The Global Signal and Observed Anticorrelated Resting State Brain Networks

Abstract

Resting state studies of spontaneous fluctuations in the functional MRI (fMRI) blood oxygen level dependent (BOLD) signal have shown great promise in mapping the brain's intrinsic, large-scale functional architecture. An important data preprocessing step used to enhance the quality of these observations has been removal of spontaneous BOLD fluctuations common to the whole brain (the so-called global signal). One reproducible consequence of global signal removal has been the finding that spontaneous BOLD fluctuations in the default mode network and an extended dorsal attention system are consistently anticorrelated, a relationship that these two systems exhibit during task performance. The dependence of these resting-state anticorrelations on global signal removal has raised important questions regarding the nature of the global signal, the validity of global signal removal, and the appropriate interpretation of observed anticorrelated brain networks. In this study, we investigate several properties of the global signal and find that it is, indeed, global, not residing preferentially in systems exhibiting anticorrelations. We detail the influence of global signal removal on resting state correlation maps both mathematically and empirically, showing an enhancement in detection of system-specific correlations and improvement in the correspondence between resting-state correlations and anatomy. Finally, we show that several characteristics of anticorrelated networks including their spatial distribution, cross-subject consistency, presence with modified whole brain masks, and existence before global regression are not attributable to global signal removal and therefore suggest a biological basis.

INTRODUCTION

Resting state studies of spontaneous fluctuations in the functional MRI (fMRI) blood oxygen level dependent (BOLD) signal have shown great promise in mapping the intrinsic functional architecture of human and primate brains (for a recent review, see Fox and Raichle 2007). A consistent observation is that regions with similar functional properties, such as the left and right somatomotor cortices, exhibit temporally coherent BOLD fluctuations even in the absence of explicit sensory stimuli or motor responses (Biswal et al. 1995; Cordes et al. 2000; De Luca et al. 2005; Fox et al. 2006; Lowe et al. 1998). Similar results have been found in visual (Cordes et al. 2000; Lowe et al. 1998), auditory (Cordes et al. 2000), language (Cordes et al. 2000; Hampson et al. 2002), and several other functional systems (Fox and Raichle 2007). Correlated spontaneous BOLD fluctuations are thought to reflect functional relationships mediated by anatomical connections (Hagmann et al. 2008; Honey et al. 2009; Johnston et al. 2008; Skudlarski et al. 2008). Although the BOLD signal is an indirect measure of neuronal activity, similarly correlated spontaneous activity has been directly shown by electrophysiological techniques (He et al. 2008; Shmuel and Leopold 2008).

In addition to positive correlations between functionally related brain regions, negative correlations between brain regions with theoretically opposed functional roles also have been reported (Kelly et al. 2008; Fox et al. 2005b; Fransson 2005; Greicius et al. 2003; Uddin et al. 2008; Wang et al. 2006). In particular, negative correlations have been observed between a set of regions routinely exhibiting activity increases during attention demanding tasks (task-positive regions) and a separate set of regions routinely exhibiting activity decreases (task-negative regions) (Fox et al. 2005b). Based on this observation, we have suggested that the task-positive and task negative networks are “intrinsically anticorrelated.” In our use, “intrinsic” means “present in patterns of spontaneous brain activity.” The task-positive system includes the dorsal attention system implicated in directed attention and working memory (Corbetta and Shulman 2002) as well as regions in the insula and anterior cingulate that have been related to salience (Seeley et al. 2007b) and task control (Dosenbach et al. 2007). The task negative system has often been referred to as the “default mode network” and has been implicated in self-referential processing and episodic memory (Buckner et al. 2008; Raichle et al. 2001; Shulman et al. 1997; Vincent et al. 2006). The concept of intrinsically anticorrelated activity has been applied toward understanding schizophrenia (Wang et al. 2006; Williamson 2007), dementia (Seeley et al. 2007a), depression (Fox et al. 2005b), behavioral variability (Kelly et al. 2008), and computational brain modeling (Honey et al. 2007; Izhikevich and Edelman 2008).

The idea that functional systems with oppositely signed responses during task performance might also exhibit spontaneously anticorrelated activity at rest is an appealing notion. However, the interpretation of observed anticorrelations in resting state BOLD data are less straightforward than originally recognized (Fox et al. 2005b). Previous reports of anticorrelated networks have relied on preprocessing to remove “nuisance regressors” or confounding variables that obscure system-specific relationships (Kelly et al. 2008; Fox et al. 2005b; Fransson 2005; Greicius et al. 2003; Tian et al. 2007b; Uddin et al. 2008; Wang et al. 2006). Of particular interest, these reports have all included some type of correction for fluctuations averaged across the entire brain, which we term the global signal. Global signal correction is reasonably common during processing of both resting-state and task-based fMRI (Aguirre et al. 1998; Macey et al. 2004; Zarahn et al. 1997) and is thought to facilitate observation of localized neuronal effects potentially obscured by BOLD fluctuations of physiological (non-neuronal) origin (Birn et al. 2006; Glover et al. 2000; Lund et al. 2006; Wise et al. 2004). However, the properties of the global signal and the effect of its removal on resting state correlation maps have been incompletely examined. This is particularly important for interpretation of negative correlations given the known potential for artifactual deactivations in task-based studies after global normalization (Aguirre et al. 1998; Desjardins et al. 2001; Gavrilescu et al. 2002; Laurienti 2004; Macey et al. 2004). Along these lines, recent resting state studies have raised questions about the interpretation of anticorrelations in the context of global signal correction and noted the importance of this issue for further study (Buckner et al. 2008; Fox and Raichle 2007; Golland et al. 2007; Honey et al. 2009; Murphy et al. 2009).

In this study, we begin by showing the effects of global signal correction on resting state correlation maps including improved specificity of positive correlations and the emergence of negative correlations. Second, we show mathematically that global signal correction mandates negative correlations, raising the possibility that anticorrelated networks could emerge as an artifact of global signal correction. Third, we examine the properties of the global signal and show that its removal by linear regression facilitates evaluation of neurophysiological relationships. Finally, we directly address the interpretation of negative correlations following global signal regression. We argue that observed negative correlations cannot be fully explained as an artifact of global signal regression, thus suggesting a biological basis.

METHODS

Subjects and data acquisition

The majority of the analyses in this study used imaging data from a previous study on the impact of spontaneous activity on behavioral variability (Fox et al. 2007). This resting state dataset is freely available as dataset BS002 at www.brainscape.org. BOLD sensitized fMRI data (3 T, 4 × 4 × 4-mm voxels, TE 25 ms, TR 2.16 s) were acquired in 17 normal right-handed young-adults using a 3T Siemens Allegra MR scanner. All subjects completed four fixation runs, each 194 frames (7 min) in duration interleaved with cued button press runs that were not used in this analysis. For fixation runs, subjects were instructed to look at a cross-hair, remain still, and to not fall asleep. Structural data (for definitive atlas transformation) included a high-resolution (1 × 1 × 1.25 mm) sagittal, T1-weighted MP-RAGE (TR = 2.1 s, TE = 3.93 ms, flip angle = 7°) and a T2-weighted fast spin echo scan.

Preprocessing of imaging data

fMRI preprocessing steps included the following: first, compensation of systematic, slice-dependent time shifts; second, elimination of systematic odd-even slice intensity differences caused by interleaved acquisition; and, third, rigid body correction for interframe head motion within and across runs. Step 3 provided a record of head position within and across all fMRI runs. Each fMRI run was intensity scaled (1 multiplicative constant over all voxels and frames) to a yield a whole brain mode value of 1,000 (not counting the 1st 4 frames) (Ojemann et al. 1997). Atlas registration was achieved by computing affine transforms connecting the fMRI run first frame (averaged over all runs after cross-run realignment) with the T2 and average T1-weighted structural images (Ojemann et al. 1997). Our atlas representative template includes MP-RAGE data from 12 normal individuals and was made to conform to the 1988 Talairach atlas (Talairach and Tournoux 1988). To prepare the BOLD data for these main analyses, each fMRI run was transformed to atlas space and resampled to 3-mm cubic voxels. This step combined movement correction within and across runs and atlas transformation in one resampling.

At each voxel, linear trends over fMRI runs were removed, and the data were spatially smoothed with a 6-mm FWHM Gaussian kernel. A temporal low-pass filter was applied with a frequency full width at half maximum cut-off of 0.1 Hz. This cut-off was used because previous work has shown that frequencies above this value do not contribute to regionally specific BOLD correlations (Cordes et al. 2001). Following the procedure of Fox et al. 2005b; several sources of spurious variance were removed by regression along with their first derivatives: 1) the six parameters resulting from rigid body correction for head motion; 2) a signal from a ventricular region of interest; 3) and a signal from a white matter region of interest (Fox et al. 2005b) (see Supplemental Fig. S1).1

Correction for global signal fluctuations

After these initial preprocessing steps, three techniques were used to correct for fluctuations in whole brain signal intensity (the global signal). In all cases, the global signal was calculated by averaging across all voxels within a whole brain mask (Supplemental Fig. S1). In most present analyses, the global signal was removed by linear regression (Fox et al. 2005b; Macey et al. 2004). A detailed mathematical description of the regression technique is presented in the appendix. The residual volumetric timeseries generated from global signal regression was used for seed based correlation mapping.

Although global signal regression is used for the primary analyses in this study and is the technique favored by our laboratory, other approaches have been used to correct for global fluctuations in resting state fMRI data and are used in this study for comparison purposes. One such approach uses multiplicative scaling to force the global mean BOLD signal to the same at all time points (frames). We refer to this strategy as frame-to-frame intensity stabilization (detailed in appendix). The primary difference between frame-to-frame intensity stabilization and global signal regression is that, for each frame, the regression technique removes the global signal in proportion to its weight at every voxel while frame-to-frame intensity stabilization uses a single scalar multiplier across all voxels. As such, global regression allows for regional heterogeneity in the distribution of the global signal, whereas frame-to-frame intensity stabilization does not (Fox et al. 2005b; Macey et al. 2004).

A third technique used for global signal correction is post hoc distribution centering. This strategy compensates for the global signal after correlation maps have been generated (Lowe et al. 1998) and has been widely used in the processing of resting state fMRI data (Hampson et al. 2002, 2004; Lowe et al. 1998, 2000; Skudlarski et al. 2008). Unlike the first two techniques, the global signal is left in the volumetric time series during computation of seed based correlation maps resulting in a voxelwise distribution of correlations that is strongly shifted toward positive values. Post hoc distribution centering directly adjusts this distribution by computing the average voxel value in the correlation map (after Fisher z-transformation) and subtracting this average value from all voxels. In this manner, the distribution of Fisher z-transformed correlation coefficients is recentered about zero.

It is important to note that all three of these strategies for compensation of global signal fluctuations forces the distribution of voxel values in a seed-based correlation map to be approximately centered about zero. This is the obvious and intended effect of post hoc distribution centering but is also a necessary mathematical consequence of both global signal regression and frame-to-frame intensity normalization (see appendix). In other words, all three strategies for global signal compensation mandate the observation of negative correlations.

Generation of seed-based correlation maps

To address the effect of preprocessing on seed-based correlation results, the BOLD data were analyzed at three stages of preprocessing. The first stage is referred to as “standard preprocessing only” and refers to the BOLD data after band-pass filtering and linear trend removal. The second stage is “movement, white matter, and ventricle regressed” and refers to data after regression of the six motion parameters as well as the signal from the white matter and ventricles. The third and final stage is “global signal regressed” and refers to the data after regression of the global signal.

At each stage of preprocessing, seed-based correlation maps were constructed by extracting the BOLD time series from a region of interest (6-mm radius sphere) and calculating the temporal correlation between this reference waveform and the time courses of all other brain voxels. Regions of interest included the posterior cingulate/precuneus (−2, −36, 37) (Fox et al. 2005b), left MT+ (−47, −69, −3) (Fox et al. 2005b), left somatomotor cortex (−39, −26, 51)(Fox et al. 2006), and right calcarine sulcus in primary visual cortex (5, −91, 0). Most coordinates were obtained from previous publications from our laboratory. The calcarine seed was placed based on anatomical landmarks in the atlas template. Resulting r values were converted to an approximately normal distribution using Fisher's r-to-z transform and entered into a random effects analysis (2-tailed, equal variance) across the 17 subjects. For the analysis using post hoc distribution centering (see Fig. 5), Fisher z-transformed correlation maps were corrected by computing the average voxel value within the whole brain mask for each subject and subtracting this value from all voxels before the random effects analysis (Lowe et al. 1998). In all analyses, resulting t maps were converted to equally probable Z-scores and corrected for multiple comparisons (thresholded at a Z of 3.0 and a cluster size of 17) (McAvoy et al. 2001). Histograms of voxel values were computed by including all voxels within the whole brain mask (Supplemental Fig. S1). For display purposes, fourfold interpolation was used to smooth voxel boundaries, and images are shown using in-house software developed on the Matlab platform (The Mathworks, Natick, MA).

Properties of the global signal

The spatial distribution of the global signal was computed by applying the same methods detailed above for seed-based correlation maps to the residual data after movement and ROI regression. Instead of a 6-mm radius sphere, the “seed” region used was the whole brain mask (Supplemental Fig. S1) and the extracted time course was therefore the global signal. To identify regions with significantly higher global signal than the whole brain mean, Fisher z-transformed single subject correlation maps were normalized to zero mean by subtraction of the whole brain average (Lowe et al. 1998). As above, results were combined across subjects using random effects analysis and corrected for multiple comparisons at P < 0.05 using a threshold of Z = 3 and a cluster size of 17. To identify peak foci in this Z-score map, it was first smoothed with a 10-mm FWHM Gaussian kernel. All peaks above a threshold of Z = 6.5 were identified, and foci closer than 20 mm were consolidated to the center of mass. Parameters were chosen to return 15–20 foci. A map of peak foci was constructed by generating 6-mm radius spheres centered on each peak coordinate.

To ensure that the global signal did not show preferential localization to the task-positive and task-negative systems, the average global signal Z-score was computed within templates of five distinct cortical systems (visual, somatomotor, auditory, task negative, and task positive; Supplemental Fig. S2). These templates were generated from seed-based correlation maps with seeds in the calcarine sulcus (5, −91, 0), left somatomotor (−39, −26, 51), left auditory (−50, −25, 8), posterior cingulate cortex (PCC) (−2, −36, 37), and left MT+ (−47, −69, −3). Single subject correlation maps were Fisher z-transformed and combined across subjects using random effects analysis. Resulting t maps were converted to equally probable Z-scores and thresholded at Z = 4. The higher threshold was chosen to prevent mask overlap and ensure that each mask was restricted to a single cortical system.

The magnitude of the global signal was determined by computing the variance of the extracted global signal waveform. To determine whether this global signal could represent the average of independent signals from distinct cortical systems, a theoretical magnitude of the global signal was also calculated by measuring the variance of the fluctuations extracted from the five cortical system templates noted above (visual, somatomotor, auditory, task negative, and task positive). The theoretical variance of the global signal was calculated by averaging the variance measured from the different cortical systems. The theoretical global variance was statistically compared with the measured variance using a Wilcoxon signed-rank test.

Correspondence between anatomical and functional connectivity

To determine the impact of global signal correction on the correspondence between anatomical and functional connectivity, authors of the most recent study evaluating BOLD correlations and anatomical connectivity were contacted and generously agreed to provide unpublished data from their analyses (C. J. Honey, P. Hagmann, and O. Sporns, personal communication). Methodological details are given in the primary publication (Honey et al. 2009). Briefly, structural connectivity was measured noninvasively in five individuals using diffusion spectrum imaging (DSI). Resting state fMRI was acquired in these same participants. The fMRI data were preprocessed by regressing out nuisance variance (ventricular and white matter signals) with and without including the global signal. Structural connectivity was assessed using streamline tractography and resting state functional connectivity was computed using Pearson correlation. These measures were computed between all pairs of 998 cortical regions of approximately equal area (∼1.5 cm²), thereby generating structural and functional 998 × 998 matrices. The correspondence between structural and functional connectivity and the correspondence between functional connectivity and fiber length was computed using Pearson correlation applied to the fMRI results obtained both with and without global signal regression. Significant differences in these correlations were assessed using a two-tailed paired t-test across the five subjects.

Creation of modified whole brain masks

To circumvent the mathematical constraint of mandatory negative correlations, modified whole brain masks were created that excluded particular systems of interest. This is similar in concept to the exclusion of activated regions from the whole bran mask for computing the global signal in task data (Andersson 1997; Gavrilescu et al. 2002). Specifically, those voxels most correlated (task-positive system) or anticorrelated (task-negative system) with the MT+ seed were eliminated with various degrees of completeness (between 0 and 95% of all voxels in the whole brain mask removed). This analysis was performed at the single subject level to allow for intersubject variability in the distribution of the correlations and assure complete removal of the involved systems. First, the single-subject Fisher z-transformed correlation map for MT+ (after whole brain regression) was computed for each subject and converted to absolute values. Second, this map was smoothed (9-mm FWHM Gaussian kernel) to prevent edge effect between adjacent positive and negative regions. Third, voxel histograms were computed, and a threshold was applied selected to remove a specified percentage of voxels from the whole brain mask. Finally, the data were preprocessed using this modified mask in place of the whole brain mask during global regression, and the correlation with MT+ was recomputed using the residual. As before, results were combined across subjects using random effects and corrected for multiple comparisons at P < 0.05.

Alternative seed regions

Although the a priori seed regions used in this analysis failed to identify significant anticorrelations without global signal regression, a post hoc analysis was performed to determine whether anticorrelations might be present with a more optimized seed region. To determine the coordinates for this seed region, random effects maps were first generated based on positive correlations for three canonical seed regions of the default network from a previously published work [seeds: MPF (−1,47, −4); PCC (−5, −49, 40); left LP (−45, −67, 36)] (Fox et al. 2005b). These maps were averaged together to generate a representative correlation map of the default network. This map was thresholded at z = 3 and clustered with an n = 17, which bounded a distinct region encompassing the anatomical location of the PCC. The center-of-mass of this region (0, −52, 27) was used as our empirically determined PCC seed based on this dataset. Note that this seed region was identified solely on the basis of positive resting state correlations within the task-negative network and was not optimized for identifying anticorrelations.

Controlling for a lagged correlation between systems

It has been suggested on theoretical grounds that a lagged correlation between the task positive and task negative networks before global regression could account for artifactual anticorrelation after global correction (Murphy et al. 2009). To ensure that this was not the etiology in the presently obtained results, time courses were extracted from the task-positive and task-negative networks as previously identified on an independent dataset (Fox et al. 2005b) (Fig. 1). The time courses were taken from the data before global regression (but including movement, white matter, and ventricle regression), and cross-correlation was performed separately on each individual to generate 17 cross-correlograms. These 17 were averaged to produce the image as shown in Supplemental Fig. S7.

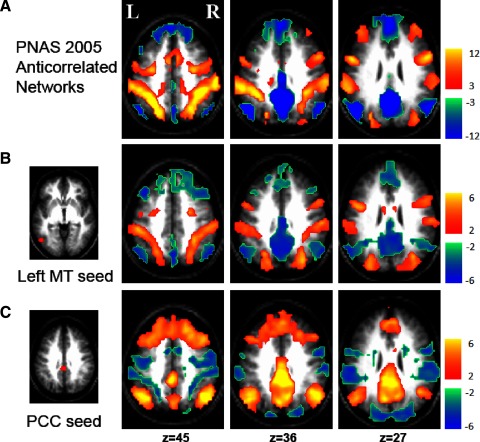
FIG. 1.

Anticorrelated brain networks are replicable across datasets and statistical technique. A: anticorrelated brain networks reproduced from the dataset of Fox et al. (2005) using fixed effects analysis showed correlations within a system and negative correlations between systems. B: Z-score map from the current independent dataset shows voxels significantly correlated with a seed in the task-positive network (area MT+) using random effects analysis. C: Z-score map from the current dataset shows voxels significantly correlated with a seed in the task negative network (posterior cingulate/precuneus) using random effects analysis.

RESULTS

The original report of anticorrelated brain systems from our group used fixed effects analysis across 10 subjects and combined results across six seed regions (Fig. 1A) (Fox et al. 2005b). This analysis defined a task-positive network (warm colors) and task-negative network (cool colors) both positively correlated within system and negatively correlated between systems. The first step in this study was to replicate the finding of anticorrelated networks in an independent dataset of 17 subjects using the more rigorous random effects analysis. As anticipated, correlations with a seed in the task-positive network (area MT+; Fig. 1B) were largely the inverse of correlations with a seed in the task-negative network (the PCC; Fig. 1C), replicating the finding of anticorrelated brain systems in a larger independent dataset.

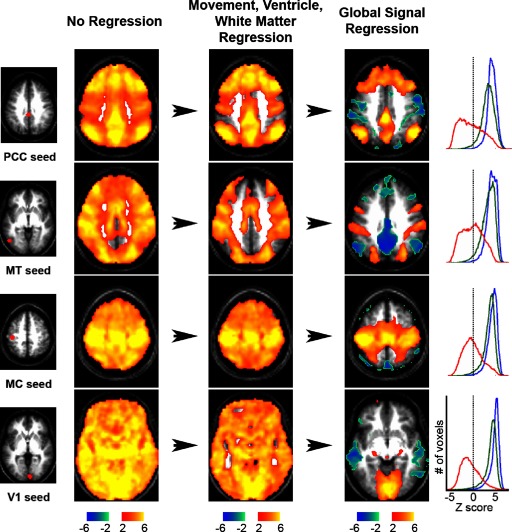
Although replicable across datasets, the finding of negative correlations was strongly dependent on preprocessing methodology (Fig. 2). Prior to regression of any nuisance variables every seed region was significantly correlated (P < 0.05) with essentially all other brain voxels and correlations were almost entirely positive. After regression of movement, white matter, and ventricle signals, this distribution changed only slightly. After removal of the global signal, either by regression (Fig. 2) or frame-to-frame intensity stabilization (Supplemental Fig. S3), the distribution of computed correlations changed dramatically: the mean correlation value became close to zero, there was a marked improvement in the neuroanatomical specificity of the significant positive correlations, and strongly negative correlations (anticorrelations) emerged.

FIG. 2.

The impact of preprocessing and global regression on seed-based correlation maps. Z-score maps show voxels significantly correlated with various seed regions at 3 processing stages: no regression (left), movement, ventricle, and white matter regression (middle), and global regression (right). Histograms of voxel intensities for the 3 processing stages are shown to the right using blue (no regression), green (movement, vent and white matter), and red (global regression) lines. The location of each seed region is shown on the far left and include the posterior cingulate cortex/precuneus (Pcc), area MT+ (MT), the somatomotor cortex (MC), and primary visual cortex (V1). Talairach slice coordinates for Z-score maps: z = 45 (Pcc); z = 36 (MT); z = 54 (MC); z = −6 (V1).

Removal of the global signal, either through linear regression or frame-to-frame intensity stabilization, ensures that, in subsequent seed-based correlation analyses performed on the residual, the sum of regression coefficients (the beta image) across all voxels within the whole brain mask must be zero. An algebraic proof is given in the appendix. Because correlation coefficients are simply regression coefficients divided by voxelwise variance, they must also sum approximately to zero. Thus global signal correction mathematically mandates the existence of negative correlations at the single subject level. This result raises important questions regarding the appropriateness of global signal regression and the interpretation of resulting anticorrelated networks.

The first step in addressing these interpretive issues was to examine the properties of the global signal and determine whether global regression facilitates or impedes the observation of physiological relationships. First, the spatial distribution and extent of the global signal were examined. If the global signal selectively localized to a small number of cortical systems (such as the task-positive and task-negative systems), global regression would be approximately equivalent to removing the mean of two signals, in which case the two systems would appear to be perfectly anticorrelated even if they were independent. However, the global signal was not restricted in this manner but rather was ubiquitously present and significant (P < 0.05) in every gray matter voxel in the brain (Fig. 3A). Voxels with a global signal correlation significantly higher than average were identified (Fig. 3B) along with peak foci of global signal localization (Supplemental Fig. S4; Supplemental Table S1). The global signal was particularly well represented in primary visual, auditory, and somatosensory cortices along with sensory thalamus, midline pericingulate regions, regions implicated in cognitive control (Vincent et al. 2008), inferior temporal cortex, and cerebellum. Importantly, the global signal did not show preferential localization to the task-positive or task-negative networks. To confirm this impression statistically, global signal correlations were compared inside several cortical systems (Supplemental Fig. S2; Supplemental Table S2). These computations showed the least global signal in the task-negative system (P < 0.05) with the greatest representation in the visual system.

FIG. 3.

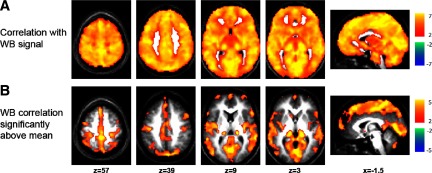
The spatial distribution of the global signal. A: Z-score map showing all voxels significantly correlated with the whole brain (WB) or global signal. B: Z-score maps showing voxels significantly more correlated with the global signal than the average voxel.

For global regression to facilitate the observation of physiological relationships, the global signal should be in addition to, not simply the average of, system-specific fluctuations. This question was addressed by measuring the variance of the global signal along with the variance of fluctuations within multiple distinct cortical systems (Supplemental Fig. S2). If the global signal is the average of independent signals in these systems, its variance should be directly computable from the system-specific variance (Supplemental Table S3). However, the global variance computed from these system-specific signals was, on average, significantly less than the measured global variance (1.55 vs. 2.51 in arbitrary units, P < 2.94 × 10⁻⁴ by the Wilcoxon signed-rank test). This finding confirms the qualitative impression of significant shared variance across cortical systems (Fig. 2) and shows that the global signal includes something in addition to contributions from the major functional systems.

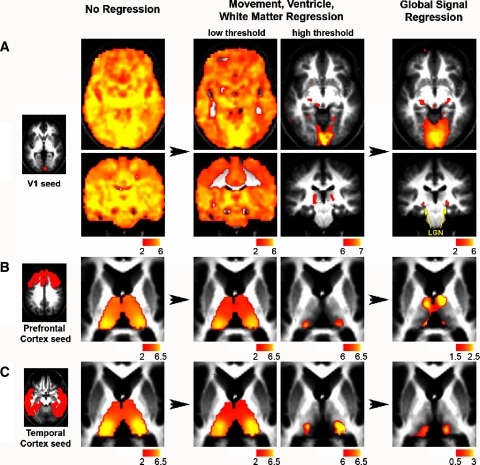
Finally, the question of whether global regression facilitates or impedes observation of physiological relationships was addressed by comparing correlation maps computed with and without global correction. Several well-established examples of cortico-thalamic connectivity were analyzed including V1 to lateral geniculate nucleus (LGN; Fig. 4A), prefrontal cortex to mediodorsal and anterior thalamic nuclei (Fig. 4B), and temporal cortex to medial pulvinar (Fig. 4C) (Zhang et al. 2008). To facilitate comparison of the correlation maps computed with and without global regression, the thresholds in the maps without global regression were allowed to vary to better approximate the specificity seen with global regression. For example, for the seed in the calcarine sulcus, the correlation map without global regression was thresholded to obtain similar specificity to the visual cortex as seen with global regression. However, only the map with global regression revealed specific correlations with the LGN (Fig. 4A). In all three cases, known functional system relationships were better observed with global regression than without it. This result suggests that removal of the global signal facilitates the observation of true physiological relationships at the systems level.

FIG. 4.

Global signal regression shows fine neuroanatomical specificity not seen without global signal correction regardless of thresholding. Z-score maps (random effects across 17 subjects) showing voxels significantly correlated with seeds in (A) the primary visual cortex (top), (B) prefrontal cortex (middle), and (C) temporal cortex (bottom) at 3 stages of processing: no regression (left), movement, ventricle, and white matter regressed (middle), and global signal regressed (right). Raising the threshold of the Z-score map after movement, ventricle, and white matter regression does not show the neuroanatomical specificity achievable with global regression such as the correlation between the visual cortex (V1) and the lateral geniculate nucleus (LGN). For the bottom 2 rows, images were masked to focus on the thalamus and cortical seed regions were generated per (Zhang et al. 2008). Transverse slices: z = −6, Coronal slices: y = −27.

To confirm the above examples in a more unbiased manner, the correspondence between BOLD correlations and anatomical connectivity was evaluated across the entire brain, and these results were compared in data preprocessed with and without global regression. A significant correspondence between anatomical connectivity, as assessed by diffusion tractography, and functional connectivity, as assessed by resting state BOLD imaging, has recently been reported (Hagmann et al. 2008; Honey et al. 2009; Skudlarski et al. 2008). Interestingly, these studies all used some type of correction for global fluctuations in the BOLD signal. To determine whether better correspondence between structural and functional connectivity would be observed with versus without global signal regression, the authors of the most recent article on this topic (Honey et al. 2009) were contacted and generously provided unpublished data (Honey, Hagmann, and Sporns personal communication). When performed in addition to ventricular and white matter signal regressions, regression of the global signal improved the correspondence between functional and structural connectivity both when considering all region pairs (r = 0.36 vs. 0.32, P < 0.03 by paired t-test) and only those pairs with significant anatomical connectivity (r = 0.53 vs. 0.45, P < 0.01). The correspondence between functional connectivity and anatomical path length also was significantly greater with versus without global signal regression (r = 0.47 vs. 0.35, P < 0.01). These results must be viewed as preliminary, because only five subjects were studied and the experiment was not specifically designed to address this question. Nevertheless, the outcome suggests that removal of the global signal improves the correspondence between fMRI correlations and anatomical connectivity as assessed by tractography.

The ubiquitous presence of the global signal across brain voxels, its large magnitude, and the improvement in the neuroanatomical specificity of positive correlations after regression all suggest that global signal regression enhances resting state fMRI. If the global signal obscures true neuroanatomical and physiological relationships within systems with respect to positive correlations, by extension, the same should be true for negative correlations. The challenge is to interpret observed anticorrelations given that they are mandated by global regression. To that end, we evaluated several properties of the anticorrelated networks not mandated by global regression including their spatial distribution, cross-subject consistency, presence with modified whole brain masks, and presence prior to global regression.

The first of these analyses examined the spatial distribution of negative correlations. Although global signal correction mandates the observation of negative correlations, it does not determine their spatial distribution. This principal is illustrated by comparing the results of global signal regression to post hoc distribution centering (Fig. 5). Both methods of global signal correction mandate the presence of negative correlations (see methods); however, the distribution of these negative correlations was quite different. Negative correlations after post hoc distribution centering localized to white matter and were similar in distribution regardless of the location of the seed ROI. This nonphysiological result may be reasonably regarded as artifact. In contrast, negative correlations after global signal regression were specific to the seed ROI and were localized to functional systems exhibiting responses of opposite sign in task-related fMRI (Fig. 5). This analysis shows that the mathematical mandate of negative correlations with global signal correction does not necessitate the interesting physiological distribution of the anticorrelated networks seen with global signal regression.

FIG. 5.

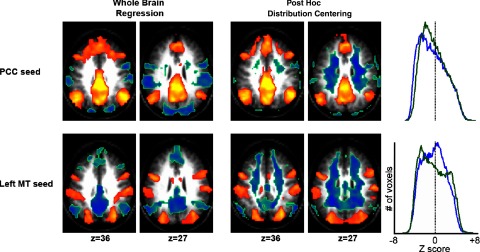
Global signal regression shows a unique distribution of negative correlations compared with post hoc distribution centering. Z-score maps showing voxels significantly correlated with seeds in the posterior cingulate (top) and area MT+ (bottom) after global signal regression (left) and post hoc distribution centering (right). Histograms show the distribution of voxel values across the entire brain (blue = whole brain regression; green = post hoc distribution centering images). Although both techniques center the distribution of correlations around 0, only global regression shows neuroanatomically specific negative correlations. Seed region locations are as shown in Fig. 1.

Second, global regression mandates negative correlations at the single subject level but does not mandate consistency of the spatial distribution across subjects. This principle is illustrated by comparing beta coefficient maps obtained using a PCC seed versus a seed in the white matter (Fig. 6). For both seed regions, the beta coefficient maps obtained in individual subjects (Fig. 6A) summed to zero, as algebraically required (appendix). However, the two seed regions varied greatly in the beta map consistency across subjects. The PCC gave rise to consistently negative regions within the beta maps, as reflected in the random effects result, whereas the white matter seed did not (Fig. 6B). A full set of slices corresponding to Fig. 6 is shown in Supplemental Fig. S5. Examination of cross-subject consistency suggests that most negative correlations seen at the single subject level with the white matter seed are likely to be an artifact of global regression, whereas those associated with the PCC were reproducible across subjects and therefore at least plausibly reflective of neurophysiology.

FIG. 6.

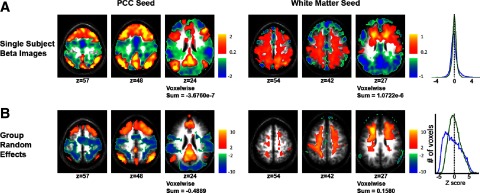
Global signal regression mandates negative correlations at the single subject level but not at the population level. A: single-subject regression coefficients (beta maps) for seeds in the posterior cingulate (left, blue line) and in the white matter (right, green line) for a representative subject. B: random effects Z-score maps show voxels significantly correlated with seeds in the posterior cingulate (left) and white matter (right) across the population of 17 subjects. The sum of voxel values across the entire brain is shown below each image and voxel histograms are shown to the right. Although the voxelwise sum of beta maps must be 0 for each subject and histograms similar, these measures can vary greatly in the population level Z-score maps depending on the consistency across subjects.

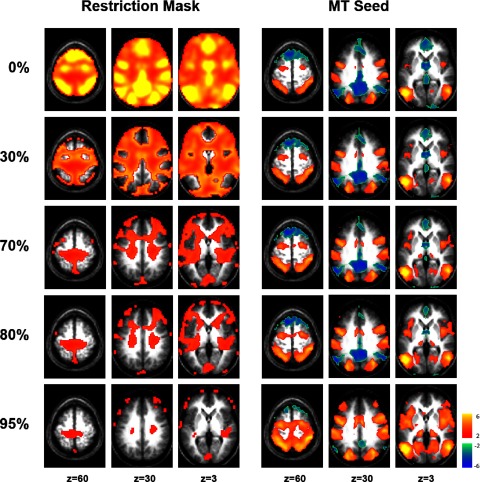
Third, global signal regression only places mathematical constraints on voxels contained within the whole brain mask. Therefore a strategy for eliminating this constraint is to restrict the whole brain mask to voxels outside the two anticorrelated networks. Correlation maps were computed using a seed ROI in area MT+, a region positively correlated with the task-positive network and anticorrelated with the task-negative network (Fig. 7). Voxels most strongly correlated or anticorrelated with area MT+ were progressively removed from the whole brain mask. Even after removing 80% of the voxels, most correlated or anticorrelated with MT+, robust anticorrelations remained (Fig. 7). As might be expected, the estimation of the global signal became less accurate and the anticorrelations less robust as the mask became more restricted. However, significant anticorrelations remained even when the global signal was computed using only the 5% of the original mask that was least correlated with either network. This result strongly suggests that the anticorrelation between these two systems is not an artifact of global regression. To insure that this modified mask approach is indeed capable of differentiating underlying anticorrelation from independence in the presence of a global signal, a simulation was performed that confirms these conclusions (Supplemental Table S4). It is worth noting that this analysis and simulation assume an independent and additive global signal, an assumption that may be challenged (see discussion.)

FIG. 7.

Anticorrelated networks persist despite modified whole brain masks that eliminate the mathematical constraints imposed by global regression. Modified whole brain masks (left) were created by removing 0, 30, 70, 80, or 95% of the voxels most correlated or anticorrelated with area MT. The intensity of the shown whole brain mask values reflects the absolute value of correlations with MT+. These masks were used to regress out a modified global signal, and Z-score correlation maps for a seed in MT+ were generated using the residual (right). The systems of interest remain anticorrelated even after being excluded from the whole brain mask, suggesting that the relationship is not an artifact of global regression. The MT+ seed region is as shown in Fig. 1.

Finally, if negative correlations are physiological and not an artifact of global regression, some evidence of these negative correlations may be present without regressing out any type of global signal at all. Although no significant negative correlations were evident before global regression using our original a priori seed regions (Fig. 2), by optimizing the location of the seed region based solely on positive correlations within the task-negative network and lowering the threshold, one can see evidence of anticorrelations even before global regression (Supplemental Fig. S6). This is admittedly a post hoc analysis and the results should be interpreted as qualitative, but they do show that anti-correlations may be present in fMRI data even without global regression.

DISCUSSION

There are three main findings in this study critical for understanding global regression and observed anticorrelations in resting-state fMRI data. First, global signal regression mathematically mandates the observation of negative values in seed-based correlation maps at the single subject level, highlighting the importance of methodological considerations in result interpretation. Second, the global signal is ubiquitously present across gray matter and obscures underlying neuroanatomical relationships, providing important validation for use of global regression as a processing maneuver. Third, multiple characteristics of anticorrelated networks are not determined by global regression, suggesting that presence of an important and interesting physiological relationship.

Methods matter

The first main finding of this study is that methodology has a pronounced impact on resting state fMRI studies and must be considered when interpreting results. We show that global signal correction places mathematical mandates on the distribution of correlation values at the single subject level, a finding consistent with other recent results (Murphy et al. 2009). As such, negative correlations in individual subjects or small sample sizes (Tian et al. 2007a) should be interpreted with caution. Furthermore, the pronounced effect of global signal correction on subsequent correlation maps and especially anticorrelations has important implications for resting state studies attempting to compare conditions or groups. Several laboratories have examined differences in both positive and negative correlations in an effort to provide insight into the physiology of brain disease (Seeley et al. 2007a; Wang et al. 2006; Williamson 2007). If global signal regression is used in such studies, it is important to consider potential group differences in the distribution of the global signal to avoid misleading results.

We have also shown that not all strategies for global signal correction generate equivalent results. While all types of global signal correction result in negative correlations, the degree to which these negative correlations represent processing artifact versus physiology may vary. For example, post hoc distribution centering induces negative correlations that are not specific to the seed region and localize to white matter (Fig. 6). A second technique, frame-to-frame intensity stabilization, for the most part, returns results similar to those obtained with global signal regression (Supplemental Fig. S3A). However, unlike global regression, this technique does not account for regional heterogeneity in the distribution of the global signal (Macey et al. 2004), a difference that becomes clear when a seed region is placed in white matter, an area with significantly less global signal than average (Supplemental Fig. S3B). Given these considerations, we advocate the use of global regression over other normalization techniques for global signal correction, especially when studying anticorrelations.

Global signal

The second main finding of this study is that the global signal obscures underlying neurophysiology and its removal through linear regression represents a valid and useful processing maneuver. This conclusion is supported by the three examples of improved cortical-thalamic relationships observed after global regression such as the correlation between V1 to LGN (Fig. 4), as well as the improved correspondence between BOLD correlations and diffusion-based structural connectivity assessed across the entire brain.

Global signal localizes primarily to gray matter, especially primary sensory cortex and thalamus, midline peri-cingulate regions, and control regions (Vincent et al. 2008), while avoiding white matter and ventricles. This distribution bears a qualitative resemblance to previous reports on the distribution of cardiac (Chang et al. 2008) and respiratory (Birn et al. 2006) related BOLD variance. However, it is important to note that the global signal does not show strong localization to the task-negative system, a finding that contrasts previous conclusions regarding localization of respiratory-related fluctuations (Birn et al. 2006).

Unambiguously, non-neuronal physiological processes give rise to widely shared variance in BOLD fMRI data (Birn et al. 2006; Wise et al. 2004). However, it remains unclear whether the origin of the global signal is predominantly neuronal or nonneuronal. Variations in neuronal activity of diffuse ascending “arousal” systems similar to the locus coeruleus may play a role. However, the presently measured distribution of the global signal (Fig. 3) only partially overlaps with previously identified brain regions associated with increases in arousal (Critchley 2005). Furthermore, it is unclear what type of arousal would localize to primary sensory cortices. This localization (to primary sensory cortices) is equally problematic for accounts of the global signal in terms of non-neuronal processes. Further insight into this question may come from analyses of non-fMRI correlates of the global signal. For example, a significant lagged correlation has been identified between the global signal and slow frequencies in respiratory variance (Birn et al. 2006). However, this correlation was significant at both positive and negative lags, begging the question of causality. Is the correlation primarily caused by fluctuations in respiration causing fluctuations in the global BOLD signal or fluctuations in global neuronal activity causing fluctuations in respiration? Future studies of the relationship between the global signal and fluctuations in cardiac activity (Chang et al. 2008), respiration (Birn et al. 2006), or indices of autonomic arousal such as skin conductance or pupil diameter will likely prove valuable.

How should we interpret observed anticorrelations?

The current evidence strongly suggests that previously observed anticorrelations between the task-positive and task-negative systems cannot be explained solely as a consequence of preprocessing using global signal correction. First, we have shown that the global signal is not preferentially localized to these systems. Hence, the observed anticorrelation cannot be explained as a trivial consequence of simply removing the average of two signals. Second, it is clear that global signal fluctuations obscure known physiological relationships with respect to positive correlations, suggesting that the same may be true for negative correlations. Third, the spatial distribution of negative correlations is not mandated by global regression, yet there exists a striking similarity between the localization of negative correlations during the resting state (Fox et al. 2005b) and sets of regions known to be modulated in opposite directions by task performance (Corbetta and Shulman 2002; Shulman et al. 1997), providing biological plausibility. Fourth, the consistency of negative correlations across subjects is not mandated by global regression; however, the task-negative and task-positive networks are routinely and specifically anticorrelated across subjects. Fifth, anticorrelated networks can be observed even when the networks of interest are removed from the whole brain mask, effectively eliminating the mathematical constraints on these systems. Finally, evidence of anticorrelations can be seen without global normalization if the location of the seed region is optimized and the thresholds lowered. These considerations argue that resting state correlation maps computed after global signal regression are informative regarding the physiological relationship between the task positive and task negative systems.

In addition to these findings, results using other techniques and modalities are also providing preliminary evidence suggesting a biological basis to anticorrelated networks. Independent components analysis (ICA) offers a means partitioning fMRI variance into neuronal and non-neuronal components without explicit global regression (Bartels and Zeki 2004; Beckmann et al. 2005; Kiviniemi et al. 2003). Negative zones corresponding to peaks in the distribution of the task-positive and task-negative networks are evident in certain ICA results (Beckmann et al. 2005). Outside the field of fMRI, recent simulations using anatomical models of the monkey (Honey et al. 2007) and human (Izhikevich and Edelman 2008) brains have shown the spontaneous emergence of anticorrelated networks based solely on anatomical connections and spontaneous neuronal firing. The later of these studies observed slow (<0.1 Hz) fluctuations in the posterior cingulate/precuneus anticorrelated with regions reminiscent of the task positive network [intraparietal sulcus (IPS) and frontal eyefield (FEF)]) (Izhikevich and Edelman 2008). Finally, recent work using subdural electrodes has reported preliminary evidence for negative correlations in band limited power and slow cortical potentials in humans (He et al. 2008). Similarly, recent electrophysiological work in cats has shown the existence of low-frequency (0.05–0.15 Hz) gamma power fluctuations anticorrelated between putative homologs of the task-positive and task-negative systems (Popa et al. 2009). Although further work is needed, these results suggest that the finding of anticorrelated networks is not limited to fMRI data processed with global signal correction.

In contrast to these conclusions, a recent article has suggested that “global signal regression is most likely the cause of anticorrelations,” causing them to be inappropriately “introduced” into the data, leading to “spurious findings” (Murphy et al. 2009). An important question is how to reconcile our results with this recent publication. Despite the difference in conclusions, the two articles are in agreement regarding multiple findings that should be present if anticorrelations are to be considered physiological. These findings include an improvement in the neuroanatomical specificity of positive correlations with global regression (Fig. 4), evidence for anticorrelations without global regression (Fig. 7; Supplemental Fig. S6), global signal distribution that does not specifically localize to the task-positive and task-negative networks (Fig. 3; Supplemental Table S2), and a difference between global regression and simply shifting the voxel distribution with post hoc distribution centering (Fig. 5). The conclusions of Murphy et al. (2009) were motivated by the absence of these findings both in their study and prior literature. However, by directly testing each hypothesis, we report clear confirmation of each of the above findings. Furthermore, Murphy et al. suggested a mechanism whereby artifactual anticorrelations could arise after global regression from a delayed correlation between systems. We directly tested for such delayed correlation between the task-positive and task-negative system and found none (Supplemental Fig. S7).

Limitations and areas for future work

There are several limitations in this study that should be noted. First, this study was limited in scope to anticorrelations between the task-positive and task-negative networks, a robust observation with respect to dataset (Fig. 1), and resting state conditions (Fox et al. 2005b). Anticorrelations outside these systems may be less reliable (Tian et al. 2007a,b) and have yet to be tested using the rigorous methods presented here. Second, some of the conclusions in this article, specifically those based on the restricted mask analysis and simulation (Fig. 7; Supplemental Table S4), relied on a model of an independent global signal added on top of interacting neuronal systems. Such a model is supported by known correlations between the global signal and physiological variables (Birn et al. 2006) and the finding that the global signal obscures underlying neurophysiology and neuroanatomy (Fig. 4). However, one could posit an alternate model in which the high degree of interconnectedness between brain regions is itself responsible for the uniformly positive correlations. We are unable to definitively rule out such a model in this study, and further work is needed to determine whether our assumption of an independent additive global signal is a valid one. Finally, this study was limited to determining whether anticorrelated networks could emerge solely as an artifact of global correction or whether they instead reflect an interesting and important physiological relationship. The precise details of this physiological relationship and the mechanisms by which this relationship are mediated require further work.

There are several approaches that may better elucidate the relationship between the task-positive and task-negative networks. One approach is identification of independent correlates of the global fMRI signal such as respiratory variance that can be used as alternate regressors in data analysis. Although removal of respiratory fluctuations alone has not shown robust anticorrelations (Birn et al. 2006; Murphy et al. 2009), removal of combined respiratory and cardiac variability (Chang et al. 2008) or alternative measures of sympathetic arousal may do so. Perhaps the definitive source for insight into the physiological relationship between anticorrelated networks is electrophysiology. In studying feline homologs of the task-positive and task-negative networks, Popa et al. (2009) showed significant nonstationarity in the relationship between the networks, with epochs of significant correlation as well as anticorrelation. Given the likely correspondence between BOLD and electrophysiologic measurements of spontaneous neuronal activity (He et al. 2008; Shmuel and Leopold 2008), nonstationarity may contribute similarly to our fMRI data. Regression of a global signal would serve to highlight even intermittent periods of anticorrelation and may partially explain these results. Temporal changes in the relationship between systems remain an underexplored aspect in fMRI studies of spontaneous activity (Fox and Raichle 2007), and electrophysiology, with its improved temporal resolution, may provide important clues to better understanding both anticorrelated networks and the brain's intrinsic dynamics in general.

Finally, additional work is needed to determine how the relationship between the task-positive and task-negative networks is mediated. One possibility is that a functional interplay between the two systems is being facilitated by a third system. For example, a right lateralized system previously implicated in task-block transitions (Fox et al. 2005a) has been proposed as mediating the switch between the task-positive and task-negative networks (Sridharan et al. 2008). Similarly, a “control network” has recently been described that is anatomically interposed between the task-positive and task-negative networks (Vincent et al. 2008) and may be involved in a competitive allocation of resources. An alternative possibility is that anatomy alone gives rise to the observed relationship between anticorrelated networks. In general, negative BOLD correlations are associated with significantly fewer anatomical connections as assessed with DTI, although there may be a slight increase in connections between regions with the strongest anticorrelations (Honey et al. 2009; Skudlarski et al. 2008). Based on models of the brain's anatomical connections, recent simulation studies have shown the spontaneous emergence of anticorrelated networks (Honey et al. 2007; Izhikevich and Edelman 2008), in some cases resembling those seen in human fMRI data (Izhikevich and Edelman 2008). These possibilities are not mutually exclusive and may all contribute in some way to the ongoing physiological interaction between the task-positive and task-negative networks.

GRANTS

This work was supported by National Institutes of Health Grants NS-06833, F30 NS-054398, and F30 MH-083483.

APPENDIX

Description of global signal regression technique

Let the BOLD data be represented as the n × m array, B, where n is number of time points (frames) and m is the number of voxels. The global mean time course, g, is an n × 1 column vector, g = (1/m)B1_m, where 1_m is the m × 1 column vector of all 1 s. Voxelwise regression of the BOLD data on g generates

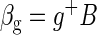where g⁺ (a 1 × n array) is the pseudoinverse of g. Thus g⁺ = [g^Tg]⁻¹g^T and g⁺g = 1.

Now, β_g is a 1 × m array (image). “Regressing out” the global signal gives the new volumetric times series

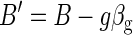This residual volumetric time series (B′) can be used to generate seed-based correlation maps.

Mandated anticorrelations following whole brain signal regression

Extending the above description, clearly, B′, like, B, is n × m. Now, suppose another regression is computed using B′ (the volumetric time series after global signal regression) on any other regressor, f. Then

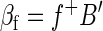where f⁺ is the 1 × m pseudoinverse of f. We want to show that the spatial mean of β_f is zero, i.e., that (1/m)f⁺β_f1_m = 0. Thus

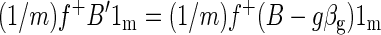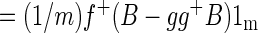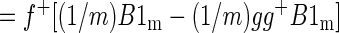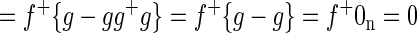The preceding proof applies to beta images rather than correlation images. However, total correlation images are equal to beta images divided by the local time series SD (square root of variance). The SD image clearly is not uniform. However, the nonuniformity of the distribution of voxelwise noise tends to be unrelated to positive versus negative regions of the beta image for regressors extracted from typical seed regions of interest. Hence, total correlation images (after whole brain signal regression) tend to exhibit an approximately zero mean property.

Description of frame to frame intensity stabilization

Using the previous notation, the intensity-stabilized volumetric time series B′ is computed as B′ = G⁻¹B, where G = diag[g] is an n × n matrix containing the (unaltered) global mean time course (as defined above) on the diagonal.

Mandated anticorrelations following frame-to-frame intensity stabilization

Using the previous notation, let B′ be the volumetric time course after frame-to-frame intensity stabilization. The stabilized global mean time course, g′ = (1/m)B′1_m, is an n × 1 column vector in which all entries are identical. We may, without loss of generality, take the value of these entries to be 1, as the subsequent argument is unchanged if B′ is scaled by any arbitrary constant. To show that g′ = 1_n, write

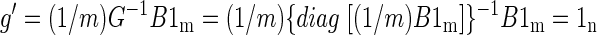The preceding equation can be verified by left-multiplying the expressions on both sides of the last equal sign by G. Thus

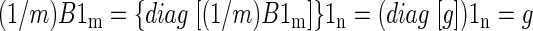Global signals must be removed before correlation analysis. Having forced the global mean value at all time points to be 1 (or any other value), this quantity must be subtracted from all entries in B′ to obtain B′. Each row of B′ (each frame) will have a whole brain mean value of 0. Algebraically, this condition is (1/m)B′1_m = 0_n. Now, suppose that B′ is regressed on some time course, f, extracted from any arbitrary ROI. As above, we have

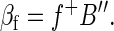We want to show that the spatial mean of β_f is 0, i.e., that (1/m)β_f1_m = 0. Performing the algebra, we obtain

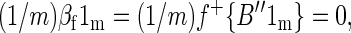which follows from the fact that the quantity in braces is an n × 1 column vector of all 0s.