Dynamics of Primate Oculomotor Plant Revealed by Effects of Abducens Microstimulation

Abstract

Despite their importance for deciphering oculomotor commands, the mechanics of the extraocular muscles and orbital tissues (oculomotor plant) are poorly understood. In particular, the significance of plant nonlinearities is uncertain. Here primate plant dynamics were investigated by measuring the eye movements produced by stimulating the abducens nucleus with brief pulse trains of varying frequency. Statistical analysis of these movements indicated that the effects of stimulation lasted about 40 ms after the final pulse, after which the eye returned passively toward its position before stimulation. Behavior during the passive phase could be approximated by a linear plant model, corresponding to Voigt elements in series, with properties independent of initial eye position. In contrast, behavior during the stimulation phase revealed a sigmoidal relation between stimulation frequency and estimated steady-state tetanic tension, together with a frequency-dependent rate of tension increase, that appeared very similar to the nonlinearities previously found for isometric-force production in primate lateral rectus muscle. These results suggest that the dynamics of the oculomotor plant have an approximately linear component related to steady-state viscoelasticity and a nonlinear component related to changes in muscle activation. The latter may in part account for the nonlinear relations observed between eye-movement parameters and single-unit firing patterns in the abducens nucleus. These findings point to the importance of recruitment as a simplifying factor for motor control with nonlinear plants.

INTRODUCTION

Eye movements are produced by changes in the firing rates of ocular motoneurons (OMNs) that alter the forces exerted by the extraocular muscles (EOMs) and so move the globe. Understanding the relationship between OMN firing and eye movement—an essential step for understanding oculomotor control in general—thus requires characterization of the dynamics of EOMs and orbital tissue (“oculomotor plant”).

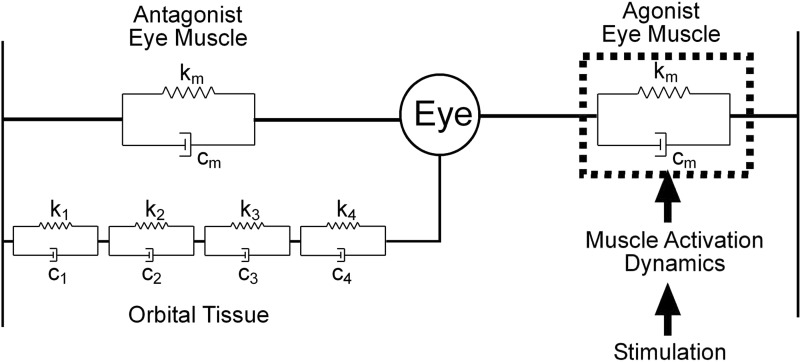
It is has been established that these dynamics are dominated by viscosity and elasticity rather than inertia and that plant viscoelasticity can be modeled as a series of Voigt elements (Robinson 1964, 1965), where a Voigt element has stiffness k, viscosity c, and time constant (TC) of c/k (Fig. 1). However, this qualitative consensus has in the past concealed quantitative confusion, about both the number of Voigt elements and the values of their time constants (see references in Sklavos et al. 2005). Since the disagreements appeared to arise from inadequate measurement of plant behavior, more recent studies have systematically analyzed the globe's return to rest after horizontal displacement in anesthetized primates. These analyses indicate that the plant can be approximated by a model with four time constants of 0.01, 0.1, 1, and 10 s (Sklavos et al. 2005, 2006). The fact that the return movements can be reproduced so accurately with a linear model suggests that, in the circumstances in which the measurements were made, the plant behaves linearly.

FIG. 1.

Model of oculomotor plant. Orbital tissue is typically modeled as a series of Voigt elements, each with elasticity k_i and viscosity c_i, giving a time constant of c_i/k_i. Evidence from studies of mechanical displacement of the eye in anesthetized primates suggests the presence of at least 4 Voigt elements. In parallel with the orbital tissue are the 2 extraocular muscles (horizontal movements only), represented by single Voigt elements. The overall behavior of the plant can still be represented by 4 time constants, but the values are not the same as those for orbital tissue alone (Sklavos et al. 2005). In the case of electrical stimulation, an additional dynamic process is involved: the transformation of electrical stimulation into muscle force, here termed “muscle activation.” It is unclear to what extent the production of muscle force is accompanied by changes in muscle dynamics.

In contrast, recordings from OMNs during eye movements in alert primates (Sylvestre and Cullen 1999) indicate that in more natural conditions the plant does not behave linearly. OMN firing rates could be related to eye-movement profiles by a differential equation corresponding to a two-Voigt-element model: however, the equation coefficients appeared to depend on movement velocity (see Fig. 14 in Sylvestre and Cullen 1999), in a manner suggestive of a significant nonlinearity.

There are a number of differences between the two sorts of study that could contribute to the differences in results, one of which is the effects of anesthetics. The “linear” measurements were obtained in animals lightly anesthetized with ketamine (Sklavos et al. 2005) or heavily anesthetized with barbiturate (Sklavos et al. 2006), whereas the OMNs were recorded in alert animals. Second, during naturally occurring eye movements, the commands to both agonist and antagonist EOMs are altered. The change in antagonist command is a potential source of nonlinearity (Sylvestre and Cullen 1999), particularly during saccades when many antagonist OMNs cease firing completely. Finally, during return movements after mechanical displacement, OMN firing rates (and thus EOM activation) presumably remain unchanged, in clear contrast to the situation during normal eye movements in alert animals. Such movements are produced by changes in innervations, causing changes in muscle activation and, consequently, changes in muscle force (Fig. 1). Although the dynamic relationship between innervation level and muscle force has proved difficult to characterize precisely (e.g., Brown and Loeb 2000) nonlinearities are clearly present (Winters 2000), so the dynamics of muscle activation are a plausible source of at least some of the nonlinearities observed in the primate oculomotor plant.

To investigate the relative importance of these factors we took advantage of data, gathered for another purpose, on the horizontal eye movements produced by microstimulation of the abducens nucleus in alert monkeys (Gandhi et al. 2008). Although individual examples of stimulation-produced eye movements have been shown previously—e.g., Robinson (1968; Fig. 1, oculomotor nerve), Pola and Robinson (1978; Fig. 6, medial longitudinal fasciculus), Sparks and Mays (1983; Fig. 11, trochlear nerve), Klier et al. (2006; Figs. 2A and 3A, abducens nerve, abducens nucleus), and Gandhi et al. (2008; Fig. 8, abducens nucleus)—no systematic analysis of movement dynamics was undertaken because the experiments used the stimulation for other purposes. However, stimulation has three properties useful for investigating the oculomotor plant: 1) It provides a way of displacing the globe that, unlike mechanical methods, can be used in alert animals. 2) Movements are produced via muscle activation (Fig. 1), a critical part of the plant that is not engaged by mechanical displacement. 3) Stimulation is unlikely to affect the antagonist muscle and the stimulated motor units are likely to fire at the same frequency. The movements produced by stimulation are thus more complex than those resulting from mechanical stimulation, but simpler than natural saccades, which involve both the antagonist muscle and variations in firing rate between agonist motoneurons (Ling et al. 2007; Sylvestre and Cullen 1999). Analysis of stimulation-induced movements is therefore likely to be particularly helpful in understanding the apparent differences in plant characteristics associated with mechanical displacements and saccades.

FIG. 2.

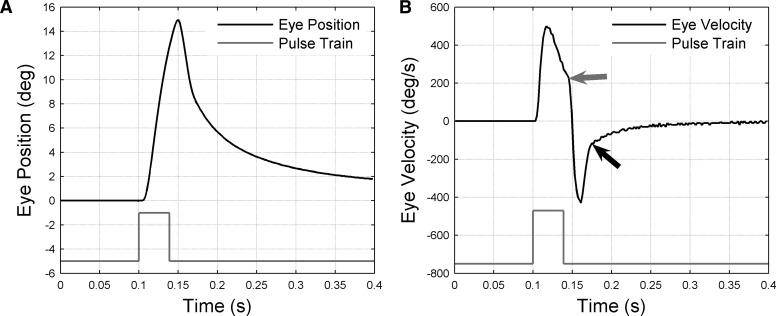
Example of eye movement produced by abducens microstimulation. A: change in eye position (black trace) resulting from 39-ms train of pulses delivered at 408 Hz (gray trace: pulse height represents stimulation frequency) delivered to monkey A when eye was in the primary position. Eye position sampled at 500 Hz. Positive eye positions correspond to abduction. B: change in eye velocity (black trace) corresponding to position change in A. Velocity derived from position trace by numerical differentiation. Discontinuities in velocity trace marked by arrows: the gray arrow indicates the point at which about 6 ms after the end of stimulation the abduction velocity starts to decrease rapidly; the black arrow indicates the point at which about 36 ms after the end of stimulation the return velocity starts to decrease slowly.

FIG. 3.

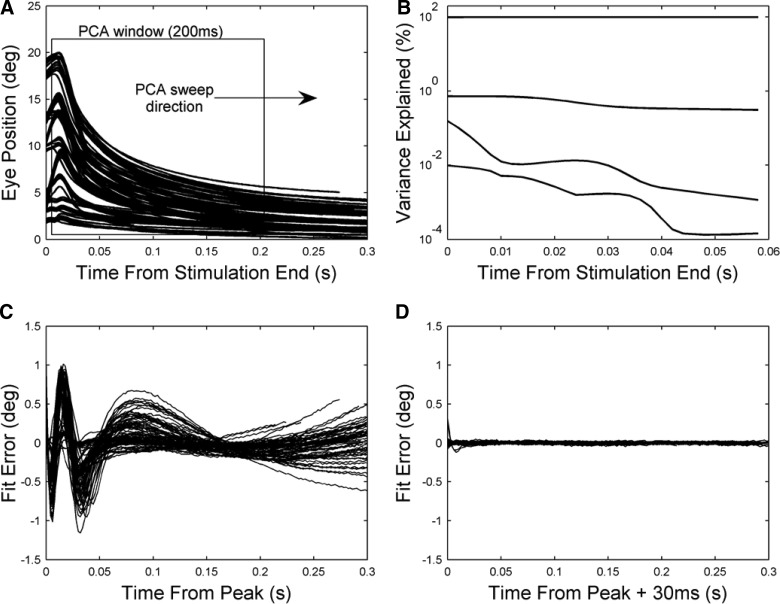
Dynamic properties of system after end of stimulation. A: principal component analysis (PCA) was applied to 200-ms segments of the eye-position traces. The starting time of the segments was varied in 2-ms steps from 0 to 100 ms after the end of the stimulation. B: results of PCA. The proportion of variance accounted for by the first 4 components is plotted as a function of segment starting time relative to the end of stimulation. C: errors resulting from fitting 3 exponential terms (methods) to eye-position traces for monkey A (n = 102), starting from the time of peak displacement (∼10 ms after end of stimulation). Each plotted curve shows the difference between the experimental and predicted values for a given eye-position trace. D: errors resulting from fitting 3 exponential terms to eye-position traces for monkey A starting 30 ms after peak displacement.

The method of analysis adopted here sought to take advantage of the fact that, although agonist activation changes dramatically during the stimulation itself, it changes little if at all once the immediate effects of stimulation are over. Eye movements during these two phases can therefore be compared. Results of the comparison indicated that the oculomotor plant in alert primates appears approximately linear for horizontal movements when muscle innervation remains constant. This suggests that, of the differences between the studies of mechanical displacement and motoneuron firing cited earlier, anesthesia plays little if any role. In contrast, changes in agonist muscle innervation can on their own produce striking nonlinearities, which appear to account in part for the nonlinearities observed in the single-unit data.

Parts of these results have previously been described in abstract form (Anderson et al. 2006; Sklavos et al. 2002).

METHODS

Surgical preparation

Three juvenile rhesus monkeys (Macaca mulatta) served as subjects. All experimental protocols were approved by the Institutional Animal Care and Use Committee at the Baylor College of Medicine and complied with the guidelines of the Public Health Service policy on Humane Care and Use of Laboratory Animals. Surgical and behavioral procedures, as well as the apparatus used for these experiments, have been described previously (Gandhi et al. 2008). Briefly, under aseptic conditions, a search coil was attached to the sclera of one eye of each monkey. Another coil, a head-restraint post, and a stainless steel chamber were secured to the skull. The cylinder was slanted laterally in the frontal plane at an angle of 26° so that a microelectrode penetration through its center would reach the midline in the interaural plane 1-mm below interaural zero. Postrecovery, the animals performed oculomotor tasks (see following text) as a microelectrode was hydraulically lowered through the chamber. The abducens region was identified by characteristic burst-tonic activity associated with saccades and by the effects of stimulation (see references in Gandhi et al. 2008). The burst-tonic activity was characterized by beehive-type sounds that varied with changes in eye position. The effects of stimulation were an ipsilateral displacement with an approximately exponential time course, generally followed by a return to the initial position also with a (different) exponential time course. In some cases, the animal made a saccade before the eyes returned to the initial position. In some other cases, the asymptotic eye position after the return fell short of the initial eye position before the stimulation. We assumed that for such sites, the stimulation may have also recruited, directly or indirectly, elements of the paramedian pontine reticular formation or the neural integrator (see results).

Histological identification of abducens stimulation sites was not performed because these animals were used for other investigations (Gandhi and Sparks 2007; Gandhi et al. 2008).

Displacement, stimulation, and recording procedures

The animals were trained on oculomotor tasks. Relevant to the current study, each trial began with the illumination of a fixation target. Unless initial eye position was the variable of interest (see following text), the fixation target was at the straight-ahead position. After 700–1,000 ms of fixation, the stimulus was extinguished. During control trials, another target was presented 100–500 ms later and the animal redirected fixation to earn a reward. In the experimental condition, stimulation was delivered 100–400 ms after the offset of the visual targets. Another 200–400 ms later, a yellow light-emitting diode was presented and the animals fixated it to obtain a reward. Typical stimulation parameters were 20–30 μA, 100–600 Hz, 10–400 ms, and 0.2-ms biphasic pulses. These are nominal values; actual values might be about 5% different, as indicated where relevant.

Experiments were conducted under both head-fixed and head-free conditions. Stimulation was applied at one site in subject A (head fixed) and seven sites (both head fixed and head free) in each of subjects B and C. The eye-position signal was sampled at 500 Hz. The velocity signal was not measured directly but was extracted from the recording of eye position by numerical differencing. Subject A was stimulated at four frequencies (100, 200, 400, and 600 Hz) each at three durations (∼9, 17, and 33 pulses; see following text).Subject B was stimulated at 200, 300, and 400 Hz for 100, 200, 300, and 400 ms. Subject C was stimulated at 100, 200, and 300 Hz for 100, 200, 300, and 400 ms.

Data selection

Data for monkey A came from a single stimulation site, with the head fixed. The main parameters varied were frequency and duration of stimulation. In most cases stimulation was applied when the eye was in the primary position (the position when the animal was looking straight ahead): the small number of instances using other starting positions were not used in the main analysis. Each eye-position trace was inspected and those that were interrupted by a saccade or had a clear vertical component were excluded from analysis. The resulting data set consisted of 102 traces. Data for monkey B were obtained from seven stimulation sites. However, only four of these sites were used, since stimulation at the remaining three produced eye movements with a strong vertical component. Both starting position in the orbit and stimulation frequency and duration were varied. Overall 715 traces were deemed suitable for analysis. Data for monkey C were similar to those for monkey B, with three of seven sites used and four rejected because of the size of the vertical component, although in general fewer conditions were run, giving a total of 201 traces for analysis. The criterion for rejecting sites was an informal one, based primarily on visual inspection, but corresponded approximately to a maximum vertical displacement of ≥6°. Later analysis indicated that inclusion of data from all sites in monkeys B and C produced only slight alterations (3–14%) in the estimated TC values shown in Fig. 4.

FIG. 4.

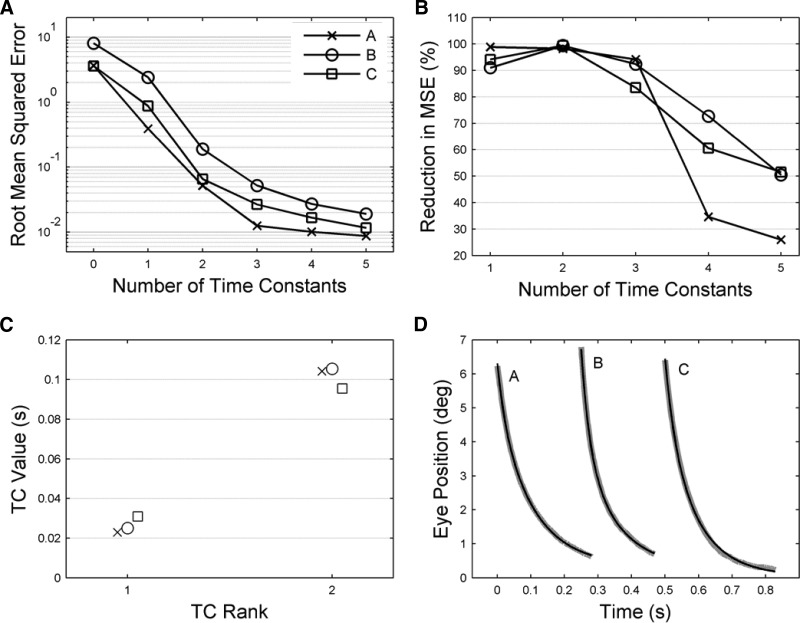
Time constant (TC) values for unstimulated plant, estimated by fitting exponential terms to return curves from 40 ms after end of stimulation. A: fitting errors plotted as a function of the number of TCs used for fitting. Fitting errors were calculated as the root mean squared errors over all traces for a given animal (methods). The value shown for zero-fitted TCs corresponds to the root mean squared values of the original data sets before fitting. The y-axis uses a logarithmic scale. B: the successive reduction in fitting error, expressed as a percentage, produced by fitting each additional TC. The x-axis starts at one, corresponding to the reduction in error of the original data sets produced by fitting a single TC. C: the values for the 2 shortest TCs, when 3 TCs were fitted. Error bars showing 95% confidence limits derived by the bootstrap method are too small to be seen at this scale. Values for the TCs for each animal are A = 23, 104 ms; B = 25, 105 ms; C = 31, 96 ms. D: examples of typical fits for each animal black lines model, gray lines data. The starting time for the traces has been advanced 250 ms for B and 500 ms for C. The VAF (variance accounted for; methods) values for each animal were A, 1.0000; B, 0.9999; C, 0.9999.

To avoid ambiguity in the use of the term “frequency” we will always refer to the pulse frequency of the stimulating pulse train as the stimulation frequency (units of pulses per second, or more concisely Hertz). When used by itself the term frequency will refer to frequency in the signal-processing sense, that is, oscillation frequency of a sinusoidal movement or modulation frequency of a sinusoidally modulated firing rate. Stimulus duration and stimulation frequency were recovered from the duration and amplitude of the recorded output of a window discriminator. In some traces for subject A the recorded duration varied significantly within a condition (≤12 ms), even though the corresponding eye movement traces had very similar time courses up to peak displacement, indicating that the stimulus duration had in fact been constant, so there must have been occasional errors in the output of the window discriminator. For 100-, 200-, and 400-Hz trains the mean of the window-discriminator outputs was used to estimate the number of pulses in the stimulation train to the nearest whole number and, from this number, the actual duration of the stimulation. The number of pulses estimated by this method for the three duration conditions was 9, 17, and 33 for each of the three frequencies and, in the case of 100-Hz trains, these estimates could be checked directly by counts of the ripples in the eye-movement record (Fig. 6). For the 600-Hz trains, this method gave a mean nominal value of 13 ms for the shortest-duration condition. However, this value corresponded to a latency to peak displacement of 15 ms, in contrast to all the other conditions, which gave values of 10–12 ms. The stimulus duration in this case was adjusted to 16 ms for consistency. The inferred number of pulses for 600 Hz was 11, 19, and 35.

Data analysis: unstimulated plant

PRINCIPAL COMPONENT ANALYSIS.

The characteristics of the oculomotor plant in its baseline unstimulated state can be assessed using the trajectory of the globe's return to its starting position, starting at the time when the effects of abducens stimulation on the lateral rectus muscle have finished. To determine that starting time, the return traces were subjected to principal component analysis (PCA).

The return traces of the globe to starting position correspond to a system driven by zero input. An nth order linear system driven by zero input can be expressed as a sum of n exponentials. The return traces of the globe should therefore be describable by this exponential model structure if the linearity assumption is correct. In this modeling scenario PCA can be used to indicate whether a system can be described by a linear system and also the order of that system: a small number n of significant principal components (PCs) that account for a large proportion of the variance of the time series suggests that the system can be modeled by an nth-order linear system (Sklavos et al. 2005).

This analysis is complicated, however, by any nonlinear effects. If the PCs change significantly with time this suggests that there is a time-varying process underlying the time series that cannot be described by a linear model. Thus a PCA sweep was applied to the return curves: a PCA window of 200-ms width was swept through the data in 2-ms increments from the end of stimulation. The resulting time-dependent sequence of PCs was assessed to determine at what time the significant variation in PCs ceased. Linear modeling of the return curves was performed using the time-series segment from this point to the end of the time series.

GROUP FITTING OF RETURN TRAJECTORIES.

The fitting procedure for the return curves of the globe was similar to that detailed in Sklavos et al. (2005). The method uses the fact that the observed output of a continuous-time linear time-invariant system with zero input is described by a sum of exponentials

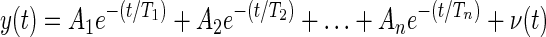(1)

where A_j is a coefficient, for j = 1, …, n; T_j is a TC; v(t) is assumed to be zero mean white measurement noise; y(t) is the measured eye rotation; and n is the model order. The TCs reflect mechanical properties of the system and are therefore constant over all the observed return curves along with the model order n. The coefficients A_j describe the extension of the corresponding jth Voigt element at time 0 and thus vary with each return curve.

The coefficients A_j and the TCs comprised the set of unknown model parameters, which were estimated using a separable least-squares algorithm (Sklavos et al. 2005). The principle of this approach was to estimate the TCs in a nonlinear regression (solved via the Matlab numerical minimization routine fminunc). The coefficients A_j “separate” from this nonlinear regression problem because they are linearly related to y(t); thus a least-squares solution is available for each A_j corresponding to each return curve for any given values of the TCs. This algorithm makes the problem of estimating the many A_j coefficients tractable for large numbers of release curves (Anderson et al. 2007).

Structure detection forms the other significant part of the modeling procedure. This corresponds to picking a model order n that most parsimoniously describes the system. The objectives are to keep the model simple and therefore of low order while accurately describing the system dynamics. These two objectives are in conflict: as model order decreases the model usually becomes less accurate. A suitable trade-off is obtained when the inclusion of an additional model term (corresponding to an exponential term in Eq. 1) does not significantly improve the accuracy. This was assessed here by visual inspection of a plot of increasing model order versus root-mean-squared (prediction) error (RMSE): the model order was chosen at the point when the RMSE began to flatten, indicating that prediction accuracy was not significantly improving. More formal model order selection methods—such as use of the Akaike information criterion (Akaike 1974)—were considered, but rejected because they can grossly overestimate model order when the residual errors have significant structure (cf. results of applying F-statistic to similar data in Sklavos et al. 2005). This was the case for our data, where fifth-order or higher-order models were selected despite tiny improvements in RMSE over the third-order models selected by visual inspection.

Parameter estimate confidence intervals were obtained using the bootstrap method (Press et al. 1992). The bootstrap method consists of sampling the M return traces of the subject (subject A: M = 102; subject B: M = 715; subject C: M = 201) with replacement to produce, in this case, 500 new sets of traces. The best-fit TCs were estimated from this new data set and the confidence intervals were then taken as the 5th and 95th percentiles.

The accuracy of the model prediction was assessed using visual inspection of the fitted return curves and quantitatively by the variance accounted for (VAF) metric, where VAF = 1 − [var (e)/var (y)] and where e denotes the vector of model prediction errors and y is the vector of fitting data.

ROBUSTNESS OF TC ESTIMATES.

The data sets for animals B and C were obtained 1) in head-fixed versus head-free conditions, 2) with varying starting positions of the eye in the orbit, and 3) from different stimulation sites. The various possible combinations of these three conditions were not administered in counterbalanced order, so here only preliminary analysis is possible. For each of the three variables listed earlier, the data were grouped over the other two. When initial eye position was the variable of interest, the data were partitioned into six groups with starting positions in 10° intervals between −30 and 30°. When stimulation site was the variable of interest, the sites were ranked according to the extent to which the release curves for that site did not decay to the primary position as expected (see results). This implied there was an unknown input acting on the plant, which we regarded as a noise signal. Since its magnitude varied by site of stimulation, we investigated the possible effect of the noise on plant TC estimates by fitting TCs separately for each stimulation site. For this procedure the third TC was also replaced by a constant term.

Data analysis: effects of stimulation

ESTIMATION OF MUSCLE FORCE PROFILES.

The effects of stimulation can be considered as a cascade of two dynamic processes: 1) the production of muscle force in the agonist muscle by stimulation (red arrows and box in Fig. 1) and 2) the action of that force on the mechanical plant (remainder of Fig. 1) to produce eye movement.

The changes in muscle force produced by abducens stimulation were not measured directly in the present study. They were instead estimated from eye-movement dynamics, using a model of the oculomotor plant used in inverse mode with eye position as input and inferred muscle force as output. The Sklavos et al. (2006) model was chosen for this purpose because it has (relative) values for the viscosities (c) and elasticities (k) of the viscoelastic elements, whereas for the alert animals only estimates for the TCs (c/k) are available. This is because in the present study the peak eye displacements were not maintained long enough to allow the viscoelastic elements to reach equilibrium. If equilibrium is reached, as in Sklavos et al. (2006), analysis of the subsequent return trajectories will permit estimates of both the relative elasticities of the elements and their time constants. If the eye is not maintained until equilibrium is reached, as in the present study, only estimates of the TCs can be made from the return trajectories on their own. These arguments are given in greater detail in Sklavos et al. (2005, 2006).

The plant model G described in Sklavos et al. (2006) has four Voigt elements with time constants of 0.01, 0.1, 1, and 10 s and corresponding compliances of 35, 35, 15, and 15%. Since eye position is related to muscle force by

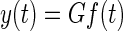(2)

where y(t) is the eye position and f(t) is the muscle force, in inverse mode we have f(t) = G⁻¹y(t) or F(s) = G(s)⁻¹Y(s) using Laplace transform notation. These inverse transforms were evaluated using the Matlab control system toolbox function lsim. However, because the inverse transfer function G(s)⁻¹ is improper (has more zeros than poles), it cannot be applied directly to y(t). To circumvent this technical limitation of lsim the proper transfer function s⁻¹G(s)⁻¹ was applied first to y(t) to get f̃(t) and the extra integration s⁻¹ was then cancelled by numerical differentiation. This was implemented as forward differencing, f(t) = Δ⁻¹[f̃(t + Δ) − f̃(t)], where Δ is the sample time.

MODELING EFFECTS OF STIMULATION DURATION AT CONSTANT STIMULATION FREQUENCY.

The force profiles estimated by the above-cited procedure (see results) turned out to be highly nonlinear functions of stimulation frequency that were very similar in appearance to the isometric-force profiles recorded from isolated lateral rectus muscle in primate by Fuchs and Luchsei (1971). To investigate whether there were further nonlinearities in the data, we attempted to model the effects of stimulus duration at constant stimulation frequency (400 Hz), using the measured isometric force profile as inputs to a refined plant model—i.e., a model G specific to our data rather than the Sklavos model defined earlier. We assumed that for a given stimulation frequency muscle force was linearly related to the duration of stimulation by

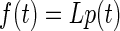(3)

where L is the linear model of force production in lateral rectus for a stimulation frequency of 400 Hz, p(t) is the pulse input signal with stimulation frequency 400 Hz, and f(t) is the force output signal. The structure of L was defined as a second-order linear transfer function (2 poles, 1 zero), which gave significantly better fits to the data than a first-order model and comparable fits to a third-order model. Parameters for the model were estimated by nonlinear regression (fminunc in Matlab), including a time delay d.

The transformation of force into eye position was then modeled using Eq. 2, with the plant G(t) represented by a linear transfer function. The order of this function was derived in part from the results of fitting the release-curve data, which suggested that the plant could be approximated by two Voigt elements in series (see results). However, to accurately describe the stimulation portion of the eye movement data, we observed that a third short TC was required that was not necessary for fitting the release curve data (see results). Thus the model G was defined as third-order (three Voigt elements in series). Additionally the model G required estimation of a compliance value corresponding to each Voigt element. In summary, the model G consisted of six parameters: time constants T₁, T₂, and T₃ and compliance values b₁, b₂, and b₃. The medium and long TCs (T₂ and T₃) were defined by fitting the release curve data. Fitting the remaining parameters of G (T₁, b₁, b₂, and b₃) is described in the following text.

To fit the short time constant in the eye mechanics model G, the force model L (described earlier) was used to generate a force profile that was used as the input to the eye mechanics model. The short time constant T₁ was adjusted in a nonlinear regression (using the function fminunc in Matlab) to optimize the fit to eye-movement data recorded from subject A at stimulation frequencies of 400 Hz only. At each iteration in the nonlinear regression the two stages of the model—force production L and mechanics G—were combined so that

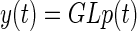(4)

This estimation procedure for T₁ needed to take into account the failure of the eye to return to the primary position on some trials, suggesting the presence of additional force input of unknown origin (see results). This input was assumed to be constant on a given trial because the return-curve data for subject A could be fitted with three exponential terms (Eq. 1), the third of which had an effectively infinite TC. The value of the unknown input α on a given trial could therefore be derived from the coefficient A₃ in Eq. 1, by use of the final-value theorem (Franklin et al. 2001), which relates constant input to constant output for a linear time-invariant system. The estimate of α for a given eye movement was appended to the recorded pulse input signal at the end of stimulation to generate a corrected pulse input signal. Thus the short TC fit was optimized with respect to this corrected pulse input signal.

The compliances b₁, b₂, and b₃ of the three Voigt elements comprising G were initially estimated along with the short time constant. However, the estimates were unreliable: examination of the cost function (obtained by fixing two compliances to optimized values and evaluating the fit error from deterministic variation of the third value) showed that it was nearly flat in wide regions for each compliance in the region of b₁ = 30%, b₂ = 10%, and b₃ = 60% (corresponding to short, medium, and long TCs). Thus the compliances were fixed to these values, which can be regarded as regularized estimates for this data set. A gain term g was estimated in the nonlinear regression along with T₁ to scale the fixed relative compliance values to the data.

EFFECTS OF STIMULATION: SUMMARY.

1) To obtain an approximate estimate of the forces produced by different stimulation frequencies we used the best model available, even though it is based on data from anesthetized animals. 2) Since the resultant force estimates were qualitatively similar to measurements of isometric force in the lateral rectus muscle, we made the assumption that the force profiles in the present study are in fact identical to the measured profiles and used that assumption to estimate compliances for the new plant model for alert animals. This enabled us to generate complete eye-movement profiles (i.e., for both “active” and “passive” phases of the movement) and compare them with data.

RELATION TO SINGLE-UNIT DATA.

Sylvestre and Cullen (1999) showed that the firing rate FR of an abducens neuron for a given eye movement can be predicted by the relationship

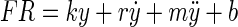(5)

where y is eye position, ẏ is eye velocity, ÿ is eye acceleration, and b is a bias term. The eye-movement records from subject A were used to obtain estimates of the model parameters at different frequencies of stimulation (100, 200, 400, and 600 Hz). The eye velocity and acceleration were obtained from the eye-position data by first-order differencing. The parameters k, r, m, and b were estimated by least-squares.

Effects of muscle stiffness on overall time constants

The transfer function H_sys(s) for the system shown in Fig. 1 consists of two component transfer functions: one for orbital tissue H_orb(s) and the other for the two muscles H_m(s). These are related by

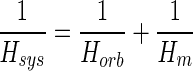so that

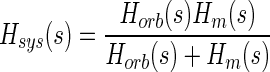(6)

The transfer function for orbital tissue used here was for a four-Voigt-element model with parameters derived from the measurements in Sklavos et al. (2005) as given in Eq. A6 of that study, with overall stiffness set at 0.45 gf/deg, estimated from the force-transducer measurements of Miller et al. (2002; Fig. 7). The combined muscles were treated as a single Voigt element

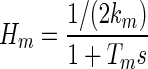(7)

with time constant T_m fixed at 0.1 s and stiffness k_m allowed to vary from 0.01 to 0.5 gf/deg. The time constants of the overall system were then plotted as a function of k_m. The value for the muscle TC was derived from measurements of passive lateral rectus muscle in cat (Collins 1971). The range of muscle stiffnesses was chosen because passive muscle stiffness appears to be about 0.03 gf/deg for primate lateral rectus in the primary position, as estimated from Fig. 4 of Fuchs and Luschei (1971); and muscle stiffness in alert humans is probably about 0.3–0.5 gf/deg (Collins et al. 1991; Robinson 1981; Simonsz and Spekreise 1996).

RESULTS

The results are organized to address the following four questions in order. First, how long do the effects of motoneuron stimulation on muscle activation continue after the stimulation has ceased? Second, does analysis of eye movements after this time (i.e., when muscle activation is constant) indicate that the plant is behaving linearly? Third, does analysis of eye movements before this time, i.e., when muscle activation is changing, indicate linear or nonlinear behavior? Finally, do any nonlinearities uncovered by these analyses throw light on the nonlinearities revealed by single-unit recording of motoneuron firing patterns?

Movement characteristics

A representative example of the eye movements produced by abducens microstimulation is shown in Fig. 2. In this case a 39-ms train of 17 pulses at 408 Hz was delivered to monkey A when the eye was in the primary position. Abduction started 5 ms after the first stimulation pulse and continued for a further 45 ms to reach maximum displacement (15°) 11 ms after the final pulse (Fig. 2A: times accurate to within ±1 ms because of 500-Hz sampling). Eye velocity reached its maximum (500°/s) at an estimated 17 ms after the start of stimulation (Fig. 2B), then declined at an approximately constant rate until 6 ms after the final pulse. At this point (marked by gray arrow) velocity began to decline much more rapidly, passing through 0 deg/s at 11 ms after the end of stimulation, corresponding to the time of maximum displacement. After this time the eye returned toward the primary position and was 2° away when the record ended 300 ms after the start of stimulation. The return velocity reached its highest absolute value (430°/s; negative according to the sign convention of Fig. 2) 11 ms after the start of the return (22 ms after the end of stimulation). This absolute value then dropped sharply to about 100°/s over a further 14 ms (36 ms after the end of stimulation, marked by black arrow). At this point the return eye velocity began to decline much more gradually, to a final value of <10°/s at the end of the record.

The initial displacement has some resemblances to a saccadic trajectory, but is roughly 50% slower and longer lasting (cf. Sparks and Mays 1983; Fig. 11): in stump-tailed monkeys (Macaca speciosa) 15° temporal saccades reach maximum velocities of around 700°/s, lasting about 30 ms (Fuchs 1967; Fig. 5). The velocity difference is presumably caused by a combination of factors, including the probable failure of the stimulation to recruit all abducens motor units and the continued presence of antagonist innervation. The return movement of course is entirely different from a saccade, reflecting the absence of the “step” from the pulse-step saccadic command, which maintains the globe in the position of maximum displacement.

FIG. 5.

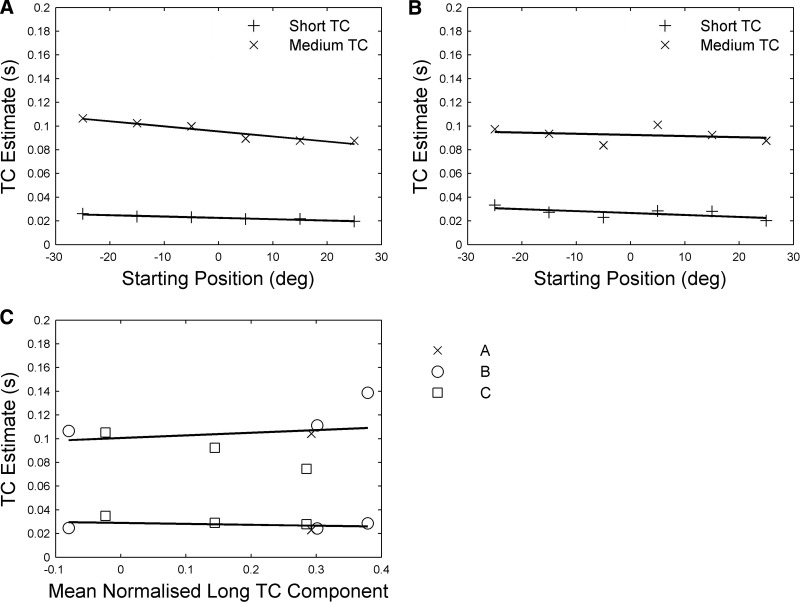
Robustness of TC estimates for unstimulated plant. A: effects on TCs of eye position at start of stimulation for subject B. Linear fits for short TC: y = −0.0001x + 0.023; for medium TC fit: y = −0.0004x + 0.96. B: effects on TCs of eye position at start of stimulation for subject C. Linear fits for short TC: y = −0.0002x + 0.027; for medium TC fit: y = 0.0001x + 0.93. C: effects on TCs of stimulation site. Each stimulation site was assigned a value corresponding to the mean normalized long TC component required to fit the mean offset of the traces produced by stimulating that site (methods). Linear fit for short TC: y = −0.0077x + 0.029; for medium TC fit: y = 0.022x + 0.10.

Return movement has two parts

A variety of evidence indicates that the mechanical properties of the unstimulated oculomotor plant are similar to those of a series of viscoelastic (Voigt) elements and that the globe's return movements after displacement can be approximated by a sum of exponentials with time constants (TCs) corresponding to the ratios of viscosity to elasticity for each element (see references in Sklavos et al. 2005). Since these are physical properties assumed not to change during the measurements, a family of return curves corresponding to different amplitudes of displacement should all be fitted by the same TCs, with only the coefficients of the exponential terms varying between curves (methods).

However, the TCs identified by this method will be inaccurate if the effects of stimulation on the muscle are still present during the period over which the traces are fitted (cf. Fig. 1). To estimate at what time the effects of stimulation could be disregarded, principal component analysis was carried out on 200-ms segments of all the return curves with the starting point of the segments systematically varied (Fig. 3, A and B). Although the proportion of variance accounted for by the first two components changed modestly or not at all as the starting point of the segment moved from 0 to 40 ms after the end of stimulation (+1 and −44%, respectively), the proportion accounted for by the next two components declined dramatically in this period (−98% in both cases). It is possible that the decline in these components is related to the discontinuity in the velocity trace observed about 36 ms after the end of stimulation in Fig. 2B.

The pattern of residual errors observed after fitting the return curves either from the time of peak displacement (∼10 ms after end of stimulation, Fig. 3C) or from 30 ms later (Fig. 3D) is consistent with the preceding analysis. The large and systematic errors in the former case are almost completely absent in the latter. These data are thus consistent with the return movement having two parts—the first influenced by the aftereffects of stimulation, the second apparently corresponding to the unstimulated state. The start of the second phase would appear to be the appropriate time at which to start fitting the return curves with sums of exponentials.

Time constants of unstimulated plant

The TC values of the unstimulated plant were therefore estimated from the return traces starting 30 ms after peak displacement, corresponding to around 40 ms after the end of stimulation. For each animal, all traces selected for analysis were fitted with the same TCs (subject A, n = 102; subject B, n = 715; subject C, n = 201) as explained in methods.

The effects of fitting different numbers of TCs on RMSE are shown in Fig. 4A. The slopes of the plots are roughly constant over the range zero to three TCs, then decrease noticeably for more than three TCs. Because the ordinate of the graph has a logarithmic scale, the roughly constant slope suggests that each successive TC reduces the fitting error by a constant factor. This is shown more clearly in Fig. 4B, which plots the percentage reduction in fitting error with each additional TC. These graphs suggest that three might be a suitable number of TCs to fit to the data.

The values obtained when three TCs are fitted are shown for the two shortest TCs in Fig. 4C. It can be seen that the values were similar for the three subjects. Estimates of the 95% confidence limits for these TC values were obtained using the bootstrap procedure (methods), but are too small to be visible in the panel. The values of the third TC (not shown) were A >10¹⁰ s, B 2.68 s, and C 144 s. This third TC was required to fit those traces that did not decay to the primary position, as expected (see, e.g., Fig. 2A). Since the magnitude of this offset varied from site to site, it appeared that there was an unknown stimulation-related input acting on the plant (see following text).

Finally, Fig. 4D shows that the typical fits to the data obtained with three TCs were good, with high values for the VAFs for each animal (>0.999).

Robustness of time constant estimates

Because animals B and C were tested under a variety of conditions, their data allow some assessment of the robustness of the two short TC estimates, even though the various conditions were tested in exploratory fashion rather than a strict counterbalanced experimental design. For each of the three variables—1) head-fixed versus head-free, 2) starting position of eye in orbit, and 3) stimulation site—the data were grouped across the other two variables for analysis. There was a slight tendency for the head-fixed estimates to be lower than head-free estimates, more noticeably for subject C than for subject B (data not shown). Of more relevance to the present study, the effects of initial eye position were also slight and not consistent between the two subjects (Fig. 5, A and B), suggesting that at least over the range of starting positions examined here the plant characteristics do not become notably nonlinear, consistent with recent findings concerning the effects of starting position on saccade-related firing in abducens neurons (Ling et al. 2007). Although few traces were available for starting positions that were displaced vertically, the TCs estimated from them were also similar to those found for traces starting from the straight-ahead position (subject A: 9 traces at 10° elevation, 10 from 20° elevation, TCs 4–8% increase; data not shown).

Finally, Fig. 5C shows the lack of effect on the short TC estimates of the location of the stimulation site, consistent with their reflecting the physical properties of the plant. More specifically, it indicates that the estimates are not influenced by the extent to which at some stimulation sites the eye appeared to be returning to a location displaced from its original position (e.g., Fig. 2, A and B). It was this phenomenon that gave rise to the requirement for a third TC that was effectively infinite (see earlier text). The amplitude of this component, expressed as a proportion of overall movement amplitude, varied from site to site over the range −8 to 38%; however, estimates of the two shorter TCs appear not to be affected by the presence of the third component (see discussion).

Nonlinear effects of stimulation frequency

The robustness of the TC estimates suggests that, under the circumstances of the present study, the unstimulated plant behaves in an approximately linear manner. However, the effects of stimulation itself are in certain respects clearly nonlinear. This can be seen from a plot of response amplitude against stimulation duration for different frequencies (Fig. 6A). The saturation ≳400 Hz and the small amplitude of the response to 100-Hz stimulation, compared with that to 200 Hz, are consistent with a sigmoidal relation between response amplitude and stimulation frequency. In addition, there is a suggestion that the time course of the response varies with stimulation frequency so that higher frequencies produce greater initial velocities than would be expected simply from the amplitude changes (Fig. 6B).

FIG. 6.

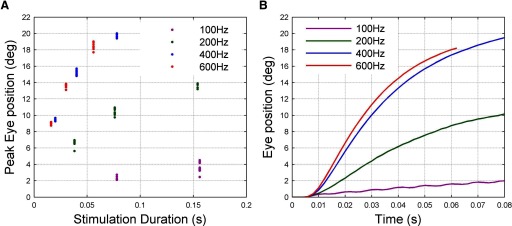
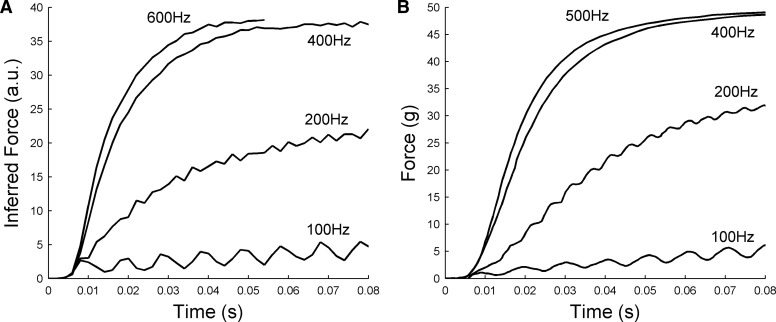
Nonlinear effects of stimulation frequency for animal A. A: peak amplitude of eye displacement as function of stimulation frequency and duration. B: time course of eye movement over first 60 or 80 ms of stimulation at each frequency.

The patterns of response shown in Fig. 6B appear similar in general terms to those previously reported for force production in isolated extraocular muscle (Fuchs and Luschei 1971). To investigate this apparent similarity, we attempted to provide an approximate estimate of the force acting on the oculomotor plant in the present study by using the plant model described in Sklavos et al. (2006) in inverse mode, so that eye displacement was the input and estimated force the output. The reasons for choosing this model are given in methods. These estimated forces are shown in Fig. 7A as a function of stimulation frequency. They differ from the eye-displacement records in reaching their asymptotic values more rapidly and that at the lowest stimulation frequency of 100 Hz the low-amplitude ripples just visible in the eye-displacement record (Fig. 6B) become much more apparent in the force record. Ripples can also be seen in the estimated-force record for 200 Hz. For comparison, actual measurements of isometric force in rhesus lateral rectus muscle (Fuchs and Luschei 1971) are shown in Fig. 7B. Despite the approximate nature of the plant model that was used to obtain the estimated-force records and the fact that in the present study the muscle forces are not isometric, the similarities are quite striking. They suggest that the plant nonlinearities shown in Fig. 6 are likely to derive in large part from nonlinearities in the mechanism of force production by the lateral rectus muscle.

FIG. 7.

Inferred force profiles for animal A compared with isometric force measurements by Fuchs and Luschei (1971). A: inferred time course of muscle force development at different stimulation frequencies, estimated from eye-movement records using an inverse plant model (details in text). B: time course of isometric lateral rectus force development at different stimulation frequencies, measured in isolated muscle. Redrawn from Fig. 3A of Fuchs and Luschei (1971).

Evidence for additional nonlinearities

The nonlinear effects of stimulation frequency on muscle force mean that a nonlinear model of muscle activation (Fig. 1) is required to simulate the full time course of the eye movements resulting from abducens stimulation over a range of frequencies and one based on standard NARMAX (Nonlinear Auto-Regressive Moving Average with eXogenous input) techniques (Chen and Billings 1985) will be described elsewhere. However, an important question for the present study is whether the eye-movement responses can be well fitted by a combination of (nonlinear) force profiles and a time-invariant linear model of plant mechanics or whether the data in fact indicate the presence of additional nonlinearities in the plant.

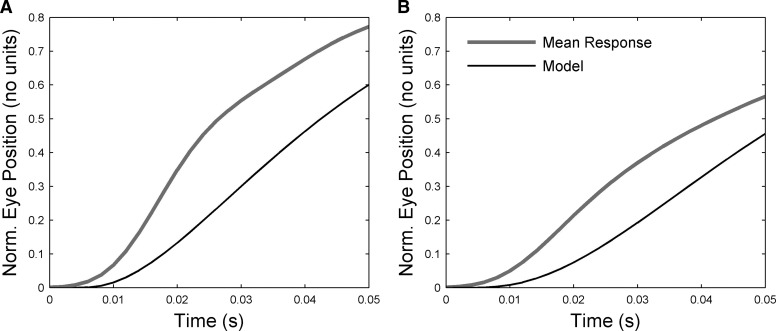
When the force profiles reported by Fuchs and Luschei (1971) were combined with the time constants identified here for the unstimulated plant, the rise times of the eye displacements produced at high stimulation frequencies were too slow. This could be seen most unambiguously for subjects B and C (Fig. 8). Whereas the shortest TC identified for the unstimulated plant was 25–30 ms (Fig. 4), the values needed to fit the data at stimulation onset were 1–4 ms (fits not shown), about an order of magnitude shorter. Some of this discrepancy may arise because the force profiles from Fuchs and Luschei (1971) differ from the actual (unknown) profiles in the present study. This cannot be the whole explanation, however, because the observed eye-displacement rise times can be obtained only with an unphysiological step input to the system if the shortest plant TC is 25 ms (results not shown). It appears either that 1) there is a very short TC element in the plant that is not picked up in the passive plotting (because the element's effects disappear in the nearly 30 ms after peak displacement before passive fitting begins) or that 2) stimulation alters the properties of the plant—that is, it produces nonlinearities additional to those illustrated in Fig. 7.

FIG. 8.

Modeling initial eye displacement for high-frequency stimulation. A: actual and modeled eye-displacements for 50 ms after stimulation onset for animal B (400 Hz). The modeled trajectory was obtained by using the time course of isometric force development measured at the appropriate stimulation frequency for the lateral rectus muscle (Fuchs and Luschei 1971) as input to a 1st-order plant with TC = 25 ms, the value derived from fitting the return curves from animal B. The gain was adjusted to fit the final value of the response. B: actual and modeled eye displacements for 50 ms after stimulation onset for animal C (300 Hz). TC used in 1st-order plant model = 31 ms, the value derived from fitting the return curves for animal C.

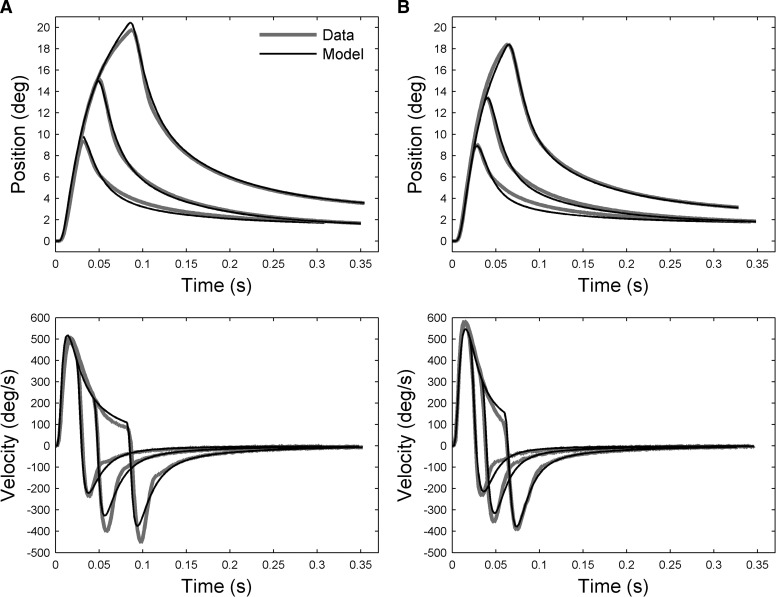
To try to distinguish between these possibilities we attempted to fit the entire duration of eye displacements produced by 400-Hz stimulation in animal A, using force input profiles derived from the data of Fuchs and Luschei (1971) in conjunction with a fixed plant model of eye mechanics (details in methods and appendix). The plant model consisted of three Voigt elements, with two TCs corresponding to those obtained for the unstimulated plant (i.e., 23 and 104 ms) and the third allowed to vary to account for the fast rise times of the eye movements (final value 5 ms; further details in the appendix). The stimulation durations at 400 Hz for animal A (∼20, 40, and 80 ms) are of the same order as the time constants of the Voigt elements in the model. They should therefore produce differential extensions of the model components, with correspondingly large variations in the maximum amplitude of the overall displacement of the eye. Thus this data set provides the strongest test of the linear model, given that the minimum stimulation duration for animals B and C was 100 ms (methods). Figure 9A shows that good fits are obtained with this procedure (VAF >0.99). Using the same plant model for the other frequencies of stimulation also produced a good fit for 600 Hz (Fig. 9B, VAF >0.99), but poor fits for 100 and 200 Hz.

FIG. 9.

Fitting entire eye-movement trajectories with input profiles derived from Fuchs and Luchsei (1971) and a linear plant model. Data from animal A: left column (A) for stimulation frequency of 400 Hz; right column (B) for 600 Hz. Top row shows eye-position traces for different durations of stimulation. Each trace represents the mean eye displacement of the individual traces obtained at that duration. Bottom row shows eye-velocity traces, derived from eye position by numerical differentiation. The modeled trajectories were obtained by using input profiles derived from isometric force measurements of primate lateral rectus muscle (Fuchs and Luschei 1971) as input to a 3rd-order plant (TCs: 5, 23, and 104 ms; further details in text).

The results shown in Fig. 9 suggest that plant nonlinearities additional to those related to stimulation frequency are of modest importance. Nonetheless, there are indications of consistent deviations between model and data, such as in the velocity traces at a time corresponding to the second inflection shown in Fig. 2 (∼36 ms after end of stimulation). It is possible that these discrepancies reflect the recruitment of motor units by the stimulation, if these units have different mechanical properties from those already recruited in the unstimulated state. This possibility is considered further in the discussion.

Relation to single-unit data

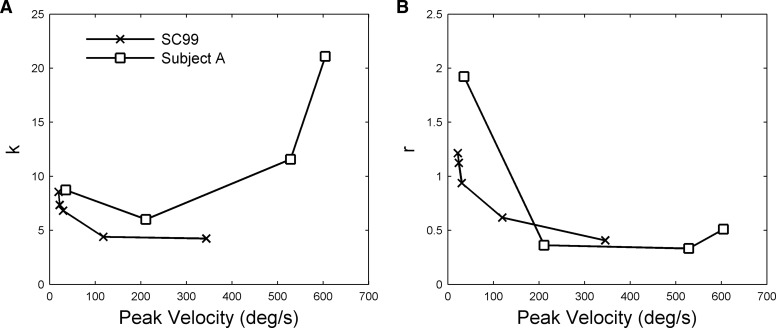
As outlined in the introduction, single-unit recordings from primate abducens nucleus show that the relation between firing rates and eye movement is nonlinear (Sylvestre and Cullen 1999). The nature of the nonlinearity is indicated in Fig. 10. Sylvestre and Cullen (1999) used what is in effect a second-order plant model and estimated its parameters as a function of eye velocity (methods, Eq. 5). If the system were linear, these parameters would be independent of eye velocity, but as shown in Fig. 10 the parameters relating firing rate to eye position (k) and firing rate to eye velocity (r) both vary with the peak eye velocity of the movement.

FIG. 10.

Comparison of nonlinearities for firing-rate and stimulation data. The firing rate curves (SC99) are taken from Fig. 14 of Sylvestre and Cullen (1999), who used a 2nd-order plant model (Eq. 5) to derive position k and velocity r coefficients. These varied with eye-movement peak velocity as shown. The same model was used to model stimulation data from subject A at 4 frequencies (100, 200, 400, and 600 Hz as shown in Fig. 6B, with the 100- and 200-Hz responses smoothed), and the derived frequencies also plotted against eye-movement peak velocity.

To assess whether the stimulation-frequency–dependent nonlinearity characteristic of the data could account qualitatively for the firing-rate nonlinearities, the same method of analysis was applied to the data from the present study illustrated in Fig. 6B. The logic behind this extrapolation was that if electrical stimulation causes motoneurons to fire at the frequency of the stimulating train, then the equation used by Sylvestre and Cullen could also be used to relate (inferred) firing rates to eye movements in the present study. Comparison of parameter variation for the two sets of data (Fig. 10) reveals some qualitative similarities.

The variation in k for the stimulation data derives from the sigmoidal relation between the amplitude of final eye displacement (in response to a step input) and stimulation frequency (Fig. 6). The gradient of this relationship is small for the flat parts of the sigmoid at low and high frequencies and larger for the linear part of the sigmoid at intermediate frequencies. Since k is the reciprocal of the gradient, it takes large values for low and high stimulation frequencies and low values for intermediate stimulation frequencies. Thus the drop in k observed in the firing-rate data may correspond to a shift from low to intermediate stimulation frequencies. As argued earlier, it seems likely that the sigmoidal relationship between eye displacement and stimulation frequency observed in the present study derives from the well-known sigmoidal relation between steady-state isometric force and stimulation frequency for extraocular (Fig. 7) and skeletal muscle (discussion).

The variation in r for the firing-rate data derives from the change in response shape to step inputs (Fig. 6B). Asymptote is reached faster for higher stimulation frequencies, corresponding to lower system time constants. Since the time constant is approximated by r/k, the value of r will decrease over the stimulation frequency range where k decreases or stays constant. Thus the drop in r observed in the firing-rate data may also correspond to a shift from low to intermediate stimulation frequencies.

The stimulation-frequency–dependent nonlinearity found in the present data may therefore account for part of the nonlinearity observed in firing-rate data by Sylvestre and Cullen (1999). Additional factors are considered in the discussion.

DISCUSSION

Previous studies of the dynamics of the primate oculomotor plant have produced apparently conflicting results. Analysis of the eye's return to rest after displacement in anesthetized animals suggested a linear plant (Sklavos et al. 2005, 2006). In contrast, recordings from abducens neurons during eye movements in alert animals indicated the presence of significant nonlinearities (Sylvestre and Cullen 1999).

The present experiment sought to help resolve this conflict by analyzing the eye movements produced by stimulation of the abducens nucleus in alert primates. First, we estimated the time after the end of stimulation at which muscle activation ceased to change then analyzed eye-movement traces starting at this time point with a previously developed group-fitting technique (Sklavos et al. 2005). The fits indicated that during constant muscle activation the plant in alert primates appears to behave approximately linearly. Second, we found that when muscle activation was changing during the stimulation itself, both inferred muscle tension and its rate of rise were nonlinear functions of stimulation frequency. Further analyses suggested that these stimulation-frequency–dependent effects probably contributed substantially to the single-unit nonlinearities characterized by Sylvestre and Cullen (1999) and that any additional nonlinearities independent of stimulation frequency were likely to be of modest importance for the present data.

Plant properties during constant muscle activation

The dynamic properties of the oculomotor plant can be identified from the relation between the force acting on the plant and the displacement it produces. When the displacement results from electrical rather than mechanical stimulation an additional dynamic process is introduced: the production of muscle force by electrical stimulation (Fig. 1). The relation between stimulation and eye-movement parameters thus reflects not only the mechanics of the oculomotor plant, but also the dynamics of the muscle activation process.

ESTIMATION OF PLANT MECHANICS.

As indicated in results, our first step in approaching this difficulty was to determine when muscle activation ceased to change after the end of stimulation. The behavior of the principal components of the poststimulation traces suggested that this occurred about 40 ms after stimulation stopped (Fig. 3C), an estimate broadly consistent with measurements of the decay of isometric force in the rhesus lateral rectus muscle after tetanic stimulation with the muscle held at its estimated resting length (Fuchs and Luschei 1971; calculated from their Fig. 3A). Although longer time decays (∼70 ms) for isometric force decay have been observed (Goldberg et al. 1998; Shall et al. 2003), in these cases the muscle was held at a greater length than the estimated resting length used by Fuchs and Luchsei (1971) and the increases of both tetanic tension and twitch fall times with muscle length are well known (e.g., Brown and Loeb 1999). The suggestion that in the present study muscle activation stayed constant after the estimated 40 ms is also consistent with the finding that the eye-movement traces starting at this time could be fitted with a small number of exponentials (Fig. 3D), unlike the same traces fitted from the time of peak displacement (Fig. 3C).

A number of features of the fitting results suggest that when muscle activation is constant, the oculomotor plant can be approximated by a simple linear model. First, all the traces from a given animal could be well fitted with the same time constants (Fig. 4D) with VAFs >0.999. Second, the time constants were similar for all three animals tested (Fig. 4C). Third, TC values were unaffected by head restraint or by variation in the site of stimulation. The TCs were also unaffected by starting position over the range investigated (Fig. 5), suggesting that overall plant properties do not change, even though the relative contributions of the agonist and antagonist muscles (Fig. 1) do vary (cf. Ling et al. 2007). These findings are thus consistent with the presence of an unchanging oculomotor plant that behaves linearly over the ranges examined. This conclusion is consistent with the results of simple mechanical displacement in anesthetized animals (Sklavos et al. 2005, 2006).

One puzzling aspect of the stimulation data is that on some trials the eye appeared not to return to its initial position, but to a new equilibrium position in the direction of the original displacement. These return traces required a third component for fitting, effectively a constant term (i.e., an infinite TC). The size of this component varied from site to site (range −8 to 38%, Fig. 5C), suggesting that it did not reflect the properties of the oculomotor plant itself, but depended on the signal delivered to the plant by the stimulation. It is as if at some sites the stimulation partially engaged the horizontal velocity-to-position integrator, in a manner that varied unpredictably from trial to trial. Fortunately for the purposes of the present study, the influence of this unintended effect of stimulation appeared not to influence estimates of plant characteristics (Fig. 5C).

IMPLICATIONS FOR PLANT MODEL.

Previous measurements of return curves in ketamine-anesthetized animals, fitted with techniques identical to those used in the present study, suggested the plant could be approximated by the model of extraocular muscles and orbital tissue shown in Fig. 1 with TCs of 0.01, 0.1, 1, and 10 s (Sklavos et al. 2005, 2006). The data here concern only the effects of brief stimulation, which would have little effect on the two longest TCs in the model: for example, a 100-ms input extends the 1-s element by about 8% (∼1–2% of total movement amplitude). The present results are therefore suitable for characterizing behavior of only the two shorter TC elements. Two issues arise.

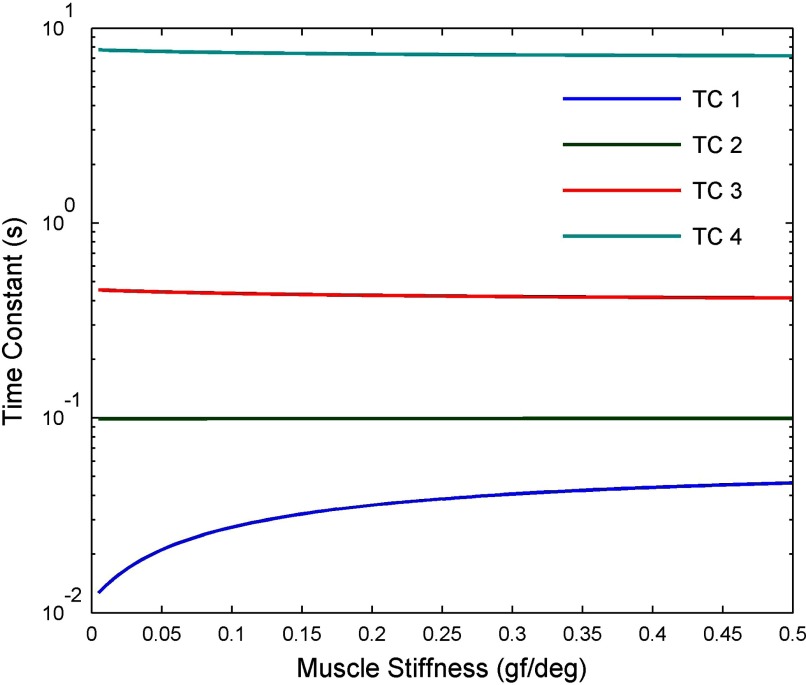
First, the TC value of 10 ms found in the previous study (Sklavos et al. 2005) appears to be transformed to 25 ms in alert animals (Fig. 3C), whereas the 100-ms value remains unchanged (Fig. 3C). A possible explanation of this transformation would be that the extraocular muscles have a TC close to 100 ms and muscle stiffness is greater in alertness than under ketamine anesthesia. The effects of changing stiffness in both muscles on the TCs of the overall plant (i.e., muscle plus orbital tissue) can be illustrated using the model shown in Fig. 1, with orbital tissue parameters derived from the measurements of Sklavos et al. (2005) (further details in methods). When the muscles' TC is kept constant at 100 ms and their stiffness changed, the shortest TC of the plant as a whole increases from 10 to 45 ms as stiffness increases from 0 to 0.5 gf/deg (Fig. 11). This result suggests that the explanation proposed here for the TC change is plausible in principle. A more precise test would require more accurate measurements of extraocular muscle properties in primates, especially their elasticity and viscosity under varying amounts of innervation.

FIG. 11.

Effects of changing muscle stiffness on system TCs in plant model shown in Fig. 1. The model was treated as a linear system (methods), so that the TCs of the system as a whole could be derived from the transfer functions of its components (i.e., orbital tissue and for muscle). In the case of orbital tissue, the transfer function was based on the measurements of Sklavos et al. (2005; Eq. A6), with overall stiffness set at 0.45 gf/deg, estimated from the force-transducer measurements of Miller et al. (2002; Fig. 7). For both muscles the TC was assumed to be 100 ms, consistent with measurements of passive lateral rectus muscle in cat (Collins 1971).

The second issue is that fitting the whole eye-movement trace, rather than the constant-activation part on its own, suggests the presence of an additional TC of about 5 ms (Figs. 8 and 9). No precise estimate is possible because the values of muscle force used in the fitting were not obtained from direct measurements, but instead inferred from others' data (Fuchs and Luschei 1971). However, it is clear that eye displacement changes too rapidly at the start of high-frequency stimulation for 25 ms to be the shortest TC value (Fig. 8). As indicated in results, an important question is whether the nearly 5-ms TC is in fact present in the unstimulated plant or is produced specifically by the stimulation itself (possibly via recruitment; see following text) and, as such, is a further example of nonlinear plant behavior. This question could be answered by displacing the globe mechanically and measuring its return trajectory after instantaneous release. However, previous studies have used only informal methods of release, such as opening forceps or letting go a suction contact lens, meaning that the first 10–20 ms of the return trajectory are influenced in an unknown way by external forces (Sklavos et al. 2005). The issue of a very short TC in the fixating alert animal is thus currently unresolved.

Properties of plant during changing muscle activation

CHANGING STIMULATION FREQUENCY.

Our second step in disambiguating the combination of dynamic properties of the oculomotor plant and those of the muscle activation process was to try to estimate the muscle force produced by electrical stimulation, by passing the eye-displacement traces back through the simple plant model derived from previous studies (Sklavos et al. 2005, 2006). When the estimated forces were related to stimulation frequency and duration (Fig. 6), the resultant curves (Fig. 7) quite closely resembled those measured for isometric force in the isolated lateral rectus muscle of rhesus monkeys held at the estimated primary position length (Fuchs and Luschei 1971).

The two main nonlinearities shown by these curves—that is, sigmoidal force-stimulation frequency relation for steady-state tension and stimulation-frequency–dependent rate of force increase—appear to be general characteristics of both skeletal (Brown and Loeb 2000; Buller and Lewis 1965; Cooper and Eccles 1930) and extraocular muscle (Asmussen and Gaunitz 1981; Barmack et al. 1971; Bishop et al. 2007; Fuchs and Luschei 1971; Goldberg et al. 1998; Lennerstrand 1974; Stelling and McVean 1988; Yamanaka and Bach-y-Rita 1970), although specific parameters (e.g., the stimulation frequency at which force saturation occurs) vary with many factors such as type of muscle, species, and muscle length. The rather close resemblance between panels in Fig. 7 suggests that stimulation of the abducens input to lateral rectus is nonlinearly related to muscle tension and thus to the consequent movement of the globe.

Although nonlinear force production and its importance for constructing an accurate plant model have been discussed by Robinson (1981), its significance has not been subsequently widely appreciated (e.g., Enderle et al. 1999; Pfann et al. 1995). The problems posed for eye-movement control are considered in the following text.

CHANGING STIMULATION DURATION.

An important question for characterizing the oculomotor plant is whether the stimulation data provide evidence for plant nonlinearities additional to those associated with stimulation frequency. An obvious potential source of such nonlinearities is that the abducens stimulation recruited motor units that were silent during fixation at the primary position, which temporarily altered the mechanical characteristics of the eye muscle (and thus the plant).

We attempted to answer this question by modeling the full eye-movement trace for different durations of stimulation at a fixed stimulation frequency, using input profiles inferred from isometric force measurements of primate lateral rectus muscle (Fuchs and Luschei 1971) with a fixed linear plant model. The goodness of the resultant fits (Fig. 9) suggests a rather modest role for additional plant nonlinearities. However, it should be noted that the plant model required for this fit differed from that deduced from the “passive” return, as discussed earlier. This difference might be expected insofar as stimulation recruits motor units that are not normally recruited in the primary position and these units are likely to be of the “global pale singly innervated type” (see references in Dean 1996; Goldstein and Robinson 1992; Khanna et al. 2007) with “fast” mechanical properties (including low viscosity) likely to reduce muscle TCs. It should be noted that the “fixed-plant” model used for Fig. 9 fails to reproduce the sudden slowing of the eye's return around 36 ms after the end of stimulation. This slowing is consistent with the increase in plant TCs expected when fast units cease to contribute. The relationship between recruitment in extraocular muscles and the mechanical properties of the oculomotor plant clearly warrants further experimental work.

Relation to single-unit data

Sylvestre and Cullen (1999) found that although the relation between the firing rates of abducens neurons and eye-movement parameters could be approximated by Eq. 5, the coefficients k and r in the equation changed with the velocity of the movement (cf. Fig. 10).

This is not in itself evidence for nonlinearity because the data analyzed were for types of movements (smooth pursuit, vestibuloocular reflex, and saccades) whose power spectra have very different frequency content. For a linear system the empirical k and r obtained for sinusoidal movements will necessarily be frequency dependent if the plant is not first order. To the extent that higher velocity movements have higher-frequency components (and such high-frequency components necessarily arise when fast movements are initiated and terminated), it is possible that the observed dependence of coefficients on movement velocity for other movement types reflects this frequency dependence. For example, if a second-order model is required, then both the position (k) and velocity (r) coefficients change as frequency (and thus maximum velocity for a sinusoidal movement) increases (Fuchs et al. 1988; Sklavos et al. 2005; Stahl and Simpson 1995). For Voigt-element models, the position coefficient would increase in these circumstances, since as frequency increases the elements with long TCs are stretched less, effectively increasing overall system stiffness and thus eye-position sensitivity.

However, in Sylvestre and Cullen's study the position sensitivity decreased with velocity (cf. Fig. 10), suggesting a nonlinear relation between firing rate and eye movement, rather than a mischaracterized linear relation. The fact that a similar position sensitivity decrease can also be seen in the stimulation data (Fig. 10) raises the possibility that the nonlinear effects of firing frequency on muscle force (Fuchs and Luschei 1971) might contribute to the nonlinear relationship described by Sylvestre and Cullen. For the stimulation data, position sensitivity k depends on both the mechanical stiffness of the plant and the conversion of firing rate into muscle force (e.g., Fig. 1). The striking comparison illustrated in Fig. 7 suggests the potential importance of the latter factor. The sigmoidal relation between asymptotic muscle force and stimulation frequency means that at low stimulation frequencies a large increase in stimulation frequency secures only a modest change in position—i.e., the system has a high eye-position sensitivity. As the stimulation frequency moves higher into the linear part of the sigmoid, the eye-position sensitivity of the system decreases. Similarly, the fact the force rises more rapidly as stimulation frequency increases corresponds to the system having a reduced eye-velocity sensitivity (i.e., to a decline in the value of r). Calculating the quantitative contributions of these factors to the single-unit nonlinearities is complicated by the fact that, because of recruitment, natural eye-movement commands cause motoneurons to fire over a range of frequencies.

A detailed distributed model of the ocular motor units may be helpful for this purpose (see next section). It would also be helpful for assessing the impact of other nonlinearities, such as 1) those related to the antagonist muscle, a factor considered in detail by Sylvestre and Cullen (1999); 2) the effects of realistic burst-tonic firing profiles in the motoneurons (Goldberg et al. 1998; Shall et al. 1996); 3) the presence of interactions between motor units caused by interconnections of muscle fibers (Shall et al. 2003); and 4) the mechanical properties of the motor units that are recruited at any given time during the movement (Shall and Goldberg 1992).

Implications for eye-movement control

The present results suggest there are circumstances in which the control signals for eye movements deal with an approximately linear plant. In alert animals, when muscle activation is held constant, the plant appears close to linear with invariant parameters. Thus small changes in muscle activation (which would correspond to movements of small amplitude and velocity) could in principle be produced by simple changes in oculomotor commands.

However, for faster movements, the substantial stimulation-frequency–related nonlinearities present in the data point to the difficulties in using nonlinear motor units for control. In general terms it should be possible to use recruitment to help with this problem, since having units fire over a range of frequencies might act to smooth out the various stimulation-frequency–related nonlinearities. Such a strategy appears to be used in a much simpler system, i.e., control of the nictitating membrane by the accessory abducens nucleus in rabbit eyeblink conditioning (Lepora et al. 2007; Mavritsaki et al. 2007), and a variety of evidence suggests that “plant simplification” (i.e., creating a virtual plant that is easy to control) may be used for skeletal muscle (Mussa-Ivaldi et al. 1994; Nichols and Houk 1976) and for the control of eye movements in three dimensions (Angelaki and Hess 2004; Demer 2006; Klier et al. 2006; Porrill et al. 2000). At present, distributed models have been used to examine the possible control of eye position (Dean 1996; Dean et al. 1999; Hazel et al. 2002), but only in a preliminary manner for actual eye movements (Hazel et al. 2002; Ling et al. 2007). Further development of such models is likely to be helpful in understanding how the oculomotor system deals with the nonlinear behavior of individual motor units.

Conclusions

Analysis of the eye movements induced by electrical stimulation of the primate abducens nucleus suggests that, when muscle activation is held constant, the behavior of the oculomotor plant can be approximated by a linear model, corresponding to Voigt elements in series, with properties independent of initial eye position. In contrast, when muscle activation changes strong frequency-dependent nonlinearities appear, very similar to those observed for force production by the lateral rectus muscle. It is likely that these nonlinearities contribute to previously described nonlinear relations between eye-movement parameters and single-unit firing patterns in the abducens nucleus. How these nonlinearities might be mitigated by, for example, recruitment to make eye-movement control simpler is an important topic for further work.

GRANTS

This research was supported by Engineering and Physical Sciences Research Council Novel Computation Initiative Grant GR/T10602/01, Biology and Biotechnology Research Council Grant 50/E13177, a Wellcome VIP award to S. R. Anderson, and National Eye Institute Grants EY-001189 and EY-015485.

APPENDIX

The model of oculomotor plant dynamics used for modeling the effects of stimulation duration at 400 Hz had two parts, corresponding to force production by the lateral rectus muscle and plant mechanics (methods).

The model of force production was identified from data extracted from Fuchs and Luschei (1971): isometric force production in response to stimulation at a frequency of 400 Hz (see methods and results). The identified force production transfer function was

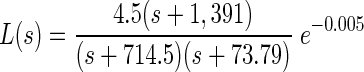(A1)

where the input to L(s) is firing rate in Hertz and the output is force in grams.

The model of oculomotor plant mechanics was identified from eye-position data recorded from subject A in conjunction with L(s), defined earlier (see methods and results). The identified mechanics transfer function was

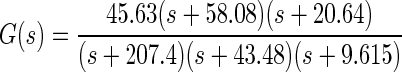(A2)

where the input to G(s) is force in grams and the output is eye position in degrees. The full oculomotor plant model P(s) is given by P(s) = L(s)G(s), where the input is firing rate in Hertz and the output is eye position in degrees. The poles of the plant correspond to TCs of 4.8, 23, and 104 ms.