Abstract
Integrated diffusion tensor-T2 measurements were made on normal and edematous rat muscle, and the data were fitted with one- and two-compartment models, respectively. Edematous muscle exhibited a short-lived component (T2 = 28 ± 6 ms) with diffusion characteristics similar to that of normal muscle and a long-lived component (T2 = 96 ± 27 ms) with greater mean apparent diffusion coefficient (ADC) and lower fractional anisotropy (FA). With this two-component description of diffusion and relaxation, values of ADC and FA estimated with a conventional pulsed-gradient spin echo sequence will depend on the echo time, relative fraction of short- and long-lived water signals, as well as the intrinsic ADC and FA values within the tissue. Based on the relative differences in water diffusion properties between long-lived and short-lived water signals, as well as the similarities between the short-lived component and normal tissue, it is postulated that these two signal components are largely reflective of intra- and extra-cellular water.
Keywords: DTI, muscle, injury, edema, multiexponential T2, ADC, FA
INTRODUCTION
Diffusion tensor imaging (DTI) is an established tool for studying microstructure in neural tissue and, in recent years, has been used to study structure in normal and injured skeletal muscle (1–8). DTI studies of skeletal muscle injury due to ischemia (5,8) and trauma (7) have shown decreased measures of fractional anisotropy (FA) and increased measures of the mean apparent diffusion coefficient (ADC) (i.e., 1/3 the trace of the diffusion tensor). These changes in FA and ADC are consistent with cellular damage and inflammation resulting in a less ordered and less restricted tissue. However, not all muscle insults result in increased ADC and decreased FA. In contrast to ischemic and traumatic injury, muscle atrophy, resulting from denervation, was shown to cause a significant increase in FA and no significant change to ADC (6).
While past studies have related DTI indices to injured muscle, more specific micro-anatomical details are unclear. Galbán et al. proposed that the second and third eigenvalues of the diffusion tensor correspond to inter- and intracellular water, respectively, diffusing perpendicular to the long axis of the of normal muscle fibers (4), but how this relates to the microanatomy of injured muscle remains unclear. In an attempt to establish a relationship between diffusion and the microanatomy of edematous muscle, independent multi-exponential decompositions of T2 and diffusion measurements were investigated as a means to relate T2s and ADCs to specific anatomical compartments (9). The results, much like similar studies in neural tissue (10,11), indicated that while multi-exponential T2 may resolve signal from different anatomical compartments, similar measures of diffusion do not.
Although direct measurements of compartmentally specific ADC of water in muscle tissue were unsuccessful, evidence from studies of neural tissue suggests such observations are possible. Several investigators have made compartmentally-specific ADC measurements of water in neural tissues by integrating diffusion- and T2-weighting (12–14). A similar approach in muscle may be possible. Therefore, the goal of this study was to use an integrated diffusion- and T2-weighting approach to probe the compartmental basis of water diffusion in edematous muscle.
MATERIALS AND METHODS
Animal Preparation
Eight male Sprague-Dawley rats (327–435 g, mean 398 g) were each given one 0.1 mL subcutaneous injection of a 1% w/v λ-carrageenan (Sigma Aldrich) saline solution into the lower hind leg to induce edema. Prior to imaging, 6 – 9 hours was allowed to pass for the inflammation to reach a plateau (15–17). Past studies have show that afflicted muscle fibers will show clear signs of muscle damage after this period (18,19). For imaging, rats were anesthetized with isoflurane (2.5 % induction, 1 – 2 % maintenance), and throughout imaging body temperature was maintained near 37 °C with a warm water blanket and warm air. All procedures were approved by the Vanderbilt University Institutional Animal Care and Use Committee (IACUC).
MRI
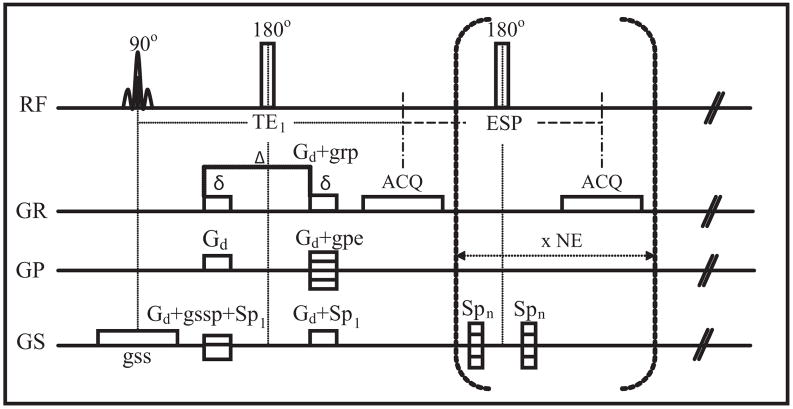
Imaging was performed at 300 MHz on a 7 T 16 cm horizontal bore magnet, equipped with a Varian Inova console (Varian Inc, Palo Alto, CA). The injected leg and a small MnCl2-doped water phantom were positioned into a 25 mm diameter Litz coil (Doty Scientific, Columbia, SC) for RF transmission and signal reception. Edematous muscle was visualized using a multi-slice fast spin echo acquisition, from which a central 2-mm thick axial slice was chosen for subsequent measurements. Integrated diffusion-T2 characteristics of this slice were studied using the single-slice diffusion-weighted, multi-echo pulse sequence shown in Fig. 1, which is similar to sequence used by one author in a previous study (14). The first echo time was TE1 = 21 ms, subsequent echo spacing (ESP) = 10 ms, number of echoes (NE) = 38, and TR = 2 sec. Spoiler gradients of modulated amplitude surrounded each non-selective composite refocusing pulse to minimize signal from unwanted coherence pathways (20). Images were encoded with 64 × 64 samples over a 35 × 35 mm2 field of view. Image acquisition was repeated 13 times: 6 non-collinear directions (1. X, Y; 2. Y, Z; 3. X, Z; 4. X, -Y; 5. -Y, Z; 6. -X, Z), each repeated with opposite polarity diffusion gradients (to cancel background and imaging gradient cross terms (21)), and one acquisition without diffusion weighting. Diffusion weighting gradients were ≈ 10.8 G/cm (in each applied direction), 6 ms in duration and separated by 12 ms, resulting in a b-value of ≈ 600 s/mm2. Two excitations were averaged resulting in a total acquisition time for the multi-echo DTI measurement of approximately 1 hour. Immediately following image acquisition, the water phantom temperature was measured.
FIG. 1.
Schematic presentation of the diffusion-weighted multi-spin-echo imaging sequence implemented for this study. Gd = diffusion gradient, grp = read gradient preparation, gpe = stepped phase encode gradient, gss = slice select gradient, gssp = slice refocusing gradient, Sp1 = spoiler gradient for first echo, Spn = spoiler gradient for nth echo, TE1 = first echo time, ESP= echo spacing, ACQ = acquisition, NE = number of echoes, δ= diffusion gradient duration, and Δ= time between onset of the two diffusion gradients. RF phases for excitation, refocusing and the receiver were ± x, + y, ±x for the two averaged excitations.
Data Analysis
The square root of the product of images gathered with opposite polarity diffusion-weighting gradients was computed; this eliminated the effect of background gradients on the diffusion measurements (21) and reduced the size of image set to 38 × 7, for each animal. The water phantom temperature (see footnote below Table 1) was used to determine the correct diffusion coefficient for water, which was then used to estimate the correct b-value for each diffusion weighting direction. Regions of interest (ROI) of normal muscle, edematous muscle, and the water phantom were manually defined and mean echo magnitudes were extracted. Care was taken in choosing both normal and edematous muscle ROIs to avoid voxels from subcutaneous or inter-muscular fat or edema. To avoid bias from the noise floor or artifacts, echo trains were truncated at the point where the echo magnitude dropped below 3×the standard deviation of the background signal, as measured adjacent to the sample (where ghosting effects were present). Also, some late echoes showing signs of stimulated echo contamination (see Fig. 3, last four echoes of edematous water ROI), were also removed.
Table 1.
Fitted parameters for normal and edematous muscle
| ρ | T2 (ms) | λ1(μm/ms) | λ2(μm/ms) | λ3(μm/ms) | ADC (μm/ms) | FA | |
|---|---|---|---|---|---|---|---|
| Normal | 1.0 | 23.7 ± 1.0 | 1.73 ± 0.08 | 1.25 ± 0.05 | 1.14 ± 0.05 | 1.37 ± 0.04 | 0.22 ± 0.03 |
| EdemaA | 0.63 ± 0.10 | 27.8 ± 5.5* | 1.58 ± 0.14 | 1.25 ± 0.10 | 1.13 ± 0.11 | 1.32 ± 0.11 | 0.18 ± 0.04 |
| EdemaB | 0.37 ± 0.10 | 95.7 ± 27.3 | 2.23 ± 0.22 | 1.92 ± 0.28 | 1.81 ± 0.25 | 1.98 ± 0.24 | 0.11 ± 0.04 |
| Phantom | 1.0 | 129 ± 5.0 | 2.60 ± 0.05 | 2.57 ± 0.05 | 2.55 ± 0.05 | 2.57 ± 0.05 | 0.01 ± 0.005 |
Mean ± SD across 8 animals studied. Spin density values, ρ, are given as fractional values for each ROI.
p = 0.077.
Mean water phantom temperature = 29.75 °C, range 29.0 – 30.5 °C.
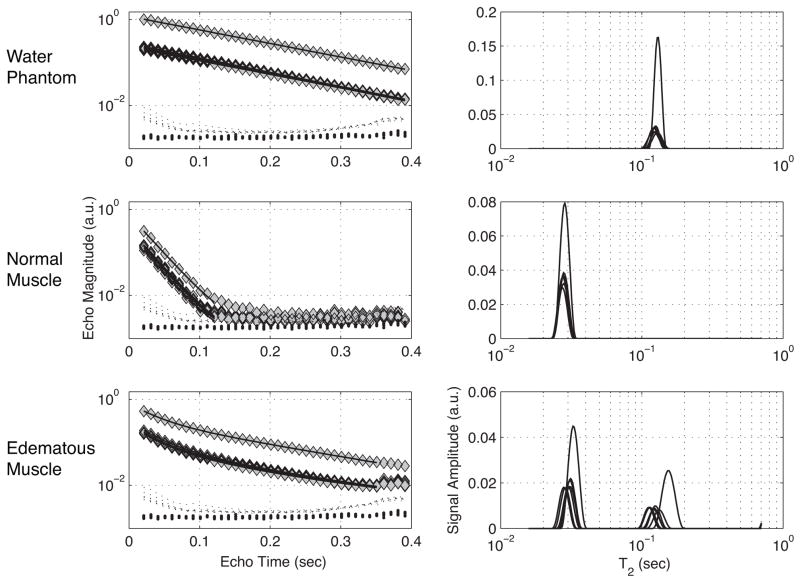
FIG. 3.
On the left are echo magnitudes from water phantom (top), normal muscle (middle) and edematous muscle (bottom), with and without diffusion weightings. On the right are corresponding T2 spectra fitted from echo magnitudes shown on the left. For both echo magnitudes and T2 spectra, the signal with the largest amplitude is that of the non-diffusion weighted measure, while the 7 diffusion-weighted measures largely overlap with a lower amplitude. The predicted echo magnitudes from these T2 spectral fits are plotted as solid lines on in the frames on the left. Also shown in these frames are background signal measures from regions in the corner (large dots) and adjacent to the sample (small dots).
For each animal, each of the 7 sets of echo magnitudes were transformed into a T2 spectrum by fitting the echo magnitudes with a broad range of decaying exponential functions (22). The spectra were then used to determine the number (one or two) of T2 components present for each ROI. The full multi-echo DTI data were then modeled either as a single compartment (Eq. [1a]), or as two compartments in slow exchange (Eq. [1b]); each compartment with a unique scalar signal amplitude, ρa or ρb, transverse relaxation time, T2,a or T2,b, and apparent diffusion coefficient, Da or Db,
| [1a] |
| [1b] |
In this equation, Si(te,b) are the echo magnitudes at each echo time, te, and b-value, b, for the ith diffusion-weighting direction (listed in MRI sub section, above), and ε is a constant signal offset term. For each animal and each ROI, the entire set of echo magnitudes was fitted unconstrained with either [1a] or [1b] nonlinearly using a Levenberg-Marquardt algorithm (implemented with the lsqcurvefit function in MATLAB (Natick, MA)). Numerical estimates of the function jacobian and the residuals to the fit were used (implemented with nlparci function in MATLAB) to estimate the uncertainty in the fitted parameters. Fitting was repeated 50 times with randomized initial conditions to ensure the global minima were found.
Diffusion tensors, D, were then constructed from linear combinations of the fitted Di values according to equations [2] and [3]:
| [2] |
| [3] |
Where i ∈ [1,2,3,4,5,6] and each number corresponds to one of the 6 previously defined non-collinear directions. Each tensor was then diagonalized, resulting in three eigenvalues, λ1, λ2, λ3 and corresponding eigenvectors. From these eigenvalues the mean apparent diffusion coefficient, ADC, and fractional anisotropy, FA, were computed as in Eqs [4] and [5]:
| [4] |
| [5] |
RESULTS
FSE images revealed edematous muscle after the λ-carrageenan injection. Figure 2 shows the differences in appearance between the normal musculature, on the left, and edematous musculature, on the right, marked with an example ROI. Typical signal from a normal muscle, edematous muscle, and the water phantom ROIs, with and without diffusion weightings are shown in Fig. 3 along with their corresponding T2 spectra. Also shown are mean background signal magnitudes from a region adjacent to the sample (includes effects of ghosting) and from the corner of the image (only thermal noise). The spectra reveal two important observations: 1) normal muscle signal was essentially mono-exponential in T2 while edematous muscle signal was clearly non-mono-exponential, and 2) diffusion weighting contrast was not the same in each T2 component of edematous muscle. It is also worth noting that the T2 components shifted in the T2 domain after diffusion weighting. This is a consequence of the T2 spectral fits, which imposes no constraint on the number or location of T2 spectral components. Thus, T2 spectra are not appropriate for fitting data to Eq. [1a] or Eq. [1b], but they do serve well to identify the number of spectral components present.
FIG. 2.
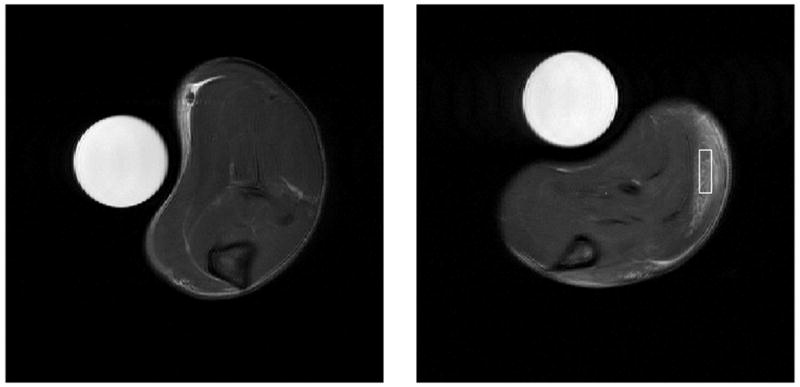
(left) FSE image of normal muscle, without λ-carrageenan injection, is shown for comparison. (right) FSE image 6 – 9 hours post λ-carrageenan injection. Note that the increased signal intensity due to edema in the area marked with an example ROI is clearly distinguishable.
Over all 8 animals studied, an average of > 99 % of the normal muscle signal could be attributed signal with T2 < 50 ms. In contrast, in all 8 animals, the edematous muscle signal had two T2 spectral components, with average relative amplitudes of ≈ 60 % (T2 < 50 ms, labeled EdemaA) and ≈ 40 % (T2 > 50 ms, labeled EdemaB). Therefore, water phantom data and normal muscle data were fitted with a single-compartment model (Eq. [1a]) and edematous muscle data were fitted with a two-compartment model (Eq. [1b]). Fitted parameters are summarized in Table 1, which shows the mean ± standard deviation (SD) across all 8 animals for each parameter. Not shown is ε, which had an absolute value of < 0.25 % of the fitted spin density for all animals and ROIs. Note that for all fitted parameters, inter-animal variance exceeded the numerically estimated variance, therefore, SD is given across animals in Table 1. Values in bold type were statistically different than the corresponding measures in normal muscle (p < 0.05, as determined by a two-tailed t-test, without the assumption of equal variances). Signal to noise ratio (SNR) of the diffusion-weighted multi-echo images was defined as the maximum non-diffusion weighted muscle signal divided by the standard deviation of the background thermal noise, measured in the corner of the image and corrected for the Rayleigh bias. Across the 8 animals, the SNR ranged from 590 to 793, mean = 674. At this high SNR, artifact in the form of small even-odd echo amplitude variation and/or ghosting was the primary contribution to the residuals of the non-linear fits (see Fig. 3). However, the root mean square amplitude of the fit residuals was < 0.3% in all cases, so the fit qualities were considered good. Also, the non-linear fitting converged to the same minimal mean square error solution in approximately 50% of the 50 repeated fitting procedures for each animal, indicating the fits were relatively insensitive to the randomized initial parameter values.
It is also worth mentioning that several data analysis strategies were investigated, and all produced similar results. For example, the specific criteria for including or excluding late echoes on the basis of contamination also had little effect on the final results. Likewise, rather than globally fitting all parameters, individual mono- or bi-exponential fits of signal amplitudes and T2 values followed by diffusion coefficient calculation from the fitting component amplitudes was also implemented. This approach yielded nearly identical results to those presented in Table 1, if the T2s were constrained to the T2s measured in the absence of diffusion weighting. Without this constraint, which is implicit in Eq. 1b and the global fitting procedure that was used, results remained broadly similar, but with greater variance of the fitted parameters for the edematous muscle.
DISCUSSION
Observations of T2 and water diffusion in normal muscle compare well with previously reports. Rat skeletal muscle T2 was previously found to be 22.8 ± 1.1 ms at 7 T (23), as compared to 23.7 ± 1.0 in this study. In human lower limb, mean skeletal muscle ADC values were reported in the range of 1.31 – 1.41 μm2/ms and mean FAs in the range of 0.20 – 0.23 for b = 500 s/mm2 (7). Similarly, in rat skeletal muscle, Damon et al. reported a mean ADC = 1.22 μm2/ms and a mean FA = 0.28 for b = 400 s/mm2 (2). Results herein, ADC = 1.37 ± 0.04 μm2/ms and FA = 0.22 ±0.03, agree well with both studies, which suggests that the λ-carrageenan injection had insignificant effect on the muscle within the normal muscle ROIs. One difference in our findings as compared to some other studies is that normal muscle was largely mono-exponential in T2. Isolated muscle has long been known to exhibit non-monoexponential transverse relaxation ((24,25), and many subsequent references), although relatively few published accounts of multi-exponential T2 exist from in vivo studies of mammalian muscle (26,27,9). The first such observation was made using a single-voxel sequence with rapid spin refocusing and extremely high SNR (27), which may be capable of revealing more T2 spectral information than the multi-echo imaging sequence used herein. Ababneh et al. found a long-lived T2 component of 6 % amplitude in rat hind paw at 4.7 T (9), although a previous study from some of the same authors found normal muscle to be mono-exponential in T2 (28). Noseworthy et al. found a long-lived component of ≈ 10 % amplitude in human leg at 1.5 T, which they attributed to intra-vascular signal (26). Such a signal might not be visible at 7 T due to the reduction in venous blood T2 at high field. In short, the absence of a long-lived T2 signal herein is not necessarily inconsistent with relevant literature.
In edematous muscle, the data were fitted well with the two-compartment model (Eq. [1b]), which presented a short-lived component (mean T2 ≈ 28 ms, slightly longer than that of normal muscle water), and a long-lived component (mean T2 ≈ 96 ms). These T2s are similar but consistently shorter than those reported by Ababneh et al. (9), possibly due to the 50 % higher field strength used in this study. The short-lived component exhibits a similar ADC value to normal muscle and a statistically significantly lower FA. Conversely, the long-lived T2 component exhibits a significantly greater ADC and ≈ 50% lower FA. Based on the similarity of the normal muscle and the short-lived edematous component, and the nature of the observed differences between the normal muscle and the long-lived edematous component, the assignment of these two edematous muscle signal components to the intracellular space of normal myofibers (short-lived component) and the extracellular space and/or space of necrotic myofibers is plausible.
Consider the effect of edema and myofiber lysis on the extracellular volume. Measurements of water dynamics in rat thigh skeletal muscle have reported intra- and extracellular proton densities of 0.89 and 0.11, respectively, and an average intra-cellular lifetime of ≈ 1.1 sec (29). Based on these numbers, the average extracellular life is ≈ 136 ms, indicating a small but significant effect of exchange on T2 measurements given observed T2 in the range of 25 – 200 ms. In edematous muscle, edema and necrosis of myofibers will cause a swelling of the extracellular volume and an approximately proportional increase in the average lifetime and decrease in the transverse relaxation rate. Both changes will drive the system toward the slow exchange limit. If we model two compartments with volume fractions and average intracellular lifetime from above and each with intrinsic T2 = 28 ms, then swelling of the extracellular volume by a factor of 4x results in intrinsic extracellular T2 ≈ 112 ms and average extracellular lifetime ≈ 544 ms. Using these values and solving the Bloch-McConnell equations (30) yields two T2 components with signal fractions and T2s of 62%, 27.3 ms and 38%, 93.4 ms, which closely resemble the values observed in edematous muscle (63%, 27.8 ms and 37%, 95.6 ms) in this study. Naturally, any number of combinations of intrinsic relaxation rates and extra-cellular volume fraction increases can yield similar results, but this example provides a plausible model that supports an interpretation of the two observed signal components as closely representing intra- and extracellular compartments.
The interpretation of the data in the previous paragraph does not account for the T2 differences between normal muscle and the short-lived T2 component in edematous muscle. One possibility is that normal extracellular T2 is actually shorter than intracellular T2, contributing to a reduced apparent T2 in normal muscle but not the extent that the signal appears bi-exponential. This seems unlikely, given the high intracellular protein/macromolecular content of muscle; however, studies in nerve have indicated extra- axonal water to have a significantly shorter T2 than axoplasmic water (13,31). Another possibility is that the edema also resulted in intracellular swelling, which increased the T2 by dilution. In order to increase T2 from 24 ms to 28 ms by simple dilution, the muscle cells would need to swell by ≈ 17%, which seems plausible (note that the area of a circle is 4/pi = 1.27 times greater than the area of a square of equal perimeter). It is also possible that metabolic changes associated with the λ-carrageenan response have an effect. There are several studies that show changes in metabolism that result from muscle injury (32–35) and these changes may have resulted in and/or contributed to an increase in intracellular T2. For example, intracellular lactate accumulation has been directly related to the increase of the observed T2 in fatigued rat skeletal muscles (36).
The simple two-compartment interpretation of the two T2 components allows for compartmental observations of water diffusion. The elevated ADC and decreased FA in the long-lived component, compared to other muscle signal, are reflective of a relatively unrestricted and less ordered space. These are consistent with a space that results from a combination of swelling and muscle fiber necrosis. If the short-lived edematous muscle signal is then ascribed to water from remaining uninjured muscle fibers within the edematous muscle ROI, then one can postulate that it is reflective of the intracellular water contribution to the normal muscle signal. Assuming the normal muscle water diffusion characteristics are simply a weighted average of diffusion rates from 89% intra- and 11% extracellular spaces, one can estimate the primary eigenvalue of the normal muscle extracellular water diffusion tensor to be λ1 = (1.73 μm2/ms - (0.89)(1.58 μm2/ms))/0.11 = 2.94 μm2/ms, which is approximately the diffusion coefficient of unrestricted water at 37 °C. This interpretation also implies that approximately 22 % of the FA observed in normal muscle results from extra-cellular water contribution, despite this water accounting for only about 11 % of the total water signal.
In the context of assessing muscle damage, this work demonstrates that a conventional diffusion tensor measurement in injured muscle reflects a muted change in ADC and FA compared to normal muscle because the changes primarily occur in only some of the observed water signal (i.e., the long-lived T2 component). Regardless of the anatomical interpretation of the two observed signal components, standard ADC and FA measurements will depend on the echo time. Based on the values in Table 1, at TE = 20 ms, a conventional DTI measurement in edematous muscle will yield ADC = 1.65 μm2/ms, and FA = 0.14, and these measurements will each change by approximately 18 % between TE = 20 and 100 ms. The magnitude of these changes will depend not only on the ADC and FA values of the long-lived water, but also on the relative fraction of long-lived water. An injury that results in a larger long-lived water component will exhibit a greater sensitivity in ADC and FA to echo time. Similarly, caution should be employed when interpreting conventional ADC or FA measures because they will change due to changes in the relative fraction of long-lived water, as well as intrinsic changes of either metric in either water compartment.
Given the dependence on echo time, when imaging purely for the purpose of contrast, it can be shown, using values in Table 1, that the contrast-to-noise ratio between normal and edematous muscle ADCs is still maximal at minimal echo time, despite an increasing edematous muscle ADC with echo time. This is because T2 contrast dominates over diffusion contrast. In fact, the maximum contrast-to-noise ratio between normal and edematous muscle in a spin echo acquisition, with isotropic diffusion weighting, maximizes with TE = 35 ms and b = 0. Furthermore, it stands to reason that, given the correspondence of the short- and long-lived T2 signals to uninjured and extracellular/necrotic fiber regions, respectively, multi-exponential T2 alone might measure the extent of muscle fiber damage in injury. Perhaps with the incorporation of diffusion weighting to a multi-echo measurement, as done herein, it may be possible to discern the biophysical basis more subtle grades of injury though the unique changes in the diffusion tensor of each T2 component. For example, Heesmskerk et al. found that in muscle recovering from arterial ligation induced ischemia, diffusion characteristics normalized sooner than T2 (8). One can postulate that such tissue includes a short-lived T2 component with low ADC and high FA derived from regenerating muscle fibers and a long-lived T2 component with high ADC and low FA derived from necrotic regions and edema. In such a case, depending on the particular compartment sizes and parameter values, a conventional ADC measure might average out to be near that of normal muscle, while a mono-exponential T2 measurement might still be high compared to that of normal muscle.
In addition to the potential application of integrated DTI-T2 measurements to experimental models of muscle injury or disease, this methodology also has potential for clinical investigations. Although the method employed in this study took an hour of data acquisition and is only suitable for single slice measurements, clinical DTI typically requires echo-planar imaging (EPI) to avoid inter-scan motion artifacts. Repeating an EPI DTI study 16 or 32 times with stepped echo times and with multiple slices only takes a few minutes, making it potentially feasible for clinical studies. This approach may not incorporate multiple spin refocusing; however, resolution of the two signal components would likely be effective given the large difference in the observed T2s.
CONCLUSIONS
Edematous muscle, resulting from λ-carrageenan injection in rat hind limb, exhibited two distinct signal components with unique T2 and diffusion tensor characteristics. The exact origin of these two signals is not clear, but based on the observed T2s, FAs, and ADCs, it is postulated that they are reflective of intra- and extra-cellular water. These observations indicate that echo time is an important parameter in diffusion measurements of injured muscle and that it may be possible to use integrated measures of diffusion and T2 to better understand the micro-anatomical basis of damage in skeletal muscle.
Acknowledgments
NIH #EB001744, NSF #0448915
The authors thank Jarrod True for support with animals and Dr. Bruce Damon and Dr. Anneriet Heemskerk for helpful conversations. MDD is supported by National Science Foundation Career Award 0448915.
List of Abbreviations
- DTI
diffusion tensor imaging
- ADC
apparent diffusion coefficient
- FA
fractional anisotropy
- NE
number of echoes
- ESP
echo spacing
- ROI
region of interest
- SD
standard deviation
- SNR
signal to noise ratio
- EPI
echo planar imaging
Footnotes
This work was presented, in part, at the International Society of Magnetic Resonance in Medicine Fourteenth Scientific Meeting (Berlin) 2007.
References
- 1.Van Donkelaar C, Kretzers L, Bovendeerd P, Lataster L, Nicolay K, Janssen J, Drost M. Diffusion tensor imaging in biomechanical studies of skeletal muscle function. Journal of Anatomy. 1999;194:79–88. doi: 10.1046/j.1469-7580.1999.19410079.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Damon B, Ding Z, Anderson A, Freyer A, Gore J. Validation of diffusion tensor MRI-based muscle fiber tracking. Magnetic Resonance in Medicine. 2002;48(1):97–104. doi: 10.1002/mrm.10198. [DOI] [PubMed] [Google Scholar]
- 3.Sinha U, Yao L. In vivo diffusion tensor imaging of human calf muscle. JOURNAL OF MAGNETIC RESONANCE IMAGING. 2002;15(1):87–95. doi: 10.1002/jmri.10035. [DOI] [PubMed] [Google Scholar]
- 4.Galban C, Maderwald S, Uffmann K, de Greiff A, Ladd M. Diffusive sensitivity to muscle architecture: a magnetic resonance diffusion tensor imaging study of the human calf. European Journal of Applied Physiology. 2004;93(3):253–262. doi: 10.1007/s00421-004-1186-2. [DOI] [PubMed] [Google Scholar]
- 5.Heemskerk A, Drost M, van Bochove G, van Oosterhout M, Nicolay K, Strijkers G. DTI-based assessment of ischemia-reperfusion in mouse skeletal muscle. Magnetic Resonance in Medicine. 2006;56(2):272–281. doi: 10.1002/mrm.20953. [DOI] [PubMed] [Google Scholar]
- 6.Saotome T, Sekino M, Eto F, Ueno S. Evaluation of diffusional anisotropy and microscopic structure in skeletal muscles using magnetic resonance. Magnetic Resonance Imaging. 2006;24(1):19–25. doi: 10.1016/j.mri.2005.09.009. [DOI] [PubMed] [Google Scholar]
- 7.Zaraiskaya T, Kumbhare D, Noseworthy M. Diffusion tensor imaging in evaluation of human skeletal muscle injury. Journal of Magnetic Resonance Imaging. 2006;24(2):402–408. doi: 10.1002/jmri.20651. [DOI] [PubMed] [Google Scholar]
- 8.Heemskerk A, Strijkers G, Drost M, van Bochove G, Nicolay K. Skeletal muscle degeneration and regeneration after femoral artery ligation in mice: Monitoring with diffusion MR imaging. Radiology. 2007;243(2):413–421. doi: 10.1148/radiol.2432060491. [DOI] [PubMed] [Google Scholar]
- 9.Ababneh Z, Beloeil H, Berde C, Gambarota G, Maier S, Mulkern R. Biexponential parameterization of diffusion and T-2 relaxation decay curves in a rat muscle edema model: Decay curve components and water compartments. Magnetic Resonance in Medicine. 2005;54(3):524–531. doi: 10.1002/mrm.20610. [DOI] [PubMed] [Google Scholar]
- 10.Niendorf T, Dijkhuizen R, Norris D, Campagne M, Nicolay K. Biexponential diffusion attenuation in various states of brain tissue: Implications for diffusion-weighted imaging. MAGNETIC RESONANCE IN MEDICINE. 1996;36(6):847–857. doi: 10.1002/mrm.1910360607. [DOI] [PubMed] [Google Scholar]
- 11.Mulkern R, Gudbjartsson H, Westin C, Zengingonul H, Gartner W, Guttmann C, Robertson R, Kyriakos W, Schwartz R, Holtzman D, Jolesz F, Maier S. Multi-component apparent diffusion coefficients in human brain. NMR in Biomedicine. 1999;12(1):51–62. doi: 10.1002/(sici)1099-1492(199902)12:1<51::aid-nbm546>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- 12.vanDusschoten D, Moonen C, deJager P, VanAs H. Unraveling diffusion constants in biological tissue by combining Carr-Purcell-Meiboom-Gill imaging and pulsed field gradient NMR. Magnetic Resonance in Medicine. 1996;36(6):907–913. doi: 10.1002/mrm.1910360613. [DOI] [PubMed] [Google Scholar]
- 13.Peled S, Cory D, Raymond S, Kirschner D, Jolesz F. Water diffusion, T-2, and compartmentation in frog sciatic nerve. Magnetic Resonance in Medicine. 1999;42(5):911–918. doi: 10.1002/(sici)1522-2594(199911)42:5<911::aid-mrm11>3.0.co;2-j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Does M, Gore J. Compartmental study of diffusion and relaxation measured in vivo in normal and ischemic rat brain and trigeminal nerve. Magnetic Resonance in Medicine. 2000;43(6):837–844. doi: 10.1002/1522-2594(200006)43:6<837::aid-mrm9>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 15.DiRosa M, Giroud J, Willough D. Studies of Mediators of Acute Inflammatory Response Inuduced in Rats in Different Sites by Carrageenan and Turpentine. Journal of Pathology. 1971;104(1):15. doi: 10.1002/path.1711040103. [DOI] [PubMed] [Google Scholar]
- 16.Doherty N, Robinson B. Inflammatory Response to Carrageenan. Journal of Pharmacy and Pharmacology. 1975;27(9):701–703. doi: 10.1111/j.2042-7158.1975.tb09537.x. [DOI] [PubMed] [Google Scholar]
- 17.Suleyman H, Buyukokuroglu M. The effects of newly synthesized pyrazole derivatives on formaldehyde-, carrageenan-, and dextran-induced acute paw edema in rats. Biologcial & Pharmaceutical Bulletin. 2001;24(10):1133–1136. doi: 10.1248/bpb.24.1133. [DOI] [PubMed] [Google Scholar]
- 18.Nantel F, Denis D, Gordon R, Northey A, Cirino M, Metters K, Chan C. Distribution and regulation of cyclooxygenase-2 in carrageenan-induced inflammation. British Journal of Pharmacology. 1999;128(4):853–859. doi: 10.1038/sj.bjp.0702866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Radhakrishnan R, Moore S, Sluka K. Unilateral carrageenan injection into muscle or joint induces chronic bilateral hyperalgesia in rats. Pain. 2003;104(3):567–577. doi: 10.1016/s0304-3959(03)00114-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Poon CS, Henkelman RM. Practical T2 quantitation for clinical applications. J Magn Reson Imaging. 1992;2(5):541–553. doi: 10.1002/jmri.1880020512. [DOI] [PubMed] [Google Scholar]
- 21.Gullmar D, Haueisen J, Reichenbach J. Analysis of b-value calculations in diffusion weighted and diffusion tensor imaging. Concepts in Magnetic Resonance Part A. 2005;25A(1):53–66. [Google Scholar]
- 22.Whittal K, Mackay A. Quantitative Interpretation of NMR Relaxation Data. Journal of Magnetic Resonance. 1989;84(1):134–152. [Google Scholar]
- 23.Cremillieux Y, Ding S, Dunn J. High-resolution in vivo measurements of transverse relaxation times in rats at 7 Tesla. Magnetic Resonance in Medicine. 1998;39(2):285–290. doi: 10.1002/mrm.1910390216. [DOI] [PubMed] [Google Scholar]
- 24.Hazlewood C, Chang D, Nichols B, Woessner D. Nuclear Magnetic-Resonance Transverse Relaxation-Times of Water Protons in Skeletal-Muscle. Biophysical Journal. 1974;14(8):583–606. doi: 10.1016/S0006-3495(74)85937-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cole W, LeBlanc A, Jhingran S. The Origin of Biexponential T2 Relaxation in Muscle Water. Magnetic Resonance in Medicine. 1993;29(1):19–24. doi: 10.1002/mrm.1910290106. [DOI] [PubMed] [Google Scholar]
- 26.Noseworthy M, Kim J, Stainsby J, Stanisz G, Wright G. Tracking oxygen effects on MR signal in blood and skeletal muscle during hyperoxia exposure. Journal of Magnetic Resonance Imaging. 1999;9(6):814–820. doi: 10.1002/(sici)1522-2586(199906)9:6<814::aid-jmri8>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- 27.Saab G, Thompson R, Marsh G. Multicomponent T-2 relaxation of in vivo skeletal muscle. Magnetic Resonance in Medicine. 1999;42(1):150–157. doi: 10.1002/(sici)1522-2594(199907)42:1<150::aid-mrm20>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- 28.Gambarota G, Cairns B, Berde C, Mulkern R. Osmotic effects on the T-2 relaxation decay of in vivo muscle. Magnetic Resonance in Medicine. 2001;46(3):592–599. doi: 10.1002/mrm.1232. [DOI] [PubMed] [Google Scholar]
- 29.Landis C, Li X, Telang F, Molina P, Palyka I, Vetek G, Springer C. Equilibrium transcytolemmal water-exchange kinetics in skeletal muscle in vivo. Magnetic Resonance in Medicine. 1999;42(3):467–478. doi: 10.1002/(sici)1522-2594(199909)42:3<467::aid-mrm9>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- 30.McConnell H. Reaction Rates by Nuclear Magnetic Resonance. The Journal of Chemical Physics. 1958;28(3):430–431. [Google Scholar]
- 31.Wachowicz K, Snyder R. Assignment of the T-2 components of amphibian peripheral nerve to their microanatomical compartments. Magnetic Resonance in Medicine. 2002;47(2):239–245. doi: 10.1002/mrm.10053. [DOI] [PubMed] [Google Scholar]
- 32.Oconnor J, Scott R, Mellick P, Caldwell M. Perfused Rat Hindlimb Wound Model - Lambda-Carrageebab Induced. American Journal of Physiology. 1982;242(5):R570–R576. doi: 10.1152/ajpregu.1982.242.5.R570. [DOI] [PubMed] [Google Scholar]
- 33.Caldwell M, Shearer J, Morris A, Mastrofrancesco B, Henry W, Albina J. Evidence for Aerobic Glycolysis in Lambda-Carrageenan-Wounded Skeletal-Muscle. Journal of Surgical Research. 1984;37(1):63–68. doi: 10.1016/0022-4804(84)90162-8. [DOI] [PubMed] [Google Scholar]
- 34.Albina J, Shearer J, Mastrofrancesco B, Caldwell M. Amino-Acid-Metabolism After Lambda-Carrageenan Injury to Rat Skeletal-Muscle. American Journal of Physiology. 1986;250(1):E24–E30. doi: 10.1152/ajpendo.1986.250.1.E24. [DOI] [PubMed] [Google Scholar]
- 35.Caldwell M. Local Glutamine-Metabolism in Wounds and Inflammation. Metabolism-Clinical and Experimental. 1989;38(8):34–39. doi: 10.1016/0026-0495(89)90137-6. [DOI] [PubMed] [Google Scholar]
- 36.Damon B, Gregory C, Hall K, Stark H, Gulani V, Dawson M. Intracellular acidification and volume increases explain R-2 decreases in exercising muscle. Magnetic Resonance in Medicine. 2002;47(1):14–23. doi: 10.1002/mrm.10043. [DOI] [PubMed] [Google Scholar]