Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2009 Jun;19(6):1107–1116. doi: 10.1101/gr.087528.108

Global networks of functional coupling in eukaryotes from comprehensive data integration

Andrey Alexeyenko 1, Erik LL Sonnhammer 1,1
PMCID: PMC2694487  PMID: 19246318

Abstract

No single experimental method can discover all connections in the interactome. A computational approach can help by integrating data from multiple, often unrelated, proteomics and genomics pipelines. Reconstructing global networks of functional coupling (FC) faces the challenges of scale and heterogeneity—how to efficiently integrate huge amounts of diverse data from multiple organisms, yet ensuring high accuracy. We developed FunCoup, an optimized Bayesian framework, to resolve these issues. Because interactomes comprise functional coupling of many types, FunCoup annotates network edges with confidence scores in support of different kinds of interactions: physical interaction, protein complex member, metabolic, or signaling link. This capability boosted overall accuracy. On the whole, the constructed framework was comprehensively tested to optimize the overall confidence and ensure seamless, automated incorporation of new data sets of heterogeneous types. Using over 50 data sets in seven organisms and extensively transferring information between orthologs, FunCoup predicted global networks in eight eukaryotes. For the Ciona intestinalis network, only orthologous information was used, and it recovered a significant number of experimental facts. FunCoup predictions were validated on independent cancer mutation data. We show how FunCoup can be used for discovering candidate members of the Parkinson and Alzheimer pathways. Cross-species pathway conservation analysis provided further support to these observations.

The high-throughput functional analysis of genes and proteins is producing vast data resources that, if integrated into interaction networks, will be key to unraveling the function of all genes in an organism (Sonnhammer 2005). While no single data set provides enough confidence and coverage, much experimental evidence from, e.g., protein–protein interactions (PPIs) and mRNA coexpression (MEX) have been integrated into interaction networks in such organisms as Saccharomyces cerevisiae, Caenorhabditis elegans, and Homo sapiens (Jansen et al. 2003; Troyanskaya et al. 2003; Bader et al. 2004; Lee et al. 2004; Li et al. 2004; Beyer et al. 2007). Srinivasan et al. (2006) also used sequence-derived interaction evidence such as correlated evolution/inheritance and chromosomal colocation to integrate interaction networks in 11 microbes.

However, as of today, using data from one organism alone is insufficient to reconstruct its interaction networks completely. It is possible to expand the data pool by transferring functional information between species via homologs (Hahn et al. 2005; von Mering et al. 2005) or orthologs (Matthews et al. 2001; Rhodes et al. 2005; Hulsen et al. 2006; Zhong and Sternberg 2006).

Furthermore, functional coupling (FC) between two proteins can have several guises: direct physical interaction (PI), protein complex members (CM), links in metabolic pathways (ML), or links in regulatory/signaling pathways (SL).

The data integration is thus multidimensional—using multiple evidence types from multiple species for predicting multiple classes of links. This puts high demands on the process, in terms of both computation and automatic parameter optimization for each new data set. It is thus necessary to develop a universal, fast, and sustainable methodology in order to discover functional connections in many eukaryotic organisms at the global scale.

To achieve this, we adopted the naïve Bayesian network framework (NBN) and advanced many procedures for supervised NBN training in order to make it optimally suited for data integration in FC network reconstruction. The innovations concerned significance testing, continuous score discretization, orthologous evidence usage, and phylogenetic profiling. A major challenge was to efficiently use data not originally produced for FC discovery. Particular attention was given to data transfer between species via orthologs—the best way to enrich sparse data sources (Rhodes et al. 2005; Hulsen et al. 2006).

These advancements allowed us to efficiently reconstruct comprehensive FC networks for eight of the most important eukaryotes: human, mouse, rat, fly, worm, yeast, Arabidopsis thaliana, and Ciona intestinalis. For these species, they are the largest reconstructed interactomes to date. For C. intestinalis, we managed to reconstruct a network in absence of any own large-scale data sets, by transferring such information from coupled orthologs only. We here present both the method and the resulting FunCoup database for discovery and analysis of FC in gene networks. To demonstrate the usefulness of network analysis in FunCoup, we applied it to discover new candidate members of important pathways, including those for Alzheimer's (AD) and Parkinson's (PD) diseases.

Results

Data integration

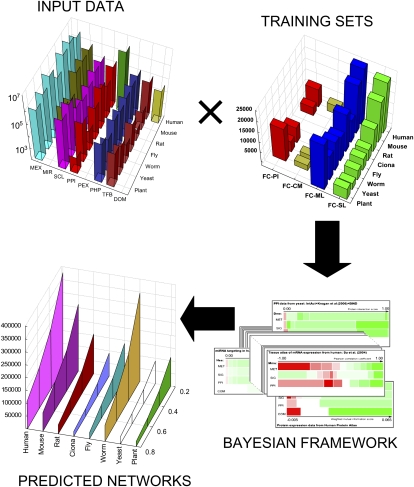
The flow of the data integration process in FunCoup is outlined in Figure 1. To infer FC between gene pairs, we collected large-scale data of a number of different types: MEX, phylogenetic profile similarity (PHP), PPI, subcellular colocalization (SCL), protein coexpression (PEX), shared transcription factor binding (TFB), co-miRNA regulation by shared miRNA targeting (MIR), and domain associations (DOM).

Figure 1.

Figure 1.

Open in a new tab

Outline of the FunCoup network reconstruction process. Amounts of input data and sizes of training sets are shown for each species in FunCoup version 1.0. Input data are as follows: MEX, mRNA coexpression; PHP, phylogenetic profile similarity; PPI, protein–protein interactions; SCL, subcellular colocalization; TFB, shared transcription factor binding; PEX, protein coexpression: MIR, miRNA targeting of transcripts; and DOM, domain associations. Training sets are as follows: ML, links between proteins from the same metabolic pathways; SL, links between proteins from the same signaling pathways; PI, experimentally observed protein–protein interactions; and CM, pairs of protein-members of the same complex. The Bayesian framework processes the input data using the training sets. The input datapoints are converted into raw interaction scores, which are grouped into discrete regions. Each such bin is assigned an FC score using the training sets. The “cards” illustrate the results of this process, showing the raw interaction score along the horizontal axis. For each training set, or functional class, the resulting bins are shown as colored rectangles: (green) positive evidence of FC; (white) either close to neutral or insignificant; (red) negative evidence of FC. Finally, the FC scores are calculated for all possible gene pairs in each species. For brevity, the predicted links of different functional classes have been combined into one network per species.

The following types of data are most abundantly available for human and the most important eukaryotic model organisms: Mus musculus (mouse), Rattus norvegicus (rat), Drosophila melanogaster (fly), C. elegans (worm), S. cerevisiae (yeast), and A. thaliana (Arabidopsis). In total, 51 data sets were collected for these species (see Fig. 1, Supplemental Table 1) (http://FunCoup.sbc.su.se/statistics_1.1.html). To avoid direct data redundancy, we made sure that the same piece of experimental information would never appear in different sets.

For each data type, we either adopted, optimized, or invented a metric to reflect the support for FC between gene pairs (Supplemental Methods). Examples of such metrics are the Pearson correlation coefficient (used for MEX), weighted mutual information (SCL), and a new probabilistic score accounting for multiple experimental reports of the same interaction (PPI). This score extracts additional FC evidence from so-called prey–prey interactions (i.e., pairs of proteins coupled indirectly via the bait), which significantly augmented available raw PPI input (Supplemental Table 6). We constructed a novel phylogenetic profile metric based on ortholog conservation in eukaryotes, which has not been done successfully before (Snitkin et al. 2006).

We compiled FC class–specific gold standard training sets (TSs) of protein–protein pairs known to belong to the respective kind of coupling. In preliminary training/prediction tests, we successfully predicted links of respective classes by integrating input data of the same collection. However, contribution to the prediction of FC classes differed across input sets. For example, mRNA coexpression usually delivered more information on CM, and experimentally reported interactions were usually more important for SL than ML. (see Fig. 3, below).

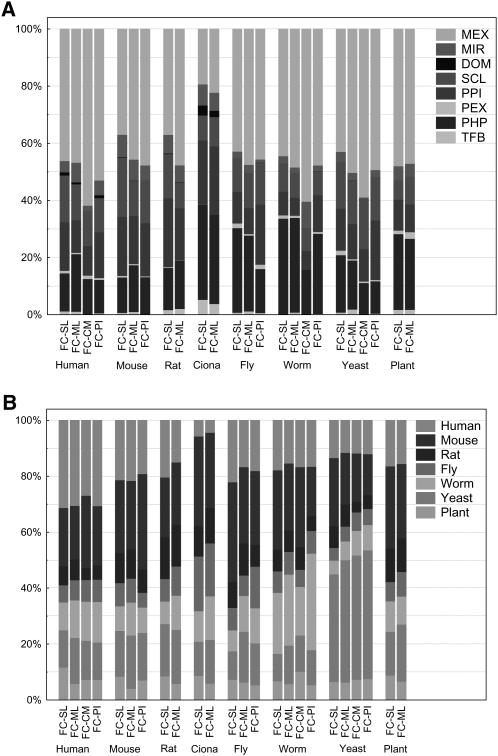
Figure 3.

Figure 3.

Open in a new tab

Relative evidence contribution to FunCoup networks viewed by input data type (A) or species (B). For each evidence category in each species and FC class, we calculated the sum of its contributions to the final Bayesian score (FBS) over the whole predicted network, i.e., the set of links with FBS > 3. Then, these sums were normalized by dividing with the sum of FBS scores over the same set. Note that no input data from Ciona was used. Data-type legends as in Figure 1.

The NBN was trained using TS of four FC classes and input data sets from seven organisms (Fig. 1). First, our novel discretization algorithm split each continuous metric's range into optimally defined bins for each combination of species, input data set, and TS. Then, the TS was used to assign probabilistic scores (likelihood ratios) to each bin. They were calculated by dividing the evidence occurrence in the positive TS with its background frequency. We predicted FC for every gene pair within a species by summing up the log likelihood ratios of their input data. This summary score, or final Bayesian score (FBS), reflects the overall chance of being functionally coupled. However to render the coupling score intuitively clear, we converted it to a probabilistic confidence value, pfc, ranging from 0 to 1 (Methods).

Each TS produced a separate prediction model. These dedicated models enabled overall accuracy improvement (Supplemental Table 2) and helped to reveal the nature of a predicted link. Supplemental Figure 9 shows that the predicted class agrees well with the GO functional annotation (Gene Ontology Consortium 2000). Figure 2 illustrates how FunCoup integrates multiple evidences, and how this leads to substantially increased confidence in the FC. Expectedly, the classes were not mutually exclusive. For example, protein kinases often produced high scores for both PI and SL links. We did not aim at a unique classification and stored all scores above FBS = 3, which constituted overall ∼1% of the processed gene–gene pairs (This fraction varies per species and functional class and can be derived from the detailed online statistics page under “Release notes” at http://FunCoup.sbc.su.se).

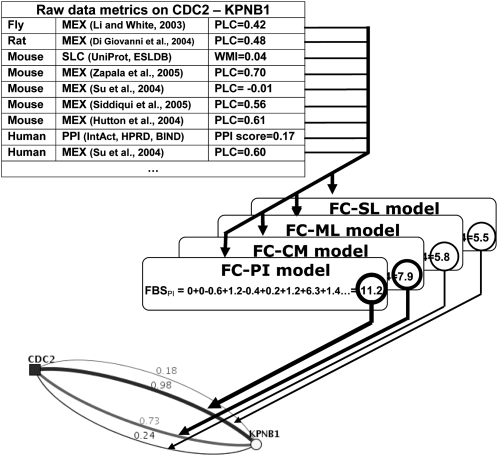
Figure 2.

Figure 2.

Open in a new tab

Example of predicting functional coupling (FC) by FunCoup's naïve Bayesian network. To evaluate the cumulative likelihood of the link CDC2–KPNB1, evidence (only nine shown) from a number of species were available. The metrics computed from each evidence were scored by the four models of FC and summed up to a total likelihood value, the final Bayesian score (FBS). In this example, a physical protein interaction (FC-PI) is more likely than membership in the same protein complex (FC-CM), a metabolic (FC-ML), or a signaling (FC-SL) link. The web interface to the database of predictions (http://FunCoup.sbc.su.se) displays likelihoods of the FC classes as four colored lines with FBS values transformed into the pfc confidence scores. This coupling was supported by many evidences from several species (top). The strongest came from the IntAct database that reported two experiments (Thelemann et al. 2005; Koch et al. 2007) where CDC2 and KPNB1 were mentioned as preys interacting with the same bait (in parallel with 219 and 68 other proteins, respectively). On its own, this is rather weak and would only yield pfc = 0.35 to prove a physical interaction (FBS = 6.3). However, combined with other evidence such as coexpression in human and mouse, the score was substantially strengthened (FBS = 11.2; pfc = 0.98). Note that the website can also display the coupling in terms of the individual evidence or species contributions. (MEX) mRNA expression; (SLC) subcellular localization; (PPI) known protein–protein interaction; (PLC) Pearson's linear correlation coefficient; (WMI) weighted mutual information score; and PPI score. See Supplemental Methods.

How much evidence was contributed from other species and from different input data types? As shown in Figure 3, mouse, human, and yeast were most influential. Strikingly, without exception the majority of the evidence came from other species, indicating the great value of transferring FC data between organisms. Even counting the links' unique origin (according to the criteria in Supplemental Table 7), more links came from other species than from the same in all cases but yeast. Among the input data types, mRNA coexpression played a dominating role, followed by phylogenetic profiles, PPI, and subcellular localization.

Optimizing NBN performance

To find the optimal combination of parameters and procedures and to make the framework universally applicable, the impact of the introduced features was tested statistically. As the influence of algorithmic details was often data set, species, and FC class specific, we only accepted modifications that significantly improved the overall performance. This was verified under holdout cross-validation in ANOVA experimental designs, always examining three to five species and usually two FC classes.

A problem with classical Bayesian predictors is the lack of a significance criterion, which can lead to nonzero likelihood ratios even in the absence of significant support by the data. We devised a simple significance test to ensure that this does not happen, which noticeably increased the performance (Supplemental Methods).

The NBN receives the input data in a discrete form, which is very practical if the likelihood of FC is irregularly distributed over the evidence data (Supplemental Fig. 1). To optimally discretize continuous data, we developed a new dynamic algorithm that is substantially superior to the flat binning (Supplemental Fig. 2). We defined optimal bin borders by comparing the frequencies of positive versus background examples in different score regions. This follows the approach of Butterworth et al. (2004) but avoids a laborious preliminary adjustment of parameters.

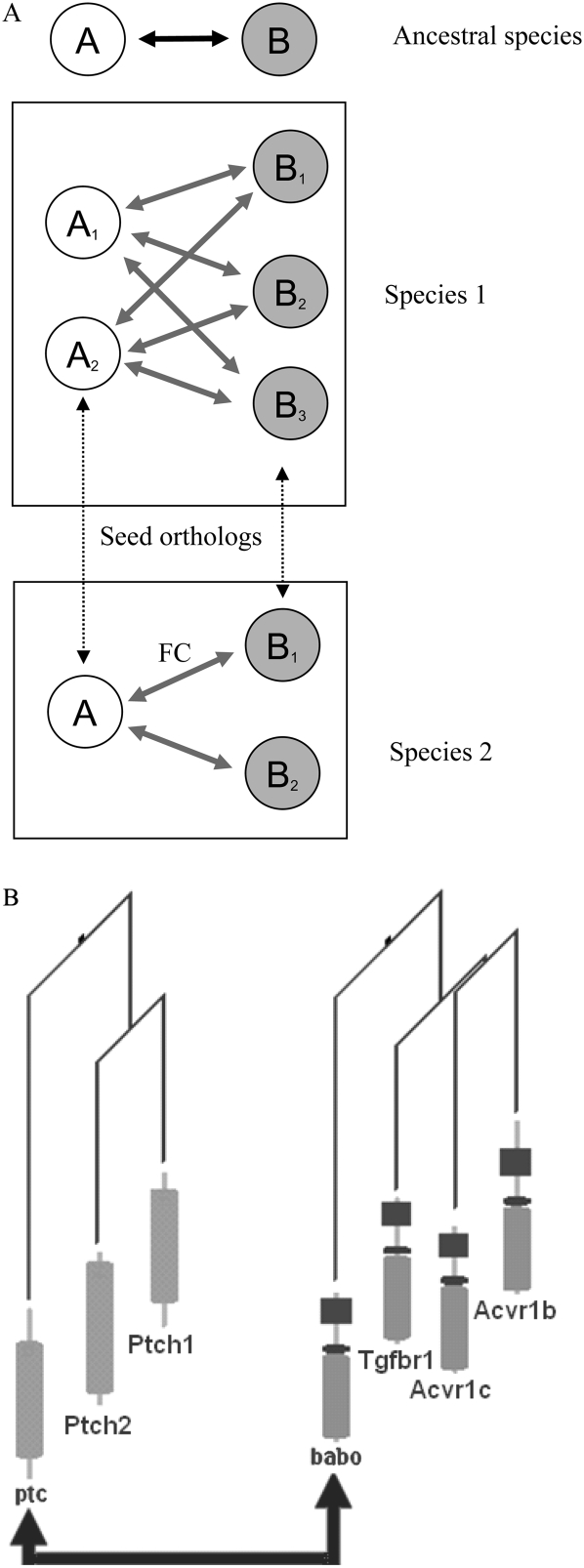
One of the most important contributions to infer FC came from orthologs in other species. We used orthologs defined by Inparanoid (Berglund et al. 2007), which has been shown to be most accurate for identifying functional counterparts (Hulsen et al. 2006). Nonetheless, the transfer can be done in many ways in case of multiple co-orthologs (inparalogs) stemming from species-specific gene duplication, which is commonplace in eukaryotes. As shown in Figure 4, the FC may evolve in different ways after the duplication. On one extreme, the interaction is limited to single inparalogs, while on the other extreme, all inparalogs may interact. By benchmarking alternative methods for using orthologs, we found that the best results are achieved by treating all alternative inparalog pairs from the same cluster equally and by using the best FC score among them (Supplemental Fig. 3). In other words, interactions are generally not considered specific to one gene copy after a duplication. However, after integrating all available FC data, from the same (or a closely related) species, a particular gene pair may receive much higher confidence.

Figure 4.

Figure 4.

Open in a new tab

Scenarios for interaction inheritance. (A) Interacting genes A and B in an ancestral species are duplicated into two and three genes in species 1, while B is duplicated into two genes in species 2. These duplicated genes are clusters of inparalogs in relation to the other species, meaning that they are co-orthologous to the corresponding A and B genes in that species. When transferring functional coupling (arrow marked FC) between orthologs, one can consider the interaction either to be valid for all inparalogs in a cluster, or to be specific for a particular inparalog pair (e.g., the seed orthologs, i.e., the two most similar ones, dotted arrows). The transfer of interaction information thus can either be done from an arbitrary inparalog in a cluster, which maximizes the coverage, or only be transferred between, e.g., seed orthologs. Benchmarking showed that transferring the best interaction in a set of inparalogs to all inparalogs in the other species yields the best results (Supplemental Material). (B) Real example of this situation: An interaction in fly ptc–babo (Shyamala and Bhat 2002) can either be considered to be valid for all six pairs of mouse inparalogs {Ptch1, Ptch2} vs. {Tgfbr1, Acvr1b, Acvr1c} or to be specific for a particular inparalog pair. Seed orthologs in this case are ptc/Ptch1 and babo/Tgfbr1. The two fly genes are connected with solid arrows; the others are mouse genes. The arrow denotes the known protein–protein interaction between ptc and babo. The leaves of the gene trees present protein domain architectures.

Independent validation tests

We developed and tested FunCoup under hold-out cross-validation (Supplemental Methods). However, the procedure employed data from the same sources for both training and testing, and thus might have involved higher order train/test dependencies. Looking for an independent proof of the predicted link's validity, we selected published research articles where investigators presented local, relatively compact subnetworks related to signaling or regulatory processes.

It was of great interest to reconstruct gene networks in organisms that themselves lack interaction data. FunCoup was particularly well suited to this task because of the integrated transfer of FC via orthologs. To demonstrate this ability, we generated a network in C. intestinalis, for which no large proteomics or genomics data set is yet available. As a positive TS, we used pathway members inferred via orthology. The input data came from the seven eukaryotes listed above, and the resulting Ciona network contained 38,445 links with a confidence pfc > 0.5, connecting 2683 genes. To validate the predicted Ciona network, we compared it to the “regulatory blueprint for a chordate embryo” (Imai et al. 2006). This is a set of 226 experimentally established functional links (mostly regulatory) between 80 genes in the ascidian embryo, referred to as the “RBP” network.

We expected to only recover a small fraction of RBP because regulatory links are indirect and very hard to find, and FunCoup was not specifically trained to find such links. Despite this, FunCoup recovered 22 (at pfc > 0.05) of the maximum achievable 116 RBP links between the 54 RBP genes in the reconstructed FunCoup network. The true discovery rate (TDR) was actually much higher than 5% (Supplemental materials). In total, the 54 RBP genes were interconnected by 180 links, which is significantly higher (P0 < 10−8) than expected by chance (39.5 links are expected for 54 randomly chosen genes in the reconstructed network).

FunCoup also identified many novel links to Ciona RBP. At pfc > 0.5, 350 new genes were coupled to RBP, and 30 of these had >30% of the evidence from both vertebrates and invertebrates, representing an evolutionarily well-supported set of novel genes in this pathway. Functions in this group included G proteins, GPCRs, protein kinases, phosphatases, etc., i.e., signaling proteins. Most of the novel genes were coupled to c-Jun (MAPK10), emphasizing its importance during embryonic development (Supplemental Fig. 4A).

The relatively low FunCoup sensitivity to RBP links emphasizes the elusive nature of the regulatory links related to embryonic development. In fact, they are equally hard to find in the better studied eukaryotes. For comparison, we took a set of “core transcriptional circuitry in human embryonic stem cells” (Boyer et al. 2005). It yielded a similar ratio: FunCoup recovered seven out of 82 regulatory links shown in the study (Supplemental Fig. 4B). Hence for this context, links predicted in Ciona had competitive confidence.

As a contrast, sensitivity of the FunCoup predictor to cancer-related pathways turned out to be very high. Such circuits are based on PPIs and complexes produced by GTPases, kinases, and DNA binding/processing proteins, and FunCoup abounded in respective input data. As a test set, we considered a map of three critical signaling pathways in the development of glioblastoma released by The Cancer Genome Atlas Research Network (2008). Figure 5 in that article depicted mutationally vulnerable segments of RTK/RAS/PI(3)K, p53, and RB pathways. Querying FunCoup with the listed genes retrieved 29 links from this map and only missed seven (Supplemental Fig. 4C). Twenty-five more FunCoup links between the mapped genes were not drawn by the TCGARN investigators but may be true novel links relevant to either cancer or normal biology. In total, FunCoup predicted as many as 896 links (pfc > 0.5) between the pathway members and other, not mapped, genes.

Figure 5.

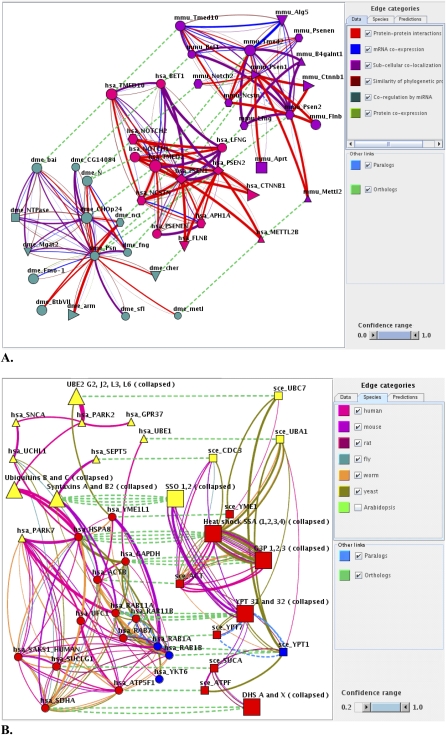
Figure 5.

Open in a new tab

Comparative network analysis in FunCoup. (A) Subnetworks in human (middle), mouse (top), and fly (left) were generated by submitting human presenilin 1 and 2 (PSEN1 and PSEN2) to FunCoup, asking for one step of network expansion keeping the 20 strongest links with P > 0.5, and inclusion of orthologous subnetworks in mouse and fly. At the lower right are two newly predicted interactors of the gamma secretase complex, BET1 and LFNG. On the right, the color legend for the links is shown in terms of evidence type. Species are indicated by gene symbol prefixes: has, human; mmu, mouse; and dme, fly. Supplemental Figure 8 presents alternative views by species source or predicted class. The jSquid XML source to this figure is available as supplementary file psen_lfng_bet.xml. (B) Using FunCoup to identify novel candidate genes in Parkinson's disease. We here employ orthologous networks in human (left) and yeast (right, squares). Novel candidates were extracted by looking for human genes that were coupled both to known PD genes and to orthologs of yeast alpha-synuclein toxicity modifiers. This resulted in 12 novel candidate PD genes (red circles). PD and alpha-synuclein toxicity modifier genes not connected to these 12 genes were omitted from the network for clarity. Edge categories are shown in the figure. Node categories are as follows: (yellow) known human PD genes from the pathway KEGG05020 (triangles) and their yeast orthologs (squares); (blue) yeast modifiers of a-synuclein toxicity (squares) and their human orthologs (circles); (red) 12 novel human PD candidate genes (circles) and their yeast orthologs (squares); and larger shapes labeled “collapsed,” grouped genes—inparalogs, except for UBE2 that represents four ubiquitin-conjugating enzymes with similar molecular function. For details on how the subnetwork was generated, see Supplemental Methods; for a large scale prospective of the presented subinteractome, see Supplemental Figure 10.

We also wanted to validate FunCoup on a raw, independently chosen, set of functionally related genes, in order to exclude any possibility of overlap between the test set and FunCoup evidence. For this purpose, we retrieved 145 somatic mutation lists, each derived for an individual patient tumor sample of glioblastoma multiforme from The Cancer Genome Atlas (TCGA). The mutations were found and experimentally validated (genotype arrays, PCR amplification, etc.) and made public according to TCGA protocols (http://tcga.cancer.gov/about/index.asp). A gene list from one tumor will generally contain two kinds of mutations: drivers and passengers. The former drive the tumor toward malignancy, while the latter passively accumulate mutations due to impaired DNA repair (Ding et al. 2008). One a priori expects the driver genes to be functionally coupled to each other in a given tumor, and passengers to not be. The nine sufficiently large (10 or more genes) mutation lists were analyzed in FunCoup to examine the connectivity. Six of these lists were significantly (P0 < 10−3) enriched with internal connections compared to random networks. Thus, using completely raw and uncurated data sets, relationships predicted by FunCoup were validated in a majority of somatic mutation cases. Details are described in Supplemental material, as well as an example network generated from a somatic mutation list. Investigating subnetworks of patient mutation sets with the help of FunCoup can be an important step toward individualized cancer treatment.

Apart from the successful validation on an orthogonal data set, the test also confirmed that our formal pfc score was a very conservative, lower-bound estimate of the TDR, i.e., the fraction of true facts among the predictions. In reality, it was probably much higher, e.g., in the TCGA-02-0114-01A-01W subnetwork TDR = 0.51 at pfc > 0.02 and TDR = 0.59 at pfc > 0.25. Respectively in the Ciona RBP case, TDR exceeded 0.20 at pfc > 0.05 (Supplemental materials).

Website

We created a web resource with networks for eight eukaryotic species, from yeast to human: http://FunCoup.sbc.su.se. Large (up to genome-wide) sets of interaction predictions are available for download in CytoScape-compatible (Shannon et al. 2003) or XML format. However, the user is typically interested in smaller subnetworks around a set of query genes.

The user can control the subnetwork retrieval and thus its information content. The evidence base can be limited to particular species or data types (e.g., “mammalian” or “coexpression” only). The query's neighborhood can be specified by subnetwork size, confidence threshold, network radius, and neighbor-search algorithm.

The subnetwork is shown with a specially designed Java applet jSquid (Klammer et al. 2008) that allows flexible user-controlled rendering of the network graph, including node grouping by pathway, organelle, or connectivity. Nodes are given a shape and color according to functional categories. The results are also shown as a table where the support from each evidence data type or species is listed for each link. This decomposition of link support is also possible in the network graph, whereby each category is shown as a distinctly colored line. Each category can be individually enabled/disabled, and the user can switch between viewing evidence data type, evidence species, and predicted FC class. Moreover, a subnetwork may be retrieved using only evidence of particular types or species, e.g., simulating a pure PPI network or a pure yeast network.

It is possible to add predefined gene groups from particular functional categories (GO), diseases (OMIM), or pathways (KEGG) to highlight a network context of interest. A multispecies view, retrieved via orthologs, provides across-species network comparisons (Fig. 5).

Cross-species network analysis using FunCoup

We used FunCoup to investigate the protein network around genes known to cause AD. Starting with human presenilin1 and presenilin2 as queries, we asked for the subnetworks of functionally coupled genes in human, mouse, and fly (Fig. 5A). The subnetworks in the three species were strikingly similar, sharing many of the known gamma-secretase associated proteins. In all three species, we detected two genes that to our knowledge have not previously been associated to AD. These were BET1 (SWISS-PROT O15155) and LFNG (SWISS-PROT Q8NES3). BET1 is a SNARE protein involved in the docking endoplasmic reticulum vesicles with Golgi (Zhang et al. 1997), and LFNG is glucosaminyltransferase found in the Golgi membrane (Haines and Irvine 2003). The FC between BET1, LFNG, and AD-related genes is supported by data from all three species and by the fact that gamma-secretase is also known to associate with Golgi. The most prominent evidence data types linking BET1 and LFNG were SCL and PPI, while no interaction class was clearly favored.

FunCoup augmented our knowledge of PD. We started from 22 genes reported by Cooper et al. (2006) to be modifiers of alpha-synuclein toxicity in a yeast model for PD. We queried FunCoup for human genes that were coupled to both the PD pathway (KEGG05020) and to orthologs of the yeast modifiers, and analyzed the corresponding human and yeast subnetworks (Fig. 5B). This revealed 12 human genes that have not previously been associated with PD to our knowledge. Their functions include vesicle trafficking, ubiquitination, and toxic substance removal, all compatible with a role in the PD pathway. An example is the metalloprotease YME1L1, whose best coupling (pfc = 0.97) is to RAB1A, ortholog to one of the strongest yeast alpha-synuclein modifiers, YPT1. Most of the evidence for this relationship comes from mRNA coexpression in mouse. Interestingly, YME1L1 has been reported to interact with presenilin (Pellegrini et al. 2001), supporting a commonality between the processes that lead to PD and AD (Suh and Checler 2002).

Another example from Figure 5B is the heat shock protein HSPA8. It had many strong couplings to the subnetwork (nine with pfc > 0.8). One of the strongest (pfc = 0.99) is to PARK7, mostly inferred from human mRNA coexpression. Further support came from the fact that its links to YME1L1 and ACTB were conserved in yeast. We noted that RAB7A (also known as RAB7), RAB11A, and RAB11B were strongly coupled to the PD pathway, even though the Cooper screen only found evidence in the yeast model for RAB1A and RAB1B. Yet the yeast model may not capture all connections. The five RAB genes were strongly interconnected in FunCoup; remarkably, they all shared transcription factors targeting their fly and plant orthologs.

Discussion

We have presented FunCoup, a general method for integrating heterogeneous data in order to reconstruct networks of FC between genes. FunCoup introduces prediction of multiple functional classes in parallel, which boosts accuracy and helps annotating of the nature of the predicted interactions. Another crucial feature of FunCoup is integration of individually weak pieces of evidence and converting them into substantially high confidence (Fig. 2).

The novel methods for adaptive data discretization and likelihood score assignment were indispensable for differential FC class prediction from the same data and enabled high performance of the FC class-specific predictors (Supplemental Fig. 9). The ability to make different quantitative conclusions from the same data was accumulated piecewise from small differences between discrete bins and their likelihood values (Fig. 1, “Bayesian framework”). Often, different TSs suggested different signs of log likelihood ratio; e.g., a negative correlation of mRNA expression might have delivered positive evidence of SL but negative evidence of ML.

Negative evidence can indeed be informative, e.g., protein localization in different compartments (strongly negative), or uncorrelated expression (weakly negative). Systematic accounting for both positive and negative evidence is thus of great value for FunCoup.

Orthologous data, i.e., FC between orthologs of a given gene pair, were treated as any other data source. This way, the FC score of orthologous data depended on its performance on the TSs in the target species. Despite reports of low conservation of PPIs between species (Mika and Rost 2006), we found that the overlap nowadays is often substantial. For instance, between the yeast IntAct set and the human high-confidence TS, 431 of the 723 shared orthologous pairs have been observed to interact in both species (including 363 with a higher PPI score, i.e., >0.5).

Input data sets of eight major types were used to generate comprehensive networks in eight eukaryotic species. Throughout the framework, we have followed the principle of automatic parameter tuning to optimize the predictive power of each data source. It is important for FunCoup as an ongoing project that evidence is transferred between organisms to predict FC with minimal human intervention yet ensuring high coverage and quality. In principle, any kind of data can be accepted, continuous or discrete, with either original or FunCoup-calculated pairwise metrics. New data sources, TSs, and species can be easily added, as their relevance to FC is estimated automatically.

How much can more data improve FunCoup's performance? We measured the accuracy as a function of adding model organisms and data sources to the system in a random order for five species and four evidence types. After addition of about 30 evidence sources, not much improvement was seen (Supplemental Fig. 5). In the yeast—an organism without close relatives in FunCoup but with much own data––other species' data sets had a lower impact. Thus, the current data collection provides an amount of information close to practical maximum. Of course, new high-throughput platforms that cover significantly more genes or entirely novel data types may breach the “ceiling” and enable even higher accuracy.

Potentially, evidence from different sources, given the same likelihood score, could differ in “quality.” We attempted to discover any potential bias and found that the “evidence quality” was uniform across data types and species and was independent of evidence magnitude (Supplemental Table 5). This analysis showed that data of different types, or from different species, could be added up in any proportion, yet the only factor that mattered was the value of log likelihood ratio—in full agreement with the NBN assumptions. Whether the main evidence came from a single species, or was spread among two or more, did not matter as well. Hence, for currently available genomics/proteomics data, the Bayesian framework based on summing up likelihood ratio scores is robust and practically unbiased. In other words, the FunCoup data integration was overall correct and efficient on the heterogeneous, sparse, and noisy data landscape. We show that the networks generated by FunCoup are scale-free (Barabasi and Albert 1999) even at the lowest confidence level, which agrees with the properties of so far known biological networks (Supplemental Fig. 11).

How different is FunCoup from STRING (von Mering et al. 2007)? The databases are built with different methodologies and only partly the same input data. An important difference is the treatment of orthologous data. To predict FC in species X with evidence EM from a model species M, STRING evaluates likelihood P(FC|EM) against training data in the same species M. In other words, EM predicts FC in any other species with the same score, although corrected for sequence dissimilarity. Thus, EM is transferred irrespective of its relevance to FC in X. On the contrary, FunCoup already at the training stage finds orthologs of M in X and evaluates P(FCX|EM) against TSs in X.

In terms of input data, STRING relies heavily on annotated resources such as comembership in KEGG pathways. FunCoup does not use curated data from, e.g., GO or KEGG as evidence of FC, as we do not think that such knowledge should be re-evaluated by the predictor, and chose to only use it for training data sets and as add-on links shown on the website. Conversely, six out of eight major FunCoup data types (PEX, MIR, TFB, DOM, SCL, and the ortholog-based eukaryotic PHP) are not used in STRING. Thus, both input data and their evaluation into scores differ between STRING and FunCoup. The Spearman rank correlation between scores of links found in both STRING and FunCoup was 0.19. The highest-ranking links in both resources often do not agree (10%–20% overlap). However, the most confident FunCoup predictions are usually (e.g., close to 70% in the human interactome) found, at some confidence, in STRING.

FunCoup represents an efficient large-scale multispecies reconstruction of global gene networks from genomics and proteomics data. As we illustrated with examples, the future modus operandi of gene function discovery is to first search a gene network resource such as FunCoup with genes of interest. This will expand the set of new genes predicted to be functionally coupled, which becomes a manageable subset of genes to investigate experimentally for their role in the studied process. By making the networks available via a powerful and user-friendly website we enable biologists to accelerate discovery of gene function.

Methods

The choice of statistical tool for integrating heterogeneous data depends on many factors. From a wide range of possible approaches, such as discriminant or regression analyses, support vector machines, or neural networks (Huttenhower and Troyanskaya 2006; Qi et al. 2006), we chose the NBN because it, (1) tolerates missing values well; (2) has been successfully applied to genome-wide data integration (e.g., Troyanskaya et al. 2003; Lee et al. 2004; Rhodes et al. 2005) and has been formally justified as optimal under certain assumptions (Zhang 2004), which hold in our case (Supplemental Methods); and (3) gives straightforward and interpretable scores, which makes it attractive to both developer and end user.

Potential drawbacks of NBNs include addition of redundant evidences and assignment of scores that are statistically insignificant due to few data points. The redundancy problem, i.e., violation of the requirement of independence between input data sets, is, however, not an issue for classification accuracy using diverse and sparse data (Zhang 2004). To ensure confident assignment of scores, we applied a statistical test (Supplemental Methods).

Training and input data sets

NBNs require training data sets with positive and negative examples, and the quality of these very much determine the resulting performance. We compiled the positive, gold standard sets of the four FC classes of interest (FC-PI, FC-ML, FC-SL, and FC-CM) from IntAct (Kerrien et al. 2007), HPRD (Mishra et al. 2006), BIND (Bader et al. 2003), KEGG (Kanehisa et al. 2002), and UniProt (Boutet et al. 2007). For each class, a set of filtering criteria (Supplemental Table 4) was applied to the raw data sets to extract highly confident FCs.

In our case, the negative TS is very difficult to obtain, as one cannot experimentally disprove an interaction. Several investigators have attempted to produce negative TSs by, e.g., selecting proteins from different subcellular localizations (Jansen et al. 2003; Rhodes et al. 2005), membership in different pathways (Li et al. 2004), or mismatching expression. However, none of these criteria guarantees the absence of interaction, and they may introduce a bias in the probabilistic space. Therefore, we used Bayes' rule in such a way that it employs the background evidence probability rather than using a negative set. The difference is actually small because only about 0.001 of the total gene pairs are expected to be functionally coupled (assuming 2 × 105 interactions of 2 × 108 possible in the human genome). A big advantage with our approach is that the background reference sample can always be made sufficiently large, which makes the training less vulnerable to errors from small sample size.

The input data may come as pairs of proteins/genes with a binary or continuous score (PPI, TFB, MIR), individual protein/gene profiles (MEX, PEX, SCL), or annotation features for protein/domain profiles (PHP, DOM). For all types, pairwise metrics were calculated as described in Supplementary Methods. This is done first with data from the same organism. Then the other organisms are searched for orthologs, and if these are found for both genes, orthologous data from other species are treated at separate input data types. All homologous gene pairs were removed from the training data sets.

Naïve Bayesian network

The NBN is trained as follows. First, the discretization algorithm finds the bins in each metric's range that produce the highest contrast in respect of FC (Supplemental Methods). In our framework, we analyzed the set ɛ of evidence features Ei ∈ ɛ to estimate the integrated support for FC given all nonempty evidences. Starting with an individual evidence, Ei, that falls in the bin j, the probability that a particular gene pair is functionally coupled is defined by Bayes' rule

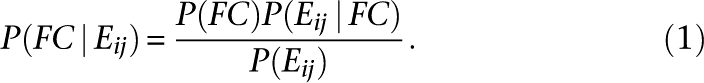graphic file with name 1107equ1.jpg

The probabilities corresponding to four different FC classes are here collapsed into one FC for brevity.

It is not possible to determine P(FC) exactly, but since this is constant, we may leave it out. Thus, without losing predictive efficiency, we integrate over all evidences by summing the logarithms of the remaining ratio in order to obtain a simplified classifier called FBS:

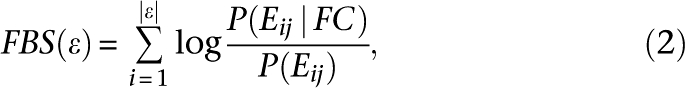graphic file with name 1107equ2.jpg

where P(Eij | FC) is estimated from occurrence of Eij in the positive TS. The background probabilities P(E) were estimated from the general population of gene pairs. Only couplings with FBS > 3 were kept.

When summing log likelihood ratios to an FBS, there is a potential danger that the particular combination of evidence types could lead to overestimation of the FBS due to redundancy. Using general regression models, we examined this effect by measuring how prediction accuracy depended on, in addition to FBS, evidence combinations of factors. The results invariably showed that FBS alone was the only significant predictor (Supplemental Table 5). In other words, the accuracy depended only on the absolute value of FBS and was independent of the evidence configuration, such as the number of distinct supporting evidences. One explanation for this robustness could be that we are treating negative evidence equal to positive evidence.

FBS is convenient to store and analyze evidence components. Some components may be negative despite an overall positive FBS. However, the FBS score does not have strict bounds and is not intuitively interpretable. We therefore used an approximation of an alternative form of Bayes' theorem (MacKay 2003) that gives an intuitive and user-friendly FunCoup confidence score between 0 and 1:

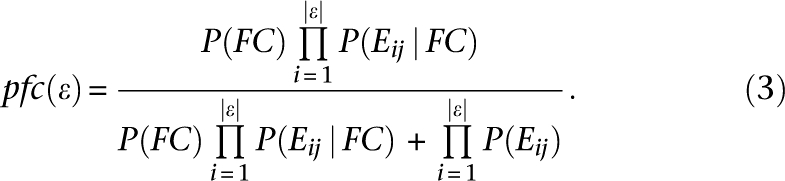graphic file with name 1107equ3.jpg

pfc is a probability estimate that the pair is functionally coupled, similar to P used in the method of Green and Karp (2004). P(FC), the prior probability that “two random proteins are functionally coupled,” is unknown. However, some expert estimates have been given by, e.g., Grigoriev (2003) and Rhodes et al. (2005), and we conservatively set P(FC) to 10−3. Note that pfc is in the interval 0…1 and monotonic with respect to P(FC). Another approximation we made was 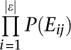Inline graphic instead of 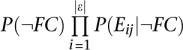Inline graphic. This numerically close substitution made the estimate even more conservative. We use pfc as a confidence value in the FunCoup database.

Discretization

The discretization algorithm that we developed for FunCoup is similar to the one by Butterworth et al. (2004), but because it is based on the Pearson χ2-statistic rather than the conditional entropy, it does not require setting a parameter (power index = 1.8…2.2) as an additional step. With a χ2-score, it tests all prospective cutpoints, i.e., ones where (1) sample counts are sufficient, (2) χ2 values are significant (P0 < 0.001), and (3) the class label swaps between the positive and background FC.

The maximally scored point splits the metric range in two initial bins. Further partitions are iteratively sought while any prospective points remain. We tested the method against the default quantile-based partitioning and found the novel method significantly superior (Supplemental Fig. 2). The algorithm usually stops at five to 10 bins, and we introduced a practically justified limit of 10 bins. When data deliver little information on FC, fewer bins are created. No splits means that positive and background labels cannot be separated significantly, and that the data set is not useful. The advantage of this procedure is that it is insensitive to a metric's distribution shape and the position of local optima (Supplemental Methods).

Significance testing

Each evidence category (bin) was subjected to a χ2 test based on the observed positive and background frequencies, and was discarded if P0 > 0.001 (Supplemental Methods).

Phylogenetic profiles

For most data sets, a continuous score, or metric, was derived that reflects the strength of the FC (Supplemental Methods). However, for phylogenetic profiles, we chose a different strategy. Here, each gene pair was classified into a discrete category describing its phylogenetic signature. For instance, the signature “mammals_insects_fungi” may characterize human genes that both have Inparanoid orthologs in mouse and/or rat, fly, and yeast but not in other species. Each signature is treated as a discrete evidence “bin” during training. We benchmarked this method against a number of earlier proposed metrics, as well as against several novel potentially useful metrics, and found it superior (Supplemental Fig. 6).

Estimating performance

To measure the predictor performance, we used the common receiver operating characteristic (ROC) curves. They map sensitivity (correctly classified fraction of the positive test set, TP/[TP + FN]) to specificity (effectively represented as “predicted non-FC” fraction of the background reference set, [TN + FP]/[TN + FP + TP + FN]) at varying cutoffs. To estimate hundreds of ROC curves in the course of testing, the area under curve (AUC) was used to measure the overall performance, as its convexity reflects the quality of the predictor. The tests were performed in regions of practical importance, i.e., when the predicted interactome reasonably compact. To ensure this, we used a cutoff such that the fraction of predictions was fixed to e.g., 1% or 4% of the total N(N − 1)/2 pairs between N proteins (Supplemental Fig. 7).

Statistical tests of NBN configuration

We analyzed the framework configuration parameters such as “maximal number of bins in discretization,” “way to use ortholog information,” “choice of a coexpression metric,” etc., for magnitude and significance under ANOVA general linear models (StatSoft, Inc., STATISTICA (data analysis software system), version 7.1, www.statsoft.com). All accepted NBN modifications were significantly efficient (P0 < 0.01). The improvements were quantified in terms of AUC. For example, introducing likelihood value check by confidence augmented AUC by 12% in the specificity region 96%–100% compared with the default configuration, i.e., “using any non-zero likelihoods.” The effects of single factors and their interactions are shown in Supplemental Figure 2. Complete balanced orthogonal ANOVA designs assured that all combinations were systematically tested. Replicates, necessary to estimate the within-combination variance, were obtained from multiple (3…10) holdout bootstraps. For each bootstrap, we randomly split the positive set and the random instance of the general population in two equal parts: one for training and the other retained for validation.

Deriving pathway members in an uncharacterized organism

At the time we generated the C. intestinalis network (December 2007), this organism was not yet present in the KEGG ortholog table. Hence, unlike the other organisms, we did not have a set of organism-specific pathway members to create a TS. We found putative Ciona pathway members in a way similar to the KEGG inference by orthology (Bono et al. 1998). Our method employs multispecies clusters of orthologs available from the MultiParanoid database (Alexeyenko et al. 2006). In each ortholog cluster, we assigned EC numbers to Ciona proteins considering the KEGG assignments to human, fly, and worm cluster members (Supplemental Methods).

Footnotes

[Supplemental material is available online at www.genome.org. FunCoup is freely available for download and query at http://funcoup.sbc.su.se.]

Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.087528.108.

References

  1. Alexeyenko A., Tamas I., Liu G., Sonnhammer E.L.L. Automatic clustering of orthologs and inparalogs shared by multiple proteomes. Bioinformatics. 2006;22:e9–e15. doi: 10.1093/bioinformatics/btl213. [DOI] [PubMed] [Google Scholar]
  2. Bader G.D., Betel D., Hogue C.W. BIND: The biomolecular interaction network database. Nucleic Acids Res. 2003;31:248–250. doi: 10.1093/nar/gkg056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bader J.S., Chaudhuri A., Rothberg J.M., Chant J. Gaining confidence in high-throughput protein interaction networks. Nat. Biotechnol. 2004;1:78–85. doi: 10.1038/nbt924. [DOI] [PubMed] [Google Scholar]
  4. Barabasi A.L., Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
  5. Berglund A.-C., Sjölund E., Östlund G., Sonnhammer E.L.L. InParanoid 6: Eukaryotic ortholog clusters with inparalogs. Nucleic Acids Res. 2008;36:D263–D266. doi: 10.1093/nar/gkm1020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Beyer A., Bandyopadhyay S., Ideker T. Integrating physical and genetic maps: From genomes to interaction networks. Nat. Rev. Genet. 2007;8:699–710. doi: 10.1038/nrg2144. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bono H., Goto S., Fujibuchi W., Ogata H., Kanehisa M. Systematic prediction of orthologous units of genes in the complete genomes. Genome Inform. Ser. Workshop Genome Inform. 1998;9:32–40. [PubMed] [Google Scholar]
  8. Boutet E., Lieberherr D., Tognolli M., Schneider M., Bairoch A. UniProtKB/Swiss-Prot: The manually annotated section of the UniProt knowledgebase. Methods Mol. Biol. 2007;406:89–112. [Google Scholar]
  9. Boyer L.A., Lee T.I., Cole M.F., Johnstone S.E., Levine S.S., Zucker J.P., Guenther M.G., Kumar R.M., Murray H.L., Jenner R.G., et al. Core transcriptional regulatory circuitry in human embryonic stem cells. Cell. 2005;122:947–956. doi: 10.1016/j.cell.2005.08.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Butterworth R., Simovici D.A., Santos G.S., Ohno-Machado L. A greedy algorithm for supervised discretization. J. Biomed. Inform. 2004;37:285–292. doi: 10.1016/j.jbi.2004.07.006. [DOI] [PubMed] [Google Scholar]
  11. The Cancer Genome Atlas Research Network. Comprehensive genomic characterization defines human glioblastoma genes and core pathways. Nature. 2008;455:1061–1068. doi: 10.1038/nature07385. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Cooper A.A., Gitler A.D., Cashikar A., Haynes C.M., Hill K.J., Bhullar B., Liu K., Xu K., Strathearn K.E., Liu F., et al. Alpha-synuclein blocks ER-Golgi traffic and Rab1 rescues neuron loss in Parkinson's models. Science. 2006;313:324–328. doi: 10.1126/science.1129462. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ding L., Getz G., Wheeler D.A., Mardis E.R., McLellan M.D., Cibulskis K., Sougnez C., Greulich H., Muzny D.M., Morgan M.B., et al. Somatic mutations affect key pathways in lung adenocarcinoma. Nature. 2008;455:1069–1075. doi: 10.1038/nature07423. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. The Gene Ontology Consortium. Gene Ontology: Tool for the unification of biology. Nat. Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Green M.L., Karp P.D. A Bayesian method for identifying missing enzymes in predicted metabolic pathway databases. BMC Bioinformatics. 2004;5:76. doi: 10.1186/1471-2105-5-76. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Grigoriev A. On the number of protein–protein interactions in the yeast proteome. Nucleic Acids Res. 2003;31:4157–4161. doi: 10.1093/nar/gkg466. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hahn A., Rahnenfuhrer J., Talwar P., Lengauer T. Confirmation of human protein interaction data by human expression data. BMC Bioinformatics. 2005;6:112. doi: 10.1186/1471-2105-6-112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Haines N., Irvine K.D. Glycosylation regulates Notch signalling. Nat. Rev. Mol. Cell Biol. 2003;4:786–797. doi: 10.1038/nrm1228. [DOI] [PubMed] [Google Scholar]
  19. Hulsen T., Huynen M.A., de Vlieg J., Groenen P.M. Benchmarking ortholog identification methods using functional genomics data. Genome Biol. 2006;7:R31. doi: 10.1186/gb-2006-7-4-r31. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Huttenhower C., Troyanskaya O.G. Bayesian data integration: A functional perspective. Comput. Syst. Bioinformatics Conf. 2006;2006:341–351. [PubMed] [Google Scholar]
  21. Imai K.S., Levine M., Satoh N., Satou Y. Regulatory blueprint for a chordate embryo. Science. 2006;312:1183–1187. doi: 10.1126/science.1123404. [DOI] [PubMed] [Google Scholar]
  22. Jansen R., Yu H., Greenbaum D., Kluger Y., Krogan N.J., Chung S., Emili A., Snyder M., Greenblatt J.F., Gerstein M.A. Bayesian networks approach for predicting protein–protein interactions from genomic data. Science. 2003;302:449–453. doi: 10.1126/science.1087361. [DOI] [PubMed] [Google Scholar]
  23. Kanehisa M., Goto S., Kawashima S., Nakaya A. The KEGG databases at GenomeNet. Nucleic Acids Res. 2002;30:42–46. doi: 10.1093/nar/30.1.42. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kerrien S., Alam-Faruque Y., Aranda B., Bancarz I., Bridge A., Derow C., Dimmer E., Feuermann M., Friedrichsen A., Huntley R., et al. IntAct: Open source resource for molecular interaction data. Nucleic Acids Res. 2007;35:D561–D565. doi: 10.1093/nar/gkl958. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Klammer M., Roopra S., Sonnhammer E.L. jSquid: A Java applet for graphical on-line network exploration. Bioinformatics. 2008;24:1467–1468. doi: 10.1093/bioinformatics/btn213. [DOI] [PubMed] [Google Scholar]
  26. Koch H.B., Zhang R., Verdoodt B., Bailey A., Zhang C.D., Yates J.R., III, Menssen A., Hermeking H. Large-scale identification of c-MYC-associated proteins using a combined TAP/MudPIT approach. Cell Cycle. 2007;6:205–217. doi: 10.4161/cc.6.2.3742. [DOI] [PubMed] [Google Scholar]
  27. Lee I., Date S.V., Adai A.T., Marcotte E.M. A probabilistic functional network of yeast genes. Science. 2004;306:1555–1558. doi: 10.1126/science.1099511. [DOI] [PubMed] [Google Scholar]
  28. Li S., Armstrong C.M., Bertin N., Ge H., Milstein S., Boxem M., Vidalain P.O., Han J.D., Chesneau A., Hao T., et al. A map of the interactome network of the metazoan C. elegans. Science. 2004;303:540–543. doi: 10.1126/science.1091403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. MacKay D.J.C. Information theory, inference, and learning algorithms. Cambridge University Press; Cambridge: 2003. [Google Scholar]
  30. Matthews L.R., Vaglio P., Reboul J., Ge H., Davis B.P., Garrels J., Vincent S., Vidal M. Identification of potential interaction networks using sequence-based searches for conserved protein–protein interactions or “interologs.”. Genome Res. 2001;11:2120–2126. doi: 10.1101/gr.205301. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Mika S., Rost B. Protein–protein interactions more conserved within species than across species. PLoS Comput. Biol. 2006;2:e79. doi: 10.1371/journal.pcbi.0020079. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Mishra G.R., Suresh M., Kumaran K., Kannabiran N., Suresh S., Bala P., Shivakumar K., Anuradha N., Reddy R., Raghavan T.M., et al. Human protein reference database: 2006 update. Nucleic Acids Res. 2006;34:D411–D414. doi: 10.1093/nar/gkj141. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Pellegrini L., Passer B.J., Canelles M., Lefterov I., Ganjei J.K., Fowlkes B.J., Koonin E.V., D'Adamio L. PAMP and PARL, two novel putative metalloproteases interacting with the COOH-terminus of Presenilin-1 and -2. J. Alzheimers Dis. 2001;3:181–190. doi: 10.3233/jad-2001-3203. [DOI] [PubMed] [Google Scholar]
  34. Qi Y., Bar-Joseph Z., Klein-Seetharaman J. Evaluation of different biological data and computational classification methods for use in protein interaction prediction. Proteins. 2006;63:490–500. doi: 10.1002/prot.20865. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Rhodes D.R., Tomlins S.A., Varambally S., Mahavisno V., Barrette T., Kalyana-Sundaram S., Ghosh D., Pandey A., Chinnaiyan A.M. Probabilistic model of the human protein–protein interaction network. Nat. Biotechnol. 2005;23:951–959. doi: 10.1038/nbt1103. [DOI] [PubMed] [Google Scholar]
  36. Shannon P., Markiel A., Ozier O., Baliga N.S., Wang J.T., Ramage D., Amin N., Schwikowski B., Ideker T. Cytoscape: A software environment for integrated models of biomolecular interaction networks. Genome Res. 2003;13:2498–2504. doi: 10.1101/gr.1239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Shyamala B.V., Bhat K.M. A positive role for Patched-Smoothened signaling in promoting cell proliferation during normal head development in Drosophila. Development. 2002;129:1839–1847. doi: 10.1242/dev.129.8.1839. [DOI] [PubMed] [Google Scholar]
  38. Snitkin E.S., Gustafson A.M., Mellor J., Wu J., DeLisi C. Comparative assessment of performance and genome dependence among phylogenetic profiling methods. BMC Bioinformatics. 2006;7:420. doi: 10.1186/1471-2105-7-420. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Sonnhammer E.L.L. Genome informatics: Taming the avalanche of genomic data. Genome Biol. 2005;6:301. doi: 10.1186/gb-2004-6-1-301. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Srinivasan B.S., Novak A.F., Flannick J.A., Batzoglou S., McAdams H.H. Integrated protein interaction networks for 11 microbes. Recomb. DNA Tech. Bull. 2006;2006:1–14. [Google Scholar]
  41. Suh Y.H., Checler F. Amyloid precursor protein, presenilins, and alpha-synuclein: Molecular pathogenesis and pharmacological applications in Alzheimer's disease. Pharmacol. Rev. 2002;54:469–525. doi: 10.1124/pr.54.3.469. [DOI] [PubMed] [Google Scholar]
  42. Thelemann A., Petti F., Griffin G., Iwata K., Hunt T., Settinari T., Fenyo D., Gibson N., Haley J.D. Phosphotyrosine signaling networks in epidermal growth factor receptor overexpressing squamous carcinoma cells. Mol. Cell. Proteomics. 2005;4:356–376. doi: 10.1074/mcp.M400118-MCP200. [DOI] [PubMed] [Google Scholar]
  43. Troyanskaya O.L., Dolinski K., Owen A.B., Altman R.B., Botstein D.A. Bayesian network for combining heterogeneous data sources for gene function prediction (in Saccharomyces cerevisiae) Proc. Natl. Acad. Sci. 2003;100:8348–8353. doi: 10.1073/pnas.0832373100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. von Mering C., Jensen L.J., Snel B., Hooper S.D., Krupp M., Foglierini M., Jouffre N., Huynen M.A., Bork P. STRING: Known and predicted protein–protein associations, integrated and transferred across organisms. Nucleic Acids Res. 2005;33:D433–D437. doi: 10.1093/nar/gki005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. von Mering C., Jensen L.J., Kuhn M., Chaffron S., Doerks T., Krüger B., Snel B., Bork P. STRING 7: Recent developments in the integration and prediction of protein interactions. Nucleic Acids Res. 2007;35:D358–D362. doi: 10.1093/nar/gkl825. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Zhang H. The optimality of naive Bayes. Proceedings of the 17th International FLAIRS conference (FLAIRS2004); Menlo Park, CA. AAAI Press; 2004. [Google Scholar]
  47. Zhang T., Wong S.H., Tang B.L., Xu Y., Peter F., Subramaniam V.N., Hong W. The mammalian protein (rbet1) homologous to yeast Bet1p is primarily associated with the pre-Golgi intermediate compartment and is involved in vesicular transport from the endoplasmic reticulum to the Golgi apparatus. J. Cell Biol. 1997;139:1157–1168. doi: 10.1083/jcb.139.5.1157. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Zhong W., Sternberg P.W. Genome-wide prediction of C. elegans genetic interactions. Science. 2006;311:1481–1484. doi: 10.1126/science.1123287. [DOI] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES