Long-range regressions to previously read words are guided by spatial and verbal memory

Abstract

To examine the nature of the information that guides eye movements to previously read text during reading (regressions), we used a relatively novel technique to request a regression to a particular target word when the eyes reached a predefined location during sentence reading. A regression was to be directed to a close or a distant target when either the first or the second line of a complex two-line sentence was read. In addition, conditions were created that pitted effects of spatial and linguistic distance against each other. Initial regressions were more accurate when the target was spatially near, and effects of spatial distance dominated effects of verbal distance. Initial regressions rarely moved the eyes onto the target, however, and subsequent “corrective” regressions that homed in on the target were subject to general linguistic processing demands, being more accurate during first-line reading than during second-line reading. The results suggest that spatial and verbal memory guide regressions in reading. Initial regressions are primarily guided by fixation-centered spatial memory, and corrective regressions are primarily guided by linguistic knowledge.

Written language offers the reader several types of modality-specific information. In contrast to spoken language, where the temporal unfolding of a transient signal determines the order in which linguistic symbols are received, written language consists of a sequence of concurrently visible and relatively permanent symbols, the order of which is determined by spatial conventions. In English, both letters and words are ordered from left to right on a line of text, and successive lines are ordered from top to bottom. Since high acuity vision is limited to a relatively small spatial area, only a subset of the available linguistic symbols can be encoded while a particular text location is viewed (fixated). Consequently, the reading of an ordered sequence of words requires action—that is, the execution of a principled sequence of eye movements that directs high-acuity vision to different locations so that sentence and passage comprehension can take place.

Most eye movements (saccades) progress with word order. Word and fixation order do not completely match, however, since a considerable proportion of eye movements—typically, from 10% to more than 25%—move the eyes to a previously read segment of the text (Rayner & Pollatsek, 1989). Most of these regressions are relatively small, extending across less than 10 letter spaces (LS), and they move the eyes to text to the left of the current fixation on either the same or the prior word (Radach & McConkie, 1998; Vitu, 2005; Vitu & McConkie, 2000). These short-range regressions appear to support the ongoing recognition of a word or of two spatially adjacent words (Vitu & McConkie, 2000). Readers also execute a small proportion of longer range regressions that move the eyes outside the range of effective vision. These memory guided regressions interrupt the temporal progression, or the temporal overlap, in the processing of consecutive words in the text. In spite of this disruption, regressions do not create the subjective experience of a “word salad” (Kolers, 1968). In fact, during silent reading, readers are generally unaware that a regression was executed.

How are inconsistencies between the temporal order of word viewing and spatial word order resolved when a regression occurs? Kolers (1968) and Kennedy (Kennedy, 1992; Kennedy, Brooks, Flynn, & Prophet, 2003; Kennedy & Murray, 1987) suggested that readers code the location of identified words and that knowledge of word location determines the word order when a regression occurs. According to Kennedy, readers apply spatial indexes to identified linguistic units so that they become spatially addressable. These indexes serve two functions: They can direct a regression to a previously read text segment when it becomes relevant during subsequent sentence and passage reading, and they maintain correct word order in case a long-range regression occurs. Spatial indexes may be established in relation to the most accessible point of reference (Kennedy et al., 2003), such as the left side margin of a line of text, a screen frame, or page boundaries. Since readers are rarely aware of their regressions, spatial indexes appear to constitute implicit spatial knowledge that can be accessed in the absence of explicit linguistic knowledge.

To examine the representational nature of readers’ knowledge of spatial word location, Kennedy et al. (2003) asked participants to read single-line materials consisting of a sentence and a subsequent question that referred to a particular target word in the sentence. Prior to the participants’ answering, the first sentence either was removed from the screen or remained visible for reinspection. Under these conditions, readers made a regression toward the location of a removed or visible target word on 13% and 50% of the trials, respectively, indicating that the visibility of prior text influenced the decision to execute a regression. Critically, an executed regression moved the eyes to, or very close to, the target word, irrespective of the visibility of the target during question answering and irrespective of the spatial distance between the launch point of a regression and the hypothesized regression target. As such, these results appear to constitute prima facie evidence for the spatial representation of the locations of previously read words and for the execution of relatively precise memory guided regressions to the location of a particular word when it becomes pertinent at a later point in time.

Effective spatial selection also occurred in other studies of reading. After the participants had read a brief passage of text, Christie and Just (1976) asked them to answer a text-related question while the text remained visible on the screen. On about a third of the trials, readers made a spontaneous eye movement to the sentence that contained question-relevant information. In Baccino and Pynte’s (1994) experiment, where participants first read a short passage of text and then pointed to the previous location of a probe word that appeared at the bottom of the computer screen, participants were able to indicate the location of the target word with a remarkable degree of accuracy. Fischer’s (1999) pointing experiments controlled the viewing duration of individual words during sentence reading (500 msec each) and viewing order, by presenting the words of an eight-word sentence from left to right on single lines of text in one condition. Under these experimental conditions, mean pointing accuracy was approximately 90%, and it reached 100% when a queried word occupied a position at or near the onset of the previously read sentence. Together, these experiments appear to converge on two conclusions: First, readers represent the precise location of previously read words; and second, they can use this knowledge to execute spatially selective responses.

Verbal memory for previously read words can also be used to determine the location of a previously read word, however, especially when to-be-remembered text occupies a single line (Inhoff, Weger, & Radach, 2005). This is because the spatial and temporal ordering of words is highly correlated, so that knowledge of the order of previously read words, together with information that can be obtained from the fixated line, can be used to determine prior word location. For instance, verbal memory can be used in the sentence/target-word sequence

The man was looking for the spade in the shed next to the barn. Spade?

to determine that the target occurred roughly in the middle of the previously read sentence, and sentence length can be determined from available visual cues, including line margins. A verbal memory guided regression that returned the eyes to a location near the middle of the previously read sentence would thus effectively position the eyes at or near the target, and this could be achieved regardless of the peripheral visibility of the previously read words. Linguistic knowledge also can be used to estimate the approximate location of a previously read text segment when more than one line of text was read (Rawson & Miyake, 2002). In fact, spatial selection can be exceedingly poor when spatial word order and temporal (linguistic) word order are no longer correlated (Fischer, 1999, Experiment 1). In one of the conditions of Fischer’s experiment, each successive word of a sentence was displayed at a randomly selected location (without replacement) within a 2-D grid that consisted of three vertically ordered lines with two or three horizontal word locations. The linguistic-temporal ordering of words thus mismatched the conventional spatial ordering of words from left to right and from top to bottom. Pointing accuracy was now very poor (13.5%) and did not differ from chance.

The relatively unusual presentation format and a relatively high criterion for accurate responses could have led to an underestimation of the use of spatial memory, however, when spatial and temporal order mismatched in Fischer’s (1999) study. Because pointing responses were considered correct only when they reached the precise location of the previously read target, accuracy rates could have been near chance, even if coarse-grained spatial knowledge was available and could be used to point to a location in the vicinity of the target. Near-chance performance in the pointing task may also be a poor predictor of regression accuracy in reading. The manual pointing at a previously viewed word location involves use of explicit knowledge; the targeting of regression in reading does not.

Consistent with this view, readers’ regressions were inaccurate, yet spatially selective, in our experiments with single-line sentence materials (Inhoff & Weger, 2005). Experiments 3 and 4 of our study used a fact-defining single-line sentence to establish a relationship between two agents and a subsequent to-be-answered question that probed knowledge of that relationship. The sentence

My father is younger than my mother. Who was born earlier?

was to be followed by the articulation of the correct response, “mother,” which we also considered the regression target. The first sentence either disappeared or remained visible while the question was read. As in Kennedy et al. (2003), regressions were much more common when the fact-defining sentence remained visible, and regressions were spatially selective, with larger regressions toward more distant targets. Regressions were rather inaccurate, however, and initial long-distance regressions rarely positioned the eyes at the target itself. Moreover, accuracy was a function of the distance of the target, regressions being less accurate when they were launched toward a relatively distant target than when they were launched toward a relatively near target.

Coarse-grained implicit knowledge of the spatial location of the previously read target or knowledge of verbal sentence content could have been used to achieve spatial selectivity in these experiments. Both theoretical accounts—which we will refer to as the spatial coding hypothesis and the verbal reconstruction hypothesis—can also accommodate the larger regression error for more distant targets by attributing it to oculomotor targeting error. In standard oculomotor aiming tasks, saccade accuracy decreases in a linear fashion with target distance (Kapoula, 1985); similarly, saccadic undershoot may have been larger for relatively distant than for relatively close targets in our experiments. The main goal of the present study was to determine the nature of the representation that guides spatially selective regressions during skilled reading—that is, whether they were guided by spatial knowledge, by verbal knowledge, or by both.

EXPERIMENT 1

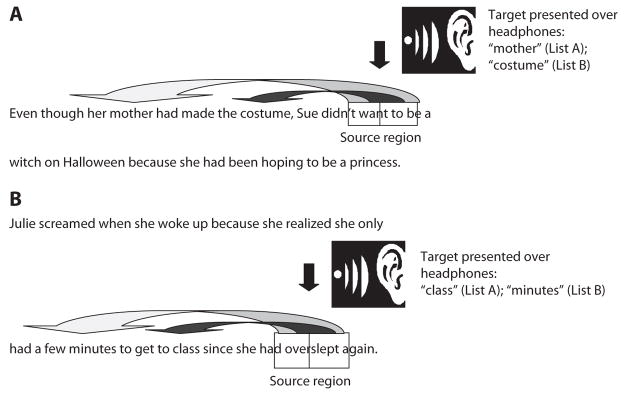
Regressions in Experiment 1 were elicited via a relatively novel experimental technique, the contingent-speech technique (Inhoff, Connine, & Radach, 2002; Inhoff & Weger, 2005), that presented a spoken target word when the eyes reached a predetermined sentence location. The location of both the target and the presentation varied from trial to trial. The visual form of the spoken target had been encountered earlier in the sentence, and readers were instructed to move the eyes back to it upon target hearing. The technique thus controlled the spatial location from which a regression was to be launched (the source area) and the spatial location of the regression target. Relatively complex sentences that extended across two lines were used to manipulate the demand of linguistic processing when a regression was to be executed; that is, regressions were to be executed either during the reading of the first line of the sentence, when linguistic processing demand was low, or during the reading of the second line, when linguistic processing demand was high. Regressions were initiated from the end of the first or second line and had to be directed to a close or more distant target in the same line. Samples of these two conditions, which will be referred to as within-line conditions (first and second lines), are depicted in Figure 1. If verbal knowledge were used to infer the location of the regression target, the spatial selectivity of a regression and its accuracy should be lower when linguistic processing demand is high—that is, during the reading of the second line—than during the reading of the first line, when linguistic processing demand is relatively low. The effect of line number on regression accuracy should be relatively small or negligible, by contrast, if spatial knowledge guided regressions. Spatial knowledge is generally implicit, and it should thus be less subject to the effects of processing demands than verbal working memory (WM) would be.

Figure 1.

Samples from the within-line conditions: (A) When the eyes enter a window at the end of the first line (invisible to the reader), a target word is presented over headphones. This target can be either close or distant. Spatial and linguistic distance are correlated in this condition. Participants are asked to discontinue reading and to directly make an eye movement to the respective word. Target length and frequency are matched across the two distance conditions. The location of targets varied across trials (between word numbers 2 and 8 in the first line and the second line), such that readers could not anticipate the location of a target. See text for details. (B) Target and source words occur in the second line.

Previous research has varied the distance between two critical text-elements as a means to manipulate linguistic processing demand—in particular, WM load. Miyake, Just, and Carpenter (1994), for instance, showed that the resolution of lexical ambiguity becomes more difficult when the distance increases between an ambiguous word and the corresponding disambiguating region. Their experiment manipulated the number of bridging words between a biased homograph and the subsequent disambiguating region. Control sentences with a matched number of bridging words contained unambiguous words. Under these conditions, increasing the number of bridging words selectively increased the viewing duration for these words in the ambiguous condition. More than one meaning of the homograph was carried forward during the reading of bridging words, and the maintenance of multiple semantic representations in WM became more difficult as the number of bridging words—and the complexity of to-be-comprehended text—increased. In the present experiment, we did not vary the actual distance between the source and the target and, hence, did not manipulate verbal WM load in a traditional sense; instead, the distances between the source and target locations were similar in the two within-line conditions. The amount of to-be-comprehended read text increased, however, from the first line to the second line, and we assumed that linguistic processing demand would be lower during the first-line reading than during the second-line one.

In addition, the experimental technique was used to pit effects of spatial distance (between the source and the target positions of a regression) against effects of temporal/linguistic distance (the number of words between the source and the target positions). This was accomplished by creating two additional conditions: one in which the regression target was spatially close to but temporally/linguistically distant from the regression source location, and one in which the regression target was spatially distant but relatively near in terms of temporal/linguistic distance. To achieve this, auditory target words were presented at the beginning of the second line in this condition, and readers had to direct their eyes to target locations in the first line. A spatially close target was now linguistically (temporally) distant, as more words—hence, longer reading time—had elapsed since the actual reading of the target word. Conversely, a spatially distant target was now linguistically (temporally) close, as fewer words—hence, a shorter reading time—had elapsed since the reading of the target word (see Figure 2A). This condition will henceforth be referred to as the between-line condition. If regression accuracy is a function of spatial distance, accuracy should be higher for spatially close but linguistically distant targets than for spatially distant but linguistically close targets in this condition. By contrast, if regression accuracy is a function of temporal/linguistic distance, accuracy should be higher for linguistically close but spatially distant targets.

Figure 2.

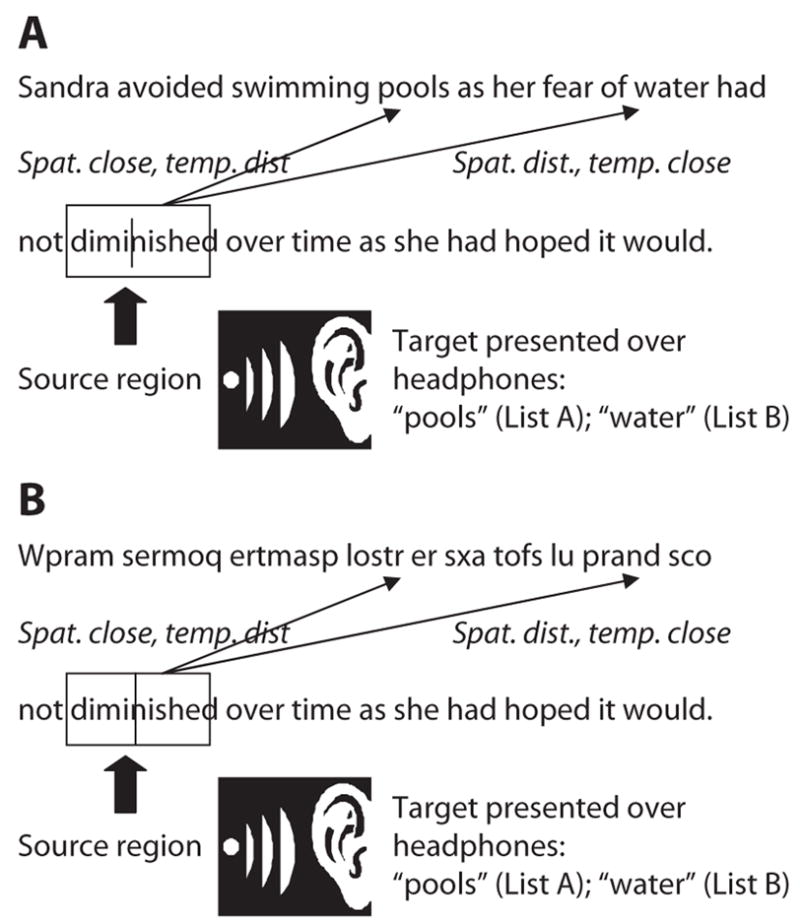
Samples from the between-line conditions. (A) The source region occurs at the beginning of the second line, and target words occur in the first line, to the right of the source. Once again, target locations vary considerably across trials, ranging from word numbers 4 to 11. Spatial and linguistic distance are dissociated in this condition: A target that is close in a spatial sense is distant in a temporal/linguistic sentence because it was encountered earlier during initial sentence reading, and vice versa. (B) In Experiment 2, the words in the first line of experimental sentences were replaced with random letters simultaneously with the presentation of the auditory target.

As is obvious from the two figures, targets in the within-line condition were always to the left of the presentation location, whereas targets in the between-line condition were to its right. Where the two conditions were directly compared, preregression durations were first analyzed to ensure that there were no systematic differences in the programming of regressions across these conditions.

Method

Participants

Twenty-four Binghamton University undergraduates participated in this experiment. They either received course credit or were paid for their participation.

Materials

Sixty-four sentences containing 15–25 words were generated. All sentences were shown in full, occupying approximately the same horizontal extent on two lines, each of which contained 52–74 characters. Each sentence contained two potential regression targets: a left-side target that occupied a location within the first half of a line of text, and a right-side target that occupied a location within the second half of the same line. None of the targets in experimental sentences occupied the first or last word location on a line. All targets were content words, and left- and right-side potential targets were matched on word frequency, which was 78 [Min., 0; Max., 509; standard deviation (SD), 105] and 81 (Min., 6; Max., 656; SD, 132) occurrences per million, respectively (Kučera & Francis, 1967) [t (63) = 0.145, p = .88], and on word length, which was 6.33 (Min., 3; Max., 11; SD, 1.8) and 6.83 LS (Min., 3; Max., 11; SD, 2.1), respectively [t(63) = 1.48, p = .14]. Each sentence also contained an 11-LS (source) region that was partitioned into two consecutive 5- and 4-character segments, plus the corresponding spaces. Two spoken words were paired with each sentence: one that matched the phonological form and meaning of a left-side visual target, and one that matched the phonological form and meaning of a right-side target. Only one of the two members of a spoken word pair was presented during sentence reading; this occurred when the eyes moved into one of the two segments of the source region. The location of target words in the between-line conditions ranged between word numbers 4 and 11, with an average of 7 and an SD of 2.4. The location of target words in the within-line conditions ranged between word numbers 2 and 8, with an average of 4.7 and an SD of 1.8.

Readers were informed that a spoken word, presented at that instant, matched a word read earlier in the sentence—the regression target—and that the eyes should return to the target upon their hearing the word. After this elicited regression, sentence reading was to be continued so that a potential question with regard to sentence content could be answered correctly.

The source region and the target occupied the same line in 32 of the sentences, with half of all regressions to the target being elicited during the reading of the first line and the other half during the reading of the second line. In these within-line regression conditions, the target was always to the left of the source region. The mean distance between the first letter of the two source segments and the first letter of a spatially close (right-side) and distant (left-side) target was 20.5 (Min., 11; Max., 30; SD, 4.8) and 42.3 (Min., 30; Max., 50; SD, 5.6) LS, respectively, when the source and target locations occupied the first line; the corresponding distances were 21.4 (Min., 13; Max., 31; SD, 4.4) versus 42.9 (Min., 34; Max., 55; SD, 5) LS when source and target occupied the second line. The spatial distance between the source and target areas was thus virtually identical in the first- and second-line conditions; linguistic processing demand, by contrast, was assumed to be substantially higher during the second-line reading than during the first-line reading.

The remaining 32 sentences were used to dissociate spatial and temporal/linguistic distance. On these trials, the source region was placed near the beginning of the second line of text, with the first letter position ranging from LS 3 to LS 15 on that line of text. The regression target in this condition always occupied the first line of text, so that a regression moved the eyes across a line of text. Left-side targets were now horizontally closer to the source region, with an onset distance of 17.2 LS (Min., 5; Max., 32; SD, 5.9), whereas right-side targets were horizontally further away, with an onset distance of 38.8 LS (Min., 28; Max., 48; SD, 5.6). Spatial and temporal/linguistic distances were now pitted against each other, since more words intervened between source and target reading in the spatially near than in the spatially distant condition. The two dissociation conditions of Experiment 1 are depicted in Figure 2A.

Although there was considerable variation in source and target locations within the 64 experimental sentences, an additional 16 filler sentences were added to further dilute expectations concerning the source and target locations. In these filler sentences, probes and targets occupied randomly selected word locations, the only constraint being that the target word should precede the source region. These filler sentences were created so as to deliberately add variability to the sentence pool: Only two of the filler sentences had nouns as targets (targets were mostly verbs or adjectives). In five cases, a target or source word occupied the first or last position of a line. In three cases, the target word was in the first half of the first line and the source region in the second half of the second line; in five cases, the target word was in the second half of the first line and the source region in the second half of the second line. In six cases, there was only one word between the target and the source. These criteria overlapped.

Apparatus

All sentences were displayed in black on a gray background on a 21-in. Liyama Vision Master 510 monitor with a screen refresh rate of 160 Hz. All text was in a Courier-type font, so that each character occupied the same horizontal area of text. A chinrest was used to stabilize the head and to reduce movements. This created a viewing distance of approximately 85 cm, at which each character subtended approximately 0.44° horizontal of visual angle. Viewing was binocular, but eye movements were recorded from the right eye only by an SR Research Eyelink II video-based pupil-tracking system. To record eye and head position, the system uses a small video camera, positioned below the right eye and held in place by a head gear, and a head position sensor mounted on the head gear. The system has a relatively high temporal and spatial accuracy, with a temporal sampling rate of 500 Hz, and an absolute spatial resolution better than one character space.

Procedure

To achieve a relatively high tracking accuracy and to minimize head movements, participants were asked to place their chins on chinrests throughout the experiment. The experiment began with a 2-D calibration of the eye-tracking system: Participants were asked to fixate a visual marker that appeared at nine different locations on the screen in random order (in the corners of the screen as well as in between and, finally, in the center). Following this, a validation cycle verified that the eye movement measurement was consistent and accurate to the nearest character space across the two measurement cycles. The calibration-validation procedure was repeated after approximately every 8–10 sentences, and drift corrections were performed after each trial to maintain a high level of tracking accuracy.

Each trial began with a fixation cross that appeared at the left side of the screen. Sentence onset was controlled by the reader, who pressed the space bar to start a trial. Once the sentence appeared, readers started reading the two lines of text. Upon crossing the left-side boundary of the source region, the target was presented via headphones, and the reader then launched an eye movement to the location of that target. Readers were instructed that the word presented via headphones had been encountered earlier during sentence reading. The task was to make a direct eye movement to that word and to fixate it briefly. After fixating the word, readers were asked to finish reading the sentence. They were free either to continue reading from the location of the target word or to return to the location where they had interrupted reading and finish the remainder of the sentence. Once they finished reading, participants were asked to press the space-bar to proceed with the experiment. The target words were recorded by a native English-speaking woman. The mean spoken (target) word duration was 728 msec, as sampled from 15 randomly selected words. Trials were excluded when inadvertent line-switches or eye-blinks caused a premature presentation of the auditory probe; this occurred on 5.5% of the trials. Instances of inaccurate calibration were also eliminated from the analyses.

A brief practice block of 10 trials preceded the experiment. To encourage reading for meaning during practice and experimental trials, comprehension questions were asked after a random number of sentences had been read, with a mean distance of approximately nine sentences. Readers answered these questions correctly on more than 90% of the probed trials. The experimental session took approximately 45 min, and participants were given a 5-min break after half of the experiment.

Design and Measurement

Two identical lists of visual sentences were used. A spoken target word was linked to each sentence on a list, and the two lists differed in that a different member of the spoken word pair (left vs. right target) was presented on experimental trials when the first and second lists were read. Both sentence lists contained an equal number of left- and right-side targets in all conditions. The order of target locations on a list was randomized, and list assignment was counterbalanced over consecutive participants.

A virtual spatial window was created as the source region, which consisted of two consecutive units, 5- and 4-LS segments long, plus the adjacent spaces, for a total source-size of 11 characters. A saccade that moved the eyes into this region initiated the presentation of the spoken target word.

Two regression measures were used: regression size and regression accuracy. Regression size was determined by measuring the size of a regression leaving the source region. In the within-line condition, two measures of regression size were used: a standard measure and a cumulative measure. The standard measure reflects the size of the outgoing regression that occurs during the first pass of a word. The cumulative size reflects the cumulated size of all consecutive regressions until the first right-directed eye movement occurs. For example, a sequence of eye movements leaving the source area may consist of an initial regression of 17 characters, followed by two consecutive regressions of 5 characters each and a final right-directed saccade of 19 characters. In this case, the standard measure would be 17 characters, and the cumulative measure would be 27 characters. In the between-line condition, only the standard measure was used. The cumulative measure was avoided, because it was difficult to compute and because it would have required forward eye movements to be cumulated. These forward movements, however, may have been instances of regular saccades that occurred because participants resumed normal reading.

Regression accuracy was determined by deducting the size of the regression from the distance between the source and the target word. The size of the regression was defined as above. The distance was defined as beginning with the center of the respective source-region unit that the regression was initiated from and ending with the center of the target word. The center of the source unit was computed by dividing the length of the respective source segment by two. The center of the target word was estimated from the average length of all target words in the experimental sentences (divided by two), yielding a standard value used for all analyses in both experiments. Absolute accuracy scores were computed so that overshoots and undershoots would not be averaged out. For example, two landing errors, one overshooting the target by +10 LS and one undershooting the target by −8 LS (undershoot), would yield an average absolute error of 9 LS.

For both size and accuracy measures, outgoing regressions in the within-line conditions were included only when they were 8 LS or larger and did not bring the eyes to a different line. The criterion of a minimum size of 8 LS was used to increase the likelihood that regressions included in these analyses were actually intended to reach the target rather than being incidental regressive eye movements. For the between-line condition, no size restrictions were used, because the line-shift criterion was sufficient to assume that the regression was launched with the intention to move the eyes toward the target. Therefore, in the between-line condition, all eye movements were used, as long they returned to the first line. Except for supplementary comparisons reported at the end of the Results section, within- and between-line regressions were analyzed separately. Where relevant, first-pass skipping rates, first-pass gaze durations, and the duration of the fixation preceding an initial regression, henceforth referred to as preregression duration (all between 50 and 1,500 msec), were also computed.

Results

To determine whether there were intrinsic processing differences between right- and left-side targets prior to the reaching of the source region, the first-pass viewing (gaze) durations and the skipping rates of target words were determined. The data are shown in Table 1. In the within-line condition, gaze durations and skipping rates showed numerically longer viewing durations for the left- than for the right-side target on the first line, 295 and 258 msec, respectively [t (23) = 1.89, p = .071]. Left-side targets were also skipped more often than right-side targets—13% and 11%, respectively—although this difference did not approach significance [t(23) = 0.75, p = .46]. Gaze durations for left- and right-side targets were more similar when they occupied the second line (278 and 258 msec, respectively) and the difference no longer approached significance [t(23) = 1.24, p = .23]. Again, the left-side target tended to be skipped more often (20% vs. 16%, respectively), although the difference was again not reliable [t(23) = 1, p = .31]. In the between-line condition, there was no difference in first-pass viewing times [273 and 267 msec for right- and left-side targets, respectively; t(23) = 0.76, p = .46], although left-side targets were again skipped more often than right-side targets [15% and 9%, respectively; t(23) = 2.46, p = .02]. Together, these analyses reveal no clear-cut processing differences between left- and right-side targets. Although there was a tendency toward longer left-side target gaze durations in the two within-line conditions, there was also a complementary tendency toward a higher skipping rate for targets at that location.

Table 1.

First-Pass Reading Times and Skipping Rates (in Milliseconds) for Targets Appearing in Left- or Right-Side Locations As a Function of Line Condition (Between or Within) in Experiment 1

	First-Pass Reading Time (Gaze)				Skipping Rate
	Left		Right		Left		Right
	M	SE	M	SE	M	SE	M	SE
Between lines	267	12.2	273	8.8	.15	.02	.09	.02
Within lines: First	295	19.0	258	9.2	.13	.02	.11	.02
Within lines: Second	278	19.0	258	11.0	.20	.04	.16	.03

Within-Line Regressions

Regression size

The regression-size data are shown in Table 2 as a function of spatial distance and linguistic processing demand. To recall, if— as maintained by the inference hypothesis—the spatial selectivity of regressions were determined by the ease with which verbal material can be used to infer the target’s prior location, second-line regressions should be less selective than first-line regressions. If spatial selectivity were based on the use of spatial knowledge, however, effects of line order might be absent or negligible. The results of a 2 (target distance: close vs. distant) × 2 (linguistic processing demand: first vs. second line) ANOVA revealed shorter regressions to close than to distant targets (20.8 and 23.1 LS, respectively). Although this effect of spatial selectivity was relatively small (2.3 character spaces), it was statistically reliable [F(1,21) = 7.2, p < .05].¹ Critically, the effect of spatial selectivity was similar for the first and second lines. Neither the main effect of linguistic processing demand [21.2 LS and 22.6 LS for the first and second line; F(1,21) = 1.4, p = .25] nor the interaction between linguistic processing demand and target location (F= 0) was reliable.

Table 2.

Regression Size and Accuracy As a Function of Sentence Location and Line for Both the Standard and the Cumulative Regression Measures in the Within-Line Condition of Experiment 1

	Standard Regression Measure								Cumulative Regression Measure
	Regression Size				Regression Deviation				Regression Size				Regression Deviation
	Left Side		Right Side		Left Side		Right Side		Left Side		Right Side		Left Side		Right Side
Target Location	M	SE	M	SE	M	SE	M	SE	M	SE	M	SE	M	SE	M	SE
First line	22.3	1.1	20.1	1.1	18.4	1.2	6.0	0.5	41.5	0.7	24.7	1.0	4.8	0.5	7.0	0.8
Second line	23.8	1.5	21.5	1.5	19.1	1.4	7.7	0.8	38.6	1.4	27.5	1.4	6.1	0.8	10.0	1.4

Note— The data are based on the 22 participants included in the analyses for which data were available in all cells.

The cumulative regression size data (see Table 2) also reveal spatial selectivity: Regressions to close targets were substantially shorter than were regressions to distant targets [26.1 and 40.1 LS, respectively; F(1,21) = 215, p < .001]. Again, there was no effect of line order (F= 0). However, in contrast to the size of the initial regression, cumulative regressions yielded a robust interaction between line order and target distance [F(1,21) = 10.47, p < .01], the difference between the spatially distant and near conditions being larger—that is, with more spatial selectivity—during the first-line reading, when linguistic processing demand was low. Verbal knowledge thus appeared to influence “corrective” regressions that occurred after an initial regression toward the target was executed. The number of saccades that contributed to a cumulative regression sequence was also computed. This number was similar for regression sequences when linguistic processing demand was low or high [F(1,21) = 0.3, p = .59]. There was a larger number of consecutive regressions when targets were distant than when they were close [2.5 vs. 1.6; F(1,21) = 127.5, p < .001]. A significant interaction between both factors showed that the effect of distance was stronger for the first than for the second line [F(1,21) = 14.17, p < .01], once more revealing more spatial selectivity when linguistic processing demand was low.

Regression Accuracy

Regression accuracy is also shown in Table 2 as a function of target distance and linguistic processing demand. A 2 (target distance: close vs. distant) × 2 (line number: one vs. two) ANOVA revealed robust effects of target distance, with a larger error for distant than for near targets [18.8 LS and 6.9 LS, respectively; F(1,21) = 83.2, p < .001]. The error was slightly, but not significantly, smaller when linguistic processing demand was low (12.2 LS) than when it was high (13.4 LS) [F(1,21) = 3.29, p = .084]. Critically, there was no interaction between the two factors [F(1,21) = 0.37, p = .55]. The regression error data thus provide further evidence for the spatial coding hypothesis according to which spatial knowledge is used to determine the size of first regressions toward the target.

Was the effect of spatial distance on regression accuracy influenced by oculomotor aiming error? To investigate this possibility, we analyzed the proportion of undershooting (the eyes’ landing position falls short of the target) and overshooting (the eyes move beyond the target) initial regressions as a function of target distance. The data are shown in Table 3. Overall, there were more undershoots than overshoots, with an average number of occurrences of 6.9 and 3 per participant [F(1,23) = 29.2, p < .001]. There was no reliable difference in the occurrence of regressions directed toward close and distant targets [F(1,23) = 2.24, p = .15]. A significant interaction indicated, however, that there were more undershoots in the distant condition than in the close condition, whereas there were more overshoots in the close condition than in the distant condition [F(1,23) = 78.3, p < .001]. It thus appears that the effect of target distance on the accuracy of initial regressions was modulated by oculomotor aiming strategies.

Table 3.

Biases of Landing Errors As a Function of Target Distance in Experiments 1 and 2

			Between Lines
	Within Lines Experiment 1		Experiment 1		Experiment 2
	M	SE	M	SE	M	SE
Close Targets
No. of undershoots	4.6	0.7	1.8	0.3	5.0	0.7
No. of overshoots	5.6	0.5	2.9	0.5	2.3	0.8
Distant Targets
No. of undershoots	9.2	0.5	4.9	0.6	5.9	0.7
No. of overshoots	0.4	0.2	0.4	0.2	0.3	0.3

Note—Reported are average numbers of occurrences per participant.

Because readers often executed additional regressions toward the target, we also computed the error for a cumulative sequence of regressions. This allowed a more detailed analysis of the effects of spatial distance and linguistic processing demand when consecutive regressions homed in on a target. A 2 × 2 ANOVA revealed an effect of distance, with a larger error for close than for distant targets [8.5 LS and 5.4 LS, respectively; F(1,21) = 8.3, p < .01]. There was also a sizable effect of linguistic processing demand, with a smaller cumulative regression error when linguistic processing demand was small (5.9 LS) than when it was high (8.1 LS) [F(1,21) = 8.63, p < .01]. The interaction between the two factors was not significant [F(1,21) = 1.1, p = .3]. Again, this line order effect indicates that corrective regressions toward a target make use of verbal knowledge. Filler sentences were analyzed for completion.²

To summarize, the initial regression toward a target word was spatially selective, being larger, although also more error prone, when directed toward a distant target. Critically, these movements were not influenced by linguistic processing demand. Additional regressions toward the target moved the eyes onto or very near the target, regardless of its distance, and they did this more successfully when linguistic processing demand was low. Spatial and verbal memory thus appear to contribute to regression planning, and they appear to do so in a functionally distinct manner at different points in time.

Pitting the Effect of Spatial Distance Against the Effect of Verbal Distance

As can be seen in Table 4, the analysis of between-line regressions revealed a clear dominance of spatial distance over linguistic/temporal distance. Specifically, initial regressions to more distant right-side targets were significantly larger than regressions to more proximal left-side targets [29.7 and 24.6, respectively; t(22) = 3.45, p < .01], and regression accuracy was higher for spatially close left-side targets than for more distant right-side targets (9.7 and 14.4 LS, respectively). Although the difference was only marginally significant [t(22) = 2.04, p = .054], it must be noted that the direction of the accuracy effect is in harmony with the predictions of the spatial coding hypothesis and directly contrary to the predictions of the verbal inference hypothesis.³

Table 4.

Regression Size and Accuracy in the Between-Line Condition As a Function of Sentence Location in Experiment 1

	Regression Size		Absolute Deviation		Relative Deviation
Side	M	SE	M	SE	M	SE
Left	24.6	1.6	9.7	1.1	2.9	1.4
Right	29.7	1.7	14.4	1.5	−14.0	1.6

Note—The data are based on the 23 participants included in the analyses for which data were available in all cells.

The proportion of overshoots and undershoots was once again investigated as a function of target distance to examine the potential contribution of spatial between-line targeting strategies. Again, there were more undershoots than overshoots [3.4 and 1.6, respectively; F(1,23) = 19.2, p < .001], and there was no reliable difference in the occurrence of regressions to close and distant targets [F(1,23) = 0.85, p = .37]. The interaction between both factors was reliable; again, there were more overshoots than undershoots in the close condition and more undershoots than overshoots in the distant condition [F(1,23) = 32.8, p < .001]. The data are also shown in Table 3. Together, the between-line data thus affirm the critical role of a spatial representation of text for the programming of initial regressions toward a previously read target word and a modulating effect of oculomotor aiming strategies.

Comparison Across the Within- and Between-Line Conditions

Regressions in the within-line condition were always launched from the second half of a line and were directed toward the left of the source region to a target on the same line. Regressions in the between-line condition, by contrast, were always launched from the first half of the second line and were directed toward the right of the source region, to a target in a different line. The programming of regressions may therefore have been different in the within- and the between-line conditions. The results of a 2 (regression-type: within or between lines) × 2 (distance: spatially close or distant target) ANOVA of preregression fixation durations was negative. It revealed an effect neither of regression type [F(1,22) = 1.32, p = .26] nor of distance [F(1,22) = 0.29, p = .6], nor an interaction between the two factors [F(1,22) = 0.53, p = .47]. For the within-line condition, there was also no reliable difference in preregression duration between the first and the second lines [330 and 355 msec, respectively; t(23) = 1.08, p = .29].

Because the programming of initial regressions was quite similar in the within- and between-line conditions, we pooled these data to conduct a more detailed supplementary analysis of spatial and verbal distance effects by creating eight spatial distance categories that ranged from 10–50 LS, with interval sizes of 5 LS (10–15, 16–20, 21–25, etc.; for details, see Table 5). For instance, in the 10–15 LS distance condition, the horizontal distance in the within-line condition was 10–15 LS, which corresponded roughly to three words (which can be seen as equivalent to a low linguistic processing demand). In the between-line condition, the horizontal distance was the same (10–15 LS), but a relatively large number of words (7.7) intervened between the source and the target. With this approach, we could directly compare regressions to targets with matched spatial distances but with substantial differences in the number of intervening words. Note that the number of intervening words changed for the various distance categories. For instance, in the distance category of 46–50 LS, linguistic processing demand was smaller in the between-line condition (4.3 intervening words) than in the within-line condition (7.4 intervening words). These proportions are also shown in Table 5.

Table 5.

Spatial Distance Conditions, Defined in Letter Spaces, Along With the Corresponding Verbal Distances in Words in Experiment 1 (Number of Words, As Computed From First Source Unit to Target Word)

	Verbal Distance				Regression Error
	Between		Within		Between		Within
Spatial Distance	M	SE	M	SE	M	SE	M	SE	df	Error Difference
10–15	7.72	0.1	3.02	0.1	11.9	2.3	5.7	0.7	58	6.2**
16–20	7.56	0.1	3.41	0.1	9.3	1.1	5.7	0.5	124	3.6***
21–25	7.54	0.1	3.73	0.05	9.1	1.0	7.2	0.6	123	1.9
26–30	6.12	0.3	4.47	0.2	10.3	1.9	8.1	1.1	48	2.2
31–35	5.06	0.4	6.85	0.15	7.6	1.2	13.7	1.7	35	−6.1***
36–40	4.12	0.1	7.14	0.1	14.6	2.3	16.5	1.2	79	−1.8
41–45	3.65	0.1	7.25	0.04	14.4	1.4	20.1	0.8	162	−5.7**
46–50	4.30	0.3	7.41	0.1	19.1	2.9	22.5	1.5	64	−3.4

Note—Average deviations, standard errors, difference scores, and significance values of within- and between-line comparisons are also provided. The data show average deviations across conditions, not participants.

^**p < .01.

^***p < .001.

The size of regressions across the two line conditions (within and between) was now directly compared for these eight spatial distance categories. The results are shown in Table 5. Due to the relatively small number of data points in each condition, raw data, rather than subject-based averages, were contrasted. An 8 (spatial distance) × 2 (regression type: between vs. within line) factorial ANOVA showed that regression error increased with distance [F(7,693) = 32.46, p < .001]. There was no effect of regression type (between or within) [F(1,693) = 0.31, p = .58], but there was a reliable interaction between the two factors: For intervals between 10 and 30 LS, errors were larger in the between- than in the within-line condition, whereas the opposite effect emerged for intervals between 31 and 50 LS [F(7,693) = 6.1, p < .001]. Separate t tests compared the differences for each of the eight distance conditions, and the data and results are also shown in Table 5. They show once again that initial regression accuracy decreased with increasing spatial distance. When spatial distance was kept constant within a category, however, regression accuracy was a function of the number of intervening words, with a larger regression error when the number of intervening words was large.

Finally, we conducted a stepwise linear regression analysis to investigate the joint contribution of spatial distance (eight categories), verbal distance (number of intervening words), and regression type (within or between line) on the magnitude of the regression error. The predictors accounted for slightly less than a third of the variability in the regression error data (R² = .31, adjusted R² = .308), and the effects of two predictors were reliable: Regression error increased with spatial distance (standardized b = .48) and with the number of intervening words (standardized b = .17). These data show that spatial distance had a stronger predictive value and, thus, dominated the effect of the number of intervening words.

Discussion

The main goal of Experiment 1 was to determine the nature of the information that was used to guide long-range regressions during reading. Descriptive aspects of long-range regressions in the experiment replicated findings of our earlier study (Inhoff & Weger, 2005). Again, initial regressions toward a same-line target word were spatially selective but relatively inaccurate. The main effect of target distance was relatively small, however, even though spatially close and spatially distant same-line targets were separated by approximately 20 LS. Readers often executed additional (cumulative) regressions that moved the eyes closer to the regression target.

Experiment 1 further revealed that the size and accuracy of same-line (initial) regressions were not reliably different when linguistic processing demand was low, which occurred when source and target locations occupied the first line, and when linguistic processing demand was high, which occurred when source and target locations occupied the second line. More detailed analyses extended this finding. When spatial distance was held constant, initial regression accuracy was lower when the number of words that intervened between source and target locations was relatively high than when it was low, and the number of intervening words was a significant predictor of regression accuracy. Linguistic processing demands thus influence the size of initial regressions.

Effects of spatial distance on regression accuracy were, however, considerably larger than were the effects of the number of intervening words, at least for the initial regression toward the target. In addition, spatial distance influenced oculomotor targeting strategies, reflected in the larger proportion of over- and undershoots for close and distant targets, respectively. Typically, oculomotor aiming errors are relatively small (see Abrams & Jonides, 1988). They may account for deviations of a few characters from the target in the present experiment, and it may have modulated the accuracy of the initial regression (this aiming error may depend on the peripheral visibility of words, a possibility investigated in Experiment 2). Together, knowledge of the spatial location of a target thus dominated the specification of the size of an initial regression toward a target, and oculomotor targeting strategies and linguistic processing demands appeared to assume a much more subordinate role.

In the present experiment, there was no particular benefit for participants to directly reach a particular target. This may have increased the likelihood for a less direct approach in which the target was reached with multiple consecutive regressions with a relatively large initial regression error. Inclusion of continuing “corrective” regressions in the cumulated regression measures revealed a sizable effect of line number, with regressions being more spatially selective and more accurate for the first line, when linguistic processing demand was low, than for the second line. Again, this finding supports a theoretical conception according to which multiple sources of information are used to direct long-range regressions. Readers primarily use knowledge of the spatial distance of the target from the source for the specification of an initial regression, linguistic distance—that is, the number of words intervening between source and target—assumed a relatively subordinate role, and there was no line-number or processing-load effect. Corrective regressions, by contrast, were more accurate during first-line reading than during second-line reading; in other words, they were guided by a more general knowledge representation that included words read prior to the regression target.

EXPERIMENT 2

In the between-line condition of Experiment 1, spatially close targets were regressed to more accurately than were spatially distant targets when effects of spatial and verbal distance were pitted against each other. Other supplementary analyses confirmed the preferential use of spatial distance knowledge for the programming of initial regressions. An alternative account for the dominance of spatial distance for the programming of between-line regressions remains viable, however. Upon the auditory presentation of the regression target, readers may have shifted visuospatial attention upward and toward the right, since the target was always upward and to the right of the source in this condition. If such a covert shift of attention occurred, and if information was obtained immediately after the attention shift, then the pitting of spatial distance against verbal distance may not have been effective in Experiment 1, since an upward shift of attention (and acquisition of useful information from the first line) would have effectively changed the spatially close but linguistically distant condition of Experiment 1 to a spatially close and linguistically close condition.

Experiment 2 once more pitted spatial and temporal/linguistic distance against each other. To prevent readers from obtaining useful linguistic information from the upper line, all words on that line in experimental trials were now replaced with strings of random letters. The display change occurred simultaneously with the onset of the auditory target presentation. The spatial location of the target word thus had to be determined solely from information available in spatial and verbal memory.

Method

Participants

Twelve Binghamton University undergraduate students participated in this experiment.

Materials and Procedure

The 32 sentences used in the between-line regression condition of Experiment 1 were used in this experiment. The 16 filler sentences were kept to diffuse expectations about the target location. From the within-line condition, only the 16 first-line sentences were included, but the presentation of target words occurred from the second line. For these filler and first-line sentences, there was no display change, so participants would not generally expect a display change. A display change occurred only on half of the trials—that is, in experimental sentences.

The procedure was the same as in Experiment 1, with the following exception: Simultaneously with to the presentation of the auditory target, the first line of text was replaced with random letters in experimental sentences (see Figure 2B). Word length information and the spacing between words were maintained, to keep the visual format of the text on the first line similar across experiments. Participants were informed about the display change in advance and were instructed to make an eye movement to the location of the target word, even though a nonmeaningful sequence of letters would occupy the target’s location. The window that triggered the auditory target and the display change occurred at the beginning of the second line but at random locations in the filler sentences. Sentence comprehension was again checked, and more than 90% of the questions were answered correctly. Inadvertent blinks of the eyes or calibration errors caused a premature presentation of the auditory probe on 22% of the trials, which were excluded from analyses. Instances in which the calibration was inaccurate were also eliminated from the analyses.

Results

As in Experiment 1, we examined target reading prior to the reaching of the source area. Again, the results revealed no reliable effect of spatial sentence location on gaze durations [t (11) = 1.44, p = .18] or skipping rates [t(11) = 1.15, p = .27]. The effect pattern is shown in Table 6.

Table 6.

Fixation Durations (in Milliseconds) and Skipping Rates As a Function of Sentence Location in the Between-Line Condition of Experiment 2

	First-Pass Reading (Gaze)		Skipping Rate
Side	M	SE	M	SE
Left	260	17.4	.16	.03
Right	285	24.0	.12	.03

Pitting the Effect of Spatial Distance Against the Effect of Verbal Distance on Initial Regressions

As can be seen in Table 7, initial regressions to spatially close but linguistically distant targets were shorter than regressions to spatially distant but linguistically close targets (10.5 and 14.6 character spaces), although the effect did not reach significance [t(11) = 1.8, p = .1].

Table 7.

Size and Accuracy of Regressions As a Function of Sentence Location in the Between-Line Condition of Experiment 2

	Regression Size		Absolute Error		Relative Error
Side	M	SE	M	SE	M	SE
Left	10.5	2.5	15.9	1.5	8.5	2.5
Right	14.6	3.3	27.7	3.3	27.4	3.5

Critically, regressions to targets that were spatially close but linguistically distant were once again more accurate than regressions to spatially distant but linguistically close targets, with regression errors of 15.9 and 27.7 LS, respectively, for the two conditions [t(11) = 3.4, p < .01]. These data are also shown in Table 7. Filler sentences were analyzed for completion.⁴

Guiding the eyes to the target at a first-line location when the line is occupied by random letters is an unnatural task that may require practice; that is, readers may have been struggling with episode specific task demands, particularly during the beginning of Experiment 2. A 2 (target location: spatially near vs. distant) × 2 (practice: first or second half of the materials) ANOVA revealed a main effect of sentence location, with landing errors being smaller in the spatially close than the spatially distant condition [16.3 and 25.9 LS, respectively; F(1,9) = 8.28, p < .05]. Notably, there was no effect of practice [F(1,9) = 0.60, p = .46] and no interaction of practice with distance [F(1,9) = 0.16, p = .7].

The effect of spatial distance on regression accuracy was thus replicated in the present experiment, and it was quite substantial in nature. The influence of aiming error seemed to be relatively small. Examination of aiming error type (over- vs. undershoot) for near and far targets revealed more undershoots than overshoots [5.5 and 1.3, respectively; F(1,11) = 32.2, p < .001] and no reliable effect of distance [F(1,11) = 1.7, p = .21]. Although the interaction between both factors was reliable [F(1,11) = 5.5, p < .05], with more undershoots for near targets, both near and far targets now were subject to more under- than overshoots. The data are reported in Table 3.

To determine the extent to which the masking of the first line influenced regression accuracy, a further supplementary analysis was conducted that examined regression accuracy in Experiments 1 and 2 as a function of target distance (spatially near vs. distant). Again, the effect of spatial target distance was highly reliable, with regressions to relatively near words being more accurate than regressions to distant words [12.8 vs. 21.1 LS; F(1,33) = 16.8, p < .001]. There was also a main effect of experiment, regression errors being smaller when the eyes regressed to a line with meaningful text in Experiment 1 (12.1 LS), than when they regressed to a line with strings of random letter combinations in Experiment 2 (21.8 LS) [F(1,33) = 35.3, p < .001]. Even though the effect of distance tended to be greater in Experiment 2 than in Experiment 1, the interaction was only marginally reliable [F(1,33) = 3.2, p = .08].

To investigate possible differences in the programming of regressions, preregression duration was also determined in Experiments 1 and 2 as a function of target distance for the between-line condition. The 2 (experiment: 1 or 2) × 2 (spatial distance: close or distant) ANOVA revealed a main effect neither of experiment [F(1,33) = 1.3, p = .27] nor of distance and no interaction between both factors (both Fs < 0.4).

Discussion

Experiment 2 replicated a key finding of Experiment 1: Effects of spatial distance once more dominated effects of temporal/linguistic distance when the two were pitted against each other. Critically, the advantage of spatially near words over distant words occurred even when readers could not obtain any information from the first line, where the target was located prior to the programming of the regression. A tendency toward longer gaze durations and lower skipping rates for right-side targets during initial sentence reading was not reliable. Supplementary analyses showed that the spatial distance advantage was not subject to the development of episode-specific regression strategies, because the advantage was present regardless of practice. Furthermore, there was a tendency to undershoot near and distant (masked) targets in Experiment 2, indicating that the spatial distance effect on regression accuracy emerges even when modulatory effects of oculomotor targeting strategies appear to be negligible.

Regression accuracy was lower in Experiment 2 than in Experiment 1, however. An explanation for this could be the occurrence of a major display change that occurred in response to the onset of the spoken word and thus immediately prior to the planning and execution of a regression. This display change was highly salient and could have interfered with the spatial targeting of the regression, and it could have been particularly detrimental when the regression target was relatively distant from the regression source.

GENERAL DISCUSSION

The present study sought to determine the nature of the information that guides long-range regressions by examining the influence of spatial distance, of temporal/linguistic distance, and of general linguistic processing demands on regression size and regression accuracy. Two theoretical conceptions were contrasted: the spatial coding hypothesis, according to which regressions to target words are guided by knowledge of the locations of previously read words (e.g., Kennedy, 1992), and the verbal inference hypothesis, according to which linguistic knowledge of previously read text is used to infer the location of the regression target (Inhoff et al., 2005; Inhoff & Weger, 2005).

The results of the present experiments provide some support for each hypothesis. In harmony with the spatial coding hypothesis, initial regressions to previously read words were spatially selective. Moreover, effects of spatial distance dominated effects of temporal/linguistic distance when the two were pitted against each other in Experiments 1 and 2. This spatial selectivity occurred even when parafoveally available linguistic information was masked before the regression could be programmed in Experiment 2, indicating that peripherally available linguistic cues provide relatively little guidance toward a long-distance regression target. This affirms prior findings according to which long-distance regressions are memory guided (Inhoff & Weger, 2005; Kennedy et al., 2003).

Supplementary examinations of initial regression accuracy also revealed an influence of other modulating factors on the accuracy of initial regressions. Analyses of under- and overshoots revealed an influence of oculomotor aiming strategies, and the number of words that intervened between the source location and a target word influenced the accuracy of initial regressions when spatial distance was held constant. The influence of the number of intervening words was considerably smaller than the influence of spatial distance, however, as indicated by the beta-weights in the regression analysis.

What is the nature of the modulating effect of the number of intervening words? On the one hand, it could be a spatial tagging effect, thus providing support for the spatial coding hypothesis, according to which recognized words are spatially tagged. For a particular spatial source–target distance, retrieval of a target’s spatial tag may be less successful when the number of intervening spatially tagged words is relatively large than when it is relatively small, because a larger number of tags may render the target tag less distinct.

Alternatively, it is tempting to speculate that the intervening word effect reflects the success with which the target word itself, rather than its spatial tag, could be accessed in verbal memory; this would be in harmony with the verbal reconstruction hypothesis. Specifically, backtracking from the source to the target may become more difficult as the number of intervening words increases, thus diminishing the success of inferential processes that use verbal knowledge to determine target location. The verbal reconstruction account is in harmony with Miyake et al.’s (1994) findings and with the results of Rawson and Miyake’s (2002) more recent study. In this study, participants read several pages of text, after which they had to relocate specific segments in the text after all useful linguistic information had been removed. Under these conditions, relocating the correct page and the correct line location was significantly better than chance. Verbal and spatial memory performance scores were also obtained in the study, and these scores were correlated with spatial relocation performance. Critically, it was participants’ verbal memory performance, rather than their spatial memory performance, that correlated significantly with relocation accuracy.

The assumption that readers used linguistic knowledge to infer the location of the target in the present experiments is also consistent with the distinct effect of line order on the magnitude of the cumulative regression error. Specifically, in the two within-line conditions, cumulative regressions were more accurate during the reading of the first line, when relatively few words had been read before the critical areas (target and source) were reached—that is, when linguistic processing demand was relatively low—than during the reading of the second line, when a relatively large number of words had been read before the critical areas were reached and when linguistic processing load was relatively high.

Alternative accounts of the line order effect are less compelling. It may be argued, for instance, that readers were less attentive when the second line was read, or that they were less inclined to execute a regression when the end of the sentence was near, thus accounting for the lower spatial selectivity of cumulative regressions during second-line reading. Although these alternatives can account for some aspects of the data, they are difficult to reconcile with other pertinent findings. There were no differences in the size of initial regressions toward a target on the first line and the second line; preregression fixation durations were virtually identical for both lines (see Vitu, 1993, for a discussion of effects of oculomotor rhythm), and there was no difference in the number of consecutive regressions. In other words, a line-dependent change in the reading strategy would have had to emerge after the first regression had been executed, and it could have influenced only the size, not the number, of executed regression. Rather than attributing line order effects on cumulative regression accuracy to changes in reading strategies, we are inclined to conclude that line order influenced not reading strategies but linguistic processing demand, which made homing in on the regression target more difficult when processing demand was high.

The term linguistic processing demand is theoretically neutral and leaves the precise source of the demand unspecified. Critically, the term is meant to be sufficiently general to include the effect of sentential context that had been read before the critical sentence locations were reached. The demand could be influenced by verbal load, and it could increase as more verbal items compete for representation in WM. However, we did not manipulate verbal WM load in the classical sense, since readers did not actively rehearse individual words. Other general factors, such as linguistic or propositional complexity, may have played a role.

Together, the findings from the present experiments thus suggest a hybrid model in which spatial WM assumes a primary role in the programming of initial regressions. This memory appears to be fovea centered, so that items in the spatial proximity of the current fixation are more prominent than are more distant items. The temporal/linguistic distance between the source and the target assumes a secondary role at that stage, because inferential processing may take time (Fischer, 1999). Continuing—or corrective—regressions are further influenced by sentence context outside the source-to-target area, since use of this linguistic knowledge for regression programming is also likely to take time.

The present findings and the proposed model are consistent with earlier findings from our laboratory that revealed two distinct movement stages for long-range regression toward a prespecified target (Inhoff & Weger, 2005). In our earlier study, readers used a large initial regression preceded by a long fixation duration to place the eyes in the vicinity of the target. This was followed by small corrective regressions preceded by short fixation durations that homed in on the target. The present work extends these findings by revealing the use of distinct types of knowledge for the specification of initial and corrective regressions. Initial regressions are primarily guided by spatial memory and rely little on linguistic knowledge, whereas corrective regressions are guided to a much larger extent by linguistic knowledge.

For a corrective regression to occur, a reader must have some means to determine the success with which the initial regression moved the eye onto the target. Information obtained after the initial regression may be matched against the content of verbal memory to determine how close to the target the eyes were when they landed. Corrective regressions, guided by inferential processes, may then be executed to backtrack the eyes until the target is reached. Corrective regressions also occur in the absence of available linguistic information, however. In Inhoff and Weger’s (2005) study, cumulative regressions moved the eyes toward the target location, whether or not the previously read sentence with the regression target was visible. Together, spatial WM, verbal WM, and linguistic knowledge of text outside the source–target area thus provide sufficient information for a relatively accurate specification of the location of a previously read target word within a sentence.

In the present study, capacity limitations, hypothesized for visuospatial and verbal WM in current models of WM, influenced regression accuracy. In Baddeley’s now classical model, for instance, items can be stored either in a phonological loop or in a visuospatial sketchpad. Both storage systems have strict capacity constraints, with the limits being around six or seven items for the verbal store and about three or four items for the visuospatial store (see Baddeley, 2003, for a recent overview). Strict limitations of spatial memory are also characteristic of Pylyshyn’s spatial indexing model (FINST; Pylyshyn, 1989; Pylyshyn & Storm, 1988). According to this model, up to four or five randomly moving objects can be simultaneously and independently indexed and retained in WM. During reading, the specific number of storable word objects could be larger or smaller than four or five, however. For instance, the number could be smaller if the similarity of visual objects and their static nature made location discrimination in spatial memory more difficult. The number could be higher because the locations were meaningfully aligned and not random. In a computational model of spatial cognition, Ballard, Hayhoe, Pook, and Rao (1997) propose the use of references or pointers to spatial locations that allow the use of cognitive or motor primitives—represented as deictic codes—to break down complex behaviors. Such deictic codes can be implemented as attentional operations, eye fixations, or motor programs, and only a single pointer is active at a given time, whereas others are kept available in WM.

Since the present study used a relatively novel technique to control regressions during reading, it may be asked whether the same types of knowledge sources are used for the programming of “spontaneous” regressions during normal reading. Regressions in the present study were experimentally elicited on each trial via the presentation of an eye-movement-contingent spoken word that specified the regression target when a predefined source area was reached. Without the spoken instruction, the frequency of regressions would have been much lower (Inhoff & Weger, 2005), and readers might not have regressed from the source location to the target. An auditorily presented regression cue may well also cause some disruption to the reading process. Consequently, the programming of experimentally (or extrinsically) elicited regressions may differ from the spontaneously executed regressions that are under the (intrinsic) control of the reader. We examined this possibility in our earlier study (Inhoff & Weger, 2005) by comparing the size and accuracy of experimentally elicited regressions with the size and accuracy of spontaneously executed initial regressions toward a hypothesized (i.e., question-relevant) regression target. Our results did not reveal any systematic differences in the size of regressions.⁵ Yet until this methodological issue is settled, it appears desirable to us that a naturalistic approach to the study of long-range regressions during reading be complemented by experimental approaches such as ours, in which the location and linguistic properties of the regression target are controlled and in which the experimenter has further control over the location from which the regression is launched and over the linguistic information that is available before a long-range regression is to be executed.