Temperature and length scale dependence of hydrophobic effects and their possible implications for protein folding

Abstract

The Lum–Chandler–Weeks theory of hydrophobicity [Lum, K., Chandler, D. & Weeks, J. D. (1999) J. Phys. Chem. 103, 4570–4577] is applied to treat the temperature dependence of hydrophobic solvation in water. The application illustrates how the temperature dependence for hydrophobic surfaces extending less than 1 nm differs significantly from that for surfaces extending more than 1 nm. The latter is the result of water depletion, a collective effect, that appears at length scales of 1 nm and larger. Because of the contrasting behaviors at small and large length scales, hydrophobicity by itself can explain the variable behavior of entropies of protein folding.

At least since the first observations concerning the significance of oil–water demixing or hydrophobic interactions in structural biology (1, 2), the temperature dependence of these interactions has been a source of speculation and puzzlement (3–8). For example, Kauzmann (1) noted the curious difference in sign between the entropy for hydrating alkane chains of modest length and that for hydrating extended hydrophobic surfaces. The former is negative in cold water (9), as Kauzmann predicted from the entropy change for disrupting small micelles. The latter is positive, as Kauzmann concluded from the temperature dependence of oil–water surface tension. Furthermore, the entropy of solvating a small hydrophobic species changes sign as temperature is increased (9), whereas the entropy of solvation for an extended oily surface, as manifested in the oil–water surface tension, is positive for both cold and warm liquid water (10).

In this paper, we show that the recently developed theory of Lum, Chandler, and Weeks (LCW) (11) is consistent with these varied behaviors. The theory is then used to analyze the concept of entropy convergence in protein folding—the idea that the hydrophobic entropy change on folding vanishes at a universal temperature, T* (3). This idea has been used for the modeling of hydrophobic contributions to the thermodynamics of protein unfolding (4–8). An important recent theoretical step showed how entropy convergence does follow from the molecular theory of small hydrophobic species (12). By extending this work to describe the alternative behaviors for hydrating small and large species, our results show that entropy convergence is not to be expected universally and that observed deviations from convergence can be understood in terms of hydrophobic solvation thermodynamics.

Structural differences between the solvation of small hydrophobic species and extended hydrophobic surfaces have been understood qualitatively at least since Stillinger's 1973 paper (13). The hydrogen bond network of water near an alkane molecule of modest length, for example, is not distorted significantly by the solute. Hydrogen bonds between neighboring water molecules can remain intact, even when these molecules make contact with small hydrophobic solutes. Hydrogen bonds simply go around the solute. There is an entropic cost to the free energy of solvation, because the presence of the small hydrophobic species limits the configuration space available for hydrogen bonding. This cost is small per water molecule in comparison with the energetic cost incurred by breaking a hydrogen bond. In contrast, the solvation of extended hydrophobic surfaces has a disruptive effect on water structure. Close proximity of water is energetically unfavorable, because it is impossible to maintain a hydrogen bond network adjacent to an extended surface. As a result, water density is depleted near the surface. This depletion is a collective effect akin to a drying transition induced by the hydrophobic surface. Because of it, there is a large energetic contribution to the free energy of hydration of extended surfaces, as manifested in the surface tension of a water interface.

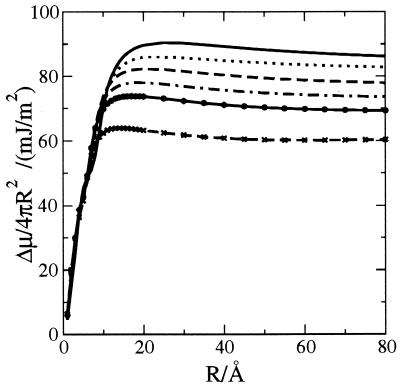
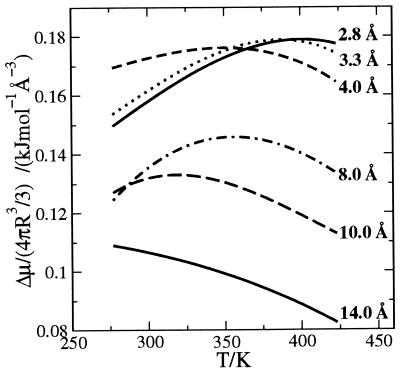
The LCW analysis (11) is the first theory to put these arguments into a generally applicable quantitative framework. The theory is relevant in the current context, because the crossover from the small to large length scale regimes occurs for surfaces extending roughly a nanometer—the characteristic length scale of protein structure. The precise crossover length depends on thermodynamic state and the shape of the hydrophobic surface. Figs. 1 and 2 illustrate this variation as we have computed it from LCW theory for ideal spherical hydrophobic solutes—bubbles—of several different sphere radii in water at several different temperatures.

Figure 1.

Excess chemical potential, Δμ, per exposed surface area for hard spheres of radius R, calculated by using the LCW theory (11), for temperatures of 277, 298, 323, 348, 373, and 423 K (the plateau decreases with increasing temperature).

Figure 2.

Excess chemical potential per solute volume as a function of temperature (T in Kelvin) for spherical bubbles of different radii (R) as indicated.

Implementation of LCW theory requires prior knowledge of the equation of state, the surface tension, and the radial distribution function of pure water. In our calculations, we have used the simple parameterization of the equation of state suggested in ref. 11, based on the isothermal compressibility, and the energy density of pure water. The entries to Table 1 list the values of the prescribed parameters. The radial distribution function is taken from the x-ray scattering measurements of it (14).

Table 1.

Parameters used in LCW theory (11) calculations at various temperatures^†

T, K	a, (kJ·cm3/mol2)‡	b, (cm3/mol)§	λ, Ŷ
277	211	14.5	4.3
298	229	14.6	3.8
323	246	14.6	3.4
348	260	14.7	3.2
373	270	14.8	3.1
423	285	14.9	2.9

^† Based on measured energy density, −an_l², isothermal compressibility, κ_T, and surface tension, γ, of pure liquid water (10). 

^‡ Bulk energy density for the uniform liquid is −an_l², where n_l is the homogeneous number density of liquid water. 

^§

Molecular volume parameter,

 

^¶

Length scale characterizing fluctuations in attractive interactions,

 

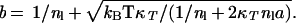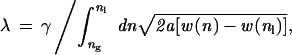where w(n) is the free energy density of a fluid of number density n. 

Fig. 1 shows consistent length scale behavior of the excess chemical potential for all temperatures studied. This behavior explains why a “microscopic” surface tension determined from the solubility of hydrocarbons in water could be smaller than the “macroscopic” surface tension measured for liquid hydrocarbon–water interfaces (15). The plateau values in Fig. 1 are close to the corresponding macroscopic surface tensions.

In the small length scale regime, Δμ is roughly proportional to the volume, as is evident from Fig. 1 for the case of spherical ideal hydrophobes. As a result, for a fixed temperature, one can identify a single length, r, close to the van der Waals radius of water, where Δμ/4π(R − r)² is roughly a constant for solute radii R > 3.3 Å. This representation has been suggested by Ashbaugh et al. (16). Complicating this apparent simplification, however, is the fact that the nontrivial temperature dependence of Δμ must be manifested in a temperature dependence of r.

A more useful observation is that the proportionality for volume remains valid for any reasonable molecular shape of small ideal hydrophobes. This fact, noticed by Ben-Naim and Mazo (28, 29), is explained and used to interpret transfer free energies successfully in the analysis of Pratt and Chandler (17). The dependence of transfer free energies on the length of small hydrocarbons is often described in terms of free energies per surface area. For such molecules, both volume and surface area are linear functions of chain length.

In the large length scale regime, it seems from Fig. 1 that another simplifying invariance holds. Here, solvation energies are proportional to surface area, independent of the precise shape of the extended ideal hydrophobic surface. Exploiting both the scaling with volume at small length scales and surface area at large length scales may lead to a simple yet accurate theory of hydrophobic solvation for biomolecules of arbitrary shape. Pursuance of this possibility, however, is beyond the scope of this paper.

Fig. 2 shows that the chemical potential decreases monotonically with temperature for solutes with radii R > 10 Å, following the dependence of the liquid–vapor surface tension of water. For smaller solutes, the temperature dependence is nonmonotonic, and the chemical potential has a maximum that moves to lower temperature as the size of the solute increases. If the statistics of the density fluctuations required to form a solute-sized cavity are Gaussian and the variance of the statistics are temperature independent (the case for water because of its low isothermal compressibility), it can be shown (12) that the chemical potential will have a maximum close to the maximum of Tn², where n is the number density of bulk water at ambient conditions. This maximum occurs near 400 K for water. Gaussian statistics do characterize density fluctuations over small length scales (18), and the assumption of such statistics is the basis of successful and closely related theories of hydration of small hydrophobic species (17–19). In the limit of small solutes, LCW theory reduces to this Gaussian model as well. On the other hand, Gaussian statistics are not expected for the density fluctuations required to form large solute-sized cavities (20). Indeed, as anticipated by Stillinger (13) and predicted as well by LCW theory (11), the disrupted water structure adjacent to such a cavity exhibits a depletion layer with a liquid–vapor interface. The maximum in the chemical potential moves to lower temperatures with increasing size of the solute and eventually disappears as the temperature dependence approaches behavior close to that of the liquid–vapor surface tension. Small shifts of the maximum to lower temperature with increasing solute size have been noted previously for the small solutes neon, argon, methane, and xenon (12). Larger shifts toward lower temperature occur for solutes large enough to promote water depletion. Further, we see from Fig. 2 that for R > 10 Å, the entropy change of solvation, ΔS = −(∂Δμ/∂T)_p, no longer passes through zero. Rather it is positive for all liquid temperatures and roughly temperature independent.

With these results in mind, let us now consider the entropy changes of protein unfolding. For a variety of globular proteins (4, 21), it has been found that this entropy change per amino acid residue converges to a common value when extrapolated to a temperature of approximately 385 K. Noting that this convergence temperature is close to the temperature at which the entropy change of solvation of a number of hydrocarbon liquids extrapolate to zero, Baldwin (3) proposed that T* is the temperature at which the contribution to the entropy change from the solvation of hydrophobic residues buried in the folded protein is zero. The residual entropy is assumed to be due to other factors such as configurational entropy and solvation of polar groups (4–8). Experimental studies of other small solutes such as n-alkanes (9), n-alcohols (9), and cyclic dipeptides (22) also show convergence of entropies of solution at ≈385 K, not far from the convergence temperature of 400 K predicted from theory for small ideal hydrophobic species (12).

In contrast, the most recent and extensive experimental study of entropies of protein unfolding finds no evidence of a convergence temperature for the entropy of unfolding (23). The proteins in all of these studies are single-domain globular proteins that unfold reversibly under heat denaturation. Several possible reasons for the scatter in the experimental data have been suggested, such as the effect of long-range interactions like electrostatics and differences in the extent of exposure to water of components in the denatured protein. We argue, however, that contributions from hydrophobic effects, usually assumed to show convergence, are themselves sufficient to produce the observed scatter. Indeed, LCW theory provides a means for interpreting why only some classes of proteins may exhibit a convergence temperature and why this temperature will generally be lower than the small molecule value of 400 K.

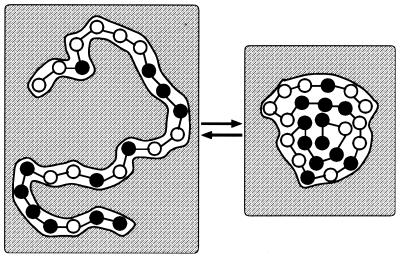
For simplicity, we assume a folded protein is a compact, spherical structure, whereas the unfolded protein is a chain in which all of the hydrophobic residues have roughly the same size. With this simplification, all of the information needed for the analysis is graphed in Fig. 2. Specifically, we conceive of protein folding as pictured in Fig. 3 and thereby write the change in the hydrophobic contributions to the entropy of unfolding per amino acid residue as

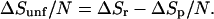1

Here, N refers to the number of residues, ΔS_r denotes the hydrophobic entropy of solvation of a residue, and ΔS_p stands for the hydrophobic entropy of solvation of the folded protein. If we were to assume that hydrophobic effects do not contribute to hydration of the folded protein, the second term in Eq. 1, ΔS_p/N, could be omitted from the analysis (3). However, typically about 50% of the exposed surface of globular proteins is classified as nonpolar, the other 50% being polar or charged (24). ΔS_p/N might therefore be significant. To estimate its size, we can consider the thermodynamics of solvation of the folded protein as a two-step process, in which a protein-sized cavity is first created and then the attractive protein-solvent interactions are turned on. To the extent that this second step is primarily enthalpic, ΔS_p should be well estimated by the entropy to solvate the cavity in the absence of protein-solvent attractions. This estimate coincides with the hydrophobic entropy change to create the protein-sized cavity.

Figure 3.

Schematic of protein-folding equilibrium. The black and white circles represent hydrophobic and hydrophilic residues, respectively. The shaded region depicts aqueous solution.

This two-step analysis of hydrophobic solvation was used to good effect by Pratt and Chandler (17). A recent simulation study of small alkanes in water supports this approach, showing that the effects of attractive solute–solvent interactions are mainly enthalpic and result in only small entropy changes (25). In this view, it is not that the average solvent density is unaffected by turning on polar interactions but that the amount of configurational space available to the solvating water molecules is not altered significantly. As such, the particular distribution and proportion of hydrophilic and hydrophobic patches on the protein surface should not affect ΔS_p.

Experimentally measured molecular volumes for amino acids in solution vary between 72 and 240 ų (26), volumes that correspond to solute radii of 2.6–3.9 Å (assuming spheres), with an average radius of 3.3 Å and a standard deviation of 0.3 Å. For this size, we see from Fig. 2 that ΔS_r increases with temperature and passes through zero. In addition, for radii within one standard deviation of the average, there is an approximate convergence in ΔS_r near zero, as noted before this report in ref. 12. This result also explains the experimentally observed entropy convergence for solvation of small hydrophobic solutes (also noted in ref. 12).

For a large number of globular proteins, the volume of the protein divided by its molecular weight is ≈0.75 cm³⋅g⁻¹ (24). Assuming this value for the proteins studied in ref. 23, the volumes for these proteins vary between 7,000 and 50,000 ų, volumes that correspond to radii (R) between 12 and 23 Å. Assuming 120 g as the average residue weight, these radii correspond to n = 48 and 340, respectively. For these radii, we see from Fig. 2 that ΔS_p/N will be positive and, to a good approximation, independent of temperature. Furthermore, from Fig. 1 we see that ΔS_p will be roughly proportional to surface area and thus scale with R², such that ΔS_p/N will scale as R^−1/3. To the extent that ΔS_r shows no dispersion in going from one protein to another, the range of values for ΔS_unf/N is the same as that for ΔS_p/N. Applying LCW theory at T = 385 K, we find that

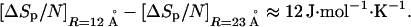2

This variation is close to the experimentally measured range of the difference in ΔS_unf/N, which is 15 J⋅mol⁻¹⋅K⁻¹ at this same temperature (23). Therefore, ΔS_p/N does seem to be significant and sufficient to explain the observed scatter in ΔS_unf/N.

The temperature at which the hydrophobic contributions to the entropy of unfolding is zero, T*, is where the curves ΔS_r and ΔS_p/N intersect. From the above considerations, T* will decrease as the size of the protein increases. Therefore, considering the variation in protein volume, one may not expect to observe a convergence temperature for the entropy of unfolding for all proteins.

Another reason concerns the idealized picture of a fully unfolded chain as essentially identical independent hydrophobic amino acid residues. This picture neglects clumping or clustering of residues. Such clustering does occur (27) and in effect produces hydrophobic units of various sizes. In that case, the typical value of ΔS_r will shift such that ΔS_r = 0 will occur at a lower temperature, as indicated by the shift in the extremum in Fig. 2. Hence, greater residue cluster size dispersion will reduce the possible value of T* further.

Abbreviation

LCW

Lum–Chandler–Weeks