Inter-sarcomere coordination in muscle revealed through individual sarcomere response to quick stretch

Abstract

The force generation and motion of muscle are produced by the collective work of thousands of sarcomeres, the basic structural units of striated muscle. Based on their series connection to form a myofibril, it is expected that sarcomeres are mechanically and/or structurally coupled to each other. However, the behavior of individual sarcomeres and the coupling dynamics between sarcomeres remain elusive, because muscle mechanics has so far been investigated mainly by analyzing the averaged behavior of thousands of sarcomeres in muscle fibers. In this study, we directly measured the length-responses of individual sarcomeres to quick stretch at partial activation, using micromanipulation of skeletal myofibrils under a phase-contrast microscope. The experiments were performed at ADP-activation (1 mM MgATP and 2 mM MgADP in the absence of Ca²⁺) and also at Ca²⁺-activation (1 mM MgATP at pCa 6.3) conditions. We show that under these activation conditions, sarcomeres exhibit 2 distinct types of responses, either “resisting” or “yielding,” which are clearly distinguished by the lengthening distance of single sarcomeres in response to stretch. These 2 types of sarcomeres tended to coexist within the myofibril, and the sarcomere “yielding” occurred in clusters composed of several adjacent sarcomeres. The labeling of Z-line with anti-α-actinin antibody significantly suppressed the clustered sarcomere “yielding.” These results strongly suggest that the contractile system of muscle possesses the mechanism of structure-based inter-sarcomere coordination.

The periodic architecture of striated muscle relies on the series connection of the basic contractile units, called sarcomeres, which are connected through the Z-line to form a myofibril. Each sarcomere is composed of a bipolar array of myofilaments, i.e., the thick (myosin) and thin (actin) filaments. The cyclic interaction of myosin with actin coupled to ATP hydrolysis produces force and motion along the long axis of the myofibril (1, 2). Such characteristics of striated muscle imply that individual sarcomeres are structurally and mechanically interconnected and interact with each other. Tension and length responses of sarcomeres to the external perturbations have revealed various mechanochemical properties of striated muscle, particularly those relating to the mechanism of force generation (3–6) and to the attachment/detachment kinetics of cross-bridges (7–9). On the other hand, the interaction between sarcomeres remains unclear, primarily because the widely used technique for measuring sarcomere response is laser light diffraction, where the individual sarcomere dynamics are obscured by the ensemble averaging of thousands of sarcomeres connected in parallel and in series in muscle fibers.

Recent developments in microscopic analysis using skeletal and cardiac myofibrils revealed various dynamic properties of individual sarcomeres (or even half-sarcomeres) upon force generation and relaxation of striated muscle (10–14). One of the particular characteristics found by this approach is the spontaneous oscillation of sarcomeres, which is observed at partial activating conditions. The myofilament-generated oscillation was first reported by Fabiato and Fabiato in skinned cardiac cells at fixed concentrations of free Ca²⁺, suggesting the existence of Ca²⁺-independent regulatory mechanism in sarcomeres (15). One decade later, we found that the steady periodic oscillation, named SPOC (SPontaneous Oscillatory Contraction), can be well reproduced at partial activation by adding exogenous ADP and inorganic phosphate (Pi) to the relaxing solution (in the presence of ATP and the absence of Ca²⁺) (16), allowing the quantitative analysis of sarcomere behavior. During SPOC, each sarcomere repeats slow-shortening and rapid-lengthening phases with a period of a few seconds, lasting from minutes to hours. In addition, the lengthening phase propagates to adjacent sarcomeres along the long axis of myofibrils (SPOC wave) at a faster rate than the diffusion of chemical components. These observations strongly suggest that the cooperative behavior of sarcomeres is not attributable to artificial non-uniform activation, but is an intrinsic property of striated muscle. Moreover, such dynamic properties of sarcomeres show a possible link to physiological functions. For example, the period of SPOC strongly correlates with that of heart beat in various animal species (17), and the relaxation of single sarcomeres propagates along the myofibril after the rapid removal of Ca²⁺ (12). These reports imply that the cooperative behavior of individual sarcomeres, which is concealed by the ensemble averaging, plays a significant role for the efficient work and motion in muscle. Hence, the analysis at the single sarcomere level must be indispensable for fully understanding the regulatory mechanism that striated muscle possesses.

In this study, we investigated the length-response of individual sarcomeres to externally applied load, using mechanical manipulation of skeletal myofibrils with microneedles. The characteristic aspects of this study are: 1) The behavior of individual sarcomeres was observed under a phase-contrast microscope simultaneously with measuring tension response (18). 2) The myofibrils were activated, in almost all cases, by adding MgADP to the relaxing conditions (19), which results in the regulation of sarcomeric activity by strong-binding (or ADP-bound) cross-bridges independently of Ca²⁺. 3) The mechanical measurements were done at partial activation, between contraction and relaxation, where the dynamic properties of sarcomeres may prominently emerge as exemplified by SPOC. These features ensure that the mechanical and structural interactions between sarcomeres are highlighted independent of the regulation by Ca²⁺.

Here we report that at partial activation conditions the sarcomeres show 2 distinct types of response to stretch: they either “resist” (only slightly elongate and then maintain the constant length, exhibiting a rectangular waveform) or “yield” (significantly elongate and then gradually shorten, exhibiting a saw-tooth waveform). This characteristic bimodal response allows us to analyze the properties of sarcomere “yielding” depending on the applied load and the mechanical properties of the Z-line structure, which shows how sarcomeres cooperatively regulate their force-generating activity with each other without the master regulator, Ca²⁺ ions.

Results

Mechanical Stretch of Skeletal Myofibrils.

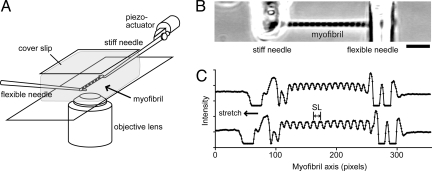
To investigate the behavior of individual sarcomeres, a single skeletal myofibril (or a thin bundle of myofibrils) was suspended between a pair of glass microneedles under a phase-contrast microscope (Fig. 1A). One of the needles was stiffness-calibrated and >50-fold more flexible than the other, so that tension could be estimated from its deflection. When the relaxing solution was exchanged to the ADP-activation solution, the myofibril responded by developing active force against a compliant load, accompanied by the shortening of sarcomeres (i.e., auxotonic contraction), and then reached a steady state. The active isometric force (P₀) was 49.5 ± 7.9 kN/m² (mean ± SE, n = 10 myofibrils) at a sarcomere length (SL) 2.0–2.5 μm, which is 5–6-fold smaller than at maximal Ca²⁺-activation (19), indicating that the myofibrils were partially activated. At the activation plateau, the myofibril was quickly stretched (0.01–0.04 P₀/ms) by moving the stiff needle away from the flexible needle, followed by holding it for 5 s and then slowly, over more than 5 s, returning it to the original position (<0.00003 P₀/ms). Such stretch protocol was repeated every 20 s, 5 times for each myofibril, with various load amplitudes. The length-responses of individual sarcomeres were analyzed from the phase-contrast image simultaneously with the tension-response (Fig. 1B and C). The analysis was performed only when the active isometric force was >95% of that during the first stretch. The striation pattern of the myofibril remained clear and uniform over the repeated stretches. During the solution exchange the spontaneous oscillation of force and SL was occasionally observed. Such oscillation usually disappeared within 30 s, although in some experiments it continued for longer than 3 min. Here, we eliminated the latter cases from the following analysis.

Fig. 1.

Overview of the stretch experiments. (A) Schematic diagram of the mechanical measurements in myofibrils under an inverted phase-contrast microscope. (B) The phase-contrast image of a myofibril. (C) The intensity profile of phase-contrast image. The profiles along the long axis of the myofibril in B, before stretch (upper trace) and 100 ms after stretch (lower trace) at ADP activation are shown. The position of the flexible needle (right) in the upper and the lower traces corresponds to those at P₀ and P₂, respectively, as defined in Fig. 2B. (Scale bar, 10 μm.)

Sarcomeres Show 2 Types of Characteristic Responses Depending on ΔP.

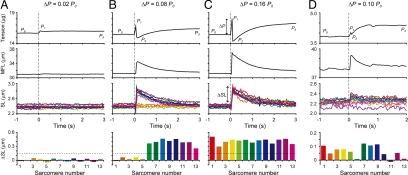
Against a stretch with the loading rate of 0.01–0.04 P₀/ms, sarcomeres exhibited 2 distinct types of responses depending on the applied load, ΔP (= P₁ − P₀) (Fig. 2). Against a small stretch corresponding to ΔP < 0.025 P₀, the sarcomeres lengthened by a few tens of nanometers on average (≈1% of initial SL), accompanied by a slight increase in tension (Fig. 2A and Movie S1, see SI Text). That is, sarcomeres retained their force-generating state against a small stretch, showing a rectangular response. We termed such sarcomeres “resisting.” In contrast, against a larger stretch corresponding to ΔP >0.125 P₀, all sarcomeres rapidly elongated by >150 nm (>6% of initial SL) within 66 ms (2 video frames) per single sarcomere (ΔSL). Following stretch, the tension first increased to P₁, with the myofibril length remaining nearly constant, and then significantly decreased to P₂ accompanied by rapid elongation of a myofibril (Fig. 2B and C; Movies S2 and S3). We termed such sarcomeres “yielding.” The “yielding” sarcomeres subsequently recovered the active force and reached a new steady level (P₃ in the top panels of Fig. 2), showing a saw-tooth response. The “yielding” phenomenon was not observed when the loading rate was less than 0.0001 P₀/ms, as far as ΔP remained <0.2 P₀ (Fig. S1). These 2 types of responses were observed irrespective of the initial SL in the range between 1.8 μm and 3.0 μm, although against the same ΔP/P₀ the “yielding” occurred less frequently at longer SLs.

Fig. 2.

Responses of individual sarcomeres in a myofibril at various ΔP. The time course of tension (top), total length of the myofibril, MFL (upper middle), and length-responses of individual sarcomeres in a myofibril (SL, lower middle) under ΔP = 0.02 P₀ (A), 0.08 P₀ (B), 0.16 P₀ (C), and 0.10 P₀ (D) loading are shown. The loading rate was 0.02 P₀/ms. Each SL is shown in a different color. The myofibril was stretched at time 0, shown by vertical dashed lines. P₀ indicates the active isometric force before stretch, P₁ is the peak force immediately after stretch, P₂ is the minimum force due to “yielding” of sarcomeres, and P₃ is the final plateau level. The spatial distributions of ΔSL of individual sarcomeres in the myofibril are shown in the bottom panels. Colors correspond to those in the SL traces. (A–C) Tension and length responses at ADP-activation. The data were obtained from the same myofibril and from the consecutive 13 out of 15 sarcomeres in the central part of the myofibril. The horizontal dashed line corresponds to ΔSL = 150 nm (see Fig. 3A). The cross-sectional area of the myofibril was determined to be 2.47 μm². (D) Tension and length responses at partial Ca²⁺-activation (pCa = 6.3). The consecutive 13 out of 17 sarcomeres in the central part of the myofibril were analyzed. Note that different myofibrils were used in (A–C) and (D). The cross-sectional area, 2.68 μm².

At partial Ca²⁺ activation, the “yielding” was observed as well, even in the absence of MgADP (n = 3 myofibrils at pCa = 6.3). Compared with the ADP-activation, however, the higher ΔP/P₀ was needed to induce the “yielding,” and ΔSL was smaller, approximately 100 nm (Fig. 2D). Within our spatial resolution the “yielding” was not clearly observed at maximal Ca²⁺-activation (pCa = 4.5). After a stretch, the sarcomeres elongated at a moderate rate accompanied by force decay, until reaching the steady-force level (Fig. S2). Since the sarcomeres non-uniformly shortened and rapidly deteriorated upon Ca²⁺ activations in contrast to the ADP-activation, quantitative measurements at Ca²⁺-activations were more complicated. The 2 types of characteristic responses as shown above were different from the viscoelastic response observed under relaxing conditions (Fig. S3), during which tension decayed exponentially following stretch, as reported previously (20).

Sarcomeres Show Bimodal Response to Intermediate ΔP.

Noticeably, when ΔP was 0.05–0.1 P₀, the sarcomeres did not show homogeneous response throughout a myofibril. Instead, the sarcomeres exhibiting 2 types of responses, “resisting” (Fig. 2A) and “yielding” (Fig. 2C), coexisted within the myofibril (Fig. 2B and Movie S2). Additionally, ΔSL of sarcomeres was not intermediate between those at 0.025 P₀ and 0.125 P₀, but corresponded to ΔSL of either “resisting” or “yielding” sarcomeres, observed at small or large ΔP, respectively. It is to be noted that “yielding” sarcomeres appeared in clusters, rather than at random, along the myofibril, as shown in Fig. 2 Bottom. Both the “resisting” and “yielding” sarcomeres recovered the initial length-distribution after the force recovery.

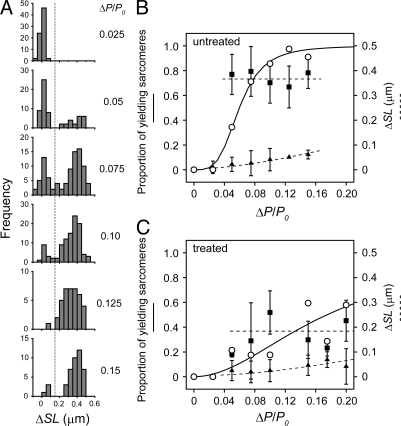
The histogram of ΔSL at various ΔP showed bimodal distribution (Fig. 3A), which clearly indicates that the sarcomeres in a myofibril adopt 2 distinct states, either “resisting” or “yielding” (corresponding to the populations on the left and the right, respectively, in Fig. 3A). The proportion of “yielding” sarcomeres at various ΔP is summarized in Fig. 3B. “Yielding” sarcomeres were clearly distinguished from the “resisting” sarcomeres by a >150 nm ΔSL (the population to the right from the vertical dotted line in Fig. 3A; see also horizontal dotted lines in the bottom panels of Fig. 2). The relationship was fitted by the Hill equation, S = (ΔP)^n_H/[(ΔP)^n_H + (ΔP₅₀)^n_H], where S is the proportion of “yielding” sarcomeres, ΔP₅₀ is the applied load at which 50% of sarcomeres are “yielding,” and n_H is the Hill coefficient (Fig. 3B). ΔP₅₀ was 0.06 P₀, and n_H was 3.8. Notably, ΔSL of “yielding” sarcomeres was almost independent of ΔP, whereas ΔSL of the “resisting” sarcomeres gradually increased with ΔP (Fig. 3B).

Fig. 3.

Bimodal sarcomere response depending on ΔP. (A) The distribution of ΔSL of individual sarcomeres at various ΔP. Each histogram is composed of the data obtained at a ΔP/P₀ in the range of the central values (shown to the right of each histogram) ± 0.0125. The data were obtained from n = 8 myofibrils at the loading rate of 0.01–0.04 P₀/ms. The vertical dashed line corresponds to ΔSL = 150 nm, which separates “resisting” and “yielding” sarcomeres. (B and C) The population and ΔSL of the bimodal response depending on ΔP. The proportion of “yielding” sarcomeres against ΔP/P₀ (open circles) in untreated (n = 8 myofibrils) and antibody-treated (n = 5 myofibrils) preparations is shown in B and C, respectively. The solid curves are the fits to the Hill equation. The average ΔSL of “resisting” (filled triangles) and “yielding” (filled squares) sarcomeres are plotted with error bars (± SD). The dotted lines were drawn by eye.

Sarcomeres “Yield” in Clusters Along a Myofibril.

To further investigate the properties of the bimodal response of sarcomeres, the myofibrils were stretched repeatedly with the same ΔP, around the ΔP₅₀ (5 times each; left panels in Fig. 4). Against repeated stretches with 0.05–0.1 P₀, the sarcomeres consistently “yielded” in clusters (left panels in Fig. 4A and B). Both the number of “yielding” sarcomeres and their location in the myofibril varied from stretch to stretch. In some cases we clearly observed that the “yielding” of one sarcomere transmitted along a myofibril to adjacent sarcomeres consecutively. This transmission spread over several sarcomeres forming a “yielding” cluster, although the size of clustering and the direction of propagation were different at every stretch. Since we did not find significant decrease in the average ΔSL of “yielding” sarcomeres against repeated stretches with 0.05–0.1 P₀, the mechanical properties of individual sarcomeres are likely to be well-maintained during the repeated stretches. These observations indicate that the inhomogeneous (or clustered) “yielding” is caused neither by the damage of particular sarcomeres nor by the inherent variability in a myofibril.

Fig. 4.

Clustered “yielding” in untreated and antibody-treated myofibrils. The spatial distribution of ΔSL along a myofibril (A), the spatial pattern of “resisting” and “yielding” sarcomeres at each stretch (B), and the distribution of ΔSL pooled over 5 stretches (C), under stretch repeated 5 times are shown. ΔP was chosen to be around ΔP₅₀ for each condition; 0.075 P₀ in untreated myofibrils (left panels) and 0.15 P₀ in antibody-treated myofibrils (right panels). The loading rate was 0.02 P₀/ms. The sarcomere responses classified as either “resisting” or “yielding” are colored in gray or orange, respectively, in B and C. The stiff needle was at the left side of the sarcomere number 1. (D) The spatial correlation of ΔSL between sarcomeres is plotted for untreated (open circles, n = 4 myofibrils) or treated (filled circles, n = 6 myofibrils) preparations. The plots were mean ± SD obtained from a total of 20 and 30 stretches, respectively (5 times in each myofibril). For details, see Materials and Methods.

Under these activation conditions, the SD of SL distribution just before stretch was typically ± 100 nm (n = 5 myofibrils), which was 2–3-fold larger than at the relaxing conditions. However, no significant correlation was found between the initial SL distribution and the probability of sarcomere “yielding” (Fig. S4). Moreover, the sarcomeres with the shortest initial length did not necessarily “yield.” Therefore, the inhomogeneity of SL distribution just before stretch is not the primary cause for the inhomogeneous “yielding.”

Antibody Binding to the Z-lines Affects the Clustered Yielding.

To examine the contribution of the Z-line to the clustered “yielding,” the myofibrils were treated with an antibody against α-actinin, a major component of the Z-line structure (21). The binding of an antibody is likely to affect the mechanical properties of the Z-line lattice structure (22, 23). The specific binding of the antibody to the Z-line was confirmed with the fluorescently labeled secondary antibody localized at regular intervals between adjacent A-bands in myofibrils (Fig. S5). After treating with a 13.9 μg/mL antibody solution (1:1,000 dilution of the stock solution), 2 distinct types of responses were observed similarly to the untreated preparations (Fig. S6); however, both ΔSL and the size of the “yielding” clusters significantly decreased compared with the untreated myofibrils (Fig. 4 A and B). We note that the “yielding” sarcomeres in the antibody-treated myofibrils were determined based on the shape of the length-response, rectangular for “resisting” or saw-tooth for “yielding,” rather than from the value of ΔSL, since the 2 peaks in the distribution of ΔSL were not clearly separated (Fig. 4C). The ΔP-dependent “yielding” frequency was also fitted by the Hill equation (Fig. 3C). Compared with the untreated myofibrils, ΔP₅₀ increased to 0.18 P₀, while n_H decreased to 2.0. The smaller size of the “yielding” clusters in the treated myofibrils was verified by the typical pattern of “yielding” in a myofibril (Fig. 4B), and by the autocorrelation analysis of the clustering pattern (Fig. 4D, see Materials and Methods for details). These results suggest that the modulation (possibly the stiffening) of the Z-line structure altered the ability of the adjacent sarcomeres to interact with each other.

The antibody treatment reduced the average active force ≈2-fold, to 23.3 ± 3.1 kN/m² (mean ± SE, n = 5 myofibrils), suggesting that the force-generating ability of individual sarcomeres was somewhat impaired. Nevertheless, all sarcomeres in the myofibril were able to shorten upon activation, showed spontaneous oscillation during activation transient, and exhibited different types of responses during each stretch, being similarly to the untreated preparations. These observations suggest that after treatment with 1:1,000-diluted antibody, the mechanical properties of individual sarcomeres were still maintained. The treatment with 1:5,000-diluted antibody resulted in responses comparable with the untreated samples, whereas less than 1:500 dilution prominently suppressed the force-generating activity and the emergence of spontaneous oscillation.

Discussion

The single-sarcomere analysis of skeletal myofibrils under phase-contrast microscope showed that at partial activation conditions force-generating sarcomeres “yield” against a stretch, rapidly elongating by more than 150 nm per sarcomere (Fig. 2). Since the thin filaments were directly activated by the strong-binding cross-bridges in the ADP-activation conditions (18, 19), the “yielding” may be induced by transient deactivation of the thin filaments due to forcible detachment of the cross-bridges, independently of the regulation by Ca²⁺. Several studies exist on individual sarcomere response to stretch at maximal activation by Ca²⁺. For example, Rassier et al. reported that sarcomeres were non-uniform along the myofibril, but stable against a stretch (13). Telley et al. reported the inhomogeneous response to stretch on the half-sarcomere level, but the quickly lengthening (or “popping”) sarcomeres were not found (14). On the other hand, a rapid but relatively small, a few tens nm, elongation of sarcomeres with a significant reduction in muscle stiffness against a stretch, termed sarcomere “give,” was observed in tetanically stimulated intact muscle fibers (24). Whereas in this study we could not detect significant rapid lengthening at maximal Ca²⁺-activation (Fig. S2), the “yielding” was observed at partial activation by Ca²⁺ (Fig. 2D), where the thin filaments are considered to be cooperatively activated by both Ca²⁺ and cross-bridges even in the absence of exogenous ADP (25). Compared with ADP-activation, sarcomeres were hardly “yielding” and ΔSL was smaller, despite the lower active isometric force (Fig. 2 B and D). Such robustness against stretch at Ca²⁺-activations is probably caused by the faster rate of cross-bridge rebinding, because cross-bridges are cycling faster due to the absence of exogenous ADP, and the thin filaments are continuously activated by Ca²⁺ even after the cross-bridges have been forcibly detached.

We emphasize 2 major characteristics of the sarcomere “yielding” observed here. First, the individual sarcomeres exhibit bimodal distribution of ΔSL. If the sarcomere response is averaged over the myofibril, it would be interpreted as a monotonic increase in ΔSL with an increase in ΔP, as shown in the upper middle panel in Fig. 2. However, the single-sarcomere analysis showed that the sarcomeres adopt either of the 2 distinct states, “resisting” or “yielding,” within a myofibril (Figs. 2B and 3A). Surprisingly, the number of “yielding” sarcomeres increased with an increase in ΔP, while the size of ΔSL remained constant (Fig. 3B). This implies that the applied load significantly affects the stability of sarcomeres to “yield,” but only slightly changes the dynamics during the lengthening phase. ΔSLs of “yielding” sarcomeres were remarkably larger than those of “resisting” ones, and the lengthening velocity was comparable to that observed upon relaxation from ADP activation (18). We therefore infer that in “yielding” sarcomeres almost all cross-bridges are transiently detached in response to stretch, followed by immediate reattachment with the active force recovery. The single-sarcomere analysis is indispensable for further elucidating the molecular mechanism underlying the “yielding” process, because in muscle fibers the non-uniformity may result in the inconsistency between force- and length-responses and therefore affect the analysis of cross-bridge dynamics (26, 27).

Second, the “yielding” occurs in clusters (or in-homogeneously) (Fig. 4), even though the sarcomeres are assumed to be uniformly loaded during stretch [note that the rate of tension transmission along the long axis of fully activated muscle fibers is reported to be 100–200 μm/μs (28)]. We verified that the main cause for the clustered “yielding” is neither the intrinsic inhomogeneity of the force-generating capacity of sarcomeres nor the inhomogeneity of SLs at the isometric tension plateau. This conclusion is based on the observations that the location of clustered “yielding” changed from stretch to stretch (Fig. 4), and the SL distribution just before stretch did not correlate with the occurrence frequency of “yielding” (Fig. S4). Thus, the clustered “yielding” is attributable to the cooperativity between adjacent sarcomeres through the structural factors (see the following paragraph). Similar phenomenon was observed during sequential relaxation of cardiac myofibrils, where a stretch can induce sarcomere relaxation only at the wave front of the already relaxing sarcomeres (29). The “yielding” sarcomeres may spread over the myofibril under isotonic conditions, where the applied load to each sarcomere is maintained nearly constant irrespective of the occurrence of “yielding.” Under the auxotonic conditions used here, however, the cluster size is limited, because every occurrence of “yielding” decreases the applied load and may therefore increase the stability of residual sarcomeres to “yielding,” allowing the analysis of clustering pattern in a myofibril.

The binding of anti-α-actinin antibody to the Z-line, which structurally connects adjacent sarcomeres, significantly increased ΔP₅₀, but decreased n_H (Fig. 3 B and C), that is, apparently stabilized sarcomere “yielding” against quick stretch. One possible reason for such stabilization may be the impairment of the sarcomere contractile ability by the antibody treatment. However, given the mosaic-type response (Fig. 4B), the faster decay of the spatial correlation between adjacent sarcomeres (Fig. 4D), and the high specificity of antibody to the Z-line (Fig. S5), we conclude that the stabilization is mainly caused by the suppression of clustered “yielding” due to the changes in the mechanical properties of the Z-line structure. Two independent results from electron microscopy (30) and X-ray diffraction (31) studies suggest that the tetragonal lattice structure of the Z-line changes between contraction and relaxation. The antibody binding may somehow inhibit these structural changes in the Z-line lattice. Recently, by tracking the process of sequential half-sarcomere relaxation along a myofibril with fluorescent markers, Telley and coworkers suggested that the cross-bridge detachment in the adjacent (half-) sarcomeres should be coupled, via the changes in the myofilament lattice structure (10, 32). Our present results clearly demonstrate that the cross-bridge detachment in a sarcomere induces that in the adjacent sarcomeres via the structural changes in the Z-line. In addition, the lattice spacing between the thick and thin filaments is likely to be compressed in response to the cross-bridge formation (33, 34), which we previously showed on the myofibrillar level (18). Taken together, these observations strongly suggest the possible mechanism of the propagation of the “yielding” phase (or the deactivation states) between adjacent sarcomeres involves the dynamic changes in the Z-line structure coupled with the expansion of the lattice spacing in the A- and I-bands, induced by the detachment of cross-bridges. In other words, the state of a sarcomere is determined not only by the longitudinal force balance between the contractile force and the external load, but also by the lateral force balance between the cross-bridge formation and the lattice structure of sarcomeres including the Z-line. The ability for the changes in the lattice structure to be transmitted along the myofibril should be important for the mechanism of SPOC wave propagation as well (11, 18). On the other hand, connectin/titin, which connects the thick filament to the Z-line and is responsible for the resting tension, is not likely to be the main player in this process, because the tryptic digestion of connectin/titin does not eliminate SPOC (35); besides, the clustered “yielding” is observed even in the region of short SLs where the resting tension is negligible. It has become recognized that the Z-line, the composition of which is more complex than previously expected, is involved in the regulation of various functions of striated muscle (36). Coupled with the previous reports, our results provide strong support to the suggestion that the Z-line not only plays an important role in the structural organization of each sarcomere but is also actively involved in force regulation by ensuring the efficient inter-sarcomere coordination.

In summary, mechanical measurements at partial activations demonstrate the dynamic response of individual sarcomeres to the applied load. We conclude that the activity of sarcomeres can be cooperatively regulated by the nearest-neighbor interaction through the structure-based mechanism involving the Z-line. Studies focusing on the lattice structure of striated muscle will give insights into the significant role of the architecture of biological systems for self-regulation. Additionally, further analysis with higher temporal resolution will reveal the contribution of force to the mechanism of long-range interaction between sarcomeres in striated muscle.

Materials and Methods

Solutions.

Rigor solution contained 2 mM free Mg²⁺, 20 mM Mops, and 4 mM EGTA. Relaxing solution contained 2 mM free Mg²⁺, 20 mM Mops, 4 mM EGTA, and 2 mM MgATP. N-benzyl-p-toluene sulfonamide (BTS) (100 μM) (37) was added to the relaxing solution when passive force response was measured. The ADP-activation solution contained 2 mM free Mg²⁺, 20 mM Mops, 4 mM EGTA, 1 mM MgATP, and 2 mM MgADP. The Ca²⁺-activation solution contained 2 mM free Mg²⁺, 20 mM Mops, 4 mM EGTA, 1 mM MgATP, and CaCl₂ of 2.2 mM (pCa 6.3; partial Ca²⁺ activation) or 4 mM (pCa 4.5; maximal Ca²⁺ activation). The pH value of all solutions was adjusted to 7.0 with KOH. The ionic strength was adjusted to 150 mM by KCl. ATP and ADP were from Roche Applied Science.

Myofibrils.

Myofibrils were prepared as described previously (38). Briefly, bundles of psoas muscle fibers were obtained from white rabbits (2–3 kg) anesthetized by sodium pentobarbital (25 mg/kg) into an ear vein. The fibers were stored in 51% (vol/vol) glycerol solution at −20 °C and used within 60 days. Myofibril suspension was prepared by homogenizing the glycerinated fibers in rigor solution and stored at 2 °C until use. The prepared myofibrils were used within 12 h. All procedures conformed to the “Guidelines for Proper Conduct of Animal Experiments” approved by the Science Council of Japan, and were performed according to the “Regulations for Animal Experimentation at Waseda University.”

Experimental Procedure.

A myofibril suspension in rigor solution was put in an experimental chamber, which was made of a pair of cover slips (Matsunami) and a Teflon block, under the phase contrast microscope (TE2000, Nikon) (Fig. 1A). A single myofibril (or a thin bundle) floating in the chamber was held by twining its ends around a pair of glass microneedles with the micromanipulators (MHW-3, Narishige) (39). After the solution had been exchanged for relaxing solution, SL was adjusted to 2.6–3.0 μm, so that sarcomeres reached SL approximately 2.3 μm at the activation plateau under auxotonic conditions. Then, relaxing solution was exchanged for activating solution. The solutions were perfused into the experimental chamber (vol. 200 μL) by a peristaltic pump (SJ-1211, ATTO) or by gravity from a syringe set at approximately 100 mm above the microscope stage, with the flow rate of 20 μL/sec. After force had reached the steady level, the stretch experiments were repeated with the same myofibril, by quickly moving the stiff needle away from the flexible one (Fig. 1B and C, see Results). The myofibrils containing 10–20 sarcomeres between the inner edges of the 2 microneedles were used in the experiments. The experiments were carried out at 25 ± 1 °C.

Phase-contrast images of myofibrils were obtained with the 40× objective (ELWD ADL 40×C; 0.60 NA, Nikon), projected onto a CCD-camera (DAGE-MTI), and recorded with a digital video recorder (SONY). Magnification was 0.25 μm/pixel. To impose mechanical perturbations on myofibrils, the stiff needle was attached to a piezoelectric stack actuator (P-841.10, Physik Instrumente) through the piezo driver (E-661, Physik Instrumente). The movement of the actuator was controlled by a self-written program in LabView 5.0 (National Instruments) through an A/D converter (PCI-MIO-16E-1, National Instruments). The other microneedle was flexible, the stiffness being 3.7 to 5.3 nN/μm (resonance frequency of ≈250 Hz in water), estimated by the cross-calibration method (39).

Data Analysis.

The intensity profile of the phase-contrast image along the long axis of a myofibril was obtained by Scion Image (Scion Corporation) every 33 ms on Macintosh PC (18). The width of ROI was set to fit the width of the myofibril. The individual SLs were defined as the distance between the centers of mass of adjacent A-bands in the intensity profile, which was calculated by the self-written Microsoft Excel macro. The rms noise of SL in relaxing conditions was ± 10 nm. The initial SL was determined by averaging 10 consecutive data points, that is, averaging over 330 ms (= 33 ms × 10), just before stretch, while the maximal SL was determined by averaging 3 consecutive data points, that is, averaging over 100 ms, just after the tension reached the minimum value (P₂). Then, ΔSL was calculated by subtracting the initial SL from the maximal SL.

The tension was estimated from the deflection of the flexible needle in the phase-contrast image. The degree of ΔP was estimated by multiplying the stiffness of the flexible needle by its displacement. The loading rate was estimated by dividing ΔP by the duration of stretch. The transient vibration of the stiff needle accompanying its rapid displacement was confirmed to be below 0.001 P₀ within the range of the examined stretch rates. The cross-sectional area of a myofibril was estimated from its width assuming that a myofibril is a uniform cylinder.

The spatial correlation in Fig. 4D was obtained by the following autocorrelation function after assigning 1 to “yielding” sarcomeres and 0 to “resisting” sarcomeres based on Fig. 4B:

where R_ΔN is the autocorrelation as a function of the distance between a given pair of sarcomeres (Δn = 1 for the adjacent sarcomeres, 2 for the second-neighbor sarcomeres, and so on), x_i is the index value of the i-th sarcomere response (either 0 or 1) in the myofibril, N_t is the total number of sarcomeres, μ is the mean, and σ is the standard deviation of the data set of x at a given ΔN.

Antibody Binding to the Z-line.

In some experiments, myofibrils were conjugated with a monoclonal anti-α-actinin antibody (A7811, Sigma-Aldrich). A myofibril, held with a pair of microneedles under the microscope, was incubated with an antibody diluted in relaxing solution for 10 min at 25 °C, and then washed with relaxing solution (5 times the chamber volume) before force measurement. To confirm the localization of the antibody to the Z-lines, the antibody-treated myofibrils obtained at the same incubating conditions were immunostained with an Alexa555-labeled secondary antibody using the Zenon labeling kit (Z25005, Invitrogen), and observed under a fluorescence microscope (IX70, Olympus) with an EM-CCD camera (iXon, Andor Technology), separately from the stretch experiment.