Correcting for Purifying Selection: An Improved Human Mitochondrial Molecular Clock

Abstract

There is currently no calibration available for the whole human mtDNA genome, incorporating both coding and control regions. Furthermore, as several authors have pointed out recently, linear molecular clocks that incorporate selectable characters are in any case problematic. We here confirm a modest effect of purifying selection on the mtDNA coding region and propose an improved molecular clock for dating human mtDNA, based on a worldwide phylogeny of > 2000 complete mtDNA genomes and calibrating against recent evidence for the divergence time of humans and chimpanzees. We focus on a time-dependent mutation rate based on the entire mtDNA genome and supported by a neutral clock based on synonymous mutations alone. We show that the corrected rate is further corroborated by archaeological dating for the settlement of the Canary Islands and Remote Oceania and also, given certain phylogeographic assumptions, by the timing of the first modern human settlement of Europe and resettlement after the Last Glacial Maximum. The corrected rate yields an age of modern human expansion in the Americas at ∼15 kya that—unlike the uncorrected clock—matches the archaeological evidence, but continues to indicate an out-of-Africa dispersal at around 55–70 kya, 5–20 ky before any clear archaeological record, suggesting the need for archaeological research efforts focusing on this time window. We also present improved rates for the mtDNA control region, and the first comprehensive estimates of positional mutation rates for human mtDNA, which are essential for defining mutation models in phylogenetic analyses.

Introduction

The use of genetic data to discern aspects of human prehistory, known as archaeogenetics,¹ is becoming increasingly important in unravelling the human past. For phylogeographic analysis, which combines phylogenetic and geographic evidence, the nonrecombining mtDNA and Y chromosome play a pivotal role, albeit most successfully in combination with other lines of evidence within a model-defined framework.² One important aspect of the phylogeographic approach in both haploid marker systems is the inclusion of a time frame based on the molecular clock, which makes it possible to estimate the age of lineages and often their dispersal times, without the need for an assumed demographic scenario.³

In recent years, the sequencing of complete mtDNA genomes has resulted in a huge increase in the resolution of the worldwide mtDNA tree, and in the potential concomitant power of phylogeographic analyses.^4,5 The tree topology confirmed that all human mtDNAs coalesce in Africa^6,7 and that all lineages that evolved outside Africa descend from two branches, referred to as haplogroups M and N, of the African haplogroup L3.^6–8 It also shed further light on the “out of Africa” dispersal process and the first colonization of each region through the detection of region-specific basal M and N lineages along the “southern coastal route”^6,7,9–18 and also on subsequent (and much more recent) prehistoric migrations.^19–23 However, many of the conclusions drawn depend to a considerable extent on the aforementioned molecular clock.

The most commonly used mutation rate for human mtDNA genomes in recent years has been a coding-region substitution rate (positions 577 to 16023 in the reference sequence²⁴) of 1.26 × 10⁻⁸ base substitution per nucleotide per year of Mishmar et al.²⁵ This mutation rate assumes a linear relation between the accumulation of substitutions and time, independent of any selection. One problem with this rate is that it omits a significant fraction of useful information from the noncoding parts of the molecules (about a third of the variation), which could be usefully employed to increase the precision of age estimates. However, the most important issue that has recently come to the fore has been the effect of selection.^26–29

The mtDNA phylogeny seems to show a higher proportion of synonymous mutations in ancient than in young branches—i.e., young branches present a higher proportion of nonsynonymous mutations in protein-coding genes and substitutions in RNA genes.^30–32 The most plausible explanation for this trend is purifying selection acting gradually over time on weakly deleterious characters, or a recent relaxation of selective constraints.^30,31 The mutation rate and the substitution rate are expected to be equal under neutral evolution,³³ but slightly deleterious mutations can persist for some time in the population with a lower fixation probability, elevating the transient mutation rate over the long-term substitution rate. (Confusingly, a misinterpretation of the same trend resulted in a proposal that the excess of nonsynonymous mutations in young branches was related to climatic adaptations,²⁵ but in fact the excess occurs in all young clades independently of location.³¹)

The potential time dependency of the mutation rate in evolutionary systems has also been discussed by Ho et al.^34–36 and Penny,³⁷ who argued that the mutation rate presents a vertically translated exponential decay curve³⁴ or a “J-shaped curve”³⁷. In other words, the mutation rate accelerates from a long-term rate in interspecific phylogenetic relationships to a higher rate nearer the present. A similar phenomenon was also proposed to explain the differences between the faster pedigree rates and the rate obtained from phylogenetic studies in the control region of mtDNA.³⁸ However, the shape of the curve may also be explained by saturation and even sequencing errors.³⁴

A possible consequence of this is that the age of young clades could be overestimated because of their higher proportion of nonsynonymous and other selectable characters. A new calibration for human mtDNA genomes has therefore been proposed, based on the rate of accumulation of synonymous mutations, thereby avoiding the selection drawback.³¹ However, this rate uses an even smaller fraction of the mtDNA genome, reducing the precision even further. Moreover, the lack of fit between this rate and a number of well-established phylogeographic patterns, such as those set up in Europe at the end of the last glaciation, leads to the suspicion that it may be an overestimate.

Endicott and Ho³⁹ recently attempted a recalibration using Bayesian estimation but assuming several highly debatable intraspecific calibration points, therefore incorporating assumptions into the estimation that a calibrated rate would preferably be employed to test. They did not analyze the time dependency of the rate, they did not provide either a time-dependent rate or an estimate of the rate for the whole mtDNA molecule, and neither their assumption that it is necessary to analyze different partitions separately when estimating divergence times nor their stipulation of intraspecific calibration points stands up to scrutiny. Even more recently, Henn et al.⁴⁰ made the first attempt to characterize the mutation-rate curve of human mtDNA, although this suffers from the same weakness regarding calibration-point assumptions.

A calibration that corrects for the evident time dependency of the mtDNA mutation rate is urgently needed in order to re-establish the credibility of mtDNA in human evolutionary research, and we therefore addressed this need in this study. We first reconstructed the global mtDNA tree by using > 2000 complete mtDNA genomes and assessed the variation of different classes of mutation at different time depths, in order to test the time dependency of the mutation rate. We then recalibrated the mtDNA molecular clock by accounting for the effect of time depth (without any prior assumption on intraspecific calibration points), incorporating the most recent fossil evidence for the time of the Homo-Pan split. We also independently estimated new synonymous mutation and control-region rates for comparison and an internal control. Finally, we reassessed a number of phylogeographic aspects of human evolution in order to cross-check the new chronology.

Material and Methods

Data Set

We compiled a database containing published complete mtDNA sequences from NCBI with the Geneious software. These included the complete mtDNA sequences from several papers^{6–9,11–25,41–52} and several deposited by Family Tree. We excluded some sets of sequences available at the beginning of this analysis^10,53 because some probably contained errors^12,54 and one was not entirely produced by direct sequencing.⁵⁵ Additionally, we added 176 unpublished sequences produced by the authors when we began this work, some of which have been subsequently published.⁵⁶ A list of the published complete mtDNA genomes used is shown in Table S1, available online. A total of 2196 complete mitochondrial genomes were used in the final analyses.

For comparative and calibration purposes, we used two sequences of Pan troglodytes,^57,58 one of Pan paniscus,⁵⁸ and two of Gorilla.^58,59 Additionally, all of the available complete mtDNA genomes from primates were retrieved from NCBI, again with the Geneious software. A list is shown in Table S2. We later included the complete mtDNA sequence of the Neanderthal for comparison.⁶⁰

Phylogenetic Reconstruction

We constructed phylogenetic trees by using the reduced-median algorithm⁶¹ of the Network 4 software and using all the substitution information in the molecule (except for 16182C, 16183C, and 16194C in polycytosine tracts containing the 16189C variant because they are inconsistently reported in the literature). The 9 bp deletion was also included. We built three trees independently, corresponding to macrohaplogroups M, N, and remaining African L sequences, because of the size of the data set.

After an initial run, we summed the statistics (counts of each mutation) obtained for each tree and used them to weight the characters from 1 to 99 with an inverted linear relation against the number of occurrences in the statistics, where a weight of 1 corresponded to the most common character in the statistics (16519) and a weight of 99 to the singletons.

We used the values of the statistics to decide which mutations happened multiple times in the reticulations. Additionally, we calculated values of ρ⁶² for the hypothetical clades or paragroups in the vertices of the reticulation in order to decide which one was likely to be older and thereby the polarity of the mutation (parallelism versus reversion).

We excluded some sequences that generated major reticulations (probably as a result of mixing fragments between samples). The errors in some of those sequences have since been confirmed by resequencing.⁶³ Combining the three trees yielded a final single tree of 2196 sequences.

Classification of Mutations

After the phylogenetic reconstruction, we classified all the mutations in the tree as control region (all the mutations present outside the coding region, encompassing positions 16024–576), 12S rDNA, 16S rDNA, tDNA, synonymous transition, synonymous transversion, nonsynonymous mutation (this class also included the synonymous/nonsynonymous mutations in the overlapping genes ATP8 and ATP6 because evolutionarily they would have been selected on the basis of the amino acid change), and other (all remaining noncoding positions not placed into any of the previous categories).

Diversity Plots for the Comparison of the Accumulation of Synonymous and Total Mutations

For each of the nodes in the final tree, we calculated a diversity value (with the ρ statistic⁶²) for each category of mutation. This allowed us to compare the accumulation of one type of mutation with any other kind for the same time depth (i.e., diverging from the same nodes). The synonymous clock, because it should not be affected to any great extent by selection effects, should approach linearity. We compared the values of ρ for every node in the tree with the proportion of the overall ρ represented by synonymous mutations (“the synonymous ρ proportion”: synonymous ρ divided by overall ρ). If the overall clock is evolving neutrally, this latter proportion will be constant on average (for all values of overall ρ). (We excluded mutations at position 16519, because the mutation rate at this site was so disproportionately fast in comparison with the rest of the molecule that its evolutionary history was sometimes difficult to track.) We modeled in R⁶⁴ the average synonymous ρ proportion as a Gompertz function of the overall ρ with least-squares. However, the data for the different nodes are correlated and the variance is not constant, so a grouping procedure was employed in an attempt to deal with this. Data points were sorted by overall ρ and averaged, from high overall ρ downward, so as to limit (below a threshold) the variance in the synonymous ρ proportion as estimated assuming we were estimating a binomial proportion with independent draws.

Saturation Curves

The absolute frequencies for each position that we obtained by counting occurrences on the tree can help us to shed light on the processes of saturation along long branches. All of the mutations we counted would correspond to independent mutation events in a tree where the level of saturation is low. If saturation were high, there would be many undetectable “hidden mutations,”⁶⁵ which could account (entirely or in part) for the “J-shaped curve” that has been attributed to purifying selection.

To test the extent of saturation, we randomly selected substitutions from the pool of total mutations, simulating the occurrence of mutations in the mitochondrial genome, according to their relative mutation rates. We assumed that the absolute frequencies of occurrences of each mutation in the tree reflected the relative mutation rate of that specific position. N_e mutations selected randomly in a specific order would reflect N_e mutations expected to occur on the evolution of a given mitochondrial sequence. Because of the rapid evolution of the mitochondrial genome, recurrences at a specific position should be frequent, and a specific substitution could occur n times in the total N_e substitutions.

A transition at a given nucleotide position occurring twice within the evolution of a single sequence—that is, an occurrence and a reversion of the position back into its original state—results in two hidden mutations in the evolution of the sequence. Given that N_e is the total number of mutations occurring in the simulations, then N_o is the observed number of mutations, so that N_e > N_o. This theoretical relation can be expressed mathematically for different values of N_e and N_o. Then, given N_e we can find N_o, and vice versa. Saturation-rate curves (y = a·x/(b+x)) presented the best fit for the data and were obtained with the CurveExpert v1.3 software.

Variation at each position is not always binary, because there are four possible bases in each position, and substitutions can be transitions or transversions. This was taken into account by considering that if a position underwent a transversion and then a transition (or vice versa) in the simulation, we would only count it as one occurrence, because we would only be able to trace the transversion when comparing the initial sequence (state 0) and the final sequence (state N). The same would happen if the position underwent a transversion and more than one transition (we would still be able to trace only one transversion).

We performed the simulations independently for different classes of mutations, for two reasons: one was that we made different assumptions in defining the portion of the mutation pool that we used (see below), and the second, more important, was related to the fact that we are mainly interested in observing the diverging variation, due to saturation, of the branch length for different classes of mutations in time. For simulations on rDNAs, tDNAs, nonsynonymous mutations, and control-region mutations, we used only mutations that were older than an overall ρ = 4, to avoid the proposed preponderance of weakly deleterious mutations in young branches, and younger than ρ = 18 (broadly corresponding to the age in mutations of macrohaplogroups M and N), to avoid a possible high degree of saturation in the deeper parts of the tree. For synonymous mutations, we used mutations that were younger than ρ = 18, because selection should not be an issue for these. We performed all of the simulations for each type of mutation at least six times, until the shape of the curve did not change with further analyses.

Is this procedure justified? Although some saturation exists in the selected part of the tree, the relative mutation rate per position obtained there should not be very misleading; however, it can be relevant for the fastest sites. Considering the fastest site in the analysis, 152 (we excluded position 16519, the fastest of all, from the main analyses), the relative mutation rate is relatively stable, whatever the portion of the tree considered, even when comparing substitutions in regions where saturation should be an issue (the older, longer branches) with substitutions within young nodes. The frequency of mutations at the 152 position within the total pool of control-region mutations is 4.59% in the total tree, 4.54% considering nodes with ρ < 20, 4.53% in ρ < 15, 4.51% in ρ < 10, 4.44% in ρ < 5, and 4.54% in nodes with ρ < 3. Using the relative mutation rate obtained, we can calculate a probability that a given mutation happens more than once per branch in a specific branch length. We used a section comprising branches between a ρ of 4 and 18 (an average of 14 mutations per branch). The probability that a substitution in position 152 happens more than once in a branch length of 14 mutations is a low 1.3 in 100—and this value does not take into account the fact that the majority of the branches are substructured. Considering that this is the position where saturation should be felt the most strongly, it seems unlikely that the relative mutation rates and the proportions in the pool of mutations are highly underestimated for the fast sites.

We applied the saturation curves (providing a value for expected mutations from the value of observed mutations) to the split between the modern human sequences and the Neanderthal, and, with due caution, to the split between the bonobo and the chimpanzee. (The relative mutation rates at each position are unlikely to be exactly the same but, considering the similarity of their mtDNA genomes, it seems reasonable to assume the curves as general models of saturation.)

Maximum-Likelihood Analysis and Calibration Points

We used a set of 193 human complete mtDNA sequences selected from the previous tree to represent all of the main branches both within and outside Africa, with two chimpanzee sequences and a bonobo sequence, to construct a maximum likelihood (ML) tree and estimate the rate of the mtDNA clock. We used PAML 3.13,⁶⁶ assuming the HKY85 mutation model with gamma-distributed rates (approximated by a discrete distribution with 32 categories) and eight partitions. Additionally, we performed the analysis with the TN93 model to test for a significant improvement in their performance. The partitions were the following: one corresponded to the rDNA sequences (12S and 16S rDNA), one to the tDNA sequences, one to the first and second positions of the codons of the protein-coding genes (broadly similar to the nonsynonymous mutations), one to the third position of the codons (broadly equivalent to the synonymous mutations), and one to noncoding regions outside the control region; finally, the control region was divided into three sections: hypervariable segment-I (HVS-I) (positions 16051 to 16400), HVS-II (positions 68 to 263), and remainder. As in the classification of mutations, the overlapping region between ATP8 and ATP6 was integrated in the nonsynonymous partition. We performed the analysis in two ways: (1) by using the entire molecule, and (2) by using only the coding region but including the Gorilla sequences where the alignment of some stretches of the control region was not completely reliable.

For an estimation of the synonymous clock, we used PAML to calculate a mutation rate per possible synonymous mutation under the mitochondrial genetic code, assuming a single value for the dN/dS ratio (ratio of nonsynonymous to synonymous mutations) and using an alignment containing only the protein-coding genes, with the ND6 gene readjusted to present the same reading direction as the other genes. In order for nonsynonymous mutations not to interfere with the calculation of the synonymous clock (as a result of differential distribution across the tree), we manually excluded the nonsynonymous substitutions from the alignment and replaced them with the ancestral base pair.

For our calibration point, we used the Homo-Pan divergence. Recent calibrations have assumed a species split of 6 mya, with an additional 0.5 My for lineage coalescence.^25,31 In the last few years, however, fossil evidence has mounted for a split time closer to 7 mya, with an approximate age of 6.5–7.4 mya for Sahelanthropus tchadensis,^67–69 5.7–6.2 mya for Orrorin tugenensis,^70,71 and 5.2–5.8 mya for Ardipithecus kadabba,^72,73 all of which have been argued to be either early hominins or close in time to the hominin-chimp split on a sister branch.^74–77 On the basis of the age of Sahelanthropus tchadensis, Benton and Donoghue⁷⁸ have recommended that 7 mya be taken as a recommended lower bound. (The discoverers of Orrorin tugenensis in fact claim an age for the split of considerably earlier than 7 mya,⁷¹ raising questions regarding older estimates of 10.5–13.5 mya obtained when nonprimate calibration points were used in molecular data,⁷⁹ but the weight of the molecular evidence argues against this.) The consensus of molecular evidence for a split 5–6 mya⁸⁰ therefore seems increasingly likely to be slightly too recent,^76,81 and can be at least in part explained by the predominant use of minimal estimates (or underestimates) for fossil divergence times deeper in the primate phylogeny, because of the nature of the fossil record.⁷⁸ Recent estimates based on large-scale genome sequencing that use more realistic divergence times (e.g., for Homo-Pongo) estimate Homo-Pan to > 6.3 mya, albeit with a possible hybridization event a little more recently.⁸² The discovery of a possible fossil gorilla ancestor, Chororapithecus abyssinicus, dating to ∼10–10.5 mya⁸³ and a possible independent line diverging from this ancestor, Nakalipithecus nakayamai, dating to 8.7–9.6 mya,⁸⁴ also, by implication, make more likely a split in the Pan-Homo branch of ∼6–7 mya, rather than 5–6 mya.

For our calibration, we therefore assumed a human-chimpanzee species split of 6.5 mya, with an additional estimated 0.5 My for mtDNA lineage coalescence. In order to check the impact of such an age on the split time of other nodes in the primate phylogeny, we built a coding-region mtDNA tree containing 31 sequences of 23 different primate species, with MrBayes 3.12,⁸⁵ and we applied the same parameters we used to calculate the molecular clock on this tree in PAML.

Human mtDNA Trees and ML Age Estimates

In order to date all of the nodes in the human mtDNA tree, we built six mtDNA trees from published data by using the reduced median (RM) algorithm of Network 4.5, and performed the ML branch-length analysis in PAML 3.13⁶⁶ with the eight partitions defined before and the HKY85 mutation model with gamma-distributed rates (approximated by a discrete distribution with 32 categories). The first tree contained all the African L sequences (including the North African haplogroups U6 and M1), as well as some additional M, N, R, and U sequences to help establish the branching structure. The second mainly contained East Asian haplogroup M sequences. The third contained all Asian N (including R) sequences. The fourth contained all Native American haplogroups along with the closest related northeast Asian sequences in the data set. The fifth contained all M, N, and R basal haplogroups from South Asia. The sixth contained the European data set (excluding North American data). As for the first, each of the remaining five trees included a few additional sequences from missing haplogroups to help establish the branching structure.

Results

Worldwide mtDNA Tree

The topology of our worldwide mtDNA tree matched published trees in most respects, with certain minor exceptions of detail. Within haplogroup N, the only instance of a different branching structure was in the separation of the putative haplogroup B6 from other members of haplogroup B (defined by a transition at the fast site 16189 and a 9 bp deletion in the COII-tRNA^Lys intergenic region;⁸⁶ instead, it grouped with R11 through 16189 and 12950, because 12950 is much slower (three occurrences) in the tree than the 9 bp deletion (16 occurrences).

Within haplogroup M, M21⁹ lost one of the subbranches of M21b that shared the M21-defining mutation, at position 11482, as well as mutations at positions 709, 15924, and 16129, all three very fast sites, and it was linked to M13 through mutations at positions 6023, 6253, 15924, and 16381, of which only 15924 is a fast site. In the weighted network, the software did not present the original link even as a reticulation.

Relative Mutation Rates

There were, in total, 10,683 substitutions throughout the tree. The count of each kind of mutation is important in order to understand the mutational spectrum of the molecule and identify mutational hotspots.

Figure 1 shows the major hotspots we identified in the mtDNA genome. The major HVS-I hotspots obtained are in reasonable agreement with the ones obtained recently by ML analysis.⁸⁷ These results quantify and greatly extend a picture already built up for the control region of the human mtDNA genome. Our approach, based on a phylogenetic reconstruction, has been little used in previous methods of relative mutation-rate determination⁸⁸ since the work of Hasegawa et al. 15 years ago.⁸⁹ Apart from the ten or so most highly mutable sites, however, the overall rates of control-region and coding-region sites are similar (in agreement with Howell et al.⁹⁰), supporting the need for an overall mutation rate. Although the control region does include some of the fastest sites in the molecule (e.g., 16311, 16189, 16129, 16093, and 16362 in HVS-I and 152, 146, 195, and 150 in HVS-II), it is primarily distinguished as including segments where a greater proportion of positions are mutable than in the coding region. The number of mutational events at the fastest site of all, position 16519, is probably considerably underestimated, and it was therefore excluded from the calibration. The most prominent transversional hotspots were G13928C (presenting 12 occurrences) and then A16265C and A16318T (with eight occurrences each). Table S3 displays all of the mutations and the number of times that they occurred.

Figure 1.

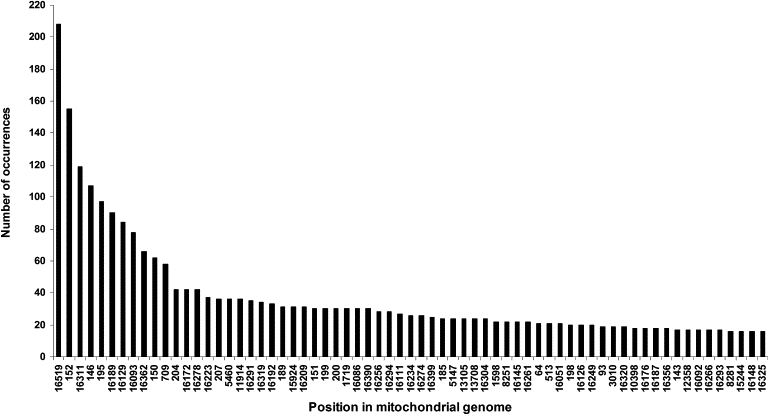
Hot Spots in the mtDNA Genome, Showing All the Positions that Appear > 25 Times in the Tree

We calculated mutation density throughout the mtDNA genome by using a sliding window at intervals of 50 bp, each overlapping by 49 bp. The two hypervariable segments are clearly recognizable, and the remaining molecule is relatively uniform. The lowest value obtained was zero, in regions 2651–2705 and regions 3028–3082. The highest value (582, or 11.64 mutations detected in the tree per nucleotide) corresponded to the interval 146–195 in HVS-II, as a result of the fact that it contains three major hotspots (146, 152, and 195). The average number of substitutions detected in the tree per nucleotide position was 0.645 for the entire molecule, 0.469 for the coding region, and 3.74 mutations for the entire control region (but excluding 16519). All 50 bp intervals with more than two substitutions detected per nucleotide were in the control region. These correspond to the regions 68–263 (5.95 detected mutations per nucleotide) and 16068–16387 (5.93 mutations detected per nucleotide), following closely the canonical definitions for HVS-II and HVS-I, respectively. Overall in the tree, 3,745 of 16,569 positions were found to mutate.

Saturation Curves

The simulations showed the relationship between the traceable variation in long branches (assuming no weakly deleterious mutations) (N_o) and total hypothetical variation, including the hidden variation in those branches (N_e). Saturation-rate curves were selected from the Curve Expert v1.3 software and corresponded to the following:

• N_o = 139.555 × N_e / (162.432 + N_e), with R² = 0.9990, for the control region obtained in the range of 0–100 observed mutations (N_o) (Figure 2A);

• N_o = 242.70155 × N_e / (241.82115 + N_e), with R² = 0.9983, for the nonsynonymous mutations obtained in the range of 0–100 observed mutations (N_o);

• N_o = 260.05817 × N_e / (326.27167 + N_e), with R² = 0.9990, for the rDNA mutations obtained in the range of 0–70 observed mutations (N_o);

• N_o = 106.85678 × N_e / (106.02999+N_e), with R² = 0.9990, for the tDNA mutations obtained in the range of 0–50 observed mutations (N_o);

• N_o = 1900.7636 × N_e / (2030.1489 + N_e), with R² = 0.9997, for the synonymous mutations obtained in the range of 0–1000 observed mutations (N_o) (Figure 2B).

Figure 2.

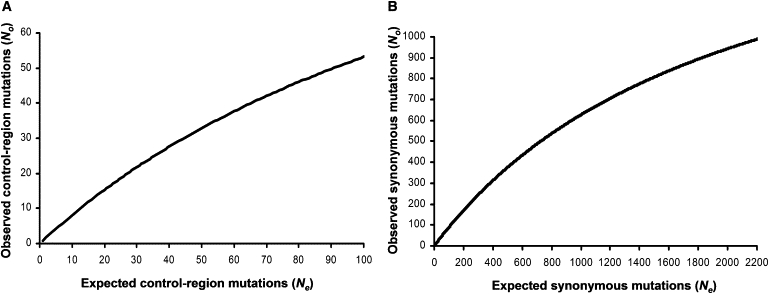
mtDNA Saturation Curves

(A) Control-region mutations.

(B) Synonymous mutations.

These saturation curves allowed us to test the effect of saturation on the increase or decrease in variation of each class of mutation and the overall number of hidden mutations in ρ calculations, as described in the next section.

Diversity and Purifying Selection: The Change in the Fraction of Synonymous Mutations over Time

Only one class of mutation is likely not to be under significant selection: the synonymous mutations. All other classes of mutation can be expected to present some combination of neutral and weakly deleterious mutations. Therefore, any value of present variation is likely to include both a neutral fraction and a fraction that is undergoing purifying selection. The neutral fraction (ρ_N) can be defined as ${\mathit{\rho }}_N=(\%syn+\%neu)\times {\mathit{\rho }}_0$, where ρ_N is the value of neutral variation of a specific observed variation (ρ₀), considering the proportion of synonymous mutations (%syn) and the proportion that are neutral or nearly neutral with a high possibility of fixation (%neu), or, $\mathit{\rho }N=(100\%-\%del)\times {\mathit{\rho }}_0$, where %del is the percentage of weakly deleterious, nonfixable mutations. However, considering these three proportions, only the proportion of synonymous mutations can be measured directly.

We plotted the synonymous ρ proportion against the overall ρ for each node to ascertain to what extent the proportion varies with time (Figure 3, filled circles). The trend is obscured because the variance in synonymous ρ proportion varies dramatically for different ρ values, but the average proportion seems to approach an asymptote for older branches. To control variance (and also to some extent the correlation of different observations), we grouped the data points as described above (Figure 3, hollow circles). This showed that the synonymous ρ proportion increases with higher values of ρ, but that the rate of increase decreases with ρ, plausibly tending to a constant. To capture this behavior, we fitted a Gompertz function to the grouped data yielding this fit: average synonymous ρ proportion = 0.479 exp(−exp[−0.0263(overall ρ + 40.28)]) (Figure 3, solid line). The average synonymous ρ proportion varies from 0.3387 when ρ = 0 to 0.4794 at ρ = ∞. The former corresponds to an estimate of the ratio of instantaneous synonymous-to-total-mutation rate.

Figure 3.

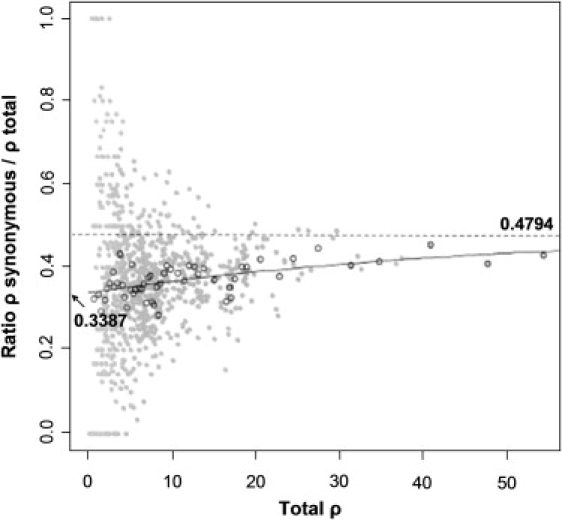
Relation between Overall ρ Values and the Synonymous ρ Proportion

Individual data points for each node in the tree are displayed as filled gray circles, and grouped points are displayed as empty circles. The solid curve is a model fit to the empty circles.

To test whether this trend could partially be explained by uneven saturation of the different classes (a plausible scenario when considering the complete genome variation, because it includes the fast-evolving control region), we used a region of the tree where saturation was low (overall ρ < 3) to obtain the proportion of mutations in each class (which should relate directly to the relative mutation rates of each class). We then estimated the variation in the proportion of these classes caused by saturation at increasing time depth and used the saturation curves calculated above to estimate a traceable number of mutations (the theoretical observed mutations in the simulations) in each class for the number of mutations occurring (the expected number of mutations in the simulations), according to the relative mutation rate of each class at a specific time depth.

Calculating the variation in the ratio of the synonymous mutations to total mutations up until an overall ρ of 60 (observed mutations), a value slightly higher than the value of ρ for the coalescence time of the human mtDNA tree, the ratio of synonymous ρ against overall ρ would not change more than 1.2% (against 10.93% in the curve) and just 0.37% until the coalescence time of the out-of-Africa macrohaplogroups, against the value of 5.51% in the data. Considering that these values are heavily overestimated, because they are the result of assuming a single long branch and do not consider the high number of recurrences and reversions that are easily detected by parsimony in a structured tree (so that this value simply provides a maximum level of saturation), saturation cannot provide the major explanation for the increase in the ratio of synonymous mutations in the mtDNA tree at higher ages. The principal remaining candidate explanation for the observed trend is the gradual continuous removal of lineages containing weakly deleterious mutations in the other classes through purifying selection, as argued by Kivisild et al.³¹ This analysis therefore substantially confirms their suggestion.

Estimates of Interspecific Molecular Clock

Before a correction for time depth could be applied, we needed to estimate the rate of the interspecific molecular clock. We used ML and a calibration point of 7 mya for the Pan-Homo mtDNA separation to estimate the interspecific mutation rate. Although the control region is highly saturated along long branches, ML would be expected to allow for this. Even so, as a precaution we also performed the ML analysis by using only the coding region, and we corrected the value by checking the relative proportions of coding-region and control-region mutations in the intraspecific human tree. This relative mutation rate was calculated with mutations with relative ages lower than ρ = 18 (in order to avoid the African long branches, where saturation could be an issue) and older than ρ = 4 (in order to avoid the majority of the deleterious mutations in both control and coding regions). This ratio of coding-region mutations to control-region mutations yielded a value of 1.57.

The values obtained for the eight partitions are shown in Table 1, as well as α and κ parameters for each. We further performed the ML analysis with the TN93 model and again without assuming a molecular clock. Likelihood-ratio tests⁹¹ did not prove significant, indicating that the clock hypothesis was not rejected (p = 0.97) and that there was no need for more complex nucleotide-substitution models (p = 0.95).

Table 1.

Substitution Rates per Nucleotide per Year for Eight Partitions of Complete mtDNA Genome of African Apes and Humans Obtained from ML Estimates

Partition	Substitution per Nucleotide per Year	α ± SE	κ ± SE
Control region: HVS-I	1.64273 × 10−7	0.245342±0.023473	45.94799±6.673706
Control region: HVS-II	2.29640 × 10−7	0.106975±0.015081	55.97029±9.681416
Control region: Remaining	1.54555 × 10−8	0.299924±0.056206	16.29045±3.316819
Protein-coding genes: 1st + 2nd positions of codon	8.87640 × 10−9	0.161436±0.010437	54.34843±2.969624
Protein-coding genes: 3rd position of the codon	1.92596 × 10−8	0.518065±0.054261	48.38462±26.01403
rDNA	8.19696 × 10−9	0.082107±0.008931	39.23242±13.33863
tDNA	6.91285 × 10−9	0.143719±0.022903	56.14882±39.16504
Others	2.48537 × 10−8	0.226347±0.096673	9.106106±4.281547

The substitution rate for the entire molecule was 1.665 × 10⁻⁸ (±1.479 × 10⁻⁹) substitutions per nucleotide per year, or one mutation every 3624 years. Using just the coding region and using the ratio of 1.57 (coding region/control region mutations) as a cross-check, we obtained a very similar value (1.708 × 10⁻⁸ ± 8.92 × 10⁻¹⁰ substitutions per nucleotide per year, or one mutation every 3533 years). The similarity of the values is not surprising considering that the ratio of the coding-region rate to the control-region rate in the eight partition calculations was 1.55.

We also included the recently published Neanderthal sequence in the tree, and we again performed the analysis with the eight-partition model. We obtained a split time between Homo neanderthalensis and Homo sapiens mtDNAs of 550 (±54) kya. Considering the widely held view that Homo neanderthalensis evolved from Homo heidelbergensis in Europe,⁹² we would expect the time of the split to be before the appearance of Homo heidelbergensis in Europe. The Boxgrove tibia (from Sussex, England), attributed to Homo heidelbergensis, dates to ∼500 kya,⁹³ so the estimate for the timing of the split fits rather well with this interpretation of the fossil record.

Assuming a human-chimp split of 6.5 mya, we obtained a value of 9.4 mya for the Gorilla-Homo versus Pan split by using the coding-region tree. These values fit well with estimates of the minimum age of the Gorilla lineage based on recent fossil discoveries^83,84—in fact, the fossil evidence suggests that they could, if anything, be even higher—indirectly supporting the assumption that the Homo-Pan split was at least 6.5 mya. Using the estimates in Table 1, we estimated the chimp-bonobo split at 2–2.5 mya, a plausible value that is in agreement with the majority of previous estimates.⁹⁴

In order to check the implications of such a Homo-Pan split time on deeper primate divergence times, we calculated ML age estimates for the whole of the primate mtDNA tree (Table 2). All of the separation times fall within the range of plausible values based on the fossil evidence,^78,81 although they are generally somewhat higher than molecular estimates. These estimates assume equal rates among primate lineages, which has been questioned at various times, for instance in the context of differing generation times.⁹⁵ We therefore checked the respective lengths of the human and chimp branches in the Bayesian analysis. They have similar lengths, with the human branch being slightly longer (1.023 longer), so rate variation between the human and the chimp does not seem to be a major issue.

Table 2.

Split Times of the Catarrhines and Groups within the Catarrhines with ML and the Coding Region of the mtDNA Genome and Assuming a Homo-Pan Split of 6.5 Mya

Split Event	Age Estimate (mya)	Standard Error (my)
Homo-Gorilla	8.85	0.30
Homo-Pongo	15.84	0.35
Homo-Hylobates	20.21	0.52
Homo-OWM (catarrhine coalescence time)	34.18	0.70
OWM coalescence time	25.52	0.63

OWM denotes Old World monkeys.

Correcting the Mitochondrial Clock to Allow for Purifying Selection

An interspecific mutation rate (M) would be linear if we were to consider only the neutral portion (ρ_N) of the variation, and the age estimate (AE) of a clade can be expressed as AE = ρ_N × M, with M expressed as the number of years taken for a single neutral mutation to happen. Considering a synonymous molecular clock, that same age estimate can be expressed as $AE={\mathit{\rho }}_0\times \%syn\times M_{syn}$, where M_syn is the synonymous mutation rate.

At and beyond a time depth when purifying selection has become irrelevant (because all deleterious mutations have been selected out), the observed variation (ρ₀) will be equal to the total neutral variation (ρ_N), i.e., $\mathit{\rho }N=(\%syn+\%neu)\times {\mathit{\rho }}_0$ and so $\%syn+\%neu=100\%$. Considering the age estimate (AE) formulas, we can deduce that ${\mathit{\rho }}_N\times M={\mathit{\rho }}_0\times \%syn\times M_{syn}$, so $M_{syn}=\frac{{\mathit{\rho }}_0\times (\%syn+\%neu)\times M}{{\mathit{\rho }}_0\times \%syn}$, leading to $M_{syn}=\frac{100\%\times M}{\%syn}$ or simply $M_{syn}=\frac{M}{\%syn}$, meaning that the mutation rate of the synonymous mutations will correspond to the overall mutation rate (expressed as mutations per site per year) divided by the observed proportion of synonymous characters in the total (fixable, neutral) characters (%synps).

However, the main objective in the calculation of the time-dependent mutation rate is to be able to estimate a theoretical fraction of neutral variation (ρ_N) at any time depth in the tree. Again considering the formulas of the age estimate, we obtain ${\mathit{\rho }}_N\times M={\mathit{\rho }}_0\times \%syn\times M_{syn}$, and that $M_{syn}=\frac{M}{\%synps}$ leads to ${\mathit{\rho }}_N\times M={\mathit{\rho }}_0\times \%syn\times \frac{M}{\%synps}$, we obtain ${\mathit{\rho }}_N=\frac{{\mathit{\rho }}_0\times \%syn}{\%synps}$ and the age estimate can be defined as $AE=\frac{{\mathit{\rho }}_0\times \%syn}{\%synps}\times M$. The main interest now is to obtain a theoretical value of the proportion of synonymous mutations corresponding to any value of total variation, in order to provide a corrected age estimate that is independent of the one calculated with the synonymous molecular clock. This correction requires an estimate of the proportion of synonymous mutations in the branches after purifying selection ceased to act or became negligible (%synps). We can express the same question in terms of the y asymptote of the curve in Figure 3.

In the human mtDNA tree, the value tended to about 44%–45%, but it is possible that selection is still operating at the coalescence time of the tree. The Gompertz function supports this, indicating a value of 47.94%. This does not necessarily mean that the ancient branches of the human mtDNA tree are still under selection, for the reason that ρ values are obtained by calculating the diversity in the present—including the possible weakly deleterious mutations—and because we do not know how far back in time the tree ceases to be effectively under selection, those weakly deleterious mutations will always be a proportion of the overall diversity despite becoming progressively more negligible moving further back in the tree.

We can compare the value of the synonymous ρ/overall ρ ratio in the modern human-Neanderthal split. This yielded the value of 55%, although it is in a time range where saturation would play an important part. Applying the saturation curves obtained above for each class brought the value down to 51.0%, close to our theoretical plateau. Beyond the coalescence time of Homo sapiens with Homo neanderthalensis mtDNAs, the nearest node we can use for comparison is the split between the bonobo and the common chimp. The bonobo-chimp branch showed an obviously higher value for the proportion of synonymous mutations (56.1%), although this should be mainly caused by uneven saturation of the different classes. Acknowledging that several assumptions are necessary, because the model was estimated with human mutation patterns, we can nevertheless obtain a heuristic value for comparison by using the saturation curves obtained. In this way, we retrieved the value of 46.6%. Once again, the value approximates our theoretical plateau value of 47.94%.

We can therefore adapt our molecular clock to any time depth, by correcting the observed overall diversity to the theoretical diversity after purifying selection has acted to remove lineages carrying deleterious mutations. This can be done through the previous formulation:

$AE=\frac{{\mathit{\rho }}_0\times \%syn}{\%synps}\times M$ or, assuming the Gompertz curve for %synonymous versus overall variation and the y asymptote value of 47.94%, we obtain:

$$AE=\frac{0.4794\times e^{-e^{-0.0263\times ({\mathit{\rho }}_o+40.2789)}}}{0.4794}\times {\mathit{\rho }}_0\times 3624,$$

or simply

$$AE=e^{-e^{-0.0263\times ({\mathit{\rho }}_o+40.2789)}}\times {\mathit{\rho }}_0\times 3624\text{.}$$

Figure 4 shows the shape of the mutation-rate curve.

Figure 4.

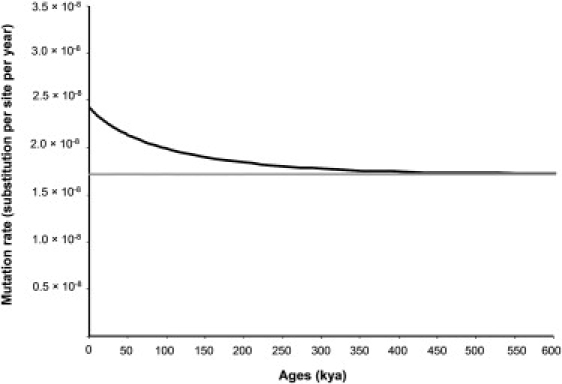
Variation of the mtDNA Mutation Rate through Time

The black curve represents the mtDNA mutation rate. The gray curve represents the interspecific mutation rate.

To assess the effect of the corrected clock on age estimates against the Mishmar et al. coding-region linear clock,²⁵ we compared both estimates within several age intervals (obtained from the corrected clock). The age estimates with the Mishmar et al. rate present differences of > 50% higher than the corrected clock at recent nodes and about 10% higher in the more ancient nodes of the tree (Table S4). The effect would be greater if the same human-chimp split time was selected (62% higher in the 0–1,000 year interval to 19% in the 100,000–200,000 year interval).

Estimates of Synonymous Mutation Rate

Obtaining an accurate mutation rate for synonymous mutations remains crucial, because it is the only class of mutations where purifying selection does not act and therefore the most likely to present a linear mutation rate (although even here there are issues related to codon usage and possible structural constraints⁹⁰). Assuming an overall interspecific mutation rate of one mutation in every 3624 years for the whole molecule, and a value of 47.94% of synonymous mutations after selection, we can readily calculate an interspecific synonymous mutation rate of one per 7557 years, by using the previously obtained relation of $M_{syn}=\frac{M}{\%synps}$.

To compare this value with that obtained by the approach of Kivisild et al.,³¹ we calculated an average distance of 51.25 synonymous transversions (52.5 from the consensus human sequence to the chimpanzee sequences and 50 to the bonobo), and an overall ρ of synonymous transversions of 0.217 within the human mtDNA tree. Converting this distance to an overall number of synonymous mutations, using the relative mutation rate of synonymous transitions to synonymous transversions in the tree (33.98:1), we obtained a mutation rate of 1 synonymous mutation every 7790 years, a value that is very close to the value we obtained from the overall mutation rate.

Using the simulation of saturation for synonymous mutations, we then calculated values for the proportion of hidden variation for the number of mutations between the human lineage and both the chimpanzee and the bonobo lineages. We obtained an average of 965 synonymous mutations from human to the chimpanzee and bonobo and converted it to 2108 total synonymous mutations, by using the formula N_o = 1900.7636 × N_e / (2030.1489 + N_e), obtained previously; and we determined a mutation rate of 1 mutation in every 6687 years, by dividing the 2108 mutations by 14 million years. The average number of synonymous transversions in these simulations was 53, a value very similar to the one observed between the Homo and Pan lineages.

The final method we employed was ML using the codon analysis without any nonsynonymous mutations in the alignment. The method yielded a final value of 0.0001053 ± 0.0000045 synonymous mutations per year, or 1 mutation every 9503 years.

An average of the methods is 1 mutation per 7884 years. Some of the methodologies are more computer intensive (ML), whereas others are more empirical but also more intuitive. For this reason we did not assume one to be intrinsically more reliable than another, and we took the average as the consensus. Additionally, we subsequently tested the rate against several archaeological calibration points in order to check its reliability (see below). Comparing average age estimates for each node by using the complete-sequence clock and the synonymous clock, we found that the latter was 0.9452 (assuming an intercept at y = 0) of the former, with R² = 0.9486, indicating that the time-dependence correction incorporated in the overall molecular clock correlates very well with the linear synonymous rate (Figure 5). This indicates that the synonymous rate is fractionally slower (because of the fact that we are using an average of four methods instead of just the one obtained directly from the complete genome mutation rate, and probably also because of some minor saturation effects in the more ancient African clades). The relative deviation from the correlation line for the data set follows a normal distribution. Considering this, and given that any age estimate inevitably presents high confidence intervals, the most likely explanation for the observed differences between the synonymous clock age estimates and the corrected complete-genome age estimates is the randomness inherent in the emergence of neutral mutations.

Figure 5.

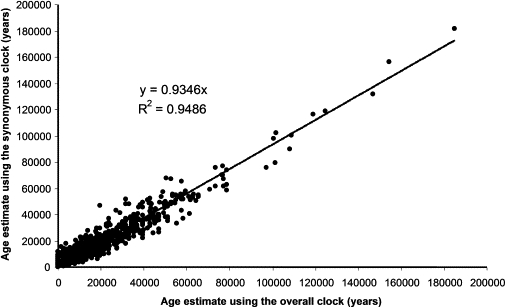
Comparison of the Age of Each Node with the Time-Dependent Complete mtDNA Genome Sequence Molecular Clock and the Synonymous Clock

Our average estimate of 1 synonymous mutation per 7884 years compares with the previously published synonymous transition rate estimate of 1 per 6764 years.³¹ This discrepancy exists, in part, because we have chosen a slightly higher divergence time for Pan-Homo for our calibration, and it is a result of the different methodologies we employed, but also very likely because the published estimate was based on far fewer data, possibly including some sequence errors such as missing polymorphisms (T. Kivisild, personal communication). Our re-estimate substantiates the suspicion referred to earlier, based on phylogeographic grounds, that this published estimate is an overestimate, leading to the underestimation of coalescence times.

Estimates of Control Region Mutation Rate

The control region of the mtDNA genome, especially the first hypervariable segment (HVS-I), has played—and indeed continues to play—an important role in the study of human evolution. This is because the high level of polymorphism in such a small region makes it highly cost-effective for researchers carrying out large-scale phylogeographic population studies on a limited budget, even though some additional typing of coding-region markers is almost always necessary to distinguish similar or identical HVS-I sequences that fall on distinct branches of the phylogenetic tree.

The most widely used molecular clock for HVS-I (e.g., it is the default value in the popular software package Network) has been 1 transition in every 20,180 years, or 1.80 × 10⁻⁷ transitions per nucleotide per year, for the region between nucleotide positions 16090 and 16365, estimated by Forster et al.^62,96 For comparative purposes, we re-estimated the rate for this region by reanalysing the ML estimate with one partition corresponding to this region. We obtained a substitution rate of 1.8899 × 10⁻⁷ mutations per nucleotide per year or 1 mutation every 19,171 years—rather similar to the Forster et al. rate, especially considering that this new estimate includes transversions. Using the value of κ for that partition to calculate the transition rate, we obtained a value of 1 mutation every 20,129 years. For a second estimate, we compared the variation (ρ) of synonymous mutations with the variation of transitions within the 16090–16365 range in each node of the tree. The variation follows a linear relation until ∼50–60 kya, after which the effect of saturation probably has a greater impact on the long ancient African branches. The correlation between the accumulation of synonymous mutations and the accumulation of transitions in the 16090–16365 interval indicated that the first was 0.4489 the rate of the second (R² = 0.9788). Considering a rate of 1 synonymous mutation every 7884 years, the rate for this interval would be 1 mutation every 17,562 years or 2.06 × 10⁻⁷ transitions per nucleotide per year, providing a second estimate. As for synonymous mutations, we took the average as the consensus (1 mutation every 18,845 years).

We also estimated the mutation rate for the larger (and nowadays more widely used) HVS-I segment from 16051–16400 (except for 16182C, 16183C, and 16194C in the polycytosine tracts containing the 16189C variant), obtaining a mutation rate of 1.62 × 10⁻⁷ mutation per nucleotide per year or 1 mutation every 17,343 years, with the partition in the ML analysis. Scaling this region against the synonymous accumulation, we obtained the value of 1 mutation per 16,011 years, or 1.784 × 10⁻⁷ substitutions per nucleotide per year. An average value would be 1 mutation every 16,677 years.

We similarly estimated a mutation rate of 2.279 × 10⁻⁷ mutations per nucleotide per year or one mutation every 22,388 years for the HVS-II (positions 68–263), and 9.883 × 10⁻⁸ mutations per nucleotide per year or 1 mutation every 9058 years for the whole of the control region.

The virtually linear relation between the accumulation of synonymous mutations and control-region mutations suggests that the control region cannot be greatly affected by purifying selection, although some possible functional constraints are still to be found.⁹⁷ The decrease in the proportion of control-region mutations compared to synonymous mutations as the time depth increases is more likely explained by a combination of saturation of control-region positions at higher time depths where the tree is less densely branching (because of the loss of many lineages by drift), with perhaps some weak effect of purifying selection. An implication of the finding that the mutation rate is approximately constant for lower ages is that some of the issues that have arisen concerning time dependency of control-region molecular clocks³⁵ are more likely caused by problematic data sets, as suggested by Bandelt.⁹⁸

Calculator

We have provided a calculator to convert ρ values (from complete mtDNA sequences, synonymous counts, HVS-I, and the entire control region), and ML estimates (from complete mtDNA sequences) to age estimates (see Document S2 in the Supplemental Data).

Discussion

Phylogeographic Cross-Checking: Dispersal out of Africa

Using the synonymous mutation rate of Kivisild et al.³¹ reduces many coalescence times previously estimated with the coding-region rate of Mishmar et al.²⁵ (see Bandelt et al.⁹⁹ for a critique of other coding-region rates on the market). This reduction is often by about one-quarter, but sometimes by up to three-quarters, of the value. Thus, it estimates the coalescence time of the mtDNA tree overall at ∼160,000 kya, L3 (the clade that evolved within Africa and gave rise to the three major non-African haplogroups—sometimes termed “macrohaplogroups”—M, N, and R) at 65 kya, and M, N, and R themselves at 40–50 kya. The latter in particular has implications for the timing of the out-of-Africa dispersal: a dispersal and settlement of Asia and Australasia at ∼45 kya would be in agreement with the “short chronology” for the arrival in Australia and intervening points (based on uncontroversial rather than contested archaeological evidence),¹⁰⁰ whereas the ages implied by the Mishmar et al. rate suggested an earlier dispersal along the southern coastal route 60–70 kya.⁹

We present a revised chronology using the complete mtDNA genome rate and an ML approach for the mtDNA tree in Figure 6, with full details of the age estimates and associated 95% confidence regions in Table S5. Broadly, the corrected complete-genome rate presented here gives ML age estimates between the previous coding-region rate²⁵ and the more recent synonymous rate,³¹ with L3 at ∼70 kya and M, N, and R at 50–70 kya. This implies that despite the poverty of archaeological evidence at present, the dispersal was indeed probably earlier than the “explosion” of evidence at ∼50 kya.¹⁰¹

Figure 6.

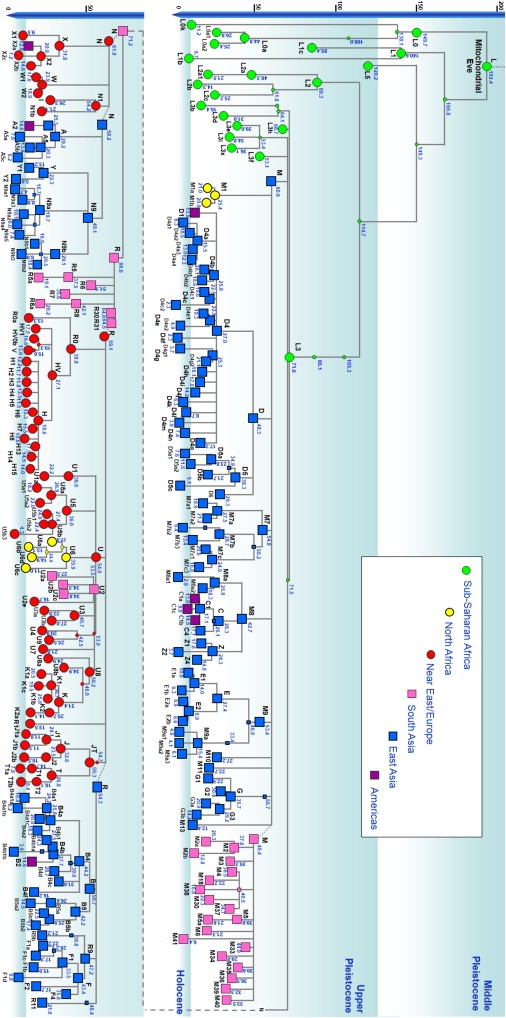
A New Chronology for the Human mtDNA Tree

The tree was obtained by combining six trees constructed separately, with branch lengths estimated with maximum likelihood and the time-dependent molecular clock. Number and presence of clades is dependent on availability of data and not on worldwide frequencies. Ages are expressed in kya.

Our ML age estimates are broadly similar to those calculated with ρ, but sometimes, at greater time depths or cases of varying branch lengths, the ML values are ∼10%–20% higher. Some of the main differences are seen among the Eurasian founders, within haplogroups M, N, and R (Table 3). These differences may in part be explained by the accounting for saturation in the tree in ML, but considering that the overall clock using ρ correlates well with the synonymous clock, we would then need to assume an implausible level of hidden mutations in the synonymous tree. Another factor to consider may be tree shape. The major differences between ρ and ML age estimates in the case of the Eurasian founders is in the West Eurasian tree, where the four R branches (HV, JT, U, and R1) present very different branch lengths, with HV much shorter than the other three and having less weight in the overall age estimate of R in ML, but a much higher impact in ρ because of its higher frequency. The ML ages might be overestimated in some cases, but in any case, the associated confidence intervals in the great majority of cases encompass the point estimates using ρ. In the following discussion, the age estimates from both methods are similar except when explicitly mentioned that this is not the case. In a phylogeographically driven paper, one should present all age estimates and compare them systematically, but here we focus on a single methodology (ML) to present a single plausible time scale.

Table 3.

Age Estimates of L3 and the Major Eurasian Founders with ρ, from Two Different Molecular Clocks, and ML

Clade	ρ Estimates		ML	Overlapping Interval
	Synonymous Positions	Complete Genome	Complete Genome
L3	73.1 (51.1; 95.0)	70.1 (52.4; 88.4)	71.6 (57.1; 86.6)	(57.1; 86.6)
N (W. Eurasia)	56.8 (37.3; 76.7)	53.6 (42.5; 65.2)	61.9 (49.2; 75.0)	(49.2; 65.2)
R (W. Eurasia)	49.4 (35.3; 63.5)	46.1 (39.1; 55.0)	59.1 (47.1; 71.4)	(47.1; 55.0)
U (W. Eurasia)	52.1 (38.8; 65.3)	48.8 (40.5; 57.2)	54.0 (43.1; 65.2)	(43.1; 57.2)
N (South Asia)	70.6 (48.9; 92.3)	64.2 (50.4; 78.3)	71.2 (55.8; 87.1)	(55.8; 78.3)
R (South Asia)	63.5 (44.9; 82.1)	54.1 (43.9: 64.6)	66.6 (52.6; 81.0)	(52.6; 64.6)
M (South Asia)	36.1 (27.7; 44.5)	38.9 (34.2; 43.7)	49.4 (39.0; 60.2)	(39.0; 43.7)
N (East Asia)	54.7 (40.4; 69.0)	56.5 (48.1; 65.1)	58.2 (44.1; 72.8)	(48.1; 65.1)
R (East Asia)	55.3 (41.3; 69.4)	55.7 (46.3; 65.3)	54.3 (41.2; 67.8)	(46.3; 65.3)
M (East Asia)	55.0 (39.0; 71.0)	46.1 (37.9; 54.5)	60.5 (47.3; 74.3)	(47.3; 54.5)

The sibling haplogroups M and N have not previously been resolvable from other members of L3. This issue is of interest because there is controversy about the number of major successful modern human dispersals out of Africa, and a clustering of M and N would provide additional support for the suggestion of a single event, rather than several. In coding-region trees, L3 shows a multifurcation in which M and N are no more closely clustered together than they are to other basal members of L3. However, in the complete-genome tree, M, N, and two other L3 subclades share a transition at position 195, clustering them in the parsimony analyses. When the new rate is used, the hypothetical subclade dates to ∼71.5 (57.0; 86.4) kya in ML. However, although the distance from the root of L3 to the root of each of its subclades is rather short, position 195 is the fifth fastest site in the mtDNA, so this could be due to recurrent mutations and “long-branch attraction.”¹⁰²

In any event, L3 probably expanded ∼70 kya, possibly associated with an improvement of the climatic conditions around that time after a long period of drought.¹⁰³ There are no “pre-M” or “pre-N” clades extant either within or outside Africa, so the out-of-Africa event could be as early as the coalescence time of L3. These data render an out-of-Africa dispersal prior to the Toba eruption in Sumatra at ∼74 kya^104,105 less likely. The upper limits of the 95% confidence intervals of some of the age estimates for the out-of-Africa macrohaplogroups do extend beyond the timing of the eruption. Nevertheless, especially given that neither M nor N in East Asia shows a 95% range that extends much further than ∼74 kya, our results do not suggest that Toba was likely to be a major factor affecting the early Eurasian settlement process. Indeed, considering the overlapping intervals of the different age estimates, only N in South Asia seems to allow the possibility (Table 3).

In the context of the southern-coastal-route model, it should be noted that although the distribution of haplogroup M has also been used to support the southern-route model,¹² the age of haplogroup M in India, at 49.4 (39.0; 60.2) kya, is significantly lower than in East Asia, at 60.6 (47.3; 74.3) kya (both are lower in ρ but the proportional difference is similar; see Table 3). At face value, this could suggest an origin of haplogroup M in East Asia and a later migration back into South Asia, suggesting that it may have been a “pre-M” lineage that initially crossed South Asia. This would seem to be contradicted by the much higher levels of basal M lineages in South than East Asia,¹² but early indications are that Southeast Asia matches South Asia in the diversity of basal M lineages, so Southeast Asia may be the point of origin of haplogroup M (preliminary dating to ∼58 kya when both the corrected and the synonymous rate are used; our unpublished data). Alternatively, if M dispersed with N and R through South Asia, M may have been caught up in a subsequent bottleneck and founder effect so that its age signals the time of re-expansion rather than first arrival. There is indeed archaeological evidence for a subsequent expansion within the Indian Subcontinent from ∼30 kya,¹⁰⁶ and this would mirror a similar effect later in Europe, as a result of the Last Glacial Maximum.¹⁰⁷

Phylogeographic Cross-Checking: The Settlement of Europe

Europe was first settled by modern humans ∼45 kya,¹⁰⁸ and it is believed that one of the branches of U, U5 or a genetically close ancestor to U5, arose among the first settlers.¹⁰⁹ The ML estimate of haplogroup U5 is 36.0 (25.3; 47.2) kya, and lower with ρ at 30.7 (21.4; 40.5) kya and 33.0 (13.3; 52.8) with our synonymous rate. The evidence suggests that the earliest branching within U5 in Europe was lost by drift or is only present in the population at very low frequencies. The closest link in the tree with the Near East is the root of haplogroup U, placing any early migration into Europe involving U5 or its ancestors between ∼55 kya and ∼30 kya.

Subsequently, the Late Glacial re-expansion of populations from the Franco-Iberian refugial areas at the end of the Ice Age from ∼15 kya is thought to have been the major demographic process,¹¹⁰ signaled in the mtDNA by the distribution of haplogroups H1, H3, V, and U5b.^20,111–114 We previously suggested that this may have been a result of dispersals into the western European refugia from a source in eastern Europe at around or shortly after the time of the Last Glacial Maximum, ∼25–19.5 kya. This may have been via cryptic northern European refugia and in association with the Badegoulian material culture, thought to be ancestral to the Magdalenian that subsequently expanded from the southwest.¹¹⁰

The age of haplogroup H, which is ∼18.6 (14.7; 22.6) kya, 15.8 (13.4; 18.3) kya in ρ and 14.5 (11.3; 19.4) kya in syn rate (compared to ∼12.8 kya with the previous syn rate), supports this postulated arrival soon after the LGM, as does the age of the eastern subclade H13,²² which dates to ∼17.5 (13.3; 21.7) kya (∼19.3 [10.7; 28.3] kya in ρ and 25.3 [7.6; 43.0] kya with our syn rate). However, apart from H6, H13, and H14, each present in the Caucasus, all the subclades in the tree present ages lower than 15 kya, so it is possible that the arrival into the rest of Europe occurred later. To test this, we calculated a founder age for the European data. We obtained an age of 14.6 (11.7; 17.6) kya, indicating a likely entrance after the LGM.

The Magdalenian expansion from the southwest refugia began ∼15 kya¹¹⁰ and, on the basis of their geographic distribution, it has been proposed that H1 and H3 (as well as V) are markers for this expansion, having evolved in the western refugium.^20,113 If this holds, their ages should then not be less than the start of the expansion (∼14 kya at the latest). H1 dates with ML to 12.2 (9.1; 15.4) kya and H3 to 11.8 (8.4; 15.4) kya. Considering their confidence intervals, these ages could be in reasonable agreement with the phylogeographic interpretation and the archaeological record. However, the point estimates are even lower when estimated with ρ, rather than ML, at 11–12 kya, and, in the case of H3, even lower when our syn rate is used (6.9 [3.4; 10.4] kya). This might suggest a possible expansion for one or both of these two lineages at the end of the Younger Dryas, 11.5 kya, rather than in the Late Glacial, although there is little archaeological evidence for a major expansion at this time.¹¹⁵ (The age estimate of H1 with the published synonymous rate is ∼9 ky, which is less readily reconcilable archaeologically with the west-east cline displayed by the clade.) This might be an issue of sampling from across the entire area of the expansion, and the result could be caused by founder effects subsequent to the one under investigation.¹¹² Given that our estimate of the arrival of H in Europe (an estimate that includes H1 and H3 data) dates to 14.6 kya, it is perhaps improbable, albeit not impossible, that H1 and H3 expanded very shortly after (14 kya) from the southwest refugia. The ancestry of haplogroup H merits further detailed study at the complete-genome level to resolve these issues, but it is worth noting that the issue that arises is that the recalibrated rate seems, if anything, a little too fast to accommodate the most plausible phylogeographic interpretation (taking into account the archaeological evidence) in this case (i.e., a large-scale Late Glacial expansion). Note also that an age of 18 kya for both H1 and H3, as assumed by Endicott and Ho,³⁹ would not fit with any plausible rate; it is too early even for the uncorrected coding-region rate of Mishmar et al., which is at variance with their suggestion of a much faster rate overall.

The sister clade of H, haplogroup V, indeed dates to ∼13.6 (9.1; 18.2) kya (13.7 [12.1; 15.2] kya in ρ and 12.2 [10.0; 14.3] kya in syn rate), fitting better the time of expansion from the Franco-Cantabrian glacial refuge. Furthermore, haplogroup V presents ancestry in Europe with its direct ancestor dating to 15.6 kya. This provides some additional corroboration for the corrected rate in the 10–20 kya time window.

Archaeological Calibration Points: Island Colonizations

Endicott and Ho³⁹ have recently argued that the human-chimp divergence is not sufficiently well known to be useful as a calibration point, and that instead we should rely upon archaeologically well-dated episodes within the time frame of modern human evolution. The suggestion that the ideal calibration points should be within the time frame of interest is clearly sensible given the nonlinear behavior of the clock. However, in practice there is a severe shortage of such uncontroversial episodes that can be unambiguously tied to particular instances of mtDNA variation. The episodes that they propose are either archaeologically controversial (as in the case of the first settlement of Australasia, or Sahul, which they tie to haplogroup P), or not sufficiently well linked to mtDNA lineages—an example being H1 and H3, already alluded to above, which they surprisingly date to the Last Glacial Maximum (rather than the Late Glacial) without any clear justification. These calibration points were also adopted by Henn and colleagues.⁴⁰ There are indeed a few such cases that can be used, but unfortunately only at very recent time depths. Nevertheless, these do have some value, because it is at very recent time depths that the impact of purifying selection is greatest on the mtDNA age estimates.

One of the few clear-cut archaeologically based calibration points that we can indeed use to corroborate the new rate is the settlement of Remote Oceania, which is readily dated archaeologically because it was a recent expansion—within the last 3.5 ky—into previously unsettled territory.¹¹⁶ A subclade of haplogroup B, B4a1a1a, known as the “Polynesian motif,” can be regarded as originating from a single founder type¹⁰⁷ with an origin to the east of Wallace's line in Island Southeast Asia.¹¹⁷ The islands of Vanuatu in the western Pacific were first settled ∼3.2 kya from the Bismarck Archipelago to the north of New Guinea,¹¹⁸ and (by using our unpublished data) we estimated a founder age for the Polynesian motif in Vanuatu of 3.45 (2.6; 4.3) kya (and 3.3 [2.5; 4.0] kya with our syn rate). This helps to corroborate the corrected rate for the mid-Holocene time frame, which is crucial also for the dating of Neolithic dispersals in other parts of the world. Note, though, that even this example is not watertight: interisland contacts probably continued until 2.9 kya (M. Spriggs, personal communication), so it is not impossible that additional diversity from the Bismarck Archipelago was brought to Vanuatu in the preceding 300 years. However, because we are dealing with a single major founder lineage in this case, the coalescence time most likely estimates the arrival time of the first settlers. Furthermore, the archaeological date is necessarily a minimum estimate, and may well increase by one or two hundred years or so.

Another fairly well-established case of first settlement is the modern human arrival in the Canary Islands. One of the subbranches of U6, U6b, presents a clade unique to the Canary Islands, U6b1b1. The population hardly presents any other subclade of U6b, suggesting that U6b1b1 emerged around the time of the first colonization. The earliest evidence for the human settlement of the Canary Islands is ∼2.2–2.4 kya¹¹⁹ so this provides a further test for the new calibration in the 0–5000 year range. The age estimate of the clade is 2.95 (2.1; 3.7) kya and 2.25 (1.7; 2.9) kya with the syn rate (our unpublished data). Again, a slightly earlier point estimate does not necessarily imply a rate that is too slow because, in the absence of a complete record, archaeological estimates are (like palaeontological estimates) almost inevitably underestimates. Clearly, in both cases, larger mtDNA sample sizes are also highly desirable.

Henn and colleagues⁴⁰ suggested the age of M7a as another well-defined point, this time for the first colonization of Japan by modern humans, which dates to at least 32 kya.¹²⁰ In our calibration, M7a dates to 27.5 (17.3; 38.2) kya, and so encompasses the age of the first human remains in the archipelago (then part of the mainland). M7a presents a northeast Asian distribution, with the two branches (M7a1 and M7a2) both present in Japan⁴² and with the latter found so far only in the archipelago, making an origin of the clade there probable. The problem with M7a as a calibration point is similar to the one described with U5 and the possibility of a lost nearest ancestor. The closest link of the clade to its sister clades is via the root of M7, which dates to nearly 55 kya, opening a large window of opportunities within which the migration might have occurred.

Archaeological Calibration Points: The Case of the Americas

A further case in which archaeological dating could be useful has proven more problematic in the past: the new rate sheds fresh light on the debate concerning the first colonization of the Americas. Previous HVS-I estimates for the founding process date to ∼20 kya or more,⁶² whereas there is no generally accepted archaeological evidence for settlement—or certainly, at least, for a major transcontinental expansion—before 15 kya.^121,122 Application of the published synonymous rate yields ages of ∼13.9 kya for the major complete mtDNA founders,¹²³ a little late in view of the recent analysis of human coprolites from ∼14.3 kya from Oregon¹²⁴ and evidence of marine-resource use in Chile from ∼14.6 kya.¹²¹ On the other hand, the use of the Mishmar et al. coding-region rate yields estimates of ∼19 kya, which are difficult to explain archaeologically without assuming coalescence among Beringian founder lineages that have subsequently become extinct.¹²⁵ Although dispersal into the continent via the Pacific coastal corridor remains a possibility, the timing of the opening of the coastal route itself remains unclear, and may not be much more than 15 kya. Our analysis of recently deposited complete genome sequences belonging to typical Native American haplogroups⁵² confirmed the extremely star-like pattern in the major Native American haplogroups, probably reflecting the major expansion through the continent, with all of the American-specific clades dating to ∼13.5–15 kya (except for C1c, dating to ∼9 [4.6; 13.6] kya, and X2a, dating to 12.8 [6.1; 19.9] kya). The average age of 14.2 kya supports a dramatic range and population expansion at around that time and is in line with the archaeological dating. This is similar to (though slightly later than) the recent estimate (∼16 ky) using a consensus of the published synonymous and Mishmar et al. rates, where evidence of distinct coastal and inland routes is also provided.¹²⁶ The poverty of inland sites in the period before the Clovis expansion ∼13.5 kya, combined with the highly star-like mtDNA phylogenies suggesting major expansions, might indeed be reconciled by a Pacific coastal dispersal from Beringia to South America ∼14–15 kya, prior to the opening of the “ice-free corridor” through central Canada,¹²⁷ paralleling the recolonization of northern Europe in the Late Glacial. An estimate of the arrival time itself, however, would require a more detailed assessment of each likely founder lineage. Such an analysis might not rule out an entry of small groups at ∼16 kya or even earlier, as suggested for a few archaeological sites, such as the Meadowcroft Rockshelter,¹²⁸ because the coalescence of the American clades in East Asia is 17.1 (12.0; 22.5) kya for haplogroup C1 and > 20 kya for A2, B2, D1, and X2a. Similar to the situation we encountered for the first settlement of Europe and Japan, the arrival of the first pioneers in America might have been at any point between the Asian coalescence time and the expansion of the Native American lineages.

Ancient DNA suggests the possibility of an alternative, nonphylogeographic approach to archaeological cross-checking, and indeed, quite recently, the first complete mtDNA genomes from ancient human remains have been obtained.^129,130 Unfortunately, though, the two genomes published to date tell us little more calibration-wise than the minimal age for the haplogroup to which they belong. The Tyrolean Iceman, at 5.35–5.1 ky old, belongs to a basal lineage within K1, which dates to > 20 kya. The Paleo-Eskimo sample, at 4.5–3.4 ky old, is slightly more informative, falling within a much younger clade dating to 6.5 (5.1; 8.0) kya (with the corrected clock) or 4.7 (3.8; 5.7) kya (with the syn clock).

Conclusions

We have confirmed that the accumulation of mutations in human mtDNA has indeed been nonlinear, most likely as a result of purifying selection (and, to a considerably smaller extent, and mainly in the control region, saturation), as predicted by Kivisild and colleagues.³¹ As a result, coalescence times near the tips of the tree have indeed been overestimated to some extent by methods that have assumed a linear coding-region clock.

However, the extent of this overestimation is less than has generally been asserted.^31,34,37 Bayesian approaches to the problem, as advocated by some researchers, are difficult to evaluate because of the opaque nature of Markov-Chain Monte Carlo simulation, but recent “relaxed-clock” estimates³⁹ provide values that seem to be mutually contradictory and make little intuitive sense. This may be because they have been based on relatively few rather unrepresentative sequences, a model for sequence evolution that includes only six rate categories and, in particular, the implausible assumptions about calibration points referred to above. The calibration points chosen (the European LGM and the colonization of Sahul) would stretch the diversity within haplogroup H (H1 and H3 dated to ∼12 kya in our time-dependent clock) while contracting that within haplogroup P (which dates to 58 [49.3; 66.8] kya with our corrected clock), producing an effect opposite to our correction for overestimation at lower time depths. Indeed, it also runs in the opposite direction from the previous time-dependent mutation-rate curve proposed by one of its authors.^34–36 Moreover, saturation is likely to have been overestimated, because it is measured as a function of pairwise incompatibility, which does not necessarily indicate saturation, but simply (usually resolvable) recurrent mutation.

Here we have instead taken the approach of estimating empirically the level of selected versus unselected variation at any time depth within the tree and using this to correct the estimates from the linear clock. This demonstrates that—contra Endicott and Ho³⁹—it is possible to combine data from throughout the mtDNA genome, with the use of the chimpanzee-human split as the primary calibration point, to provide reliable time-depth estimates for the entire window of anatomically modern human evolution, without making any a priori assumption regarding age of clades that should be tested rather than taken as given^39,40 and avoiding the issue of circularity. The results mean that disperal-time estimates using mtDNA can be set on a new and more reliable footing. However, they also show that, contrary to the alarmist claims made in recent years, the outcome does not require a wholesale re-evaluation of the chronology of human mtDNA evolution.

Supplemental Data

Supplemental Data include five tables and our ρ and ML genetic distance value conversion calculator and can be found with this article online at http://www.ajhg.org/.

Web Resources

The URLs for data presented herein are as follows:

• Geneious, http://www.geneious.com

• Network 4, http://www.fluxus-engineering.com/sharenet.htm

• Timetree database, http://www.timetree.org