Volumetric capnography and chronic obstructive pulmonary disease staging

Abstract

Spirometry is difficult for some COPD patient to perform. Volumetric capnography could be a second choice test to evaluate the severity of functional disturbances. The aim of this work is to test this hypothesis. A total number of 98 subjects were classified either as normal ex-smokers (N = 14) or COPD patients. The latter were staged following GOLD recommendations. Spirometry and volumetric capnography recordings were obtained from each patient. Spirometry parameters, Bohr Dead Space (V_D ^Bohr), Airways Dead Space from the pre-interface expirate corrected curve (V_D ^aw), Phase III slope (Sl_III) and Volume of alveolar ejection (V_AE) were measured. Index of Ventilatory Efficiency (IVE), and Index of Airways Heterogeneity (IAH) were calculated as: IVE = V_AE/(V_T – V_D ^aw) and IAH = 1 – [(V_T – V_D ^Bohr)/(V_T – V_D ^aw)]. In ANOCOVA analysis IAH showed the greatest association with stage (F > 40), with no significant covariant dependence on V_T. A receiver operating characteristics curve analysis showed values of the area under the curve greater than 0.9 for IAH and IVE at all stage levels, with a sensitivity = specificity value greater than 80%. We conclude that IAH and IVE can be used when spirometry cannot be reliably performed, as an alternative test to evaluate the degree of functional involvement in COPD patients.

Introduction

Stable chronic obstructive pulmonary disease (COPD) can be evaluated by means of standard spirometry in a large majority of patients. In fact, spirometry is the gold standard to diagnose and classify COPD patients, and the severity of the disease. When properly performed, spirometry is the most reproducible, standardized and objective way of measuring flow limitation. A correct spirometry manoeuvre, however, requires the ability to clearly understand the manoeuvre, the intellectual capacity to perform it, and the absence of clinical limitations which might prevent several maximal forced expiratory manoeuvres from being performed. It is relatively common to deal with subjects with disabled intellectual capacity, with language difficulties, or clinical situations that make the forced expiratory manoeuvres painful or may even preclude them (chest pain, coronary vascular disease, minimal efforts dyspnoea, etc) In such cases spirometry is a poor cost/benefit procedure. Other situations such as intubation or tracheotomy, or patients lying in bed also limit the application of standard spirometry.

Pulmonary heterogeneity is, together with airways obstruction, a cardinal feature in the functional impairment of COPD. Heterogeneity, mostly dependent of peripheral involvement, is seen to increase with the severity of the disease; therefore, volumetric capnography, a technique that basically explores regional distribution, can be expected to correlate with the severity of disease in COPD patients. Previous authors have outlined the good relationship between changes in volumetric capnography parameters and the severity of COPD (Kars et al 1995; Kars et al 1997; Wilschut et al 1999; and Koulouris et al 2001); however, the diagnostic value of volumetric capnography has not been systematically explored. Recent studies reduce the intrinsic variability of the parameters, either by using internal relationships (Romero 2001), a procedure that reduces the noise-to-signal ratio, or by using the reference values reported by Åström et al (2000) in normal people.

Volumetric capnography parameters are measured in continuous scales. Their use as a diagnostic test requires the selection of a cut-off value in the original scale in order to define positive and negative test outcome. Comparison of the dichotomised test results with the clinical status of the patient, evaluated as the disease stage from Global Initiative for Chronic Lung Disease (GOLD) classification (a spirometry based criterion) (GOLD 2006), allows estimation of the test’s diagnostic sensitivity (Se) and specificity (Sp), and determines the cut-off values that concurrently optimise Se and Sp. According to the hypothesis that volumetric capnography could be an alternative test to determine the amount of functional involvement in COPD patients, we have designed a study to compare the diagnostic value of volumetric capnography with spirometry as gold standard.

Methods

Subjects

A group of 84 patients (18 women, 66 men; age 60 ± 13 years, mean ± standard deviation) with clinical symptoms of COPD have been selected from patients attending the Pulmonary Function Laboratory. This protocol was approved by the Hospital’s Research Committee. Patients were asked to give their consent for statistical use of the results of functional studies. The selection criteria were: clinical diagnosis of COPD based on clinical symptoms and history of exposure to cigarette smoking. Age limits were 30 to 80 years, and body mass index (BMI) was limited to 35. Exclusion criteria were cardiovascular comorbidity disease, sequelae of tuberculosis on the chest X-ray or any other coexistent lung disease, and neuromuscular or other diseases causing loss of ventilatory capacity. In order to exclude asthmatics, patients with a change of more than 12% in FEV₁ after bronchodilator were excluded. Subjects were classified according to the Global Initiative for Chronic Lung Disease (GOLD) criteria (GOLD 2006) into five groups:

• – Group 0 (N = 33) or subjects at risk, with normal spirometry (FEV%FEC ≥70%, FEV₁%pred ≥80%), but symptoms (cough, sputum).

• – Group I (N = 1) or mild COPD, with FEV₁%FVC <70%, but FEV₁%pred <80%.

• – Group II (N = 20) or moderate COPD, with FEV₁%FVC < 70%, and 50% ≤FEV₁%pred <80%.

• – Group III (N = 19) or moderate to severe COPD, with FEV₁%FVC <70%, and 30% ≤FEV₁%pred<50%.

• – Group IV (N = 18) or severe COPD, with FEV₁%FVC <70%, and FEV₁%pred <30%.

In these five groups FEV₁ and FVC post-bronchodilator in percent of predicted were considered. A group of 14 normal subjects (6 women, 8 men; age 48 ± 11 years, mean ± SD), ex-smokers (more than 10 years of cessation) but free of symptoms was also studied, and is called “Ex-Smok” Group. The same exclusion criteria were applied. Table 1 shows the descriptive and spirometric data for the different groups. All COPD subjects were in a stable situation, with no changes in respiratory symptoms during the month prior to the study, and no acute episodes of respiratory failure more than six months. Patients were asked not to have any inhaled therapy in the previous twelve hours. They sat down for at least half an hour before the procedure.

Table 1.

Descriptive statistical data of the different groups of subjects studied

Group	N	Sex ♀/♂	Age yrs	BMI	FEV1 %pr	FVC %pr	MEF50 %pr
Ex-Smok	14	6/8	48 ± 11.1	24.2 ± 2.04	100.3 ± 8.9	93.2 ± 7.78	109.3 ± 14.7
GOLD 0	26	13/13	52 ± 14.8	27.1 ± 4.37	86.3 ± 16.2	84.2 ± 17.3	67.8 ± 18.0
GOLD I	1	0/1	57	32	88.6	98.5	42.9
GOLD II	20	2/18	63 ± 11.4	26.5 ± 4.16	58.4 ± 7.32	73.5 ± 13.0	26.1 ± 8.2
GOLD III	19	3/16	64 ± 13.1	25.5 ± 4.5	40.1 ± 5.73	59.2 ± 10.1	16.2 ± 7.8
GOLD IV	18	0/18	62 ± 9.5	25.8 ± 4.49	22.4 ± 5.2	42.4 ± 14.9	7.42 ± 2.72

Abbreviations: BMI body mass index; FEV₁%pr, forced expiratory volume at the first second in percent of predicted; FVC%pr, forced vital capacity in percent of predicted; MEF₅₀%pr, maximal expiratory flow at 50% FVC in percent of predicted.

Note: Mean ± Standard Deviation.

Instrumentation

The equipment used was a Cosmo Plus System (Novametrix Medical Systems Inc, Wallinford, CT, USA), which measures CO₂ concentration by means of a mainstream infrared cell, and airflow by an integrated pitot type pneumotachograph. Optical CO₂ calibration and zero flow were performed before each measurement. The instrumental dead space (mouthpiece plus pneumotachograph and infrared cell chamber) was 18 ml. Pneumotachograph linearity was confirmed in the experimental range of flows, with increasing static flows measured by means of a rotameter (Collins, Braintree, Mass, USA). Expiratory flow and volume are expressed in BTPS conditions. Response characteristics of mainstream capnograph, as well as the validity of optical calibration, was determined by flowing a gas mixture containing 5% (in) or 0% (out) CO₂ in air by means of a syringe at step changing flow rates in the range of the physiological rates. Delay between flow and capnographic signal and capnograph time constant were determined by analyzing the system’s step response between 5% and 0% CO₂ in air. In all cases delay was measured as the time elapsed between the beginning of flow transition according to the pneumotachographic recording, and the breakpoint of the capnographic recording. Average delay was 58.9 ± 16.2 ms. Time constant was determined as the time to reach 63.2% of the total step response, and was 24.4 ± 2.35 ms. Capnographic signal was time shifted according to the time delay.

Measurements: Capnographic recording was always performed before spirometry. Subjects were sitting during the recording procedure, breathing through a mouthpiece and with a nose clip. After two to three minutes of stable breath, CO₂ and flow signals were continuously recorded for two more minutes, digitalised at sampling frequency of 100 Hz and stored in magnetic media. Forced spirometry was performed with patient in standing position by means of a Fleisch pneumotachograph (GS-System, Collins, Braintree, MA, USA) according to ATS/ERS Standardization of Spirometry (ATS/ERS, http://www.thoracic.org/sections/publications/statements/pages/pfet/pft2.html, update 2006). Spirometry was processed by GS software, and results expressed in BTPS conditions. To accept spirometry results, at least three manoeuvres with a reproducibility of 5% and a difference between the best and second best FEV₁ and FVC below 150 ml had to be recorded. A maximum of eight forced expiratory manoeuvres were performed. Maximal values of forced expiratory flow in one second (FEV₁), Forced Vital Capacity (FVC) and Maximal Mid Expiratory Flow between 25 and 75% of FVC (MMEF) were retained. The minimum time between manoeuvres was three minutes (of longer if requested by the patient). Spirometric manoeuvres were repeated 15 minutes after inhalation of 400 μg of salbutamol by means of a spacing chamber. According to recorded observations, time consumption by spirometric tests oscillated between about 20 minutes (the fastest) and 50 minutes (the slowest) plus the time consumed by the reversibility test. Predicted spirometric values were calculated from age, height and sex according to Roca et al (1986).

Volumetric capnography parameters: A recording containing a minimum of fifteen complete breathing cycles, at a minimal tidal volume of 150 ml was processed for every patient. Every cycle was identified from the pneumotachographic signal, isolated and analysed separately by a computer procedure. Cycles not accepted for measurements were those with a P_ETCO₂ 5 mmHg lower or higher than the average P_ETCO₂. Also discarded were cycles with a tidal volume above or below 25% of average V_T. Final results give the average of the measurements done on seven to fifteen cycles for each patient.

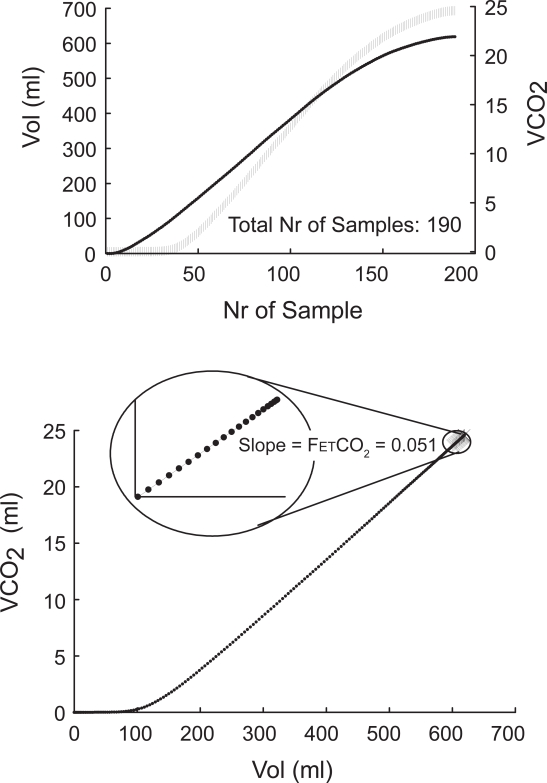
End tidal CO₂ fractional concentration (F_ETCO₂): to avoid the artefact of cardiac oscillations, F_ETCO₂ was measured on the CO₂ elimination (VCO₂) versus expired volume (V) curve [VCO₂ = ∫F_ECO₂·dV], as the linear slope between expired volume and VCO₂ of the segment defined by the end expiratory 10% of the total number of expiratory samples of each breath (Figure 1). End-tidal partial pressure of CO₂ (P_ETCO₂) was calculated from barometric pressure (P_B) as: F_ETCO₂·(P_B – P_H2O).

Figure 1.

Top: Expired volume and VCO₂ sampled curves. Bottom: Measurements of end expiratory CO₂ concentration. For detail please see the text.

Bohr Dead Space (V_D^Bohr) was calculated according to classical principles, assuming that end-tidal fraction of CO₂ represents alveolar fractional concentration in the equation:

$${\text{V}}_{\text{D}}^{\text{Bohr}}/{\text{V}}_{\text{T}}=1-({\text{V}}_{\text{E}}{\text{CO}}_2/{\text{V}}_{\text{T}})/{\text{F}}_{\text{ET}}{\text{CO}}_2$$ [1]

where V_ECO₂ is the CO₂ eliminated by breath.

Pre-interface expirate (PIE) was calculated according to Wolff and Brunner’s method (Wolff and Brunner 1984). In short, the volume expired when CO₂ has reached half of the end-expiratory value is doubled, the rest of the points are excluded from further analysis. Then the first derivative of the signal (dF_ECO₂/dV) is plotted against the volume, and the mean of this normalized distribution function is calculated. The volume at which this mean value is obtained represents the minimal mean volume of the convective airways, also called the pre-interface expirate or PIE (Wolff and Brunner 1984). Physiologically speaking, PIE represents the expired volume at which the interface between airways and alveolar gas is appreciated at airways opening.

Phase III slope (Sl_III ): the curve between PIE and V_T is divided into four segments. According to Åström et al (2000), Sl_III was calculated as the slope of the linear regression between F_ECO₂ and Volume for the two central segments.

Series dead space (V_D ^ser): The curve was corrected for the Sl_III between PIE and end tidal volume. From the corrected new curve, serial dead space volume (V_D ^ser) was calculated by the equal area method. This procedure prevents overcorrection of phase II (Åström et al 2000). Airways dead space (V_D ^aw) was obtained by subtracting Instrumental Dead Space (18 ml) from V_D ^ser.

Index of Alveolar Inhomogeneity (IAH): According to previous studies (Kars et al 1995; Romero 2001) the difference between V_D ^ser and V_D ^Bohr is mainly due to impairment of regional distribution, which distorts the curve beyond PIE. An index of heterogeneity was calculated by relating both magnitudes according to:

$$IAH(\%)=\left[1-\frac{\left(V_T-V_D^{Bohr}\right)}{\left(V_T-V_D^{ser}\right)}\right]\times 100$$ [2]

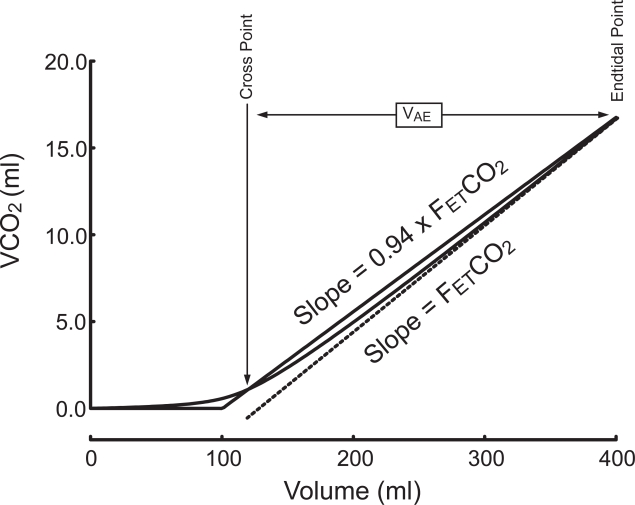
Index of Ventilatory Efficiency (IVE): Alveolar exhaled volume or V_AE was determined from the VCO₂ versus expired volume or VCO₂(V) curve, according to previous studies (Romero et al 1997; Blanch et al 1999). In short, after the linear fitting of the last end-expiratory segment previously described, the slope of this curve was decreased by 6% by pivoting on the end expiratory point. The new straight line crosses the VCO₂(V) curve at a single point. The volume between this and the end-expiratory point corresponds to V_AE (Figure 2). This volume tends to decrease as serial contamination of alveolar gas, heterogeneity, and phase II increase. As V_AE directly depends on V_T and V_D ^ser, it seemed appropriate to express it in relation to these magnitudes. An index of ventilatory efficiency (IVE) has been calculated as follows:

$$IVE(\%)=\frac{V_{AE}}{V_T-V_D^{ser}}\times 100$$ [3]

We used a 6% change in end tidal slope of VCO₂(V) curve rather than the 5% used in previous studies in ventilated patients, because we have observed less variability in spontaneously breathing patients when using 6% (CVar% ± SD: 9.14 ± 3.34, and 10.98 ± 4.16 at 6% and 5% respectively. N = 16 patients, twenty consecutive cycles each).

Figure 2.

Measurement of the volume of alveolar ejection (VAE) from the VCO₂ versus expired volume curve. For detailed instructions, please see the text.

Statistical analysis: tests of normality (Kolmogorof-Smirnof) and homogeneity of variances (Levene homocedasticity test) were applied to data prior to deciding which test to use to compare the groups identified according to GOLD classification. For variables normally distributed, and with homogeneous variances, ANOVA analysis was performed. Tidal volume was added as covariant when necessary. If normality and homocedasticity tests failed at an error of 5%, the Kruskal-Walis rank test was applied to evaluate the differences between groups.

A multivariate model including Height, Body Mass Index, age, FEV₁%pred, Tidal volume and MMEF%pred was used to determine the association of capnography parameters with functional data, and the possible confounding effect of factors relatively independent of respiratory functional abnormalities.

Receiver operating characteristic (ROC) curve analysis was performed to test the ability of each volumetric capnography parameter to detect the different levels of disease characterised by the GOLD Stages. The analysis was performed by cutting-off the population at increasing GOLD Stages of the disease. For each Stage Level, each parameter, considered as one-class classifier, was progressively increased or decreased in step values (threshold changes). Sensitivity (Se) and specificity (Sp) were calculated for each threshold change and expressed as a percentage. For each parameter at every stage ROC curves were constructed by plotting sensitivity against the false positive rate (100-specificity). The area under the curve (AUC) and confidence intervals at 95% were calculated to determine the degree and limits of accuracy of the curves, allowing paired comparisons. To determine cut-off points for each parameter at every stage, we calculated the point at which sensitivity equals specificity (Se = Sp). Positive and Negative Predicted Values were calculated using Bayes theorem (Greiner and Gardner 2000) based on COPD prevalence observed by Kornmann et al (2003) at stages levels II, III and IV, and internal prevalence at stage 0. MedCalc^® and SPSS^® statistical packages were used for statistical analysis.

Results

Table 2 shows the descriptive statistics (mean, standard deviation) of capnography parameters in the COPD groups, as well as statistical data from ANOVA test. Variables ΔSl_III and IVE did not meet the criteria of homocedasticity, and the Kruskal-Wallis test was applied. Group I was excluded, because it had only one subject. Although no significant between groups difference was observed for V_T, this parameter was used as covariant in the ANOVA analysis because of the documented tidal dependence of capnography variables (Åström et al 2000; Kornmann et al 2003), and the high dispersion of V_T. In Table II values of F (or χ²) and P are given for between groups difference (F(χ²)_group, and P_group) and V_T covariant effect (F_cov, and P_cov).V_D ^aw showed no significant between-groups difference, but did show high dependence on V_T. P_ETCO₂ showed mainly group, but also some V_T dependence. V_D ^Bohr/V_T showed both group and tidal volume dependence. When corrected for predicted value, however, (Δ = real-predicted, ΔV_D ^Bohr/V_T) the covariant effect disappeared, but the group effect was maintained. Finally, IAH showed strong group but no V_T dependence.

Table 2.

Comparison of groups by ANOVA or Kruskal-Wallis test. VT is used as covariant in ANOVA test. Values of χ² are marked with an asterisk

Group	N	STAT	VT ml	VDaw ml	PETCO2 mmHg	IAH %	IVE %	VDBohr/VT %	Δ(VDBohr/VT) %	ΔSlIII mmHg/L
Ex-smok	14	mean ± SD	548 ± 209	115 ± 34	38.2 ± 3.76	4.62 ± 1.46	84.8 ± 8.16	32.0 ± 6.27	7.48 ± 4.25	12.78 ± 7.14
GOLD 0	26	mean ± SD	530 ± 176	99 ± 23	34.2 ± 5.37	7.54 ± 2.81	70.0 ± 13.9	31.6 ± 4.50	7.40 ± 4.02	17.18 ± 9.05
GOLD II	20	mean ± SD	697 ± 227	126 ± 38	31.4 ± 3.31	11.9 ± 3.30	51.5 ± 12.1	33.2 ± 5.94	10.45 ± 4.39	19.35 ± 11.57
GOLD III	19	mean ± SD	572 ± 247	107 ± 37	33.5 ± 6.1	13.5 ± 2.57	48.0 ± 6.97	36.6 ± 6.72	11.82 ± 4.35	32.84 ± 26.9
GOLD IV	18	mean ± SD	558 ± 205	117 ± 39	37.4 ± 7.08	17.5 ± 3.23	39.9 ± 6.5	40.9 ± 6.76	15.43 ± 5.33	40.46 ± 44.5
ANOCOVA		F(χ2)group	1.76	1.54	3.299	45.79	64.45*	12.28	10.07	36.59*
		Pgroup	0.128	0.185	0.009	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001
		Fcov	--	116.6	4.722	0.761	--	63.08	4.40	--
		Pcov	--	<0.0001	0.032	0.209	--	<0.0001	0.039	--

Abbreviations: V_T, tidal volume; V_D ^aw, airways dead space; P_ETCO₂, end-tidal CO₂ partial pressure; IAH, index of alveolar heterogeneity; IVE, index of ventilatory efficiency; V_D^Bohr/V_T, Bohr dead space ratio; Δ(V_D ^Bohr/VT), V_D ^Bohr/V_T ratio real minus predicted; ΔSl_III, Slope of phase III real minus predicted.

Note: F_corr and P_corr are values corrected for V_T effect in ANOVA analysis.

Table 3 shows the results of the multivariate linear regression. Significance P gives the probability associated to the rejection of the null hypothesis stating that the regression coefficient (Coeff) for a given independent variable is different from zero, at an alpha error below 5%. Variables in the equation (P < 0.05) are marked in bold. The Beta statistic or regression coefficient for typified variables, allows a non dimensional comparison of the degree of association between dependent and independent variables. The narrowest association between FEV₁%pred and capnography parameters was observed for IAH. This association was not confounded by other associations with the independent variables considered. In contrast, ΔV_D ^Bohr/V_T showed some extra dependence on age, but its association with FEV₁%pred was still high. ΔSl_III also showed a good correlation with FEV₁%pred, but was greatly confounded by a high dependence on V_T. Finally IVE was well defined by a model including FEV₁%pred, MMEF%pred, and age.

Table 3.

Results of the multivariant analysis. Variables in the model are in bold

Parameter	Height T (Sig T) beta	BMI T (Sig T) beta	Age T (Sig T) beta	VT T (Sig T) beta	FEV1%pred T (Sig T) beta	MEF%pred T (Sig T) beta	R(multi)
IVE	−1.40 (0.164)	1.85 (0.067)	−2.41 (0.018)	−0.70 (0.48)	2.78 (0.006)	2.82 (0.006)	0.825
	−0.084	0.110	−0.159	−0.042	0.379	0.379
IHA	1.38 (0.170)	−1.07 (0.29)	1.40 (0.16)	−0.31 (0.76)	−14.4 (<0.0001)	−1.66 (0.099)	0.826
	0.079	−0.061	0.090	−0.017	−0.826	−0.218
ΔVDBohr/VT	0.050 (0.96)	−0.46 (0.64)	2.15 (0.034)	−1.74 (0.08)	−4.57 (0.0003)	0.80 (0.42)	0.560
	0.004	−0.041	0.205	−0.146	−0.436	0.158
ΔSlIII	1.87 (0.06)	0.87 (0.38)	0.084 (0.93)	−6.44 (<0.0001)	−6.33 (<0.0001)	0.63 (0.53)	0.683
	0.155	0.066	0.007	−0.483	−0.475	0.112
VDaw	1.54 (0.13)	−0.078 (0.94)	1.46 (0.15)	11.06 (<0.0001)	0.078 (0.94)	0.519 (0.13)	0.748
	0.115	−0.005	0.098	−0.130	0.005	0.035

Abbreviations: V_T, Tidal volume; V_D ^aw, airways dead space; IAH, index of alveolar heterogeneity; IVE, index of ventilatory efficiency; Δ(V_D ^Bohr/V_T), V_D ^Bohr/V_T ratio real minus predicted; ΔSl_III, slope of phase III real minus predicted.

Using capnography parameters as independent variables, FEV₁% pred was well defined (R = 0.836) by a multivariate linear model including IAH and ΔV_D ^Bohr/V_T (beta = −0.976, and 0.200 respectively) with the equation:

$$\begin{array}{l}{\mathit{\text{FEV}}}_1(\%\mathit{\text{pred}})=112.08-5.60\times \mathit{\text{IAH}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+1.10\times \Delta ({\text{V}}_{\text{D}}^{\text{Bohr}}/V_T)\end{array}$$

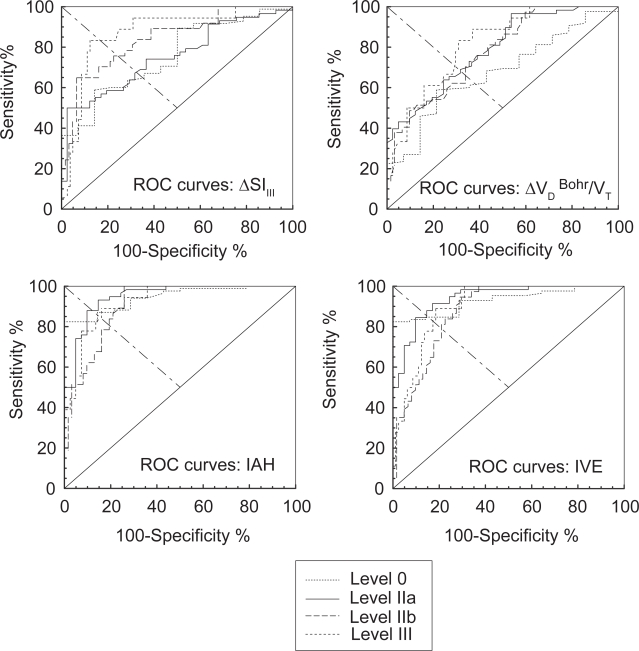
Figure 3 shows the ROC curves constructed for 0, II, III and IV threshold stages of the disease at increasing values of IAH, Sl_III, and ΔV_D ^Bohr/V_T, or decreasing values of IVE. Table 4 shows the numerical analysis of the ROC curves, including AUC with 95% confidence intervals, the cut-off value at which sensitivity equals specificity, the value of sensitivity (or specificity) at this cut-off, positive predicted value (PPV), and negative predicted value (NPV) calculated either from internal prevalence at stage level 0, or from the cumulative prevalence calculated from Kornmann et al (2003) for the remaining stage levels. A visual inspection of the ROC curves in Figure 3 shows that IAH and IVE seem more accurate than Sl_III, and ΔV_D ^Bohr/V_T to stage COPD patients. More precise information about the accuracy of capnography indices is obtained from numerical analysis of ROC curves. AUC, taken as a global summary statistic of diagnostic accuracy, shows higher values for IAH and IVE than Sl_III, and ΔV_D ^Bohr/V_T, especially for diagnosis at low stage levels of the disease. Paired comparison between AUC showed the following differences with IAH: Sl_III, and ΔV_D ^Bohr/V_T at stages 0 and II; ΔV_D ^Bohr/V_T and IVE at stage III; and ΔV_D ^Bohr/V_T at stage IV. Sensitivity (and specificity) was similar and higher than 80% at all threshold levels for IAH, and IVE. In all cases PPV decreased with the threshold level of the disease, and the opposite was observed for NPV. The positive likelihood ratio (PLR) (ratio between the probability of observing the test result in diseased individuals, and the probability of observing the same result in non-diseased individuals) was globally high in IAH, followed by IVE, and ΔSLIII but only at stage IV.

Figure 3.

Receiver operating characteristics curve for each capnography parameter are plotted in separate boxes (ΔV_D ^Bohr: Bohr dead space minus predicted value, ΔSl_III: Slope of alveolar phase or phase III minus predicted value, IAH: Index of Alveolar Heterogeneity, IVE: Index of Ventilatory Efficiency). In every box, each curve corresponds to a different stage of the disease.

Table 4.

Receiver operating characteristics analysis (internal pevalence)

	Stage (cut-off)	AUC (95% C.I.)	Cut-off (95% C.I.) sens = spec	PPV (range)	NPV (range)
IAH	Stage II	0.908 (0.884–0.982)	9.76 (9.43–10.1)	91.1 (89.5–92.6)	82.9 (82.1–83.3)
	Stage III	0.908 (0.833–0.957)	11.9 (11.1–12.7)	70.7 (69.6–75.8)	86.2 (81.5–92.3)
	Stage IV	0.926 (0.855–0.969)	14.2 (13.6–14.9)	53.6 (53.3–59.0)	95.8 (94.7–97.1)
IVE	Stage II	0.939 (0.873–0.977)	57.2 (55.6–58.7)	89.5 (88.2–92.3)	83.3 (80.0–85.6)
	Stage III	0.879 (0.798–0.936)	50.6 (49.9–51.3)	68.2 (67.7–69.4)	84.5 (67.6–69.1)
	Stage IV	0.902 (0.826–0.952)	45.5 (44.2–46.7)	51.7 (50.0–51.9)	95.7 (94.5–97.0)
ΔVDBohr/VT	Stage II	0.788 (0.694–0.864)	9.6 (8.54–10.74)	76.0 (72.0–78.7)	59.8 (62.2–59.6)
	Stage III	0.777 (0.683–0.855)	11.0 (9.26–12.8)	52.3 (51.8–65.5)	74.5 (73.9–81.4)
	Stage IV	0.816 (0.725–0.886)	12.4 (10.7–14.1)	35.1 (34.0–42.0)	90.6 (88.3–96.2)
ΔSlIII	Stage II	0.753 (0.656–0.834)	18.0 (16.9–19.1)	74.7 (72.7–74.9)	58.1 (56.0–59.1)
	Stage III	0.841 (0.753–0.906)	21.1 (20.5–21.7)	63.5 (62.9–66.7)	83.3 (84.1–83.0)
	Stage IV	0.871 (0.788–0.930)	28.4 (25.5–31.3)	85.2 (75.0–82.5)	80.6 (76.3–80.9)

Discussion

According to our results, volumetric capnography parameters seem to be a good tool to determine the degree of functional involvement in COPD patients. It is generally considered that volumetric capnography reflects the degree of pulmonary regional homogeneity in relation to gas exchange (Wolff and Brunner 1984; Fletcher and Jonson 1984; Hoffbrand 1966). From this point of view it seems reasonable to expect that volumetric capnography will reflect the progression of alveolar heterogeneity in parallel with that of the disease. Previous studies have shown some relationships between functional involvement in obstructive lung disease and specific indices obtained either from time based capnography (Toulou 1966; Smidt 1976; Worth 1986; You et al 1992) or from volumetric capnography in humans (Kars et al 1995; Kars et al 1997) and horses (Herholz et al 2002). However, no systematic analysis of the diagnostic capabilities of volumetric capnography in COPD patients has been carried on until now in humans. Recent technical and conceptual advances have allowed anticipation of better perspectives for clinical applications of capnography.

On the volumetric capnography parameters

We have used classical (V_D ^Bohr, Sl_III) and newly developed parameters (VAE, PIE, V_D ^ser), as well as combinations of both (IAH, IVE). Historically, the clinical use of volumetric capnography has been limited for several reasons, one of them being the lack of a reliable measurement of V_D ^aw. The over-correction of phase II induces a phase III-dependent error in the classical, and most popular, equal area method. Nowadays, we can avoid this problem by taking into account the interface expired (Kars et al 1997; Åström et al 2000; Romero et al 1997). In fact, the finding that V_D ^aw, calculated according to Wolff and Brunner (1984), is unrelated to the disease stage in COPD supports this hypothesis.

Another factor that has limited the clinical use of volumetric capnography is the tidal dependence of the more usual capnography parameters. The use of predicted values means tidal dependence can be smoothed for V_D ^Bohr /V_T, by subtracting the predicted value. A better result is obtained by using a common mode rejection ratio: IAH to completely eliminates the tidal dependence of V_D ^Bohr by referring it to V_T–V_D ^aw (Equation 2). IVE, based on the alveolar ejection volume (V_AE) measured on the VCO₂(V) curve, also uses V_T–V_D ^aw as reference eliminate the tidal dependence of V_AE. Both IAH and IVE parameters are related to functional troubles expressed during the alveolar phase of the capnogram. They are, therefore, physiologically related to regional distribution impairment as has been suggested by previous studies on normal subjects and COPD patients (Wilschut et al 1999; Hoffbrand 1966); however, the strong tidal dependence of Sl_III could not be corrected even after subtraction of the predicted value calculated from tidal volume.

In 1997 Kars et al observed a good correlation between the degree of airways obstruction and the V_D ^Bohr normalised at 1 L V_T (R = −0.66). Our results are in concordance with this observation, as ΔV_D ^Bohr/V_T has shown a significant correlation with FEV₁% pred. In the multivariate model we have used, however, age is significantly correlated with ΔV_D ^Bohr/V_T, a fact that was not noticed by Kars (1997) in COPD patients, or by Åström (2000) in normal subjects. In the study by Kars, only simple regressions were performed. Perhaps the age dependence we have observed is a surrogate dependence on the clinical evolution of the disease. Unfortunately, there is no way to verify this hypothesis from our present data.

ROC curves analysis

In order to obtain an estimation of the diagnostic accuracy of each parameter, as well as to determine the cut-off for each stage level of the disease, we have performed a receiver operating characteristics (ROC) curve analysis. A reliable definition of the disease and a good estimation of its prevalence, are the key elements for using ROC curves with a high degree of statistical power. Clear guidelines for staging COPD patients have been published by the GOLD group. The staging process is based on spirometry, a completely standardised and reproducible technique, which leaves only a narrow margin for ambiguity. Prevalence data of COPD stages have been recently published by Kornmann et al 2003). Because their results are somewhat different from the internal prevalence calculated in our population, they have been used to obtain the cumulated prevalence for Positive and Negative Predicted Values and Likelihood Ratio calculations, except for Stage 0 level which does not represent a true prevalence of COPD disease, but simply a cut-off point for a reference population of ex-smokers (cessation for more than 10 years) with no clinical symptoms. Our population was not chosen to calculate the prevalence of COPD and that is why Stage Level 0 ROC Predicted Values and Likelihood Ratio do not correspond to the social prevalence of the disease. Furthermore, the stage-related variation of PPV and NPV may be influenced by their prevalence-dependence because we have used the cumulative prevalence in the ROC curve analysis. In contrast, sensitivity and specificity values, AUC and cut-off points, which are prevalence-independent are therefore valid for all stages, including stage 0.

The area under the ROC curve (AUC) is a global summary statistic of diagnostic accuracy. According to an arbitrary guideline (based on a suggestion by Swets in 1988), it is possible to distinguish between non-informative (AUC = 0.5), less accurate (0.5 <0.7 ≤0.9), highly accurate (0.9 <AUC <1) and perfect tests (AUC = 1). It has been recognised that AUC is equivalent to the probability that a randomly drawn individual from the positive reference sample has a higher (or lower) test value than a randomly drawn individual from the negative reference sample. As AUC gives equal weighting to sensitivity and specificity, we have considered the point at which specificity equals sensitivity as the cut-off point for all stages. However, other criteria could be used if we consider, for instance, the misclassification cost (False Positive and False Negative Cost, CFP and CFN respectively), which require quantification of the consequences of misclassification (Greiner et al 2000). Without better information we have a priori considered that CFP = CFN, and we have given equal weight to sensitivity and specificity.

In a previous study Herholtz et al (2002) studied the diagnostic value of volumetric capnography parameters in a population of horses suffering from recurrent airways obstruction (a veterinary equivalent of COPD in horses). In their study the best accuracy was obtained for V_D ^Bohr/V_T (AUC = 0.70, Se = Sp = 63%) in the staging between without symptoms and with symptoms horses, equivalent to our stage 0 for which we have obtained nearly identical results using ΔV_D ^Bohr/V_T (AUC = 0.68, Se = Sp = 63%). However practically all our AUC have been over 0.7.

In conclusion, capnography parameters seem to be useful for staging COPD patients when spirometry is difficult to perform because of technical or clinical constraints. Capnography is an easy-to-perform technique that requires no special effort or particular knowledge of the manoeuvre, and can be performed in severely disabled patients. It can be used as an alternative test to diagnose the severity of functional impairment in these patients. The Index of Alveolar Heterogeneity seems to be the best parameter for use in clinical practice.

Abbreviations

ANOVA

Analysis of variance

AUC

Area Under the (ROC) Curve

BMI

Body Mass Index

CFN

False Negative Cost

CFP

False Positive Cost

COD

Coefficient of Determination

ΔSl_III

Slope of phase III real minus predicted

ΔV_D^Bohr/V_T

V_D ^Bohr/V_T ratio real minus predicted

F_cov

Fisher F for covariance analysis

P_ETCO₂

End tidal CO₂ partial pressure

FEV₁%pred

Forced Expiratory Volume in one second in percent of predicted

F_group

Fisher For inter-group comparison

IAH

Index of Alveolar Heterogeneity

IVE

Index of Ventilatory Efficiency

MMEF%pred

Maximal Mid Expiratory Flow in percent of predicted

NPV

Negative Predicted Value

P_cov

Probability associated to F_cov

P_group

Probability associated to F_group or χ² _group

PIE

Pre-interface expirate

PLR

Positive Likelihood ratio

PPV

Positive Predicted Value

ROC

Receiver Operating Characteristics Curve

Se

Sensitivity

Sl_III

Slope of Phase III or alveolar phase in the capnogram

Sp

Specificity

VAE

Volume of alveolar ejection

VCO₂(V)

Curve of VCO₂ versus exhaled volume

V_D^aw

Airways Dead Space

V_D^ser

Serial Dead Space (includes instrumental dead space)

V_ECO₂

CO₂ rejected by breath

V_T

Tidal Volume

χ²_group

Chi squared from Kruskal-Wallis rank test