CALCULATING CONTINGENCIES IN NATURAL ENVIRONMENTS: ISSUES IN THE APPLICATION OF SEQUENTIAL ANALYSIS

Abstract

Analysis and interpretation of behavior–environment relations are increasingly being conducted with data that have been derived descriptively. This paper provides an overview of the logic that underlies a sequential analytic approach to the analysis of descriptive data. Several methods for quantifying sequential relations are reviewed along with their strengths and weaknesses. Data from descriptive analyses are used to illustrate key points. Issues germane to contingency analysis in natural environments are discussed briefly. It is concluded that the conceptual distinctions among contiguity, contingency, and dependency are critical if the logic of sequential analysis is to be extended successfully to a behavior-analytic account of reinforcement in natural environments.

Dependencies involve consequences that follow some or all instances of behavior but are not observed in the absence of behavior. Dependencies can be arranged experimentally in analog conditions, allowing one to exhibit a perfect contingency between behavior and environmental events. Experimental procedures used in operant models of behavior explicitly arrange dependencies between responses and consequences by isolating and manipulating antecedent- or consequence-based variables (Skinner, 1938). For example, social consequences can be delivered dependent on problem behavior in analogue functional analyses to demonstrate the effects of contingent reinforcement. Under such controlled conditions, moment-by-moment changes in behavior can be understood with a great deal of precision, particularly in relation to reinforcement effects. By contrast, in less controlled settings, in which descriptive data are collected during naturally occurring social interactions, the behavior–environment dependencies can be difficult to ascertain. However, Vollmer and Hackenberg (2001) presented several examples to show that dependencies are not necessary to demonstrate reinforcement effects, and more than one conceptual framework and set of empirical procedures to derive contingent relations in social behavior in natural contexts have been outlined (Martens, DiGennaro, Reed, Szczech, & Rosenthal, 2008; Vollmer, Borrero, Wright, Van Camp, & Lalli, 2001).

Increasingly, applied researchers are using contingency analyses to detect order in behavior–environment relations in naturally occurring social interactions (Borrero & Vollmer, 2002; Martens et al., 2008; Sloman, Vollmer, Cotnoir, & Borrero, 2005; Snyder & Patterson, 1995; Symons, Hoch, Dahl, & McComas, 2003; Wehby, Symons, & Shores, 1995). Sequential analysis is conducted to determine whether a sequential relation exists between two events of interest in naturally occurring social interactions (Yoder, Short-Meyerson, & Tapp, 2004) and has been applied to socially appropriate and destructive behavior of individuals with developmental disabilities (Hoch & Symons, 2007).

Yoder and Feurer (2000) cautioned about the potential for misuse of sequential analysis techniques. Because of this and the lack of a standardized approach to the analysis of descriptive data sets, the main purpose of this paper is to provide an overview of the logic that underlies the application of sequential analysis to analyze behavior–environment relations in natural contexts. First, the basic principles and uses of sequential analysis are outlined. Next, several specific indexes of sequential association are reviewed along with corresponding statistical analysis issues. Then, we use an existing data set to illustrate a number of issues specific to sequential analysis and relevant for behavior analysis in general. We conclude by discussing the clinical and theoretical relevance of showing that two events are or are not sequentially related.

Sequential Analysis: An Overview

Sequential analysis is a set of techniques used to identify temporal patterns embedded within sequences of coded behaviors or stimulus events (Quera & Bakeman, 2000). Sequential analysis can be conceived of as a tool to tease apart temporal relations among events by analyzing event sequences unfolding in time. Reduced to its core essence, sequential analysis of social interactions serves a single theme: to determine if and how an action or event is related to another action or event (Morgan, Dumas, & Symons, 1992). Sequential analysis is generally used for one or both of the following purposes: (a) to identify whether a particular sequence of behavior and stimulus events occurs to a greater or lesser extent than might be expected by chance alone, and (b) to determine whether a given sequence of behavior and stimulus events differs significantly across conditions, individuals, or groups.

The terminology of sequential analysis is relatively straightforward. However, confusion is sometimes created because sequential analysis and behavior analysis share some common terms that have slightly different meanings. For example, the term antecedent as it is used in sequential analysis can cause some confusion. In a sequential analysis, an antecedent refers to the first of two events, and target refers to the second event. Thus, in some analyses, the antecedent may be adult behavior and the target may be subsequent child destructive behavior. Or, in a different set of analyses, the antecedent may be child destructive behavior and the target is the subsequent adult social interaction. Another example of terminology that can be confusing is how the terms conditional and transitional probabilities are used. These two terms are often used interchangeably, but technically, a conditional probability is the likelihood that two events co-occur within some predesignated time frame. The calculation involves dividing the occurrences of the antecedent–target relation by the total occurrences of the antecedent. For example, the likelihood of a child displaying disruptive behavior (target) in the presence of the teacher (antecedent) can be calculated as a conditional probability in which the number of intervals in which the child was disruptive in the presence of the teacher is divided by the total number of intervals in which the teacher was present. A transitional probability is a special instance of the more general class of conditional probabilities in which time is preserved, and the specific order of events is relevant (Bakeman & Gottman, 1997). Specifically, a transitional probability indicates the likelihood that one event follows another in sequence. The calculation is the same, but the nature of the relation between the antecedent and target is specifically a sequential one. For example, the likelihood of a child displaying disruptive behavior following a teacher instruction would be calculated as a transitional probability in which the number of times the child displayed disruptive behavior following a teacher instruction is divided by the total number of times the teacher provided an instruction. For the purposes of examining whether and what type of relation exists in behavior sequences, transitional probabilities are preferred to conditional probabilities and are used henceforth in this paper.

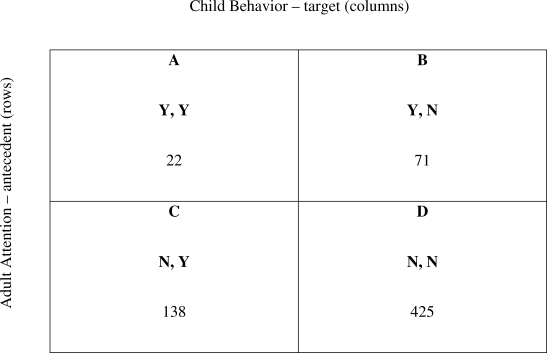
The unit of analysis in sequential analysis is a two-event sequence recorded via an observational protocol that consists of operationally defined behaviors sampled across some period of time or across conditions or contexts. Pairs of events are organized into a 2 × 2 contingency table (see Figure 1). By convention, the antecedent occupies the rows, and the target occupies the columns. The cells are labeled A, B, C, and D, with A and B in the top row, left to right, and C and D in the bottom row, left to right. Cell A contains the tallies of the behavior–event pair of interest within the stream of behavioral codes recorded. For example, the top panel of Figure 1 shows the number of times child behavior was preceded by teacher attention in Cell A. Cell B contains instances of teacher attention that were not followed by child behavior. Cell C represents the occurrence of the target event (child behavior) in the absence of the antecedent event (teacher attention). Cell D represents all other pairs of coded events that did not include the specified antecedent (teacher attention) or target (child behavior). From such a 2 × 2 contingency table, a number of indexes can be derived to examine the nature of the behavior–event sequence of interest.

Figure 1.

Sample 2 × 2 matrix for tallying and computing sequential relations between adult attention and child behavior. Observed frequency of the event pair of interest is given in Cell A. Y,Y (antecedent, target) indicates yes antecedent occurred, yes target occurred as next event in sequence. Observed frequencies of other event pairs are given in Cells B, C, and D.

Indexes of Sequential Associations

A number of basic statistics can be generated to aid interpretation of the nature of the association between observed two-event sequences (Wampold, 1992). To begin, the simple probability of two events occurring in sequence could be calculated as a summary level statistic. Simple probabilities have been considered but disregarded as a measure of sequential association because they do not control for chance occurrences of the two-event sequence (Yoder et al., 2004). The calculation for simple probabilities is the number of tallies in Cell A of the 2 × 2 matrix divided by the sum of the tallies in Cells A, B, C, and D; this only yields information on how often that two-event sequence was observed in all the observed sequences. The simple probability does not provide information about that two-event sequence relative to anything; thus, it is difficult to interpret the resulting probability. For example, imagine that the child behavior depicted in the matrix in Figure 1 is hand raising, and the adult behavior is asking questions. The simple probability of the child raising his or her hand following an adult question is 3%. That is, 3% of all observed sequences involved the child raising his or her hand following an adult question. The problem is that we do not know how to interpret that 3% because we do not know anything about how often the teacher asked questions. Therefore, it is desirable to examine the probability conditional on the number of times the teacher asked questions. Thus, transitional probabilities are calculated to yield an index of how well one event (the antecedent) predicts another (the target) as the next event in the sequence relative to the overall occurrence (referred to as the base rate) of the antecedent [A/(A + B)].

Using the example from Figure 1, the transitional probability would be 24%; that is to say that 24% of the time that the teacher asked a question, the student raised his or her hand. Transitional probabilities represent one of the simplest means of describing a contingent relation between antecedent and target events because they represent how often a target event follows a particular antecedent event (Bakeman & Gottman, 1997). Although transitional probabilities are among the most commonly used index to represent the sequence of interest, their use as an index of sequential association is limited and can be problematic for at least two reasons. First, although they do take into account the overall occurrence of the antecedent, they do not take into account the overall occurrence of the target event. This is problematic because it is difficult to interpret the likelihood of a target event in the absence of consideration of the overall occurrence of that target event. For example, we might know that 24% of the time a teacher asks a question, the child raises his or her hand, but we don't know the overall occurrence of hand raising or what proportion of hand raising follows teacher questions. It might be that 100% of the time he or she raises his or her hand, it is after the teacher asked a question, or it could be that 5% of the time that he or she raises his or her hand, it is after the teacher asked a question. In fact, across observations, conditions, individuals, or groups, the overall frequency of the target event may vary substantially, making a transitional probability of 24% for a child who raises his or her hand frequently different and difficult to compare to a transitional probability of 24% for a child who rarely raises his or her hand. Second, transitional probabilities do not provide information regarding the probability of a two-event sequence relative to chance. Taken together, these two limitations are problematic when comparing transitional probabilities across conditions, individuals, or groups because transitional probabilities of the same value may represent different levels of sequential association due to differences in overall frequencies (Bakeman & Gottman, 1997). Based on these reasons, Yoder and Feurer (2000) suggested that transitional probabilities should not be used because (a) readers will make implicit but inappropriate comparisons between transitional probabilities of sequences from different conditions or groups, and (b) more appropriate alternative statistics exist for making comparisons. A variety of appropriate alternative indexes and data transformations, including z scores (Bakeman & Gottman), transformed kappa (Wampold, 1992), and Yule's Q (Yoder & Feurer) have been recommended for making comparisons across conditions, individuals, or groups.

Z scores are useful for identifying whether a particular transitional probability deviates significantly from its expected value (Bakeman & Gottman, 1997). This statistic, unlike transformed kappa, Yule's Q, and phi, which provide strength-of-association measures, provides a p value. As Wampold (1992) noted, a z score may allow rejection of a null hypothesis of randomness and allow the conclusion that a particular transition is present beyond that which would likely be obtained by chance, but it does not indicate the degree to which a pattern is present. Accordingly, using z scores in conjunction with one of the other indexes may provide investigators with a better understanding of their data.

Although z scores are an appropriate statistic for assessing whether a particular transitional probability deviates significantly from its expected value, the critical problem associated with their use as a dependent measure is that their numeric “value is influenced directly by the rate of occurrence of the given act itself” (Morgan et al., 1992, p. 73). As Bakeman and Gottman (1997) described, for an effect of a specific size, the z score becomes larger as the number of tallies increases. That is, all things being equal, when contingency tables possess an unequal number of two-event pairings, the p value of a z score based on a contingency table with more tallies will be less (e.g., .01 instead of .05) than the p value of a z score based on a contingency table with fewer tallies, even when the underlying sequential association is the same (Yoder & Tapp, 1990). Despite these caveats, a z statistic appears to be a safe option for assessing whether a particular transitional probability differs significantly from that which might be expected by chance. The fact that a z score is one of the only tests of sequential dependency that provides a p value may be of interest to some investigators. However, the z score's sensitivity to the total number of tallies makes it less appropriate as a dependent measure for comparisons across subjects, groups, conditions, or observation sessions.

Because of the relatively limited utility of z scores, other indexes have been tested as measures of sequential dependency. Transformed kappa provides an index of effect size (Wampold, 1992) that may be used in the analysis of singular transitions for a given event to a target event, but for a number of reasons related to properties of its sampling distribution (i.e., skewness), its use as a dependent variable in parametric analyses is not recommended (see Bakeman, McArthur, & Quera, 1996). The phi coefficient controls for the total number of coded behaviors, but it may be an unreliable index because it reaches its maximum values only when antecedent and target events occur the same number of times throughout an observation session (Yoder & Feurer, 2000).

Yule's Q is a statistic based on a transformed odds ratio that controls for both the total number of tallies and the simple probability of target events (Yoder & Fuerer, 2000). Like transformed kappa and phi, it produces easy-to-interpret values that range from −1 to 1, with zero indicating no sequential association between given and target events. However, unlike the other indexes of sequential association that have been reviewed (z scores, transformed kappa, and phi), Yule's Q does not incorporate marginal totals (from the 2 × 2 table) in its calculation. Unlike alternative indexes that are either sensitive to the total number of tallies or the total number of target or given events, Yule's Q is immune to this problem because it does not incorporate marginal totals in its calculation. Therefore, Yule's Q appears to provide a viable index of sequential association for assessing both singular transitional probabilities and differences between or across transitional probabilities. The following analyses will illustrate the implications of using simple probabilities, transitional probabilities, and Yule's Q for comparing social-interaction data between 2 child–adult dyads.

APPLICATION OF SEQUENTIAL ANALYSIS FOR DESCRIPTIVE DATA

Purpose

The purpose of the following section is to illustrate a number of issues described previously, to demonstrate how to appropriately answer basic questions about two events unfolding in time, and to quantify the magnitude of their association. For this demonstration we selected observation sessions from an existing descriptive observational data set of social interactions in child–teacher dyads. Our primary conceptual interest was in describing and quantifying the social interaction between preschool children and teachers during naturally occurring free-play activities in preschool settings consistent with a reinforcement effects model. For the purpose of this illustration, our specific research question was whether adults were positively responsive to appropriate child social initiations. To begin to answer this question, sequential analytic techniques were applied.

Method

Two preschool children (boy, 36 months old; girl, 42 months old) and one preschool teacher were directly observed for three 20-min sessions over the course of 1 week at a university-affiliated preschool program. Observations occurred during free-play activity times and sessions were selected based on availability of the child and the classroom schedule. The antecedent event was an appropriate child social initiation (CI) in the form of child statements, questions, vocalizations, or gestures directed towards an adult that invited prosocial interaction (e.g., “let's play,” “hi, what's going on”). The target event was a positive adult social (AS) response in the form of positive talk (e.g., praise statements, affirmative interactions) directed toward the child. Other forms of adult (e.g., neutral, negative) and child (e.g., inappropriate social initiation, aggression or destruction) behavior were also observed and coded. Briefly, prior to beginning data collection, the observers were trained (until reaching 80% agreement criteria on all codes) by calibrating to videotaped samples of participants. Mean overall agreement (number of agreements divided by the number of agreements plus disagreements) for prosocial child behavior was 96% (see McComas, Johnson, & Symons, 2004, for the complete data set, coding definitions, and training procedures).

The primary unit of analysis was the two-event sequence CI followed by AS. Written as a transitional probability, it can be represented as p(AS/CI) or the probability of AS as the next coded event given CI. For each dyad, data were pooled across all observation sessions combined, and pairs of events were organized into a 2 × 2 contingency table for each dyad (see Figure 2). Cell A contains the tallies of the event pair of interest (i.e., any two-event pairing when the child exhibited an appropriate social initiation, and the next coded event involved adult social interaction). This is referred to as an event-based lag 1 analysis. Cell B represents instances of the occurrence of CI that is not followed by AS. Cell C represents occurrence of the target event (AS) in the absence of the antecedent event (CI). Cell D represents all other pairs of coded events that did not include the specified antecedent (CI) or the target (AS).

Figure 2.

Matrix of tallies of child initiations and adult social behavior for computing sequential relations for Dyad 1 (top) and Dyad 2 (bottom).

Results

Summary-level analyses

Summary-level analysis was used to quantify the frequency (responses per minute) of prosocial behavior of each CI and AS. These data were derived prior to construction of the 2 × 2 matrix and do not appear in the figures. For Dyad 1 (D1), mean CI was 1.7 per minute, and mean AS was 3.1 per minute. For Dyad 2 (D2), mean CI was 2.2 per minute, and mean AS was 1.0 per minute.

Sequential-level analyses

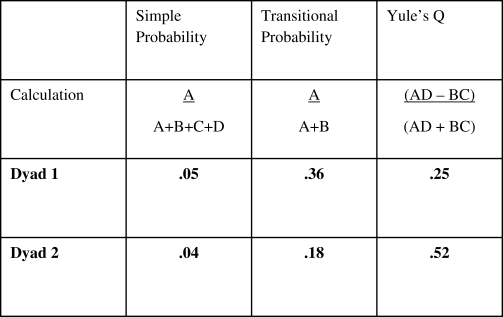
Sequential-level analysis was used to address the issue of whether teachers were responsive (i.e., responded contingently) to appropriate social initiations of each child. To demonstrate the logic that underlies sequential analysis and the influence of different base rates across individuals, we computed three indexes (see Figure 3). First, simple probabilities of AS following CI were calculated. Second, transitional probabilities of each target CI and AS were calculated. Next, Yule's Q scores associated with the transitional probabilities were calculated (Bakeman et al., 1996). As described above, Yule's Q is a transformed odds ratio bound by −1 and 1 that controls for the total number of coded behaviors (Quera & Bakeman, 2000).

Figure 3.

Formulas and computational results of sequential relations for Dyads 1 and 2.

Simple probabilities

The simple probability of the two-event sequence is the proportion of event sequences including the antecedent event (CI) and the target event (AS) and is calculated by A/(A + B + C + D). The simple probability of a child initiation followed by an AS was .05 for Dyad 1 and .04 for Dyad 2. The simple probability of an AS following a CI is nearly identical for the 2 dyads. What does this tell us? The simple probability is limited to indicating that in all observed sequences, the probability of an AS following a CI was about the same for both children, regardless of how often the 2 children displayed social initiations. There is no information concerning the contingency between appropriate child social initiations and positive adult social responses because it is not known to what proportion of each child's initiations the adult responded.

Controlling for antecedent base rate: Transitional probabilities

The transitional probability is the proportion of instances of the antecedent or given behavior (CI) that are followed by an instance of the target behavior (AS) and is calculated by A/(A + B). Transitional probabilities improve our ability to predict the target event by considering what event precedes it, shedding some light on the sequential nature of the relation between the two designated events or behaviors. The transitional probability of a positive AS given an appropriate CI was .36 for Dyad 1 and .18 for Dyad 2. It is important to note that transitional probabilities control for differences in the overall frequency of the antecedent event. Because the base rate of the antecedent (CI) was different for Dyad 1 (frequency was 99) and Dyad 2 (frequency was 134), it needed to be controlled to clarify the possible sequential relation between the antecedent (CI) and the target (AS). Thus, the transitional probability improves our ability to predict the target event by considering preceding events and controlling for any base-rate differences in the frequency of the antecedent. However, because transitional probabilities can be influenced by the simple probability of the target behavior and because there were differences between Dyad 1 (AS frequency was 183; simple probability AS was .27) and Dyad 2 (AS frequency was 61; simple probability AS was .09), a more interpretable descriptive index of the sequential relation than transitional probabilities is required.

Controlling for target base rate: Yule's Q

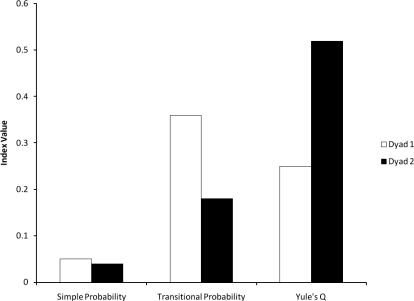
If the base rates of the target are not equivalent, transitional probabilities are uninterpretable across units of analyses (conditions, individual subjects, groups). For this demonstration, Yule's Q was an appropriate index of sequential dependency because it is not influenced by the base rate of the target (or antecedent) and provides an implicit comparison with an estimate of chance occurrence of AS after appropriate CI, whereas transitional probabilities do not (Yoder & Feurer, 2000). Yule's Q is calculated by (AD − BC)/(AD + BC). Figure 4 shows that the sequential association between positive adult social and appropriate child social initiation is greater for Dyad 2 than Dyad 1. Note the resulting transitional probability was greater for Dyad 1 than for Dyad 2. Thus, the Yule's Q statistic suggests the opposite inference of the transitional probability.

Figure 4.

Three sequential indexes arrayed for Dyad 1 (D1) and Dyad 2 (D2), illustrating the variation in the strength of sequential association between appropriate child social initiations (CI) and positive adult responses (AS) using three indexes. SP  =  simple probability of the two-event sequence; TP  =  transitional probability; YQ  =  Yule's Q.

SUMMARY AND CONCLUSIONS

Operant models that rely on experimental analyses explicitly arrange dependencies between responses and consequences. In descriptive studies, the dependency is not programmed and is largely unknown (Vollmer et al., 2001). One purpose of sequential analysis is to quantify the magnitude of association between events, a key feature of the dependency. Yule's Q (and other indexes appropriately used) are critical for interpretation of the magnitude of the relation for two-event sequences, but are not necessarily magic bullets for a complete behavioral analysis. In fact, the best measures of contingency strength are not yet known; therefore, an approach that involves multiple evaluations of contingency on the same set of descriptive data appears warranted to examine behavior–environment relations so that important relations are not missed.

How good a tool is sequential analysis for identifying reinforcement contingencies in the natural environment in the absence of experimental manipulation? It depends, in part, on how reinforcement contingency is defined and operationalized. As reported earlier, a dependency is not a necessary condition to demonstrate reinforcement effects (Vollmer & Hackenberg, 2001). Instead, contingent relations have been used to infer reinforcement effects in natural sequences of behavior–environment events (e.g., Borrero & Vollmer, 2002; Sloman et al., 2005; Symons et al., 2003; Vollmer et al., 2001). A contingency between a response and a consequence exists when the response is both necessary and sufficient to generate that consequence (Watson, 1979). The sufficiency of a response in producing a consequence can be considered as the conditional probability of the consequence given the response. The necessity of a response in producing a consequence can be considered by comparing the conditional probability with the simple probability of the consequence (Rescorla, 1988; Snyder & Patterson, 1995). Thus, there appears to be both logical and emerging empirical support for the use of contingency analyses to infer reinforcement effects in descriptively derived data.

The utility of sequential analysis for identifying reinforcement contingencies also depends on the correct application of sequential analytic techniques (i.e., accounting for or correcting for differences in base rates, choice of index of sequential association). In this paper, our primary purpose was to address the issue by introducing, describing, and demonstrating an application of sequential analysis. As illustrated, different conclusions can be reached depending on the point at which the sequential analysis is stopped. In this application, opposite conclusions would be made about the nature of the relation between the 2 children's appropriate social interactions and their teachers' social behavior. Knowing when the analysis is complete depends on consideration of the context in which the data are collected and the types of planned comparisons to be made (Symons, 2005).

In terms of inferring a reinforcement effect, in some approaches (including our own), statistical analyses are applied to a priori specified sequences of interest to determine whether the target event occurs more or less often than expected by chance (i.e., a p value is assigned), and the magnitude of association between the two events is calculated. Then, the logic and procedures of a matching law analysis are applied to determine whether the relation between the two events fits or is consistent with a reinforcement effects model (Sloman et al., 2005; Symons et al., 2003). We recognize that other researchers do not conduct statistical tests of significance because statistically significant differences are not a necessary condition to observe reinforcement effects. Clearly, behavior can be maintained in the absence of a statistically significant difference. Consider, for example, a situation in which a single instance of a reinforcer presentation is sufficient to maintain behavior (Skinner, 1956). This is yet another reason to consider use of multiple approaches to contingency analysis in evaluating descriptive data.

There are a number of additional issues beyond the immediate scope of this paper that warrant consideration in the application and extension of sequential analysis to applied behavior analysis, including (a) establishment of a mutually exclusive and exhaustive code set; (b) the question of whether consecutive codes may or may not repeat; (c) the impact of autocorrelation; (d) modifications to account for differences among interval-based, time-based, or event data; and (e) the value and utilization of sampling permutations or randomization tests (see Bakeman & Gottman, 1997, for further elaboration of these points).

For behavior analysis, critical conceptual and definitional distinctions remain central to the issue of inferring functional relations from descriptive data sets; these include contiguity, contingency, and dependency. Sequential analysis can be a powerful tool to clarify critical features of the relations between and among variables in descriptive data sets, but like all analytic tools, it is limited by the nature of the data and the conditions of their generation.