Dynamic mechanisms of blood vessel growth

Abstract

The formation of a polygonal configuration of proto-blood-vessels from initially dispersed cells is the first step in the development of the circulatory system in vertebrates. This initial vascular network later expands to form new blood vessels, primarily via a sprouting mechanism. We review a range of recent results obtained with a Monte Carlo model of chemotactically migrating cells which can explain both de novo blood vessel growth and aspects of blood vessel sprouting. We propose that the initial network forms via a percolation-like instability depending on cell shape, or through an alternative contact-inhibition of motility mechanism which also reproduces aspects of sprouting blood vessel growth.

1. Introduction

The phenomena of biological development often seem much too complex to treat from the perspective of applied mathematics. The simulation results of the Hogeweg group at Utrecht University on the development of the cellular slime mould, Dictyostelium discoideum, have nevertheless shown that even apparently intentional behaviours (like phototaxis [1]) can arise from the uncoordinated interactions of a few cell types interacting via a few simple biophysical mechanisms. While the mechanisms (adhesion, chemotaxis, diffusion, light capture, stimulated secretion and stochastic differentiation) individually are incapable of producing complex behaviours and while single cells exhibiting combinations of these mechanisms are also very limited in their behaviours, the combination of multiple mechanisms and many cells can produce genuinely emergent complex behaviours. In the case of Dictyostelium discoideum (often abbreviated as Dicty.), the same cell types, obeying the same rules, can produce spiral waves, stream aggregates, a crawling slug and a stalk and fruiting body, all depending on initial conditions. The lesson of Dicty. is that even apparently hopelessly complex biological phenomena can (though they need not) result from instabilities which we can understand theoretically. The Dicty. model has shown a hidden unity underlying the apparently disparate behavioural phases of the Dicty. life-cycle.

This paper presents an example of underlying unity in a different context, the growth of blood vessels, which appears to occur via two completely different mechanisms. Blood vessels form de novo during embryonic development, when dispersed endothelial cells (ECs: the cells lining the inner walls of fully-formed blood vessels) organize into a vascular network (vasculogenesis), or later during development and in adult life by sprouting or splitting of existing blood vessels (angiogenesis). Many computer models exist to explain and describe either, but not both, de novo [2-7] or sprouting blood vessel growth [8-10]. However, the same genetic machinery regulates both mechanisms, which are closely related at the molecular and cellular levels [11], so a plausible mechanism must explain both. We suggest a set of cell behaviours and a fundamental instability mechanism that reproduces phenomenology of both cases and show a second, cell-shape dependent instability mechanism for de novo blood vessel growth. We aim to encourage the reader to attempt to develop more abstract models of these phenomena to explain in a rigorous way the origin of the instabilities we observe.

A popular experimental model of blood vessel development is human umbilical-vein endothelial-cell (HUVEC) culture, which cultures blood vessel wall cells obtained from umbilical cords in a protein gel obtained from Matrigel, a commercial product which mimics the environment in which blood vessels normally grow. Initially the cells are randomly but isotropically distributed over the gel. The growth factors in the Matrigel stimulate the cells to elongate and interconnect to form an initially fine network, which progressively coarsens. Both the patterns and their kinetics resemble embryonic, de novo blood vessel growth. The cells do not penetrate into the Matrigel, forming instead a quasi-two-dimensional vascular-like pattern. HUVEC culture closely resembles quasi-two-dimensional blood vessel growth in the yolk sacs of avian and mammalian embryos. Sprouting blood vessel growth roughly involves the following steps. First the basement membrane—a tough wall of connective tissue surrounding most blood vessels—degrades enzymatically. Then ECs migrate through it, proliferate and assemble, forming an initial sprout. Finally, a new basement membrane forms as the vessels mature. We have focused our initial models on quasi-two-dimensional cases, to facilitate comparison of simulations to experiments and to keep the simulations computationally tractable.

1.1. Cell-centred modelling

Previous models of blood vessel formation focused on tissue-level phenomena, describing densities of ECs rather than the behaviours of individual cells [2-7] or describing growing blood vessels as branching networks of pipes whose elements were tubular lengths of vessel [8-10]. Here, we explicitly model the behaviour of individual ECs.

Individual cells of a given type are almost indistinguishable between organisms of the same kingdom. Instead, differences between multicellular organisms arise primarily from how their cells recombine to form new patterns. Genome evolution studies suggest that after gene and genome duplication events, duplicates of intercellular communication pathways stay in the genome (and diverge from their original copies), while intracellular house-keeping genes decay quickly after duplication (see e.g. [12, 13]). This difference in the frequency of duplication and the rate of evolutionary diffusion suggests that the regulation of cell interactions diversifies much faster than the behaviours of individual cells. Genetic information controls blood vessel growth (and development more generally) only indirectly; so modelling cell interactions accurately is more important than modelling genetic and metabolic regulation within cells. We therefore employ a simplified, phenomenological model of the relationship between genome and cell behaviour and a much more detailed model of how cell interactions lead to the development of tissues. This choice vastly simplifies our models, since the interactions of roughly 10⁴–10⁵ gene products reduce to ten or so cell behaviours. In our case, we consider only a subset of these behaviours: our cells can move, stick to each other, change shape, exert forces and secrete and absorb chemicals.

We have described in detail elsewhere [14] how to build such a cell-centred model. We must first infer individual cell behaviour from biological experiments, e.g. cell cycle times, cell death rates, mean cell velocities, adhesion strengths and hierarchies, shapes, rates and triggers of cell differentiation. We can sometimes obtain cell-behaviour data from the scientific literature, or we may need to perform additional experiments. In some cases we must make plausible guesses by analogy with other cell types or organisms. Qualitative data are fairly abundant, quantitative data rare. Because of the relative sparseness and poor quality of quantitative data, our models must be quite robust to substantial changes in parameter values in order to be credible. Once we have identified how individual cells behave, we can describe the essentials of that behaviour in a conceptual biological model.

Philosophically, because of the paucity of experimental data and our desire to identify fundamental mechanisms, and also because a biological model can only ever prove sufficiency rather than correctness, we always attempt to build the simplest possible model consistent with the biological observations. To minimize the number of model parameters, we always start with a minimal model and then gradually add mechanisms as needed, rather than attempting to simulate all known behaviours from the beginning. We then pick a scale (or range of scales) of description (subcellular, cellular, tissue-level) and translate the biological model into a mathematical and algorithmic model, which might take the form of a set of coupled partial differential equations (PDEs) and a set of rules describing cell division and differentiation. Such mathematical models, usually at the tissue scale (i.e. neglecting the behaviour of individual cells) are the type most familiar to applied mathematicians.

Often, the PDE approach suffices. However, when we have structures or behaviours which occur at the scale of single cells, continuum approaches can give qualitatively incorrect results. For example, ECs are highly anisotropic and form vascular plexi only a few cell-widths thick, both of which are difficult to include in continuum PDE models. In this case, we then must implement the mathematical model computationally using an approach that preserves the identity and behaviour of individual cells (we use Glazier and Graner’s CPM approach, but many other approaches are equally valid). This computational description must phenomenologically reproduce the individual cells’ behaviour. Our phenomenological single-cell model is purely descriptive and has no explanatory value per se. It becomes useful when we simulate many single-cell models simultaneously to determine whether the behaviours we included in the single-cell model suffice to explain the tissue-level patterns and physiological functions we find in experiments. If the model results match experimental observation, we can further test our model by making experimental predictions. What happens to the cell ensemble if we eliminate one of the single-cell behaviours? Can we remove the same element in an experiment, e.g. with a genetic knock-out, and find similar tissue-level ensemble behaviour? Also, we might ask which networks of genes steer this set of single-cell behaviours and how they do it. In this way, we can describe and understand the role of gene networks in multicellular phenomena, instead of merely observing that knocking a gene out disrupts a multicellular function.

The cell-centred model we develop will reproduce aspects of our target phenomenon (here de novo and sprouting blood vessel growth) but will not reproduce all details of experiments. By identifying which phenomenology our model reproduces and which it fails to reproduce, we can identify essential cell behaviours.

Following our general outline for the modelling of developmental phenomena, we first identify a small set of experimentally confirmed EC behaviours and try one by one whether these could explain the formation of vascular networks. EC (a) secrete a morphogen [15] which slowly degrades, (b) preferentially extend protrusions (filopodia) up morphogen gradients, causing cell movement up those gradients [16], (c) rapidly elongate after contact with the extracellular matrix (ECM) [17] (internal remodelling of the actin cytoskeleton drives this shape change [20]) and (d) stick to each other through the adhesion receptor vascular-endothelial–cadherin (VE–cadherin) [18] (this receptor also allows the cells to sense when they are in contact with each other and to change both their global behaviour and their local membrane activity [19]).

A PDE model [4, 5] explains vasculogenesis from the chemotactic aggregation of ECs. This model derives from the astrophysical Burgers equations and assumes that ECs secrete a chemoattractant, which diffuses and decays in the ECM:

$$\begin{array}{l}\frac{\partial n}{\partial t}+\nabla ·(n\overrightarrow{\upsilon })=0,\\ \frac{\partial \overrightarrow{\upsilon }}{\partial t}+\overrightarrow{\upsilon }·\nabla \overrightarrow{\upsilon }=\mu \nabla c,\\ \frac{\partial c}{\partial t}=D{\nabla }^{2}c+\alpha n-{\tau }^{-1}c,\end{array}$$ (1)

where n is the density of ECs, υ⃗ the velocity field and c the chemoattractant concentration. According to this model, ECs accelerate in chemoattractant gradients. In the highly viscous environment which the cells experience, however, ECs have no inertia. Instead, they move as long as they exert or experience a force and stop when it is removed. Thus, cell inertia seems biologically implausible, although the authors argue that it can represent EC’s persistence of motility [7]. Studies in other organisms show that cells, while they do exhibit persistence, do not accelerate in response to gradients, primarily because their maximum velocity is limited [21]. While persistent motion due to the time a cell takes to assemble and disassemble its motility apparatus (flilopodia or lamellipodia) can significantly affect the kinetics of pattern evolution in highly frustrated environments where cell diffusion or superdiffusion sets timescales (e.g. cell sorting), we neglect it here for three reasons. (1) The typical persistence time for cells is a minute, while the vascular pattern forms over the course of hours. (2) The cells primarily interact with each other via a chemoattractant which diffuses rapidly relative to the timescales of cell diffusion (thus chemical rather than cell diffusion sets the timescale for cells to sense each other’s presence). (3) All cells are equivalent and interact in an environment with no mechanical barriers which require low-probability ‘thermally activated’ processes (thus the pattern timescale depends on the mean cell speed rather than the frequency of rare large-amplitude events; equivalently the energy is a smooth function of configuration with a single global minimum attracting nearly all initial conditions and few if any local minima). We therefore modify the Gamba and Serini equations to set the cell velocity rather than the cell acceleration to be proportional to the chemoattractant gradient. Further, we assume that (as is observed biologically) the response of the cell to the gradient is local along the membrane rather than occurring at the cell centre.

Because we are attempting to reproduce experiments on quasi-two-dimensional vascular patterns, which form in yolk sacs and in in vitro experiments, we employ a two-dimensional model of our cells. Working in two dimensions greatly simplifies our modelling because the cells move on top of the ECM rather than through it and extracellular signals diffuse through the underlying ECM rather than through the complex and moving volume around cells in three dimensions. Releasing hundreds of such virtual ECs into an ‘in silico petri dish,’ we then study how cell-level phenomenology drives morphology and dynamics at the tissue scale.

2. Methods

We model EC behaviour at a mesoscopic level using Glazier and Graner’s cellular Potts model [22] (CPM), a flexible, lattice-based, Monte Carlo approach, which includes cell–cell adhesion, cell migration and chemotaxis (cell movement up or down chemical gradients which occur when we bias membrane fluctuations and extensions of filopodia according to the concentration of a diffusible chemoattractant). We describe chemoattractant diffusion macroscopically, using a continuum approximation. An energy-minimization philosophy, a set of constraints and auxiliary conditions determine how the cells move. Intercellular junctions determine an adhesive (or binding) energy between cells. Cells move to promote stronger rather than weaker bonds and shorter rather than longer cell boundaries. An energy constraint regulates cell volume, which is a surface area in two dimensions. Additional constraints or auxiliary conditions easily extend the CPM [23].

The CPM represents biological cells as patches of identical lattice spins σ(x⃗) on a square lattice, where each spin identifies or ‘labels’ a single biological cell. Connections between neighbouring lattice sites of unlike spin σ(x⃗) ≠ σ(x⃗′) represent membrane bonds, where the bond energy is J_{σx⃗,σx⃗′}, assuming that the types and number of VE–cadherin and other adhesive cell-surface proteins determine J. An energy penalty increasing with the cell’s deviation from a designated target area A_σ imposes a volume constraint on the biological cells. We define the pattern Hamiltonian:

$$H=\sum _{\overrightarrow{x},\overrightarrow{x}\text{'}}{J}_{{\sigma }_{\overrightarrow{x}},{\sigma }_{\overrightarrow{x}\text{'}}}(1-{\delta }_{{\sigma }_{\overrightarrow{x}},{\sigma }_{\overrightarrow{x}\text{'}}})+\lambda \sum _{\sigma }{(a_{\sigma }-A_{\sigma })}^2,$$ (2)

where λ represents a cell’s resistance to compression and the Kronecker delta is δ_x,y = {1, x = y; 0, x ≠ y}. Each lattice site represents an area of 2 μm×2 μm. We assume that cells do not divide or grow during patterning, with A_σ = 50 lattice sites and λ = 25 for all cells. The cells reside in an extracellular fluid medium which is a generalized CPM cell without a volume constraint and with σ = 0. We define a special, high cell-border energy J_cB = 100 to prevent cells from adhering to the lattice boundaries (we could equally conveniently use non-physical periodic boundary conditions).

To mimic cytoskeletally-driven membrane fluctuations, we randomly choose a lattice site, x⃗, and attempt to copy its spin σ_x⃗ into a randomly chosen neighbouring lattice site x⃗′. For better isotropy we use the twenty first to fourth nearest neighbours [24]. During a Monte Carlo step (MCS) we carry out n copy attempts, where n is the number of sites in the lattice. We calculate how much the Hamiltonian would change if we performed the copy and accept the attempt with probability:

$$P(\mathrm{\Delta }H)=\{e^{-\mathrm{\Delta }H/T},\mathrm{\Delta }H\ge 0;1,\mathrm{\Delta }H<0\}.$$ (3)

All our simulations use a Boltzmann temperature T = 50.

To mimic cell elongation due to cytoskeletal remodelling we add a cell-length constraint to the free energy:

$$H^{\text{'}}=H+{\lambda }_L\sum _{\sigma }{(l_{\sigma }-L_{\sigma })}^2,$$ (4)

where l_σ is the length of cell along its longest axis, L_σ its target length and λ_L is the strength of the length constraint. Assuming that cells are ellipses, we can derive their length from the largest eigenvalue of their inertia tensor I [25, 26]. The length constraint could cause cells to split into disconnected patches. We prevent this artefact by introducing a connectivity constraint, which reflects the physical continuity and cohesion of the actual cell [26].

3. Results

3.1. Chemotactic cell aggregation

Our initial cell-centred model of vasculogenesis implements the basic assumption of the Gamba and Serini model [4, 5]: ECs migrate towards the chemoattract they themselves secrete. We use the basic CPM and add a PDE layer which describes the diffusion and secretion of the chemoattractant in the uniform substrate underlying the cells:

$$\frac{\partial c}{\partial t}=\alpha {\delta }_{{\sigma }_{\overrightarrow{x}},0}-(1-{\delta }_{{\sigma }_{\overrightarrow{x}},0})\mathit{\in }c+D{\nabla }^{2}c,$$ (5)

where δ_σx⃗,0 = 1 inside the cells. α = 10⁻³ is the rate at which the cells release chemoattractant, ∈ = α is the decay rate of the chemoattractant and D = 10⁻¹³. Every site within the CPM cells secretes the chemoattractant, which only decays in the substrate. We solve this PDE numerically using a finite-difference scheme on a lattice that matches the CPM lattice, using 15 diffusion steps per MCS with Δt = 2 s. In this way we assume one MCS takes about 30 s. At this value the cells move at approximately natural velocities and the pattern develops at a rate corresponding to experiments [26]. For these parameters, the chemoattractant diffuses more rapidly than the cells, enabling us to ignore advection as the cells push the substrate.

We implement a preferential extension of filopodia in the direction of chemoattractant gradients [16]—which drives chemotaxis—by allowing for an extra energy drop at the time of copying [27]:

$$\mathrm{\Delta }{H}_{\mathrm{chemotaxis}}=-\mu (c(\overrightarrow{x}\prime )-c(\overrightarrow{x})),$$ (6)

where x⃗′ is the neighbour into which site x⃗ copies its spin and μ = 500 and μ = 0 at cell–substrate and cell–cell interfaces, respectively. We use a value of μ = 500 to obtain sufficient chemotactic migration. In our initial simulations the cells do not adhere without chemotaxis (J_cc = 2J_cM).

Figure 1(a) shows that chemotactic aggregation alone, without cell adhesion, cannot account for growth of vascular networks. Starting from a random configuration, the ECs organize into a number of round cellular clusters instead. Intuitively we can understand this patterning as follows: initially higher cell densities will create local ‘bumps’ of chemoattractant which isotropically attract the surrounding cells. For reasons we explain below, in this simulation we use the length constraint (equation (4)) to keep the cell shapes round, but the results hold for unconstrained cells.

Figure 1.

Hypothetical mechanisms of de novo vascular development. (a) Rounded cells aggregate into isolate vascular islands. (b) Autonomously elongating virtual cells organize into a vascular network with coarsening dynamics corresponding to in vitro observations. (c) Short, steep gradients cause the cells—whose shape we do not constrain—to elongate and organize into vascular networks. (d) Strong adhesivity also causes the cells to elongate. (e) Contact-inhibition of motility drives a cell-shape-independent mechanism of vasculogenesis.

Indeed, our result resembles the famous Keller–Segel equations of chemotactic aggregation [28]. The classic Keller–Segel equations, however, ignore the cells’ finite volume and lead to ‘blow-ups,’ single points at which all cell mass concentrates. A recent paper [29] derives a Keller–Segel-type model from the Gamba–Serini PDE model of vasculogenesis [4,5] which includes a pressure term to mimic cell-volume effects, and gives the conditions under which such a pressure term prevents a blow-up. This paper provides a mathematical framework that might allow a rigorous analysis of the morphogenetic instabilities we discuss here.

Thus, our basic model apparently misses an essential biological mechanism needed for vasculogenesis. In the rest of this paper, we discuss four additional mechanisms which could result in vascular patterning. The mechanisms fall into two broad categories: those which the cell shape change drives and those which the contact-inhibition of chemotaxis drives. The two categories seem to produce different patterning instability mechanisms.

3.2. Cell shape changes

ECs dramatically change shape during angiogenesis and vasculogenesis. Are these shape changes coincidental, or are they important to the ECs’ self-organization into vascular networks?

To explore this question, we used a length constraint (equation (4)) to mimic cell elongation due to internal, cytoskeleton remodelling. Figure 1(b) shows the virtual ECs’ aggregation for cells of length about 50 lattice sites (100 μm). Elongated ECs rapidly organize into an initially fine-grained network with vascular cords enclosing lacunae. With time the pattern remodels: small lacunae collapse and large lacunae grow larger.

Alternative mechanisms can also explain the organization of ECs into network patterns. Figure 1(c) shows a simulation where the chemoattractant diffuses much more slowly than in the previous simulation, resulting in short, steep gradients. The gradients ‘trap’ the virtual ECs, which elongate as a result. These passively elongated cells also organize into networks. Strong intercellular adhesion can also result in cell elongation necessary for vascular network formation, as in figure 1(d) [23]. These two mechanisms depend on the cells’ elongated shape: when we kept the cells round (using the length constraint to keep the longest axis equal to the mean diameter) the cells organized into round, disconnected clusters similar to those in figure 1.

Elongated cells do not randomly walk like round cells. Instead they move more easily along their long axis than along their short axis (not shown). Consequently, elongated cells migrating along a curved chemotactic gradient must reorient before moving again at full speed. This orientational variation in motility gives elongated cells’ motion a longer persistence length than for rounded cells, and might explain why previous work [4,5] needed cell inertia for vascular patterning. Persistence of motion and alignment of ECs results in elongated cell clusters which may interconnect and form a percolating vascular network.

3.3. Contact-inhibition of motility

In addition to the mechanism described above, we identified a second class of mechanisms which does not depend on cell shape [30]. Blood vessel growth requires the cell-adhesion molecule, VE–cadherin [18], which clusters at EC interfaces and modulates vascular-endothelial growth-factor-A’s (VEGF-A) effect on ECs; VEGF-A is a potent growth-factor, which stimulates blood vessel sprouting. In the presence of VE–cadherin binding, VEGF-A inhibits EC motility and proliferation. In the absence of VE–cadherin binding, VEGF-A activates pathways related to actin polymerization and the cell cycle, triggering cell motility and proliferation in sub-confluent monolayers [19, 31]. Thus, we hypothesize that VE–cadherin binding at cell–cell interfaces represses the formation of chemotactic surface projections (filopodia), while filopodia normally form at unbound parts of the cell surface.

We introduce such contact-inhibition of motility in our models by setting μ = 0 (equation (6)) at cell–cell interfaces and μ = 500 at cell–substrate interfaces. This mechanism drives vascular patterning even if we use the length constraint to keep the cell shape round (figure 1(e)).

3.4. Angiogenesis

Interestingly, unlike the cell-shape-driven mechanisms we described above, contact-inhibition can also drive a mechanism reminiscent of sprouting angiogenesis, the biological mechanism by which new blood vessels sprout from existing vessels. In figure 2 we initiate our simulation with a mass of ECs, keeping all other parameters the same. After an initial ‘roughening,’ the blob’s surface digitates into a structure reminiscent of a vascular network (figure 2 and cover page), the first structure to develop both in de novo and in sprouting blood vessel growth [32]. Thus in our simulation sprouting and de novo blood vessel growth seem to be two manifestations of a single process at the level of ECs.

Figure 2.

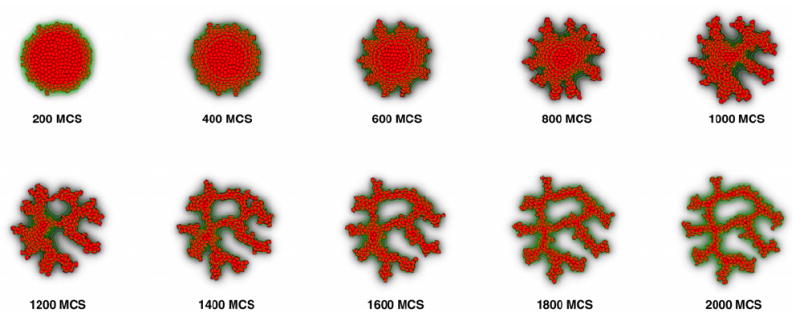
Sprouting instability in a simulation initiated with a clump of virtual ECs experiencing contact-inhibition.

These results suggest a mechanism by which contact-inhibited directed migration can drive blood vessel sprouting, which we currently understand intuitively. Near the surface of the cluster, the chemoattractant has an exponential profile: the gradient is shallow outside the cluster and becomes steeper in the interior, while it levels off at the centre. Thus, surface cells closer to the centre push inwards more strongly than other peripheral surface cells, which thus move outwards. The balance between the inward, chemotactic force and the outward force determines the direction in which surface cells move. Without contact-inhibition the interior cells also attempt to migrate inwards, thus resisting displacement by the surface cells, essentially behaving as a solid body.

4. Conclusion

In this paper we have described two classes of instability mechanisms which may be responsible for aspects of de novo and sprouting blood vessel growth. The first instability mechanism depends on cell shape: elongated cells align and form elongated blobs which interconnect to form a vascular pattern. The second mechanism needs contact-inhibition and is independent of cell-shape. Although we can verbally explain these instability mechanisms, many open questions remain. How can cell shape drive the formation of network-like patterns? Is it due to the elongated cells’ anisotropic cell diffusion and the resulting directional persistence, or is cell alignment and percolation more important? Another open problem is the correspondence between our cell-centred models and the Gamba–Serini PDE model [4, 5]. Our basic cell-centred model generates disconnected blobs (figure 1(a)), while network patterns require extra (biologically plausible) assumptions that the Gamba–Serini model seemingly does not need. What is the essential difference between the two models? Does network formation indeed depend on directional persistence [7] (as possibly dictated by cell shape [26]) or is our contact-inhibition mechanism—which suppresses chemotaxis at cell–cell interfaces but otherwise allows cells to move freely—equivalent to the pressure terms the Gamba–Serini model needs to prevent blow-up? Abstract mathematical models should help to more rigorously explain these open questions and the instability mechanisms described in this paper.