Spatial Linear Mixed Models with Covariate Measurement Errors

SUMMARY

Spatial data with covariate measurement errors have been commonly observed in public health studies. Existing work mainly concentrates on parameter estimation using Gibbs sampling, and no work has been conducted to understand and quantify the theoretical impact of ignoring measurement error on spatial data analysis in the form of the asymptotic biases in regression coefficients and variance components when measurement error is ignored. Plausible implementations, from frequentist perspectives, of maximum likelihood estimation in spatial covariate measurement error models are also elusive. In this paper, we propose a new class of linear mixed models for spatial data in the presence of covariate measurement errors. We show that the naive estimators of the regression coefficients are attenuated while the naive estimators of the variance components are inflated, if measurement error is ignored. We further develop a structural modeling approach to obtaining the maximum likelihood estimator by accounting for the measurement error. We study the large sample properties of the proposed maximum likelihood estimator, and propose an EM algorithm to draw inference. All the asymptotic properties are shown under the increasing-domain asymptotic framework. We illustrate the method by analyzing the Scottish lip cancer data, and evaluate its performance through a simulation study, all of which elucidate the importance of adjusting for covariate measurement errors.

1 Introduction

Spatial data are common in ecology, environmental health and epidemiology, where sampling units are geographical areas or spatially located individuals (Cressie (1993)). Analysis of spatial data is challenged by the spatial correlation among the observations. Mixed effects models provide a convenient framework to model the spatial correlation using random effects that are assumed to follow some spatial correlation structure, such as the conditional autoregressive (CAR) structure (Yasui and Lele (1997); Waller, et al. (1997)) or the Matèrn correlation structure (Stein (1999)). Asymptotic theory for spatial linear mixed models was established by Mardia and Marshall (1984).

Spatial data are susceptible to measurement errors in covariates. For example in ecological studies, covariates are often collected from a small survey sample in each area and sample averages are used as surrogates for the true population aggregated values, such as the percentage of smokers in a county (Xia and Carlin, 1998). Measurement errors can be substantial when the areas are small, especially in nutritional ecological studies (Prentice and Sheppard (1995)), where additional measurement errors arise due to inaccuracy in measuring nutrition intakes, such as fat intake, using conventional instruments and using 24 hour food recall. In environmental health studies, the air pollution level, e.g., PM10 or ozone, in an area is difficult to measure and is often approximated by using the distance from a polluted site or by using the measures at a few monitoring sites (Carroll, et al., 1997).

There is a vast literature on modeling measurement error for independent data. For an overview, see Carroll, Stefanski and Ruppert (1995). Several authors have considered measurement error in covariate in generalized linear mixed models for clustered data, such as longitudinal data (Wang and Davidian (1996); Wang, et al. (1998)). However, only limited work has been done in modeling measurement error in covariates for spatial data. Bernardinelli, et al. (1997) and Xia and Carlin (1998) accounted for measurement error in covariate using hierarchical models in disease mapping. These authors mainly concentrated on parameter estimation using Gibbs sampling. Little is understood about the theoretical effect of measurement error on the asymptotic biases in regression coefficients and variance components when measurement error is ignored. To our knowledge, our work is the first attempt to understand the theoretical properties of maximum likelihood estimation in spatial measurement error mixed effects models.

We first study the asymptotic bias in the naive estimator when measurement error is ignored. Our results show that ignoring measurement error results in attenuated regression coefficients and inflated variance components. We then proceed by applying the structural modeling approach to make valid maximum likelihood inference by accounting for measurement error. An EM algorithm is proposed to compute the maximum likelihood estimator. The proposed methods are illustrated through an application to the Scottish lip cancer data and their performance is evaluated through a simulation study.

2 The Spatial Linear Mixed Measurement Error Model

Suppose that the data are obtained from n geographical areas with continuous outcome variable Y_i, unobserved true covariate X_i (assumed to be a scalar), observed X_i-related covariate W_i, and other accurately observed covariates Z_i at the ith area (i = 1,…, n). Conditional on the site-specific random effects b_i that model the spatial correlation, the spatial linear mixed model of Y given X and Z can be written as

$$Y_i={\beta }_0+X_i{\beta }_x+{\mathbf{Z}}_i^T{\mathit{\beta }}_z+b_i+{\epsilon }_i,$$ (1)

where the random effect vector (b₁,…, b_n) is N{0, V(θ)} and θ is a vector of variance components, the residuals ε_i are N(0, ${\sigma }_{\epsilon }^2$), and b_i and ε_i are independent to each other and are independent of the covariates X and Z.

The covariance matrix V(θ) models the spatial correlation and admits many choices. For instance, we might parameterize the (i, j)th component of V(θ) as V_ij(θ) = θρ(||s_i − s_j||), where correlation function ρ(.) is an isotropic correlation function that decays as the Euclidean distance d_ij = ||s_i − s_j|| between two individuals increases. A widely adopted choice for this correlation function is the Matèrn function $\frac{1}{2^{\nu -1}\mathrm{\Gamma }(\nu )}{(2\eta \sqrt{\nu }d)}^{\nu }{K}_{\nu }(2\eta \sqrt{\nu }d)$, where η measures the correlation decay with the distance and ν is a smoothness parameter, Γ(·) is the conventional Gamma function and K_ν(·) is the modified Bessel function of the second kind of order ν (see, e.g. Abramowitz and Stegun (1965)). This spatial correlation model is rather general, special cases including the exponential model

$$\rho (d)=exp(-d)$$ (2)

when the smoothness parameter ν = 0.5 and the ‘decay parameter’ η = 1, and the Gaussian correlation model

$$\rho (d)=exp(-d^2)$$ (3)

corresponding to ν → ∞ and η = 1 (see, e.g., Waller and Gotway (2004), p. 279). Our theoretical development in the ensuing sections focuses on these two widely used cases of the Matèrn family.

The conditional auto-regressive (CAR) structure is also a popular choice. It has appealing theoretical properties, computational advantages and attractive interpretation (Cressie (1993)). A common CAR structure takes the form (Yasui and Lele (1997))

$$\mathbf{V}=\theta {(\mathbf{I}-\gamma \mathbf{MQ})}^{-1}\mathbf{M}=\theta {({\mathbf{M}}^{-1}-\gamma \mathbf{Q})}^{-1},$$ (4)

where Q = {q_ij} is an n × n symmetric matrix; M is an n × n diagonal matrix with diagonal elements 1/q_i+, with q_i+ = Σ_j q_ij, −1 < γ < 1 is the spatial dependence parameter that controls the amount of information in an area provided by its neighbors, and θ is a scale parameter. The quantity q_ij controls the strength of connection between areas i and j, and often takes value 0 when areas i, j are not neighbors. When area i and area j are neighbors, a common choice is q_ij = 1 to reflect equal weights from neighbor areas. Note the flexibility of the CAR structure that allows a more general neighborhood concept than geographical proximity.

In the presence of measurement error we cannot observe X directly, but see instead its error-contaminated version W. The spatial linear mixed measurement error model is completed by assuming an additive measurement error model to relate W and X as

$$W_i=X_i+U_i,$$ (5)

where U_i is the measurement error and is N(0, ${\sigma }_u^2$), independent of the unobserved covariate X_i. Note that the measurement error variance ${\sigma }_u^2$ often needs to be estimated using replicates or a validation data set.

Since the covariate X is unobserved, we use the structural modeling approach in the measurement error literature (Carroll, Ruppert and Stefanski (1995)) by assuming a parametric model for X and proceed with maximum likelihood estimation. The classical measurement error model often assumes X to be an independent and identically distributed Gaussian random variable. However since we are dealing with spatial data, it is likely that spatial correlation exists not only in the outcome variable Y, but also in the covariate X. Hence we assume a spatial linear mixed model for the unobserved covariate X,

$$X_i={\alpha }_0+{\mathbf{Z}}_i^T{\mathit{\alpha }}_z+a_i+e_i$$ (6)

where the random effect vector (a₁,…, a_n) ~ N{0,Σ(ζ)}, Σ(ζ) models the spatial correlation among the X_i, and the residuals e_i are independent N(0, ${\sigma }_e^2$). We assume the a_i and the e_i are independent of the Z_i. Let W = (W₁, W₂, …, W_n)^T, with X, Y, Z, a, b defined similarly. Note that we allow the spatial correlation structure Σ(ζ) among the X_i to be different from the spatial correlation structure V(θ) among the Y_i. In practice, since X and Y both come from the same area, it is often reasonable to assume that they share the same spatial correlation structure with possibly different parameter θ and ζ.

It follows that the likelihood of the observed data Y, W conditional on Z is

$$L(\mathbf{Y},\mathbf{W}\mid \mathbf{Z})=\int L(\mathbf{Y}\mid \mathbf{X},\mathbf{Z})L(\mathbf{W}\mid \mathbf{X},\mathbf{Z})L(\mathbf{X}\mid \mathbf{Z})d\mathbf{X}.$$

Since all the conditional distributions inside the integral are Gaussian, the joint distribution of (Y, W|Z) has the closed form,

$$\ell (\mathbf{Y},\mathbf{W}\mid \mathbf{Z})=-\frac{(2n)}{2}ln(2\pi )-\frac{1}{2}ln\mid \mathbf{\Lambda }\mid -\frac{1}{2}{\left(\begin{array}{l}\mathbf{Y}-{\mu }_y\hfill \\ \mathbf{W}-{\mu }_w\hfill \end{array}\right)}^T{\mathbf{\Lambda }}^{-1}\left(\begin{array}{l}\mathbf{Y}-{\mu }_y\hfill \\ \mathbf{W}-{\mu }_w\hfill \end{array}\right)$$ (7)

where μ_y = (β₀ + β_xα₀)1 + Z(β_xα_z + β_z), μ_w = α₀1 + Zα_z and

$$\mathbf{\Lambda }=cov(\mathbf{Y},\mathbf{W}\mid \mathbf{Z})=\left(\begin{array}{cc}{\beta }_x^2\mathbf{\sum }(\mathit{\zeta })+\mathbf{V}(\mathit{\theta })+({\beta }_x^2{\sigma }_e^2+{\sigma }_{\epsilon }^2)\mathbf{I}& {\beta }_x\{\mathbf{\sum }(\mathit{\zeta })+{\sigma }_e^2\mathbf{I}\}\\ {\beta }_x\{\mathbf{\sum }(\mathit{\zeta })+{\sigma }_e^2\mathbf{I}\}& \mathbf{\sum }(\mathit{\zeta })+({\sigma }_e^2+{\sigma }_U^2)\mathbf{I}\end{array}\right),$$

with I an n-dimensional identity matrix.

3 The Asymptotic Bias Analysis

It is of substantial interest to investigate the effect of measurement error by investigating the bias caused by ignoring measurement error, i.e., simply replacing X in model (1) by its error-prone version W. This problem, albeit common in spatial data and cautioned by many authors, is never formally addressed. Specifically, the direction and magnitude of biases in naive estimators obtained by ignoring measurement error are not well understood. The goal of this section is to study their asymptotic biases. Our asymptotic bias analysis shows that ignoring measurement error results in an attenuated regression coefficient estimator and an inflated variance component estimator.

We assume the spatial linear mixed measurement error model (1) only contains a single covariate X (no Z) with

$$\begin{array}{l}{Y}_i={\beta }_0+X_i{\beta }_x+b_i+{\epsilon }_i\\ X_i={\alpha }_0+a_i+e_i,\end{array}$$ (8)

where the distributions of b_i, ε_i, a_i, e_i are the same as those in (1) and (6). The naive estimators of (β₀, β_x, θ, ${\sigma }_{\epsilon }^2$) are obtained by simply replacing X_i with the error-prone observation W_i and fitting

$$Y_i={\beta }_{0,\text{naive}}+W_i{\beta }_{x,\text{naive}}+b_{i,\text{naive}}+{\epsilon }_{i,\text{naive}}$$ (9)

where b_i ~ N{0, V(θ_naive)} and ${\epsilon }_i\sim N(0,{\sigma }_{\epsilon ,\text{naive}}^2)$. Let 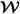= (1, W), β_naive = (β_0,naive, β_x,naive)^T, ${\mathbf{\Lambda }}_{\text{naive}}(\mathit{\vartheta })=\mathbf{V}({\theta }_{\text{naive}})+{\sigma }_{\epsilon }^2{\mathbf{I}}_n$, and ${\mathit{\vartheta }}_{\text{naive}}={({\theta }_{\text{naive}},{\sigma }_{\epsilon ,\text{naive}}^2)}^T\stackrel{\mathit{def}}{=}{({\vartheta }_1,{\vartheta }_2)}^T$. The naive estimates would be obtained by maximizing the likelihood that ignores measurement error,

$$-\frac{n}{2}log(2\pi )-\frac{1}{2}log\mid {\mathbf{\Lambda }}_{\text{naive}}\mid -\frac{1}{2}{(\mathbf{Y}-\mathcal{W}{\mathit{\beta }}_{\text{naive}})}^T{\mathbf{\Lambda }}_{\text{naive}}^{-1}(\mathbf{Y}-\mathcal{W}{\mathit{\beta }}_{\text{naive}}).$$ (10)

Specifically, they solve

$$\begin{array}{r}\frac{1}{n}{\mathcal{W}}^T{\mathbf{\Lambda }}_{\text{naive}}^{-1}(\mathbf{Y}-\mathcal{W}{\mathit{\beta }}_{\text{naive}})=0\\ \frac{1}{2n}\left[{(\mathbf{Y}-\mathcal{W}{\mathit{\beta }}_{\text{naive}})}^T\frac{\partial {\mathbf{\Lambda }}_{\text{naive}}}{{\vartheta }_j}{\mathbf{\Lambda }}_{\text{naive}}^{-1}\frac{\partial {\mathbf{\Lambda }}_{\text{naive}}}{{\vartheta }_j}(\mathbf{Y}-\mathcal{W}{\mathit{\beta }}_{\text{naive}})-\text{tr}\left({\mathbf{\Lambda }}_{\mathit{naive}}^{-1}\frac{\partial {\mathbf{\Lambda }}_{\text{naive}}}{{\vartheta }_j}\right)\right]=0.\end{array}$$ (11)

We seek the probability limits of the naive estimates as functions of the true values as n → ∞; with a slight abuse of notation, these are β_naive and ϑ_naive.

We resort to the increasing domain asymptotics framework when studying bias, as opposed to infill asymptotics. Zhang and Zimmerman (2005) compared these two frameworks and found that, for certain consistently estimable parameters of exponential covariograms, approximations corresponding to the two frameworks perform about equally well, but for those parameters that cannot be estimated consistently or are highly correlated, infill asymptotic approximation may be preferable. It is usually difficult to derive infill asymptotic properties, so the increasing domain asymptotic framework is used in this work.

Consider Λ in (10), which depends on $\mathit{\vartheta }=(\theta ,{\sigma }_{\epsilon })\stackrel{\mathit{def}}{=}({\vartheta }_1,{\vartheta }_2)$. Let Λ_i = ∂/∂ϑ_iΛ(ϑ) and Λ_ij = ∂²/∂ϑ_i∂ϑ_jΛ(ϑ), where the differentiation is element-wise for i, j = 1,2. Now let λ₁ ≤ … ≤ λ_n be the eigenvalues of Λ, and let those of Λ_i and Λ_ij be ${\lambda }_k^i$ and ${\lambda }_k^{ij}$ for k = 1,…,n, respectively, with $\mid {\lambda }_1^i\mid \le \dots \le \mid {\lambda }_n^i\mid$ and $\mid {\lambda }_1^{ij}\mid \le \dots \le \mid {\lambda }_n^{ij}\mid$ for i, j = 1, 2. We consider the following modified regularity conditions of Mardia and Marshall (1984).

• (c.1) lim sup λ_n < ∞, $limsup\mid {\lambda }_n^i\mid <\infty ,limsup\mid {\lambda }_n^{ij}\mid <\infty$, for all i, j = 1, 2.

• (c.2) $\parallel {\mathbf{\Lambda }}_i\mid {\mid }^{-2}=O(n^{-\frac{1}{2}-\delta })$ for some δ > 0 for i = 1, 2, $\parallel \mathbf{A}\parallel =\sqrt{tr({\mathbf{A}}^T\mathbf{A})}$.

• (c.3) A = (a_ij)_2×2 is invertible, where for all i, j = 1,2, a_ij = {t_ij/(t_iit_jj)^1/2} exists and t_ij = tr(Λ⁻¹Λ_iΛ⁻¹Λ_j).

• (c.4) lim( ^T )⁻¹ = 0.

These conditions ensure the growth and convergence of the information matrix from (10), which allows the usage of the general results of Sweeting (1980) to guarantee the convergence of the naive estimates. In practice, (c.1) and (c.2) are difficult to verify. However, using some basic matrix norm properties, we show in Appendix A.0 that the common geostatistical models, for example the exponential, Gaussian, and CAR models, satisfy (c.1) and (c.2). Condition (c.3) is an identifiability condition, ensuring that the variance components (ϑ₁, ϑ₂) are not linear dependent, which is satisfied in our settings. Condition (c.4) ensures that the observed covariates are not trivial and is satisfied for the measurement error models (5) and (6). Then if (c.1)–(c.4) hold, required limits exist (Sweeting (1980)) and satisfy the asymptotic equations (Harville (1977)),

$$\begin{array}{r}\underset{n\to \infty }{lim}\frac{1}{n}E\left\{{\mathcal{W}}^T{\mathbf{\Lambda }}_{\text{naive}}^{-1}(\mathbf{Y}-\mathcal{W}{\mathit{\beta }}_{\text{naive}})\right\}=0,\\ \underset{n\to \infty }{lim}\frac{1}{2n}\left[E\left\{{(\mathbf{Y}-\mathcal{W}{\mathit{\beta }}_{\text{naive}})}^T\frac{\partial {\mathbf{\Lambda }}_{\text{naive}}}{{\vartheta }_j}{\mathbf{\Lambda }}_{\text{naive}}^{-1}\frac{\partial {\mathbf{\Lambda }}_{\text{naive}}}{{\vartheta }_j}(\mathbf{Y}-\mathcal{W}{\mathit{\beta }}_{\text{naive}})\right\}-\text{tr}\left({\mathbf{\Lambda }}_{\mathit{naive}}^{-1}\frac{\partial {\mathbf{\Lambda }}_{\text{naive}}}{{\vartheta }_j}\right)\right]=0,\end{array}$$ (12)

where the expectations are taken under the true law of (Y, W) in (1) (omitting Z). In particular, we can calculate the asymptotic biases in the naive regression coefficients β_naive. The result is summarized in Theorem 1 and the proof is given in Appendix A.1 (on-line supplement), which can be found on-line at http://www.stat.sinica.edu.tw/statistica.

Theorem 1

(Asymptotic Biases in the Regression Coefficients) Under (c.1)–(c.4), the following hold, (i) The probability limit of the naive estimator β_naive is

$${\beta }_{x,\text{naive}}={\lambda }_{\ast }{\beta }_x,{\beta }_{0,\text{naive}}={\beta }_0+{\alpha }_0(1-{\lambda }_{\ast }){\beta }_x,$$ (13)

where

$${\lambda }_{\ast }=\underset{n\to \infty }{lim}\frac{\text{tr}\left[{\left\{\mathbf{V}({\theta }_{\text{naive}})+{\sigma }_{\epsilon ,\text{naive}}^2\mathbf{I}\right\}}^{-1}\{\mathbf{\sum }(\mathbf{\zeta })+{\sigma }_e^2\mathbf{I}\}\right]}{\text{tr}\left[{\left\{\mathbf{V}({\theta }_{\text{naive}})+{\sigma }_{\epsilon ,\text{naive}}^2\mathbf{I}\right\}}^{-1}\{\mathbf{\sum }(\mathbf{\zeta })+{\sigma }_e^2\mathbf{I})\}\right]+{\sigma }_u^2\text{tr}\left[{\left\{\mathbf{V}({\theta }_{\text{naive}})+{\sigma }_{\epsilon ,\text{naive}}^2\mathbf{I}\right\}}^{-1}\right]},$$ (14)

and hence 0 ≤ λ_* ≤ 1.

(ii) If Y and X have the same spatial covariance structure with different scale parameters,

$$\mathbf{V}(\mathbf{\theta })=\theta \mathbf{R},\mathbf{\sum }(\mathbf{\zeta })={\sigma }_{\mathrm{\sum }}^2\mathbf{R},$$ (15)

where R is a known matrix, then λ_* in (14) is

$${\lambda }_{\ast }=\underset{n\to \infty }{lim}\frac{{\sum }_{l=1}^n({\delta }_l{\sigma }_e^2+{\sigma }_{\mathrm{\sum }}^2)/({\delta }_l{\sigma }_{\epsilon ,\text{naive}}^2+{\theta }_{\text{naive}})}{{\sum }_{l=1}^n\{{\delta }_l({\sigma }_e^2+{\sigma }_u^2)+{\sigma }_{\mathrm{\sum }}^2\}/({\delta }_l{\sigma }_{\epsilon ,\text{naive}}^2+{\theta }_{\text{naive}})},$$ (16)

where {δ_l} are the eigenvalues of R⁻¹.

(iii) For regular (square) grid data and the conditional auto-regressive spatial correlation structure (4) defined using the adjacent neighborhood spatial correlation structure of Breslow and Clayton (1993),

$${\lambda }_{\ast }\ge \frac{{\sigma }_{\mathrm{\sum }}^2+{\sigma }_e^2(4+4\gamma )}{{\sigma }_{\mathrm{\sum }}^2+({\sigma }_e^2+{\sigma }_u^2)(4+4\gamma )};$$ (17)

for regular grid data and an exponential or Gaussian spatial correlation structure,

$$0\le {\lambda }_{\ast }\le 1-\frac{{\sigma }_u^2}{{\sigma }_u^2+{\sigma }_e^2+4{\sigma }_{\mathrm{\sum }}^2/{(1-e^{-1/\sqrt{2}})}^2}.$$ (18)

The results in Theorem 1 show that ignoring the measurement error causes the regression coefficient estimates to be attenuated. Calculations of the attenuation factor λ_* can be quite complicated in general. Therefore the results in (ii) are particularly useful for numerically computing λ_*, since it avoids the inversion of large matrices. Note that the eigenvalues therein do not depend on data if the spatial dependence parameter γ is known. For grid data, exponential and Gaussian correlation structures are often used. In these cases, (iii) provides a bound of the attenuation factor that can be easily computed.

We state in Theorem 2 the asymptotic bias in the naive variance component ϑ_naive; the proof is given in Appendix A.2 (on-line supplement).

Theorem 2

(Asymptotic Biases in Variance Components) Suppose Y and X have the same spatial covariance structure with different scale parameters as at (15). Under (c.1)–(c.4), the asymptotic limits of the naive estimators of the spatial variance component and the residual variance satisfy,

$${\theta }_{\text{naive}}=\theta +{(1-{\lambda }_{\ast })}^2{\sigma }_{\mathrm{\sum }}^2{\beta }_x^2,{\sigma }_{\epsilon ,\text{naive}}^2={\sigma }_{\epsilon }^2+\{{(1-{\lambda }_{\ast })}^2{\sigma }_e^2+{\lambda }_{\ast }^2{\sigma }_U^2\}{\beta }_x^2,$$ (19)

where λ_* is defined in (16).

Theorem 2 shows that when Y and X possess the same spatial covariance structure, a reasonable assumption in practice since they come from the same spatial area, the naive estimators of the spatial variance component and the residual variance both overestimate the corresponding true values. For more general cases when the spatial covariance structure of Y and X differ, the asymptotic limits of the naive estimators are difficult to calculate, and no analytic expressions are available.

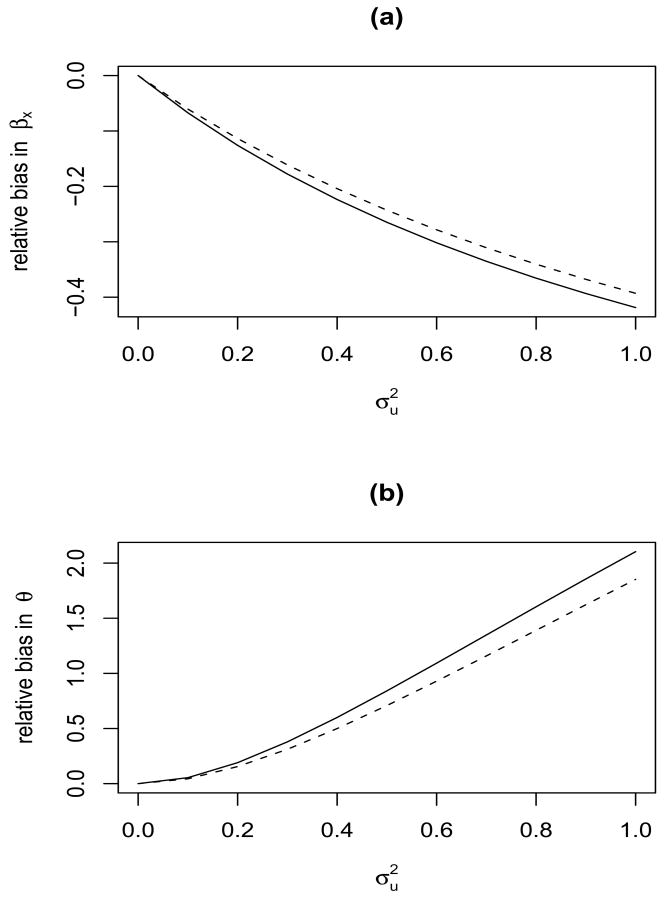
The asymptotic relative biases in the naive estimators of the regression coefficients and the variance components, assuming the adjacent neighborhood spatial correlation structure is illustrated in Figure 1. Since the computation of λ_* involves n → ∞, we approximate λ_* with n = 1024 on a 32 × 32 lattice. The spatial dependence parameter γ in (4) are taken as γ = 0.2 and γ = 0.95. The regression coefficient is β_x = .5, variance components are θ = 1 and ${\sigma }_{\epsilon }^2=.3$. The parameters in the X models are α₀ = 1.4, ${\sigma }_{\mathrm{\sum }}^2=1.2$, and ${\sigma }_e^2=.5$. We iteratively calculate λ_* using (16) and (19). In our experience, convergence is often achieved within 5 iterations. Then we obtain the expected naive estimates from (13) and (19). The bias curves for the naive estimates of β_x and θ are plotted as a function of the measurement error variance ${\sigma }_u^2$. It should be noted that the bias curves in fact correspond to the finite sample exact bias.

Figure 1.

Asymptotic relative biases in the naive estimates of β_x and θ. The CAR spatial covariance structure with spatial dependence parameter γ = 0.2 and 0.95 was used. The true parameter values were β_x =.5, θ = 1, ${\sigma }_{\epsilon }^2=0.5,{\sigma }_{\mathrm{\sum }}^2=1.2,{\sigma }_e^2=.5$. Variance of measurement error ${\sigma }_u^2$ varied between 0 and 1.0. The two curves in each plot correspond to the spatial dependence parameter γ: ——— γ = 0.2; - - - γ = 0.95.

Figure 1 shows that the naive estimate of the regression coefficient β_x is attenuated, while the naive estimate of the variance component θ is inflated. The biases increase with the measurement error variance ${\sigma }_u^2$, but decrease with the spatial dependence parameter γ. The reason for the latter phenomenon is explained by the fact that stronger dependence implies that neighbor areas can provide more information, and hence the estimates are more resistant to the effect of measurement error.

4 Maximum Likelihood Estimation

We consider the large sample results for the maximum likelihood estimator for the spatial linear mixed measurement error models (1), (5) and (6). In particular, we show for some commonly used spatial models, the MLEs are consistent and asymptotically normal. To proceed, we assume mild regularity conditions on the parameter space and the observed covariate Z.

• (d.1) The unknown parameters Ω in (1), (5) and (6) lie in a compact set of an Euclidean space.

• (d.2) Let Z̃ = (1, Z), where 1 is an n × 1 vector of 1’s. Assume lim n⁻¹Z̃^TZ̃ = Z₀ in probability, where Z₀ is a positive definite matrix.

It follows that, for the common geostatistical models, such as the exponential, Gaussian and CAR models, the maximum likelihood estimator is consistent and asymptotically normal, as summarized in the following theorem. The proof is deferred to Appendix A.3 (on-line supplement).

Theorem 3

(Consistency and Asymptotic Normality of MLEs) Let Ω₀ be the true unknown parameters in (1), (5) and (6) and Ω̂ be its maximum likelihood estimator. Suppose that Y and X have the exponential, Gaussian or CAR [eq. (4)] spatial covariance structure on regular grid. Then, under (d.1) and (d.2), Ω̂ is consistent and Γ^1/2(Ω̂ − Ω₀) → N(0, I_p) in distribution, where Γ^1/2 is the Cholesky decomposition of $\mathbf{\Gamma }\stackrel{\mathit{def}}{=}{E}_{{\mathbf{\Omega }}_0}\{-{\partial }^2\ell /\partial \mathbf{\Omega }\partial {\mathbf{\Omega }}^T\}$, Ω₀ is the truth, ℓ is as defined in (7), and I_p is the identity matrix of dimension of p, the dimension of Ω₀

Theorem 3 does not require X and Y to have the same correlation structure, but, since X and Y both come from the same area, it may be reasonable to assume that they do. In such a situation we propose an EM algorithm to compute the MLEs; in particular, we assume the spatial covariance structures of the random effects b and a take the same form (15) with different scale parameters. The EM algorithm for a general spatial covariance structure is similar. The complete data are (Y, W, X, Z, b, a), where (Y, W, Z) are observed data and X, b, and a are missing data. The complete data loglikelihood is

$$\begin{array}{l}\ell (\mathbf{Y},\mathbf{W},\mathbf{X},\mathbf{b},\mathbf{a}\mid \mathbf{Z})=-\frac{n}{2}log({\sigma }_{\epsilon }^2)-\frac{1}{2{\sigma }_{\epsilon }^2}\parallel \mathbf{Y}-{\beta }_0\mathbf{1}-{\beta }_x\mathbf{X}-\mathbf{Z}{\mathit{\beta }}_z-\mathbf{b}\mid {\mid }^2\\ -\frac{n}{2}log(\theta )-\frac{1}{2\theta }{\mathbf{b}}^T{\mathbf{R}}^{-1}\mathbf{b}-\frac{n}{2}log({\sigma }_u^2)-\frac{1}{2{\sigma }_u^2}\parallel \mathbf{W}-\mathbf{X}\mid {\mid }^2\\ -\frac{n}{2}log({\sigma }_e^2)-\frac{1}{2{\sigma }_e^2}\parallel \mathbf{X}-{\alpha }_0\mathbf{1}-\mathbf{Z}{\mathit{\alpha }}_z-\mathbf{a}\mid {\mid }^2-\frac{n}{2}log({\sigma }_{\mathrm{\sum }}^2)-\frac{1}{2{\sigma }_{\mathrm{\sum }}^2}{\mathbf{a}}^T{\mathbf{R}}^{-1}\mathbf{a},\end{array}$$

where || · || denotes the square norm.

Let X̃ = (1, X, Z), Z̃ = (1, Z), $\mathit{\beta }={({\beta }_0,{\beta }_x,{\mathit{\beta }}_z^T)}^T$, and $\mathit{\alpha }={({\alpha }_0,{\mathit{\alpha }}_z^T)}^T$. At the (t + l)th step, let the estimator of β be β̂^(t+1) and the estimator of α be α^(t+1), and define the variance component estimates similarly. In the M step, we update the regression coefficients

$$\begin{array}{l}{\widehat{\mathit{\beta }}}^{(t+1)}=E{({\stackrel{\sim }{\mathbf{X}}}^T\stackrel{\sim }{\mathbf{X}}\mid \mathbf{Y},\mathbf{W},\mathbf{Z},{\widehat{\xi }}^{(t)})}^{-1}E({\stackrel{\sim }{\mathbf{X}}}^T(\mathbf{Y}-\mathbf{b})\mid \mathbf{Y},\mathbf{W},\mathbf{Z},{\widehat{\xi }}^{(t)})\\ {\widehat{\mathit{\alpha }}}^{(t+1)}={({\stackrel{\sim }{\mathbf{Z}}}^T\stackrel{\sim }{\mathbf{Z}})}^{-1}{\stackrel{\sim }{\mathbf{Z}}}^{T}E(\mathbf{X}-\mathbf{a}\mid \mathbf{Y},\mathbf{W},\mathbf{Z},{\widehat{\xi }}^{(t)}),\end{array}$$

where E(·|Y, W, Z,ξ̂^(t)) is the expectation conditional on the observed data (Y, W) with all parameters taking the values of the current estimates ξ̂^(t) We update the variance components by

$$\begin{array}{l}{\widehat{\theta }}^{(t+1)}=\frac{1}{n}E({\mathbf{b}}^T{\mathbf{R}}^{-1}\mathbf{b}\mid \mathbf{Y},\mathbf{W},\mathbf{Z},{\widehat{\xi }}^{(t)}),\\ {\widehat{\sigma }}_{\epsilon }^{2(t+1)}=\frac{1}{n}E(\parallel \mathbf{Y}-{\widehat{\beta }}_x^{(t+1)}\mathbf{X}-\mathbf{Z}{\widehat{\mathit{\beta }}}_z^{(t+1)}-\mathbf{b}\mid {\mid }^2\mid \mathbf{Y},\mathbf{W},\mathbf{Z},{\widehat{\xi }}^{(t)}),\\ {\widehat{\sigma }}_{\mathrm{\sum }}^{2(t+1)}=\frac{1}{n}E({\mathbf{a}}^T{\mathbf{R}}^{-1}\mathbf{a}\mid \mathbf{Y},\mathbf{W},\mathbf{Z},{\widehat{\xi }}^{(t)}),\\ {\widehat{\sigma }}_e^{2(t+1)}=\frac{1}{n}E(\parallel \mathbf{X}-{{\widehat{\alpha }}_0}^{(t+1)}\mathbf{1}-\mathbf{Z}{\mathit{\alpha }}_z^{(t+1)}-\mathbf{a}\mid {\mid }^2\mid \mathbf{Y},\mathbf{W},\mathbf{Z},{\widehat{\xi }}^{(t)}).\end{array}$$

In the E step, we compute the conditional expectations that appeared in the above equations. The closed-form expressions of these conditional expressions are derived and can be found in Appendix A.4 (on-line supplement). These steps can be easily implemented since all the quantities involved have closed form and no numerical integration is needed. Finally, the standard errors of the maximum likelihood estimates can be obtained by inverting the Fisher information matrix.

5 Simulation Study

Our simulation study aims at evaluating the finite sample performance of the naive estimates obtained by ignoring the measurement error and the maximum likelihood estimates obtained by accounting for the measurement error. We took the data to be on a regular grid. We considered the Y model (1) with a single covariate X. We assumed the adjacent neighborhood CAR spatial correlation structure (4) for both the random effects {b_i} and {a_i} in the Y and X models, neighbors being defined as the four adjacent areas for each location except for those on the edge. The weight q_ij was set to be 1 if areas i and j are neighbors and 0 otherwise. The spatial dependence parameter was γ = 0.95, mimicking what was obtained in the data example in the next section. The unobserved covariate X was generated under model (6) with mean 1.4 and variance components 1.2 and 0.3, respectively for the spatial covariance and residual error term. The observed error-contaminated version W was generated by adding Gaussian noise with variance ${\sigma }_u^2=0.50$ to X. To generate the outcome variable Y, the regression coefficients were taken as (β₀, β_x)^T = (0.0,2.0)^T, and the variance components for the spatial covariance and residual error term were taken as 1.0 and 0.5. For each generated data set, we computed the naive estimates that ignored the measurement error and the maximum likelihood estimates that accounted for the measurement error using the EM algorithm. We varied the grid size to be 7(n = 7 × 7), 10(n = 10 × 10) and 20(n = 20 × 20). The averages and variances of the estimates from 500 replications are given in Table 1.

Table 1.

Results of a simulation study from 500 replications under the CAR model. A regular 20 × 20 grid design and an adjacent neighborhood covariance structure with γ = 0.95 were used. The true parameters were β₀ = 0, β_x = 0.5, $\theta =1{\sigma }_{\epsilon }^2=0.3,{\sigma }_{\mathrm{\sum }}^2=1.2,{\sigma }_e^2=0.5$ and α₀ = 1.4. The measurement error variance was ${\sigma }_u^2=0.5$. Inside the brackets are estimated standard errors

Sample Size	Parameter	Mean of naive est	model based Var. of naive est	MSE	Mean of MLE	model based Var. of MLE	MSE
49	β0	0.221	0.095 (0.161)	0.200	−0.045	0.150 (0.210)	0.210
	βx	0.326	0.011 (0.012)	0.040	0.513	0.030 (0.043)	0.043
	θ	1.141	0.355 (0.383)	0.401	1.041	0.283 (0.367)	0.368
	${\sigma }_{\epsilon }^2$	0.461	0.054(0.063)	0.090	0.374	0.045 (0.056)	0.061
100	β0	0.261	0.062(0.072)	0.14	−0.042	0.079 (0.090)	0.09
	βx	0.323	0.005 (0.005)	0.036	0.507	0.0157 (0.0157)	0.016
	θ	1.066	0.222 (0.265)	0.269	0.957	0.209 (0.239)	0.240
	${\sigma }_{\epsilon }^2$	0.399	0.0268 (0.033)	0.043	0.326	0.0312 (0.029)	0.030
400	β0	0.247	0.0160 (0.0154)	0.076	0.0032	0.020 (0.022)	0.022
	βx	0.318	0.0012 (0.0012)	0.034	0.503	0.0035(0.0035)	0.0035
	θ	1.015	0.067 (0.073)	0.073	0.989	0.062 (0.072)	0.072
	${\sigma }_{\epsilon }^2$	0.376	0.0068 (0.0069)	0.012	0.304	0.0068 (0.0072)	0.0072

We next examined the performance of the MLE when the spatial correlation structure was specified to be the exponential model as well as the Gaussian model. The locations of subjects were sampled uniformly over region [0, $\sqrt{n}$]², where n is the number of subjects. We set n = 49,100,400 in our simulations. The results are documented in Tables 2 and 3.

Table 2.

Results of a simulation study from 500 replications under the Gaussian model. The locations of subjects were sampled uniformly over the region [0, $\sqrt{n}$]², where n is the number of subjects. The true parameters were β₀ = 0, β_x = 0.5, $\theta =1{\sigma }_{\epsilon }^2=0.3,{\sigma }_{\mathrm{\sum }}^2=1.2,{\sigma }_e^2=0.5$ and α₀ = 1.4. The measurement error variance was ${\sigma }_u^2=0.5$. Inside the brackets are estimated standard errors

Sample Size	Parameter	Mean of naive est	model based Var. of naive est	MSE	Mean of MLE	model based Var. of MLE	MSE
49	β0	0.276	0.107 (0.110)	0.186	−0.038	0.136 (0.191)	0.192
	βx	0.320	0.010 (0.012)	0.044	0.532	0.031 (0.038)	0.039
	θ	1.076	0.168 (0.180)	0.185	0.970	0.150 (0.156)	0.156
	${\sigma }_{\epsilon }^2$	0.365	0.019 (0.018)	0.022	0.300	0.020 (0.021)	0.021
100	β0	0.218	0.043 (0.041)	0.119	−0.022	0.055 (0.057)	0.057
	βx	0.338	0.0057 (0.0056)	0.032	0.512	0.0128 (0.0134)	0.013
	θ	1.049	0.077(0.078)	0.081	0.982	0.071 (0.066)	0.066
	${\sigma }_{\epsilon }^2$	0.373	0.0153 (0.0158)	0.0211	0.298	0.0150 (0.0150)	0.0150
400	β0	0.176	0.0076 (0.0084)	0.039	0.034	0.009 (0.006)	0.006
	βx	0.369	0.0015 (0.0018)	0.0189	0.498	0.002 (0.002)	0.002
	θ	1.027	0.026 (0.022)	0.022	1.019	0.023 (0.024)	0.024
	${\sigma }_{\epsilon }^2$	0.386	0.013 (0.014)	0.021	0.303	0.0108 (0.0108)	0.011

Table 3.

Results of a simulation study from 500 replications under the exponential model. The locations of subjects were sampled uniformly over the region [0, $\sqrt{n}$]², where n is the number of subjects. The true parameters were β₀ = 0, β_x = 0.5, $\theta =1{\sigma }_{\epsilon }^2=0.3,{\sigma }_{\mathrm{\sum }}^2=1.2,{\sigma }_e^2=0.5$ and α₀ = 1.4. The measurement error variance ${\sigma }_u^2=0.5$. Inside the brackets are estimated standard errors

Sample Size	Para meter	Mean of naive est	model based Var. of naive est	MSE	Mean of MLE	model based Var. of MLE	MSE
49	β0	0.223	0.145 (0.179)	0.228	−0.030	0.187 (0.239)	0.239
	βx	0.339	0.010 (0.012)	0.038	0.528	0.0270 (0.0323)	0.033
	θ	1.079	0.220 (0.268)	0.274	0.966	0.191 (0.235)	0.236
	${\sigma }_{\epsilon }^2$	0.408	0.0535 (0.0670)	0.079	0.364	0.052 (0.063)	0.067
100	β0	0.216	0.062 (0.073)	0.108	−0.021	0.071 (0.079)	0.079
	βx	0.350	0.0057 (0.0058)	0.028	0.509	0.012 (0.013)	0.013
	θ	1.037	0.114 (0.130)	0.131	0.982	0.113 (0.134)	0.134
	${\sigma }_{\epsilon }^2$	0.399	0.037 (0.042)	0.038	0.314	0.036 (0.037)	0.037
400	β0	0.168	0.009 (0.010)	0.038	−0.002	0.011 (0.011)	0.011
	βx	0.374	0.0015 (0.0015)	0.017	0.495	0.0026 (0.0026)	0.0026
	θ	1.037	0.040 (0.030)	0.031	1.010	0.037 (0.045)	0.045
	${\sigma }_{\epsilon }^2$	0.387	0.022 (0.014)	0.021	0.298	0.020 (0.024)	0.024

All the results (Tables 1–3) show that the naive estimate of β_x is attenuated while the naive estimates for θ and ${\sigma }_{\epsilon }^2$ are inflated, agreeing with our asymptotic bias analysis. The maximum likelihood estimates computed using the EM algorithm, on the other hand, performed very well. The mean of the estimates of the regression coefficients and the variance components were very close to the corresponding true values. As expected, there was a bias-variance tradeoff. The MLEs effectively eliminated the biases in the naive estimators but had larger variances. As an overall measure of performance using the MSE, the MLEs had smaller MSEs than the naive estimators. The MSE gain was more apparent as n increased.

Finally, to compare the empirical results with our theoretical asymptotic bias analysis results, we computed the theoretical values of the naive estimate using the results in Theorems 1 and 2. For example, under the CAR model with γ = 0.95, these values were 0.254, 0.318, 1.039, 0.367 for β₀, β_x, θ and ${\sigma }_{\epsilon }^2$, compared with 0.247, 0.318, 1.027, 0.376 of the average naive estimates based on 500 simulations for grid size 20 (n=400) (see Table 1). Hence, our theoretical values do match with our simulation results.

6 Analysis of Scottish Lip Cancer Incidence Data

The Scottish lip cancer incidence data were collected in each of the 56 counties of Scotland (Breslow and Clayton (1993)). For each county, the number of lip cancer cases among males from 1975–1980 and the percentage of AFF employment in all employed population were reported. Earlier analysis found that the rates were higher in counties with higher proportion of the population employed in agriculture, forestry, and fishing (AFF) – the professions that require working outdoors. This observation reflects the biological plausible causal relationship between ultraviolet rays and lip cancer. Breslow and Clayton (1993) applied spatial mixed models to study the association between the percentage of the AFF employment and the lip cancer incidence. However the exposure of main interest is the exposure to sunlight, a known risk factor for lip cancer. The AFF employment variable serves as a surrogate for the degree of exposure to sunlight. Since we mainly focused on the association between lip cancer and the exposure to sunlight, we need to account for the measurement error in using the AFF employment variable to measure the degree of exposure to sunlight.

Breslow and Clayton (1993) modeled the standardized morbidity ratios calculated by dividing the observed number of cancer cases by the age-adjusted expected cancer cases using a Poisson regression model. To apply our methodology, we first took a square root transformation of the observed SMR; the transformed SMR approximated a normal distribution well, which was verified using the Shapiro-Wilks test. We applied the spatial linear mixed measurement error model to account for the measurement error.

Following Breslow and Clayton (1993), we assumed the adjacent neighborhood spatial correlation structure for the square-root transformed SMR. These authors also noted that the covariate, the percentage of the AFF employment, exhibited the same spatial aggregation as the SMR. We hence assumed the same spatial correlation structure with a different scale parameter for the AFF variable.

The analysis results are given in Table 4. The naive analysis showed a strong effect of the AFF employment on the SMR (β_x = 0.139 and SE=0.091), and the spatial correlation seemed to dominate in the total variation (θ̂ = 0.310, ${\widehat{\sigma }}_{\epsilon }^2=0.0389$). We next considered the spatial linear mixed measurement error model to account for the measurement error in the AFF employment. Since no validation data set was available, the measurement error variance ${\sigma }_u^2$ could not be estimated directly from the data. We fit a linear random intercept CAR model on W. This allowed us to estimate the sum of ${\sigma }_e^2$ and ${\sigma }_u^2$ as 0.041. We then did sensitivity analysis by varying ${\sigma }_u^2$ from 0.0, naive analysis, to moderate measurement error, ${\sigma }_u^2=0.020$, to severe measurement error, ${\sigma }_u^2=0.035$. The estimates of the dependence parameter γ were 0.922 when ${\sigma }_u^2=0$, 0.928 when ${\sigma }_u^2=0.02$ and 0.932 when ${\sigma }_u^2=0.035$, all of which were close to the estimate of 0.93 obtained by Yasui and LeLe (1997), and indicated a strong spatial dependence. Second, all the analyses indicated that working outdoors was associated with the risk of lip cancer. Third, ignoring measurement error did attenuate the regression coefficient estimates. As ${\sigma }_u^2$ increased, the estimates of the regression coefficients became larger. For example, the estimate of the coefficient of ‘AFT’, with estimated standard error in brackets, increased from 0.132 (0.093) when ${\sigma }_u^2=0$, to 0.153 (0.099) when ${\sigma }_u^2=0.02$, and to 0.172 (0.104) when ${\sigma }_u^2=0.035$, while the variance component for the spatial correlation part was estimated as 0.434 (0.245) when ${\sigma }_u^2=0$, 0.414(0.234) when ${\sigma }_u^2=0.02$, and 0.394 (0.228) when ${\sigma }_u^2=0.035$. These results indicated that that accounting for measurement error increased the magnitude of the estimated effects of ‘AFT’ while it decreased the overestimation of the spatial variance component.

Table 4.

Sensitivity analysis of Scottish Lip Cancer Incidence Data: Outcome variable is the square root of SMR; the covariate is AFF/10. The measurement error variance varied between 0 (naive), 0.02 (moderate) and 0.035 (severe)

Estimate ± standard error
Parameter	naive	moderate	severe
	${\sigma }_u^2=0.0$	${\sigma }_u^2=0.02$	${\sigma }_u^2=0.035$
γ	0.922 ± 0.072	0.928 ± 0.044	0.932 ± 0.043
β0	0.939 ± 0.164	0.923 ± 0.168	0.908 ± 0.171
βx	0.132 ± 0.093	0.153 ± 0.099	0.172 ± 0.104
θ	0.434 ± 0.245	0.414 ± 0.234	0.394 ± 0.228
${\sigma }_{\epsilon }^2$	0.017 ± 0.045	0.021 ± 0.044	0.024 ± 0.044
${\sigma }_{\mathrm{\sum }}^2$		1.258 ± 0.258	1.183 ± 0.256
${\sigma }_e^2$		0.0001 ± 0.0005	0.0001 ± 0.0003
α0		0.8033 ± 0.258	0.8030 ± 0.258

7 Discussion

In this paper we have proposed spatial linear mixed measurement error models to account for covariate measurement error and spatial correlation in spatial data. Our asymptotic bias analysis shows that, by ignoring the measurement error, the naive estimators of the regression coefficients are attenuated and the naive estimators of the variance components are inflated. We give formulae for calculating these biases for a general case, and provide simplified forms or bounds for some commonly-used spatial correlation structures. Our numerical calculation also shows that the biases are related to the spatial dependence parameter γ for an adjacent neighborhood structure.

We have developed a structural modeling approach to accounting for the covariate measurement error in spatial data, where spatial linear mixed models are assumed for both the outcome and the unobserved covariate, and an additive model is assumed for the observed error-prone covariate. An EM algorithm is developed to compute the maximum likelihood estimate. Our simulation study shows that the maximum likelihood estimator works well in finite samples and appropriately corrects for the bias in the naive estimator. We find that the maximum likelihood estimators correct the biases in naive estimators, but are associated with larger variances.

On the computational side, our algorithm requires operations of matrices of large size, including inversion of large matrices. We alleviate the computational burden by diagonalizing the matrices simultaneously. Since the sizes of the matrices involved increase rapidly with the grid size of the spatial areas, many operations on these matrices are needed in each EM iteration. These cause problems in handling large data sets with the EM algorithm. Here it might be more convenient to adopt an MCMC algorithm, especially if one uses the conditional autoregressive spatial covariance structure.

Ou structural modeling approach, where a parametric model is assumed for the unobserved covariate X, might be sensitive to misspecification of the distribution of X. An alternative estimation in the measurement error literature is functional modeling, such as SIMEX (Carroll, et al. (1995)), which makes no distributional assumption on X. However it can be less efficient than the MLE when the distribution of X is correctly specified. It is of interest in future research to compare these two approaches in terms of their robustness and efficiency.

We have concentrated in this paper on Gaussian spatial outcomes. Work is underway to extend the results to non-Gaussian spatial outcomes, with measurement error in the covariate, within the framework of spatial generalized linear mixed models (e.g. Diggle et al. (1998)).