Quantification of Hormesis in Anticancer-Agent Dose-Responses

Abstract

Quantitative features of dose responses were analyzed for 2,189 candidate anticancer agents in 13 strains of yeast (Saccharomyces cerevisiae). The agents represent a diverse class of chemical compounds including mustards, other alkylating agents, and antimetabolites, inter alia. Previous analyses have shown that the responses below the toxic threshold were stimulatory and poorly predicted by a threshold dose-response model, while better explained by a hormetic dose-response model. We determined the quantitative features of the hormetic concentration-responses (n = 4,548) using previously published entry and evaluative criteria. The quantitative features that are described are: (1) the width of the concentration range showing stimulation above 10% of the control (mean of 5-fold), (2) the maximum stimulation of the concentration-responses (mean of 27% above the control), and (3) the width from the maximum stimulation to the toxicological threshold (mean of 3.7-fold). These results show that 52.5% of the 2,189 chemicals evaluated display hormetic concentration-responses in at least one of the 13 yeast strains. Many chemicals showed hormesis in multiple strains, and 24 agents showed hormesis in all 13 strains. The data are compared to previously reported quantitative features of hormesis based on published literature.

INTRODUCTION

This study presents an analysis of the concentration-response relationships of 2,189 candidate anticancer compounds evaluated by the National Cancer Institute (NCI) in its Yeast Anticancer Drug Screen (Holbeck 2004; Holbeck and Simon 2007). These compounds were tested on a panel of 13 yeast strains, each having one or two mutations affecting damage-response functions (DNA damage repair or cell cycle control) homologous to those mutated in human cancers. Previous analyses of these NCI data have shown that responses below the toxic threshold were poorly predicted by the threshold model, yet highly consistent with a hormetic, inverted U-shaped concentration-response model (Calabrese et al. 2006a, 2008). The initial studies evaluated the individual responses of concentrations and their replication below estimated Benchmark Doses (BMDs) but they did not explore the individual concentration-response relationships or the magnitude of stimulation with respect to hormesis. This presentation extends the initial reports by addressing each of these limitations.

Hormesis is a dose-response relationship that represents either overcompensation to a disruption in homeostasis or a direct stimulatory response (Calabrese and Baldwin 2002). The quantitative features of both of these types of hormetic responses are similar, with the magnitude of the maximum stimulatory response typically being 30–60% greater than controls, the width of the stimulatory or hormetic zone averaging approximately 10-fold, and the interval from the zero equivalent point to the maximum stimulation averaging 4–5-fold (see Figure 1; Calabrese and Baldwin 1997; Calabrese and Blain 2005).

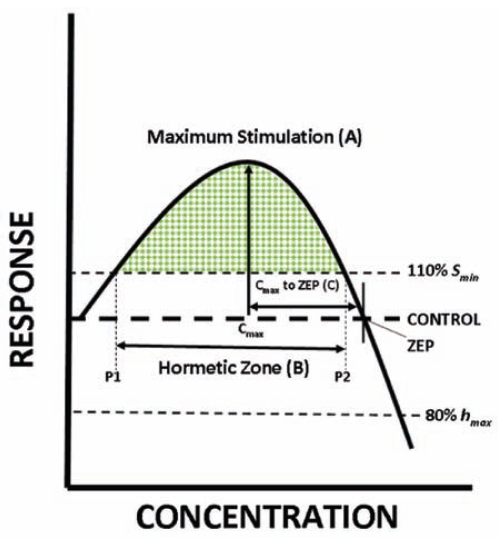
FIGURE 1.

Parameters of the hormetic concentration-response curves (shaded region). (A) The maximum stimulatory response. (B) The width of the stimulatory response calculated from the lowest (P1) to the highest (P2) concentration showing a response that is 110% of the control response. (C) Distance from the concentration of the maximum stimulatory response (C_max) to the highest concentration with a response equal to the control, the zero equivalent point (ZEP) [after Calabrese and Baldwin, 2003]. In order for a concentration-response to be evaluated it had to have a response in the low-concentration region ≥110% (S_min) and a response at a higher concentration ≤ 80% (h_max) of the control.

The work presented here extends the findings of Calabrese et al. (2006a, 2008) by evaluating the quantitative features of the hormetic concentration-responses in the NCI Yeast Anticancer Drug Screen database. The individual hormetic concentration-responses in this paper were quantified by measuring the width of the hormetic zone, the interval from the maximum stimulatory concentration to the zero equivalent point, and the amplitude of the maximum stimulation. These data were then compared to quantitative features of previously described hormetic dose-responses in other biological model systems following exposure to chemicals or radiation (Calabrese and Blain 2005).

This paper represents the first work that focuses entirely on quantitative features of hormetic responses in a single large-scale study (e.g., the NCI Yeast Anticancer Drug Screen). It thus complements and extends previous analyses that quantitatively described dose-response relationships in published literature (Calabrese and Blain 2005). This analysis has the advantage of exploring 28,457 concentration-responses that were derived from identical experiments conducted in the same laboratory.

METHODS

NCI Laboratory Methods

The NCI data that are used in this evaluation are from the “Stage 2” Yeast Anticancer Drug Screen (YACDS) and are available to the public on the Internet (http://dtp.nci.nih.gov/yacds/download.html). The data set has been described by Holbeck (2004) and by Holbeck and Simon (2007). Our use of the database for the study of hormesis is consistent with the methods of Calabrese et al. (2006a, 2008). This analysis includes 2,189 agents that were tested at five concentrations (1.2, 3.7, 11, 33, and 100 μM) in 13 genetically different yeast strains. Most of the strains harbor one or two mutations in genes involved in DNA damage repair (mgt1, mlh1, rad14, rad18, rad50, rad52 or sgs1) or cell cycle control (bub3, CLN2oe or mec2). Descriptions of the genotypes are on the NCI website [http://dtp.nci.nih.gov/yacds/exp_design.html]. This group of genetically altered Saccharomyces cerevisiae strains is collectively referred to as the yeast panel and it represents 11 strains with genetic alterations and two “wild-type” strains. The latter, designated wt and SPY50780, are not classically defined wild types but are wild type with respect to the DNA damage and cell cycle control genes in the other 11 strains.

The available data are derived from the fraction of growth of the yeast strain exposed to the chemical relative to the growth of the same strain in a solvent control (i.e., DMSO). Yeast in the exponential phase of growth were inoculated into synthetic medium containing 2% glucose that included the chemical agent. The initial cell density was 10⁴ cells per well containing 200μl of medium.

In the replication procedure each of the 2,189 chemicals was tested four times at the same five concentrations in each of the 13 strains. Each 96-well plate contained 80 chemicals at the same concentration (either 1.2, 3.7, 11, 33 or 100 μM) with the outer wells serving as controls. Plates for the five concentrations of each chemical were incubated over the same 12-hour period. The 16 control wells included four unexposed controls, eight solvent controls, and four controls using cycloheximide. The assay was considered invalid if there was growth in the presence of cycloheximide as all strains were cycloheximide sensitive.

The available data consist of a ratio of the optical density (OD) at 600 nm of a single response well for the treatment divided by the mean of the eight OD₆₀₀ readings of the solvent control wells for each concentration. This process was repeated on a second day, and the ratios from the two days were averaged to yield what this paper refers to as a replication response. Two replication responses were produced for each of the 28,457 experiments, and the data on the NCI website provide the average of the two replications and the difference between the two values. The original OD values are not available (see: Calabrese et al. 2006a) the absolute value of the difference in response between the replications was provided by the NCI. The replicate values at each concentration were derived as described by Calabrese et al. (2006a, 2008).

Selection of Hormetic Concentration-responses

A concentration-response in this study is defined as the response of a single yeast genotype to a single chemical (referred to as an NSC agent by the NCI) evaluated over 5 concentrations (1.2, 3.7, 11, 33, and 100 μM). Hormetic concentration-responses were selected using a priori entry criteria to evaluate the 28,457 individual concentration-response curves in the NCI “Stage 2” database (NCI 2007). This process ensured that concentration-responses displayed evidence of low dose stimulation followed by higher dose inhibition, and displayed a characteristic β-shaped (inverted U-shaped) concentration-response (Figure 1). The screening procedure used to define an inhibitory response (h_max) and a stimulatory response (s_min) set h_max ≤ 80% of the control response and S_min ≥ 110% of the control response. These values were consistent with a typical hormetic (β) concentration-response curve (Calabrese and Baldwin 1997).

The chemical concentrations were represented with the subscript i, where i = 1,…,5 indicates the lowest concentration (1.2 μM) to the highest concentration (100μM), the concentration as d_i, and the corresponding average response as Y_i. Using these definitions, the stimulatory concentration was defined as:

$$d_s=\text{min}[d_i|Y_i\ge s_{\text{min}}].$$

This concentration represents the lowest concentration where the response is greater than or equal to the minimum stimulatory response.

The inhibitory concentration in the concentration-response was defined as:

$$d_h=\text{min}[d_i|Y_i\le h_{\text{max}}].$$

Finally, if the concentration-response had both a d_h and a d_s and d_h>d_s, then the concentration-response for the chemical was classified as having a hormetic concentration-response.

There was no measure of statistical significance for the individual mean responses at each of the five concentrations in a given concentration-response study. Instead, we used criteria established by Calabrese and Baldwin (1997), as these permitted us to compare hormetic responses in this tightly defined database with those in the broader toxicological literature. Thus, if a concentration-response had inhibition below 80% of the control at the highest concentration, and the remaining 4 concentrations below the ZEP had mean responses between 100% and 110% of the control, it would not be included in this analysis. The value of ≥10% above the controls was chosen as it has been previously used as the “criterion for evidence of hormesis” when evaluating inverted U-shaped concentration-responses in dose-range studies (Calabrese and Baldwin 2003).

Quantification of Hormetic Parameters

The features of the hormetic concentration-responses (green pattern/shaded region in Figure 1) that were quantified include the maximum stimulatory response, the width from the maximum stimulatory response to the zero equivalent point (ZEP, i.e., the highest dose showing a response equal to the control response), and the width of the hormetic zone in each of the concentration-response studies.

Maximum Stimulatory Response and the Width from Max Stimulation to the ZEP

The maximum stimulatory response (parameter A, Figure 1) is the response of the greatest magnitude at the 1.2, 3.7, 11, or 33 μM concentration. If the largest response was the same at two concentrations (e.g., 130% at both the 1.2 and 11 μM concentrations), the lower concentration was chosen as the C_max. This was done so as to conservatively estimate the width of the stimulatory response. The concentration that corresponds to the maximum stimulatory response is termed the C_max. The distance from that concentration to the ZEP is parameter C (i.e., C = ZEP − C_max, not; Figure 1). The ZEP was calculated by determining the concentration (on the abscissa) where the response (on the ordinate) is equal to the control (ordinate value of 100%). The ZEP calculations were performed by interpolating (on the logarithmic scale) the concentration from the response immediately below and above the ZEP. For example, if the ZEP falls between the response at the 33 μM and 100 μM concentration, the ZEP would be:

$$\begin{array}{c}\text{ZEP}=\text{exp}[\text{log}(33)+((100-33\mu \text{M\hspace{0.17em}Response})\times (\text{log}(100)-\\ \text{log}(33)))/(100\mu \text{M\hspace{0.17em}Response}-33\mu \text{M\hspace{0.17em}Response})].\end{array}$$

Width of the Hormetic Zone

The width of the hormetic zone (parameter B, Figure 1) is defined as the width of the stimulatory region that is ≥ 110% of the control. It therefore extends above and below the concentration of the maximum stimulatory response (P2 – P1 = B, Figure 1) but does not reach the ordinate or the ZEP.

The concentration at which the response is estimated to have increased 10% above the control value before reaching the concentration of the maximum stimulatory response (termed P1) was estimated for the concentration-responses selected for evaluation in this analysis. The average of two replications expressed as percent of control responses, was used to determine the 10% increase in response. The P1 was estimated by the following procedure:

1. If the C_max = 1.2 μM then let P1 = 1.2 μM. If not, then proceed to step 2.

2. The largest concentration < C_max with an average response < 110% of the control was identified. This concentration was defined as P₁X_below, and the associated response was termed P₁Y_below.

3. The next highest concentration was defined as P₁X_above, and the associated response was defined as P₁Y_above.

4. The P1 was then estimated by linear interpolation on the log concentration scale:

$$\begin{array}{c}\text{P}1=\text{exp}[\text{log}({\text{P}}_1{\text{X}}_{\text{above}})+(110-{\text{P}}_1{\text{Y}}_{\text{above}})\hspace{0.17em}(\text{log}({\text{P}}_1{\text{X}}_{\text{below}})-\\ \text{log}({\text{P}}_1{\text{X}}_{\text{above}}))/({\text{P}}_1{\text{Y}}_{\text{below}}-{\text{P}}_1{\text{X}}_{\text{above}})].\end{array}$$

The concentration > C_max where the associated response has decreased to < 10% above the control value (P2) was similarly estimated for the concentration-responses from the average of two replications. The P2 was estimated by the following procedure:

1. The lowest concentration > C_max with an average response < 110% of the control was identified. This concentration was termed P₂X_below, and the associated response was P₂Y_below.

2. The first concentration immediately < P₂X_below was defined as P₂X_above, and the associated response was defined as P₂Y_above.

3. The P2 was then estimated by linear interpolation on the log concentration scale:

$$\begin{array}{c}\text{P}2=\text{exp}[\text{log}({\text{P}}_2{\text{X}}_{\text{above}})+(110-{\text{P}}_2{\text{Y}}_{\text{above}})\hspace{0.17em}(\text{log}({\text{P}}_2{\text{X}}_{\text{below}})-\\ \text{log}({\text{P}}_2{\text{X}}_{\text{above}}))/({\text{P}}_2{\text{Y}}_{\text{below}}-{\text{P}}_2{\text{Y}}_{\text{above}})].\end{array}$$

RESULTS

Identification of Hormetic Concentration-Responses

There are a total of 28,457 concentration-responses in the publicly available “Stage 2” data in the NCI YACDS database (2,189 anticancer agents × 13 yeast strains). Of those concentration-responses, 78.0% (n = 22,208) have an inhibitory response (h_max) ≤ 80% of the control. From those 22,208 responses, 20.5 % (n = 4,548) also have at least one stimulatory response (s_min) ≥ 110% of the control response. These 4,548 concentration-responses are the sample described in this study.

Quantification of Hormetic Parameters

The results of these analyses are presented in Table 1. In this evaluation of 4,548 hormetic concentration-responses, the mean maximum stimulatory response (parameter A, Figure 1) is 127.2% of the control with individual values ranging from 110% to 254%. The mean width of the hormetic zone (parameter B, Figure 1) was 9.2 μM, with individual concentration-responses ranging from 0 to 64.5 μM. The mean distance from the concentration of the maximum stimulatory response to the ZEP (parameter “C”, Figure 1) is 12.3 μM, with individual values ranging from 0.14 to 68.6 μM. The mean ZEP for the 4,548 responses was 16.9 μM (standard deviation 13.7) with individual ZEP values ranging from 1.3 to 77.4 μM.

TABLE 1.

Parameters of the 4,548 hormetic dose-responses in the YACDS database. The parameters are illustrated in Figure 1.

Parameter	Concentrations Below ZEP	N	Mean	St Dev	Q1	Median	Q3	Min	Max
A Maximum stimulation (%)	1	438	118.81	9.65	112	115	122	110	173
	2	1338	125.87	16.07	114	121	133	110	237
	3	1925	128.53	17.33	115	124	137	110	254
	4	847	130.57	18.25	116	125	141	110	207
	All data	4548	127.19	16.85	115	122	135	110	254
B Width of hormetic zone (μM)	1	438	0.38	0.34	0.12	0.29	0.55	0	1.85
	2	1338	2.68	1.64	1.34	2.76	3.68	0	7.80
	3	1925	8.99	5.52	4.37	9.93	12.80	0	24.84
	4	847	24.52	14.58	11.95	26.88	35.52	0	64.47
	All data	4548	9.20	10.82	1.57	4.86	12.63	0	64.47
C Maximum-to-ZEP interval (μM)	1	438	1.18	0.61	0.67	1.13	1.70	0.14	2.35
	2	1338	4.00	1.89	2.79	3.66	5.11	0.39	9.45
	3	1925	12.51	5.52	9.17	11.56	15.35	1.18	30.72
	4	847	30.56	12.33	24.37	32.33	37.87	3.79	68.60
	All data	4548	12.28	11.69	3.50	8.81	16.03	0.14	68.60
ZEP (μM)	1	438	2.38	0.61	1.87	2.33	2.90	1.34	3.55
	2	1338	6.15	1.85	4.60	5.68	7.49	3.70	10.67
	3	1925	16.85	5.03	12.91	15.39	19.35	11.00	32.25
	4	847	41.44	7.47	35.94	39.31	44.84	33.00	77.36
	All data	4548	16.89	13.73	5.80	12.97	22.39	1.34	77.36
Cmax (μM)	1	438	1.20	0.00	1.2	1.2	1.2	1.2	1.2
	2	1338	2.15	1.21	1.2	1.2	3.7	1.2	3.7
	3	1925	4.34	3.86	1.2	3.7	3.7	1.2	11.0
	4	847	10.88	11.53	1.2	11.0	11.0	1.2	33.0
	All data	4548	4.61	6.46	1.2	1.2	3.7	1.2	33

DISCUSSION

The results are in general agreement with previous reports of hormesis for over 5,600 concentration-response relationships from over 900 different exposures to chemical and radiation stress (Calabrese and Baldwin 1997; Calabrese and Blain 2005). In those studies, Calabrese and others reported that the maximum amplitude of the stimulatory response is generally modest, usually only 30% greater than the control response. They reported that nearly 80% of the concentration-responses are less than 200% of the control response, which is also in general agreement with the present evaluation. The mean maximum stimulatory response (parameter A, Figure 1) in the present study was approximately 127% of the control, being <135% in about 75% of the dose responses

The experimental design with a dose range of ~100-fold (1.2 – 100 μM) was somewhat restrictive in assessing hormetic concentration-responses given the a priori entry criterion that at least one of the responses must be less than or equal to 80% of the control response (h_max). Thus, the entry criteria and experimental design limit the width of the maximum stimulatory zone to approximately 75 μM. Despite the potential limitation, the mean width of the hormetic zone was found to be only 9.2 μM with 75% of the data below 12.6 μM (Table 1). In fact, for the 4,548 concentration-responses the width of the stimulatory response extended on average from 2.3 μM (parameter P1, Figure 1) to 11.5 μM (parameter P2, Figure 1), thus constituting a 5-fold (11.5/2.3) difference in dose. This result corresponds well to published hormetic responses for microbial growth. In an evaluation of 165 dose-response studies involving microbes, the width of the hormetic zone was between 1 and 10-fold 54% of the time (Calabrese and Blain 2005). One might expect a homogeneous population to show a narrower range of stimulatory response than that observed in heterogeneous systems (Calabrese and Blain 2005). This might explain why 90% of the hormetic concentration-responses in our study had a stimulatory width less than 25.2 μM.

The mean difference between the maximum stimulatory response and the ZEP (parameter C, Figure 1) was 3.7-fold. This was calculated on the basis of an average ZEP of 16.9 μM and an average stimulatory concentration of 4.6 μM. The 3.7-fold interval is within the value of 3- to 6-fold reported in the published literature (Calabrese and Baldwin 1997).

The number of concentrations below the ZEP strongly influenced the parameters assessed in this study. When there were more concentrations below the ZEP, the zone of stimulation (parameter B) was wider, the distance from the maximum stimulatory concentration (C_max) to the ZEP (parameter C) was larger, and the ZEP itself was greater (Table 1). The number of concentrations below the ZEP also had an impact on the amplitude (parameter A) of the maximum stimulated response. The amplitude increased approximately 12% (from 118.8% to 130.6%; Table 1) when going from 1 to 4 concentrations below the ZEP. The increase at each category of “numbers of concentrations below the ZEP” was statistically significant (p < .05, two sample t-test) relative to the preceding category (i.e., 1 vs. 2; 2 vs. 3; 3 vs. 4).

It is highly unlikely that a single toxicological mechanism can explain the multitude of observed biphasic concentration-responses. Calabrese (2001) has suggested that the stimulatory response at low concentrations is generally the result of an initial disruption in homeostasis, and it appears to represent a modest overcompensation response. The stimulatory response is usually slight because a compensatory process only modestly overshoots the original physiological set-point. This slight overshoot, or overcompensation phenomenon, ensures that the system efficiently returns to homeostasis, thus avoiding an unnecessary and excessive waste of resources. The data presented here are consistent with a slight overcompensation, represented by a relatively small stimulatory response averaging 27% above controls. A more complete analysis of the magnitude would require inclusion of a temporal component to examine the concentration-responses over time, which is not possible in the NCI database.

It is also difficult to speculate on a specific molecular mechanism that may account for the various hormetic concentration-response curves observed here because the compounds represent diverse chemical structures and biological activity. They include spindle poisons (such as vinca alkaloids, taxanes, benzimidazoles), ribonucleotide reductase inhibitors (such as triapine), antipsychotics (such as Haldoperidol), antibiotics (such as congocidine), mustard agents, histological stains (such as toluylene blue and acridine yellow), halocarbonyls, and nitroaromatics, to name only a few (Holbeck and Simon, 2007; NCI, 2007). While many of the compounds are effective at inhibiting the proliferation of a particular mutated yeast strain, their precise molecular targets and mechanisms of action are not known in many cases (Holbeck and Simon 2007). Thus, it is difficult to speculate on the molecular mechanisms that stimulate cell proliferation at low concentrations. While a single mechanism is unlikely to apply to all of the compounds in this drug screen, a common general mechanism that has emerged in a study of over 120 different anticancer drug biphasic concentration-responses is that of a 2-receptor subtype model (Calabrese 2005). In this scenario, one receptor would have high and the other low affinity for the agonist. A biphasic concentration-response would result from the high affinity receptor becoming activated at the lower concentrations and the low affinity/high capacity receptor becoming dominant at the higher concentrations (Szabadi 1977).

Studies related to drug development should be designed in a way that accurately estimates the NOEL (no observed effect level, or the highest dose that is not statistically different from the control value) so that hormesis can be assessed (Calabrese et al 2006b). Assessment of hormesis can be important clinically; for example, if an anticancer drug were to stimulate tumor cells at low doses, hormesis would be an adverse effect to be avoided. In this database of approximately 28,500 concentration-responses only about 22,200 (78%) showed the requisite high dose inhibition (h_max) required by our a priori criteria, and 17,660 of these did not show stimulation (S_min) of at least 10% greater than the control value. Thus, more concentrations in the sub-threshold zone would be needed for about 62% of the concentration-responses in order to accurately assess the possibility of hormetic effects.

It has been proposed that an initial screening should accurately estimate the toxic threshold (such as the ZEP), and then follow-up testing should be done to evaluate the presence of hormesis (Calabrese et al. 2006b). This may be prudent given that 52.5% (n = 1,150) of the 2,189 anticancer agents evaluated in the NCI Yeast Anticancer Drug Screen display hormetic concentration-responses in at least one of the 13 yeast strains, and 24 putative anticancer agents showed hormetic concentration-responses in all of the 13 strains (Table 2). The amplitude of stimulation, width of the hormetic zone, and distance from the maximum stimulatory response to the ZEP were generally greater when hormetic responses for a given agent were observed in more yeast strains (Table 2). There is also a tendency for the quantified parameters of the hormetic region (i.e., A, B, or C in Figure 1) to increase as the slope of the distance from the IC50 to the ZEP becomes greatest (i.e., the IC50-ZEP value is smallest).

TABLE 2.

The mean value of the quantified features of the hormetic concentration-responses. The “No. of Strains Hormetic” refers to the number of yeast strains that a particular “Chemical Agent” passed the a priori entry and evaluative criteria. For example, there were 24 chemical agents that passed the entry criteria in all 13 yeast strains yielding a total of 312 concentration-responses.

			Mean Value of Respective Parameter
No. of Strains Hormetic	Chemical Agents	Concentration-Responses	A (% Control)	B (μM)	C (μM)	ZEP (μM)	IC50 (μM)
1	419	419	120.31	5.78	10.18	16.18	47.83
2	183	366	121.21	7.18	11.18	17.36	45.91
3	91	273	119.92	5.92	10.42	16.27	47.26
4	75	300	119.74	7.25	10.89	16.02	45.98
5	64	320	121.13	7.65	10.30	15.62	54.09
6	55	330	122.52	8.90	12.60	16.93	48.45
7	46	322	124.14	10.04	13.22	17.94	45.70
8	49	392	124.45	7.86	10.46	14.54	46.94
9	38	342	126.85	11.40	14.31	18.95	39.49
10	29	290	129.94	10.32	14.09	17.28	45.36
11	42	462	134.54	11.36	13.42	16.89	46.35
12	35	420	141.42	12.83	13.90	17.62	44.05
13	24	312	142.48	12.07	14.54	18.19	42.91

Caution is required when attempting to identify chemical structures of “hormetic” compounds because the structures of all compounds have not been unequivocally verified. For example, Holbeck and Simon (2007) report a case in which one of the compounds identified as a specific inhibitor of the rad50 and rad52 strains had a different structure than was indicated by the supplier.

The observation of hormetic responses in over 50% of the chemicals evaluated and all 13 yeast strains suggests that the biphasic dose-response is generalizable for many different chemical agents and varied genotypes. Thus, the responses following exposure to alkylating agents, antimetabolites, DNA cutters, DNA binders, and many other classes of compounds (Holbeck and Simon 2007) exhibit similar quantitative features. The results reported here are consistent with quantitative features of hormetic responses seen in published literature for various biological models, (i.e., plant, microbe, invertebrate, vertebrate, in vitro, in vivo), endpoints (e.g., growth, fecundity, tissue repair, cognition, lifespan) and stressors (toxicants, endogenous agonists, synthetic agonists, radiation, physical stressor) [Calabrese and Blain 2005]. The consistency of the findings for a large database of systematically conducted tests with excellent quality control (Holbeck 2004; Holbeck and Simon 2007) and the toxicological literature more broadly (Calabrese and Blain 2005) argues that there is coherence in the quantitative attributes of hormesis. This suggests a broadly based biological plasticity that may represent a general biological principle in responding to stress.