Attentional Modulation of Visual Responses by Flexible Input Gain

Abstract

Although it is clear that sensory responses in the cortex can be strongly modulated by stimuli outside of classical receptive fields as well as by extraretinal signals such as attention and anticipation, the exact rules governing the neuronal integration of sensory and behavioral signals remain unclear. For example, most experiments studying sensory interactions have not explored attention, while most studies of attention have relied on the responses to relatively limited sets of stimuli. However, a recent study of V4 responses, in which location, orientation, and spatial attention were systematically varied, suggests that attention can both facilitate and suppress specific sensory inputs to a neuron according to behavioral relevance. To explore the implications of such input gain, we modeled the effects of a center-surround organization of attentional modulation using existing receptive field models of sensory integration. The model is consistent with behavioral measurements of a suppressive effect that surrounds the facilitatory locus of spatial attention. When this center-surround modulation is incorporated into realistic models of sensory integration, it is able to explain seemingly disparate observations of attentional effects in the neurophysiological literature, including spatial shifts in receptive field position and the preferential modulation of low contrast stimuli. The model is also consistent with recent formulations of attention to features in which gain is variably applied among cells with different receptive field properties. Consistent with functional imaging results, the model predicts that spatial attention effects will vary between different visual areas and suggests that attention may act through a common mechanism of selective and flexible gain throughout the visual system.

INTRODUCTION

Attention is by definition flexible: its utility depends on its ability to be directed to particular features, objects, or locations on the basis of behavioral context. This flexibility, however, makes it difficult to construct models of attention modulation that can generalize across different subjects and tasks. Indeed although it is clear that spatial attention modulates neuronal responses in a variety of visual areas, several fundamental questions concerning the mechanisms underlying attentional improvements in performance remain controversial. For example, while several studies have concluded that spatial attention can alter visual representations at a cellular level, for example by refining (Spitzer et al. 1988) or changing (Luck et al. 1997; Moran and Desimone 1985; Reynolds et al. 1999) receptive field selectivites, other studies are consistent with attention simply increasing responsiveness without any change in selectivity (McAdams and Maunsell 1999). Similarly, while some studies have concluded that attention only enhances responses to stimuli that are weak (Reynolds et al. 2000) or competing with other stimuli for behavioral relevance (Luck et al. 1997), other studies have found robust attentional modulation with single stimuli of high contrast (McAdams and Maunsell 1999; Motter 1993). Finally, the influence of attention directed to a particular location on behavior and physiological responses at distant locations (Boudreau et al. 2006; Lavie 1995; Muggleton et al. 2008) varies between different studies. Although differences in task design or stimulus configuration may be responsible for some of the apparent inconsistencies, substantial behavioral and physiological variation is often observed even between individual subjects within the same study (Boudreau et al. 2006; Ito and Gilbert 1999). This suggests that if multiple strategies may be employed to solve a particular task, then those strategies may largely determine the manner in which attention modulates sensory responses.

To quantitatively explain the effects of different attentional strategies on visual processing, a complete physiological model of attention must allow for differences in receptive field structure and organization as well as differences in the magnitude and spatial distribution of attention. One such model, the input gain model, incorporates nonlinear spatial summation and attentional modulation of neuronal inputs and can explain neuronal responses in area V4 to single and paired stimulation under a variety of attentional conditions (Ghose and Maunsell 2008). In this model, attention acts according to localized activity gain in which visual signals at a particular retinotopic location are scaled by a constant factor in the presence of attention but that scaling can vary between different locations. After the inputs are scaled according to their behavioral relevance of the location they represent, they are combined according to summation rules that are constant over different attentional conditions. These rules can accommodate well-described nonlinearities in response generation in the visual system including divisive normalization, gain control, and surround suppression. Significantly, the model is able to reconcile observations based on single stimulus responses suggesting that attention simply increases responsiveness with observations based on paired stimulus responses in which attention biases the influence of particular stimuli within the receptive field.

The input gain model stipulates that attention can either increase or decrease the influence of particular inputs on the basis of behavioral relevance. In the V4 data set, many neuronal responses were best described by a combination of facilitation of the inputs corresponding to attended portion of the receptive field and suppression of those inputs corresponding to the ignored region. However, because of the time constraints of electrophysiological recordings, the model could only be validated over a limited set of stimuli and attentional conditions. In this paper, we apply a generalized model of input gain to predict the responses to a range of stimuli and attentional allocations. Based on psychophysical (Cutzu and Tsotsos 2003; Suzuki and Cavanagh 1997) and electrophysiological (Moore and Armstrong 2003) measurements of the spatial organization of facilitation and suppression from frontal cortex, we choose to model the spatial distribution of attentional modulation with a center-surround model in which attention modulates inputs at the focus of attention with facilitatory gain and surrounding inputs with suppressive gain. The exact characteristics of center-surround attentional modulation were derived from models of sensory center-surround interactions with an additional provision that the spatial extent of the center-surround gain field is flexible. This flexibility allows for attention to modulate neuronal signals in accordance with the spatial extent of behaviorally relevant information in a particular task (Eriksen and St James 1986; Eriksen and Yeh 1985; LaBerge 1983; LaBerge and Brown 1986).

In this paper, we show that this input gain model, when applied to existing models of sensory integration, can explain numerous and seemingly disparate electrophysiological observations of attentional modulation. If attention is broadly distributed in space with respect to a neuron's receptive field, then attention gain is close to uniform among the inputs to the neuron, and the effect is similar to an increase in responsiveness without any change in selectivity. On the other hand, if attention is narrowly focused in space, then attentional gain would only be applied to the subset of inputs, and the influence of those inputs, relative to other inputs, would be increased consistent with biased competition-based models of attention (Reynolds et al. 1999). Similarly, the model explains how either suppression or facilitation can occur at points distant from the center of attention (Boudreau et al. 2006) depending on the particular attentional strategy employed by the subject. By incorporating potential misalignments between attention and receptive fields, the model can explain how attention can shift receptive fields by selectively amplifying inputs corresponding to a particular spatial location (Connor et al. 1997; Womelsdorf et al. 2006) and modulate the influence of stimuli outside the classical receptive field (Ito and Gilbert 1999). Finally, because of the differential contrast sensitivity of excitatory and inhibitory inputs in certain cells, the input gain model is also able to explain how attentional modulation might be preferentially observed for weaker stimuli of low contrast (Reynolds et al. 2000; Williford and Maunsell 2006).

METHODS

V4 spatial summation

Data describing the effects of spatial attention and visual stimulation within the receptive fields of individual V4 neurons were acquired while animals performed a spatially specific orientation change detection task for juice or water rewards. Experiments were conducted at the Baylor College of Medicine in accordance with institutional and National Institutes of Health animal care guidelines. Data from two monkeys (Macaca mulatta) have been described previously (Ghose and Maunsell 2008), whereas data from a third animal, the task of which slightly varied from that performed by the other two monkeys, have not been previously published. During each behavioral trial, animals were required to fixate on a small dot (∼0.1°, fixation widow width: ± 0.5–0.7°) while two or four stimuli were presented peripherally. The monkeys' task was to release a lever as soon as the stimulus at the cued location changed orientation (changes from 60 to 90°), while ignoring any changes occurring at other locations. Each animal's performance, excluding fixation breaks, was >90% correct and did not depend on the time at which the behaviorally relevant change occurred. Overall performance did not vary according to the particular stimulus presented or the attended location. Early releases prior to this change, failures to release, and eye movements outside the fixation window immediately ended the trial without reward. Because the orientation changes at all locations occurred at random times (≤2,500 ms after stimulus onset), and the animals had a limited time window with which to respond (between 250 and 450 ms), chance performance in the task is close to zero. Moreover, spatial attention is required for this task because a random behavioral response to the first change that occurs among four possible locations would result in only 25% correct performance.

Trials were presented in block mode in which the behaviorally relevant location, but not the visual stimulus, was fixed between trials within a block. This relevant location was cued by instruction trials presented at the start of each block in which only a single stimulus was presented. Thus prior to each trial within a block, the relevant location, but not the actual visual stimuli, could be anticipated by the animals. Trial types or conditions were defined according to the stimuli within the receptive field and the location to which attention was directed. Only cells with at least four repetitions of each condition were included. Stimuli outside the receptive field (in the opposite visual quadrant) were randomly varied between different repetitions of the same attention+within receptive field stimulus condition.

Recordings were made from individual neurons in area V4 on the surface of the prelunate gyrus in daily sessions using transdural electrodes (0.5–1.5 MΩ at 1 kHz) and conventional extracellular recording techniques. Action potentials were recorded with a resolution of 1 ms using a time base that was synchronized with the vertical retrace of the monitor. Once a single unit was isolated, its receptive field position, optimal orientation, and optimal spatial frequency were estimated by presenting achromatic counter-phasing Gabors with manually chosen parameters. Spatial receptive fields were confirmed quantitatively using single Gabor stimuli at eight adjacent positions around a central point. Gabor size and center point of the eight position array were chosen so that responses to the central four positions were approximately equal and that responses significantly above spontaneous activity were observed at all eight positions. Orientation tuning was assessed by measuring the responses of a single Gabor of varying orientation at the central point.

One or two Gabors were presented at two central positions defined by this receptive field mapping. For each Gabor, orientation assumed one of three values corresponding to the preferred, intermediate, and null orientation of the neuron under study. The behaviorally relevant location was kept constant during an attentional block within which all possible combinations of Gabors were presented in a randomly interleaved trials. Because stimulus variations were matched between different attention blocks, attention modulation could be measured for all possible stimulus combinations within the receptive field. Two monkeys performed a four-target task, where all four locations could potentially be behaviorally relevant. The third monkey performed a two-target task, in which there were only two locations of potential behavioral relevance. In this task, the most foveal Gabor within the cued quadrant was behaviorally relevant. For the four-target task, conditions in which attention was directed to different locations in the opposite visual quadrant were combined to yield a single attend-out data set. Thus there were a total of 39 conditions (attend in position 1: 12, attend in position 2: 12, attend out: 15). For the two-target task, there were a total of 30 conditions (attend in: 6 singles + 9 pairs, attend out: 6 singles + 9 pairs). For the two-target task, the Gabors were located along the line connecting receptive field center with fixation (iso-polar angle), and the monkey had to attend to the inner most stimuli either within the receptive field (attend in) or in the opposite visual quadrant (attend out). For the four-target task, Gabors were located perpendicular to this line (iso-eccentricity), and the behavioral relevant location could be at four possible locations (attend in: position 1, attend in: position 2, attend out: position 3, attend out position 4). Stimulus and attention specific responses were characterized by the mean firing rate of discharge during epochs of positive change probability (500–2,500 ms) and prior to any orientation change within the receptive field.

To test for interactions between the effects of attention and stimuli, three-factor ANOVAs were done on the responses from each neuron. To allow for multiplicative effects on neuronal responses, spike rates were log-transformed before this analysis. Thus if the effects of orientation and attention are separable in the same sense that stimulus parameters such as orientation and spatial frequency are for V1 neurons, the ANOVA would reveal no significant interaction between the factors of orientation and attention. Specifically, an output gain model specifies that there would be no significant interaction term. Because the log-transform required positive values, for those few trials in which no spikes were observed, a fractional response was defined to be half of the average response rate over all trials multiplied by the time epoch of the trial. For trials in which a single stimulus was presented within the receptive field, the ANOVA factors were: position within the receptive field (2 levels: position 1 and position 2), orientation (3 levels: preferred, intermediate, and null), and the spatial locus of attention (2 levels: attention directed within the receptive field, and attention directed outside of the receptive field). For trials in which pairs of Gabors were presented within the receptive field, the ANOVA factors were: orientation at position 1 (3 levels), orientation at position 2 (3 levels), and attention position (3 levels: position 1, position 2, and outside of the receptive field at positions 3 and 4). Significant effects were defined by P < 0.05.

Single stimulus and paired stimulation responses were used to fit a spatial summation model for each neuron. We used a variant of a generalized model that has been used to explain paired stimulus responses in other visual areas (Britten and Heuer 1999). In this model, the response to paired stimulation (R_1,2) is related to the responses to individual stimuli (R₁ and R₂) according to the equation

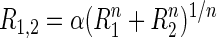(1)

This model can accommodate several classic models of spatial summation including winner-take-all (large n), averaging (n = 1, α = 0.5), and normalization (n = 0.5, α = 1) (Simoncelli and Heeger 1998). In both area V4 (Ghose and Maunsell 2008) and MT (Britten and Heuer 1999), many cells cannot be described by these simpler single parameter models and require the full generalized model with two free parameters to adequately describe paired stimulus responses. To evaluate the effects of spatial attention, we compared responses during trials with same stimulus conditions from the three different attention blocks (attend position 1, attend position 2, and attend out). Single stimulus responses from attend out trials were used to predict the paired responses to all three attentional conditions. This was done by introducing two additional parameters describing the attentional gain at each position (β₁ and β₂) so that

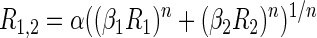(2)

When attention is directed outside of the receptive field, β values were set equal to 1.0. Facilitatory gain (β > 1) selectively applied to a particular stimulus would therefore increase the influence of that stimulus. Such a model can also incorporate suppression: in the case of a single stimulus, no inputs are suppressed, whereas in the case of multiple stimuli, suppressive gain (β < 1) might be applied to the inputs associated with suppressed stimuli.

For all spatial summation and attention models, optimal parameters were obtained by minimizing mean square error (MSE) weighted according to the variance of the experimental observations using the downhill simplex method. This weighted MSE was then normalized to the explainable variance (variance of the means of the observations - variance of a typical observation). Models with different numbers of free parameters were statistically compared using an F-test based on the sum of residuals weighted according the variance of the experimental observations. The F-test takes into account sample size and degrees of freedom in determining whether the improvement in fit observed with the addition of a free parameter is significant (Zar 1999).

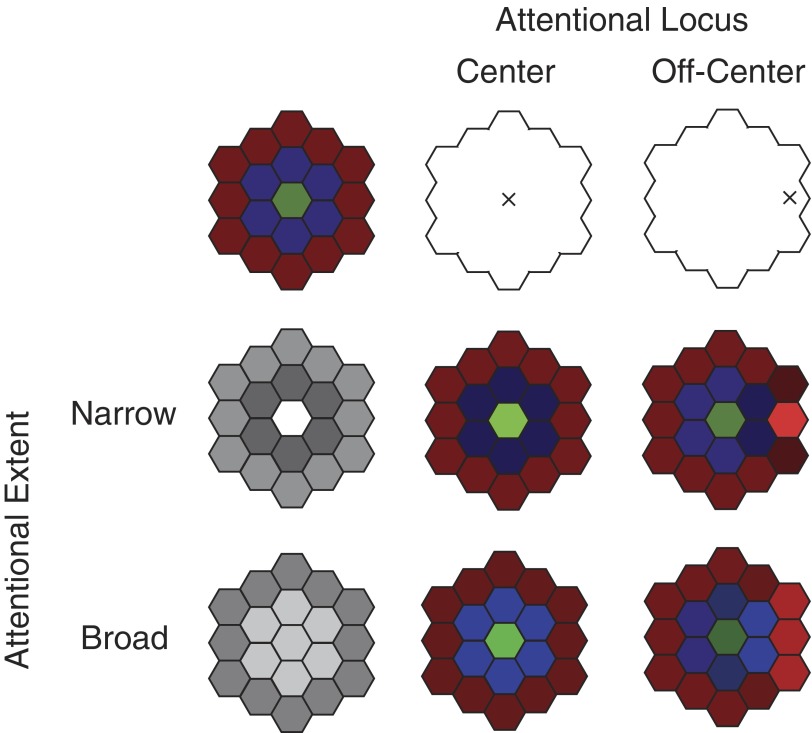
Divisive surround suppression model

To apply an attention model to a range of behavioral requirements and visual stimuli beyond that of the V4 data, both the flexibility of attentional allocations and the sophistication of receptive field (RF) properties must be incorporated. With regard to attentional allocation, we wish to incorporate the ability to direct attention to different locations and over different spatial extents (Fig. 1). With regard to RF properties, we wish to incorporate the possibility of spatial heterogeneity in which sensory selectivity or sensitivity varies within RFs. Although the input gain model can incorporate arbitrary RFs, its principles can be easily illustrated for a model neuron with a spatial center-surround organization such that the sensitivities or selectivity vary according to distance from the center of the RF. In the absence of any behavioral context, such as in an anesthetized preparation, the overall response of the neuron to a stimulus depends on how the stimulus activates the inputs associated with these distinct selectivities within the RF and how the activated inputs are combined. For example, if the center of the RF (green in Fig. 1) has a different contrast sensitivity that the surround (red), then the overall contrast sensitivity of the cell will depend on the size of the stimulus (Cavanaugh et al. 2002a). For such a center-surround RF, the input gain model dictates that a narrow focus of attention will have very different effects depending on its locus (Fig. 1, middle row): attention limited to the center will result in overall response properties mimicking those found in the center, while conversely, when attention is directed to a portion of the surround, surround selectivites would dominate. Thus a spatially restricted allocation of attention has a heterogeneous effect at the population level because of variations in the distance between the attentional locus and the RF centers of responding neurons. When attention is broadly distributed in space, the model states that the facilitation at any particular attended location is weaker than it would have been had attention been narrowly focused on that location (Fig. 1, bottom left vs. center left). When attention is broadly distributed, the effect on stimulus selectivities or sensitivities is far less than with narrow distributions for two reasons: the relative weighting of inputs is not strongly altered because gain is applied to a broad range of inputs, and the magnitude of gain effects on inputs are relatively modest compared with more focused attention. Similarly, because the spatial modulation is broadly distributed, the exact location of the center of attentional allocation is less relevant than for a narrow attentional focus. Thus because a broadly distributed attentional focus minimally alters the weighting of different inputs to a neuron, its effects are similar to output gain in which responses increase without any change in selectivity or sensitivity. Similarly, the effects on a population level are more homogeneous and the relative activity levels of different neurons are unaltered. Because in many tasks subjects can perform adequately with a variety of different attentional allocations, the model predicts that the action of attention on neuronal selectivities depends on the particular attentional strategy employed by the subject. For example, if a subject chooses to broadly distribute attention across the space, the effects of attention of individual neuronal responses are more modest and consistent with output gain than if a subject narrowly focuses attention on a particular region or stimulus.

FIG. 1.

Input gain model of spatially variant attentional modulation for a center-surround receptive field. Responses in the absence of attention are determined by the relative activation of different sets of inputs (red, green, and blue; top left). Attention modulates the gain of those inputs in a spatially specific manner so that neuronal response reflects the relative activation of behavioral modulated inputs. In this cartoon, attentional modulation varies over space according to a center-surround organization (left), with facilitation (white) at the center, and suppression (dark gray) at the surround. The effect of attention varies according to both the locus and spread of attention. Highly localized attention can substantially alter the relative weighting of different sensory inputs depending on its locus (right), while broadly distributed attention does not substantially alter the relative activity of a particular subset of inputs.

Both the spatial distribution of attentional modulation and integration of sensory inputs were derived from a divisive normalization model of excitatory and inhibitory inputs used to describe center-surround interactions in primate V1 neurons (Cavanaugh et al. 2002a). V1 data were used because neurons in this area have been the most systematically studied with respect to spatial integration, but our results are generalizable to any RF with center surround organization. In this model, excitatory and inhibitory inputs are described by co-extensive two-dimensional (2-D) Gaussians envelopes in which the centers of the Gaussians (defining the RF center) are aligned and sensitivity decreases with distance from the centers. By analogy, net attentional gain was defined as the difference between co-aligned facilitatory (F) and suppressive (S) Gaussians, such that maximal facilitation was observed at the center of attentional focus and the effect of attention decreased away from the center. Because the two Gaussians are centered with respect to one another and are radially symmetric, this attentional gain field has four parameters: the center magnitude of the two Gaussians (F and S), and their spatial extents (σ_F and σ_S)

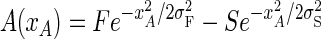(3)

where x_A is the distance from the center of attention. For these simulations, these parameters were defined so as to be consistent with both V1 center-surround parameters of sensory integration and the average magnitude of attentional modulation seen at the attended and unattended locations for the V4 data. The magnitudes of the Gaussians (F and S) were set according to the average ratio of excitatory and inhibitory Gaussians in the V1 data (F = 2S) and the requirement that their difference be equal to the average input gain observed at the attended location in the V4 data (F − S = 1.56). The spatial extents were set according to the average ratio of excitatory and inhibitory Gaussian in the V1 data (σ_S = 2.5σ_F) and average input gain at the unattended location in the V4 data (0.9 in the 4-target data set, and 1.0 in the 2-target data set). Because we assume that attentional modulation at any one point decreases as attention is more broadly distributed over visual space, an additional magnitude constraint was introduced such that the total area of the facilitatory and suppressive Gaussians was kept constant by inversely scaling magnitude with spatial extent

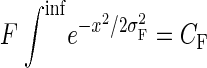(4)

and

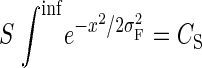(5)

for all σ. To study how this attentional modulation model would affect responses under a broader range of conditions than was explored in the V4 data, we applied spatially variant attention gain to inputs of various RF models. To explore how attentional modulation might affect sensory interactions within and beyond the classical RF, we used the V1 divisive model comprised of an excitatory and inhibitory input. In this model, the response R to a stimulus of size s in the absence of attention is given by

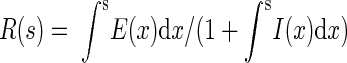(6)

where E and I are excitatory and inhibitory inputs with Gaussian spatial profiles, and x is the distance from the center of the RF. The effect of input gain was implemented by multiplying E(x) and I(x) by the aforementioned center-surround gain field. To study the effects of attention on the broad population of neurons activated by a particular stimulus, we place no constraint on the centering of attention with respect to any particular RF; the Gaussians associated with input gain (F and S) can differ in both position and spatial extents from the sensory inputs E and I.

RESULTS

Attentional modulation with single and paired stimuli

The input gain model provides a quantitative framework for predicting how the adoption of different strategies in the spatial allocation of attention will affect sensory responses. Boudreau et al. (2006) provided direct evidence that spatial strategies of attention allocation can substantially alter the nature of attentional modulation seen in individual neurons. Animals were cued to attend to changes in one of the two locations while ignoring any changes in the other location. Easy and difficult changes were presented in block mode, and the performance on changes of intermediate difficulty was measured. In their study, the effect of increased difficulty on visual responses to behaviorally irrelevant stimulation varied between animals: in one animal, a suppression of responses was observed, whereas in the other two, a facilitation. These differences occurred despite a large distance between the attended and unattended locations, which were located in opposite visual quadrants and were accompanied by corresponding differences in behavioral performance to probes of intermediate difficulty: the animal in which physiological responses were strongly suppressed at the unattended location also exhibited strongly impaired performance at that location. The suggestion that the animals employed different spatial strategies when confronted with a difficult task was corroborated by a behavioral study in which both locations were cued. In this study, for the first two animals, difficulty still had an effect on behavior, consistent with a broad allocation of spatial attention with increased difficulty, whereas in the third animal, no such difference was observed.

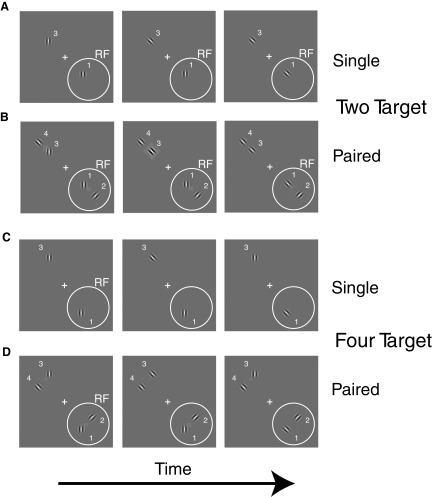
To test whether such differences in the spatial allocation of attention could also been seen over distances on the order of RFs, we measured responses to single and paired stimuli presented within V4 RFs while the animals attended to different locations within and outside the RF. Three animals were trained to respond with a lever release when a randomly timed orientation change occurred at a single Gabor while ignoring such changes in the other Gabors. For paired stimulation, two Gabors were placed adjacent to each other within the RF of the neuron under study, while two additional Gabors were symmetrically located in the opposite visual quadrant (Fig 2). Responses to single stimuli at the two positions were also measured in trials randomly interleaved among the paired stimulus trials. For the two animals, the data of which have been published previously (Ghose and Maunsell 2008), the four Gabors were located at identical eccentricities, and all four Gabors could potentially be cued (4 target, Fig 2B). For the third animal, adjacent Gabors were located at identical polar angles but different eccentricities, and only the Gabor closest to the fixation point was potentially relevant (2 target, Fig 2A). The probability of orientation change was identical at all locations for all three animals.

FIG. 2.

Spatially localized orientation change detection tasks. Left to right: temporal sequence of stimuli; +, fixation point; •, the receptive field (RF) of the V4 neuron under study. Monkeys were cued to pay attention to a particular location (location 1 in A–D) and only release a lever immediately after an orientation change occurred at that location, (center to right panels), while ignoring changes at all other locations (left to center panels). The behaviorally relevant location was cued with an instruction trial (not shown) in which only 1 stimulus was present. Subsequent trials within a cued location block included conditions in which only a single stimulus was present in the RF (A and C) and conditions in which pairs of stimuli were present (B and D).

The effects of attention were assessed by comparing responses in which the RF stimulation was identical but the cued location differed using ANOVA on log-transformed response rates. Single stimulus and paired stimulus responses were analyzed separately. Single stimulus responses were categorized according to the factors of orientation (3 levels), location (2 levels), attended location (2 levels: in and out of RF), while paired stimulus responses were categorized according to orientation at location 1 (3 levels), orientation at location 2 (3 levels), and attended location (3 levels: position 1, position 2, or positions 3 or 4). The ANOVA determines whether the responses of a neuron are significantly modulated by the factors of stimulus or attentional locus. With log transformed data, a significant interaction between these factors indicates a lack of multiplicative separability. Thus for a strict output gain model in which the effect of attention is a multiplicative increase in responsiveness irrespective of the stimulus (McAdams and Maunsell 1999), this interaction should be zero. In such a gain model, the incidence of significant attentional modulation should be similar for single and paired stimulus responses, and, for paired stimulus responses, there should be no significant interactions between attention and location or orientation. The data from two-target cells (n = 43) are largely consistent with these expectations: the incidence of attentional effects was similar for single and paired stimulus responses (36 vs. 37), and, given our number of repetitions, few significant interactions between attention and stimulation were observed in paired stimulus trials (attention × orientation at location 1: 7, attention × orientation at location 2: 4, attention × orientation at location 1 × orientation at location 2: 2).

By contrast, the responses of four-target cells were consistent with attentional modulation being dependent on stimulus conditions. For four-target cells (n = 159), attentional effects were more often visible when pairs of stimuli, as opposed to single stimuli, were presented within the RF (121 vs. 86). This is consistent with a “biased competition” model of attention in which attentional modulation is preferentially observed for nearby stimuli that are in maximal competition for driving the response of a neuron. Moreover, for four-target cells, significant interactions between attention and RF stimulation were relatively common with paired stimuli responses (n = 159): (attention × orientation at location 1: 48; attention × orientation at location 2: 55; attention × orientation at location 1 × orientation at location 2: 28). Thus a change in paired stimulus configuration (radial in 2 target vs. tangential in 4 target) that was maintained throughout training was associated with a large change in the stimulus dependency of attentional modulation. Specifically, while paired stimulus responses in the two-target cells could largely be explained by stimulus-independent attentional modulation, many paired stimulus responses in the four-target cells could not.

The two- and four-target data demonstrate that results consistent with both output gain and biased competition can be observed in V4 responses to paired stimulation. To investigate whether changes in the spatial allocation of attention might be able to explain the differences between the data sets requires quantitative models of how neurons respond to paired stimulation. Only once such a model is obtained for a particular neuron can we make predictions about how various attentional models would affect the ensemble of responses evoked by different stimulus combinations. In a previous study analyzing the four target data (Ghose and Maunsell 2008), we demonstrated that a generalized model of spatial summation adopted from observations in area MT (Britten and Heuer 1999) was able to explain the stimulus dependencies with respect to orientation and location of a large fraction of V4 neurons. This model accommodates nonlinearities in input summation and, depending on the particular parameters, can describe classic models such as winner-take-all, averaging, and normalization. When different attentional models were incorporated into this model of spatial summation by altering the strength on particular inputs according to behavioral relevance, the best fit for many cells was obtained when attentional modulation was not uniform among their inputs but instead was larger at the particular location within the RF to which attention was directed. We termed this model input gain because the effect of attention was quantitatively modeled as a multiplicative modulation that could vary across the different inputs to a neuron.

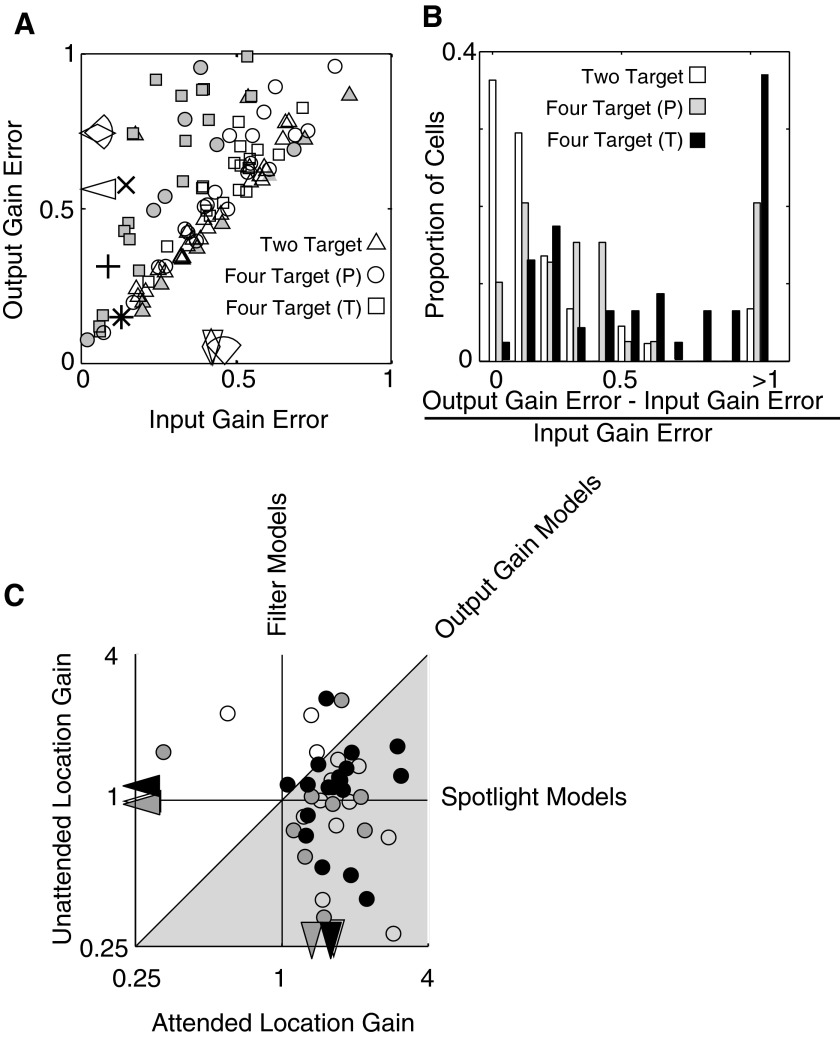
We initially tested two attention models for every neuron in the two-target and four-target data sets. In the generalized input gain model, the magnitude of attentional modulation is free to vary between the unattended and attended locations (βs in Eq. 2), whereas in an output gain model the magnitude of attention modulation is locked between the two locations (β₁ = β₂). Each neuron was tested separately and thus produces a different set of parameters depending on its spatial summation and attentional modulation. No population data were ever used to model individual neurons. For each neuron, once a quantitative spatial summation model (α and n in Eq. 1) is determined on the basis of responses when attention is directed outside of the RF, the ability of the two models to explain responses when attention is directed within the RF can be compared. Only cells that were well fit by the spatial summation model, as defined by a normalized error of <0.5, (90 of 159, 4 target, and 43 of 43. 2 target) were included in this testing of attention models. Because the two attention models have a different number of free parameters, we used an F-test to evaluate whether the addition of extra parameter in the input gain model resulted in a significant improvement in fit. While, for many individual neurons in the four-target sample (37 of 90, F-test, P < 0.05) the output gain model is significantly worse than the more generalized input gain model, the incidence of input gain superiority is significantly less (binomial, P < 0.05) in the two-target data set (12 of 43, F-test, P < 0.05; Fig. 3, A and B). The median error for the output gain model is also larger in the four-target data set. As expected from these observations, when the two models are tested on average neuronal responses (sorted according to orientation and location preference) within the two sets, the input gain is only superior for the four-target data (+ and x vs. * in Fig 3A). Further distinctions can be seen when comparing the two parameters of the input gain model (attentional modulation to the attended stimulus and to the unattended stimulus) for the two-target and four-target data sets (Fig. 3C). In particular, three special cases of input gain model can be examined: the previously mentioned case in which attention modulation is constant within the RF (output gain), a case in which modulation only occurs at the attended location (“spotlight”), and a case in which modulation only occurs at the unattended location (“filter”). For both data sets, relatively few cells have input gain parameters consistent with simpler models (Fig. 3), even among the two-target data. However, the two-target population is notably different from the four-target population in that there is no consistent difference between attentional modulation at the two locations (paired t-test, 2 target P = 0.179; 4 target P < 0.001). The results underlie that apparent shifts between output gain and input gain can be explained by a simple change in the spatial extent of attentional modulation.

FIG. 3.

Input gain model fit and parameters for 2-target (monkey Y) and 4-target data (monkeys P and T). Normalized error (sum of errors squared divided by explainable variance) for the input gain vs. output gain models is plotted for the 2-target (triangles, n = 43) and 4-target (circles: monkey P, n = 39; squares: monkey T, n = 51) data sets (A). Filled symbols indicate significant difference in error (F-test, P < 0.05) between input gain model, in which attention is free to vary between the 2 locations within the RF and the output gain model, in which attentional gain is locked throughout the RF. Median errors are indicated along the axes (triangles, monkey Y; diamonds: monkey P; arcs, monkey T). While input gain is clearly superior to output gain in explaining the 4-target data for many cells, fewer cells in the 2-target sample are preferentially fit by the input gain model. Similarly, input gain is clearly superior to output gain in explaining the average response observed for the 4-target monkeys (plus and x) but not for the average for the 2-target monkey (asterisk). For the 4-target data (gray, monkey P; black, monkey T), the responses from <10% of cells were equally well explained by the 2 models (B), whereas for the 2-target data (white), the 2 models were equally valid for >35% of neurons. Despite the equivalent behavioral significance of attended and unattended stimuli between recording sessions, gain parameters vary substantially between neurons in both data sets (C). Median input gain parameters for the attended and unattended location are indicated by triangle markers on the axes. There is no obviously clustering of points along the lines corresponding with the simpler single parameter attention models (vertical: filter, diagonal: output gain, and horizontal: spotlight) in any animal. Attended stimulus gains were significantly larger than unattended gains for the 4-target data (filled circles, P < 0.001, paired t-test) but not for the 2-target data (open circles, P = 0.179). Average gain across the sampled neuronal population is significantly positive at the attended location (2-target, P = 0.012; 4-target,P < 0.001) but not significantly different from zero at the unattended location (2-target, P = 1.00; 4-target, P = 0.184).

Center-surround attentional modulation

The diversity in input gain parameters among cells and between tasks suggests that not only the magnitude but also the exact spatial distribution of attention modulation is flexible. Such flexibility is consistent with psychophysical observations of attentional windows, in which the spatial extent of attentional effects can be adjusted according the spatial distribution of behavioral relevance (Eriksen and St James 1986; Eriksen and Yeh 1985; LaBerge 1983; LaBerge and Brown 1986). Moreover, the prevalence of negative coefficients among the modulations seen for unattended stimuli, especially with the four-target data, is consistent with psychophysical observations of behavioral impairment at locations surrounding the attentional locus (Cutzu and Tsotsos 2003; Suzuki and Cavanagh 1997). Finally, microstimulation within an area associated with saccadic planning (FEF) produces facilitation among V4 neurons with corresponding RF locations and suppression for neurons with noncorresponding RFs (Moore and Armstrong 2003). One simple model that can accommodate all of these observations is one in which the spatial distribution of attentional modulation is characterized by a center surround organization in which facilitatory effects are spatially localized and surrounded by a region of suppression. To account for task-dependent differences in the spatial extent of attentional effects (Cutzu and Tsotsos 2003; Suzuki and Cavanagh 1997), the size of the facilitatory and suppressive envelopes are flexible. Such a model is appealing in that center-surround organization is a defining characteristic of RFs throughout the visual pathway. Thus a model in which attentional modulation is also governed by center-surround organization is a potentially elegant solution for distribution of attentional modulation across a map of visual space because it could potentially make use of the same set of biophysical and circuitry properties responsible for sensory RF organization. When attentional modulation is distributed in such a center-surround fashion, it can exert a “push-pull” effect by selectively increasing the influence of inputs representing attended regions or stimuli and conversely decreasing the influence of inputs representing unattended regions or stimuli.

We adopted a center-surround model of attentional modulation based on sensory center-surround interactions of V1 neurons in which a divisive process best explains the surround suppression. We chose V1 observations as a starting point because the spatial summation of individual neurons in the area has been the most extensively studied and quantified (Bair et al. 2003; Cavanaugh et al. 2002a,b; Levitt and Lund 2002; Rust et al. 2005; Smith et al. 2006). However, because we define all spatial parameters relative to RF size, the same model applies to any RF with center-surround properties, including those in areas V2 (Burkhalter and Van Essen 1986), V3 (Gaska et al. 1987), V4 (Desimone and Schein 1987; Tanaka et al. 1986), and MT (Born and Tootell 1992; Pack et al. 2005; Raiguel et al. 1995; Xiao et al. 1995). We define attentional facilitation according to excitatory Gaussian region of facilitatory gain and attentional suppression according to a co-extensive Gaussian with suppressive gain. When the suppression is weaker but broader in spatial extent, this produces attentional modulation consistent with input gain model: facilitation at the center of attention, suppression surrounding this center, and decreasing modulation with increasing distance from the center of attention. Consistent with the averages seen among V1 cells, we initially define the ratio of surround/center radii to be 2.5, and the surround/center amplitude to be 0.5 at the center of attention. These parameters define the relative, but not absolute, sizes of center facilitation and surround suppression. The only remaining free parameters are therefore the size of central attentional facilitation (σ_F) and its amplitude (A_F). For the parameters of unattended and attended gains, we used the results of the input-gain modeling described previously on the average responses (+, x, and * in Fig. 3A) within the two- and four-target data set. Attended gain was set at 1.38, an average of the values obtained in the two-target (1.42) and four-target (1.34) sets. The RF sensitivity was modeled as a single excitatory Gaussian of width σ_R. Because Gabors were well centered, the average difference in sensitivity between the two locations was small (0.24σ_R). As shown in Fig. 4, a change in extent of facilitatory modulation by attention is sufficient to explain the observed differences in input gain parameters between the two- and four-target samples (Fig. 3): the attentional window is smaller in the four-target case (σ_F = 0.2σ_R), creating, on average, suppression of the unattended location (gain = 0.92), and slightly broader in the case of the two-target case (σ_F = 0.46σ_R), resulting in positive modulation at the unattended location (gain = 1.1). If attention is centered on the RF of the neuron under study, as was approximately the case for both the two- and four-target studies, this center-surround modulation produces relatively modest changes in the spatial sensitivity of a neuron. This can be seen by modeling the RF by a Gaussian profile consistent with the average inputs in the spatial summation models without attention (Fig. 4B): the resulting RF profiles are similar for both the two-target and four-target case (Fig. 4B), despite the large difference in the effect of attention on unattended stimuli. This highlights that careful modeling of spatial summation is a necessary prerequisite for quantitative measurements of attentional modulation.

FIG. 4.

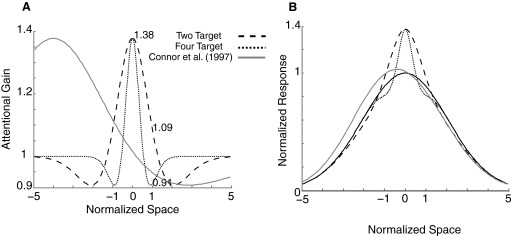
Center surround models of input gain fit according the parameters in Fig. 3A. Gain at the attended location is assumed to be maximal at the center of the RF for the 2-target (- - -) and 4-target (···) cases and fixed at 1.38, while gain at the unattended location (x = 1) is 1.1 for 2 targets and 0.91 for 4 targets. Visual sensitivity over space in the absence of attention is modeled by a Gaussian of SD 2 (black, B). RF differences between the 2- and 4-target attention allocations are only apparent near the center of the RF: beyond x = 2, visual sensitivity is virtually identical (B). On the other hand, when attention is directed outside of the receptive field (gray, A), a notable shift toward the direction of attention is apparent in the spatial weighting of the receptive field (gray vs. black), consistent with experimental observations.

If attention is not centered on the RF but rather centered just outside of the RF, a more substantial change in RF profile is observed. To test the effects of such attentional misalignment, we introduced a spatial offset between RF center and attentional focus consistent with that used by Connor et al. (1997) in their study of V4 responses when attention was directed outside of RFs (4 σ_R). If attention was distributed with a similar extent to RF size (σ_F = 1.5σ_R), then RFs shift notably in the direction of attention (Fig. 4B). Under such conditions, our model produced a facilitation factor, which compares visual sensitivity in the direction of attention with sensitivity away from the focus of attention of 0.10, which corresponds well with the average across the neuronal population reported by Connor et al. of 0.15.

For these analyses, the magnitude of attentional modulation at the center of attentional focus was held fixed. We term this factor, which corresponds with the input gain parameter of the attended stimulus in the previous analyses, “attention gain.” This can vary substantially between animals and depends on nonspatial parameters such as task timing (Ghose and Maunsell 2002), difficulty (Boudreau et al. 2006; Spitzer et al. 1988), and featural attention (Boynton 2005; Martinez-Trujillo and Treue 2004; Maunsell and Treue 2006; Treue and Martinez-Trujillo 1999). An increase in attention gain would not alter the fundamental difference seen at the unattended location between the two- and four-target stimulation (facilitation vs. suppression) but would increase the RF shift seen when attention is directed outside the RF. For example, if maximal attentional gain were increased from 1.38 to 1.93, the facilitation factor quantifying RF shift would match the average reported by Connor et al. On the other hand, if we assume that difficulty and timing to be constant, we would expect this magnitude to depend on the spatial extent of attention: when expectations are broadly spread over space, the behavioral effects are more modest at a particular location than when expectations are highly localized. To generalize the model across large changes in the spatial extent of attention allocation, we therefore postulate that overall attention gain decreases with increases in the size of attentional focus (Eqs. 4 and 5).

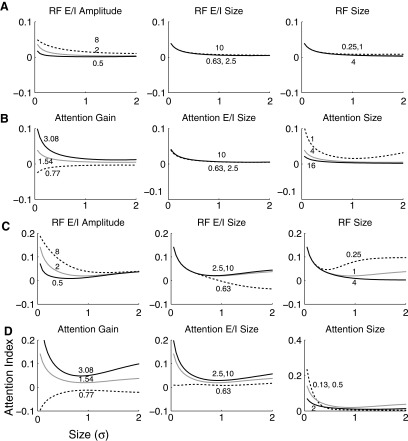
With this more generalized model and the incorporation of divisive normalization among the facilitatory and suppressive sensory inputs to a neuron, we can explore how RF and attentional parameters might alter spatial sensitivity profiles by plotting attention modulation as a function of stimulus size. Attentional modulation was quantified according to an attention index that is the difference between attended and unattended responses divided by the sum of attended and unattended responses to identical visual stimulation. Thus positive values indicate facilitation, and negative values, suppression. In these cases, attention was centered on the stimulus and the RF of a model neuron. When attention is broad compared with RF size (4 σ_E, where σ_E is the width of the excitatory input Gaussian), attentional effects are constant with changes in the size of the sensory facilitation (RF size), the size of the sensory suppression (“RF E/I size”), and the size of the attentional suppression (“attention E/I size;” Fig. 5 A). Thus attentional effects would be relatively constant across the variations in RF size parameters expected among the neuronal population within a given area such as V1. However, our model does predict that attentional effects would vary modestly with the strength of sensory suppression with slightly larger modulation seen for RFs that are not strongly length tuned. In a pure output gain model, there would no dependency of attentional effect on stimulus size. Except for the very smallest stimuli, attentional modulation is largely independent of stimulus size for a wide range of receptive parameters, consistent with what would be observed with an output gain model.

FIG. 5.

Attentional modulation as a function of stimulus size when parameters of the center-surround gain model are varied. Attention index is the difference between attended and unattended responses divided by the sum of the responses. Space is normalized according to the size of the central excitatory Gaussian in a divisive normalization model of the RF, and attention is centered at the center of the RF (x = 0). The spatial extent of attentional facilitation is defined to be 1 in A and B and 0.5 in C and D. For almost all parameter variations, the effects of attention decrease as stimulus size increases: the strongest attentional effects are seen for small well-centered stimuli. Attention effects are more dependent on RF properties such the strength and size of the surround when attention is narrowly focused (C vs. A). Under most conditions, the exact size of the suppressive region of attention (attention E/I) has a minimal effect of responses. Attention gain, associated with nonspatial factors such as anticipation and task difficulty, is the biggest determinant of the magnitude of attention effects (B and D).

When the spatial extent of attention modulation is better matched to the size of the visual RF (1 σ_E, Fig. 5, C and D), the departures from output gain predictions are more substantial. For small stimuli, the strength of length tuning has a larger effect on attentional modulation than is seen when attention is more broadly distributed (RF E/I amplitude, C vs. A). When attention is more localized, the effects across of a population of neurons with different RF properties are more diverse than seen with broadly distributed attention. For example, neurons with limited regions of sensory suppression (RF E/I size) can be suppressed by attention, while neurons with large suppressive zones are facilitated.

The input gain model also provides an explanation for a common observation in attentional studies: the presence of a small proportion of neurons with “negative” attention effects, in which responses are reduced when attention is directed within the RF. Although response suppression is to be expected when subjects are actively ignoring a region of space (corresponding with negative attention gain in Fig. 5, D and E, left), the presence of response suppression with selective behavioral facilitation has been difficult to explain. The input gain model, on the other hand, offers an explanation for the presence of such neurons by predicting that attention suppresses the responses to large stimuli that activate neurons with particularly strong suppressive surround regions.

Attentional effects on surround properties

The V4 data suggest that spatial attention is not necessarily uniform within RFs. This heterogeneity suggests that under some circumstances, spatial attention could alter the balance of facilitatory and suppressive influences underlying phenomena such as length tuning or surround suppression. To see whether our model might explain observations of attention affecting V1 surround interactions, we modeled responses under different attentional allocations as a function of stimulus size with a RF defined according to the averages found among V1 cells (E/I size = 2.5). Ito and Gilbert (1999) reported that spatial attention could either increase or decrease the facilitation seen when a stimulus was added just outside the classic RF. To study this effect, we compared the response to a well centered stimulus of size 0.25 σ_E with the response for a stimulus that extends just beyond the classic RF (1.5 σ_E, determined by the closest location of a subthreshold difference between facilitatory and suppressive inputs), and used the same facilitation index developed by Ito and Gilbert (Fig. 6). We modeled two cases: one in which suppression was weak (E/I = 5) and surround facilitation was observed, (Fig 6, center) and another where suppression was strong (E/I = 0.25) and responses decreased as the stimulus extended beyond the RF (Fig. 6, right). For the cell with strong spatial suppression (Fig. 6, right), attention had little effect on the decrease in response seen with increasing stimulus size. For cells with facilitation immediately outside the classic RF, however, attention can strongly affect the amount of that facilitation. Without attention, or with attention directed away from the neuron's RF, these two cases yield a facilitation index of +0.90 and −0.14, respectively (Fig. 6A). When attention is broadly distributed (4σ_E), these indices are relatively unchanged (Fig. 6B), consistent with Ito and Gilbert's observations. When attention is narrowly distributed (0.5 σ_E), facilitation decreases substantially, from 0.90 to 0.55, consistent with one of the animals in the Ito and Gilbert study (Fig. 6C, center). This occurs because attention selectively increases responses near the center of the RF, and therefore the relative increase with stimulus size is less. Conversely, a strong increase in facilitation can occur if the center of narrow attention is offset from the center of the RF (0.90–1.18) because spatially selective attention is directed toward the edge of the classical RF where the surround facilitation is located.

FIG. 6.

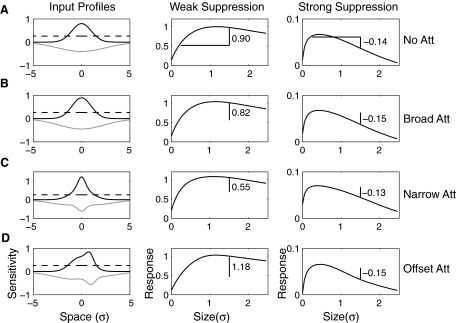
Attentional effects on extra-RF facilitation and suppression. Spatial summation is described by center and surround inputs with Gaussian profiles in the absence of attention (A, left). Responses are defined by applying a threshold (dotted line) after the inputs of center (black) and surround (gray) inputs (arbitrary units) are multiplied by gains describing their relative influence and then normalized by divisive normalization (Cavanaugh et al. 2002a). Because of this threshold responses to stimuli extending beyond the classical receptive field can be larger than those that are well confined if the surround influence is relatively weak (center). A facilitation index is computed by subtracting one from the ratio of the response to larger stimulus to the response to the smaller stimulus. If the surround influence is weak (surround/center gain = 0.2), a positive facilitation index is observed (center), while if the surround is strong (right, surround/center gain = 4), a negative index, reflecting response suppression, is observed (right). While attention has relatively modest effects of the magnitude of suppression for strongly length-tuned neurons (A vs. B–D, right), it can either increase or decrease facilitation in the case of weak surrounds (A vs. B–D, center). Narrowly focused attention can decrease facilitation (C, center) by selectively increasing the weight of central inputs (C, left). However, narrowly focused attention, if is not centered on the RF, can also increase the relative influence of noncentral inputs (D, left) and therefore increase facilitation (D, center).

The results indicate that the amount of facilitation observed with attention depends critically on the alignment of attention to the RF center. Ito and Gilbert observed that in one animal, facilitation increased with spatial attention, and in another, it decreased. If such differences were due to the animals deploying attention at different locations, one would expect corresponding behavioral differences as well. For example, when attention was well centered on the RF, the flanking stimulus in the surround should have little influence on behavior. On the other hand, if attention was not properly aligned and instead was directed in between the center and flanking stimuli, the presence of the flanking stimulus should affect behavioral performance. These behavioral predictions of attentional allocations are consistent with the performance of the animals: behavioral suppression of the flanking stimulus was only observed in the animal the neurons of which exhibited a decrease in spatial facilitation with attention. For the other animal, no such behavioral suppression was observed, consistent with an attentional locus in between the center and flanking stimuli and therefore offset from the center of the RF.

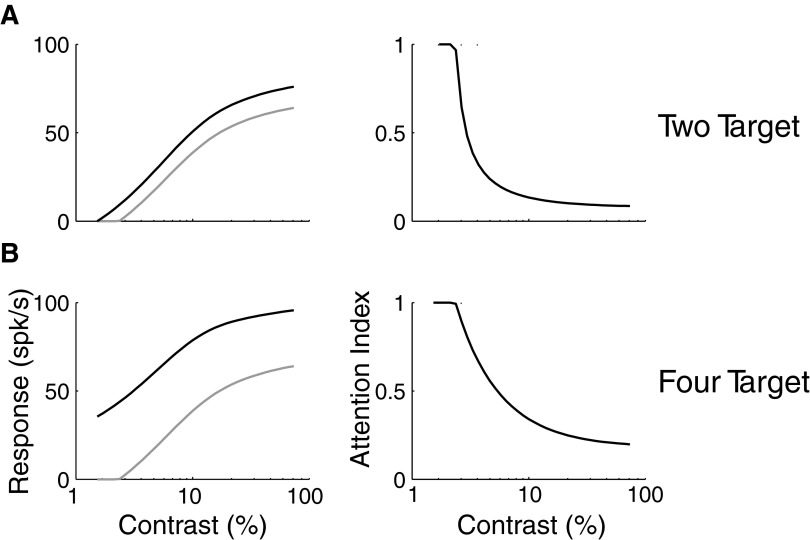
Contrast-dependent attention

The two predominant models for how attention interacts with contrast are response gain and contrast gain (Williford and Maunsell 2006). In response gain, the effect of attention is to multiplicatively increase responses independent of contrast. Thus, for this model to be strictly true, the attentional index would have to be constant across all contrasts. On the other hand, in a pure contrast gain model, the effect of attention is equivalent to an increase in contrast. Because of response saturation responses at high contrasts are relatively unaffected by attention in this model. Conversely, at low contrasts, because of spontaneous activity, a shift in effective contrast produces minimal changes in response. Thus attentional modulation is strongest for stimuli around contrast threshold.

To study how attention might affect contrast response properties in our model, we incorporated the differential contrast sensitivity of excitatory and inhibitory inputs (E and I in Fig. 6) in the Cavanaugh model of V1 sensory RFs (Cavanaugh et al. 2002a). As with the center-surround model (Eq. 6), we chose V1 data as a starting point because contrast sensitivity within V1 RFs has been the most extensively studied and because all spatial parameters in our model are relative to RF size. However, it is likely that differential contrast sensitivity between excitatory and inhibitory inputs is a common feature in the visual system. For example, in area MT, contrast sensitivity varies between the excitatory center and inhibitory surround (Pack et al. 2005). In both V1 and MT, this difference results in the size of sensory RFs, defined by a suprathreshold difference between excitation and inhibition, depending on contrast, and suggests the possibility that when attentional effects on the inputs are incorporated, contrast-dependent attentional modulation may also be observed. We computed responses for four different stimulus sizes (0, 0.5, 1, and 4σ_E) and three different attentional allocations (none; narrow, 0.5 σ_E; broad, 4σ_E) as a function of contrast (Fig. 7, left). To quantify the effect of attention, we computed attentional indices, where zero indicates no attentional effect, as a function of contrast. Consistent with many observations, but inconsistent with a pure contrast gain model, attention increases responses even at suprathreshold contrasts. For a stimulus that is small and perfectly centered, attentional modulation is constant across contrast, consistent with an output gain model (Fig. 7A). However, for a variety of stimuli and attentional allocations, deviations from a pure output gain model are apparent, especially just below contrast threshold (Fig. 7, B–D). This range of contrasts is where attentional modulation would be maximal under a pure contrast gain model. Thus the model predicts that under many circumstances, attentional modulation would exhibit both contrast- and activity-gain-like behavior (Williford and Maunsell 2006) and that ability of one or the other of these models to describe individual experiments would depend both the stimulus size and the spatial extent of attention.

FIG. 7.

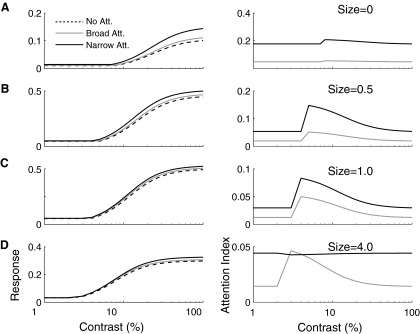
Contrast dependence of attention modulation as a function of stimulus size and the spatial extent of attention. Neuronal responses (left) are in arbitrary units, and attentional modulation (right) is quantified according to the same attention index used in Fig. 5. As with previous figures, stimulus size is normalized according the SD of the central Gaussian in the divisive normalization model. In accordance with Fig. 5, the effect of attention is the greatest for very small well centered stimuli (A). For such stimuli, irrespective of the size of the attentional gain field, attention modulation is consistent across variations in contrast. However, for larger stimuli (B–D), especially those on the order of the size of the RF (C), attentional modulation is larger at intermediate contrasts near threshold then it is for high-contrast stimuli, consistent with a shift in contrast response functions.

Contrast-dependent attentional effects have also been reported when pairs of stimuli of different contrasts and movement directions were presented within the RF of MT neurons (Martinez-Trujillo and Treue 2002). Because normalization across different sensory inputs applies even at low contrasts, the interpretation of attentional effects in this situation depends on the spatial summation properties of MT neurons, just as was necessary for V4 neurons (Figs. 2 and 3). We have modeled the inputs associated with the null direction as being 0.1 the magnitude of those associated with the preferred direction and used a normalization model based on a squaring of the inputs. We assume that there is no modulation of the unattended stimulus, analogous to the allocations seen in the two-target case for V4 neurons. To study contrast dependency, we applied a sigmoidal contrast dependence to the inputs in which we have defined threshold as the contrast value at which half-maximal response is observed (c₅₀ = 10%). We also applied a slight contrast correction to the normalization in accordance with experimental observations (Heuer and Britten 2002). Based on the input gain models of the V4 data, we applied two models of attention: one in which the attended stimulus input was multiplied by 1.63 and the unattended stimulus input was not changed (2-target model, Fig. 8 A), and one in which the attended stimulus was facilitated and the unattended stimulus suppressed (4-target model, Fig. 8B). In both cases, attention increases responses across all contrasts but has the greatest effect at low contrast. Attentional modulation is observed to increase just below threshold, just as was observed with the center-surround model of Fig. 7. Also similar to the center-surround model, attentional modulation is present even at full contrast, so that the overall effect is consistent with neither a pure contrast gain nor a pure output gain model (Williford and Maunsell 2006).

FIG. 8.

Contrast dependence of attention modulation in MT responses to paired stimulation. Attended (null direction) and unattended (preferred direction) stimuli were modulated according the mean input gain parameters of the 2- and 4-target data (Fig. 4), and the contrast of the unattended stimulus was modulated. Responses with attention (black, A) were increased across all contrasts relative to responses without attention (gray, A). However, this increase was not uniform and, consistent with the responses to single stimuli in Fig. 7, was larger for contrasts near threshold.

DISCUSSION

Experimental observations of the responses of neurons in area V4 to changes in stimulation and behavioral relevance suggest that spatial attention can selectively change the gain of specific inputs to a neuron. These observations suggest that attention in a variety of situations may act through a common mechanism by altering the gain of specific subpopulations of neurons in accordance with behavioral relevance. In this paper, we implement a specific spatial pattern of gain modulation in which central facilitation is surrounded by suppression. The model is accordance with psychophysical observations of center-surround facilitation and suppression of performance as well as established patterns of spatial summation seen in neurons with primary visual cortex. By assuming that the spatial extent of this facilitation and suppression is flexible and reflects the spatial expectations of a subject, the model can reconcile numerous observations in the attention literature that appear contradictory. These include variable effects of center-surround sensory interactions, variations between experiments employing paired and single stimuli within RFs and variations in the degree to which attention preferentially affects responses to low-contrast stimuli.

Flexible attentional allocations

Attention is by definition flexible in that it can selectively enhance the perception of particular locations, objects, or epochs of time. The allocation of attention can potentially vary substantially between different tasks and between different subjects (Boudreau et al. 2006; Ito and Gilbert 1999) and is likely to be responsible for the observed differences between the two- and four-target data sets. Although many factors may alter a subject's spatial allocation of attention, two factors are likely to be particularly significant. The first is past experience or training: even for identical tasks and stimuli, different subjects may choose to attend to a broad or a narrow region of visual space if either strategy is sufficient to accomplish the task (Boudreau et al. 2006). Similarly, subjects may attend to different locations relative to stimulation as is suggested by the Ito and Gilbert results. We feel that adoption of different attentional strategies, due to a slight change in stimulus configuration that maintained throughout training, is the most likely explanation for the differences between the four-target data, which were acquired from two animals, and the two-target data, which were acquired from a third animal. Most factors were very similar between the two data sets including task timing, stimulus type and contrast, and reward scheduling. Moreover, physiological parameters, such as the magnitude of responses and typical RF location and size, were also similar between the two data sets. On the other hand, the behavioral strategy employed from the two-target animal appeared different from that of the other two animals: after two-target training and neurophysiological recording, he was unable to consistently perform well in the four-target task but always able to perform the two-target task even after 9 mo of training. This suggests that the strategy used by the third animal, for which the most foveal stimulus within a cued quadrant was behaviorally relevant, was distinct from those employed by the other two animals. It is therefore possible that the third animal invoked attentional mechanisms fundamentally distinct from those employed in the four-target animals. However, as demonstrated by our analysis, it is not necessary to invoke a completely different theory of attentional modulation to explain such variations: the input gain model provides a single parsimonious theory with testable predictions that can explain variations between subjects even when testing conditions are identical (Boudreau et al. 2006; Ito and Gilbert 1999).

Because of the slight difference in stimulus configuration, we similarly cannot rule out the possibility that intrinsic sensory or attentional biases may have also contributed. For example, highly visible and spatially distinct stimuli might be associated with lower and spatially diffuse attentional allocation, whereas stimuli that are less visible or in more crowded environments are associated with higher and more localized attentional allocation. Biases with respect to visual eccentricity might explain the discrepancy between the input gain parameters of the two- and four-target data. Because in the two-target task the attended stimulus was always more foveal to the unattended stimulus, even without attention, it was more salient and therefore on average required less spatially selective attention. It is also possible that attentional modulations themselves have an intrinsic bias toward low eccentricities irrespective of training, which would have selectively affected the two-target results because of the eccentricity difference between the attended and unattended stimulus.

Whether due to the adoption of different strategies or slight differences in stimulus configuration, the differences between the two- and four-target data emphasize the importance of simultaneous behavioral and physiological measurements. For example, the two-target data are certainly consistent with a broader spatial allocation of attention, but without behavioral evidence of such allocation, other explanations cannot be excluded. Behavioral measurements are especially important if the exact magnitude and spatial distribution of attention is not strongly constrained by task design because fluctuations in attention over space or time might also contribute to neuronal response variance. Behavioral variability might explain inconsistencies in the literature with regard to the attentional modulation of visual responses to high-contrast singleton stimuli. In studies reporting minimal attentional effects for such stimuli (Moran and Desimone 1985; Reynolds et al. 2000), subjects may not bother allocating attention for readily detectable changes, whereas in studies reporting attentional modulation for such stimuli (McAdams and Maunsell 1999; Salinas and Abbott 1997; Treue and Martinez-Trujillo 1999), the required change may have been sufficiently difficult or infrequent so that subjects more consistently allocated attention. Similarly, the relatively wide variations seen between different cells in input gain parameters (Fig. 3), may reflect fluctuations in the spatial allocation of attention in addition to differences in the overall sensitivity to attention between different neurons. Because attention can be modulated rapidly (<100 ms) (Ghose and Maunsell 2002), to measure the contribution of such behavioral fluctuations to response variability, it may be necessary to continually assess the magnitude and spatial extent of behavioral modulation during physiological measurements.

Model validation

In our model, we used a psychophysically documented flexibility in the spatial extent of attention (Eriksen and St James 1986; Eriksen and Yeh 1985; LaBerge 1983; LaBerge and Brown 1986) to explain specific observations of attentional modulation with different tasks and stimuli. In the case of single-cell responses, the input gain model states that the same nonlinearities encountered when superimposing multiple stimuli in the absence of attention, or when attention is directed outside of the RF, should also apply when attention is directed within the RF. For example, if strong nonlinearities exist such that modest changes visual stimulation result in large changes in neuronal output, then even a very weak attentional input could have a dramatic effect on output. In such a situation, the magnitude of attentional effects at a cellular level would depend not only on the strength of the attentional inputs but also on the degree of nonlinearity within individual neurons. Because nonlinearities can vary substantially between individual neurons, a careful examination of the nonlinearity and parameters of sensory summation provides a critical test for the input gain model. Although there have been several quantitative studies of how sensory inputs are integrated at the cellular level in a variety of visual areas (Britten and Heuer 1999; Zoccolan et al. 2005), few of these studies have incorporated spatial attention. Similarly, most studies of spatial attention have not rigorously examined sensory summation and integration. Although the V4 data set examined both spatial summation and attentional modulation simultaneously, many neurons in that area exhibit higher-order feature selectivity that precludes a easy modeling of spatial summation: only half the neurons in that study had responses to paired stimuli that could be explained according to their responses to the stimuli separately. This likely due a mismatch between our stimulus set (single orientation sinusoidal gratings) and RF selectivities in V4. For example, if a neuron was selective to a particular conjunction of orientations (like a cross), then its responses would not necessarily be well characterized by the responses to the constituent orientations separately, just as orientation selectivity in V1 neurons is not predictable by responses to small unoriented dots.

To better test the input gain model, the combined summation and attention approach should be applied using stimuli and neurons for which good RF models have already been demonstrated. For example, length tuning in area V1 can be quantitatively modeled using a divisive surround model (Cavanaugh et al. 2002a), so studying attentional modulation as a function of size would provide a robust test for the input gain model, provided that the spatial extent of attention could be verified behaviorally. As shown in Fig. 5, the input gain model generates very specific predictions regarding the sign and magnitude of attentional modulation as a function of RF properties. For example, for very small RFs with strong surround suppression (E/I size small), the model predicts that broadly distributed attention should suppress responses (Fig. 6C center). Conversely, for neurons with minimal suppression (E/I amplitude large), attentional modulation should be inversely related to stimulus size (Fig. 5C, left).

The input gain model could also be tested by seeing whether the variations in the effect of attention on contrast sensitivity seen among different cells are correlated with differences in spatial summation. In the model, the only way contrast-dependent modulation can occur is when there is a difference between the contrast sensitivities of the excitatory and inhibitory inputs. Such can be evaluated by measuring size tuning curves (such as those of Figs. 5 and 6) with different contrasts (Cavanaugh et al. 2002a). The input gain model states that the strongest deviations from activity gain should occur for those neurons whose size tuning is most dependent on contrast. Additionally the model predicts that effects consistent with contrast gain should be preferentially observed with larger stimuli (Fig. 7) because inhibitory influences are the most significant for such stimuli.

In all cases of attention allocation and RF configurations, the model predicts that maximal attentional modulation will be observed for small stimuli that are well centered on the RF. Because robust attention effects provide the best test of any attentional model, it is advantageous to study neurons with relatively large RFs and simple rules of stimulus summation. In this regard, neurons in two extrastriate areas are good candidates for validating the input gain model. For most neurons in area MT, responses to pairs of preferred direction stimuli can be predicted by individual stimuli responses according to Eq. 1 (Britten and Heuer 1999). Furthermore, MT neuronal responses are modulated by attention (Cook and Maunsell 2002; Seidemann and Newsome 1999; Treue and Martinez-Trujillo 1999; Womelsdorf et al. 2006), and certain observations with paired stimulation are consistent with a competition-like model (Treue and Maunsell 1999). Thus an experimental design similar to that employed for the V4 data, in which attention was directed to particular locations within the RF while responses to single and paired stimulation are measured, could be applied by measuring MT responses to localized motion stimuli. Another area for which relatively simple rules of sensory summation are applicable is area IT when object pairs are presented (Zoccolan et al. 2005). In the case of IT neurons, once object preferences are established for a particular neuron, the input gain model could be tested using combinations of preferred and nonpreferred stimuli with attention directed to one of the stimuli.

Comparison with other attention models

Several mechanistic models have been proposed to describe the effects on spatial attention on neuronal responses. Reynolds et al. (1999), for example, proposed a dynamic model in which the influence of specific inputs to a neuron could be targeted by attention and that incorporated a divisive normalization of excitatory and inhibitory inputs similar to that described in our formulation of center-surround interactions (Eq. 6). Our model is similar to theirs in that it incorporates the potential for heterogenities in the effect of attention on a neuron's inputs as well as nonlinearities in input summation. However, our formulation and approach differs from theirs in a number of respects. Most notably their model is relatively inflexibile with regard to the implementation of attention: it stipulates that attention modulation occurs by a fivefold amplification of synaptic gain of input neurons. Physiological data clearly show that attentional modulation varies between different neurons and varies across space and time (Ghose and Maunsell 2002) according to task demands. To explain this variability within the Reynolds model requires changes in the balance of excitation and inhibition that would necessarily change sensory RF integration. Thus unlike the input gain model, different attentional effects can only be explained with changes in the integration of inputs. Furthermore because the model stipulates that attentional modulation occurs without any change in the actual responses of input neurons, it does not readily accommodate observations consistent with gain changes (McAdams and Maunsell 1999). This is a critical distinction with our input gain model, which specifically relies on gain changes in the responses of input neurons rather than synaptic modification of the afferents of those neurons.

Because of this inflexibility it is unclear how well the Reynolds model can explain an experimental data set containing both paired and single stimulus response. Unlike the input gain model (Ghose and Maunsell 2008), the Reynolds et al. model was never tested with data from neuronal recordings; instead it was applied to a population of simulated neurons with a random distribution of input parameters. For example, the model is described as consistent with response averaging but that is never explicitly tested. By contrast, response averaging was tested using our spatial summation model and found to be a poor model for most V4 neurons (Ghose and Maunsell 2008). Similarly because the Reynolds model does not incorporate spatial RF properties such as center-surround organization and the differential contrast sensitivity of excitatory and inhibitory inputs, it is also unclear how consistent it is with known rules of sensory integration. This makes it difficult to generalize to a variety of RFs so as to produce testable predictions that are the crux of this manuscript.

More recently Ardid et al. (2007) have implemented a neural network model in which the population activity in a working memory layer of neurons directs attentional modulation onto a sensory layer of neurons. The authors compare their model to experimental observations of attentional modulations observed in MT neurons and, as with the model described here, are able to produce both gain and biased competition phenomenology. In this sense, the model may provide a mechanistic explanation of our input gain model. However, this model employs very specific assumptions regarding both the connectivity within the layers of neurons and between the layers, and it is therefore unclear how well it can explain attentional modulations in a wide range of visual areas especially early visual areas that provide input to MT. For example, in their model, the sensory layer has strong recurrent inhibition while the memory layer has strong recurrent excitation, and the rich connectivity between different visual areas (Felleman and Van Essen 1991) is ignored. Although the model does describe interactions with different stimuli, just as with the Reynolds model, it is not clear whether it can accommodate commonly observed spatial RF properties such as center-surround organization or how the effects on attention might vary between neurons with different RF properties.

Attention in the visual hierarchy

Attention is a process of selective perceptual enhancement, so the proposal that attentional modulation can vary among the inputs to a particular cell may seem trivial. However, the generalizability of the model to the numerous areas associated with vision depends on a distributed allocation of attention effects: if attentional modulation was restricted to a certain visual area, then the input gain model would apply only to neurons receiving input from this area and not to any of the neurons providing input to the area. Although imaging studies suggest that attentional modulation can be seen in a variety of visual areas, suggesting that attentional effects are highly distributed among different areas (Hopf et al. 2006; O'Connor et al. 2002), the exact nature of this distribution remains controversial. Anatomical and physiological evidence suggests that visual areas are organized into a hierarchy in which RF size and complexity increases at higher areas (Felleman and Van Essen 1991; Riesenhuber and Poggio 1999). Most functional imaging and electrophysiological studies also suggest the magnitude of attentional modulation is larger in higher visual areas (Cook and Maunsell 2002; O'Connor et al. 2002). Our model suggests how this might arise simply by virtue of differences between the spatial extent of attentional allocation (Eriksen and St James 1986; Eriksen and Yeh 1985; LaBerge 1983; LaBerge and Brown 1986) and RF size, without requiring any fundamental difference in the nature or distribution of attentional inputs to different areas. As seen in Fig. 5, when attention is widely distributed with respect to RF size, the magnitude of modulation is modest over a large range of stimulus sizes: the largest modulations are seen when attention is distributed consistent with receptive size and for small stimuli. Because most spatial attention tasks use stimuli that are large with respect to RF sizes in the earliest visual areas, if attention was allocated according the stimulus size, attentional effects would be larger in higher visual areas simply by virtue of the larger RFs encountered in such areas. Our model further predicts that attentional modulation should be highest in the particular visual area the RFs of which are best matched to the spatial extent of attention as has been observed in a recent functional imaging experiment (Hopf et al. 2006).

Because of the evidence that attentional effects can be seen in a variety of visual areas (Hopf et al. 2006; O'Connor et al. 2002), any model of attention must consider how attentional effects in one area would propagate to other areas. In our model, when attention is broad with respect to the RF, the effect is comparable to activity gain, and thus the retinotopic extent of attentional modulation would be preserved in the output of this area to other areas. Thus it is possible that attentional inputs could selectively enter the visual system at the earliest stages of visual processing (O'Connor et al. 2002) or that the retinotopic distribution of attention inputs is similar for all visual areas. This also simplifies the control circuitry necessarily for the modulation of sensory signals at specific locations (Awh et al. 2006) because visuotopic feedback can either be consistently applied across different visual areas or restricted to an early visual area such as V1 or V2. On the other hand, a strict interpretation of activity gain, in which attention directed anywhere within a RF multiplicatively increases responses, is problematic for a distributed system because low-resolution (large RF) spatial representations would be amplified in the same manner as more appropriate high-resolution spatial representations. If behavioral performance was based on the distributed activity in multiple visual areas or the activity only in higher visual areas, then the degree to which attentional facilitation could be spatially selective would be necessarily limited. A strict interpretation of biased competition, in which attention is solely directed toward cells the RFs of which encompass potentially relevant stimuli, also seems problematic with respect to attentional control in that it requires a specific targeting of attentional inputs to a specific population within specific visual areas. For example, the Reynolds et al. (1999) formulation specifies that attention specifically modulates the synaptic gain of specific inputs but not the activity level of the neurons providing input. It also requires that the attentional inputs have higher spatial resolution than the affected neurons and that these inputs do not target the sensory representations that match their spatial extent. Thus for every spatial scale of attention allocation, a separate population of visuotopic attentional inputs with a distinct pattern of connectivity would have to be activated.

Attentional models typically distinguish between bottom-up modulations, in which signals propagate in feedforward manner from early areas in the visual hierarchy to higher areas, and top-down modulations governed by feedback connections. Our model does not put strong constraints on the relative role of feedforward and -back connections because both sets of connections potentially provide significant inputs to neurons. Because our model is fundamentally based on sensory integration, the relative importance of feedforward and -back connections in attentional modulation is determined by the relative contributions of these connections to underlying RF properties. For example, the spatial extent and dynamics of sensory surround suppression in area V1 suggests that it is not solely mediated by long-range horizontal connections within V1 but also involves feedback for higher visual areas (Cavanaugh et al. 2002a; Levitt and Lund 2002) In this case, our model stipulates that for neurons that exhibit strong surround suppression due to feedback connections, top-down attentional modulations may be more important than they are for neurons with little surround suppression.

One aspect that is not explicitly specified in our model is the mechanism by which the breadth of attentional focus is modified. While psychophysical experiments clearly point the plasticity of attention windows, they do not suggest the basis of this effect. In an oculomotor control scheme for attention (Awh et al. 2006; Moore et al. 2003), for example, the breadth of attentional window would be related to the spatial distribution of potential saccadic targets. In this case, the spatial distribution of activity within areas, such as FEF, typically associated with saccadic preparation and planning areas would critically control the retinotopic extent of attentional modulation.

Attention to features

Attention can be directed to both spatial locations and specific visual features. There are numerous studies which demonstrate that attention can be directed to features irrespective of location (He et al. 2008; Mitchell et al. 2004; Yantis and Serences 2003). Because featural attention can shift quite rapidly (Hayden and Gallant 2005), many tasks designed to explore spatial attention may also invoke featural attention (Boynton 2005). For example, in the two- and four-target experiments, once the Gabor at the cued location is identified, featural attention could be directed in accordance with that Gabor's orientation. In these experiments, it is clear that featural attention is not of primary importance: performance would be only 20% correct if subjects consistently looked for a particular orientation change irrespective of location. Moreover, from the lack of interactions seen in the ANOVAs of the single stimulus data, it is clear that any rapid deployment of featural attention does not have suppressive effects on other features, as was observed in a featural attention study (Martinez-Trujillo and Treue 2004). However, it is not clear whether the additive effect of spatial and featural attention reported by previous studies using single stimuli (McAdams and Maunsell 2000; Treue and Martinez-Trujillo 1999) also applies to paired stimulus responses and the extent to which object-based attention is dependent on spatial attention (Hayden and Gallant 2008; Lavie and Driver 1996). Physiologically, the question of whether attention to a particular feature has a spatially uniform effect throughout the RF remains to be examined.

One model that incorporates both the output gain effects seen in single stimulus studies of attention with featural specific enhancement and suppression is the feature-similarity gain hypothesis (Martinez-Trujillo and Treue 2004; Maunsell and Treue 2006). In this model, attention to a particular feature selectively enhances the responses of those neurons preferring that feature in a multiplicative manner and suppresses those neurons preferring different features. If visual space is considered a feature, this model is entirely consistent with our center-surround model of spatial attention: neurons that best matched to the attended location by virtue of their RF location are facilitated, whereas neurons that are mismatched are suppressed. The feature-similarity gain model was proposed on the basis of measurements obtained using single stimuli placed with MT RFs, so it is not clear how generalizable it is to situations in which in multiple stimuli are present within a RF. However, because it relies on gain-like effects on neuronal responses, feature-specific attentional effects could be easily incorporated into our model by making the attention coefficients (βs in Eq. 2) in our input gain formulation dependent on the attended feature. For example, in a situation in which attention was directed to particular orientation over an spatial window, the excitatory and inhibitory inputs underlying center surround organization (Eq. 6) would be modulated both according the spatial distribution of attention and the distribution of attention with respect to the feature of orientation. In this way, if an input was strongly tuned to a particular feature, then attention to that feature could increase the influence of that input beyond the effects seen with a purely spatial allocation of attention. As stated previously, the extent to which attention to features can be readily incorporated in such a manner requires further experimental studies in which the two types of attention are systematically varied.

Our model of attention modulation was motivated both by physiological studies of center-surround sensory interactions and by psychophysical evidence of a suppressive surround for spatial attention. The attentional suppression invoked, although relatively modest in magnitude, would localize the spatial distribution of activity in cortical areas, such as V1, with relatively strict retinotopic maps. In such areas, the model stipulates that focused attention creates a center-surround pattern of activity modulation over the cortical surface. If this physiological distribution of modulation was also seen in higher visual areas, in which attributes other than retinal location are mapped along the cortical surface, then nonspatial representations might also be selectively enhanced by similar circuitry. For example, if nearby neurons in inferotemporal cortex share object preferences (Wang et al. 1996), then such modulation would increase the relative strength of a particular object representation while suppressing the representations of other similar objects. Similarly, given the columnar organization with regard to preferred directions of motion in area MT, a center-surround modulation of activity over the surface of MT would create facilitation of attended directions of motions and suppression of unattended directions consistent with experimental observations (Martinez-Trujillo and Treue 2004). Thus if center-surround modulation is a common feature of cortical architecture, then the model described here to explain spatial attention may also be relevant to the physiological modulations underlying attention to specific features, attributes, or objects.

GRANTS

This work was supported by National Eye Institute Grant EY-014989 and the Alfred P. Sloan Foundation.