Functional Consequences of Neuronal Divergence Within the Retinogeniculate Pathway

Abstract

The neuronal connections from the retina to the dorsal lateral geniculate nucleus (dLGN) are characterized by a high specificity. Each retinal ganglion cell diverges to connect to a small group of geniculate cells and each geniculate cell receives input from a small number of retinal ganglion cells. Consistent with the high specificity of the connections, geniculate cells sharing input from the same retinal afferent are thought to have very similar receptive fields. However, the magnitude of the receptive-field mismatches, which has not been systematically measured across the different cell types in dLGN, seems to be in contradiction with the functional anatomy of the Y visual pathway: Y retinal afferents in the cat diverge into two geniculate layers (A and C) that have Y geniculate cells (Y_A and Y_C) with different receptive-field sizes, response latencies, nonlinearity of spatial summation, and contrast sensitivity. To better understand the functional consequences of retinogeniculate divergence, we recorded from pairs of geniculate cells that shared input from a common retinal afferent across layers and within the same layer in dLGN. We found that nearly all cell pairs that shared retinal input across layers had Y-type receptive fields of the same sign (i.e., both on-center) that overlapped by >70%, but frequently differed in size and response latency. The receptive-field mismatches were relatively small in value (receptive-field size ratio <5; difference in peak response <5 ms), but were robustly correlated with the strength of the synchronous firing generated by the shared retinal connections (R² = 0.75). On average, the percentage of geniculate spikes that could be attributed to shared retinal inputs was about 10% for all cell-pair combinations studied. These results are used to provide new estimates of retinogeniculate divergence for different cell classes.

INTRODUCTION

Visual information is transferred to the brain through multiple pathways that originate in different types of retinal ganglion cells and remain relatively well segregated through the dorsal lateral geniculate nucleus (dLGN) until they reach visual cortex (Cleland and Lee 1985; Cleland et al. 1971a; Hamos et al. 1987; Mastronarde 1992; Sincich et al. 2007; Usrey et al. 1999). In the cat, there are two main pathways (X and Y) that differ in their response properties and axonal projections. Whereas most X retinal afferents project to a single dLGN layer (i.e., layer A), and virtually each X dLGN afferent projects to a single cortical area (area 17), Y retinal afferents can diverge into two dLGN layers (i.e., A and C) and Y dLGN afferents can project to multiple cortical areas (for review see Sherman 1985). Y afferents, both retinal and thalamic, not only project to more brain structures than X afferents, but they are also likely to target more cells in each structure since they have larger axonal terminals (Freund et al. 1985; Humphrey et al. 1985; Sur and Sherman 1982). Therefore although originating in a small number of cells in the retina (Illing and Wassle 1981; Stein et al. 1996), the Y pathway is widely represented at the cortical level. This ample Y divergence in the cat is reminiscent of the primate magnocellular pathway in which also a minority of cells in the retina (∼8% of all retinal ganglion cells; Masland 2001) dominate half of layer 4C in primary visual cortex (Callaway 1998; for a more detailed comparison of Y and M pathways see Yabuta and Callaway 1998).

The functional significance of the large amplification of the Y pathway remains unclear, but one possibility is that it serves to diversify the sparse Y receptive-field array available in the retina (Mastronarde 1992; Yeh et al. 2003). Consistent with this hypothesis, here we demonstrate that Y geniculate cells sharing a common retinal afferent (as estimated by their precise synchronous firing) have receptive fields that show subtle mismatches in position, size, and timing. Moreover, we demonstrate that the strength of the synchronous firing generated by the shared retinal inputs is robustly correlated with the magnitude of the receptive-field mismatches—the stronger the synchrony, the smaller the receptive-field mismatches. In addition, we show that the percentage of dLGN synchronous spikes driven by common retinal afferents is relatively independent of cell class and is an order of magnitude lower than the percentage of spikes driven by dominant retinal afferents (Carandini et al. 2007; Cleland and Lee 1985; Cleland et al. 1971a; Sincich et al. 2007; Weyand 2007). Finally, our results provide new estimates of retinogeniculate divergence within the three major visual pathways (Y_A, Y_C, X_A). Preliminary results were previously presented in abstract form (Yeh et al. 2004).

METHODS

Surgery and preparation

Details of the surgical procedures have been described previously (Weng et al. 2005; Yeh et al. 2003). Young adult cats were initially anesthetized with ketamine and placed in a stereotaxic apparatus after being intubated. An intravenous catheter (Johnson & Johnson, Arlington, TX) was placed in each hindlimb to allow continuous infusions of thiopental sodium for anesthesia and atracurium besylate for muscle paralysis. All vital signs were closely monitored and carefully maintained within normal physiological limits. Saline was also supplied intravenously to maintain the animal hydration (the total fluid was given at a rate of 6 ml·kg⁻¹·h⁻¹). Nictitating membranes were retracted with neosynephrine, pupils were dilated with atropine sulfate, and contact lenses were inserted to protect the corneas and focus visual stimuli in the retina. By using a fiber-optic light source, the positions of the optic disk and the area centralis were plotted on the tangent screen that was placed 114 cm in front of the animal. The data reported in this study were collected from 23 cats that were also used for other research projects on thalamocortical connectivity over a period of time that spanned >5 yr. All procedures were performed in accordance to the guidelines of the U.S. Department of Agriculture and approved by the Institutional Animal Care and Use Committee at the University of Connecticut and the State University of New York, State College of Optometry.

Electrophysiological recordings and data acquisition

A matrix of seven independently movable electrodes arranged circularly was used to simultaneously record from multiple geniculate cells with spatially overlapping receptive fields (Thomas Recording, Marburg, Germany). The matrix was introduced into the brain (anterior: 5.5; lateral: 10.5) with a precise angle (∼25–30° anterior–posterior; ∼2–5° lateral–medial). The dLGN was identified by its precise retinotopic organization: small adjustments in the multielectrode position led to small changes in the receptive-field position of the recorded neurons that were consistent with the retinotopic map of dLGN. Several multielectrode penetrations had to be performed to find the retinotopic location where it was possible to simultaneously record from cells in layers A and C with overlapping receptive fields (see Fig. 1A). At this retinotopic location, an electrode penetration encountered a sequence of geniculate cells (all with superimposed receptive fields) that were driven by the contralateral eye (layer A), then the ipsilateral eye (layer A1), and then the contralateral eye again (layer C), with an approximate distance between layers of 500 μm.

FIG. 1.

Tight correlated firing was used to identify layer A and layer C cells sharing input from a common retinal afferent. A: retinotopic map of the cat lateral geniculate nucleus (adapted from Sanderson 1971) and cartoon illustrating the simultaneous recordings from 3 different cell types: X cell from layer A (X_A in blue), Y cell from layer A (Y_A in orange), and Y cell from layer C (Y_C in green). B: receptive fields, impulse responses, and cross-correlograms for a tightly correlated Y_A–Y_C cell pair. The receptive fields from the Y_A and Y_C cells were both off-center and were overlapped by 88% (1st column from the left). The impulse responses were nearly identical (2nd column) and the correlograms (3rd to 5th columns) had a narrow peak centered at the zero, indicating that they shared input from a common retinal afferent. This narrow peak was observed under different stimulus conditions such as sparse noise (Jones and Palmer 1987) and moving bars. The receptive fields from this cell pair were previously illustrated (Yeh et al. 2003; Fig. 2B, bottom). C: example of an X_A–Y_C cell pair that was not tightly correlated. Both cells had off-center receptive fields that were completely overlapped but differed in size and response latency (Y_C/X_A receptive-field size ratio = 4; X_A − Y_C peak-time difference = 12.4 ms). The receptive fields from this cell pair were previously illustrated in Yeh et al. (2003; Fig. 5). In all correlograms from this study the bins with negative values correspond to spikes from layer C cell preceded by spikes from layer A cell.

Signals from recording electrodes were amplified, filtered, and collected by a computer running the Discovery software package (Datawave Systems, Longmont, CO). Spike waveforms from each cell were initially identified during the experiment and later carefully verified off-line with spike-sorting software (Datawave Systems and Plexon, Dallas, TX). All cells in this study were recorded within 10° of the area centralis (in most cases between 5 and 10°). There is evidence that the percentage of Y geniculate cells increases with eccentricity both in retina (Fukuda and Stone 1974; Peichl and Wassle 1979; Stein et al. 1996) and in dLGN (Hoffmann et al. 1972; LeVay and Ferster 1977); however, recording from tightly correlated cells across different layers and different eccentricity ranges would have been technically very challenging. Therefore the conclusions of this study are restricted to the range of eccentricities that we sampled.

The simultaneous recordings from cells with overlapping receptive fields minimize potential sources of variability (e.g., anesthesia level, eccentricity) in the measurements of response properties. Consequently, our measurements of neighboring geniculate cells revealed some striking receptive-field similarities even among geniculate cells located in different layers. Although we cannot completely discard electrode bias as a potential source of the receptive-field similarities, the peak times of the recorded Y geniculate cells ranged from 15.5 to 46.5 ms (see Fig. 2A of Yeh et al. 2003), a range that is similar to that reported in recordings with high-impedance electrodes (Saul and Humphrey 1990). Our electrodes also occasionally recorded Y-lagged cells (see impulse response illustrated in blue in Fig. 2B of Weng et al. 2005), a type of cell that is relatively rare and whose frequency has been estimated to range between 5% (Mastronarde et al. 1991) and 18% (Saul and Humphrey 1990; see also Hartveit and Heggelund 1994; Humphrey and Murthy 1999).

FIG. 2.

Tight correlated firing was found in only a small proportion of A–C cell pairs with overlapping receptive fields. A: example of 6 geniculate cells that were simultaneously recorded from layers A and C of the dorsal lateral geniculate nucleus (dLGN). Receptive-field centers (middle column) are shown separately for each cell (above) and superimposed (below; only the 20% contour lines are shown for clarity). On-center cells are shown as continuous lines and off-center cells as discontinuous lines. Cross-correlograms obtained with white-noise stimuli were used to identify A–C cell pairs that shared input from a common retinal afferent. In this example, only one of 5 A–C cell pairs was tightly correlated. B: tight correlated firing was found in only a small number of A–C cell pairs with overlapping receptive fields (12%, n = 18/153) of the same sign (both on or both off). Notice that this figure includes all A–C cell pairs recorded regardless of cell type (Y_A–Y_C, X_A–X_C, X_A–Y_C, Y_A–X_C). C: most of the tightly correlated cells were Y cells (83%, n = 15/18). D: only 22% of Y cell pairs (n = 15/69) showed tight correlated firing. Notice that B, C, and D include only cell pairs with receptive fields overlapped ≥20%. Throughout the study we select only cell pairs with receptive-field overlap ≥20% because all neighboring neurons within dLGN, which are close enough to be in the vicinity of the axonal arbor from the same retinal afferent, have their receptive fields overlapped by ≥20% (see Fig. 5).

Receptive-field mapping

Visual stimuli were generated with an AT-vista graphics card (Truevision, Indianapolis, IN) and shown on a 20-in. monitor (Nokia 445 Xpro, Salo, Finland; frame rate = 128.8 Hz). Receptive fields were mapped with white noise (16 × 16 pixels, pixel size: 0.9 × 0.9°, 2–64 pixels per geniculate center) and calculated by reverse correlation (Cai et al. 1997; Jones and Palmer 1987; Reid et al. 1997). For each cell, we calculated the receptive field for a total of 13 different delays (receptive-field frames) between stimulus and response (from 0 to 186 ms with a 15.5-ms interval; stimulus update: 64.4 Hz). The receptive-field frame with the strongest response (usually at the 31-ms delay) was used to classify the cell either as on-center or off-center. Throughout the study on-center receptive fields are shown as continuous lines and off-center receptive fields as discontinuous lines. We usually collected nearly 6,000 geniculate spikes during the 8 min of white-noise stimulation.

Receptive fields were normalized by the maximum response and represented as contour plots smoothed with a cubic spline (Matlab, The MathWorks, Natick, MA). The most peripheral contour line represents 20% of the maximum response and each additional contour line represents a 20% increment in response strength. To be consistent with previous studies (Alonso et al. 1996, 2001, 2008; Weng et al. 2005; Yeh et al. 2003), the 20% contour line was chosen to measure the receptive-field overlap and the receptive-field size (measurements <20% would be less accurate due to the presence of surround responses and background noise). The receptive-field overlap between two cells was calculated as the percentage of pixels from the cell with the smaller receptive field that were superimposed with pixels from the cell with the larger receptive field. The receptive-field size was quantified as the number of pixels within the 20%-contour line (see following text for additional measurements with a different method). To estimate the error in the calculation of receptive-field size, we obtained repeated measurements in 14 Y_A and 11 Y_C geniculate cells. Each measurement was obtained during 8 min of white-noise stimulation and repeated measurements were separated from each other by around 10–60 min. In 16 cells, the receptive-field size was identical in the two separated measurements. In the other 9 cells, there was a difference of 1 pixel, which corresponds to a receptive-field size ratio (larger size/smaller size) of 1.14–1.25, depending on the receptive-field size of each cell (e.g., 1.14 for a cell pair with receptive-field sizes 8/7, 1.25 for a cell pair with receptive-field sizes 5/4). Based on these measurements, the average error in receptive-field size ratio was 1.07 ± 0.10. Assuming a normal distribution, the receptive-field size ratio was considered significant if it was larger than the average error plus 2SDs (1.27), which is equivalent to a probability value of <0.05. It should be emphasized that these measurements of receptive-field overlap and receptive-field size refer exclusively to the receptive-field center and not the surround. The receptive-field sizes obtained with this simple 20%-contour method were virtually identical to those obtained after fitting the receptive fields with a difference of Gaussians (DoG) function (Cai et al. 1997; see following text and results for details). More precise measurements of receptive-field size could be obtained by increasing the number of pixels within the receptive-field center. However, if the pixels are too small, the geniculate cells become poorly driven, making it difficult to obtain significant correlograms in 8 min of white-noise stimulation. Moreover, the pixel size has to be adjusted to drive cells with small and large receptive fields simultaneously. Therefore the pixel size was adjusted for each cell group to maximize the accuracy of the measurements for both receptive-field size/overlap and synchronous firing.

A DoG function was used to measure the receptive-field center and surround for each geniculate cell (Cai et al. 1997; Rodieck 1965). The two-dimensional spatial receptive field (at the response peak) was first transformed into a one-dimensional receptive field by summing the values along the y-axis. The one-dimensional receptive field was then fitted with the following DoG function

(1)

where A_C and A_S are the amplitudes of the center and surround Gaussians, x_C and x_S are the center positions, and 2σ_C and 2σ_S are the sizes (defined as the width of the Gaussian at a criterion level 0.367-fold the amplitude; Cai et al. 1997). Three parameters were extracted from the DoG fit: the receptive-field center size (2σ_C), the surround size (2σ_S), and the amplitude ratio between surround and center (A_S/A_C). The spatial receptive fields were accurately fitted with the DoG functions (average R² = 0.95).

We also estimated the error in the calculation of receptive-field surround by obtaining repeated measurements in 14 Y_A and 11 Y_C geniculate cells. The average error in receptive-field surround size ratio was 1.11 ± 0.10. Assuming a normal distribution, the receptive-field surround size ratio was considered significant if it was larger than the average error plus 2SDs (1.31), which is equivalent to a probability value of <0.05.

Time course of the visual response

The time course of the visual response was also calculated from responses to white noise by reverse correlation. The impulse response was defined as the time course of the response evoked by the most effective stimulus pixel within the receptive-field center (Alonso et al. 1996, 2001; Weng et al. 2005; Yeh et al. 2003). Most impulse responses were biphasic and, by convention, the first phase was positive for on-center geniculate cells and negative for off-center geniculate cells. For example, the impulse response of an on-center cell had a positive first phase (on-peak) followed by a negative second phase (off-rebound). Impulse responses were normalized by the maximum response of the first phase and subsampled with a cubic spline at 1.55 ms (Matlab). A not-a-knot end condition was chosen to interpolate bins of 15.5 ms, from the 0- to the 186-ms bin. This method allowed us to make accurate temporal comparisons between pairs of impulse responses with an error <1.85 ms. We estimated the error by making repeated measurements of the impulse responses in 14 Y_A and 11 Y_C cells under white-noise stimulation. In 18 of the cells, the values of peak time (see definition in the following text) were identical in the two repetitions and in 7 cells there was a difference of 1.55 ms, which resulted in an average error of 0.43 ± 0.71 ms. Assuming a normal distribution, the peak-time difference was considered significant if it was larger than the average error plus 2SDs (1.85 ms), which corresponds to a probability of <0.05.

The response time course of each geniculate cell was measured at several points and intervals of the impulse response. The peak-time was defined as the time when the first phase of the impulse response reached its maximum absolute value. The rebound time was defined as the time when the second phase of the impulse response reached its maximum absolute value. The zero-crossing time was defined as the zero point at the crossing between the two phases. The half-duration was defined as the difference between the rebound time and the peak-time (Yeh et al. 2003). We also calculated a ratio between the first phase and the second phase of the normalized impulse response, either as a biphasic index (Cai et al. 1997) or rebound index (Alonso et al. 2001; Usrey and Reid 2000). The biphasic index (BI) was defined as −1·(rebound amplitude)/(peak amplitude). The rebound index (RI) was defined as −1·(rebound area)/(peak area), where the peak area is the integral of the impulse response before the zero-crossing and the rebound area is the integral of the impulse response after the zero-crossing. Almost all geniculate cells recorded here were nonlagged cells with BI ≤1 (Cai et al. 1997; Mastronarde 1987b; Saul and Humphrey 1990; Wolfe and Palmer 1998). In our experience, the differences in the time course of the impulse responses are better captured by making direct measurements from subsampled raw data than by fitting functions to the data. The fitting functions describe well the general shape of the impulse response but fail to reveal subtle differences in response latency (e.g., average peak-time differences of 2.5 ms between Y_C and Y_A cells; Yeh et al. 2003). Therefore all measurements of response time course reported here were obtained directly from impulse responses interpolated with cubic splines.

Static nonlinearity

A linear–nonlinear (LN) model (Chichilnisky 2001) was used to measure the static nonlinearities of the geniculate neurons. The LN model assumes that the neuron's spike rate is determined by the linear sum of visual input over the receptive field of the neuron followed by a rectifying static nonlinearity (see also Baccus and Meister 2002; McAdams and Reid 2005; Zaghloul et al. 2005). For each geniculate cell, we calculated the predicted linear output (LO) by convolving the spatiotemporal receptive field (RF) with the white-noise stimulus sequence (WN)

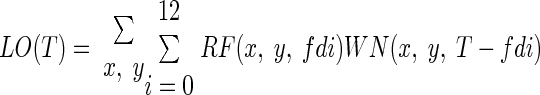(2)

where x and y represent the spatial positions of each pixel, fd is twofold the duration of a monitor frame (fd = 2 × 7.76364 = 15.5 ms; the stimulus was updated every two frames), and T is time in 15.5-ms steps. The values of the predicted output were normalized (scaled from +1 to −1) and paired with their corresponding actual spike rates using bins of 15.5 ms. To calculate the static nonlinearity, the paired values were first sorted in ascending order of the predicted linear outputs and then separated into groups of 60 paired values. The averaged pair values (normalized linear output and its corresponding actual spike rate) were then fitted with a half-wave rectifying static nonlinearity to yield gain and threshold parameters (Lesica et al. 2007)

(3)

where x is the normalized linear output, α is the gain, and θ is the offset (threshold). The gain (α) represents the overall sensitivity to the linear output and the offset (θ), the response selectivity to the stimuli.

Cross-correlation analysis

Geniculate cell pairs that shared input from the same retinal afferent were identified by cross-correlation analysis under white-noise stimulation. Most cell pairs were also tested with other stimulus conditions such as sparse noise (Jones and Palmer 1987) and moving bars. However, with the exception of the correlograms from Fig. 1, all correlograms shown herein (and all correlogram measurements reported) were obtained under white-noise stimulation.

The correlograms were represented in a 10-ms time window with a 0.1-ms bin width. A narrow peak (<1-ms width) centered at zero of the correlogram was taken as an indication that a cell pair shared a common retinal input (Alonso et al. 1996, 2008; Usrey et al. 1998; Yeh et al. 2003). A positive correlation was considered significant if it met the two following criteria. First, the peak of the correlogram was 3.1SDs above the baseline noise, which is equivalent to a probability of 0.02, assuming a normal distribution. Second, the width of the peak above the 3.1SDs was >0.5 ms (the jitter of geniculate spikes triggered by a retinal input is >0.5 ms; Cleland et al. 1971a; Mastronarde 1987b, 1992; Usrey et al. 1999). To calculate the significance of the peak, the correlograms were band-pass filtered between 75 and 700 Hz (the low-frequency filter eliminates stimulus-dependent correlations and the high-frequency filter eliminates correlogram noise that could lead to false positives in some rare cases). Notice that all correlograms shown herein are unfiltered; the filtering was used only to calculate statistical significance.

The strength of the 1-ms synchronous firing was calculated from the unfiltered correlograms obtained under white-noise stimulation as the ratio between the peak magnitude and the total number of geniculate spikes. The peak magnitude was defined as the integral of the correlogram within the central 1 ms after subtracting the baseline. The baseline was defined as the average integral of the correlogram obtained at both sides of the peak (between −1 and −2 ms and between 1 and 2 ms). The synchrony strength was calculated for each cell independently (i.e., peak magnitude/spikes from geniculate cell 1; peak magnitude/spikes from geniculate cell 2) and then the two values obtained for each cell were averaged to obtain the synchrony strength for the cell pair (called correlation strength in Alonso et al. 1996).

The measurements of synchrony strength were restricted to the central 1-ms peak because this approach provides the most accurate estimation of the percentage of geniculate spikes that can be attributed to the shared retinal afferent. The correlogram between monosynaptically connected retinal cells and geniculate cells also has a peak of around 1-ms width (Mastronarde 1992; Usrey et al. 1999) and most geniculate spikes are preceded by a retinal excitatory postsynaptic potential within <1 ms (Carandini et al. 2007; Kaplan and Shapley 1984; Sincich et al. 2007; Weyand 2007).

Classification of geniculate cells

X and Y geniculate cells were classified based on their linearity of spatial summation, measured with contrast reversing sinusoidal gratings. The linearity of spatial summation was quantified as the ratio between the second and first Fourier harmonics (F₂/F₁). If the F₂/F₁ ratio was >1 in more than half of the spatial phases tested, the cell was classified as Y; otherwise, the cell was classified as X. The average of the F₂/F₁ ratios obtained from all spatial phases was used to represent the spatial linearity of each cell. Cells that responded poorly to full-field gratings (fewer than five spikes in a 50-ms bin, in four stimulus repetitions) were labeled as unclassified and were discarded from this sample. We also discarded cells recorded deep within layer C (>500 μm below the transition A1–C), where most W cells are found (Wilson et al. 1976). Consistent with previous physiological studies, cells recorded deep within layer C had very slow impulse responses (peak times slower than 36 ms and >4.5 ms slower than the slowest layer-A cell simultaneously recorded; Yeh et al. 2003).

Overall, we measured the synchronous firing of 198 pairs of cells that were simultaneously recorded across layers (X_A–X_C: 13; X_A–Y_C: 92; Y_A–X_C: 8; Y_A–Y_C: 85; 75% of this sample was also used in Yeh et al. 2003). In addition, we studied 233 cell pairs recorded within each of the layers to measure the probability of synchronous firing across the different cell-type combinations (X_A–X_A: 108; X_A–Y_A: 51; Y_A–Y_A: 20; X_C–X_C: 5; X_C–Y_C: 10; Y_C–Y_C: 39). Eighty-six percent of the total 431 cell pairs were previously used to measure stimulus modulations of synchrony strength in Alonso et al. (2008). Interestingly, cell pairs with receptive fields of the same sign (both on or both off) were more frequently recorded than cell pairs with receptive fields of different sign, consistent with the notion that there is clustering for receptive-field sign in dLGN (Berman and Payne 1989; Bowling and Wieniawa-Narkiewicz 1986; Jin et al. 2008). The clustering for receptive-field sign reached significance for pairs of X cells within layer A (P = 0.03, chi-square test). Because of this sampling bias, the estimates of retinogeniculate divergence made in this study are based on probability values obtained for cell pairs with receptive fields of the same sign (Table 4). We also included 112 cell pairs (X_A–X_A: 31; Y_A–Y_A: 32; X_A–Y_A: 23; Y_C–Y_C: 26) recorded with the same electrode tip to measure the similarity in the response properties of neighboring geniculate cells (Fig. 5). Statistical comparisons were assessed with a Wilcoxon signed-rank test (for paired data), Mann–Whitney test (for nonpaired data), and Pearson's correlation (for correlations between receptive-field parameters and strength of synchronous firing).

TABLE 4.

Estimates of retinogeniculate divergence: number of geniculate cells sharing a common retinal afferent

Parameter	YC	YA	X
Cell density c, relay cells/mm3	10,000	7,400	14,800
Volume of retinal axonal arbor v, × 10−3 mm−3	2.9	8.7	2.4
Probability of tightly correlated firing p, RF of same type, sign, and overlap ≥ 20%	0.74	0.40	0.31
Number of geniculate cells sharing a retinal afferent, D	12	20	10

We calculated the number of relay cells sharing a retinal afferent (D) based on three parameters: cell density (c), volume of the retinal axonal arbors within each layer of dLGN (v), and probability of tightly correlated firing (p). The cell densities were calculated (Madarasz et al. 1978) by assuming 1) 25% of dLGN neurons are interneurons (LeVay and Ferster 1977, 1979); 2) 22% of neurons in C layers of dLGN are Y cells (Wilson et al. 1976); 3) the volume of layer C occupies about one third of the volume of the C layers (Bickford et al. 1998); and 4) the X/Y ratio in layer A is around 2, to match the sampling bias in the probability measurements. The volume of retinal axonal arbors were retrieved from the results of Sur et al. (1987), assuming that the volume of the Y axonal arbor is one third smaller in layer C than in layer A. The probability of tightly correlated firing was taken from our data (Table 1).

FIG. 5.

Receptive-field diversity measured in pairs of neighboring geniculate cells recorded from the same electrode tip. Response properties of neighboring geniculate cells were compared in paired-cell recordings obtained with the same electrode tip. A: the percentage of neighboring cells with receptive fields overlapped ≤80% was only 19% for neighboring X cells (blue circles) but it was 53% for neighboring Y_A cells (orange circles) and 58% for neighboring Y_C cells (green squares). In other words, although most X–X cell pairs (81%) had receptive fields overlapped >80% only 42–47% of Y–Y cell pairs had receptive fields overlapped >80%. The relation between receptive-field overlap and accumulated cell-pair percentage can be accurately fit with exponential functions (R² = 0.99 for each of the possible pair combinations). The equations of these exponential fits are: X_A–X_A cell pair: y = 0.11·e^0.068x, X_A–Y_A pair: y = 0.42·e^0.055x, Y_A–Y_A pair: y = 2.19·e^0.038x, Y_C–Y_C pair: y = 3.39·e^0.034x. B: neighboring Y geniculate cells tended to be better matched in their response latencies than neighboring X geniculate cells. The mean peak-time difference of neighboring X cells (6.40 ms) was about 2.5-fold larger than for neighboring Y_A cells (2.72 ms, P < 0.001, Mann–Whitney test) and 3-fold larger than for neighboring Y_C cells (2.03 ms, P < 0.001, Mann–Whitney test). Symbols of different sizes are used to represent the number of cell pairs. C: similar comparisons for peak-time ratio. D: similar comparisons for receptive-field size ratio.

RESULTS

Geniculate cells in layers A and C of the cat dLGN were simultaneously recorded with a multielectrode matrix. The matrix was lowered into the brain with a precise angle to record from multiple cells with spatially overlapping receptive fields (Fig. 1A). Cell pairs that shared a common retinal afferent were identified by their tight synchrony or correlated firing, characterized by a narrow peak of <1-ms width centered at zero in the correlogram (Alonso et al. 1996, 2008; Usrey et al. 1998; Yeh et al. 2003). Figure 1, B and C shows examples of two A–C cell pairs: a tightly correlated pair of Y cells (Y_A–Y_C, Fig. 1B) and a pair of an X cell and a Y cell that were not tightly correlated (X_A–Y_C, Fig. 1C). The cells from the tightly correlated pair (Y_A in orange and Y_C in green) had off-center receptive fields that were similar in size, position, and response latency (Fig. 1B, left). The cell pair that was not tightly correlated (X_A in blue and Y_C in green) also had off-center receptive fields that were well overlapped but differed in their size and response latency (Fig. 1C, left). Tightly correlated A–C cell pairs showed a narrow peak centered at the zero of the correlogram whose width was relatively independent of the stimulus conditions (Fig. 1B, right).

Specificity of retinogeniculate connections within the Y visual pathway

Tight correlated firing was found in a small proportion of simultaneously recorded A–C cell pairs with overlapping receptive fields (18/153, 12%). Figure 2A shows a simultaneous recording from six different geniculate cells, which resulted in only one A–C cell pair that was tightly correlated (three and six; three other correlograms are shown as examples). All tightly correlated cells had receptive fields of the same sign (i.e., both off-center or both on-center; Fig. 2B) and were mostly Y cells (Fig. 2C). Among all the Y_A–Y_C cell pairs with overlapping receptive-field centers, only 22% were tightly correlated (Fig. 2D). This low percentage is similar to the percentage of correlated X_A–X_A cell pairs (19%, Table 1) but it is almost an order of magnitude larger than the percentage of correlated X_A–Y_C cell pairs (3%, Fig. 2D and Table 1). The low percentage of X_A–Y_C cell pairs indicates that, although there is some mixing between X and Y pathways (Alonso et al. 1996; Cleland and Lee 1985; Hamos et al. 1987; Mastronarde 1992; Usrey et al. 1999), most divergent retinal connections synchronize geniculate cells of the same type.

TABLE 1.

Probability of tightly correlated firing for different cell-type combinations

Property	YA–YC	YC–YC	YA–YA	XA–XA	XA–YA	XA–YC
A. All cell pairs
Correlation probability
≥20% RF overlap	22% (69)	49% (35)	22% (18)	19% (103)	12% (50)	3% (67)
≥40% RF overlap	31% (49)	63% (27)	29% (14)	22% (89)	14% (42)	3% (60)
≥80% RF overlap	59% (22)	64% (11)	40% (5)	37% (38)	13% (16)	6% (34)
B. Cell pairs with same-sign RFs
Correlation probability
≥20% RF overlap, same sign	36% (42)	74% (23)	40% (10)	31% (61)	21% (29)	7% (29)
≥40% RF overlap same sign	52% (29)	85% (20)	50% (8)	35% (55)	23% (26)	7% (28)
≥80% RF overlap same sign	93% (14)	88% (8)	67% (3)	57% (23)	22% (9)	13% (16)
C. Average RF properties of tightly correlated cells pairs
Receptive-field overlap
Mean ± SD	89.5 ± 11.1%	74.1 ± 17.1%	76.3 ± 20.6%	84.7 ± 20.3%	79.5 ± 16.8	95.0 ± 7.1%
Receptive-field size ratio
Mean ± SD	1.7 ± 0.9	1.7 ± 0.8	1.3 ± 0.5	1.3 ± 0.3	1.6 ± 0.3	1.5 ± 0.3
Peak-time difference, ms
Mean ± SD	2.1 ± 1.6	0.6 ± 0.8	0.4 ± 0.8	1.6 ± 1.9	7.0 ± 3.2	3.1 ± 2.2

The probabilities were calculated for cells with different receptive field (RF) overlap, either including all pairs or selecting only cell pairs with receptive fields of the same sign. The bottom three rows of the table provide average values for receptive-field overlap, receptive-field size ratio, and peak-time difference. The numbers in parentheses represent the sample sizes.

Correlated Y_A and Y_C cells had receptive fields that overlapped ≥70% (Fig. 3A) but frequently differed in their spatial and temporal properties. On average, Y_C cells tended to have larger receptive fields (Fig. 3B) and faster response latencies (Fig. 3C) than those of Y_A cells, in both correlated and uncorrelated Y_A–Y_C cell pairs (Table 2; see also Yeh et al. 2003). The differences in receptive-field size and response latency were similarly distributed among correlated and uncorrelated cell pairs, although the distribution range was slightly wider in uncorrelated cell pairs, both for receptive-field size ratio (uncorrelated: 0.5 to 6.25; correlated: 0.62 to 4.75) and peak-time difference (uncorrelated: −10.85 to 12.4 ms; correlated: −4.65 to 1.55 ms). The comparisons between the distributions of correlated and uncorrelated cells have to be interpreted with caution because the receptive fields from each cell pair differ in multiple dimensions. For example, many uncorrelated cell pairs that showed a precise match in response latency (peak-time difference = 0) had poorly overlapped receptive fields or had receptive fields of opposite sign (e.g., on-center superimposed with off-center).

FIG. 3.

Correlated Y_A and Y_C cells had overlapped receptive fields that frequently differ in size and timing. A: the receptive fields of tightly correlated Y_A–Y_C cell pairs were well overlapped. B: most Y_C cells had larger receptive fields than those of Y_A cells. The dashed line represents the tick mark for equal receptive-field sizes. C: most Y_C cells had faster response latencies than those of Y_A cells. The dashed line represents the tick mark with the same peak-time. This figure includes only Y_A–Y_C cell pairs with receptive fields overlapped ≥20%.

TABLE 2.

Receptive-field differences between correlated and uncorrelated Y_C–Y_A cell pairs

	Peak-Time Difference (YC − YA)	Zero-Crossing Difference (YC − YA)	Rebound Time Difference (YC − YA)	Half-Duration Difference (YC − YA)	Biphasic Index (YC/YA)	Rebound Index (YC/YA)
Tightly correlated (n = 15)	−1.86**	−3.00**	−4.65*	−2.79*	1.10	1.07
Uncorrelated (n = 69)	−2.40***	−3.77***	−4.74***	−2.34**	1.07	1.04

	RF Center Size (YC/YA)	RF Surround Size (YC/YA)	RF Surround/Center Amplitude (YC/YA)	Response Gain (YC/YA)	Response offset (YC − YA)	Spatial Linearity (YC/YA)
Tightly correlated (n = 15)	1.55*	1.52	1.79	1.20	0.00	1.63
Uncorrelated (n = 69)	1.67***	1.41	2.23	1.26	0.02	3.65**

Peak-time difference: the Y_A peak time was subtracted from the Y_C peak time (i.e. Y_C − Y_A) for each cell pair and then the results were averaged (same for zero-crossing, rebound time, half-duration, and response offset). Biphasic index: it was calculated separately for each cell and then the Y_C/Y_A ratios were averaged for all cell pairs (same for receptive-field surround/center amplitude and spatial linearity). Receptive-field center size: a ratio was calculated for each cell pair (Y_C RF center size/Y_A RF center size) and then the results were averaged (same for RF surround size and response gain). The receptive-field size ratio was obtained from the DoG fits.

^***P < 0.001;

^**P < 0.01;

^*P < 0.05, Wilcoxon signed-rank test.

To precisely compare receptive-field similarity between correlated and uncorrelated cell pairs, we selected only cell pairs with overlapping receptive fields of the same sign (n = 42; correlated: 15; uncorrelated: 27) and calculated a combined index of receptive-field mismatch in size and response latency (size-timing mismatch [STM]). The STM was defined as the product between the normalized size ratio and normalized peak-time difference for each cell pair (normalization was obtained after dividing by the maximum value measured for each parameter). As illustrated in Fig. 4A, almost all cell pairs with receptive fields overlapped >70% were tightly correlated (black filled circles). The only two exceptions were a cell pair that had an exceptionally large STM mismatch and another cell pair that had poor receptive-field overlap (the value of receptive-field overlap for this cell pair was near the minimum measured among correlated Y_A–Y_C cell pairs). Figure 4, B and C illustrates the receptive-field mismatches in timing and receptive-field size for each cell pair.

FIG. 4.

Most Y_A–Y_C cell pairs with overlapping receptive fields (>70%) of the same sign were correlated. The 3 panels of the figure show only cell pairs that had receptive fields of the same sign (e.g., both on-center), for correlated (filled circles) and uncorrelated (open circles) cell pairs. A: cell pairs plotted as a function of their receptive-field overlap and size-timing mismatch (STM: the product of the normalized receptive-field size ratio and peak-time difference). B and C: the same cell pairs plotted as a function of their peak-time difference and receptive-field size ratio (the number of filled circles in B and C is <15 because some cell pairs had the same size-ratio/peak-time-difference values and the circles are shown superimposed). Notice that all but 2 cell pairs with receptive fields overlapping ≥70% were correlated. The 2 exceptions were one cell pair with receptive fields that were 100% overlapped but showed an exceptionally large mismatch in timing and size (peak-time difference: −6.2 ms, size ratio: 6.25) and another cell pair with a low receptive-field overlap (71%, at the limit that separates correlated and uncorrelated cell pairs).

The results from Fig. 4 indicate that Y cells sharing a retinal afferent across layers have receptive fields of the same sign that overlap >70% but can show substantial mismatches in size and timing.

Receptive-field mismatch among neighboring dLGN neurons

The finding that synchronous geniculate cells can be mismatched in receptive-field size and timing raises a question about the magnitude of these mismatches within neighboring dLGN neurons. Although response timing and receptive-field size have been repeatedly measured in dLGN (e.g., Bonin et al. 2005; Cai et al. 1997; Lesica et al. 2007; Mastronarde 1987a; Nolt et al. 2004; Saul and Humphrey 1990; So and Shapley 1979; Wolfe and Palmer 1998), very few studies have made comparative measurements from neighboring neurons that were simultaneously recorded (Bowling 1989). Our previous studies compared neurons recorded with different electrodes that were separated by 100–300 μm (e.g., Alonso et al. 1996); however, the ideal comparison could be made in dLGN neurons recorded with the same electrode tip, which are likely to be adjacent to each other. Figure 5 illustrates measurements of receptive-field overlap (Fig. 5A), peak-time difference (Fig. 5B), peak-time ratio (Fig. 5C), and size ratio (Fig. 5D) obtained in different combinations of cell pairs recorded with the same electrode tip (X_A–X_A: 31; Y_A–Y_A: 32; X_A–Y_A: 23; Y_C–Y_C: 26). Notice that this is a separate sample that was used only for the measurements reported in Fig. 5; all correlation measurements reported herein were obtained from cells recorded with different electrodes.

The results from the same-electrode recordings demonstrate that all neighboring neurons within dLGN have receptive fields that overlap >20%. They also show a tendency for neighboring Y–Y cell pairs to have receptive fields that are less overlapped (Fig. 5A), better matched in peak time (Fig. 5, B and C), and slightly better matched in receptive-field size (Fig. 5D) than neighboring X–X cell pairs. The ranges of peak-time differences and receptive-field size ratios measured in recordings from Y–Y cell pairs were comparable to the ranges measured in uncorrelated Y_A–Y_C cell pairs recorded with different electrodes (Fig. 3, B and C). Therefore we conclude that the samples of cell pairs recorded with different electrodes show the same diversity in receptive-field sizes and response timing observed among neighboring neurons in dLGN.

Strength of Y_A–Y_C synchronous firing

The results presented earlier indicate that the magnitude of the temporal receptive-field mismatch is similar in cells that share and those that do not share a retinal afferent. In other words, the magnitude of the temporal mismatch is not related with the probability that two Y cells will share a retinal afferent. Given this lack of relation between temporal mismatch and probability of connection, it was very surprising to find a strong correlation between the temporal mismatch and the strength of the synchrony generated by the shared retinal afferents. (The terms “synchrony” and “correlated” have the same meaning throughout this study. In this section, we prefer to use the term “synchrony” instead of “correlated” to avoid confusion with the “correlations” measured between the magnitude of receptive-field mismatches and the synchrony strength.)

Figure 6 shows the receptive fields, impulse responses, and cross-correlograms of 15 tightly correlated Y_A–Y_C cell pairs, arranged in order of synchrony strength. A simple visual inspection of this figure reveals a close relation between synchrony strength and timing similarity. Whereas the three cell pairs with the strongest synchronous firing (pairs 174, 62, and 6) had nearly identical impulse responses (peak-time difference = 0), the three cell pairs with the weakest synchrony (pairs 103, 64, and 12) all showed significant differences in response latency (peak-time difference >4 ms).

FIG. 6.

Receptive fields, impulse responses, and cross-correlograms from simultaneously recorded pairs of Y_A and Y_C cells (15 tightly correlated and 1 uncorrelated). Y_A–Y_C cell pairs are ordered based on their synchrony strength (shown as a percentage at the top right corner of each correlogram). Each cell pair is represented in 3 panels that illustrate, from left to right, the receptive fields, impulse responses, and correlogram. In most cell pairs the receptive field is larger and the response latency is faster for the Y_C cell than for the Y_A cell. The correlograms from all cell pairs (except pair 69) have a narrow peak centered at the zero, indicating that the 2 Y cells shared input from a common retinal afferent. The asterisks represent significant differences in receptive-field size ratio (bottom left corner) and peak time (next to the peak-time). ***P < 0.001; **P < 0.01. The receptive fields of cell pairs 174, 56, 64, and 106 were previously illustrated in Yeh et al. (2003).

Although the differences in the impulse responses may seem small, they are large enough to generate strong asymmetries in the relative spike timing of Y_A and Y_C cells (as can be seen in the stimulus-dependent correlograms of some cell pairs). The stimulus-dependent correlograms generated by white noise have a broad crest of around 15 ms that can be seen at the base of the 1-ms narrow peak. In some cell pairs the differences in the impulse responses make the stimulus-dependent crest asymmetric with respect to zero (e.g., pairs 129, 9, 103, and 12). Because most impulse responses are faster in Y_C than in Y_A cells, the maximum of the crest is displaced toward the left (and not the right) side of the correlogram. In some correlograms, it is also possible to see the contribution from another type of synchrony that originates in the retinal circuitry (Mastronarde 1983; Pillow et al. 2008). This retinal synchrony is usually lower in amplitude and less precise than the geniculate synchrony described here. It can be seen as a broad bump (>2 ms), usually of low amplitude, at the base of the narrow peak in the correlogram. The strongest retinal synchrony in this figure can be seen at the base of the correlogram from cell pairs 6 and 174.

To quantify the relation between the strength of the geniculate synchrony and the magnitude of the receptive-field mismatches, we calculated three indices of receptive-field similarity: a spatiotemporal index (STSI) that measures receptive-field similarity in both space and time, a spatial similarity index (SSI) that measures receptive-field similarity in visual space, and a temporal similarity index (TSI) that measures timing differences at three points of the impulse response.

The spatiotemporal similarity index (STSI) was calculated as the correlation coefficient between the two entire receptive-field movies (RF₁ and RF₂)

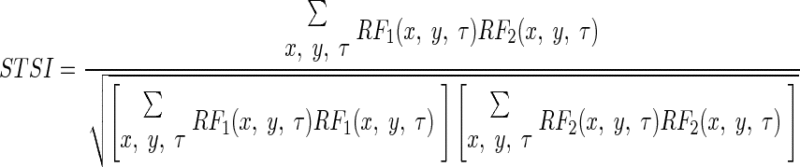(4)

where x and y represent the spatial positions of each pixel and τ is the time from 0 to 186 ms with steps of 15.5 ms.

The spatial similarity index (SSI) was calculated as the correlation coefficient between the receptive fields at peak of the impulse response

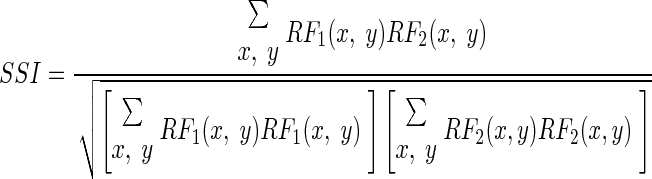(5)

where x and y represent the spatial positions of each pixel.

Finally, the temporal similarity index (TSI) was calculated as the sum of the timing differences obtained at three time points of the impulse response [the peak-time (P), the zero-crossing time (Z), and the rebound time (R)]. The timing differences were normalized by the maximum difference (MAX) measured for each parameter within the entire sample of cell pairs (adapted from Alonso et al. 1996)

(6)

All three indices of receptive-field similarity were robustly correlated with synchrony strength (Fig. 7A), although the temporal similarity index showed the strongest correlation (r = 0.76, P = 0.001). The strong correlation between synchrony strength and temporal similarity is interesting for two main reasons. First, it was unique of Y_A–Y_C cell pairs: synchrony strength was not correlated with the temporal similarity index in Y_C–Y_C and X_A–X_A cell pairs (r = 0.13, P = 0.62 for Y_C–Y_C; r = 0.4, P = 0.09 for X_A–X_A), although it was correlated with the spatial similarity index in all cell pairs (r = 0.71, P = 0.003 for Y_A–Y_C; r = 0.67, P = 0.003 for Y_C–Y_C; r = 0.47, P = 0.04 for X_A–X_A). Second, synchrony strength in Y_A–Y_C cell pairs was linearly correlated with most temporal parameters measured including peak time, zero-crossing time, rebound time (Fig. 7B), half-duration, and biphasic ratio (Fig. 7C). These correlations are surprisingly strong given the narrow range of the timing differences (e.g., <5 ms difference in peak time) and the relatively coarse time resolution of the measurements (15.5 ms). To our knowledge, this is the first demonstration of a significant relation between response–latency differences and the amount of synchrony caused by divergent connections in the visual system. Third, many spatial measurements such as receptive-field overlap, center distance, and size ratio were not linearly correlated with Y_A–Y_C synchrony strength (Fig. 7D). The only correlated spatial measurement was the spatial similarity index (Fig. 7A), which is a combined measurement of multiple spatial parameters including receptive-field overlap, distance, and size ratio. These results indicate that although a Y_A–Y_C cell pair with 100% receptive-field overlap can sometimes show weaker synchrony than that of a Y_A–Y_C cell pair with 80% overlap, a Y_A–Y_C cell pair with identical impulse responses will rarely show weaker synchrony than that of a cell pair that is temporally mismatched.

FIG. 7.

Y_A–Y_C synchrony strength is correlated to receptive-field similarity. A: the strength of synchronous firing was significantly correlated to 3 different indices of receptive-field similarity: spatiotemporal index (left: r = 0.71, P = 0.003), spatial index (middle: r = 0.56, P = 0.03), and temporal index (right: r = 0.76, P = 0.001). B: the strength of the synchronous firing was significantly correlated to the Y_C–Y_A peak-time difference (left: r = 0.61, P = 0.016), the Y_C–Y_A zero-crossing time difference (middle: r = 0.66, P = 0.008), and the Y_C–Y_A rebound-time difference (right: r = 0.75, P = 0.001). C: the strength of the synchronous firing was significantly correlated to the Y_C–Y_A half-duration difference (left: r = 0.57, P = 0.026) and the Y_C/Y_A proportion of biphasic ratios (middle: r = 0.63, P = 0.012), but not to the Y_C/Y_A proportion of rebound indices (right: r = 0.13, P = 0.645). D: the strength of synchronous firing was not correlated to receptive-field overlap (left: r = −0.01, P = 0.972), receptive-field center distance (middle: r = −0.21, P = 0.459), or receptive-field size ratio (right: r = −0.47, P = 0.08). E, left: the strength of the synchronous firing is best predicted by a model that incorporates 4 critical receptive-field parameters: receptive-field sign (sign), receptive-field overlap (OV), receptive-field size ratio (SR), and timing differences (TDs; we used differences in rebound time). This model could be use to accurately predict the measured synchrony (R² = 0.75; P < 0.0001). Middle: multiple regression analysis indicates that the receptive-field overlap, the response latency, and the receptive-field size ratio all contribute significantly to synchrony strength. The receptive-field sign was not included in the multiple regression analysis and can take only 2 values: 0 (different sign) or 1 (same sign). Parameter ranges: [70%, 100%] for receptive-field overlap, [−13.95, 1.55] for response-latency difference (measured at the rebound of the impulse response), and [0.6, 4.75] for receptive-field size ratio. Right: correlation between the model prediction and the measured synchrony strength. The regression line had a slope of 0.77 and an intercept of 1.86. ***P < 0.001; **P < 0.01; *P < 0.05; Pearson's correlation.

As indicated by these results, geniculate cells that are most strongly synchronized by the retinal inputs have the most similar receptive fields. Therefore it should be possible to predict the strength of the synchronous firing from the magnitude of the receptive-field mismatches. To estimate the relative importance of the different receptive-field mismatches in predicting the synchronous firing of geniculate cells, we did multiple regression analysis. We used synchrony strength as the dependent variable and the different types of receptive-field mismatches as the independent variables. After testing different combinations of receptive-field parameters, we found that the receptive-field overlap, receptive-field size ratio, and rebound time difference provided the strongest correlation coefficients (Fig. 7E, middle). We then combined these receptive-field parameters in a simple linear model in an attempt to predict the synchrony strength of each Y_A–Y_C cell pair that shared retinal input. In this simple model (Fig. 7E, left), the receptive-field sign works as a switch that allows only Y_A and Y_C cells with receptive fields of the same sign (Sign = 1) to share a retinal afferent. For those Y_A–Y_C cell pairs with receptive fields of the same sign, the synchrony strength is estimated from a linear combination of receptive-field overlap (OV), receptive-field size ratio (SR), and the timing difference (TD). The weights of OV, SR, and TD in the model are given by the standardized coefficients obtained with multiple regression analysis (Fig. 7E, middle). The synchrony strength estimated with this model was strongly correlated with the measured synchrony (Fig. 7E, right, R² = 0.75) and explained 77% of the variance in the synchrony measurements [residual variance measured as in Cano et al. (2006)].

On average, the synchrony strength generated by shared retinal afferents was 8% in Y_A–Y_C cell pairs and 10–13% in other cell-pair combinations (X_A–X_A: 10%; Y_C–Y_C: 9.8%; Y_A–Y_A: 13.4%; Table 3). That is, on average, 8–13% of the spikes generated by two geniculate neurons were synchronized by shared retinal afferents. Importantly, the average synchrony strength did not differ >6% across different cell-pair combinations, including X–X/X–Y and same-layer/different-layer comparisons (Table 3). Moreover, the average synchrony strength (∼10%) was almost an order of magnitude lower than the percentage of geniculate spikes generated by s-potentials (∼90%; Carandini et al. 2007; Cleland and Lee 1985; Cleland et al. 1971a; Sincich et al. 2007; Weyand 2007). Such low-average synchrony suggests that retinogeniculate convergence plays a more important role in driving geniculate responses than previously thought. Notice, however, that the strongest average synchrony measured in Y–Y cell pairs (26.3% for Y_A–Y_A) was close to two times weaker than the strongest synchrony measured in X_A–X_A cell pairs (46.9%), a finding that is consistent with the notion that Y geniculate cells receive more convergent retinal inputs than X geniculate cells (Mastronarde 1992).

TABLE 3.

Strength of synchronous firing in different cell types

Property	YA–YC	YC–YC	YA–YA	XA–XA	XA–YA	XA–YC
A. All cell pairs
Synchrony strength
≥20% RF overlap	8.0 ± 4.7% (15)	9.8 ± 5.9% (17)	13.4 ± 10.7% (4)	10.0 ± 10.0% (20)	7.7 ± 1.9% (6)	12.0 ± 14.7% (2)
≥40% RF overlap	8.0 ± 4.7% (15)	9.8 ± 5.9% (17)	13.4 ± 10.7% (4)	10.0 ± 10.0% (20)	7.7 ± 1.9% (6)	12.0 ± 14.7% (2)
≥80% RF overlap	8.1 ± 4.7% (13)	10.0 ± 4.5% (7)	22.2 ± 5.8% (2)	12.0 ± 11.3% (14)	10.0 ± 0.1% (2)	12.0 ± 14.7% (2)
B. Average and maximum strength
Average synchrony strength	8.0 ± 4.7% (15)	9.8 ± 5.9% (17)	13.4 ± 10.7% (4)	10.0 ± 10.0% (20)	7.7 ± 1.9% (6)	12.0 ± 14.7% (2)
Maximum synchrony strength	17.7%	24.1%	26.3%	46.9%	10.1%	22.5%

The numbers in parentheses represent the sample sizes. All tightly correlated cell pairs had receptive fields of the same sign except one X_A–X_A cell pair.

Center–surround organization and static nonlinearities of Y_A and Y_C cells

To gain a better understanding of the neuronal mechanisms responsible for the receptive-field mismatches between Y_A and Y_C cells that shared a retinal afferent, we compared their center–surround organization and static nonlinearities. The spatial receptive field of each geniculate cell was fitted with a difference of Gaussians (DoG) function (Fig. 8A; Cai et al. 1997; Rodieck 1965) and, from this function, we extracted three different receptive-field parameters: center size (2σ_C), surround size (2σ_S), and a ratio of surround/center amplitudes (A_S/A_C; see methods for details). The measurements of center size obtained with the DoG fits were equivalent to those obtained directly from the spatiotemporal receptive fields with our 20%-contour method (r = 0.86, P < 0.0001, Fig. 8B), although the DoG fits seemed to be more sensitive at identifying differences in center size between correlated Y_A and Y_C cells (see following text). Consistent with previous studies in retinal ganglion cells (Linsenmeier et al. 1982) and geniculate cells (Bonin et al. 2005; Irvin et al. 1993; Xu et al. 2002), the size of the geniculate surround was roughly 3.9-fold larger than the center size, although surround size and center size were not correlated with each other. Instead, the center size was inversely correlated with the ratio of surround/center size (r = −0.53, P = 0.003, Fig. 8C). That is, cells with small receptive-field centers tended to have comparatively larger receptive-field surrounds than those with larger receptive-field centers.

FIG. 8.

Receptive-field center and surround of tightly correlated Y_A and Y_C cells. A: receptive fields of tightly correlated Y_A and Y_C cells were fitted with a difference of Gaussians (DoG) function (Cai et al. 1997; Rodieck 1965). The 2-dimensional receptive fields of the Y_A (top left) and Y_C (top right) cells were first transformed into one-dimensional receptive fields (middle) by summing values along the y-axis (solid dots) and then fitted with the DoG function (solid curves). The receptive-field center and surround were quantified as 2σ_C and 2σ_S (bottom). This cell pair was previously illustrated in Fig. 7 of Yeh et al. (2003). B: the measurement of receptive-field center size obtained with the DoG fit was equivalent to that obtained directly from the spatiotemporal receptive field with our 20%-contour method (r = 0.86, P < 0.0001). C: a strong correlation was found between the center size and the ratio of surround size and center size for Y geniculate cells (r = −0.53, P = 0.003). D: on average, the receptive-field center size was significantly larger for the Y_C cell than for the Y_A cell (Y_A: 1.71 ± 0.91, Y_C: 2.31 ± 0.81, shown as mean ± SD, P = 0.036, Wilcoxon signed-rank test); however, about half of the Y_A–Y_C cell pairs had similar center sizes and lie along the unity line. E: the surround sizes of correlated Y_A–Y_C cell pairs were not significantly different (Y_A: 6.71 ± 3.89, Y_C: 6.87 ± 3.17, P = 0.61, Wilcoxon signed-rank test). F: the ratios of surround amplitude and center amplitude were not significantly different either (Y_A: 0.27 ± 0.18, Y_C: 0.35 ± 0.24, P = 0.17, Wilcoxon signed-rank test).

The Gaussian amplitude and size of the receptive-field surround were also inversely correlated (r = −0.65, P < 0.001), but this was not the case for the amplitude and size of the receptive-field center (data not shown). The DoG fits provided an excellent description of the center–surround organization of geniculate cells and revealed a significant tendency for Y_C cells to have larger receptive-field centers than those of Y_A cells on average (Y_A: 1.71 vs. Y_C: 2.31, P = 0.036, Wilcoxon signed-rank test, Fig. 8D and Table 2). However, notice that many Y_A–Y_C cell pairs had similar receptive-field sizes (Fig. 8D) and we did not find significant differences in other spatial properties, such as the average size of the receptive-field surround (Y_A: 6.71 vs. Y_C: 6.87, P = 0.61, Wilcoxon signed-rank test, Fig. 8E) or the average surround/center amplitude ratio (Y_A: 0.27 vs. Y_C: 0.35, P = 0.17, Wilcoxon signed-rank test, Fig. 8F).

To measure possible differences in static nonlinearities between Y_A and Y_C cells that shared a retinal afferent we used a linear–nonlinear (LN) model that has been very successful at characterizing response properties within early stages of the visual pathway (Baccus and Meister 2002; Chichilnisky 2001; McAdams and Reid 2005; Zaghloul et al. 2005). For each geniculate cell, we calculated a linear output by convolving the white-noise stimulus with the spatiotemporal receptive field (Fig. 9A) and then the values of the linear output were paired with the corresponding spike rates of the neuron to define the static nonlinearity (see methods for details). Two parameters from the static nonlinearity were extracted: the gain (α) and the offset (θ, Fig. 9B). These two parameters were negatively correlated in Y_A cells (r = −0.70, P = 0.003) but not Y_C cells (Fig. 9C) and a positive correlation was also found between the offset and the peak time in Y_A cells (r = 0.64, P = 0.01) but not in Y_C cells (data not shown). On average, tightly correlated Y_A and Y_C cells did not differ significantly in either gain (Y_A: 243.6 vs. Y_C: 261.8, P = 0.39, Wilcoxon signed-rank test, Fig. 9D) or offset (Y_A: 0.16 vs. Y_C: 0.16, P = 0.96, Wilcoxon signed-rank test, Fig. 9E). Moreover, the mean firing rates of correlated Y_A and Y_C cells were similar (Y_A: 12.6 spikes/s, Y_C: 12.3 spikes/s, P = 0.89, Wilcoxon signed-rank test; data not shown).

FIG. 9.

Static nonlinearities of tightly correlated Y_A and Y_C cells. A: the static nonlinearities of tightly correlated Y_A and Y_C cells were measured with the 2-stage linear–nonlinear (LN) model (Chichilnisky 2001). Top: the linear outputs of Y_A (left) and Y_C (right) cells were calculated as single numerical values by convolving the white-noise stimulus sequence with the spatiotemporal receptive field. Bottom: the linear output was arbitrarily scaled from −1 to +1 and shown at 60 different stimulus frames (15.5 ms/frame), together with the measured neuronal spiking rate. Note that both Y_A and Y_C cells tended to fire more spikes when the linear output was positive (solid lines) than when it was negative (dashed lines). B: the static nonlinearities of the Y_A and Y_C cells (solid lines) were defined by the mean values of the sorted linear outputs with their corresponding spiking rates and fitted with a half-wave rectifier function (each circle here represents the mean of 546 values). Two parameters were extracted from the static nonlinearity: the gain (α) and the offset (θ, inset). C: the gain and the offset of the static nonlinearity were negatively correlated (for Y_A cells only, r = −0.70, P = 0.003). D: the gains of tightly correlated Y_A and Y_C cells were not significantly different (Y_A: 243.6 ± 83.0, Y_C: 261.8 ± 57.1, shown as mean ± SD, P = 0.39, Wilcoxon signed-rank test). E: the offsets of tightly correlated Y_A and Y_C cells were not significantly different (Y_A: 0.16 ± 0.06, Y_C: 0.16 ± 0.08, P = 0.96, Wilcoxon signed-rank test).

Divergence within the Y retinogeniculate pathway

Our measurements of correlated firing within dLGN allow us to provide new estimates of retinogeniculate divergence (D) within the Y and X visual pathways in the cat. These estimates are based on the probability of tight correlated firing (p), cell density (c), and the volume of retinal axon arbors within dLGN (v, Table 4), as given by

(7)

where n is the number of geniculate cells covered by the axonal arbor from a single retinal ganglion cell and it is calculated by multiplying cell density (c) by the arbor volume and dividing by two [n = (cv)/2]. The division by two is necessary because retinogeniculate connections are restricted to cells with receptive fields of the same sign (either on-center or off-center). We used the volume of the axonal arbor instead of number of synapses because the arbor volume can be directly related to dLGN volume and cell density. The equation for divergence (D) was derived as follows. First, we calculated the number of cell pairs within the axonal arbor volume by using a two-combination equation [n(n − 1)/2]. This equation was multiplied by the probability of correlated firing estimated in our study (p, Table 1) to obtain the number of correlated cell pairs [pn(n − 1)/2]. The number of correlated cell pairs was also obtained by using a two-combination equation based on divergence (D) as [D(D − 1)/2]. From this equivalence [pn(n − 1)/2 = D(D − 1)/2], we obtained Eq. 7, assuming that [D(D − 1) ≅ D²].

Based on the results from this equation, we estimate that X retinal afferents diverge into 10 X_A cells and Y retinal afferents diverge into 20 Y_A cells and 12 Y_C cells (Table 4). These divergence values are consistent with the scant anatomical data that are available on retinogeniculate divergence. Hamos et al. (1987) reconstructed nearly one third of the volume from an X axon terminal in layer A (nearly one fifth of the synapses) and found 3 X geniculate targets, which would lead to a divergence of 9 X cells if we used axonal-arbor volume to calculate divergence. The divergence for the Y pathway has also been estimated to be 20–30, based on the total number of Y cells in retina and dLGN (Friedlander et al. 1981).

Our estimates of divergence can vary depending on how the probability of synchrony is calculated. To estimate more accurately how geniculate synchrony varies along the diameter of an axonal arbor, we plotted the probability of synchrony (Fig. 10A) and synchrony strength (Fig. 10B) as a function of receptive-field overlap. As shown in Fig. 10, the probabilities of synchrony and synchrony strength fall very rapidly when the receptive-field overlap is <50% (see also Tables 1 and 3). Moreover, the synchronous geniculate cells of the same type show a wider range of receptive-field overlap than synchronous geniculate cells of different type (compare top and bottom panels of Fig. 10A). If we assume that the axonal arbor from the retinal afferent covers a population of neighboring geniculate cells with receptive fields overlapping >20% and use the probability functions illustrated in Fig. 10A, then the probability of synchrony would be lower than that reported in Table 4 (0.10 for X_A, 0.21 for Y_A, and 0.46 for Y_C) and would reduce the estimates of divergence to 5 X_A cells, 15 Y_A cells, and 9 Y_C cells.

FIG. 10.

Distributions of probability of synchrony and synchrony strength for different combinations of cell pairs in dLGN. A: probability of synchrony plotted as a function of receptive-field overlap for cell pairs of different types (X_A–Y_A, X_A–Y_C, Y_A–Y_C, top) and those of the same type (X_A–X_A, Y_A–Y_A, Y_C–Y_C, bottom). B: synchrony strength plotted as a function of receptive-field overlap for cell pairs of different types (X_A–Y_A, X_A–Y_C, Y_A–Y_C, top) and those of the same type (X_A–X_A, Y_A–Y_A, Y_C–Y_C, bottom).

Our estimates of divergence also depend on current measurements of axonal-arbor volumes. The volume of Y axonal arbors is inversely correlated with eccentricity (Sur and Sherman 1982) and, at 5–10° (where our recordings were performed), the mean volume of the axonal arbor is fivefold larger for Y cells than for X cells (Sur and Sherman 1982). If we use the mean volume of the Y axonal arbor at 5–10° eccentricity (instead of the mean across all eccentricities) together with the probability functions of Fig. 10, the divergence would be similar to that reported in Table 4, particularly for Y cells (5 X_A cells, 21 Y_A cells, and 13 Y_C cells).

DISCUSSION

We have investigated the functional consequences of neuronal divergence within the retinogeniculate pathway by simultaneously recording from pairs of geniculate cells that share input from a retinal afferent. We demonstrate that geniculate cells sharing retinal input across layers are mostly Y cells with overlapping receptive fields. The Y receptive fields are always of the same sign but show small mismatches in position, size, and response timing (Figs. 2 and 3). These receptive-field mismatches are subtle but functionally significant since their magnitude is strongly correlated with the strength of the synchronous firing generated by the divergent retinal afferents. Consequently, the cells with the best-matched receptive fields will generate the strongest synchronous firing and will be the most effective in driving common postsynaptic targets (Alonso et al. 1996; Bruno and Sakmann 2006).

Importantly, we have shown that the average synchronous firing caused by divergent retinal afferents is independent of cell type and is close to 10% across all pair combinations studied (Y_A–Y_C: 8%; X_A–X_A: 10%; Y_A–Y_A: 13%; Y_C–Y_C: 10%; Table 3, Fig. 10B). This value of synchrony (∼10%) is almost an order of magnitude lower than the percentage of geniculate spikes driven by s-potentials (∼90%), which are large excitatory postsynaptic potentials generated by a single retinal afferent (Carandini et al. 2007; Cleland and Lee 1985; Cleland et al. 1971a; Kaplan and Shapley 1984; Sincich et al. 2007; Weyand 2007). Therefore our finding indicates that most dLGN spikes are independently driven, even in cells that share input from common retinal afferents.

Our results also provide new estimates of retinogeniculate divergence across different cell classes and support previous findings that divergent neuronal connections confine the strongest synchrony to groups of cells with the most similar receptive fields (Alonso et al. 1996, 2008; Bruno and Sakmann 2006;Roy and Alloway 2001; Usrey et al. 2000). We also document the range of receptive-field mismatches, probability of synchrony, and synchrony strength across different cell-pair combinations of geniculate cells sharing a retinal afferent (Tables 1 and 3, Fig. 10). These data can be used to draw a more detailed diagram of retinogeniculate wiring than that currently available. Figure 11 illustrates a possible circuitry diagram that would replicate the main types of synchrony and range of synchrony strengths reported in this study.

FIG. 11.

Cartoon representing a group of dLGN cells synchronized by inputs from common retinal afferents. Left: dLGN synchrony strength predicted by Cleland (1986), assuming that each geniculate cell receives input from one or two retinal afferents. Right: synchrony strengths measured in this study. The numbers are based on the synchrony strengths reported in Table 3 for different cell-type combinations. The average synchrony for all geniculate cell pairs is about 10% regardless of their type. The size of the black dots represents the percentage of the total synaptic contribution from a single retinogeniculate afferent to its multiple geniculate targets.

Specificity of retinogeniculate divergence

Although our findings confirm the existence of certain X–Y mixing in the retinogeniculate pathway (see also Alonso et al. 1996; Cleland et al. 1971b; Hamos et al. 1987; Mastronarde 1992; Usrey et al. 1999), they show that the probability of synchrony is highest among cells of the same type (Table 1, Fig. 10A). The synchronous firing between X and Y cells across layers was very rare (Fig. 2C, Table 1), even if X cells are far more abundant than Y cells in layer A (e.g., Humphrey and Murthy 1999; Mastronarde 1992; Saul and Humphrey 1990; So and Shapley 1979). The finding that X and Y cells are about fourfold more frequently synchronized within layer A than across layers (12 vs. 3%, Table 1) could be explained if X_A cells shared more retinal input with Y_A than with Y_C cells. This explanation is consistent with the notion that Y_C cells receive more convergent retinal input than Y_A cells.

Our results indicate that the probability of finding synchronous Y_A–Y_C cell pairs is strongly determined by their receptive-field sign and receptive-field overlap. None of the Y_A–Y_C cell pairs with receptive fields of different sign shared input from the same retinal afferent, although some had 100% receptive-field overlap and identical response latencies. Moreover, nearly all Y_A–Y_C cell pairs with receptive fields of the same sign that overlapped >70% shared retinal input, independently of their differences in receptive-field size and response latency (Fig. 4). The finding that synchronous Y_A–Y_C cells have receptive fields overlapping >70% is consistent with the pronounced sparseness of the Y receptive-field array in the retina (Wassle et al. 1975).

The synchronous Y_A–Y_C firing generated by shared retinal inputs was strongly correlated with the temporal similarity of the receptive fields. Although Y_A–Y_C cell pairs with 100% receptive overlap showed a wide range of synchrony strengths (from the weakest to nearly the strongest measured; Fig. 7D, left), the Y_A–Y_C cell pairs with the best-matched impulse responses consistently showed the strongest synchrony (Figs. 6 and 7, A, right and B). Several previous studies have demonstrated a relation between the average synchrony strength and receptive-field overlap in both retina and dLGN (Alonso et al. 1996; Brivanlou et al. 1998; Mastronarde 1983; Meister et al. 1995; Shlens et al. 2006). However, a relation between synchrony (caused by direct neuronal divergence) and temporal similarity has not been demonstrated before in the visual system and, as shown here, it seems to be restricted to Y_A–Y_C cell pairs in dLGN.

Strength of the synchronous firing generated by divergent retinal afferents

Our findings indicate that the average synchrony generated by divergent retinal afferents is relatively similar in X and Y pathways, even if Y geniculate cells are thought to receive more convergent retinal inputs (Mastronarde 1992). This could not be expected from our current knowledge of retinogeniculate connections. It has been estimated that around 90% of the geniculate spikes can be attributed to inputs from retinal afferents (Carandini et al. 2007; Cleland and Lee 1985; Cleland et al. 1971a; Mastronarde 1992; Sincich et al. 2007; Weyand 2007). Moreover, Cleland (1986) estimated that if a retinal afferent diverged into two geniculate cells that received no other additional retinal input, the synchrony between the two cells should approach 81% (0.9 × 0.9). These estimates of geniculate synchrony proposed by Cleland in the 1980s (Cleland 1986) were based on two main assumptions. First, retinogeniculate convergence is very limited (up to two retinal inputs in most geniculate cells). Second, the geniculate synchrony can be estimated from the product of the retinogeniculate efficacies. The finding that the average geniculate synchrony is nearly 10% across all different cell types suggests that neuronal convergence plays a more important role in driving geniculate neurons than previously thought. An average synchrony of about 10% could be explained by the presence of weak retinal inputs that add to the most frequently studied dominant inputs (Carandini et al. 2007; Cleland and Lee 1985; Cleland et al. 1971a; Sincich et al. 2007; Weyand 2007). Studies performing simultaneous recordings from retina and dLGN indicate that each retinal afferent can drive from 1 to 100% of all geniculate spikes (Cleland et al. 1971a; Mastronarde 1992; Usrey et al. 1999). Moreover, the largest value of geniculate synchrony measured to date is around 46.9% for X–X cell pairs (46.9% in this study and 43% in Alonso et al. 1996; both in X_A–X_A cell pairs) and 26.3% for Y–Y cell pairs (this Y_A–Y_A example is illustrated in great detail in Alonso et al. 2008). Therefore it is likely that most geniculate neurons receive at least two convergent retinal inputs, although some of these inputs are weak and contribute with only a small percentage of the geniculate spikes.

The percentage of geniculate spikes driven by retinal afferents depends on the stimulus conditions and the temporal summation of the excitatory postsynaptic potentials generated by the retinal afferents (Augustinaite and Heggelund 2007; Carandini et al. 2007; Rowe and Fischer 2001; Sincich et al. 2007; Usrey et al. 1999; Weyand 2007). Because the stimulus also modulates the strength of the geniculate synchrony (Alonso et al. 2008), all the comparisons of synchrony strength across cell classes must be obtained under the same stimulus conditions (in our study, white noise). The synchrony measurements are very stable across stimulus repetitions (Alonso et al. 2008), which makes it unlikely that they would be affected by factors such as synaptic depression and changes in the level of anesthesia. In fact, if the synchrony measurements would show pronounced fluctuations with the level of anesthesia, it would have been impossible to demonstrate the strong correlations between the receptive-field mismatches and synchrony strength that we report in Fig. 7. Also, a recent study has found very low levels of synaptic depression in retinogeniculate synapses (Carandini et al. 2007).

It is well established that the percentage of geniculate spikes driven by a dominant retinal input is ≥90% in different animals and brain states (Carandini et al. 2007; Cleland and Lee 1985; Cleland et al. 1971a; Mastronarde 1992; Sincich et al. 2007; Weyand 2007). In contrast, the efficacy of the retinogeniculate connections (the percentage of retinal spikes that generate a geniculate spike) can fluctuate depending on the level of anesthesia, arousal, cortical feedback, and stimulus conditions (Cano et al. 2006; Nolt et al. 2007; Przybyszewski et al. 2000; Sillito et al. 1994). In theory, if a retinal afferent had an average efficacy of 50% and drove each geniculate neuron independently, the amount of synchrony could not reach the 81% value predicted by Cleland (1986). Under this scenario, generating synchronous geniculate spikes would be equivalent to flipping two coins and landing both heads up. In reality, retinal afferents do not drive geniculate neurons independently (Carandini et al. 2007; Rowe and Fischer 2001; Usrey et al. 1998, 1999; Weyand 2007). The ongoing activity of neighboring neurons is highly correlated and most of the geniculate spikes are generated by trains of retinal spikes with short interspike intervals. In fact, the efficacy of retinogeniculate connections can exceed 90% when retinal spikes are separated by <10 ms in awake cats (Weyand 2007). Therefore although the low retinogeniculate efficacy may reduce the synchronous firing of geniculate cells to some extent, the average value of 10% that we report is most likely a consequence of retinogeniculate convergence.

Neuronal mechanisms underlying Y_A–Y_C receptive-field mismatches

What could be the neuronal mechanisms that are responsible for the receptive-field mismatches of Y_A–Y_C cells sharing a retinal afferent? The mechanism that we favor the most is a simple difference in retinogeniculate convergence: strong, shared, retinal inputs could explain the receptive-field similarities between correlated Y_A and Y_C cells and the nonshared retinal inputs could explain some of the differences. Moreover, greater retinogeniculate convergence within layer C than that within layer A could explain the larger receptive fields, faster response latencies, and higher contrast sensitivities of Y_C cells (Frascella and Lehmkuhle 1984; Lee et al. 1992; Yeh et al. 2003). A greater retinogeniculate convergence within layer C is supported by two main findings. First, the probability for two geniculate cells to share a retinal afferent is greater in Y_C–Y_C and Y_A–Y_C cell pairs than in any other cell-pair combination (Table 3 and Fig. 10A). Second, Y–Y cell pairs showed weaker synchrony across different layers than within the same layer; the differences were small but consistent in both the average (8 vs. 9.8–13.4%) and the maximum synchrony measured (17 vs. 24–26%). For example, the weaker synchrony across layers could be explained if a Y_C–Y_C cell pair shared input from multiple geniculate afferents but only one of these afferents was shared with a Y_A cell.

Although a mechanism purely based on retinogeniculate convergence could explain our results, other mechanisms should also be discussed. In particular, intrageniculate inhibition could be important since it has been shown to modulate the strength of both classical and suppressive surrounds in geniculate receptive fields (Bonin et al. 2005) and it is known to play a role in diversifying response timing within dLGN (Humphrey and Murthy 1999; Humphrey and Weller 1988; Mastronarde 1987b, 1992; Saul and Humphrey 1990; Wolfe and Palmer 1998). Intrageniculate inhibition clearly plays an important role in receptive-field construction within dLGN, although it is unlikely that it could explain the differences in response latency and receptive-field size of Y_A and Y_C cells (Table 2). Although the intrageniculate inhibitory circuitry is known to differ between layer A and layer C, it is thought to be similar for Y_A and Y_C cells (Dankowski and Bickford 2003; Datskovskaia et al. 2001). Moreover, although systematic differences in intrageniculate inhibition would make Y_A and Y_C cells different in the strength of their receptive-field surrounds, response gains, offsets, and mean firing rates (Bonin et al. 2005), none of these differences was revealed by our measurements (Figs. 8 and 9 and Table 2). As a second possible mechanism, Y_A and Y_C cells may differ in the strength of the feedback inputs that they receive from the cortex. This mechanism is also unlikely because, whereas cortical feedback is thought to modulate the strength of the receptive-field surround and response gain (Murphy and Sillito 1987; Nolt et al. 2007; Przybyszewski et al. 2000), we did not find systematic differences between Y_A and Y_C cells in either of these two parameters. Finally, other mechanisms based on differences in nonlinear membrane properties would be hard to reconcile with the lack of significant differences in static nonlinearites reported here (Fig. 9 and Table 2). Therefore our results suggest that the amount of retinogeniculate convergence plays a major role in shaping the spatiotemporal structure of the geniculate receptive fields; however, properties such as the strength of the receptive-field surround, gain, offset, and mean firing rate are likely to be more determined by other factors such as intrageniculate circuitry, neuronal membrane properties, and cortical feedback.

Relation with previous work

Previous studies have shown that geniculate neurons sharing input from a retinal afferent fire in precise 1-ms synchrony. These studies identified the retinal inputs to synchronous geniculate cells through s-potential recordings (Alonso et al. 1996) or recording directly from the retina (Usrey et al. 1998). The precise synchrony generated by shared retinal afferents has been shown to involve neurons with similar receptive fields (Alonso et al. 1996, 2006, 2008; Yeh et al. 2003), although it was not known whether the magnitude of the receptive-field mismatches depended on cell type. Y cells located in different layers share input from the same retinal afferent (Sur et al. 1987; Yeh et al. 2003), but differ in a large number of response properties including contrast sensitivity, linearity of spatial summation, receptive-field size, response latency, and response transiency (Frascella and Lehmkuhle 1984; Lee et al. 1992; Yeh et al. 2003). Therefore the expectation was to find larger receptive-field mismatches within the Y pathway than within the X pathway. Interestingly, we found that the receptive-field mismatches in the Y pathway are small even across geniculate layers (peak-time difference <5 ms; size ratio <2 in most pairs; Fig. 7).

We cannot completely discard the possibility that Y_A and Y_C cells may differ in other response properties that were not tested in our experiments. Most of our analyses were obtained by spike-trigger-averaging the stimulus, a technique that does not capture response nonlinearities in Y geniculate cells. However, it should be noticed that Y_A–Y_C synchronous cells did not show pronounced differences in their linearity of spatial summation measured with contrast reverse gratings (Table 2). Importantly, the synchrony generated by shared retinal afferents was robustly correlated with the magnitude of the Y_A–Y_C receptive-field mismatch (R² = 0.75, Fig. 7). Such a strong correlation between receptive-field mismatch and synchrony strength would not be expected if we would have missed a major factor in the retinal inputs that distinguishes Y_A and Y_C cells.

The synchronous firing of geniculate cells that share a retinal afferent (called here geniculate synchrony) is remarkably precise compared with the synchrony generated by other circuits. For example, geniculate cells with overlapping receptive fields are continuously synchronized by stimuli; however, this stimulus-dependent synchrony is several times broader than the geniculate synchrony (Desbordes et al. 2008). Another type of synchrony that originates from the direct inputs to the retinal ganglion cells is more precise than the stimulus-dependent synchrony but less precise than the geniculate synchrony (Mastronarde 1983; Pillow et al. 2008) (Fig. 6).

Divergence within the Y retinogeniculate pathway

Based on our measurements of correlated firing within dLGN, we estimate that X retinal afferents diverge into 10 X_A cells and Y retinal afferents diverge into 20 Y_A cells and 12 Y_C cells (Table 4). These large divergence values, together with the relatively low percentage of tightly correlated spikes generated by Y retinal afferents, indicate that retinogeniculate convergence may be more functionally important than previously thought. It is frequently assumed that most geniculate cells are dominated by just one retinal afferent (Carandini et al. 2007; Chen and Regehr 2000; Mastronarde 1992; Sincich et al. 2007). However, it is very possible that convergent, weaker retinal afferents are more important in receptive-field construction than previously thought. Simultaneous recordings from geniculate cells and s-potentials have consistently demonstrated that >90% of the geniculate spikes can be generated by a single, dominant retinal afferent during visual stimulation (Cleland and Lee 1985; Cleland et al. 1971a; Sincich et al. 2007; Weyand 2007). However, it is not known whether the same retinal afferent can dominate the responses of multiple geniculate cells. Our results clearly demonstrate that this is unlikely. If each dominant afferent generates >90% of the spikes from a given geniculate cell and multiple geniculate cells share input from the same dominant-retinal afferent, synchrony strengths >80% should be found, as predicted by Cleland (1986). In contrast, the strongest correlation that we found was 46.9% for X_A–X_A cell pairs. Even if the synchrony strength is considerably reduced by low retinogeniculate efficacies, the average value reported here of around 10% can hardly be explained without retinogeniculate convergence.

Current estimates indicate that the number of retinal afferents converging on the same geniculate cell can range from 1 to 4 (Cleland et al. 1971a,b; Mastronarde 1992; Usrey et al. 1999). Our values of retinogeniculate divergence can be used to estimate convergence because the ratio of divergence/convergence equals the ratio of geniculate cells to retinal ganglion cells. However, our estimates are limited by the accuracy of current retinal ganglion cell counts. Whereas the numbers of geniculate cells seem to be quite consistent across individual cats [503,000 in Williams et al. (1993); 557,000 in Madarasz et al. (1978)], the number of retinal ganglion cells can vary by a factor >2 [90,000–128,000 in Stone (1965) and Stone and Campion (1978); 150,000 in Illing and Wassle (1981); and 170,000–240,000 in Hughes (1975, 1981)]. Taken into account this important limitation, if we assume that our animals had 90,000–128,000 retinal ganglion cells (Stone 1965; Stone and Campion 1978), 5% Y and 50% X (Wassle and Boycott 1991), and that the X/Y ratio across the entire dLGN was 5 (Humphrey and Murthy 1999; Mastronarde 1992; So and Shapley 1979), then the average retinogeniculate convergence would be roughly 2–3 for X_A and Y_A cells and 4–5 for Y_C cells. Because the maximum synchrony measured in dLGN is twice as large in X_A than that in Y_A cell pairs, most cells receiving a single retinal input are likely to be X_A and not Y_A cells (Mastronarde 1992).

The pronounced divergence of the Y pathway reported here raises an intriguing question: why do we need so many Y geniculate cells covering the same point of visual space? We propose that retinal receptive fields are multiplexed within the dLGN by a weighted sum of retinal inputs (Alonso et al. 2006). In this weighted sum, the center of gravity of the geniculate receptive field is mostly determined by a dominant-retinal afferent but the additional retinal inputs introduce slight variations in receptive-field position, size, and response latency that are important to increase dLGN receptive-field diversity. In this scheme, each retinal ganglion cell would provide the sole retinal input to one geniculate cell to pass a copy of the original retinal receptive field to the next stage of visual processing. In addition, it would provide weaker inputs to many other geniculate cells, which together with inhibitory dLGN circuits (Mastronarde 1987b) would enrich the temporal and spatial receptive-field properties of the thalamic receptive-field array. The strategy of multiplexing the retinal receptive fields could be particularly important in sparse retinal arrays such as those of Y cells (Masland 2001) and could provide the visual cortex with a more diverse and uniform representation of visual space than that available at the retina.

GRANTS

The research was supported by National Eye Institute Grant EY-05253 and Research Foundations in the University of Connecticut and the State University of New York.