Abstract
Most behavioral tasks have time constraints for successful completion, such as catching a ball in flight. Many of these tasks require trading off the time allocated to perception and action, especially when only one of the two is possible at any time. In general, the longer we perceive, the smaller the uncertainty in perceptual estimates. However, a longer perception phase leaves less time for action, which results in less precise movements. Here we examine subjects catching a virtual ball. Critically, as soon as subjects began to move, the ball became invisible. We study how subjects trade-off sensory and movement uncertainty by deciding when to initiate their actions. We formulate this task in a probabilistic framework and show that subjects' decisions when to start moving are statistically near optimal given their individual sensory and motor uncertainties. Moreover, we accurately predict individual subject's task performance. Thus we show that subjects in a natural task are quantitatively aware of how sensory and motor variability depend on time and act so as to minimize overall task variability.
INTRODUCTION
Real world behavior requires the brain to combine a stream of sensory information and motor actions over time. This problem is complicated given that sensory inputs and motor outputs are subjected to noise and, more generally, uncertainty (Faisal et al. 2008). In the sensory domain, it has previously been shown that human subjects have knowledge about the uncertainty in their sensory modalities and can combine these modalities in a statistically optimal fashion to reduce overall sensory uncertainty (van Beers et al. 1996; Ernst and Banks 2002; Hillis et al. 2004; Jacobs 1999; Knill 2003; Sober and Sabes 2005; van Beers et al. 1999). However, these studies examine only synchronous presentation of stimuli and therefore ignore the role of time in acquiring sensory information. In the motor domain, goal-directed movements seem to be conducted in such a way as to reduce motor variability (Harris and Wolpert 1998) and minimize the task relevant parts of movement uncertainty (Todorov and Jordan 2002). Thus in action and perception tasks, subjects behave in a way to minimize the negative consequences of uncertainty (Battaglia and Schrater 2007). Unlike previous studies, most natural situations involve asynchronous (and possibly overlapping) episodes of sensory information acquisition and motor action, from reaching to an object that you have previously looked at to using your side view mirror while driving. Thus successful behavior requires a combination of sensation and action across time. Here, we examine how subjects choose to allocate time to perception and action.
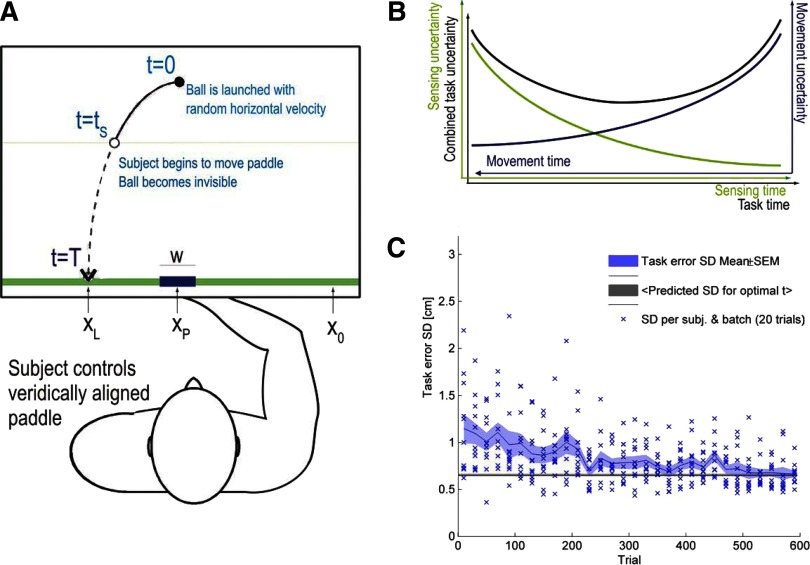
To do this we used a simple virtual reality experiment, catching a falling ball with a paddle (Fig. 1A). We enforced a trade-off between perception and action phases by making the ball invisible once movement is initiated, such that no additional sensory information can be acquired about the ball's trajectory and landing position. Therefore subjects can trade-off their sensory and movement uncertainties by choosing the amount of time they allocate to perception and the amount of time remaining for action before the ball touches the ground—that is, by making the decision when to switch from perception to action. Our approach is to measure independently the time dependence of sensory variability and motor variability and to predict their combined effect on the ball catching task. Note that the use here of the term variability encompasses many sources. For example, motor variability (here the endpoint variability of the position of the paddle) is constituted by signal-dependent motor noise (Harris and Wolpert 1998), motor planning variability (Churchland et al. 2006; van Beers et al. 2004), noise in nerve fibers of the CNS and PNS (Faisal and Laughlin 2007), and other sources (Faisal et al. 2008).
FIG. 1.
Overview of the ball catching experiment. A: the ball is launched from a central position with random horizontal velocity and is accelerated by artificial gravity toward the ground (green line); the total task time to touchdown is therefore constant. Subject controls a veridically aligned paddle of varying width w (the subjects hand center underneath the flat screen is matched to the paddle center). After the ball is launched, the subject chooses when to start moving the paddle from the far right start position (x = 0). Once paddle movement begins, the ball becomes invisible as it falls toward the ground. At all times, a thin horizontal line indicates the vertical position of the ball. A successful catch occurs when the ball center touches ground level within the width of the paddle; otherwise, to provide feedback, the ball is rendered visible and continues its trajectory until it disappears at the bottom of the screen. B: time and uncertainty relationships in the ball catching experiment. In general, sensory uncertainty (green curve and axis) decreases with time, and so does motor uncertainty (blue curve and axis). However, because of the design of the experiment, the more task time is spent sensing, the less task time remains for movement. Therefore as task time progresses and the ball approaches ground level, motor uncertainty increases. Thus the switching between sensory and motor uncertainty causes a combined uncertainty (black curve) with a globally minimal task error at the accordingly optimal switching time. C: task error (measured as ball landing position minus final paddle position) SD plotted vs. trial [batch of 20 trials for each subject (blue crosses), mean across 11 subjects (blue line), and SE (shaded region)]. The horizontal level line represents the minimal task error across subjects if they would have used the optimal switching times for each trial.
We investigate whether subjects have knowledge of the time dependence of their uncertainty in both perception and action by examining whether they choose the optimal switching time so as to minimize the overall variability of the task and maximize their chances of catching the ball.
We can consider an ideal actor whose aim is to maximize the probability of catching
the ball by minimizing the distance between the paddle and ball at touchdown. Both
sensory and motor variability contribute to the overall variability of where the
paddle is placed relative to the ball (see Fig.
1B for illustration). The longer the actor
perceives, the lower the sensory variability about where the ball will land (Fig. 1B, green curve and axes)
but the higher the motor variability, because the remaining time for movement
decreases (Fig. 1B, blue curve
and axes). An ideal actor should therefore choose a switching time that minimizes
the combined effect of sensory and motor variability (Fig. 1B, black line). To predict the optimal switching
time for each subject, we independently quantify in two separate experiments the
time dependence of the sensory and motor variability (by their variance). We assume
that the two sources of sensory and motor variability are independent, and therefore
the combined task variability 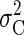 is the sum of the time-dependent sensory variability variance
is the sum of the time-dependent sensory variability variance 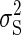 and motor variability
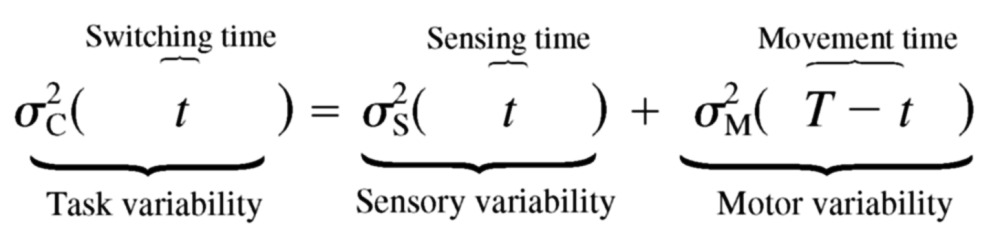
and motor variability 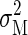 Therefore if the total task time is T and
subjects switch from perception to action at time t, this means
they have time t for sensing and the remaining time
(T − t) for moving. Therefore we would
predict that the task variability is given by
Therefore if the total task time is T and
subjects switch from perception to action at time t, this means
they have time t for sensing and the remaining time
(T − t) for moving. Therefore we would
predict that the task variability is given by
 |
(1) |
This allows us to find the value for the switching time t that
minimizes 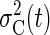 and thus maximizes the probability of catching the ball.
and thus maximizes the probability of catching the ball.
We can directly predict the subject's performance with respect to their task instruction (catching as many balls as possible). Using Eq. 1 , we calculate the probability of catching the ball for the ideal actor and compare it to the subject's actual performance for each paddle width. The subject's catch performance will be systematically worse than the optimal prediction if the subject chooses suboptimal switching times, if another source of variability has a notable effect (as captured by a third variability term in the sum of Eq. 1 ), or if significant correlations between sensory and motor error exist.
Preliminary results were presented at the Neural Control of Movement Conference 2007 (abstract dated December 15, 2006).
METHODS
Subjects and manipulandum
After providing written informed consent, 11 subjects (6 naïve university students and 5 naïve laboratory members) participated in the main study. A second sequence-controlled study was carried out with six different right-handed naïve university students. All subjects were right-handed and between 19 and 37 yr old. The experiments were carried out in accordance with institutional guidelines, and a local ethics committee approved the experimental protocols.
Subjects controlled the horizontal movement of a paddle with the aim of catching a falling ball on the computer screen. While seated, subjects held the handle of a robotic manipulandum with two degrees of planar freedom of which only the horizontal axis was used to control the task. The manipulandum is a custom-built device (vBOT) consisting of a parallelogram constructed mainly from carbon fiber tubes that were driven by rare earth motors via low-friction timing belts. Software control of the robot was achieved by means of a control loop running at 1-kHz measuring position of the handle. A planar virtual reality system was used that prevented subjects seeing their hand and allowed us to present visual images into the plane of the movement (for full details of the setup, see Kording et al. 2004). The setup was calibrated such that the position of the paddle center lined up visually with the center position of the grasped handle. Each subject completed a sequence of three experiments in the following sequence: catching (600 trials), sensory variability (560 trials), and motor variability (560 trials).
Ball catching experiment
The ground level (y = 0 cm) was marked by a horizontal 38-cm bar (Fig. 1A). A virtual paddle could be moved along ground level (x = 17 cm corresponded to the horizontal center of the screen—positive values of x are to the left of the starting point) and was veridically aligned with the invisible manipulandum handle underneath it. Before each trial, a paddle of width w = {0.5, 1, 2, 4} cm was chosen randomly and displayed. Each trial began with the subject having to move the paddle's center to its start position at 0 cm (close to the right corner of the screen) and remain there within a centered 5-mm tolerance window until the ball appeared.
After the paddle initial position is reached, the ball (represented by a filled white circle of 8 mm diam) appeared at its initial position. In every trial, the ball fell from x = 17 cm, y = 25 cm down toward the bottom edge of the screen. At all times, a green horizontal bar (1 mm high and 38 cm wide) was displayed that tracked the vertical position of the ball throughout the trial. When the green bar appeared, the task started and the ball began to move. Up to this point, any movement of the paddle beyond its tolerance window would trigger a repetition of the trial (mistrial). The ball fell under simulated gravity and was launched with a horizontal velocity that was drawn uniformly between −7.5 and 7.5 cm/s, such that landing positions resulted in uniformly distributed movement distances between 6.5 and 27.5 cm. The gravity constant was set to g = 25.5 cm/s2 so that the total ball motion time (from launch to landing) was T = 1,400 ms.
At any time when the ball was falling, the subject could start moving the paddle to catch the ball. As soon as the paddle was outside its tolerance window, the ball would become invisible, but the falling bar would still be visible and continue to move. If the center of the ball was within the paddle width at ground level, the trial was successful and the screen turned green. If the ball was not caught, the trial was unsuccessful, the screen turned red, and the ball became visible as it crossed the ground level and remained visible for a further 3 cm of trajectory. To motivate the subjects, the current score was displayed as the number of successful trials minus the number of unsuccessful trials and mistrials. Each paddle width was tested on 150 trials, resulting in 600 trials in total.
Sensory variability experiment
We measured subjects' sensory uncertainty by letting them observe the falling ball for varying durations and asking them to indicate ball's landing position by moving the paddle (here, a 1-mm-wide white line) to the estimated position and clicking a button. They were allowed arbitrary time to make this estimate to minimize the effects of motor variability. After clicking, the subjects were briefly shown the correct landing position of the ball by displaying the ball and a 1-mm-wide black dot marking its center. The ball's initial velocity was chosen randomly so that its landing positions varies over x = 17 cm + {9.8, 7.7, 4.2, 2.1, −1.4, −4.2, −6.3} cm, as were observation durations t = 200, 400, 650, 1100 ms, and each pair of observation duration and ball landing position was tested 20 times. The 560 trials took ∼50 min to complete.
Motor variability experiment
We measured a subjects' motor variability with respect to the movement time and distance moved. The paddle was a 1-mm-wide white line. At the start of each trial, a fixed ball location (x) was marked on the ground, which remained visible throughout the trial, such that time-dependent sensory uncertainty was reduced to a minimum. Subjects observed a horizontal bar falling at a constant speed from a height of 25 cm to ground level, which provided timing information. During this time, the subjects were instructed not to move (any action would have triggered a mistrial). The duration of the falling bar indicated visually how much time the subject was allowed on this trial. After the bar had reached the ground, it was positioned again at the top and subjects could start the trial at any time by moving >5 mm from the paddle's initial position (the target was visible at all times). Subjects were required to reach to the target with their paddle as accurately as possible, within the indicated movement time. As soon as subjects initiated their movement, the bar began to fall again at the same rate, indicating the total time that subjects had to perform the movement. Their paddle froze the moment the bar touched the ground. The distance between the paddle's frozen position and the target was recorded as the trial's motor error.
The movement times were chosen randomly from t = 300, 500, 750, 1100 ms. Ball landing positions were chosen randomly from x = 17 cm + {6.4, 4.9, 2.4, 0.9, −1.6, −2.6, −5.1} cm. Each pair of movement time and ball landing positions was tested 20 times. The 560 trials took ∼50 min to complete. For the successive analysis, we removed the trials with movement times of 300 ms, because subjects showed a consistent movement bias, reflecting their inability to move fast enough to reach the target, thereby undershooting on the majority of trials. Because subjects almost never moved this fast in the combined task (cf. Fig. 3; fastest movement time had a mean of 427 ms across subjects), we fitted the motor variability using only the slower movement times (500, 750, 1100 ms).
Note that the ball landing positions and movement distances in the sensory variability and motor variability experiments were different from those used in the actual ball catching experiment. This minimizes the effect of training subjects to specific ball landing positions. In particular, the ball catching experiment tested a range of positions uniformly, whereas the sensory and motor variability experiments tested seven discrete positions to allow a defined measurement of variability at each position. In the sequence-controlled experiments, the sensory and motor positions were the same (as by balancing the sequences we could factor out training effects). The ball catching task imposes an explicit trade-off between perception and action. We therefore assume that by the time the subjects decide to initiate their movement, they have also decided where to move. Thus their movement toward their estimated ball landing position should be analogous to their movement toward the displayed ball in the motor variability experiment.
Sequence controlled study
In the first study, each subject experienced the ball catching task first. This was done to ensure that they did not become trained in knowing about their own sensory and motor variability simply through the sensory and motor experiments. To test whether the order of our experiments could have affected our results, we ran a second set of experiments with six different naïve subjects. Each subject experienced one of the six possible sequences of sensory, motor, and ball catching experiments with a single paddle width (2 cm), as shown in Table 1.
TABLE 1.
Sequence order of the 3 experiments
| Subject | Sensory | Motor | Ball Catching |
|---|---|---|---|
| A | 1 | 2 | 3 |
| B | 1 | 3 | 2 |
| C | 3 | 1 | 2 |
| D | 3 | 2 | 1 |
| E | 2 | 3 | 1 |
| F | 2 | 1 | 3 |
The subject labels match those of Fig. 4.
To further corroborate our findings, we ran these subjects on a different set of parameter values: subjects had to move faster (total task time T = 1000 ms, by setting the gravity constant to g = 50 cm/s2) and over longer distances (movement distances for ball landing positions were 9.6–30.5 cm), while the paddle width was held constant at 2 cm. In the sensory experiment, ball landing positions of x = 20 cm + {9, 6, 3, 0.5, −3, −6, −9} cm and times t = 250, 375, 500, 750 ms were probed, whereas in the motor experiment, movement distances of positions of x = 20 cm + {9, 6, 3, 0.5, −3, −6, −9} cm and times t = 375, 500, 750 ms were probed.
Analysis
SENSORY VARIABILITY EXPERIMENT.
The sensory variability experiment was used to calculate the SD of error between the ball's true landing location and the sensory estimate of the location [σs(t)]. This was calculated separately for each subject and each observation's duration. We collapsed these estimates across different landing positions for each subject. To provide a parameterized model of how the SD depends on observation durations, t, we fit a power law to estimate two parameters (a, b) for each subject, σs(t) = a × tb. The power law had the highest R2 values among two-parameter exponential and power law fits.
MOTOR VARIABILITY EXPERIMENT.
The motor variability experiment was used to calculate the SD of error between the ball's fixed location and the position of the paddle center, σM(t, x). This was calculated separately for each subject, each movement time t, and movement distance x. To model the distance and movement time-dependent variability σM(t,x), we made use of Fitt's law (Fitts 1954). This empirical law states that pointing towards a target of width V at a distance U requires a movement time MT = c + d log2(2U/V), where c and d are task- and subject-specific parameters. We equated movement distances U = x and movement time MT = t. We used the SD of movement variability towards pointing to a point-like target (our task) as equivalent measure of pointing towards a target of size V = σM. To provide a parameterized model of how the SD depends on movement time and distance, we solved Fitts' law for the movement variability σM to estimate two parameters (c, d) for each subject
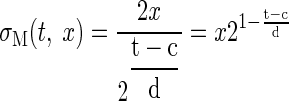 |
Modeling the combined task
For each trial of the ball catching task, we measured the switching time from perception to action. The task error was defined as the distance between the center of the paddle and the ball's landing position (independent if the ball was caught or not). Given the independent measures of sensory and motor variability in the previous two experiments, we can predict the optimal switching time from perception to action and the probability of a successful trial in the ball catching task. We assume that the contribution of motor planning variability to overall motor variability is similar in the motor variability experiment and the ball catching experiment, because the movement is quite simple.
To predict optimal switching times, we make two assumptions. First, we assume that the sensory and the motor errors are independent of each other. Second, we assume that subjects aim to move the center of the paddle to where they estimate the ball will land—that is, they are unbiased (in addition, we examined a model where subjects were optimally biased, but this has minimal effect because optimal bias is well below movement variability). We model the variance in the ball catching task as the sum of the variances of the independent sensory and motor tasks (assuming the movement is to the ball's true landing position). Therefore on a trial with total task time, T, where the ball will land a distance, x, from the starting paddle position and the switching time is t, the predicted variance is
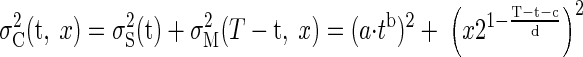 |
(2) |
where a, b, c, and d are the predetermined parameters that characterize each subject's sensory and motor variability. Therefore for any setting of switching time t and ball landing location x, we can predict the combined variance using Eq. 2 . By varying the switching time, t, we can find the optimal switching time to minimize the error.
Subjects controlled a paddle moving along the horizontal axis by moving a manipulandum that was free to move in a plane. However, any variability in the vertical axis does not affect the paddle position. We examined the final vertical deviation at the end of the movement in both the motor task and the combined task across all subjects and landing positions. The variability measured in SD was similar in the two tasks (0.87 ± 0.05 vs. 0.99 ± 0.04 cm). Thus any effect of vertical movement to the results should contribute equally to both the combined task and the motor variability task. Hence, we analyze and fit the data with respect to only the horizontal (task-relevant) movement distance.
Prediction of catch performance
To predict the probability of catching the ball we assume that the sensory and
motor variability have a distribution that is Gaussian. Therefore the
probability of catching is simply the integral of the zero mean Gaussian
distribution with variance 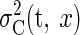 over the paddle width (from –w/2
to w/2—that is, the paddle being under the ball).
over the paddle width (from –w/2
to w/2—that is, the paddle being under the ball).
We can predict the catch probability in two ways: First, we use the empirical switching times and ball landing position on each trial for each subject to calculate the catch for the sensory and motor variability. We average the catch probabilities over all trials of a certain paddle width and compare these with actual catch probabilities for each subject. This prediction can be used to test our assumption that the sensory and motor variability are Gaussian distributed, independent, and additive in the catching task. Second, we can test the hypothesis that subjects are optimal by predicting the catch probability based on subjects using the predicted optimal switching times instead of the actual switching times for each trials.
RESULTS
We devised three experiments to study the trade-off between the time allocated to perception and action. We measured the time dependence of sensory and motor uncertainty independently (see methods for details) in two experiments, as well as a combined perception-action task of ball catching. We present the results of the ball catching experiment here, whereas we relegate the results of our repetition using the sequence-controlled experiments in the supplementary information,1 because we are reporting similar results.
Sensory variability experiment
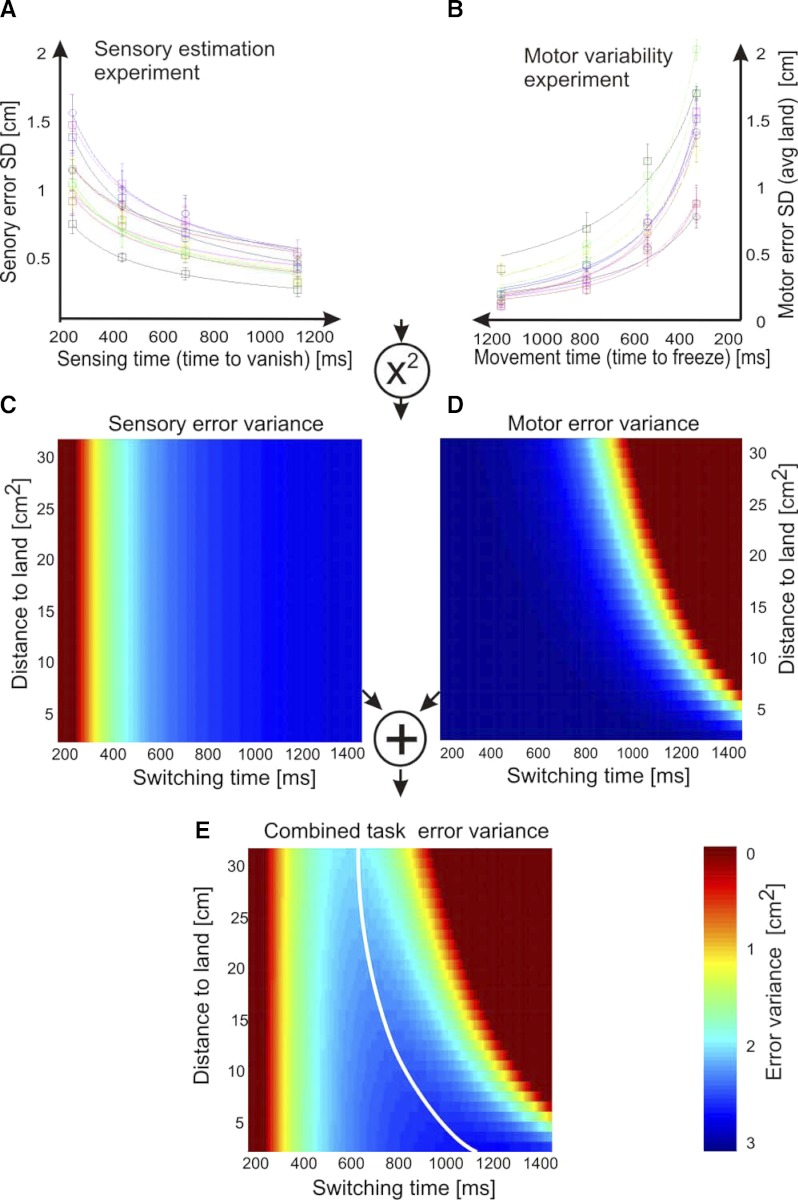
In this experiment, we measured the time dependence of the sensory variability, in a situation in which motor uncertainty was negligible. On each trial, a ball was launched from the same upper central screen location with a random horizontal velocity component and fell toward the lower edge of the screen under artificial gravity. The ball fell with a parabolic trajectory for 1,400 ms before landing on the ground. The ball vanished after a randomly prescribed time (sensing time) and subjects had to indicate, without time constraints, where the ball landed and were given feedback as to the actual ball landing position. The levels of sensory variability were individual to each subject and dependent on time. For a sensing time of 200 ms, subjects' sensory variability, as measured by the SD between actual and estimated positions, ranged between 0.73 and 1.61 cm (median, 0.96 cm), whereas for a 1,200-ms sensing interval, the range was between 0.27 and 0.51 cm (median, 0.38 cm; Fig. 2A). Subjects' mean sensory error bias was small; the range of mean sensory error was −0.16 to 0.24 cm with a median of −0.03 cm. To quantify the time dependence of the sensory variability, we fit (after visual inspection of the data) a power law of the SD of the sensory error (calculated for each sensing time, pooled across ball landing positions) to the sensing time (median R2 = 0.51; R2 range, 0.36–0.76). Subjects showed an inverse square root time dependence of the SD of the sensory error—that is, a power law exponent of −0.55 ± 0.03 (SE) across subjects. In our model, we assume that sensory error is not dependent on the balls landing location, because the measurable dependence is weak (median R2 = 0.05; R2 range, 0–0.15). We can thus interpolate the subject's sensory variability for other sensing times and ball landing positions using the time-dependent square root power law.
FIG. 2.
Construction of the task variability surface from the sensory estimation and motor variability experiments. A: the time dependency of the sensory error (means ± SE) is fitted by square root power-law for each of the 11 subjects. B: the time- and position-dependent motor error is fitted by Fitt's law; here the time-dependency fit (curves) is shown alone by averaging over all landing positions. A and B show the data (means ± SE) for each of the 11 subjects. The sensory and motor error SD is converted into variances by squaring. C: the sensory error variance surface is constructed by interpolating the fitted sensory error relationship for all possible switching times (the switching time corresponds to the time available for sensing) and landing positions. D: the motor error surface is obtained as in C by using Fitt's law to interpolate the motor variability SD and squaring the values. Note that in the ball catching experiment, we equate the movement time of the motor experiment with the remaining task time after switching. We plot the motor error in terms of the switching time t and therefore the motor error increases in the direction of the switching time axis. E: we assume that sensor and motor error (surfaces) are independent of each other and we can thus obtain an estimate of the ball catching task variability surface by summing both C and D together. This combined error surface resembles a “river valley” with a minimum task error curve (white line) that shows the optimum switching time for every ball landing position.
The sequence-controlled version of the experiment produced similar results. For a sensing time of 250 ms, subjects' sensory variability, as measured by the SD between actual and estimated positions, ranged between 1.2 and 2.4 cm (median, 1.45 cm), whereas for a 750-ms sensing interval, the range was between 0.47 and 0.92 cm (median, 0.65 cm). Thus sensing error was considerably larger in this faster version of the sensor variability experiment. Subjects' mean sensory error bias was small; the range of mean sensory error was −0.73 to 0.46 cm, with a median of −0.13 cm.
Motor variability experiment
In the second experiment, we measured subject's movement variability. The sensory uncertainty about the target location was reduced to a minimum by ensuring that the target was always visible and stationary. The experiment was similar to the sensory experiment; however, subjects were first shown a falling bar, indicating the time they had to reach the ball at its fixed position on the ground (the ball was always visible). Subjects could initiate the trial by starting to move from their start position, resulting in the bar falling again. The trial ended when the bar hit the ground, at which point the paddle position froze. The difference between the subject's final paddle position and the ball position reflected their motor error. The subjects' motor error bias was small (range of subjects' mean motor error, −0.07 to 0.17 cm; median, 0.08 cm) compared with their motor variability SD.
In contrast to the sensory error, the movement error also depends on the distance the paddle had to be moved to reach the ball's position. We used Fitts' law (Fitts 1954) to describe the relation between motor error SD with movement time and distance. This nonlinear relationship was fit by the data across subjects (median R2 = 0.72; R2 range, 0.22–0.96; Fig. 2B). This fit allowed us to interpolate the motor error SD for other ball landing positions and movement times.
The separate sensory and motor experiments allowed us to measure the individual terms on the right-hand side of Eq. 1 . However, because the motor error is distance dependent, we reflect this by the distance dependence of the combined task error ( Eq. 2 )
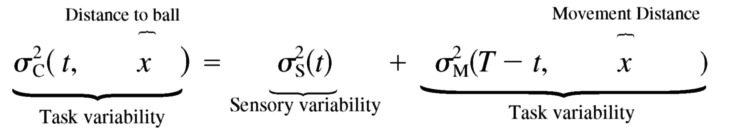 |
(3) |
The sequence-controlled version of the experiment produced similar results. Five subjects' motor error bias was small (range of subjects' mean motor error, −0.06 to 0.06 cm; median, −0.04 cm). We used Fitts' law (Fitts 1954) to describe the relation between motor error SD with movement time and distance. This nonlinear relationship was fit by the data across subjects (median R2 = 0.86; R2 range, 0.76–0.94). One subject had difficulty at moving very fast over a long distances, which resulted in an overall bias of −1.8 cm and a fit value R2 = 0.18 (subject A in Fig. 4).
Ball catching task experiment
Subjects controlled the horizontal movement of the paddle with the aim of catching the falling ball and we recorded their time of switching from perception to action given the ball landing position (and the paddle width) of the trial. As in the sensory experiment, the ball was launched with random initial horizontal velocity. The subject's task was to catch the ball by moving the paddle to beneath the ball before the ball reached the ground (Fig. 1A). To ensure distinct perception and action phases, as soon as subjects began to move the paddle, the ball disappeared and moved on its trajectory invisibly. To avoid any uncertainty about when the ball would hit the ground, the vertical position of the ball was indicated at all times (even when the ball became invisible) by a horizontal line passing through the ball's center. Thus subjects could choose to observe for a long period, thereby reducing sensory uncertainty, but only have a short movement time left that would increase motor uncertainty. Alternatively, they could choose to move early to reduce motor variability but with an increased sensory uncertainty in the ball's landing location. After the ball hit the ground, subjects were given feedback about task success. We also varied the paddle width on each trial to explore how catch performance depends on paddle width.
Performance varied across subjects. Task error remained low for some subjects (Fig. 1C, blue crosses), whereas it was initially large for other subjects; however, over the first 1–250 trials, all subjects had settled (Fig. 1C, shaded area and line) and their task error was near to the optimal task error achieved by using optimal transition times (Fig. 1C, black line). The least accurate subject caught on average 50% of the balls, whereas the most accurate subject caught 69% of the balls (median, 59%).
The actual switching times depend on the balls' landing position. To predict the
task performance as a function of both switching time and ball landing position,
we constructed two-dimensional variability surfaces for both sensory variability 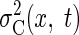 and motor variability
and motor variability 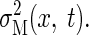 Because sensory variability is independent of the landing
location of the ball, the variability only varies over the sensing time
(switching time) axis (Fig.
2C). However, movement variability depends on both
movement time (total time − switching time) and distance to the ball
(Fig. 2D). To predict
performance on the catching task, we can add these two variability surfaces to
obtain the combined task error variability
Because sensory variability is independent of the landing
location of the ball, the variability only varies over the sensing time
(switching time) axis (Fig.
2C). However, movement variability depends on both
movement time (total time − switching time) and distance to the ball
(Fig. 2D). To predict
performance on the catching task, we can add these two variability surfaces to
obtain the combined task error variability 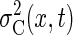 (
Eq. 2
). The resulting task variability surface (Fig. 2E) is characterized by a single curved error
“valley.” The switching times along the minimum in the
valley represent the optimal switching time curve (Fig. 2E, white line), traced by the switching time
which minimizes task error for a given ball landing position. These values can
be used to predict the switching times for each subject.
(
Eq. 2
). The resulting task variability surface (Fig. 2E) is characterized by a single curved error
“valley.” The switching times along the minimum in the
valley represent the optimal switching time curve (Fig. 2E, white line), traced by the switching time
which minimizes task error for a given ball landing position. These values can
be used to predict the switching times for each subject.
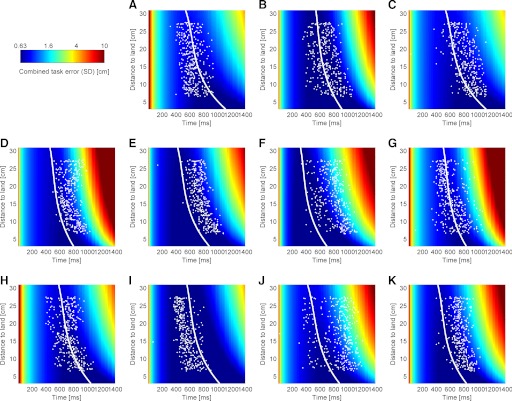
Each subject had characteristic sensory and motor variability surfaces. Correspondingly, their combined task variability surfaces (Fig. 3) and switching times varied (Fig. 3, white dots showing individual trials). Therefore the key feature we are trying to predict is the mean switching times for a given target distance. For each subject, the empirical mean switching time curve (least square fit of the white dots in Fig. 3 by a 2nd-order polynomial) and the optimal switching time curves had matching shapes for all 11 subjects (R2 median = 0.97; R2 range, 0.73–0.99; as can also be seen in the matching curvature of the black curve and the blue curve in Supplementary Fig. S1). Switching time curves varied between subjects and ranged from (averaged across landing positions) 431 to 733 ms. The variability in trial-by-trial switching times around the mean switching time curve had an SD (across landing positions) of 130 ± 12 (SE) ms (across subjects). This can also be seen in Supplementary Fig. S1, where we plot the 95% confidence intervals (red curves) for the data around the mean switching time curve (black). The optimal switching time curves were within the confidence interval of the timing noise around the mean switching time curves in 96% (median across subjects; range, 0–100%) of trials. Two of the 11 subjects caused the large range between 0 and 100%. Their optimum curve was systematically outside the confidence interval; however, it matched the curvature of the mean switching time curve. These two outliers and an additional two suboptimal subjects had <50% of the switching times within the confidence bars.
FIG. 3.
Switching times and task variability surfaces for all 11 subjects. A–K: each subplot shows the behavior for each subject and the combined variance. Individual trials of the ball catching experiment are shown as white dots, marking the distance of the paddle's initial position to the ball's landing position (i.e., the required movement distance) and the chosen switching time. The same color coding scale (log units of variance) is used for all subjects to highlight the individuality of each subject's error surface. The task variability surfaces (see text and Fig. 2) are computed from the sum of the sensor and motor error surfaces, as determined independently for each subject in the sensory and motor estimation experiment. The optimal switching time curve (white curve) lies in the valley (blue region) of the minimum of the task variability surface. Subjects in A–C, H, and I are naïve members of the laboratory.
The sequence-controlled version of the experiment confirmed the above findings even though it required faster perception and action over longer movement distances (cf. Figs. 4 and 3). The combined task variability surfaces (Fig. 4) and optimal switching times (white curve) varied as predicted among subjects. For each subject, the empirical mean switching time curve (least square fit of the white dots in Fig. 4 by a 1st-order polynomial) and the optimal switching time curves had matching shapes for all six subjects (R2 median = 0.98; R2 range, 0.97–0.99). Note, we chose here a first-order polynomial, because subject's switching times were better fitted than using the second-order polynomial used for the non-sequence- controlled version of the experiment. This is probably because of the weak curvature of the optimal switching time curve in this much faster version of the experiments. The variability in trial-by-trial switching times around the mean switching time curve had an SD (across landing positions) of 61 ± 8 (SE) ms (across subjects). Switching time curves varied between subjects and ranged from (averaged across landing positions) 231 to 500 ms. The variability of the optimal switching times (averaged across landing positions) had an SD of 91 ms across subjects.
FIG. 4.
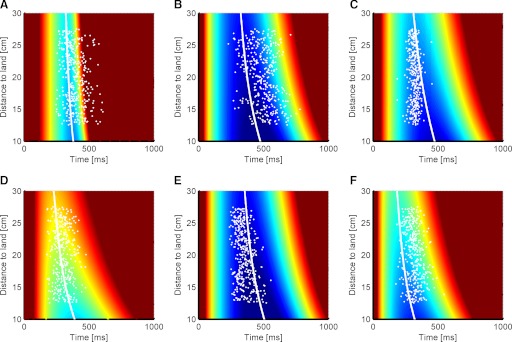
Switching times and task variability surfaces for 6 different subjects in the faster and more difficult sequence-controlled version of the experiments (A–F). Individual trials of the ball catching experiment are shown as white dots, marking the distance of the paddle's initial position to the ball's landing position (i.e., the required movement distance) and the chosen switching time together with the optimal switching time curve (white line). The same color coding scale (log units of variance) and conventions apply as in Fig. 3. Note how the overall level of the combined error surface is higher in this version of the task than that one in Fig. 3, reflecting increased difficulty as subjects have to act within higher sensory and motor uncertainties. Note subject A had difficulty in completing fast movements (<500 ms) over the full range of possible landing positions. All subjects were naïve.
We tested if subjects had specific knowledge of their own individual time- and distance-dependent sensory and motor variability or were just following a general strategy. For each subject, we calculated the combined error surface and optimal switching times of the 121 possible combinations of the 11 sensory and 11 motor error surfaces. We calculated the root mean square error (RMSE) of the 121 optimal switching times with the subject's empirical switching times. We also calculated the most general measure of each subject's performance: the paddle width-dependent catch rates for the 121 possible combinations of sensory and motor error. The R2 between the actual catch rate and the optimal catch rate curves is a measure of how close to optimum a subject performed with respect to the optimum. Across all subjects, cross-validation showed that the match between optimal and actual switching times were on average 6.6% (median, 6.5%) better when using the subject's own sensory and motor variability than the average across all possible combinations. This was further supported by cross-validation in the sequence-controlled version of the experiment with the faster and harder version of the ball catching experiment (6 subjects, 36 possible combinations). Here it was shown that subjects switching times were on average 10% better explained by the optimal switching time calculated using the subject's own sensory and motor variability than the average across all possible combinations.
In our task, it is not the switching time that determines performance per se but the catching of the ball. It is important to distinguish between subjects choosing an optimal parameter value and the sensitivity of the behavioral task (ball catching performance) that is being optimized to variations in the parameter. Therefore to evaluate whether subjects are optimal, we need to ultimately measure how close they are to the optimal catch probability and not how close the switching times are to the optimal switching times. This is particularly important because the valley of the combined error surface in Figs. 3 and 4 (blue regions) is relatively shallow so that subjects can show variation in switching times in this region without degrading performance. The topology of the error surface implies that varying switching time around the optimum will affect catch performance little, because the level of task error remains close to the minimum level and within the width of three to four paddles, and subjects had little incentive or need to exactly choose the optimum switching time. Thus to avoid penalizing switching times at levels close to the minimum and to underweight switching times at task error levels high above the optimum, we measured the proportion of trials where combined task error was within a certain level of the lowest possible task error SD at the optimal switching time (the relevant parameter with respect to catch performance). Subjects behaved such that 27% (median; range, 12–40%) of trials had switching times within 2.5% of the minimum achievable task SD. Moreover, 61% (median; range, 23–73%) of trials were within 10% of the minimum achievable task SD. Thus subjects showed near optimal performance in choosing switching times with respect to the minimum of the combined task variability surface, thus maximizing task performance.
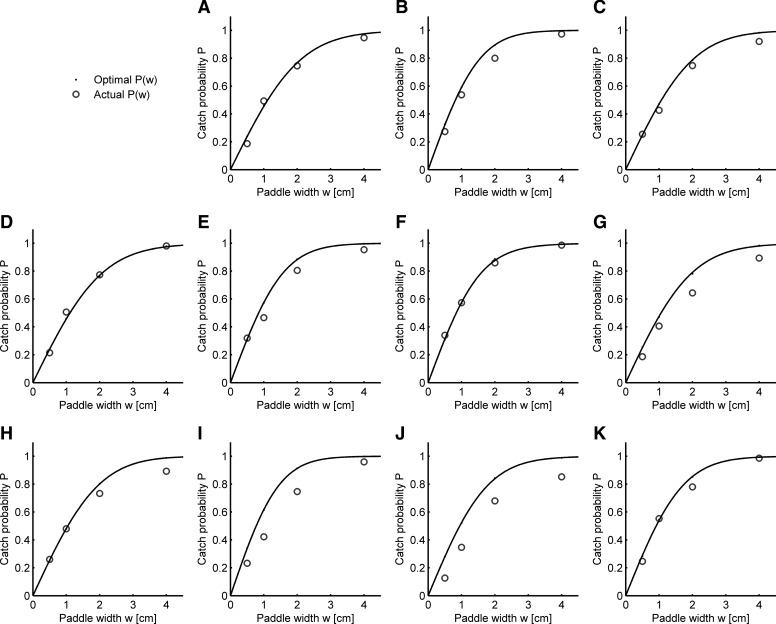
Using the optimal switching time relationship ( Eq. 2 ), we can predict the individual catch performance of each subject. In the ball catching task, we varied the width of the paddle used to catch the ball from trial to trial, which shows a nonlinear relationship between catch performance (i.e., the chance to catch a ball) and paddle width (Fig. 5, circles in the subfigures for each subject). We developed a probabilistic model of task performance that accounts for each individual's variability in the task. We modeled how likely it is that the subject's paddle will be under the ball at touch down by using the independently measured sensory and motor variability to obtain a Gaussian distribution (zero mean, variance equal the combined task variance as computed by Eq. 2 ) of paddle positions under the ball. The area under the Gaussian distribution half a paddle's width to the left and right of its center corresponds to the catch probability. We can predict the catch performance's dependence on the paddle width for all subjects Fig. 5 (black curve) regression between predicted performance (using actual switching times for each trial) and actual performance for four paddle widths: R2 median = 0.99; R2 range, 0.96–0.99. Similarly, we can also use optimal switching times for each trial to predict the optimal catch performance and find very similar results (R2 median = 0.98; R2 range, 0.94–0.99). Therefore our prediction of catch performance confirms that we can model the combined task error as a sum of Gaussian distributed, zero mean sensory and motor errors, which variance is given by the landing position and switching time used. Moreover, the catch probability analysis shows that subjects choose to act very close to the minimum of the task variability surface. These results confirm that, because the task variability surface is shallow near the optimal switching time, subjects can achieve near optimal catch performance despite their timing variability around the mean switching time curve.
FIG. 5.
Catch probability given paddle width (data pooled over all landing positions) for all 11 subjects (arranged to correspond with Fig. 3). A–K: each plot shows the optimal catch performance achieved by using optimal switching times (black curve) and subject's actual catch performance (circles) for each paddle width.
Similarly to the above cross-validation of switching times, we tested whether random combinations of sensory and motor variability surfaces could predict catch performance better than using the subject's own sensory and motor variability surfaces. Across all subjects, the subject's actual catch rate matched the optimal catch rate for the subject's own variability surfaces on average 2.8% (median 5%) better than calculations using other combinations of sensory and motor variability surfaces. This translates into an average of 5.4% (median 7.4%) more balls caught using the subject's own variability surfaces compared with other subject's surfaces. This is a substantial advantage in the final score (the worst and best subjects' catch score differed by only 19%). Similarly, in the sequence-controlled experiment (which used a single paddle width of 2 cm), the catch rate was predicted on average 7% better by using the subject's own surfaces. Thus, on average, subjects' own sensory and motor uncertainties provide a better explanation of their behavior: their switching times are closer to the optimal switching times and their actual catch rate was closer to the optimal catch rate than other combinations of sensory and motor surfaces.
DISCUSSION
We developed a ball catching task in which subjects can choose when to switch from a distinct perception phase to an action phase. Because the total task time was fixed, increasing the perception phase reduced the time available for movement. We used two additional and separate experiments to measure the variability in sensing and variability in moving as a function of time. Using this data, we developed a full probabilistic model of the perception-action task, which allowed us to predict the optimal behavioral decision, when to start moving, as well as the overall performance in the task, the probability of catching the ball. We found that different subjects had idiosyncratic time-dependent variability in both perception and action; however, we were able to predict individual performance and switching times, showing that subjects behaved close to optimal. We showed that, by selecting the minima of the summed sensory and motor variability, we could account for each subject's individual switching times and catch performance. By following this computational strategy, subjects behave statistically optimal in the maximum-likelihood sense.
Our pure perception task measured endpoint estimation error of the ball's landing position as a function of time for which the ball was visible. A ball's parabolic trajectory is a composition of an object falling with constant acceleration vertically and moving with constant speed horizontally. Several previous studies have shown that subjects are accurate at estimating the location of objects moving with constant horizontal speed behind an occlusion (Brouwer et al. 2005; Brown et al. 2007) or estimating the time of contact of occluded objects falling under gravity-like acceleration (Gottsdanker et al. 1961; Indovina et al. 2005; Rosenbaum 1975; Zago et al. 2004). These studies showed that subjects perform poorly when predicting target motion under either horizontal acceleration or under vertical constant velocity motions (Brouwer et al. 2002; Zago et al. 2004). Few studies looked at the estimation of parabolic trajectories (Brouwer et al. 2006; Oudejans et al. 1997; Saxberg 1987). We measured here the extrapolation of parabolic trajectories in the time domain, quantified by sensory endpoint estimation error SD, which was well fit by an inverse square root of time and increasing sensory precision over a period of more than a second.
Our pure motor task measured endpoint estimation error of the paddle's position as a function of allowed movement time and the indicated ball landing position. Because of the veridical experimental setup, moving the paddle was comparable to the hand's reaching movement for the ball (Gordon et al. 1994). Accordingly, we were able to use movement time and the distance from the paddle's starting position to the target position to fit the movement error using Fitt's law (Fitts 1954). Our predictions for the combined perception-action task are solely based on measurements made in independent experiments that measured the individual relationships of sensor and motor error on time. We applied these predictions to the ball catching task, enabling us to assess the full behavioral loop by a direct measure of behavioral performance.
The fact that we can model the catch probability accurately in 7 of 11 suggests that these subjects behave optimally in choosing their switching times. Moreover, other sources of variability beyond the measured sensory and motor variability are negligible or their catch rate would have been much lower than optimum. This is true of any extra source of variability present in the combined task than in the sum of sensory and motor variability.
Four subjects have partially somewhat lower catch performance than optimum. This could be because of several factors, such as positive correlations between sensory and motor error, as well as impact of time-dependent sources of variability that we do not account for in our model. For example time-dependent motor variability could be higher in the ball catching experiment because of the limited amount of time to form a motor plan. Our motor variability experiment incorporates both movement variability from, for example, signal-dependent motor noise (Harris and Wolpert 1998), as well as variability resulting from motor planning (Churchland et al. 2006; van Beers et al. 2004), when there is no time constraint on motor planning. We assume that the contribution of motor planning variability to overall motor variability is similar in the motor variability experiment and the ball catching experiment, because the movement is quite simple.
A recent study (Battaglia and Schrater 2007) suggested a similar effect of sensor-motor timing trade-offs for a random dot pointing task. In their experiment, random dots clustered around an invisible target that was on an arc a fixed distance from the initial hand position. The sensory information changed discretely with the appearance of new dots, unlike our task where sensory information changed continuously. Moreover, the movement distance was always fixed; therefore, it was not possible to test if subjects had full knowledge of the motor variability as a function of both time and distance. In addition, the task was quite unnatural (with time indicated by an hourglass), and the predicted switching times were weakly correlated with mean empirical switching times (subject's median R2 = 0.79; R2 range from 0.56 to 0.93 based on 3 mean switching times conditions measured per subject; Fig. 7 in Battaglia and Schrater 2007, calculated from data kindly provided by Peter Battaglia) compared with our match between the optimal and empirical mean switching time curve (subject's median R2 = 0.97; R2 range, 0.73–0.99, based on 350 mean switching time conditions measured per subject). In contrast, we show here that subject's integrate the nonlinear relationship (measured at 350 different positions) between sensing time, movement time, and movement distance such that depending on the estimated ball landing position switching times vary accordingly along a continuous optimal switching time curve (as predicted by our ideal actor) instead of specific, discrete switching times. Over trials, the task error (distance between ball landing position and paddle center) was low from the beginning of the experiment for some subjects or decreased within the first 250 trials to near optimal levels (see Fig. 1C, blue crosses). Correspondingly, the ball catch performance was stable after 250 trials (Supplemental Fig. S2). This suggests that subjects could not have probed the relationship between switching time, movement distance, and catch performance sufficiently to learn the optimal switching times in dependence of movement distance.
Trading off multiple sources of uncertainty has been studied in pure perceptual tasks. It was shown that humans integrate synchronously presented sensory cues to form a statistically optimal estimate: each sensory source is weighted by the inverse of its uncertainty (the variance of the single cue estimation), such as combining information from vision to determine object width (Ernst and Banks 2002) and depth (Hillis et al. 2004; Jacobs 1999; Knill 2003), vision and hearing to estimate position (Alais and Burr 2004), and proprioception and vision to locate the hand (van Beers et al. 1996; Sober and Sabes 2005; van Beers et al. 1999). However, unlike these existing sensory studies assumed, we mostly act in natural settings, where sources of sensory information and movements occur asynchronously—as in our perception-action task. We show here that subjects must have some form of explicit knowledge of their sensory and motor error as a function of time (and distance) because they are able to combine perceptual and action uncertainty (asynchronously) across time.
It was previously shown that in trading off reward and uncertainty in pure action tasks, humans choose near-optimal strategies when planning their movement and can base their selection in an explicit reward-and-punishment framework (Trommershauser et al. 2006). In such a framework, subjects were able to compensate artificially induced changes of sensor and motor uncertainties by the experimenter (Trommershauser et al. 2005). Our study presents a novel combination of perception and action tasks. We show that by forcing a trade-off between sensor and motor uncertainty in natural tasks, humans make use of knowledge about time dependence in their natural sensory and motor uncertainty to make an optimal decision about when to start moving such as to maximize reward (number of caught balls).
Our ball catching task is a natural world task with distinct perception and action stages. We showed that subjects have knowledge of how their sensor and motor error change as a function of time and are able to decide when to move such as to minimize the combined task error. The decision when to move is not straightforward, because motor error depends on how far one has to move in a nonlinear way, suggesting that subjects have an explicit representation of the sensor and motor error as functions of time. Although subjects mean switching time curves were highly correlated with their predicted optimal switching time curves (median R2 = 0.97), subjects showed trial-by-trial variability of ∼130 (SD) ms (median across subjects) around their mean timings. Variability in timing could result from either a subject's uncertainty in the shape of the task variability surface, the precision with which subject's could time switching, or a mixture of both. Studies that measure timing variability in the initiation of discontinuous, i.e., nonperiodical, hand movements report timing precisions of 65–90 (SD) ms in similar time intervals (data extracted from Spencer et al. 2003). Our findings were similar in the faster sequence controlled version of the experiments, where the task error valley was narrower and subject's timing precision somewhat higher (cf. spread of white dots and the blue regions in Figs. 3 and 4). These findings suggest that the majority of switching timing variability observed here can be explained by the baseline precision to initiate an action at a desired instant in time.
Subject task performance can be explained by the variability of their sensory and motor systems and not their individual strategy chosen, because across the catch performance range (50–69%) subjects chose near optimal switching times. We showed that cross-validation (i.e., randomly interchanging the predicted variability surfaces from sensory and motor experiments across subjects and the chosen switching times in the combined experiments) led to less optimal subject behavior, suggesting that subjects shaped their responses based on their specific time- and distance-dependent sensory and motor uncertainty and not on some general strategy. Moreover, subjects switching time variability decreased by 29% as the speed of the task increased by 31%, suggesting that subjects were aware that the size of the optimal switching time valley had decreased correspondingly (cf. Figs. 3 and 4). Individual's knowledge of their task variability surface is important in real world tasks with dynamic environments. This occurs when we have to distribute the time of visual attention allotted to various directions around us, for example, when moving in complex terrains or in reducing motor error in grasping and estimating grasp relevant object properties. A similar trade-off of perception versus action could apply to saccading eye movements and the estimation of where to look next, as during a saccade visual perception, is blocked.
Our quantitative perception-action framework provides a novel approach to study speed–accuracy trade-offs, allowing for straightforward manipulation by deciding when to start moving and stop sensing. Moreover, we are able to quantitatively predict the subject's performance in terms of their actual task instruction (catching as many balls as possible). These characteristics make our sensorimotor task directly applicable to clinical testing of motor disorders or for experiments of decision-making in time and allow novel ways to probe sensor and motor speed–accuracy trade-offs in conjunction. Our task lends itself to identify and study the underlying neuronal mechanisms that process such decisions, for example, by perturbing the activity of selected neuronal populations and quantifying how catch performance and switching times are affected. We note that the performance in our ball catching game was explained by the subject's sensory and motor uncertainty and did not depend on specific movement strategies; this may suggest that, in related sports disciplines, technique is ultimately less important than simply having the lowest possible (innate) sensory and motor uncertainties.
GRANTS
This work was supported by the Wellcome Trust, HFSP, and European project SENSOPAC IST-2005-028056.
The costs of publication of this article were defrayed in part by the payment of page charges. The article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. Section 1734 solely to indicate this fact.
Footnotes
The online version of this article contains supplemental data.
REFERENCES
- Alais and Burr 2004.Alais D, Burr D. The ventriloquist effect results from near-optimal bimodal integration. Curr Biol 14: 257–262, 2004 [DOI] [PubMed] [Google Scholar]
- Battaglia and Schrater 2007.Battaglia PW, Schrater PR. Humans trade off viewing time and movement duration to improve visuomotor accuracy in a fast reaching task. J Neurosci 27: 6984–6994, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beers et al. 1996.Beers RJ, Sittig AC, Denier JJ. How humans combine simultaneous proprioceptive and visual position information. Exp Brain Res 111: 253–261, 1996 [DOI] [PubMed] [Google Scholar]
- Brouwer et al. 2002.Brouwer AM, Brenner E, Smeets JB. Perception of acceleration with short presentation times: can acceleration be used in interception? Percept Psychophys 64: 1160–1168, 2002 [DOI] [PubMed] [Google Scholar]
- Brouwer et al. 2006.Brouwer AM, Lopez-Moliner J, Brenner E, Smeets JB. Determining whether a ball will land behind or in front of you: not just a combination of expansion and angular velocity. Vision Res 46: 382–391, 2006 [DOI] [PubMed] [Google Scholar]
- Brouwer et al. 2005.Brouwer AM, Smeets JB, Brenner E. Hitting moving targets: effects of target speed and dimensions on movement time. Exp Brain Res 165: 28–36, 2005 [DOI] [PubMed] [Google Scholar]
- Brown et al. 2007.Brown LE, Wilson ET, Goodale MA, Gribble PL. Motor force field learning influences visual processing of target motion. J Neurosci 27: 9975–9983, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland et al. 2006.Churchland MM, Yu BM, Ryu SI, Santhanam G, Shenoy KV. Neural variability in premotor cortex provides a signature of motor preparation. J Neurosci 26: 3697–3712, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ernst and Banks 2002.Ernst MO, Banks MS. Humans integrate visual and haptic information in a statistically optimal fashion. Nature 415: 429–433, 2002 [DOI] [PubMed] [Google Scholar]
- Faisal and Laughlin 2007.Faisal AA, Laughlin SB. Stochastic simulations on the reliability of action potential propagation in thin axons. PLoS Comput Biol 3: e79, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faisal et al. 2008.Faisal AA, Selen LP, Wolpert DM. Noise in the nervous system. Nat Rev Neurosci 9: 292–303, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitts 1954.Fitts PM The information capacity of the human motor system in controlling the amplitude of movement. J Exp Psychol 47: 381–391, 1954 [PubMed] [Google Scholar]
- Gordon et al. 1994.Gordon J, Ghilardi MF, Ghez C. Accuracy of planar reaching movements. I. Independence of direction and extent variability. Exp Brain Res 99: 97–111, 1994 [DOI] [PubMed] [Google Scholar]
- Gottsdanker et al. 1961.Gottsdanker R, Frick JW, Lockard RB. Identifying the acceleration of visual targets. Br J Psychol 52: 31–42, 1961 [DOI] [PubMed] [Google Scholar]
- Harris and Wolpert 1998.Harris CM, Wolpert DM. Signal-dependent noise determines motor planning. Nature 394: 780–784, 1998 [DOI] [PubMed] [Google Scholar]
- Hillis et al. 2004.Hillis J, Watt S, Landy M, Banks M. Slant from texture and disparity cues: optimal cue combination. J Vision 4: 967–992, 2004 [DOI] [PubMed] [Google Scholar]
- Indovina et al. 2005.Indovina I, Maffei V, Bosco G, Zago M, Macaluso E, Lacquaniti F. Representation of visual gravitational motion in the human vestibular cortex. Science 308: 416–419, 2005 [DOI] [PubMed] [Google Scholar]
- Jacobs 1999.Jacobs RA Optimal integration of texture and motion cues to depth. Vision Res 39: 3621–3629, 1999 [DOI] [PubMed] [Google Scholar]
- Knill 2003.Knill DC Mixture models and the probabilistic structure of depth cues. Vision Res 43: 831–854, 2003 [DOI] [PubMed] [Google Scholar]
- Kording et al. 2004.Kording KP, Ku SP, Wolpert DM. Bayesian integration in force estimation. J Neurophysiol 92: 3161–3165, 2004 [DOI] [PubMed] [Google Scholar]
- Oudejans et al. 1997.Oudejans RR, Michaels CF, Bakker FC. The effects of baseball experience on movement initiation in catching fly balls. J Sports Sci 15: 587–595, 1997 [DOI] [PubMed] [Google Scholar]
- Rosenbaum 1975.Rosenbaum DA Perception and extrapolation of velocity and acceleration. J Exp Psychol 1: 395–403, 1975 [DOI] [PubMed] [Google Scholar]
- Saxberg 1987.Saxberg BV Projected free fall trajectories. II. Human experiments. Biol Cybern 56: 177–184, 1987 [DOI] [PubMed] [Google Scholar]
- Sober and Sabes 2005.Sober S, Sabes P. Flexible strategies for sensory integration during motor planning. Nat Neurosci 8: 490–497, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer et al. 2003.Spencer RM, Zelaznik HN, Diedrichsen J, Ivry RB. Disrupted timing of discontinuous but not continuous movements by cerebellar lesions. Science 300: 1437–1439, 2003 [DOI] [PubMed] [Google Scholar]
- Todorov and Jordan 2002.Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci 5: 1226–1235, 2002 [DOI] [PubMed] [Google Scholar]
- Trommershauser et al. 2005.Trommershauser J, Gepshtein S, Maloney LT, Landy MS, Banks MS. Optimal compensation for changes in task-relevant movement variability. J Neurosci 25: 7169–7178, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trommershauser et al. 2006.Trommershauser J, Landy MS, Maloney LT. Humans rapidly estimate expected gain in movement planning. Psychol Sci 17: 981–988, 2006 [DOI] [PubMed] [Google Scholar]
- van Beers et al. 2004.van Beers RJ, Haggard P, Wolpert DM. The role of execution noise in movement variability. J Neurophysiol 91: 1050–1063, 2004 [DOI] [PubMed] [Google Scholar]
- van Beers et al. 1996.van Beers RJ, Sittig AC, Denier JJ. How humans combine simultaneous proprioceptive and visual position information. Exp Brain Res 111: 253–261, 1996 [DOI] [PubMed] [Google Scholar]
- van Beers et al. 1999.van Beers RJ, Sittig AC, Gon JJDvd. Integration of proprioceptive and visual position-information: an experimentally supported model. J Neurophysiol 81: 1355–1364, 1999 [DOI] [PubMed] [Google Scholar]
- Zago et al. 2004.Zago M, Bosco G, Maffei V, Iosa M, Ivanenko YP, Lacquaniti F. Internal models of target motion: expected dynamics overrides measured kinematics in timing manual interceptions. J Neurophysiol 91: 1620–1634, 2004 [DOI] [PubMed] [Google Scholar]