Representation of Dynamic Interaural Phase Difference in Auditory Cortex of Awake Rhesus Macaques

Brian H Scott; Brian J Malone; Malcolm N Semple

doi:10.1152/jn.00678.2007

. 2009 Jan 21;101(4):1781–1799. doi: 10.1152/jn.00678.2007

Representation of Dynamic Interaural Phase Difference in Auditory Cortex of Awake Rhesus Macaques

Brian H Scott ¹, Brian J Malone ¹, Malcolm N Semple ¹

PMCID: PMC2695633 PMID: 19164111

Abstract

Neurons in auditory cortex of awake primates are selective for the spatial location of a sound source, yet the neural representation of the binaural cues that underlie this tuning remains undefined. We examined this representation in 283 single neurons across the low-frequency auditory core in alert macaques, trained to discriminate binaural cues for sound azimuth. In response to binaural beat stimuli, which mimic acoustic motion by modulating the relative phase of a tone at the two ears, these neurons robustly modulate their discharge rate in response to this directional cue. In accordance with prior studies, the preferred interaural phase difference (IPD) of these neurons typically corresponds to azimuthal locations contralateral to the recorded hemisphere. Whereas binaural beats evoke only transient discharges in anesthetized cortex, neurons in awake cortex respond throughout the IPD cycle. In this regard, responses are consistent with observations at earlier stations of the auditory pathway. Discharge rate is a band-pass function of the frequency of IPD modulation in most neurons (73%), but both discharge rate and temporal synchrony are independent of the direction of phase modulation. When subjected to a receiver operator characteristic analysis, the responses of individual neurons are insufficient to account for the perceptual acuity of these macaques in an IPD discrimination task, suggesting the need for neural pooling at the cortical level.

INTRODUCTION

Behavioral studies using focal lesions have established that auditory cortex is necessary for sound-directed behavior (Heffner and Heffner 1990; Jenkins and Merzenich 1984; Malhotra et al. 2004; Neff et al. 1956). Broad tuning for the location of a sound source has been observed in single neurons of the auditory cortex in several species, including cats (Brugge et al. 1996; Mickey and Middlebrooks 2003; Middlebrooks et al. 1994) and primates (Tian et al. 2001). Neurons in core auditory cortex (Kaas and Hackett 2000) of the awake macaque are sensitive to sound source location and movement (Ahissar et al. 1992; Benson et al. 1981; Recanzone et al. 2000; Woods et al. 2006) and this tuning presumably derives from both binaural and monaural spatial cues (Schnupp et al. 2001). Despite a resurgence of interest in the awake primate model of auditory cortex, the predominance of free-field stimulation has left the representation of binaural cues at the level of single cells relatively unexplored (Brugge and Merzenich 1973; Malone et al. 2002; Scott et al. 2007).

A prominent binaural cue underlying sound localization along the azimuth is the difference in arrival time of a sound at the two ears. Physiological sensitivity to this interaural time difference (ITD) arises from a coincidence-detection mechanism in the superior olivary complex (SOC) of the brain stem, where cells are tuned for a particular temporal delay—on the order of microseconds—between sound arriving from the contralateral and ipsilateral ears (Goldberg and Brown 1969; Yin and Chan 1990). For periodic stimuli, such as pure tones, this ITD manifests as an ongoing interaural phase difference (IPD; Rayleigh 1907) as well as an onset delay. This IPD dominates onset delay as the primary cue for both neural tuning (Kuwada and Yin 1983) and human spatial perception (Buell et al. 1991; Shackleton et al. 1991). Neural tuning to IPD, once established in the brain stem, is preserved through the inferior colliculus (IC) in the midbrain (Kuwada and Yin 1983; Rose et al. 1966; Spitzer and Semple 1991; 1993) and relayed via the medial geniculate nucleus (MGN) of the thalamus to the primary auditory cortex (AI) (Brugge and Merzenich 1973; Fitzpatrick and Kuwada 2001).

The preferred IPD and tuning sharpness of a neuron may be determined from repeated presentations of dichotic tones spanning the full range of IPD. A more efficient stimulus for the assessment of IPD tuning is the binaural beat, an ongoing modulation of IPD produced by presenting tones of slightly different frequencies to the two ears (Yin and Kuwada 1983a,b). This produces a percept of auditory motion in human listeners, such that a tone appears to move within the head at a rate determined by the frequency difference between the ears. As the difference between the two tones is increased (beyond ∼20 Hz), the perceived beat loses its spatial quality and becomes a fluctuation or roughness (Licklider 1950; Perrott and Musicant 1977). We used binaural beats to probe the spatial, spectral, and temporal properties of the binaural system by recording single neurons in auditory cortex of awake macaques.

Binaural beats evoked strong, synchronized discharges in low-frequency neurons of the auditory cortex. In stark contrast to earlier studies that report transient responses to the beat cycle in anesthetized cortex (Reale and Brugge 1990), neurons in awake cortex typically respond robustly throughout the period of the beat. These broadly tuned responses imply different mechanisms of neural coding than would have been possible under anesthesia and are compatible with theories of sound localization that stress population codes among broadly tuned neurons (Fitzpatrick et al. 1997; Harper and McAlpine 2004; Middlebrooks et al. 1994; Stecker et al. 2005). Furthermore, the macaques were trained to discriminate IPD (Houben and Gourevitch 1979; Scott et al. 2007; Wegener 1974), allowing us to compare psychophysical performance to single-neuron tuning in the same animals. The animals' perceptual ability exceeds the accuracy of single neurons, lending further support to the notion of population coding in the binaural auditory system.

METHODS

Subjects, recording procedure, and stimuli

All procedures were in accordance with the Society for Neuroscience guiding principles on the care and use of animals and were approved by the Institutional Animal Care and Use Committee of New York University. Subjects were two male rhesus macaques (referred to as X and Z), trained to discriminate the laterality of IPD around midline and accustomed to sitting quietly between behavioral sessions to allow the collection of additional physiological data in the passive state (Malone et al. 2002; Scott et al. 2007). Animals were monitored by video and given periodic rewards (between stimulus sets) to maintain alertness. Recording cylinders were implanted over the interaural axis in a sterile surgical procedure, first over the left hemisphere and later moved to the right. In daily sessions monitored on closed-circuit video, animals sat in a Plexiglas chair (Crist Instrument, Hagerstown, MD) in a double-walled anechoic room (IAC, Bronx, NY) with their heads immobilized by a surgically implanted headholder.

Physiology and stimulus generation

A stepping microdrive was secured on the recording cylinder under aseptic conditions to allow a vertical approach to auditory cortex (Pfingst and O'Connor 1980) by resin-coated tungsten microelectrodes (10–12 MΩ; FHC, Bowdoin, ME). The signal was amplified (variable gain), filtered (typically 0.3–10 kHz), and processed by a MALab event timer (Kaiser Instruments) communicating with a Macintosh computer. Spikes from single neurons were discriminated by setting voltage/time windows and waveforms were monitored for consistency throughout the recording; spike times were logged at a precision of 1 μs and responses displayed on-line.

Stimulus generation was controlled by the MALab software, which drives a hardware synthesizer that feeds the left and right signals to a Stax amplifier and, in turn, to electrostatic speakers [Stax Lambda (STAX, Saitama, Japan) in Sokolich Custom Sound Systems housings] coupled to custom-made ear inserts. Each channel was calibrated for sound pressure level (SPL, in dB re: 20 μPa, from 50 to 30,000 Hz) and phase (from 50 to 3,000 Hz) prior to each session using a probe microphone (4133, Brüel & Kjær, Nærum, Denmark) positioned within the ear insert.

Entry into auditory cortex was typically preceded by a gap in physiological activity consistent with passage through the lateral sulcus. When a responsive cell was isolated, best frequency (BF, the frequency eliciting the highest spike rate at a supratheshold level) was quantified by an isolevel contour, typically at 60 dB SPL, or an effective level chosen audiovisually (as was sometimes necessary for strongly nonmonotonic responses). Tones were 100 ms in duration, gated with a 5-ms cosine-squared ramp, and presented binaurally at zero ITD. Monaural tones were used only if binaural stimulation was ineffective; this was the case for only 7% of low-frequency neurons (BF ≤2.5 kHz).

Phase sensitivity was assessed using binaural beats, an ongoing modulation of interaural phase produced by presenting two tones of slightly different frequency to the two ears. A positive IPD value corresponds to a phase advance at the ipsilateral ear and a binaural beat in the positive direction denotes an increasing phase advance at the ipsilateral ear. A +2-Hz binaural beat at a center frequency of 1,000 Hz is produced by presenting 999 Hz to the contralateral ear and 1,001 Hz to the ipsilateral, evenly spacing the actual tone frequencies about the center frequency. Beats were typically presented as two 10-s trials, with a 2-s “off” time between presentations. A neuron's response first was measured across a range of center frequencies, at an SPL chosen audiovisually to elicit a high spike rate and well-synchronized response. The center frequency at which the product of rate and synchrony was maximal (spike rate × vector strength; see following text) was used for subsequent manipulations of other parameters (e.g., SPL, beat frequency, and beat direction). The center frequency eliciting the strongest beat response (as measured by the Rayleigh statistic; see following text) exactly matched the tone-derived BF for 59% of neurons; in cases where the frequencies differed, the difference was slight, such that only 4% of neurons had best beat responses ≥1 octave from the BF.

Statistical analysis of synchrony

In this study the term “synchrony” is always used in reference to the stimulus beat cycle. The binaural beat is a cyclical modulation of IPD: over one cycle of a 2-Hz beat, the signals begin in phase (IPD = 0°), modulate to a maximal left ear lead at 0.25 s (IPD = 180°), and then realign after 0.5 s to begin the cycle again (IPD = 360° = 0°; Fig. 1A). This circular axis confines the stimulus space and requires the use of circular statistics. Each spike fired is treated as a unit vector in a polar coordinate system with the angle representing the instantaneous phase of the beat and the direction of the sum of those vectors defines the mean phase of the response. Normalized to the number of spikes, the length of that mean vector is dependent on how tightly the spikes cluster about that one point in the stimulus cycle. This vector strength (VS; Goldberg and Brown 1969) is a measure that varies between zero (e.g., a flat period histogram) and one (all spikes at one phase). The product of spike rate × VS was computed on-line and used to select optimal stimulation parameters (e.g., center frequency, as described earlier). In post hoc analysis, the significance of the VS measurement was assessed by the Rayleigh statistic, a spike-rate–dependent statistical criterion for the nonuniformity of a circular distribution

where R is computed from the total number of spikes n and the VS [Rayleigh (1880), cited in Fisher (1996)]. A response was considered significantly synchronized if R was >13.816 the P < 0.001 level (Mardia and Jupp 2000). In practice, the functions described by rate × VS and R are very similar because both reflect the combined strengths of spike rate and temporal synchrony. Both VS and R are problematic for testing nonunimodal distributions, but clear bimodal responses to binaural beat stimuli were not observed in our sample.

FIG. 1. — Dynamic interaural phase difference (IPD) elicits robust, time-locked responses in single neurons of low-frequency auditory cortex. A: schematic depiction of 1 s of a binaural beat stimulus, illustrating the phase relationship between tone stimuli at the 2 ears (the sine waves are depicted at very low frequency and differing amplitude, only for visual clarity). The frequency at the ipsilateral ear (black) is 2 Hz lower than that at the contralateral ear (gray), causing a phase advance of one full cycle every 0.5 s. B: single-unit response to a 2-Hz binaural beat presented as two 10-s trials (2-s intertrial interval). Spike raster at *top* is binned into a peristimulus time histogram (PSTH) showing 20 peaks of spike discharge each corresponding to one cycle of the beat. Spike rate on the ordinate is computed within each 50-ms bin (overall spike rate for the 10-s trial was 29 spikes/s). Spike rate does not adapt over the course of the trial. Stimulus was presented at 80 dB SPL, centered at the cell's best frequency (BF) of 1,600 Hz (1,599 Hz to the right/contra ear, 1,601 Hz to the left/ipsi). C: histogram folded on the period of modulation, showing spikes from all 40 cycles of modulation (2 trials × 10 s × 2 Hz) in 10-ms bins. Overlaid in gray is the tuning curve derived from presentations of static IPD at 8 values (spike rates on right ordinate, in gray). Both responses have been shifted on the (circular) phase axis to illustrate more clearly the relative phase and vector strength (VS) of the beat and static responses. The lower abscissa indicates milliseconds from the beginning of the beat period, the upper abscissa indicates the corresponding instantaneous phase of the beat and the phase of the static IPD stimulus (because the stimulus is cyclical, ±180° are the same point, and −90° is equivalent to 270°). As is typical for the population, the mean phases of these 2 responses are very similar (295 and 314° for the beat and static IPD, respectively). As a reference, the VS values for the beat and static responses are 0.56 and 0.42, respectively.

Quantification of IPD tuning width

For each neuron, the strongest response (measured by R) to a 2-Hz beat was binned into a modulation period histogram of fifty 10-ms bins (see following text, Fig. 1C). A five-point moving average was used to identify the peak bin and the histogram was rotated on the phase axis to center the peak at 0°. The minimum of the smoothed function was subtracted off as baseline firing rate and the resultant histogram was fit by a Gaussian (normal) distribution with three free parameters: amplitude, mean, and SD (Fig. 12; Matlab curve fit toolbox, The MathWorks, Natick, MA). Tuning width was defined as twice the SD value, in degrees of IPD. By visual inspection, the fits seemed to capture tuning width well for strongly modulated responses (see results). Population analysis of the raw histograms revealed median values of skewness and kurtosis consistent with Gaussian functions (median skew 0.02, median kurtosis 2.81, indistinguishable from 0 and 3 by Wilcoxon signed-rank; measured using built-in functions of Matlab Statistics Toolbox). Because responses were deeply modulated, the baseline firing rate that was subtracted was generally small, whether expressed as actual values (median 0.5 spike/s, <5 spikes/s in 90% of neurons) or the ratio of baseline to peak firing rate (median 0.03, 90% <0.44).

Although IPD is a cue to sound location along the azimuth, degrees of IPD do not map directly to external space. Under some circumstances, however, an equivalent angle in azimuth can be computed from an IPD value. Such a computation was applied to provide a reference in actual space for the IPD tuning widths estimated from binaural beat responses. The +1 SD point on the Gaussian fit (described earlier) was taken to indicate half the width of the IPD “receptive field” (from the center, at the peak of the Gaussian, to the edge). That SD value was converted from degrees of IPD into ITD, by expressing it as a fraction of the tone period

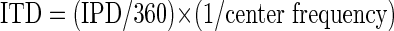In the relevant frequency range, ITD is effectively independent of center frequency and can be translated into the equivalent angle along the azimuth, relative to midline

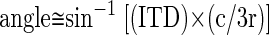(rearranged from Eq. 6 of Kuhn 1977), where c is the speed of sound (3.43 × 10⁻⁴ m/μs) and r is the head radius (∼0.045 m). This angle was doubled to estimate the width of the receptive field if it were centered at midline.

Under ecological conditions, maximal ITD occurs for a sound source 90° from midline and is determined by the animal's head size; for macaques, this limit is around 400 μs. The use of dichotic stimuli (such as the binaural beat) allows the presentation of interaural disparities greater than those that could occur under natural listening conditions. If an IPD value corresponds to an ITD >400 μs, the term in parentheses in the preceding equation will exceed ±1 and the inverse sine operation become ambiguous; thus angles >90° of azimuth cannot be defined. At center frequencies <500 Hz, where the tone period is long, the edge of the IPD receptive field often corresponded to an ITD beyond the ecological range, so an equivalent angle in azimuth could not be computed. Nevertheless, IPD is a powerful cue to location in this low-frequency range.

Recording sites

Histology in both animals and postmortem magnetic resonance imaging in animal X confirmed the recording locations to be within the core auditory cortex (the primary auditory field AI and the rostral field R). Assignment of recording locations to cortical fields is based on physiological criteria, in particular the reversal of the tonotopic gradient at the border of AI and R, and the degradation in efficacy of pure-tone stimuli at the border of core and belt (Kosaki et al. 1997; Rauschecker et al. 1995; Recanzone 2000; Scott 2004). For the analyses presented in the following text, the population has been defined physiologically and has not been segregated by animal, hemisphere, or cortical field.

RESULTS

Vigorous responses to binaural beats were found in a largely contiguous area around rostral, low-frequency AI, extending into the adjacent field R. Entry into low-frequency AI was often marked by an audible “hash” synchronized to a binaural beat, suggesting relatively homogeneous responsiveness among the local population of neurons. This was especially true in the middle layers of cortex (as estimated by depth relative to entry into the superior temporal plane), although responses could be obtained throughout the depth of the tissue. Outside of the AI/R border, some units isolated in the belt responded to low-frequency tones or band-passed noise, but were not phase sensitive when tested with binaural beats.

Table 1 shows the number of cells with best frequencies in the range where sensitivity to IPD might be expected, based on the limits of phase-locking in the primate auditory nerve (Rose et al. 1967) and the number of those cells tested with the binaural beat stimulus. Quantitative data were collected from 283 cells (186 in monkey X, 97 from Z) from AI and R. (Recording chamber positions in monkey X were optimal for recording from the low-frequency border of AI and R, resulting in a disproportionate sample of phase-sensitive neurons from this animal.) Of cells studied quantitatively, 268 (95%) discharged with significant synchrony (Rayleigh test, P < 0.001) to a binaural beat, although these cells represent only 68% of the total number of cells tested (cells that showed no sensitivity to the qualitative test were less likely to be studied in further detail). In one hemisphere, an additional 57 neurons with BFs >3 kHz were tested with a standard set of binaural beats at center frequencies between 250 and 1,500 Hz; although 24% of these neurons showed some significant synchrony, in all cases the significance was marginal (R < 20). This suggests that entrainment to the binaural beat is restricted to the low-frequency population described here.

TABLE 1.

Number of cells studied with binaural beats

	Rhesus X	Rhesus Z	Total
Total cells with BF <2.5 kHz	290	256	546
Qualitatively studied	226	171	397
Quantitatively studied	186	97	283
Showing synchrony to beat	178	906	268^*

Open in a new tab

168 AI, 91 R, 9 belt.

The following analysis is intended to provide a comprehensive survey of binaural beat responses, allowing comparison with the existing (largely subcortical) literature, as well as the processing of other modulated sounds in auditory cortex. After the general properties of a beat response are introduced, the effects of beat frequency, center frequency, and beat direction are discussed in turn. The widths of IPD “receptive fields” are then quantified and, finally, the neural responses are compared with psychophysical thresholds for the perception of dynamic IPD.

An example of a single-unit response to a 2-Hz binaural beat is shown in Fig. 1B as a spike raster, binned into a peristimulus time histogram (PSTH). Cycling through IPD induced a synchronized firing pattern evident in the PSTH and emphasized in the modulation period histogram (MPH; Fig. 1C), in which responses to 40 cycles of the beat (two 10-s presentations at 2 cycles/s) are superimposed on a common time axis by “folding” on the beat duration of 500 ms. This profile was typical of responses to binaural beats in the awake cortex (see Figs. 1, 3, 7, 12, and 13) and differs markedly from previous observations in anesthetized cat AI, where cells responded transiently with a single spike per beat cycle at comparable rates of modulation (Reale and Brugge 1990).

FIG. 3. — Responses from 2 single units tested across binaural beat frequency illustrate the influence of the rate of IPD modulation on the profile of the modulation period histogram (MPH). Each period is divided into 100 bins, with the ordinate indicating spike count in each bin. All stimuli were of equal duration (10 s, presented twice in A and once in B), so the 10-Hz histogram represents 10-fold as many IPD cycles as the 1-Hz histogram, and so forth. Functions at *bottom* summarize the effects of beat frequency on vector strength, mean phase, and spike rate (temporal, phase, and rate modulation transfer functions [tMTF, pMTF, and rMTF, respectively]) for each neuron. Only points with significant synchrony are plotted in pMTFs.

FIG. 7. — The dual tuning of cortical cells in the center frequency and IPD dimensions represented as a contour plot in phase/frequency space, where black indicates the maximal response. The maximal response rates averaged over 40 total beat periods were 68.8 (A) and 70.0 (B) spikes/s. Significant mean phase points and a linear fit (weighted by Rayleigh strength) are overlaid. Slope and intercept values are 0.00013 cycle/Hz and 221° in A, −0.00028 cycle/Hz and 339° in B.

FIG. 12. — Gaussian fits of the binaural beat period histogram were applied to the strongest response of each neuron (as determined by Rayleigh strength) at 2-Hz beat frequency. In the *top panel*, the response was phase-shifted to center it on the phase axis before fitting with a 3-parameter Gaussian (filled gray bars and upper abscissa: original response; open bars and lower abscissa: shifted response). This response yielded the best fit (r² = 0.94) in the population, with SD of 63.5°. The *center* and *bottom panels* show the median and 25th percentile, respectively, of goodness-of-fit. Although weaker responses were fit less well than stronger ones, the median skewness and kurtosis of the period histograms across the population suggest that a Gaussian distribution was an appropriate model.

FIG. 13. — Gaussian fits of binaural beat period histograms quantified the width of IPD tuning across the neural population. A: the distribution of IPD tuning width (double the SD of each fit, as measured in Fig. 12) at various cutoff levels of fit quality. B: IPD tuning width across frequency. Filled circles mark the mean phase of the response, with vertical error bars spanning ±1SD of the Gaussian fit. For visual clarity, only the 50th percentile is displayed (n = 123) and the frequency values have been randomly “jittered” to separate points at commonly tested frequencies. Phases above the dashed gray line correspond to azimuth contralateral to the recorded hemisphere. There was no correlation between IPD tuning width and center frequency (P = 0.29). C: for those responses that could be mapped from degrees of IPD to degrees of azimuth, the width of the tuning functions in azimuth decreased at higher center frequencies, but were seldom narrower than roughly 45°. Line is a linear least-squares fit (y = 128 − 0.05x, r² = 0.32; significant by ANOVA, P < 0.0001). Points displayed in gray could not be converted into an unambiguous value of azimuth (see text). D: distribution of mean phases, corresponding to the peaks of the Gaussian fits (black bars), on the same axis as the distribution of “slopes,” the inflection point of the Gaussian fits at +1SD, where the spike rate/IPD function is steepest (gray bars). Each function has 2 slope points; the one closer to midline was included. The median value of the IPD peak was −49° (contralateral to midline), whereas the median point of maximal slope was 12°, reflecting the fact that the slopes better span the midline.

The binaural beat proved to be an efficient stimulus for measuring the phase tuning of neurons in the primate cortex, as was demonstrated in cat IC (Yin and Kuwada 1983a,b). Overlaid in gray on the period histogram (Fig. 1C) is a tuning curve obtained from presentations of static phase offsets at eight values of IPD. The mean phases computed from the beat and static IPD responses are similar, reflecting a common underlying phase selectivity. The degree of selectivity for phase (and, in the dynamic case, synchrony to the beat cycle) was measured by the VS of the response (see methods), which is sharper for the binaural beat (beat: 0.56; static: 0.42). In 46 units, phase sensitivity was studied with both static IPD and binaural beats, allowing a comparison of the mean phase and VS estimates afforded by the two stimuli. Figure 2A confirms that a 2-Hz beat gives a reliably similar estimate of mean phase when compared with estimates from static IPD stimuli presented at the same carrier frequency (r² = 0.92, slope = 0.97; arrow indicates cell from Fig. 1). Although a given mean phase estimate could differ by ≥45° between the two measures, there was no consistent tendency for the binaural beat mean phase to lead or lag the static estimate (paired t-test, P = 0.90). Vector strengths of the two measures (Fig. 2B) were correlated, but (as suggested by the example unit in Fig. 1C) were consistently higher for beat responses (r² = 0.45, paired t-test, P < 0.0001), which was also the case in anesthetized cortex (Reale and Brugge 1990). This may be attributed to nonselective transient responses that could be present at the onset of every tone used in a static IPD procedure, but the difference in VS remained if the first 100 ms of the response to static IPD was excluded from analysis. Alternatively, gliding smoothly through phase rather than presenting static IPDs in isolation may enhance a neuron's selectivity (Malone et al. 2002; Spitzer and Semple 1991, 1993). The generality of this sharpening at higher rates of IPD change is addressed in the next section.

FIG. 2. — Binaural beat and static IPD stimuli generate similar estimates of mean phase, but beats yield consistently higher VS. Each point represents the response of one neuron; arrows indicate data from the neuron depicted in Fig. 1; dashed line is identity (slope = 1). A: mean phase of the response to a 2-Hz binaural beat vs. mean phase of static IPD tuning functions (same frequency and SPL). Solid line is a linear least-squares fit (slope = 0.97, r² = 0.92). A paired t-test revealed no difference in mean phase as measured by the 2 stimuli. B: VS of binaural beat responses vs. static IPD tuning functions. The 2 are roughly correlated (fit not shown; slope = 0.64, r² = 0.45), but beat vector strengths are consistently higher (paired t-test P < 0.0001).

Effects of binaural beat frequency

The frequency disparity between the ears was varied about a common center frequency to produce a range of binaural beat frequencies. Responses from two cells tested across beat frequency are shown in Fig. 3, both as MPHs of spike times and summarized as a family of modulation transfer functions (MTFs). At low binaural beat frequencies, synchrony to the beat is seen in the deeply modulated profile of the MPHs. At high beat frequencies (50–100 Hz, Fig. 3, top panels), the MPH of the cell in Fig. 3A has flattened, whereas the cell in Fig. 3B continues to synchronize its discharges. The temporal MTF (tMTF) captures this effect as a plot of vector strength across modulation frequency. The tMTF in Fig. 3A exemplifies the typically observed low-pass function rolling off above 20 Hz. A more unusual example is depicted in Fig. 3B: the tMTF reveals synchrony up to ≥50 Hz. Also apparent in both neurons is a shift in the mean phase of the response at beat frequencies >5 Hz: the MPH profile seems to slide rightward (later in the period) and at 20 Hz “wraps around” to center, captured by the phase MTFs (pMTFs; only points with significant synchrony are plotted; see also Fig. 5). Last, overall spike rate is affected by the rate at which the binaural beats cycle through IPD, as demonstrated in the rate modulation transfer functions (rMTFs) in the bottom panel (and Fig. 6).

Effects of beat frequency on vector strength

A neuron was classified as beat responsive if it showed significant synchrony at any beat frequency. All beat-responsive neurons had synchronized discharges at a beat frequency of 2 Hz (e.g., Figs. 1 and 2), but a range of higher frequencies (up to ≥20 Hz) was tested to determine how synchrony between the beat and the neural discharge degraded at higher rates of IPD modulation. The enhanced IPD tuning sharpness for binaural beats (relative to the static IPD stimulus) shown in Fig. 2B exists only at low beat rates. When the differences between VS measured from beats and static IPD pips were compared, VS was higher for beats from 2 to 10 Hz (data not shown; Wilcoxon signed-rank, P < 0.05). To assess the effect of beat frequency on VS across the population, all recorded measurements were pooled from those cells in which beats were presented across modulation frequency (n = 183). Figure 4A plots the median VS, along with the 10th and 90th percentiles, across beat frequency. The median degrades from 0.5 to 0.2 with increasing beat frequency and the 90th percentile traces a weakly band-pass curve peaking at 5–10 Hz but falling toward the median at higher rates, where synchrony becomes uniformly poor.

FIG. 4. — Effects of binaural beat frequency on VS across the population. A: all recorded VS measurements were pooled from those cells in which beats were presented across modulation frequency (n = 183; beat frequencies tested were 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, and 200 Hz). Median VS (heavy line) is plotted along with the 10th and 90th percentiles (dashed lines), across beat frequency. The median degrades from 0.5 to 0.2 with increasing beat frequency and the 90th percentile traces a weakly band-pass curve peaking at 5–10 Hz but falling toward the median at higher rates (>50 Hz), where synchrony becomes uniformly poor. B: survival plot of synchrony cutoff. For 97 cells tested beyond the limit of significant synchrony, a line was fit between the Rayleigh statistic at the highest significant point and that at the next highest frequency; the frequency at which this point intercepted the P < 0.001 significance criterion was the interpolated cutoff. Survival indicates the proportion of cells that could synchronize at or below the frequency on the abscissa. The median cutoff (gray dashed line) was 20 Hz, beyond which only half the tested population could synchronize to the beat envelope.

The highest beat frequency eliciting a significantly synchronized response indicates the maximal velocity of IPD change that can be represented. Cutoff frequency was determined in 97 cells for which beat frequency was tested beyond the range of synchrony. [A linear interpolation was performed between R at the highest synchronized frequency and the adjacent lowest unsynchronized frequency; the frequency at which this line crossed the Rayleigh threshold of 13.816 was taken as the cutoff (Liang et al. 2002).] Figure 4B is a survival plot of these interpolated cutoffs, plotting the percentage of cells that could fire in synchrony at or above a given beat frequency. The median cutoff, at which the survival plot crosses 50%, is 20 Hz. Although faster beats are generated by increasing the frequency difference between the ears, synchrony cutoff did not vary significantly with the BF of the neuron or the center frequency used (ANOVA, P = 0.3 and 0.09, respectively).

Each cell could be assigned a best modulation frequency (BMF) on the basis of firing rate, synchrony, or their product. The distributions of BMFs generated from each measure were essentially identical, with a mode at 5 Hz. As with synchrony cutoff, there was no dependence of BMF on BF (ANOVA, P > 0.89). As suggested by the MPHs in Fig. 3 and the distribution of cutoffs, IPD is represented by instantaneous spike rates over a wide range of beat frequencies, so the assignment of a BMF is not especially informative (Malone et al. 2007).

Effects of beat frequency on mean phase

Whereas a slow 2-Hz beat generates a mean phase equivalent to that estimated from static IPD stimuli, increasing beat rates elicit a phase lag deriving (presumably) from the conduction time from ear to cortex. For example, a latency of 20 ms is only 4% of the 500-ms cycle of a 2-Hz beat (i.e., by the time the cell fires, the instantaneous IPD has shifted 14°), but the lag will be tenfold larger relative to the shorter period of a 20-Hz beat. The difference in mean phase between the beat response and static tuning curve was measured, at each beat frequency eliciting significant synchrony, for the 64 cells in Fig. 2. This difference is significantly >0 at all beat frequencies ≥5 Hz (P < 0.001, Wilcoxon signed-rank). Data from three individual units are plotted in Fig. 5A to emphasize the constancy of mean phase estimates in the low-frequency regime (0.1–5 Hz) and the shift in phase as beat frequency increases and latency effects become more prominent. For the cells illustrated, and the population in general, binaural beats in the “negative” (contralateral ear lead) direction produced mean phase plots that were the mirror images of those produced by “positive” frequencies. Figure 5, B and C illustrates this phase lag for eight units tested across beat frequency in the positive and negative directions. The four units in Fig. 5B showed a diversity of mean phases at low beat frequencies and a linear shift in mean phase at higher beat frequencies. The cells in Fig. 5C had similar mean phase values and were tested to greater extremes, but showed consistent mean phase shifts to modulations ≥100 Hz in either direction.

FIG. 5. — Binaural beats accurately predict a neuron's static preferred IPD at low beat frequencies, but higher rates of IPD modulation elicit a lag in the phase of the response. A: data from 3 example neurons, plotted to emphasize the constancy of mean phase estimates <5 Hz, before the transition to a linear shift in phase with beat frequency. Arrow indicates the 2-Hz beat frequency used in Fig. 2. B: mean phase of the response shifts linearly with beat frequency in the positive or negative direction. These 4 units show a wide range of mean phase values at low beat frequencies and their phase/frequency functions remain parallel out to 50 Hz in either direction. C: additional units tested to greater extremes of beat frequency. Linear fits such as in B and C were used to measure group delay.

The slope of the function relating mean phase to beat frequency should provide an estimate of the fixed delay in the system (the neural latency) causing the phase lag. Least-squares linear fits, like the examples in Fig. 5, B and C, were weighted by R at each point. Delay estimates from these slopes were compared with minimum first-spike latencies in response to diotic pure tones for 124 single units. Both the tones and the binaural beats were presented well above threshold (≥60 dB SPL), but were not matched in SPL. The two measures are weakly but significantly correlated (r² = 0.22; P < 0.0001, ANOVA), with first-spike latency estimates showing a slight but statistically insignificant tendency to be shorter (paired t-test, P = 0.08). There was no effect of BF on delay (P = 0.76, ANOVA). The poor fit between the two latency estimates suggests that onset responses may be attributed to a mechanism distinct from that which induces the phase lag. Adaptation to repeated stimulus cycles could also explain a longer estimate of delay (Eggermont 1999).

Effects of beat frequency on discharge rate

The overall spike rate at which a neuron fires may carry information about the binaural beat stimulus in addition to, or in the absence of, synchronized firing at a preferred phase. In anesthetized cortex, cells typically fire only one spike per cycle, making firing rate a monotonic function of beat frequency (Reale and Brugge 1990). In awake animals, by contrast, cortical neurons often respond throughout the IPD cycle (see Figs. 1 and 3), so spike rate need not increase linearly with beat rate. Figure 6A shows normalized rMTFs from six cells tested with beat frequencies from 0.1 to 100 Hz. All are nonmonotonic functions, indicating an optimal range of beat frequencies between 5 and 20 Hz where the cell discharges maximally over the 20 s of stimulus presentation. Figure 6B shows the data from the same cells in terms of average spikes fired per beat cycle. In every case, the number of spikes per cycle falls off roughly as a power function. At a low beat rate of 1 Hz, the cells fire on the order of 10–100 spikes/s (or spikes/beat), but at higher rates (20–100 Hz in these cells) they begin to behave as described in anesthetized cortex, firing only one or two spikes per cycle, then skipping cycles as the curves drop to <1 spike/beat at very high rates of modulation.

FIG. 6. — Neurons discharge many spikes per cycle at most beat frequencies and their overall discharge rate is band-pass tuned. A: spike rate modulation transfer functions (rMTFs) for 6 units, normalized to maximum spike rate for each run (actual rates: 142, 85, 63, 35, 33, 20 spikes/s). All show some degree of band-pass tuning to binaural beat frequency (measured over the full 20 s of stimulation)—a phenomenon rarely observed in midbrain neurons. All peaks occur at beat rates between 5 and 20 Hz. B: the same data plotted in terms of average number of spikes per beat cycle, which falls off as a power function (linear on log axes). Values <1 spike/beat (gray dashed lines) indicate the response is skipping cycles. This contrasts sharply with responses to binaural beats in anesthetized cortex (see text).

Spitzer and Semple (1998) examined the effect of beat frequency on overall spike rate in the IC, where responses generally resemble those in awake cortex: spikes are fired throughout the phase cycle. In most IC neurons (35/44), beat rate (and direction) did not affect spike rate. To obtain a similar estimate in this sample, an index of firing rate contrast was computed for each unit tested across beat frequency

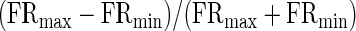where FR_max and FR_min denote the maximum and minimum evoked firing rate; a contrast of 0.33 would indicate a doubling of spike rate at one beat frequency relative to another. Of 183 cells, 73% had a rate contrast of ≥0.3, which corresponded well to band-pass rate tuning by visual inspection of rMTFs. Band-pass rate tuning to beat frequency in awake cortex, like that seen in Fig. 6A, is the rule rather than the exception, a seemingly emergent property observed rarely in the IC and never in the SOC (Spitzer and Semple 1998).

Effects of center frequency: characteristic delay and characteristic phase

The low-frequency, IPD-tuned neurons of core auditory cortex respond over a finite range of carrier frequencies and carrier frequency can exert a systematic influence on the binaural beat response, particularly its mean phase. The dual tuning of low-frequency cells in auditory cortex to frequency and IPD is exemplified in Fig. 7, in which spike rate is represented as a contour map in phase-frequency space for two cells. A vertical slice through the contours at any frequency would be the beat period histogram at that center frequency. Significant mean phase points and a linear fit (weighted by R) are overlaid. The example in Fig. 7A has a circumscribed phase/frequency response area, with little effect of frequency on mean phase. The range of IPDs over which the cell responds is broadest when the center frequency is at the BF (1.6 kHz, as defined by discharge rate). The neuron in Fig. 7B shows a clear phase advance with increasing frequency and a broader range of effective carrier frequencies (>1 octave in Fig. 7B, compared with ∼0.5 octave in Fig. 7A).

The slope of the regression line tracking mean phase across frequency may reflect a fixed delay in a linear system, called the characteristic delay (CD) of the neuron. This term was introduced by Rose et al. (1966) to denote the ITD evoking maximal (or minimal) discharge regardless of center frequency (Yin and Kuwada 1983b). The intercept of that function represents the characteristic phase (CP; Yin and Kuwada 1983b), the preferred phase regardless of frequency. Both terms refer to characteristics of binaural coincidence detection in the brain stem, originally assessed by the alignment of ITD tuning functions measured across frequency. The point of alignment indicated the CD and a CP of 0° indicated that the CD occurred at the point of maximal discharge in those functions (the “peak”); a CP of 180° indicated a CD at the point of minimum discharge (the “trough”; reviewed in Kuwada et al. 1997). For the example neurons in Fig. 7, the slopes are 0.00013 and −0.00028 cycles of IPD per Hz in Fig. 7, A and B, respectively; thus CD = 130 μs in A and −280 μs in B. The intercept in Fig. 7A falls between peak and trough, at 221°, whereas CP in Fig. 7B falls nearer the peak, at 339°.

For all cells showing significant synchrony to the binaural beat at three or more carrier frequencies, phase/frequency plots were subjected to linear regression, weighted by R at each point. A simple bootstrap technique was used to determine statistical significance of each fit (see appendix in Yin and Kuwada 1983b). Significant linear phase/frequency functions were collected from 150 cells (83% of 180 tested). Of these, 100 cells (67%) had negative slopes, indicating a progressive phase lead with increasing frequency. Figure 8 shows a collection of phase–frequency plots with both negative (Fig. 8A) and positive (Fig. 8B) slopes.

FIG. 8. — Mean phase of the binaural beat response as a linear function of center frequency. A: linear phase/frequency plots with negative slopes. These were common among the population and indicative of a preference for a lead at the contralateral ear. The slope of each function indicates the cell's characteristic delay (CD) and the “zero-frequency” intercept its characteristic phase (CP). B: cells with positive slopes to their phase/frequency functions were less common and fits were often poorer.

The populations of CD (slope, converted to microseconds) and CP (intercept, in cycles) values are plotted against one another in Fig. 9A, with marginal distributions for both metrics. An inset circular histogram replots the CP values to emphasize the clustering of their distribution at a mean phase of 333° on the circular axis; the significance of this clustering can be assessed by the same metrics used for spikes (VS = 0.34, P < 0.001 by Rayleigh test; the mean CP and VS of the left and right hemisphere distributions were almost identical, so data have been pooled). This unimodal distribution (Hartigan's dip test, P = 0.94) is significantly shifted from a mean of zero (Wilcoxon signed-rank, P = 0.002), suggesting that CDs in cortex most often occur at intermediate values corresponding to the slope of the ITD tuning curve, rather than the peak or trough. The distribution of CDs (top histogram) shows a bias toward negative values, again indicating a preference for a lead at the contralateral ear (mean CD = −100 μs, different from zero by Wilcoxon signed-rank, P < 0.0001). There is no clear dependence between the two metrics, in contrast to that described in the IC (McAlpine et al.1996; their Fig. 15).

The range of interaural delays that might be encountered in the environment is restricted by the head size of the animal and the speed of sound (Kuhn 1977). Nearly all CDs (133/150, 89%; Fig. 9, A and B) fell into the range of ecologically plausible ITDs for macaques, about ±400 μs [as computed from the measured head sizes of our animals and consistent with direct measurements by Spezio et al. (2000)].

A dependence of preferred ITD on BF has been observed in the IC of the guinea pig (McAlpine et al. 2001) and cat (Hancock and Delgutte 2004), using delayed noise stimuli, which would predict a similar effect on CD in primate cortex. Figure 9B plots CD against the BF of each neuron (n = 150) and indicates no relation between the two (ANOVA, P = 0.30). In all three species, however, BF was not seen to exert a strong effect on CP.

Characteristic delay is abstracted from a neuron's response across a range of center frequencies and does not address how the population responds to an ITD in a tone of a given frequency. Figure 9C plots all measured preferred ITDs, computed from all significant mean phases of binaural beat responses (1,280 responses, from 162 cells in monkey X, 86 in Z; 425 responses from the left hemisphere, 855 right). For values over 0.5 cycle, one cycle was subtracted (because there is no way to disambiguate ITDs longer than half a period using a cyclical stimulus). Thus the maximum range of ITDs at each frequency is constrained to half the stimulus period, defining the outer edges of the distribution (thin hyperbolic lines). At every center frequency, the distribution of preferred ITDs in the population response spans the possible range of ITD values, regardless of ecological range. The relevance of this distribution in relation to prior studies is addressed in the discussion.

Directional sensitivity and perceptual relevance

The ability of these animals to discriminate IPD sweeps from midline has been described previously (Scott et al. 2007). Figure 10 reproduces the psychophysical thresholds of both animals across carrier frequency, overlaid on the distribution of center frequencies for all significant binaural beat responses (gray histogram). Thresholds are low in the frequency range where the bulk of beat-sensitive neurons are tuned, and thresholds rise as the IPD sensitivity of the population wanes at higher carrier frequencies. This relationship is only correlational, but it merits a comparison of cortical binaural beat responses to psychophysical discrimination of IPD.

FIG. 10. — Behavioral performance of IPD discrimination mirrors the frequency range for binaural beat synchrony in auditory cortex. Thresholds for lateralization of shifts in IPD from midline across carrier frequencies in both macaques are overlaid on the distribution of center frequencies for all significant binaural beat responses (gray bars, n = 1,280) (adapted from Scott et al. 2007). Both animals performed poorly or refused to work at frequencies outside the range shown and both show elevated thresholds at frequencies >1,750 Hz (filled circles: monkey X; open squares: monkey Z). Sensitivity to IPD among the neural population seems to decline with the rise in thresholds.

Effect of beat direction on discharge rate and synchrony

Cells that fire selectively for IPD shifts in a particular direction would provide an obvious substrate for the discrimination task performed by these animals. However, the prevailing characteristic among cells tested with beats in both directions was symmetry, of both rMTFs and tMTFs. In other words, overall firing rate and synchrony were dependent on absolute beat frequency, but largely independent of which ear was advancing in phase. Figure 11A plots rMTFs for four cells tested over a wide range of beat frequencies in both directions and, regardless of absolute firing rate, the functions are symmetric about zero. For all beat frequencies tested in two directions (n = 661), the firing rates elicited show a slight bias toward the positive direction (P = 0.002 by paired t-test; mean difference is only 1 spike/s), but this is likely a result of adaptation: beats in the positive direction were presented first, as a block, in 78% of cases. To examine direction selectivity cell by cell, a rate Direction Selectivity Index (rDSI) was computed at each beat rate

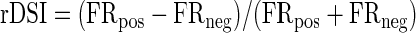where FR is firing rate and the subscript indicates the positive or negative beat direction. (By convention, “negative” denotes apparent motion into the contralateral hemifield as it passes midline.) An average rDSI was computed for each neuron (n = 135), the distribution of which is shown in Fig. 11C. Values of ±0.33 would indicate a doubling of firing rate in one direction relative to the other, but the bulk of the values fall below ±0.2 and there is no directional bias in the distribution (median not different from zero, P = 0.78, Wilcoxon signed-rank). The same analysis was carried out for all VS points (Fig. 11D) and the temporal DSI showed a somewhat broader distribution but no significant bias away from 0 (Fig. 11E). Although 6 of 135 cells showed a doubling of firing rate or VS in one direction, most cortical neurons encode IPD modulation regardless of the direction of apparent motion.

FIG. 11. — Population measures of spike rate and temporal synchrony do not reveal a preference for direction of apparent motion. A: rMTFs for cells tested with binaural beats in the positive and negative directions are generally symmetrical, showing no rate coding of IPD modulation direction. Filled symbols mark the diotic tone control values (0 Hz). B: population summary of spike rates evoked by beats of equal frequency in the positive and negative directions (n = 661, from 135 neurons). Line indicates identity; there is a weak trend across the population for points to fall above or below the line, but the mean difference of 1 spike/s is likely due to adaptation (a block of stimuli in the positive direction was presented before a block in the negative direction). C: distribution of the rate Direction Selectivity Index (rDSI) metric (see text) averaged for each neuron used in B. The mean of the distribution is not different from zero. For a doubling of spike rate (on average) in one direction, rDSI = 0.3; very few cells show this behavior. D: population of VS values from the same responses shown in B, again with no consistent directional bias in synchrony. E: temporal (t)DSI values, averaged for each neuron as in C. The distribution of tDSI is broader than that of rDSI, but the mean is not different from zero and only 6 cells exhibit a doubling of vector strength in one direction over the other.

IPD tuning width and receptive field distribution

To substantiate the claim that neurons in awake AI respond over a broad range of IPD, the MPH of each neuron's strongest response (by maximal R value, at a 2-Hz beat rate) was fit with a Gaussian distribution (Fig. 12). Tuning width was defined as twice the SD of the Gaussian. As the three examples in Fig. 12 imply, stronger responses (with high R) resulted in better goodness-of-fit (expressed as r²) and more meaningful estimates of tuning width (the three panels show the best fit, median of the population, and the 25th percentile). [Statistically, r² values correlated with the magnitude of R (P < 0.0001), and r² inversely correlated with tuning width (P < 0.0001).] The population histogram (Fig. 13A) shows a high-end tail of wide tuning widths that disappears if poor fits are excluded: median tuning width for the full population (n = 246) and the 25th, 50th, and 75th percentile of fit quality were 164, 158, 150, and 142°, respectively (medians of the 50th and 75th percentile distributions are significantly lower than the full population by Wilcoxon rank-sum, P < 0.005).

The location and extent of IPD receptive fields are displayed across frequency in Fig. 13B, for responses in the 50th percentile of fit quality (n = 123). There was no correlation between IPD tuning width and center frequency (P = 0.29, using the full population). To reference these IPD receptive fields to spatial hearing, tuning width was converted from degrees of IPD to an approximation of azimuthal angle (see methods). A property of the binaural beat stimulus (and dichotic stimuli in general) is that it can generate IPDs that would not be possible under natural listening conditions and thus cannot be mapped unambiguously to external space. Under that condition, the receptive field width could not be defined for some neurons, particularly at low frequencies. Figure 13C plots spatial receptive field width as a function of frequency, for all neurons with an IPD tuning width that could be defined in azimuth (159/246). Angles of >180° could not be defined, but are indicated by points beyond the range of the ordinate. Because tuning width in IPD did not vary with center frequency and the period is shorter at higher frequencies, it would be predicted that spatial tuning would be more narrow at high center frequencies. This is confirmed by Fig. 13C (ANOVA, P < 0.0001), although even the sharpest receptive fields still encompassed around 45° of azimuth. Consistent with the CD and ITD data in Fig. 9, the peaks of the MPHs tend to occur with a phase lead at the contralateral ear, placing the slope of the MPH near midline, which is illustrated in the distributions of peak and slope location in Fig. 13D.

Given the broad tuning and absence of directional preference in cortical neurons, how do these animals reliably discriminate the direction of small shifts in IPD (Fig. 10)? It is plausible that IPD is represented by the instantaneous firing rates of a population of broadly tuned neurons. The following section will attempt to quantify those changes in firing rate on which discrimination may depend.

d′ analysis of IPD tuning functions

The d′ statistic is an index of how reliably two stimuli can be discriminated on the basis of evoked firing rates. It is a measure of the separation between distributions of spike rates under two conditions (e.g., two adjacent values of IPD), assuming those rates to follow a Gaussian distribution. Such an analysis is illustrated for an example neuron in Fig. 14A. Spike times were sorted into matrices of 16 columns, each corresponding to a phase bin of 22.5°. Each row of the matrix represented spike counts from one period. Treating each period as an individual “trial” allowed an estimate of the SD of spike count within each phase bin. Figure 14A graphs mean spikes/period with error bars representing 1SD (same cell used in Fig. 1). d′ was computed between each phase bin and the following bin as

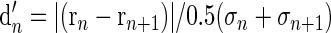where n is a given phase bin, r is the mean spike rate, and σ is the SD of spike rate. The d′ function is overlaid in gray in Fig. 14A (right-hand axis). The response peaked at 270°, but the d′ statistic shows that discriminability does not reach its maximum near the peak of the response. To the contrary, d′ dips at the maximum and minimum firing rates and peaks on the slopes of the response at 0 and 180°, where local dynamic range is maximal. A cell like this one, with d′ maximal at 0°, should be an ideal neural unit for detecting IPD modulation at the midline.

Figure 14B shows d′ functions from ten example units, with maximal discriminability spanning a range of IPDs. When these functions are aligned to the peak response of each cell (Fig. 14C), it is apparent that the properties described in the example unit from Fig. 14A apply more broadly: discriminability is greatest on the slopes of the response and is minimal at the peak and trough of the response (the peak is 0° on this axis, the trough 180° away). The asymmetry in the d′ functions may reflect an effect of varying IPD dynamically and/or an asymmetry in the static IPD tuning underlying the binaural beat response. From the 46 neurons for which static IPD functions were measured (Fig. 2), the steepness of the function was estimated at each IPD value as the slope (change in firing rate) between the discharge rate at the two flanking IPD values (Kuwada et al. 1997; McAlpine et al. 2001). The steepest point on the IPD tuning curve fell to the negative side of the peak in most cases (32/46), with a clear mode at −45° relative to the peak response. This is qualitatively similar to the bias in d′ values shown in Fig. 14C, suggesting that an asymmetry in the underlying static IPD tuning contributes to the asymmetric discriminability functions measured from binaural beats.

Neurometric analysis

Binaural beat responses were used to construct neurometric functions (Britten et al. 1992; Parker and Hawken 1985; Skottun 1998; Skottun et al. 2001; Tolhurst et al. 1983), allowing a comparison between the IPD discrimination of the animal and individual neurons of the auditory cortex. Signal detection theory (Green 1966) was applied to the binaural beat response to produce the receiver operator characteristic (ROC) of a given neuron (Bradley et al. 1987; Britten et al. 1992; Skottun et al. 2001). An advantage of ROC analysis over d′ is that no assumptions are made about the distribution of spike rates (because spike rates cannot go negative, they are seldom normally distributed around low mean rates).

This analysis is explained for an example neuron in Fig. 14. The bin in Fig. 14A marked with an asterisk was used as the “noise” distribution of spike counts and counts from the three bins before and after were the “signal,” compared at a range of criterion values spanning the full dynamic range of the response. The probability of a spike count from the signal being higher than the criterion was defined as P_hit and the probability of a spike count from the noise being higher than the criterion was P_{false alarm}. Plotting P_hit against P_{false alarm} for each criterion produces ROC curves; integrating under each curve yields a point in the neurometric function. This function was fit with a cumulative Weibull distribution, as plotted in Fig. 14D (open squares). The neurometric functions from this cell (and a similarly tuned cell from the same location) are plotted on the same axes as the psychometric function for dynamic IPD discrimination. The carrier frequency for the beat response and the task is 1,600 Hz.

The animal's behavioral function is far steeper than either of the neurometric functions. This result generalizes to the larger sample of neurons shown in Fig. 15, which depicts neurometric functions sorted by animal and frequency band. The data are the same as those depicted in Fig. 13B—the strongest response (by maximal R) of 125 neurons representing the upper 50th percentile of Gaussian fit quality. For each response, the seven phase bins comprising the rising edge of the response (bounded by the peak) were analyzed, taking the fourth bin as the “noise” distribution as described in Fig. 14A. The slopes of the resulting neurometric functions are visibly more shallow than the psychometric functions of the monkeys at each corresponding frequency, confirming that the animals' ability to discriminate changes in IPD around the midline far outstrips its most sensitive cortical neurons.

FIG. 15. — Neurometric functions of individual cortical neurons, constructed by ROC analysis of binaural beat responses, are not as steep as psychometric functions for dynamic IPD discrimination. Data are divided by animal (macaque X in the *left column*; macaque Z on the *right*) and binned by frequency: neurometric functions (light gray curves) span the frequency range indicated above each set of panels and psychometric functions (bold curves) were measured (in Hz) at 350 (*top panels*), 500 (*2nd from top*), 750 (*3rd from top*), 1,000 and 1,250 (black and gray respectively, *4th from top*); and 1,500, 1,700, and 2,000 (black, gray, and dashed lines respectively, *bottom panels*). Functions were constructed from the rising phase of the binaural beat response; cumulative Weibull fits revealed no difference in function slope between animals.

DISCUSSION

These data reveal several features previously unobserved in the neural representation of continuously varying IPD. In the absence of anesthesia, sustained, modulated responses to dynamic IPD are widespread in low-frequency primate auditory cortex. Qualitatively, the audible modulation of the hash in response to binaural beats suggested a homogeneity of tuning in the local neural population, especially in the middle (thalamorecipient) layers. This synchronized activity may underlie the neuromagnetic signal in response to slow binaural beats reported in human cerebral cortex (Karino et al. 2006). Rather than exhibiting a phasic response at a single IPD value as in anesthetized cat cortex (Reale and Brugge 1990), neurons typically modulate their rate of spike discharge throughout the IPD cycle, consistent with observations in awake rabbits (Fitzpatrick et al. 2000). This study extends that observation to include manipulations of binaural beat frequency and direction in the awake state, as well as comparisons to psychophysical performance in the same subjects.

Binaural beat frequency

Cortical neurons in awake primate synchronized their discharges to faster binaural beat rates than have been previously observed. The median synchrony cutoff of 20 Hz is consistent with the reported limit of 35–45 Hz under anesthesia (Reale and Brugge 1990), but nearly one third of neurons tested to the limit of synchrony could entrain beyond 45 Hz and 8% beyond 100 Hz (Fig. 4B). How the limit of temporal synchrony for binaural beats changes as the signal ascends the auditory pathway is unclear. Prior evidence placed the limit of synchrony to binaural beats in the IC at 80 Hz (Yin and Kuwada 1983a), about the upper limit we observed in cortex (Fig. 4B). However, evidence from a small sample of IC neurons suggests that synchrony may extend to beat frequencies an order of magnitude higher (Joris et al. 2006). More recently, Siveke et al. (2008), using a novel stimulus comparable to a broadband binaural beat, demonstrated synchrony to rates of interaural modulation as high as 500 Hz in the gerbil brain stem. The relevance of these physiological phenomena to perception is discussed in the following text.

Under anesthesia, spike rate was effectively a monotonic function of beat frequency (Reale and Brugge 1990), as would be predicted for a phasic response; this contrasts with our finding of band-pass rate tuning and the power-law decrease in the average number of spikes fired per cycle of IPD (Fig. 6). Band-pass tuning, although predominant in our sample of cortical responses, is nonexistent in the SOC and rare in the IC of the anesthetized gerbil (Spitzer and Semple 1998). The emergence of rate tuning between midbrain and cortex may result from successive filtering (e.g., synaptic integration) at each synapse between brain stem, midbrain, thalamus, and cortex. The rate tuning functions peaked within the range where synchrony was still prevalent (5–20 Hz), suggesting that discharge rate tuning need not emerge at the expense of temporal fidelity or beyond the range of synchrony, as has been proposed for the processing of amplitude modulations (e.g., Langer and Schreiner 1988; Liang et al. 2002). Rather, the greatest changes in discharge rate occur over the frequency range where responses are synchronized to the binaural beat (Fig. 6A), as has been shown for modulations of amplitude in the same preparation (Malone et al. 2007).

The binaural system previously has been characterized as “sluggish,” based on the discrepancy between rapid temporal resolution of monaural modulations and slow resolution of binaural disparities (Grantham 1982; Grantham and Wightman 1978). This perceptual phenomenon is perhaps surprising, given the remarkable temporal acuity of neurons in the auditory brain stem. A report of fast binaural resolution in IC neurons suggests that midbrain responses similarly fail to mirror binaural perception, leading the authors to speculate that the limitation stems from an inability to read out a fast temporal code at higher levels of the brain (Joris et al. 2006). However, competing evidence suggests that the incongruity between physiological and psychophysical temporal limits may depend on the stimulus used (Siveke et al. 2008).

The temporal characteristics of binaural beat responses in macaque cortex closely match psychophysical results in human listeners, who report hearing two individual tones, rather than a beat, at frequency separations between 25 and 30 Hz (Licklider 1950). The decay of synchrony in the neural population at beat frequencies >20 Hz corresponds well to this observed transition between perceived “fluctuations” and “roughness” (Licklider 1950), but is well above the limit for clear perception of auditory motion, around 2–5 Hz (Blauert 1972; Grantham and Wightman 1978). Even a 5-Hz binaural beat may exceed the expected range of ecological relevance for auditory motion, however, so perhaps the appropriate question is not “why is the binaural system slower than the monaural at tracking modulations?” but rather, “why is the binaural system so fast in the first place?” The synchrony to very fast rates of dynamic IPD observed in the present study may bear no obvious utility to tracking acoustic motion; rather, the ability of cortical neurons to follow such rates could arise from the precision of the cross-correlator in the brain stem, leaving a considerable degree of synchrony preserved at the cortical level.

Coding of sound azimuth

Neurons in the auditory cortex of alert macaques are selective for the location of sounds presented in the free field (Recanzone et al. 2000). Tuning for azimuth appears to be sharpest among neurons in the caudolateral belt field, where the median receptive field width is close to 90° (Woods et al. 2006). Although IPD is only one of several cues contributing to sound source localization, the breadth of these receptive fields for broadband stimuli is consistent with the azimuthal tuning width estimated here from pure-tone IPD responses in AI and R (Fig. 13). Transient responses to binaural beats in anesthetized cortex (Reale and Brugge 1990) implied a sharply focused spatial receptive field, whereas the responses reported here from awake cortex are more consistent with a broadly tuned spike rate code in single neurons (e.g., Middlebrooks et al. 1994).

Binaural properties have not been studied in lower stations of the primate auditory pathway, so the IPD tuning widths in cortex cannot be compared with other structures in the same species. Recordings from awake rabbits reveal a sharpening of tuning to ITD between brain stem and thalamus (Fitzpatrick et al. 1997; Kuwada et al. 2006), but the tuning widths in rabbit thalamus are narrower than those in primate cortex. Converting the Gaussian fit tuning widths into ITD, the mean width is 766 μs for neurons with BF between 300 and 1,500 Hz (compatible with Fig. 8 of Kuwada et al. 2006). In both cases, ITD tuning was measured using binaural beats, at comparable sound levels, although with slightly different measures of tuning width. From the extant data in primate, it cannot be resolved whether ITD tuning is broader at all stages of the pathway or whether the sharpening described in rabbit does not apply in this species.

A long-standing model of sound location coding (Jeffress 1948) is based on neurons receiving convergent binaural inputs at a fixed delay between the ears; coincidence detection thus converts binaural temporal differences into a place code, with an array of neurons tuned for every possible value of interaural delay. A linear model of binaural coincidence detection predicts that optimal summation for excitatory (EE) interactions would occur for signals arriving in phase, whereas excitatory–inhibitory (EI) summation would yield maximal responses when signals are out of phase (Goldberg and Brown 1969). It would follow that CP values should cluster at the peaks and troughs of the ITD tuning functions (0 and 180°, respectively) in the SOC, the site of binaural convergence.

A bimodal distribution of CP has been reported in the SOC of awake rabbit (Batra et al. 1997), although other studies find a unimodal cluster around 0° with little or no evidence of “trough”-type interactions at 180° (gerbil: Spitzer and Semple 1995; anesthetized cat: Yin and Chan 1990). Even at the level of the brain stem, CPs at intermediate values have been observed, as have nonlinear phase/frequency functions (Batra et al. 1997). In the IC, the distribution of CP is more widely distributed than that in the brain stem and reports differ as to whether values cluster near zero (Kuwada et al. 1997; Yin and Chan 1990) or tend to fall between peak and trough (Yin and Kuwada 1983b). In the cortical population reported here, CP does not show a bimodal distribution, but instead forms a messy cluster centered at 333° (Fig. 9A). This is consistent with the phase/frequency plots shown by Reale and Brugge (1990), which show a variety of intercept values in cat cortical cells, and the data of Fitzpatrick et al. (2000) from awake rabbit, which show a broad distribution of CP. By the criterion of those authors, neurons in the present study were 66% peak type and 34% trough; however, because the distribution of CPs was not bimodal, they were not divided in any of our analyses. Although 83% of cells tested possess an identifiable CD and CP in awake primate cortex, the spread in CP values suggests that the peak/trough dichotomy is of diminishing significance at higher levels of the auditory pathway.

The distribution of CDs reported here (Fig. 9A) conforms to a trend toward broader distributions in higher auditory stations, as has been described between the medial superior olive (MSO) and IC (Yin and Chan 1990) and between the dorsal nucleus of the lateral lemniscus and IC (Kuwada et al. 2006). The distribution is shifted farther from zero than has been reported in the cat IC (Yin and Kuwada 1983b), yet 89% of CDs fell within the ecological range for the macaque. Consistent with observations in awake rabbit cortex (Fitzpatrick et al. 2000), about two thirds of neurons (95/150; 63%) had CDs corresponding to ipsilateral delays, as would be generated by sounds originating in contralateral space; by comparison, 93% of CD values meet this criterion in MSO (Yin and Chan 1990). A dependence of CD on the BF of the recorded neuron has been reported in the IC (Hancock and Delgutte 2004; McAlpine et al. 1996, 2001), but was absent in our data (Fig. 9B). Whether this discrepancy stems from methodological differences (species, anesthetic state, or definitions of BF) or a difference between midbrain and cortex remains to be resolved. We recorded few neurons with BF <300 Hz, the range in which the longest CDs were observed (e.g., McAlpine et al. 1996; their Fig. 15B), which may have obscured the trend in cortex.

When mean phases of the binaural beat responses are converted to ITDs, their distribution is not constrained to the ecological range at low frequencies (Fig. 9C), demonstrating that in some cases, the IPDs that elicit the highest discharge rates during the beat cycle are IPDs that cannot occur naturally. This echoes findings in IC of the guinea pig (McAlpine et al. 2001) and cat (Hancock and Delgutte 2004), where preferred ITDs in some low-BF neurons exceeded the range of delays a small-headed animal could experience. However, this interpretation has been challenged by Kuwada et al. (2006) who contend that preferred ITDs fall within the ecological range at frequencies >400 Hz in their own data (from brain stem and IC of awake rabbit) and those of McAlpine et al. (2001). Also apparent in the Kuwada et al. (2006) data is a wider distribution of preferred ITD values in IC as compared with brain stem (their Fig. 5, C and F), such that more preferred ITD points lie outside the ecological range at low frequencies. Our data from awake primate cortex, in which preferred ITDs were distributed throughout the possible range of ITD values, would be consistent with a trend toward broader distributions of preferred ITD at higher auditory stations.

Although the peaks of some noise-delay functions in guinea pigs fall outside the ecological range, the slopes of these functions were steepest at the midline (McAlpine et al. 2001), where perceptual acuity in human listeners is greatest (Yost 1974; but see Middlebrooks and Green 1991). Cortical neurons in awake primate are broadly tuned to IPDs away from midline (Fig. 13), consistent with a mechanism of low-frequency sound localization that exploits the slopes of IPD tuning functions (Fitzpatrick et al. 2000; McAlpine et al. 2001), within broadly tuned spatial channels (Middlebrooks et al. 1994; Stecker et al. 2005). The comparison of these data to psychophysical performance is discussed in the following text.

Neural sensitivity to auditory motion

One previous study has examined sensitivity to auditory motion in AI of the alert macaque, using noise stimuli from a moving free-field speaker (Ahissar et al. 1992). In accordance with the present study, the tuning of single units in azimuth was not sharp enough to account for the ability of monkeys to localize similar stimuli (Brown 1978), but the authors did observe that most neurons showed the largest modulation in response magnitude for changes in sound location around the midline, regardless of their preferred azimuth. Whereas we report no overall sensitivity to the direction of simulated motion among the population when assessed by spike rate or synchrony (Fig. 11), Ahissar et al. (1992) drew a different conclusion from a qualitatively similar data set (cf. Fig. 11B, their Fig. 5B). They reported a preponderance of units preferring movement toward the contralateral hemifield, but only among the 28% of units exhibiting a significant directional preference. The absence of an overarching directional preference among our population may stem from differences between the stimuli and methods of analysis in the two studies; a white-noise stimulus presented in the free field would engage interaural level difference mechanisms and generate spectral cues from filtering by the pinna (Spezio et al. 2000).

A model of responses to dynamic phase in the IC (Borisyuk et al. 2002) replicates many characteristics observed in vivo (Spitzer and Semple 1998) and predicts several response properties observed in cortex. In accordance with a previous model (Cai et al. 1998), firing rate adaptation and IPD-tuned excitatory and inhibitory inputs can produce sharper tuning in response to beats than static IPD stimuli and predict the phase lag seen at faster beat frequencies. The model also predicts a phase lead at very low beat rates (i.e., the curves in Fig. 5A should sag before going upward), as the latter half of the modulation histogram is eroded by adaptation, effectively advancing the mean phase of the response. Such a lag was not seen in the present study, although this discrepancy could be accounted for in the model by the inclusion of a transmission delay that masked phase advance at low frequencies (Borisyuk et al. 2002). Under no circumstances did the IC model predict band-pass tuning of spike rate to beat frequency. A similar effect was observed, however, in a model of primary visual cortex neurons (Chance et al. 1998) in which rapid synaptic depression (in the absence of inhibition) engendered a band-pass frequency response function, analogous to the rate-tuned rMTFs emergent in cortex (Fig. 6A).

Comparing neural and psychophysical discriminability

The neurometric analysis used here rests on the presumption that thresholds for perception of change in IPD may be predictable from the neural response to those changes—a relationship posited previously in the visual domain (Britten et al. 1992; Tolhurst et al. 1983). In the auditory system, Skottun et al. (2001) found the best thresholds in the population of guinea pig IC neurons to be comparable to ITD thresholds in humans, when tested with sufficient resolution. This is compatible with the “lower-envelope hypothesis” (reviewed in Parker and Newsome 1998), whereby psychophysical threshold represents the tuning of only the most selective neurons in the population. Our finding does not accord with this hypothesis, but is consistent with comparisons of psychophysical and neuronal performance in the visual system. For example, neural sensitivity in visual cortex falls short of psychophysical sensitivity for contrast, orientation, spatial frequency, position, and acuity (reviewed in Parker and Newsome 1998).

If the lower-envelope hypothesis were true for IPD in cortex, several factors could explain why neural tuning commensurate with performance was not observed. Perhaps these neurons were not encountered in our sample, but the survey of low-frequency primary cortex was extensive. The animals were not actively engaged in listening to the binaural beats during data collection, but a prior study examined the effect of behavior on responses to dynamic IPD and found no consistent effects of active discrimination (Scott et al. 2007). The neurons examined in that study are a subset of the population analyzed here, so it is reasonable to presume that the neural discriminability computed from these binaural beat responses would not be substantially changed had the animals been actively listening. A final caveat is that the stimuli used in the psychophysical discrimination task contained dynamic IPD, but differed from binaural beats. The beat is a continuous modulation, whereas the psychophysical stimuli consisted of a steady-state zero IPD, followed by a modulation of IPD to a second steady-state value (Scott et al. 2007). Because these stimuli effectively embedded a short segment of a binaural beat between steady-state IPDs, they provided additional information that could have been used to perform the discrimination. It has previously been shown that the context in which a dynamic IPD is presented can alter neural tuning (Malone et al. 2002; Spitzer and Semple 1991, 1993). Similar context-induced changes in rate coding could enhance the information conveyed by single neurons.

If it is correct that single neurons in AI do not match the animals' behavioral sensitivity, it may be more likely that discrimination depends on the pooled activity of the neural population. Neural sensitivity commensurate with lateralization acuity may emerge in areas downstream of AI, such as the caudal belt regions (Recanzone et al. 2000; Tian et al. 2001; Woods et al. 2006). Convergence of primary cortical IPD-tuned inputs to a secondary cortical area could improve signal-to-noise by integrating across units with uncorrelated noise (Britten et al. 1992; Shadlen et al. 1996). A pooling model has been developed for ITD discrimination in SOC, IC, and thalamus (Fitzpatrick et al. 1997), which predicts a progressive sharpening in ITD tuning at sequentially higher centers, a sharpening that was also demonstrated empirically. Hancock and Delgutte (2004) demonstrated the necessity of pooling ITD responses in cat IC across BF to predict human psychophysical acuity. In macaque AI, the discrimination performance of individual neurons may not be the best predictor of psychophysical performance.

Organization of auditory cortex

Experiments using free-field stimuli have shown that neurons in the auditory cortex of awake macaque are tuned to sound source location, with the caudomedial belt showing possible enhancement of tuning relative to core or rostral belt areas (Recanzone et al. 2000; Tian et al. 2001; Woods et al. 2006). Anatomical data (Hackett et al. 1998) indicate that cells in the belt receive strong inputs from the adjacent core and thus may construct their spatial tuning by pooling feedforward inputs from the primary fields. Neurons in low-frequency AI and R possess binaural tuning properties consistent with the origin of a spatial stream of cortical processing, but projections from the low-frequency core most likely target multiple fields in the auditory belt and parabelt, including the proposed nonspatial streams (Romanski et al. 1999). Existing tracer studies in the macaque temporal lobe either did not use physiology to determine the frequency region where injections were made (Hackett et al. 1998) or made injections only into the lateral belt (Morel et al. 1993), so the patterns of inputs from the low-frequency core to downstream cortical fields are not yet fully established. In human listeners, binaural interactions can contribute to phenomena like auditory streaming and the “cocktail-party effect,” in which separation of sound sources aids speech intelligibility (Bregman 1990; Cherry 1953). The “what versus where” model of auditory processing (Tian et al. 2001) awaits further evidence from fields beyond the core, although the IPD-sensitive population described here could contribute to both.

GRANTS

B. H. Scott was supported by National Institute on Deafness and Other Communication Disorders Grant DC-05287-01 and a James Arthur Fellowship from New York University. B. J. Malone was supported by National Institute of Mental Health Grant MH-12993-02. M. N. Semple was supported by the W. M. Keck Foundation.

Acknowledgments

Present addresses: B. H. Scott: Laboratory of Neuropsychology, NIMH/National Institutes of Health, 49 Convent Dr., Room 1B80, Bethesda, MD 20892 (brianscott@mail.nih.gov); B. J. Malone: Keck Center for Integrative Neuroscience, 513 Parnassus Ave., San Francisco, CA 94143-0444.

The costs of publication of this article were defrayed in part by the payment of page charges. The article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. Section 1734 solely to indicate this fact.

REFERENCES

Ahissar et al. 1992.Ahissar M, Ahissar E, Bergman H, Vaadia E. Encoding of sound-source location and movement: activity of single neurons and interactions between adjacent neurons in the monkey auditory cortex. J Neurophysiol 67: 203–215, 1992. [DOI] [PubMed] [Google Scholar]
Batra et al. 1997.Batra R, Kuwada S, Fitzpatrick DC. Sensitivity to interaural temporal disparities of low- and high-frequency neurons in the superior olivary complex. I. Heterogeneity of responses. J Neurophysiol 78: 1222–1236, 1997. [DOI] [PubMed] [Google Scholar]
Benson et al. 1981.Benson DA, Hienz RD, Goldstein MH Jr. Single-unit activity in the auditory cortex of monkeys actively localizing sound sources: spatial tuning and behavioral dependency. Brain Res 219: 249–267, 1981. [DOI] [PubMed] [Google Scholar]
Blauert 1972.Blauert J On the lag of lateralization caused by interaural time and intensity differences. Audiology 11: 265–270, 1972. [DOI] [PubMed] [Google Scholar]
Borisyuk et al. 2002.Borisyuk A, Semple MN, Rinzel J. Adaptation and inhibition underlie responses to time-varying interaural phase cues in a model of inferior colliculus neurons. J Neurophysiol 88: 2134–2146, 2002. [DOI] [PubMed] [Google Scholar]
Bradley et al. 1987.Bradley A, Skottun BC, Ohzawa I, Sclar G, Freeman RD. Visual orientation and spatial frequency discrimination: a comparison of single neurons and behavior. J Neurophysiol 57: 755–772, 1987. [DOI] [PubMed] [Google Scholar]
Bregman 1990.Bregman AS Auditory Scene Analysis: The Perceptual Organization of Sound. Cambridge, MA: MIT Press, 1990.
Britten et al. 1992.Britten KH, Shadlen MN, Newsome WT, Movshon JA. The analysis of visual motion: a comparison of neuronal and psychophysical performance. J Neurosci 12: 4745–4765, 1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brown et al. 1978.Brown CH, Beecher MD, Moody DB, Stebbins WC. Localization of pure tones by Old World monkeys. J Acoust Soc Am 63: 1484–1492, 1978. [DOI] [PubMed] [Google Scholar]
Brugge and Merzenich 1973.Brugge JF, Merzenich MM. Responses of neurons in auditory cortex of the macaque monkey to monaural and binaural stimulation. J Neurophysiol 36: 1138–1158, 1973. [DOI] [PubMed] [Google Scholar]
Brugge et al. 1996.Brugge JF, Reale RA, Hind JE. The structure of spatial receptive fields of neurons in primary auditory cortex of the cat. J Neurosci 16: 4420–4437, 1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
Buell et al. 1991.Buell TN, Trahiotis C, Bernstein LR. Lateralization of low-frequency tones: relative potency of gating and ongoing interaural delays. J Acoust Soc Am 90: 3077–3085, 1991. [DOI] [PubMed] [Google Scholar]
Cai et al. 1998.Cai H, Carney LH, Colburn HS. A model for binaural response properties of inferior colliculus neurons. II. A model with interaural time difference-sensitive excitatory and inhibitory inputs and an adaptation mechanism. J Acoust Soc Am 103: 494–506, 1998. [DOI] [PubMed] [Google Scholar]
Chance et al. 1998.Chance FS, Nelson SB, Abbott LF. Synaptic depression and the temporal response characteristics of V1 cells. J Neurosci 18: 4785–4799, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cherry 1953.Cherry EC Some experiments on the recognition of speech with one and with two ears. J Acoust Soc Am 25: 975–979, 1953. [Google Scholar]
Eggermont 1999.Eggermont JJ The magnitude and phase of temporal modulation transfer functions in cat auditory cortex. J Neurosci 19: 2780–2788, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fisher 1996.Fisher NI Statistical Analysis of Circular Data. Cambridge, UK: Cambridge Univ. Press, 1996, p. 277.
Fitzpatrick et al. 1997.Fitzpatrick DC, Batra R, Stanford TR, Kuwada S. A neuronal population code for sound localization. Nature 388: 871–874, 1997. [DOI] [PubMed] [Google Scholar]
Fitzpatrick and Kuwada 2001.Fitzpatrick DC, Kuwada S. Tuning to interaural time differences across frequency. J Neurosci 21: 4844–4851, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fitzpatrick et al. 2000.Fitzpatrick DC, Kuwada S, Batra R. Neural sensitivity to interaural time differences: beyond the Jeffress model. J Neurosci 20: 1605–1615, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
Goldberg and Brown 1969.Goldberg JM, Brown PB. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J Neurophysiol 32: 613–636, 1969. [DOI] [PubMed] [Google Scholar]
Grantham and Luethke 1988.Grantham DW, Luethke LE. Detectability of tonal signals with changing interaural phase differences in noise. J Acoust Soc Am 83: 1117–1123, 1988. [DOI] [PubMed] [Google Scholar]
Grantham and Wightman 1978.Grantham DW, Wightman FL. Detectability of varying interaural temporal differences. J Acoust Soc Am 63: 511–523, 1978. [DOI] [PubMed] [Google Scholar]
Green and Swets 1966.Green DM, Swets JA. Signal Detection Theory and Psychophysics. New York: Wiley, 1966, p. 476.
Hackett et al. 1998.Hackett TA, Stepniewska I, Kaas JH. Subdivisions of auditory cortex and ipsilateral cortical connections of the parabelt auditory cortex in macaque monkeys. J Comp Neurol 394: 475–495, 1998. [DOI] [PubMed] [Google Scholar]
Hancock and Delgutte 2004.Hancock KE, Delgutte B. A physiologically based model of interaural time difference discrimination. J Neurosci 24: 7110–7117, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
Harper and McAlpine 2004.Harper NS, McAlpine D. Optimal neural population coding of an auditory spatial cue. Nature 430: 682–686, 2004. [DOI] [PubMed] [Google Scholar]
Heffner and Heffner 1990.Heffner HE, Heffner RS. Effect of bilateral auditory cortex lesions on sound localization in Japanese macaques. J Neurophysiol 64: 915–931, 1990. [DOI] [PubMed] [Google Scholar]
Houben and Gourevitch 1979.Houben D, Gourevitch G. Auditory lateralization in monkeys: an examination of two cues serving directional hearing. J Acoust Soc Am 66: 1057–1063, 1979. [DOI] [PubMed] [Google Scholar]
Jeffress 1948.Jeffress LA A place theory of sound localization. J Comp Physiol Psychol 41: 35–39, 1948. [DOI] [PubMed] [Google Scholar]
Jenkins and Merzenich 1984.Jenkins WM, Merzenich MM. Role of cat primary auditory cortex for sound-localization behavior. J Neurophysiol 52: 819–847, 1984. [DOI] [PubMed] [Google Scholar]
Joris et al. 2006.Joris PX, van de Sande B, Recio-Spinoso A, van der Heijden M. Auditory midbrain and nerve responses to sinusoidal variations in interaural correlation. J Neurosci 26: 279–289, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kaas and Hackett 2000.Kaas JH, Hackett TA. Subdivisions of auditory cortex and processing streams in primates. Proc Natl Acad Sci USA 97: 11793–11799, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
Karino et al. 2006.Karino S, Yumoto M, Itoh K, Uno A, Yamakawa K, Sekimoto S, Kaga K. Neuromagnetic responses to binaural beat in human cerebral cortex. J Neurophysiol 96: 1927–1938, 2006. [DOI] [PubMed] [Google Scholar]
Kosaki et al. 1997.Kosaki H, Hashikawa T, He J, Jones EG. Tonotopic organization of auditory cortical fields delineated by parvalbumin immunoreactivity in macaque monkeys. J Comp Neurol 386: 304–316, 1997. [PubMed] [Google Scholar]
Kuhn 1977.Kuhn GF Model for interaural time differences in the azimuthal plane. J Acoust Soc Am 62: 157–167, 1977. [Google Scholar]
Kuwada et al. 1997.Kuwada S, Batra R, Fitzpatrick DC. Neural processing of binaural temporal cues. In: Binaural and Spatial Hearing in Real and Virtual Environments, edited by Gilkey RH, Anderson TR. Mahwah, NJ: Erlbaum, 1997, p. 399–426.
Kuwada et al. 2006.Kuwada S, Fitzpatrick DC, Batra R, Ostapoff E-M. Sensitivity to interaural time differences in the dorsal nucleus of the lateral lemniscus of the unanesthetized rabbit: comparison with other structures. J Neurophysiol 95: 1309–1322, 2006. [DOI] [PubMed] [Google Scholar]
Kuwada and Yin 1983.Kuwada S, Yin T. Binaural interaction in low-frequency neurons in inferior colliculus in the cat. I. Effects of long interaural delays, intensity, and repetition rate on interaural delay function. J Neurophysiol 50: 981–999, 1983. [DOI] [PubMed] [Google Scholar]
Langner and Schreiner 1988.Langner G, Schreiner CE. Periodicity coding in the inferior colliculus of the cat. I. Neuronal mechanisms. J Neurophysiol 60: 1799–1822, 1988. [DOI] [PubMed] [Google Scholar]
Liang et al. 2002.Liang L, Lu T, Wang X. Neural representations of sinusoidal amplitude and frequency modulations in the primary auditory cortex of awake primates. J Neurophysiol 87: 2237–2261, 2002. [DOI] [PubMed] [Google Scholar]
Licklider et al. 1950.Licklider JCR, Webster JC, Hedlun JM. On the frequency limits of binaural beats. J Acoust Soc Am 22: 468–473, 1950. [Google Scholar]
Malhotra et al. 2004.Malhotra S, Hall AJ, Lomber SG. Cortical control of sound localization in the cat: unilateral cooling deactivation of 19 cerebral areas. J Neurophysiol 92: 1625–1643, 2004. [DOI] [PubMed] [Google Scholar]
Malone et al. 2002.Malone BJ, Scott BH, Semple MN. Context-dependent adaptive coding of interaural phase disparity in the auditory cortex of awake macaques. J Neurosci 22: 4625–4638, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
Malone et al. 2007.Malone BJ, Scott BH, Semple MN. Dynamic amplitude coding in the auditory cortex of awake rhesus macaques. J Neurophysiol 98: 1451–1474, 2007. [DOI] [PubMed] [Google Scholar]
Mardia and Jupp 2000.Mardia KV, Jupp PE. Directional Statistics (2nd ed.). New York: Wiley, 2000.
McAlpine et al. 2001.McAlpine D, Jiang D, Palmer AR. A neural code for low-frequency sound localization in mammals. Nat Neurosci 4: 396–401, 2001. [DOI] [PubMed] [Google Scholar]
Merzenich and Brugge 1973.Merzenich MM, Brugge JF. Representation of the cochlear partition of the superior temporal plane of the macaque monkey. Brain Res 50: 275–296, 1973. [DOI] [PubMed] [Google Scholar]
Mickey and Middlebrooks 2003.Mickey BJ, Middlebrooks JC. Representation of auditory space by cortical neurons in awake cats. J Neurosci 23: 8649–8663, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
Middlebrooks et al. 1994.Middlebrooks JC, Clock AE, Xu L, Green DM. A panoramic code for sound location by cortical neurons. Science 264: 842–844, 1994. [DOI] [PubMed] [Google Scholar]
Middlebrooks and Green 1991.Middlebrooks JC, Green DM. Sound localization by human listeners. Annu Rev Psychol 42: 135–159, 1991. [DOI] [PubMed] [Google Scholar]
Morel et al. 1993.Morel A, Garraghty PE, Kaas JH. Tonotopic organization, architectonic fields, and connections of auditory cortex in macaque monkeys. J Comp Neurol 335: 437–459, 1993. [DOI] [PubMed] [Google Scholar]
Neff et al. 1956.Neff WD, Fisher JF, Diamond IT, Yela M. Role of auditory cortex in discrimination requiring localization of sound in space. J Neurophysiol 19: 500–512, 1956. [DOI] [PubMed] [Google Scholar]
Parker and Hawken 1985.Parker A, Hawken M. Capabilities of monkey cortical cells in spatial-resolution tasks. J Opt Soc Am A 2: 1101–1114, 1985. [DOI] [PubMed] [Google Scholar]
Parker and Newsome 1998.Parker AJ, Newsome WT. Sense and the single neuron: probing the physiology of perception. Annu Rev Neurosci 21: 227–277, 1998. [DOI] [PubMed] [Google Scholar]
Perrott and Musicant 1977.Perrott DR, Musicant AD. Rotating tones and binaural beats. J Acoust Soc Am 61: 1288–1292, 1977. [DOI] [PubMed] [Google Scholar]
Pfingst and O'Connor 1980.Pfingst BE, O'Connor TA. A vertical stereotaxic approach to auditory cortex in the unanesthetized monkey. J Neurosci Methods 2: 33–45, 1980. [DOI] [PubMed] [Google Scholar]
Rauschecker et al. 1995.Rauschecker JP, Tian B, Hauser M. Processing of complex sounds in the macaque nonprimary auditory cortex. Science 268: 111–114, 1995. [DOI] [PubMed] [Google Scholar]
Rayleigh 1907.Rayleigh (Strutt JW 3rd, Baron of Rayleigh). On our perception of sound direction. Philos Mag 13: 214–232, 1907. [Google Scholar]
Reale and Brugge 1990.Reale RA, Brugge JF. Auditory cortical neurons are sensitive to static and continuously changing interaural phase cues. J Neurophysiol 64: 1247–1260, 1990. [DOI] [PubMed] [Google Scholar]
Recanzone 2000.Recanzone GH Response profiles of auditory cortical neurons to tones and noise in behaving macaque monkeys. Hear Res 150: 104–118, 2000. [DOI] [PubMed] [Google Scholar]
Recanzone et al. 2000.Recanzone GH, Guard DC, Phan ML, Su TK. Correlation between the activity of single auditory cortical neurons and sound-localization behavior in the macaque monkey. J Neurophysiol 83: 2723–2739, 2000. [DOI] [PubMed] [Google Scholar]
Romanski et al. 1999.Romanski LM, Tian B, Fritz J, Mishkin M, Goldman-Rakic PS, Rauschecker JP. Dual streams of auditory afferents target multiple domains in the primate prefrontal cortex. Nat Neurosci 2: 1131–1136, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rose et al. 1967.Rose JE, Brugge JF, Anderson DJ, Hind JE. Phase-locked response to low-frequency tones in single auditory nerve fibers of the squirrel monkey. J Neurophysiol 30: 769–793, 1967. [DOI] [PubMed] [Google Scholar]
Rose et al. 1966.Rose JE, Gross NB, Geisler CD, Hind JE. Some neural mechanisms in the inferior colliculus of the cat which may be relevant to localization of a sound source. J Neurophysiol 29: 288–314, 1966. [DOI] [PubMed] [Google Scholar]
Schnupp et al. 2001.Schnupp JW, Mrsic-Flogel TD, King AJ. Linear processing of spatial cues in primary auditory cortex. Nature 414: 200–204, 2001. [DOI] [PubMed] [Google Scholar]
Scott 2004.Scott BH Physiological Organization of Auditory Cortex in Awake Macaque (PhD thesis). New York: New York Univ., 2004, p. 324.
Scott et al. 2007.Scott BH, Malone BJ, Semple MN. Effect of behavioral context on representation of a spatial cue in core auditory cortex of awake macaques. J Neurosci 27: 6489–6499, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shackleton et al. 1991.Shackleton TM, Bowsher JM, Meddis R. Lateralization of very-short-duration tone pulses of low and high frequencies. Q J Exp Psychol 43: 503–516, 1991. [DOI] [PubMed] [Google Scholar]
Shadlen et al. 1996.Shadlen MN, Britten KH, Newsome WT, Movshon JA. A computational analysis of the relationship between neuronal and behavioral responses to visual motion. J Neurosci 16: 1486–1510, 1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
Siveke et al. 2008.Siveke I, Ewert SD, Grothe B, Wiegrebe L. Psychophysical and physiological evidence for fast binaural processing. J Neurosci 28: 2043–2052, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Skottun 1998.Skottun BC Sound localization and neurons (Letter). Nature 393: 531, 1998. [DOI] [PubMed] [Google Scholar]
Skottun et al. 2001.Skottun BC, Shackleton TM, Arnott RH, Palmer AR. The ability of inferior colliculus neurons to signal differences in interaural delay. Proc Natl Acad Sci USA 98: 14050–14054, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Spezio et al. 2000.Spezio ML, Keller CH, Marrocco RT, Takahashi TT. Head-related transfer functions of the rhesus monkey. Hear Res 144: 73–88, 2000. [DOI] [PubMed] [Google Scholar]
Spitzer and Semple 1991.Spitzer MW, Semple MN. Interaural phase coding in auditory midbrain: influence of dynamic stimulus features. Science 254: 721–724, 1991. [DOI] [PubMed] [Google Scholar]
Spitzer and Semple 1993.Spitzer MW, Semple MN. Responses of inferior colliculus neurons to time-varying interaural phase disparity: effects of shifting the locus of virtual motion. J Neurophysiol 69: 1245–1263, 1993. [DOI] [PubMed] [Google Scholar]
Spitzer and Semple 1995.Spitzer MW, Semple MN. Neurons sensitive to interaural phase disparity in gerbil superior olive: diverse monaural and temporal response properties. J Neurophysiol 73: 1668–1690, 1995. [DOI] [PubMed] [Google Scholar]
Spitzer and Semple 1998.Spitzer MW, Semple MN. Transformation of binaural response properties in the ascending auditory pathway: influence of time-varying interaural phase disparity. J Neurophysiol 80: 3062–3076, 1998. [DOI] [PubMed] [Google Scholar]
Stecker et al. 2005.Stecker GC, Harrington IA, Middlebrooks JC. Location coding by opponent neural populations in the auditory cortex. PLoS Biol 3: e78, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
Tian et al. 2001.Tian B, Reser D, Durham A, Kustov A, Rauschecker JP. Functional specialization in rhesus monkey auditory cortex. Science 292: 290–293, 2001. [DOI] [PubMed] [Google Scholar]
Tolhurst et al. 1983.Tolhurst DJ, Movshon JA, Dean AF. The statistical reliability of signals in single neurons in cat and monkey visual cortex. Vision Res 23: 775–785, 1983. [DOI] [PubMed] [Google Scholar]
Wegener 1974.Wegener JG Interaural intensity and phase angle discrimination by rhesus monkeys. J Speech Hear Res 17: 638–655, 1974. [DOI] [PubMed] [Google Scholar]
Woods et al. 2006.Woods TM, Lopez SE, Long JH, Rahman JE, Recanzone GH. Effects of stimulus azimuth and intensity on the single-neuron activity in the auditory cortex of the alert macaque monkey. J Neurophysiol 96: 3323–3337, 2006. [DOI] [PubMed] [Google Scholar]
Yin and Chan 1990.Yin TC, Chan JC. Interaural time sensitivity in medial superior olive of cat. J Neurophysiol 64: 465–488, 1990. [DOI] [PubMed] [Google Scholar]
Yin and Kuwada 1983a.Yin TC, Kuwada S. Binaural interaction in low-frequency neurons in inferior colliculus of the cat. II. Effects of changing rate and direction of interaural phase. J Neurophysiol 50: 1000–1019, 1983a. [DOI] [PubMed] [Google Scholar]
Yin and Kuwada 1983b.Yin TC, Kuwada S. Binaural interaction in low-frequency neurons in inferior colliculus of the cat. III. Effects of changing frequency. J Neurophysiol 50: 1020–1042, 1983b. [DOI] [PubMed] [Google Scholar]
Yost 1974.Yost WA Discriminations of interaural phase differences. J Acoust Soc Am 55: 1299–1303, 1974. [DOI] [PubMed] [Google Scholar]

[r1] Ahissar et al. 1992.Ahissar M, Ahissar E, Bergman H, Vaadia E. Encoding of sound-source location and movement: activity of single neurons and interactions between adjacent neurons in the monkey auditory cortex. J Neurophysiol 67: 203–215, 1992. [DOI] [PubMed] [Google Scholar]

[r2] Batra et al. 1997.Batra R, Kuwada S, Fitzpatrick DC. Sensitivity to interaural temporal disparities of low- and high-frequency neurons in the superior olivary complex. I. Heterogeneity of responses. J Neurophysiol 78: 1222–1236, 1997. [DOI] [PubMed] [Google Scholar]

[r3] Benson et al. 1981.Benson DA, Hienz RD, Goldstein MH Jr. Single-unit activity in the auditory cortex of monkeys actively localizing sound sources: spatial tuning and behavioral dependency. Brain Res 219: 249–267, 1981. [DOI] [PubMed] [Google Scholar]

[r4] Blauert 1972.Blauert J On the lag of lateralization caused by interaural time and intensity differences. Audiology 11: 265–270, 1972. [DOI] [PubMed] [Google Scholar]

[r5] Borisyuk et al. 2002.Borisyuk A, Semple MN, Rinzel J. Adaptation and inhibition underlie responses to time-varying interaural phase cues in a model of inferior colliculus neurons. J Neurophysiol 88: 2134–2146, 2002. [DOI] [PubMed] [Google Scholar]

[r6] Bradley et al. 1987.Bradley A, Skottun BC, Ohzawa I, Sclar G, Freeman RD. Visual orientation and spatial frequency discrimination: a comparison of single neurons and behavior. J Neurophysiol 57: 755–772, 1987. [DOI] [PubMed] [Google Scholar]

[r7] Bregman 1990.Bregman AS Auditory Scene Analysis: The Perceptual Organization of Sound. Cambridge, MA: MIT Press, 1990.

[r8] Britten et al. 1992.Britten KH, Shadlen MN, Newsome WT, Movshon JA. The analysis of visual motion: a comparison of neuronal and psychophysical performance. J Neurosci 12: 4745–4765, 1992. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r9] Brown et al. 1978.Brown CH, Beecher MD, Moody DB, Stebbins WC. Localization of pure tones by Old World monkeys. J Acoust Soc Am 63: 1484–1492, 1978. [DOI] [PubMed] [Google Scholar]

[r10] Brugge and Merzenich 1973.Brugge JF, Merzenich MM. Responses of neurons in auditory cortex of the macaque monkey to monaural and binaural stimulation. J Neurophysiol 36: 1138–1158, 1973. [DOI] [PubMed] [Google Scholar]

[r11] Brugge et al. 1996.Brugge JF, Reale RA, Hind JE. The structure of spatial receptive fields of neurons in primary auditory cortex of the cat. J Neurosci 16: 4420–4437, 1996. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r12] Buell et al. 1991.Buell TN, Trahiotis C, Bernstein LR. Lateralization of low-frequency tones: relative potency of gating and ongoing interaural delays. J Acoust Soc Am 90: 3077–3085, 1991. [DOI] [PubMed] [Google Scholar]

[r13] Cai et al. 1998.Cai H, Carney LH, Colburn HS. A model for binaural response properties of inferior colliculus neurons. II. A model with interaural time difference-sensitive excitatory and inhibitory inputs and an adaptation mechanism. J Acoust Soc Am 103: 494–506, 1998. [DOI] [PubMed] [Google Scholar]

[r14] Chance et al. 1998.Chance FS, Nelson SB, Abbott LF. Synaptic depression and the temporal response characteristics of V1 cells. J Neurosci 18: 4785–4799, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r15] Cherry 1953.Cherry EC Some experiments on the recognition of speech with one and with two ears. J Acoust Soc Am 25: 975–979, 1953. [Google Scholar]

[r16] Eggermont 1999.Eggermont JJ The magnitude and phase of temporal modulation transfer functions in cat auditory cortex. J Neurosci 19: 2780–2788, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r17] Fisher 1996.Fisher NI Statistical Analysis of Circular Data. Cambridge, UK: Cambridge Univ. Press, 1996, p. 277.

[r18] Fitzpatrick et al. 1997.Fitzpatrick DC, Batra R, Stanford TR, Kuwada S. A neuronal population code for sound localization. Nature 388: 871–874, 1997. [DOI] [PubMed] [Google Scholar]

[r19] Fitzpatrick and Kuwada 2001.Fitzpatrick DC, Kuwada S. Tuning to interaural time differences across frequency. J Neurosci 21: 4844–4851, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r20] Fitzpatrick et al. 2000.Fitzpatrick DC, Kuwada S, Batra R. Neural sensitivity to interaural time differences: beyond the Jeffress model. J Neurosci 20: 1605–1615, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r21] Goldberg and Brown 1969.Goldberg JM, Brown PB. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J Neurophysiol 32: 613–636, 1969. [DOI] [PubMed] [Google Scholar]

[r22] Grantham and Luethke 1988.Grantham DW, Luethke LE. Detectability of tonal signals with changing interaural phase differences in noise. J Acoust Soc Am 83: 1117–1123, 1988. [DOI] [PubMed] [Google Scholar]

[r23] Grantham and Wightman 1978.Grantham DW, Wightman FL. Detectability of varying interaural temporal differences. J Acoust Soc Am 63: 511–523, 1978. [DOI] [PubMed] [Google Scholar]

[r24] Green and Swets 1966.Green DM, Swets JA. Signal Detection Theory and Psychophysics. New York: Wiley, 1966, p. 476.

[r25] Hackett et al. 1998.Hackett TA, Stepniewska I, Kaas JH. Subdivisions of auditory cortex and ipsilateral cortical connections of the parabelt auditory cortex in macaque monkeys. J Comp Neurol 394: 475–495, 1998. [DOI] [PubMed] [Google Scholar]

[r26] Hancock and Delgutte 2004.Hancock KE, Delgutte B. A physiologically based model of interaural time difference discrimination. J Neurosci 24: 7110–7117, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r27] Harper and McAlpine 2004.Harper NS, McAlpine D. Optimal neural population coding of an auditory spatial cue. Nature 430: 682–686, 2004. [DOI] [PubMed] [Google Scholar]

[r28] Heffner and Heffner 1990.Heffner HE, Heffner RS. Effect of bilateral auditory cortex lesions on sound localization in Japanese macaques. J Neurophysiol 64: 915–931, 1990. [DOI] [PubMed] [Google Scholar]

[r29] Houben and Gourevitch 1979.Houben D, Gourevitch G. Auditory lateralization in monkeys: an examination of two cues serving directional hearing. J Acoust Soc Am 66: 1057–1063, 1979. [DOI] [PubMed] [Google Scholar]

[r30] Jeffress 1948.Jeffress LA A place theory of sound localization. J Comp Physiol Psychol 41: 35–39, 1948. [DOI] [PubMed] [Google Scholar]

[r31] Jenkins and Merzenich 1984.Jenkins WM, Merzenich MM. Role of cat primary auditory cortex for sound-localization behavior. J Neurophysiol 52: 819–847, 1984. [DOI] [PubMed] [Google Scholar]

[r32] Joris et al. 2006.Joris PX, van de Sande B, Recio-Spinoso A, van der Heijden M. Auditory midbrain and nerve responses to sinusoidal variations in interaural correlation. J Neurosci 26: 279–289, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r33] Kaas and Hackett 2000.Kaas JH, Hackett TA. Subdivisions of auditory cortex and processing streams in primates. Proc Natl Acad Sci USA 97: 11793–11799, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r34] Karino et al. 2006.Karino S, Yumoto M, Itoh K, Uno A, Yamakawa K, Sekimoto S, Kaga K. Neuromagnetic responses to binaural beat in human cerebral cortex. J Neurophysiol 96: 1927–1938, 2006. [DOI] [PubMed] [Google Scholar]

[r35] Kosaki et al. 1997.Kosaki H, Hashikawa T, He J, Jones EG. Tonotopic organization of auditory cortical fields delineated by parvalbumin immunoreactivity in macaque monkeys. J Comp Neurol 386: 304–316, 1997. [PubMed] [Google Scholar]

[r36] Kuhn 1977.Kuhn GF Model for interaural time differences in the azimuthal plane. J Acoust Soc Am 62: 157–167, 1977. [Google Scholar]

[r37] Kuwada et al. 1997.Kuwada S, Batra R, Fitzpatrick DC. Neural processing of binaural temporal cues. In: Binaural and Spatial Hearing in Real and Virtual Environments, edited by Gilkey RH, Anderson TR. Mahwah, NJ: Erlbaum, 1997, p. 399–426.

[r38] Kuwada et al. 2006.Kuwada S, Fitzpatrick DC, Batra R, Ostapoff E-M. Sensitivity to interaural time differences in the dorsal nucleus of the lateral lemniscus of the unanesthetized rabbit: comparison with other structures. J Neurophysiol 95: 1309–1322, 2006. [DOI] [PubMed] [Google Scholar]

[r39] Kuwada and Yin 1983.Kuwada S, Yin T. Binaural interaction in low-frequency neurons in inferior colliculus in the cat. I. Effects of long interaural delays, intensity, and repetition rate on interaural delay function. J Neurophysiol 50: 981–999, 1983. [DOI] [PubMed] [Google Scholar]

[r40] Langner and Schreiner 1988.Langner G, Schreiner CE. Periodicity coding in the inferior colliculus of the cat. I. Neuronal mechanisms. J Neurophysiol 60: 1799–1822, 1988. [DOI] [PubMed] [Google Scholar]

[r41] Liang et al. 2002.Liang L, Lu T, Wang X. Neural representations of sinusoidal amplitude and frequency modulations in the primary auditory cortex of awake primates. J Neurophysiol 87: 2237–2261, 2002. [DOI] [PubMed] [Google Scholar]

[r42] Licklider et al. 1950.Licklider JCR, Webster JC, Hedlun JM. On the frequency limits of binaural beats. J Acoust Soc Am 22: 468–473, 1950. [Google Scholar]

[r43] Malhotra et al. 2004.Malhotra S, Hall AJ, Lomber SG. Cortical control of sound localization in the cat: unilateral cooling deactivation of 19 cerebral areas. J Neurophysiol 92: 1625–1643, 2004. [DOI] [PubMed] [Google Scholar]

[r44] Malone et al. 2002.Malone BJ, Scott BH, Semple MN. Context-dependent adaptive coding of interaural phase disparity in the auditory cortex of awake macaques. J Neurosci 22: 4625–4638, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r45] Malone et al. 2007.Malone BJ, Scott BH, Semple MN. Dynamic amplitude coding in the auditory cortex of awake rhesus macaques. J Neurophysiol 98: 1451–1474, 2007. [DOI] [PubMed] [Google Scholar]

[r46] Mardia and Jupp 2000.Mardia KV, Jupp PE. Directional Statistics (2nd ed.). New York: Wiley, 2000.

[r47] McAlpine et al. 2001.McAlpine D, Jiang D, Palmer AR. A neural code for low-frequency sound localization in mammals. Nat Neurosci 4: 396–401, 2001. [DOI] [PubMed] [Google Scholar]

[r48] Merzenich and Brugge 1973.Merzenich MM, Brugge JF. Representation of the cochlear partition of the superior temporal plane of the macaque monkey. Brain Res 50: 275–296, 1973. [DOI] [PubMed] [Google Scholar]

[r49] Mickey and Middlebrooks 2003.Mickey BJ, Middlebrooks JC. Representation of auditory space by cortical neurons in awake cats. J Neurosci 23: 8649–8663, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r50] Middlebrooks et al. 1994.Middlebrooks JC, Clock AE, Xu L, Green DM. A panoramic code for sound location by cortical neurons. Science 264: 842–844, 1994. [DOI] [PubMed] [Google Scholar]

[r51] Middlebrooks and Green 1991.Middlebrooks JC, Green DM. Sound localization by human listeners. Annu Rev Psychol 42: 135–159, 1991. [DOI] [PubMed] [Google Scholar]

[r52] Morel et al. 1993.Morel A, Garraghty PE, Kaas JH. Tonotopic organization, architectonic fields, and connections of auditory cortex in macaque monkeys. J Comp Neurol 335: 437–459, 1993. [DOI] [PubMed] [Google Scholar]

[r53] Neff et al. 1956.Neff WD, Fisher JF, Diamond IT, Yela M. Role of auditory cortex in discrimination requiring localization of sound in space. J Neurophysiol 19: 500–512, 1956. [DOI] [PubMed] [Google Scholar]

[r54] Parker and Hawken 1985.Parker A, Hawken M. Capabilities of monkey cortical cells in spatial-resolution tasks. J Opt Soc Am A 2: 1101–1114, 1985. [DOI] [PubMed] [Google Scholar]

[r55] Parker and Newsome 1998.Parker AJ, Newsome WT. Sense and the single neuron: probing the physiology of perception. Annu Rev Neurosci 21: 227–277, 1998. [DOI] [PubMed] [Google Scholar]

[r56] Perrott and Musicant 1977.Perrott DR, Musicant AD. Rotating tones and binaural beats. J Acoust Soc Am 61: 1288–1292, 1977. [DOI] [PubMed] [Google Scholar]

[r57] Pfingst and O'Connor 1980.Pfingst BE, O'Connor TA. A vertical stereotaxic approach to auditory cortex in the unanesthetized monkey. J Neurosci Methods 2: 33–45, 1980. [DOI] [PubMed] [Google Scholar]

[r58] Rauschecker et al. 1995.Rauschecker JP, Tian B, Hauser M. Processing of complex sounds in the macaque nonprimary auditory cortex. Science 268: 111–114, 1995. [DOI] [PubMed] [Google Scholar]

[r59] Rayleigh 1907.Rayleigh (Strutt JW 3rd, Baron of Rayleigh). On our perception of sound direction. Philos Mag 13: 214–232, 1907. [Google Scholar]

[r60] Reale and Brugge 1990.Reale RA, Brugge JF. Auditory cortical neurons are sensitive to static and continuously changing interaural phase cues. J Neurophysiol 64: 1247–1260, 1990. [DOI] [PubMed] [Google Scholar]

[r61] Recanzone 2000.Recanzone GH Response profiles of auditory cortical neurons to tones and noise in behaving macaque monkeys. Hear Res 150: 104–118, 2000. [DOI] [PubMed] [Google Scholar]

[r62] Recanzone et al. 2000.Recanzone GH, Guard DC, Phan ML, Su TK. Correlation between the activity of single auditory cortical neurons and sound-localization behavior in the macaque monkey. J Neurophysiol 83: 2723–2739, 2000. [DOI] [PubMed] [Google Scholar]

[r63] Romanski et al. 1999.Romanski LM, Tian B, Fritz J, Mishkin M, Goldman-Rakic PS, Rauschecker JP. Dual streams of auditory afferents target multiple domains in the primate prefrontal cortex. Nat Neurosci 2: 1131–1136, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r64] Rose et al. 1967.Rose JE, Brugge JF, Anderson DJ, Hind JE. Phase-locked response to low-frequency tones in single auditory nerve fibers of the squirrel monkey. J Neurophysiol 30: 769–793, 1967. [DOI] [PubMed] [Google Scholar]

[r65] Rose et al. 1966.Rose JE, Gross NB, Geisler CD, Hind JE. Some neural mechanisms in the inferior colliculus of the cat which may be relevant to localization of a sound source. J Neurophysiol 29: 288–314, 1966. [DOI] [PubMed] [Google Scholar]

[r66] Schnupp et al. 2001.Schnupp JW, Mrsic-Flogel TD, King AJ. Linear processing of spatial cues in primary auditory cortex. Nature 414: 200–204, 2001. [DOI] [PubMed] [Google Scholar]

[r67] Scott 2004.Scott BH Physiological Organization of Auditory Cortex in Awake Macaque (PhD thesis). New York: New York Univ., 2004, p. 324.

[r68] Scott et al. 2007.Scott BH, Malone BJ, Semple MN. Effect of behavioral context on representation of a spatial cue in core auditory cortex of awake macaques. J Neurosci 27: 6489–6499, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r69] Shackleton et al. 1991.Shackleton TM, Bowsher JM, Meddis R. Lateralization of very-short-duration tone pulses of low and high frequencies. Q J Exp Psychol 43: 503–516, 1991. [DOI] [PubMed] [Google Scholar]

[r70] Shadlen et al. 1996.Shadlen MN, Britten KH, Newsome WT, Movshon JA. A computational analysis of the relationship between neuronal and behavioral responses to visual motion. J Neurosci 16: 1486–1510, 1996. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r71] Siveke et al. 2008.Siveke I, Ewert SD, Grothe B, Wiegrebe L. Psychophysical and physiological evidence for fast binaural processing. J Neurosci 28: 2043–2052, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r72] Skottun 1998.Skottun BC Sound localization and neurons (Letter). Nature 393: 531, 1998. [DOI] [PubMed] [Google Scholar]

[r73] Skottun et al. 2001.Skottun BC, Shackleton TM, Arnott RH, Palmer AR. The ability of inferior colliculus neurons to signal differences in interaural delay. Proc Natl Acad Sci USA 98: 14050–14054, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r74] Spezio et al. 2000.Spezio ML, Keller CH, Marrocco RT, Takahashi TT. Head-related transfer functions of the rhesus monkey. Hear Res 144: 73–88, 2000. [DOI] [PubMed] [Google Scholar]

[r75] Spitzer and Semple 1991.Spitzer MW, Semple MN. Interaural phase coding in auditory midbrain: influence of dynamic stimulus features. Science 254: 721–724, 1991. [DOI] [PubMed] [Google Scholar]

[r76] Spitzer and Semple 1993.Spitzer MW, Semple MN. Responses of inferior colliculus neurons to time-varying interaural phase disparity: effects of shifting the locus of virtual motion. J Neurophysiol 69: 1245–1263, 1993. [DOI] [PubMed] [Google Scholar]

[r77] Spitzer and Semple 1995.Spitzer MW, Semple MN. Neurons sensitive to interaural phase disparity in gerbil superior olive: diverse monaural and temporal response properties. J Neurophysiol 73: 1668–1690, 1995. [DOI] [PubMed] [Google Scholar]

[r78] Spitzer and Semple 1998.Spitzer MW, Semple MN. Transformation of binaural response properties in the ascending auditory pathway: influence of time-varying interaural phase disparity. J Neurophysiol 80: 3062–3076, 1998. [DOI] [PubMed] [Google Scholar]

[r79] Stecker et al. 2005.Stecker GC, Harrington IA, Middlebrooks JC. Location coding by opponent neural populations in the auditory cortex. PLoS Biol 3: e78, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r80] Tian et al. 2001.Tian B, Reser D, Durham A, Kustov A, Rauschecker JP. Functional specialization in rhesus monkey auditory cortex. Science 292: 290–293, 2001. [DOI] [PubMed] [Google Scholar]

[r81] Tolhurst et al. 1983.Tolhurst DJ, Movshon JA, Dean AF. The statistical reliability of signals in single neurons in cat and monkey visual cortex. Vision Res 23: 775–785, 1983. [DOI] [PubMed] [Google Scholar]

[r82] Wegener 1974.Wegener JG Interaural intensity and phase angle discrimination by rhesus monkeys. J Speech Hear Res 17: 638–655, 1974. [DOI] [PubMed] [Google Scholar]

[r83] Woods et al. 2006.Woods TM, Lopez SE, Long JH, Rahman JE, Recanzone GH. Effects of stimulus azimuth and intensity on the single-neuron activity in the auditory cortex of the alert macaque monkey. J Neurophysiol 96: 3323–3337, 2006. [DOI] [PubMed] [Google Scholar]

[r84] Yin and Chan 1990.Yin TC, Chan JC. Interaural time sensitivity in medial superior olive of cat. J Neurophysiol 64: 465–488, 1990. [DOI] [PubMed] [Google Scholar]

[r85] Yin and Kuwada 1983a.Yin TC, Kuwada S. Binaural interaction in low-frequency neurons in inferior colliculus of the cat. II. Effects of changing rate and direction of interaural phase. J Neurophysiol 50: 1000–1019, 1983a. [DOI] [PubMed] [Google Scholar]

[r86] Yin and Kuwada 1983b.Yin TC, Kuwada S. Binaural interaction in low-frequency neurons in inferior colliculus of the cat. III. Effects of changing frequency. J Neurophysiol 50: 1020–1042, 1983b. [DOI] [PubMed] [Google Scholar]

[r87] Yost 1974.Yost WA Discriminations of interaural phase differences. J Acoust Soc Am 55: 1299–1303, 1974. [DOI] [PubMed] [Google Scholar]

PERMALINK

Representation of Dynamic Interaural Phase Difference in Auditory Cortex of Awake Rhesus Macaques

Brian H Scott

Brian J Malone

Malcolm N Semple

Abstract

INTRODUCTION

METHODS

Subjects, recording procedure, and stimuli

Physiology and stimulus generation

Statistical analysis of synchrony

FIG. 1.

Quantification of IPD tuning width

Recording sites

RESULTS

TABLE 1.

FIG. 3.

FIG. 7.

FIG. 12.

FIG. 13.

FIG. 2.

Effects of binaural beat frequency

Effects of beat frequency on vector strength

FIG. 4.

Effects of beat frequency on mean phase

FIG. 5.

Effects of beat frequency on discharge rate

FIG. 6.

Effects of center frequency: characteristic delay and characteristic phase

FIG. 8.

FIG. 9.

Directional sensitivity and perceptual relevance

FIG. 10.

Effect of beat direction on discharge rate and synchrony

FIG. 11.

IPD tuning width and receptive field distribution

d′ analysis of IPD tuning functions

FIG. 14.

Neurometric analysis

FIG. 15.

DISCUSSION

Binaural beat frequency

Coding of sound azimuth

Neural sensitivity to auditory motion

Comparing neural and psychophysical discriminability

Organization of auditory cortex

GRANTS

Acknowledgments

REFERENCES

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases