Linearly Additive Shape and Color Signals in Monkey Inferotemporal Cortex

Abstract

How does the brain represent a red circle? One possibility is that there is a specialized and possibly time-consuming process whereby the attributes of shape and color, carried by separate populations of neurons in low-order visual cortex, are bound together into a unitary neural representation. Another possibility is that neurons in high-order visual cortex are selective, by virtue of their bottom-up input from low-order visual areas, for particular conjunctions of shape and color. A third possibility is that they simply sum shape and color signals linearly. We tested these ideas by measuring the responses of inferotemporal cortex neurons to sets of stimuli in which two attributes—shape and color—varied independently. We find that a few neurons exhibit conjunction selectivity but that in most neurons the influences of shape and color sum linearly. Contrary to the idea of conjunction coding, few neurons respond selectively to a particular combination of shape and color. Contrary to the idea that binding requires time, conjunction signals, when present, occur as early as feature signals. We argue that neither conjunction selectivity nor a specialized feature binding process is necessary for the effective representation of shape–color combinations.

INTRODUCTION

In visual search, it is easy to find a red circle among green circles or a green circle among green squares but it is difficult to find a green circle among intermingled red circles and green squares (Treisman and Gelade 1980). In the latter case, the target is distinguished from the collection of distracters only by its unique conjunction of color and shape. The fact that conjunction search is difficult has led to the view that the visual system does not form representations of feature conjunctions at the stage when attention is distributed across an array but rather does so through a specialized “binding” process only when attention is focused on a single object (Treisman 1996, 2006). The process of binding, it has been suggested, takes time. When a red grating oriented at 0° alternates with a green grating oriented at 90°, subjects require longer frame durations to reliably report a red grating at 0° than to report the color red or the orientation 0° (Bodelón et al. 2007).

The idea that there is a specialized binding process is by no means universally accepted. It has been questioned on the ground that there are efficient models of visual object recognition in which detection of feature conjunctions proceeds by the same parallel bottom-up processing stages as detection of isolated features (Mel 1997; Riesenhuber and Poggio 1999). It has also been questioned on the ground that conjunction-selective neurons in high-order visual cortex could signal the presence of conjunctions by a mechanism no more complicated than passing the summed input from afferents representing a preferred set of features through a nonlinear activation function (Ghose and Maunsell 1999; Shadlen and Movshon 1999). Apparent conjunction selectivity has been demonstrated in monkey inferotemporal cortex (IT) by experiments involving a method of “reduction” or “simplification,” whereby parts are successively removed from an effective image until a neuron ceases to respond to it (Tanaka 1996; Tanaka et al. 1991; Tsunoda et al. 2001). In such an experiment, a neuron might respond to a bar projecting from a disk while responding neither to the bar alone nor to the disk alone (Tanaka et al. 1991). It is commonly assumed that this indicates selectivity for the conjunction of bar and disk but it might alternatively indicate selectivity for a local feature created by putting the two together (the 90° angle at the joint). All experiments treating shapes as conjunctions of parts suffer to some degree from this interpretational problem (Brincat and Connor 2004, 2006; Tsunoda et al. 2001). In a handful of experiments in which the manipulated features were kept physically separate—on opposite ends of a baton—to preclude the creation of juxtapositional features, conjunction selectivity, although present in a few neurons, was not common (Baker et al. 2002; De Baene et al. 2007).

Stimuli incorporating shape and color in various combinations are well suited for testing the notion that IT neurons are conjunction selective because shape can be changed without affecting color and vice versa. However, relatively little is known about how IT neurons encode shape–color combinations. Only one study has systematically compared selectivity for shape and color (Komatsu and Ideura 1993). In this study, even though the test set was small, a majority of IT neurons was selective for shape and/or color. The two forms of selectivity were distributed independently, with the consequence that as many as a third of neurons were selective for both attributes. In a subset of such neurons tested for color selectivity in the context of more than one shape, the order of preference for colors was correlated across shapes. This might seem to imply that there is linear summation of shape and color signals but, in fact, it is compatible with the existence of nonlinear interactions favoring one combination. Another study compared responses to natural images rendered with veridical color, with false color and without color (Edwards et al. 2003). IT neurons discriminated best among images rendered with veridical color. This might be taken to imply that color modulates form selectivity—and thus that color and form interact nonlinearly in driving the neuronal response—but it could also arise if neurons differentiated better among images containing natural combinations of colors than among those containing unnatural combinations. No such chromatic advantage exists for arbitrarily colored shapes (Tompa et al. 2004). In studies based on the reductive method, the occasional IT neuron has been found to respond selectively to a particular combination of shape and color—in one example, to a green star but not to a green square or a red star (see Fig. 10 in Tanaka et al. 1991). However, because testing of shape–color conjunction selectivity was not carried out systematically, it is not clear how common such cases are.

Thus the representation of shape–color conjunctions, although occupying a canonical place in theoretical discussions of the binding problem, has not yet been thoroughly investigated in monkey IT. The aim of the present study was to redress this shortcoming by systematically measuring the responses of IT neurons to a simple stimulus set consisting of four items obtained by crossing two shapes (mortise and tenon) with two colors (red and green). Two questions were at the forefront. First, do color and shape interact nonlinearly in such a way that a neuron responds particularly well to one conjunction of the two? Second, in cases where this is so, does the nonlinear conjunction signal develop later than signals representing color alone and shape alone, as expected if conjunction coding depended on a specialized time-consuming process?

METHODS

Surgery and recording

Two adult rhesus macaque monkeys [laboratory designations Ca and Eg, here referred to as m1 (female, 4.1 kg) and m2 (male, 10.2 kg)] were used. All experimental procedures were approved by the Carnegie Mellon University Animal Care and Use Committee and were in compliance with the guidelines set forth in the United States Public Health Service Guide for the Care and Use of Laboratory Animals. At the outset of the training period, each monkey underwent sterile surgery under general anesthesia maintained with isoflurane inhalation. The top of the skull was exposed, bone screws were inserted around the perimeter of the exposed area, a continuous cap of rapidly hardening acrylic was laid down to cover the skull and embed the heads of the screws, a head-restraint bar was embedded in the cap, and scleral search coils were implanted on the eyes, with the leads directed subcutaneously to plugs on the acrylic cap. After initial training, a 2-cm-diameter disk of acrylic and skull overlying the right hemisphere was removed to allow for the positioning of a vertically oriented cylindrical recording chamber.

At the beginning of each day's session, a varnish-coated tungsten microelectrode with an initial impedance of several megohms at 1 kHz (FHC, Bowdoinham, ME) was advanced through the dura into the underlying cortex. The electrode was introduced through a transdural guide tube advanced to a depth such that its tip was about 10 mm above IT. The electrode could be advanced reproducibly along tracks forming a square grid with 1-mm spacing. The action potentials of a single neuron were isolated from the multineuronal trace by means of an on-line spike-sorting system using a template-matching algorithm (Signal Processing Systems, Prospect, Australia). The spike-sorting system, on detection of an action potential, generated a pulse whose time was stored with 1-ms resolution. Eye position was monitored by means of a scleral search coil system (Riverbend Instruments, Birmingham, AL) and the x and y coordinates of eye position were stored with 4-ms resolution. All aspects of the behavioral experiment, including stimulus presentation, eye position monitoring, and reward delivery, were under control of a Pentium PC running Cortex software (NIMH Cortex). Recording chambers in both monkeys were centered at Horsley–Clarke coordinates (18 anterior and 18 lateral). Physiological recordings were obtained primarily from the ventral convexity of area TE lateral to the anterior middle temporal sulcus and included anterior ventral and anterior dorsal subdivisions (TEav and TEad) (Saleem and Tanaka 1996). A minority of cells (11%) were recorded in the lower bank of the superior temporal sulcus.

Stimulus and task design

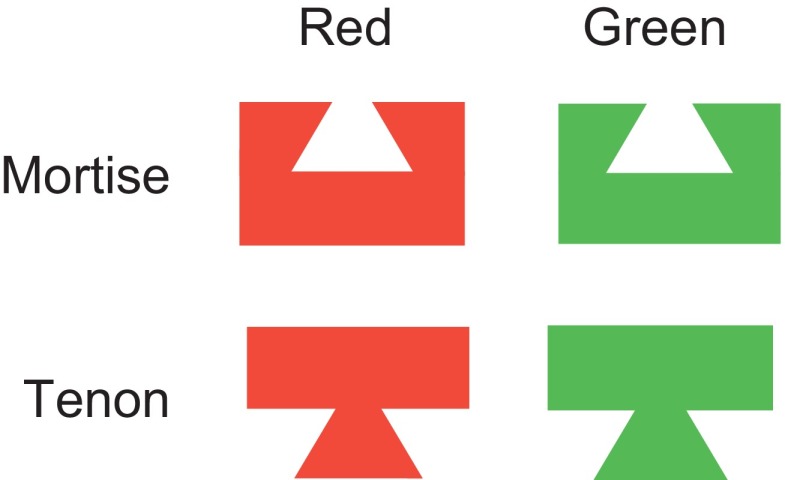
The visual stimuli—red and green mortises and tenons—were roughly equivalent in their content of local features but were markedly different at the level of global shape (Fig. 1). They were equiluminant (∼30 cd/m²) and had CIE x and y indices of approximately 0.571 and 0.386 (for red shapes) and 0.243 and 0.641 (for green shapes), as measured by a Tektronix J17 photometer and colorimeter. There were minor variations from session to session in the configuration of the mortise–tenon boundary contour (which could contain a variable number of either straight or curved line segments), but in all cases the two were strictly complementary in the sense that, if locked together, they would have formed a 2.9 × 2.9° square. On preliminary testing of each neuron, we identified a location or locations within 4° of fixation at which the stimuli appeared to elicit consistent visual responses. We then carried out systematic testing. On each trial, 200–300 ms after the monkey had attained fixation within 1.5° of a central white spot 0.1° in diameter, a single stimulus was presented for 400–700 ms. If it overlapped the fixation spot, then it occluded the fixation spot. The four stimuli were presented in pseudorandom sequence according to the rule that each had to be presented once in each block of four trials. The interval from the end of one trial to the beginning of the next was about 400 ms. Testing continued until each stimulus had been presented an average of 21 times (range: 6–46).

FIG. 1.

The 4 standard stimuli obtained by crossing 2 shapes with 2 colors.

Selection of neurons

We quantified the firing rate evoked by a visual stimulus by counting spikes within a time window of 80–400 ms following stimulus onset. To assess whether neurons were visually responsive, we conducted a paired t-test comparing the evoked visual response to the baseline firing rate obtained during fixation within a time window 200 ms in duration immediately prior to stimulus onset. Neurons were excluded from further analysis if they failed to display a significant positive visual response to any of the stimuli at a threshold of alpha = 0.05 after Bonferroni correction for multiple comparisons.

Peg–hole analysis

The peg–hole index—a measure of the degree to which any interaction effect favored (peg) or opposed (hole) conjunction selectivity—was computed as

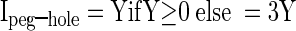where

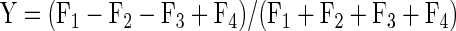and where F₁, F₂, F₃, and F₄ are the firing rates elicited by the four stimuli ranked in order of strength. This index has the property that values approaching +1 indicate peg selectivity (meaning that one stimulus evoked a high response and the other three stimuli evoked equal lesser responses; Fig. 4A) and values approaching −1 indicate hole selectivity (meaning that three stimuli evoked equally high responses and the one remaining stimulus evoked a low response; Fig. 4C).

The P value representing the level of significance of the combined presence of all three effects necessary for a peg or hole pattern was calculated as

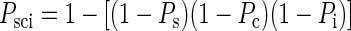where P_s, P_c, and P_i are the P values associated, respectively, with the main effect of shape, the main effect of color, and the interaction effect in the ANOVA.

Three-way model comparison

We conducted a three-way comparison of competing models of color and shape selectivity using Akaike's Information Criterion (AIC). This method, based on information theory, assigns a relative probability weight to each of the models under consideration rather than assigning a P value based on hypothesis testing (Motulsky and Christopoulos 2004). The AIC method has two key advantages over the more commonly used nested F-test. First, it can be applied to both nested and nonnested models. Second, it can be used to simultaneously compare more than two models. We used it to compare the following three models.

1. Full Nonlinear Model (4 DF).

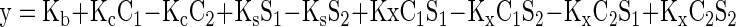where y is the firing rate; Kb is the free parameter for baseline activity; Kc is the free parameter for color main effect; Ks is the free parameter for shape main effect; Kx is the free parameter for color–shape interaction effect; C1 = 1 if the color is red, else 0; C2 = 1 if the color is green, else 0; S1 = 1 if the shape is mortise, else 0; S2 = 1 if the shape is tenon, else 0.

2. Reduced Linear Model (3 DF).

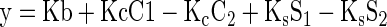where the variables are defined as in the preceding model.

3. Conjunction Model (2 DF).

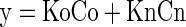where Ko is the free parameter for the response to best stimulus; Kn is the free parameter for the responses to the three non-optimal stimuli; Co = 1 if the single optimal stimulus is displayed, else 0; Cn = 1 if any of three nonoptimal stimuli is displayed, else 0.

To compare the three models, we first computed a corrected AIC value for each

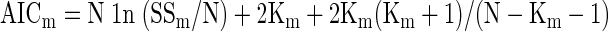where m is the index of the model (1, 2, or 3), N is the number of observations, SS_m is the sum of squared variance explained by the model, and K_m is the number of free parameters in the model. We then computed the difference between each AIC_m and the minimum of AIC₁, AIC₂, and AIC₃

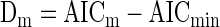Finally, we computed an Akaike weight for each model

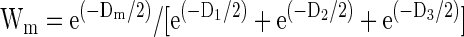Each Akaike weight represents the probability that the corresponding model best accounts for the data.

Latency of discriminative activity

To compute the latency of each neuron's discriminative signal (Fig. 6B), we assessed the magnitude of the signal within a temporal window ranging from 40 to 200 ms in duration and beginning 50 to 200 ms after stimulus onset, with each range covered in 10-ms steps. The discriminative signal was defined as (P − N)/(P + N), where P and N are the mean firing rates elicited, respectively, by the preferred and nonpreferred shapes (in shape-selective neurons), colors (in color-selective neurons), and diagonals of the shape–color matrix (in neurons with interaction effects). Having identified the window in which this index was maximal, we took as an estimate of discriminative signal latency the interval between stimulus onset and the window's early edge.

RESULTS

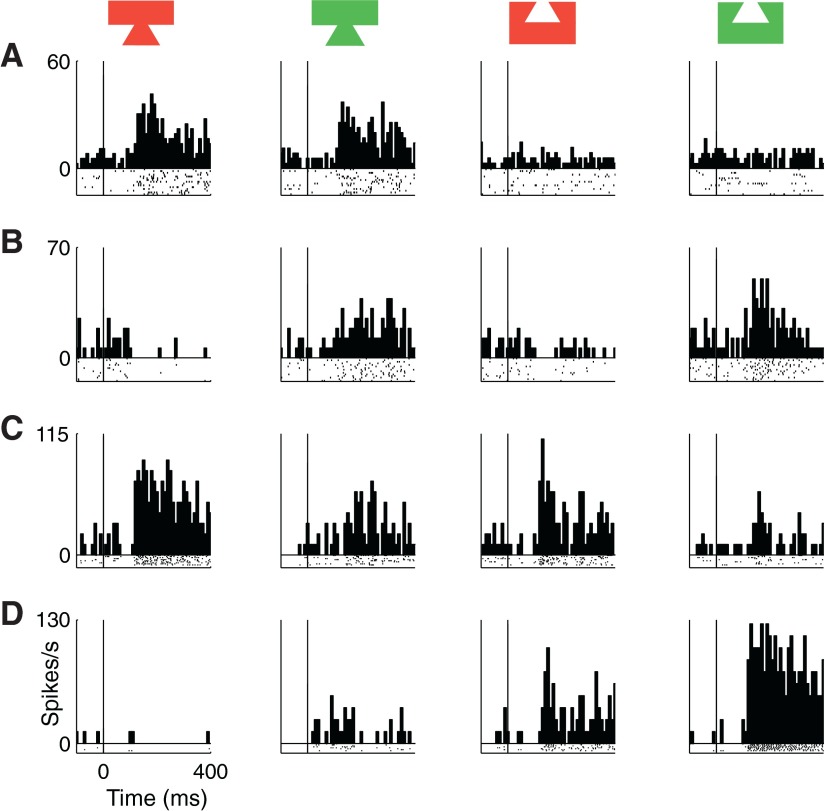
We collected data from 139 neurons in the anterior IT of the right hemisphere of two monkeys (m1 and m2) during presentation of the four-stimulus test set (Fig. 1). Twenty neurons were rejected on the basis of off-line analysis indicating that they were not visually responsive (t-test, alpha = 0.05, Bonferroni corrected to P ≥ 0.0125). This left 119 neurons (74 from m1 and 45 from m2) on which subsequent steps of data analysis were carried out. Among these neurons, the median strength of the visual response (the mean firing rate in a window 80–400 ms following onset of the best stimulus minus the prestimulus baseline firing rate) was 9.6 spikes/s (interquartile range = 5.9 to 15.0 spikes/s). On casual inspection of the data, it was apparent that neurons varied dramatically in their patterns of selectivity for the four stimuli. There were cases in which the strength of the visual response depended primarily on shape (Fig. 2A), primarily on color (Fig. 2B), on both shape and color in such a way that the two influences approximately summed (Fig. 2C), and on both shape and color in such a way that a single conjunction of the two was most effective (Fig. 2D).

FIG. 2.

Data from 4 inferotemporal cortex (IT) neurons embodying different patterns of shape and color selectivity (bin width = 10 ms for all histograms). A: shape-selective neuron favoring tenon over mortise (main effect of shape, P < 0.0001). B: color-selective neuron favoring green over red (main effect of color, P < 0.0001). C: neuron linearly independently selective for shape (tenon over mortise) and color (red over green) (main effects of shape and color, both P < 0.0001). D: neuron responding to a preferred shape–color conjunction (green mortise) far more strongly than expected from linear summation of shape and color signals (main effects of shape and color and an interaction effect, all 3: P < 0.0001).

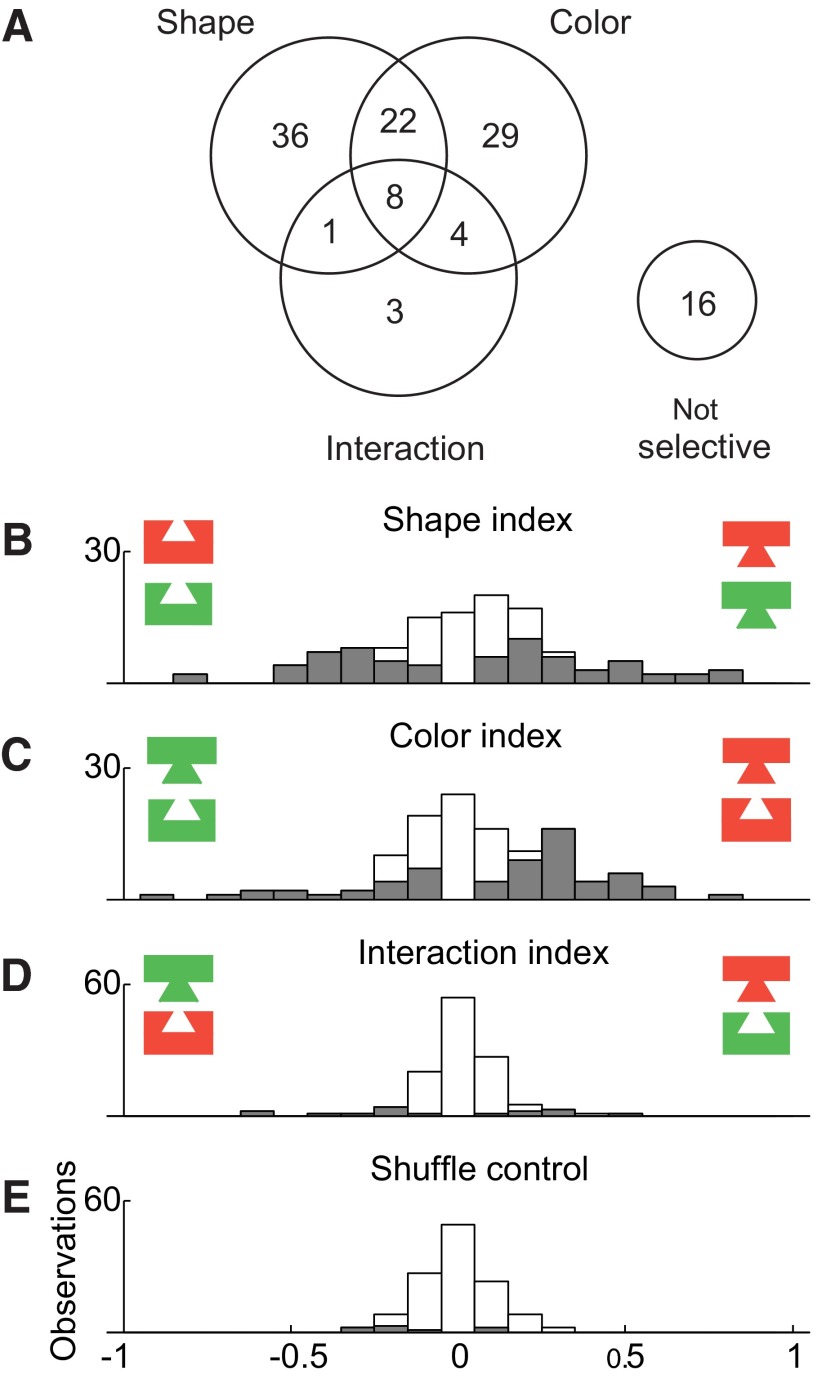
To assess the relative frequency of linear and nonlinear effects, we carried out an ANOVA on data from each neuron, with the spike count in a window 80 to 400 ms following stimulus onset as the dependent variable, with shape (mortise or tenon) and color (red or green) as factors and with P < 0.05 the criterion for significance. Counts of neurons exhibiting the various possible combinations of shape main effect, color main effect, and shape–color interaction effect are presented in Fig. 3A. Main effects of shape were common (67/119 = 56%) as were main effects of color (63/119 = 53%). The two traits were distributed independently in that the observed frequency with which neurons exhibited main effects of both shape and color (30/119 = 25%) was not significantly different from the multiple of the frequencies with which they exhibited a main effect of shape and a main effect of color (30%) (χ² test with Yates correction, P = 0.066). Shape–color interaction effects, although more frequent than expected by chance (χ² test with Yates correction, P = 0.0001), were rare (16/119 = 13%). The ANOVA on which these counts were based, because it involved a 2 × 2 design, was equally sensitive to main and interaction effects. Thus interaction effects (indicating that the influences of shape and color combined nonlinearly) were genuinely far less frequent than main effects.

FIG. 3.

A: counts of neurons (n = 119) exhibiting various combinations of significant effects (P < 0.05) in an ANOVA with shape (mortise or tenon) and color (red or green) as factors. B–D: distribution across neurons of shape, color, and interaction indices

where Tr is the firing rate elicited by the red tenon, Mg is the firing rate elicited by the green mortise, and so on. Cases in which the corresponding effect was significant in an ANOVA with shape and color as factors (P < 0.05) are indicated by shading. E: distribution across neurons of interaction indices computed after randomly shuffling the condition labels attached to each neuron's trials. This constitutes an estimate of the distribution expected by chance. Bin width = 0.1.

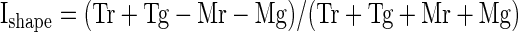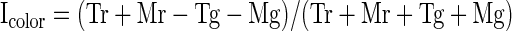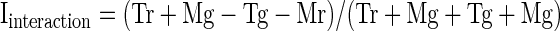As a complement to the analysis based on statistical categorization, we computed for each recorded neuron indices reflecting the strength of shape selectivity, color selectivity, and interaction selectivity (Fig. 3, B–D). Each index was computed as (A − B)/(A + B), where A and B are, respectively, the firing rates elicited by the tenon and mortise stimuli (for the shape index), red and green stimuli (for the color index), and stimuli along the diagonals of the shape–color matrix (for the interaction index). The mean of the absolute values of the indices was 0.24 for shape, 0.21 for color, and 0.090 for interaction, compared with 0.070 for a random control (indices computed after randomly shuffling the condition labels of each neuron's trials; Fig. 3E). The shape and color indices significantly exceeded the interaction indices in magnitude (paired t-test on absolute values, P < 0.0001). The interaction indices, on the other hand, did not significantly exceed the level expected by chance (paired t-test on absolute values of observed vs. shuffle-based interaction indices, P = 0.19). Thus interaction signals were much weaker than shape and color signals.

A recent study by Köteles et al. (2008) assessed the selectivity of neurons in IT for stimulus shape, texture, and shape × texture interactions. In that study, the authors assessed the magnitude of each effect in terms of the omega-squared metric (Keppel 1991), which is defined as the fraction of variance explained by a given effect (shape, texture, or interaction) divided by the total variance (shape + texture + interaction + error). Because their study used an experimental design similar to the design used here, we applied the same measure to our data set for the sake of comparison. The omega-squared values were as follows: ω_shape² = 0.1, ω_color² = 0.05, and ω_interaction² = 0.007. These values are roughly comparable to the results obtained by Köteles et al. (ω_shape² = 0.04, ω_texture² = 0.08, and ω_interaction² = 0.02).

Neuronal visual responses in IT are known to become weaker over multiple presentations of the same stimulus. This phenomenon, known as repetition suppression, results in a uniform down-scaling of visual response strength and therefore does not affect stimulus selectivity (McMahon and Olson 2007). Nevertheless, it is conceivable that repetition-induced decreases in visual response strength affected our results. To assess this possibility, we repeated the analyses after filtering out trials on which the stimulus was the same as that on the previous trial. All trends noted earlier persisted and remained significant.

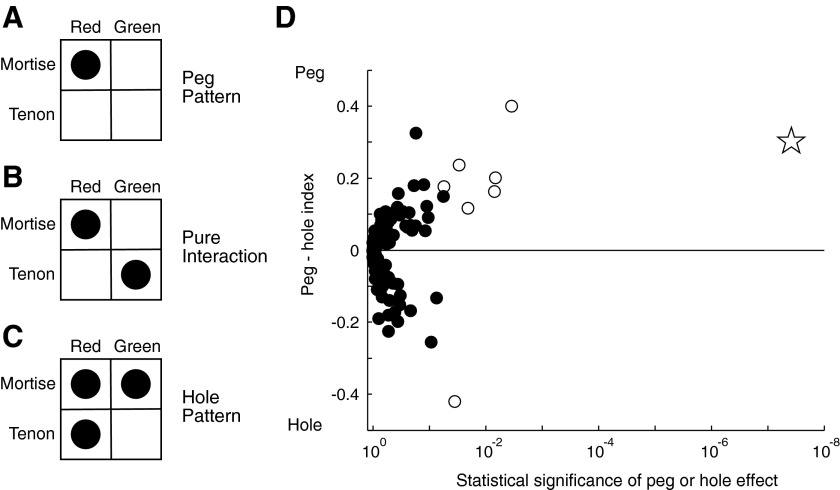
The occurrence of a few interaction effects does not in itself indicate that neurons were conjunction selective. An interaction effect arises from a difference in the counts along the two diagonals of the shape–color matrix (Fig. 4B : pure interaction pattern). For conjunction selectivity to be present, main effects of shape and color must accompany the interaction effect and must be matched to it in the sense that the stimulus favored by main effects occupies the diagonal favored by the interaction effect (Fig. 4A: peg pattern). If two main effects are present but are mismatched to the interaction effect, then the neuron responds especially weakly, not especially strongly, to one of the four stimuli (Fig. 4C: hole pattern). For every recorded neuron, we computed an index that varied in the range −1 to +1, with negative values representing effects that tended toward the hole pattern and positive values representing effects that tended toward the peg pattern. We then plotted the peg–hole index as a function of a P value representing the combined significance of the two main effects and the interaction effect (Fig. 4D). Among neurons with an especially low P value (therefore with an especially high probability that two main effects and an interaction effect were present), peg effects predominated. In particular, a peg effect was present in seven of eight neurons exhibiting two significant main effects and a significant interaction effect in the ANOVA (open symbols in Fig. 4D). The strongly conjunction selective neuron of Fig. 2D was a dramatic outlier (star in Fig. 4D). We conclude that nonlinear interactions between shape and color, although they occur in only a small fraction of IT neurons and generally are weak, are systematic in the sense that they tend to induce selectivity for a particular conjunction of shape and color.

FIG. 4.

Nonlinear interaction of shape and color signals could take a variety of forms ranging from (A) a peg pattern (an especially strong response to one of the 4 stimuli) through (B) a pure interaction pattern to (C) a hole pattern (an especially weak response to one of the 4 stimuli). In each diagram, the size of the disk in each cell of the shape–color matrix indicates the strength of the neuronal response to a stimulus incorporating the corresponding shape and color. D: the value of each neuron's peg–hole index (positive for peg effects and negative for hole effects in the range +1 to −1) is plotted against a P value representing the level of significance of the combined presence of the 3 effects. A point is shown for each of 119 recorded neurons. Open symbols represent neurons in which the ANOVA revealed significant main effects of both shape and color and a significant interaction effect. The star indicates the neuron shown in Fig. 2D.

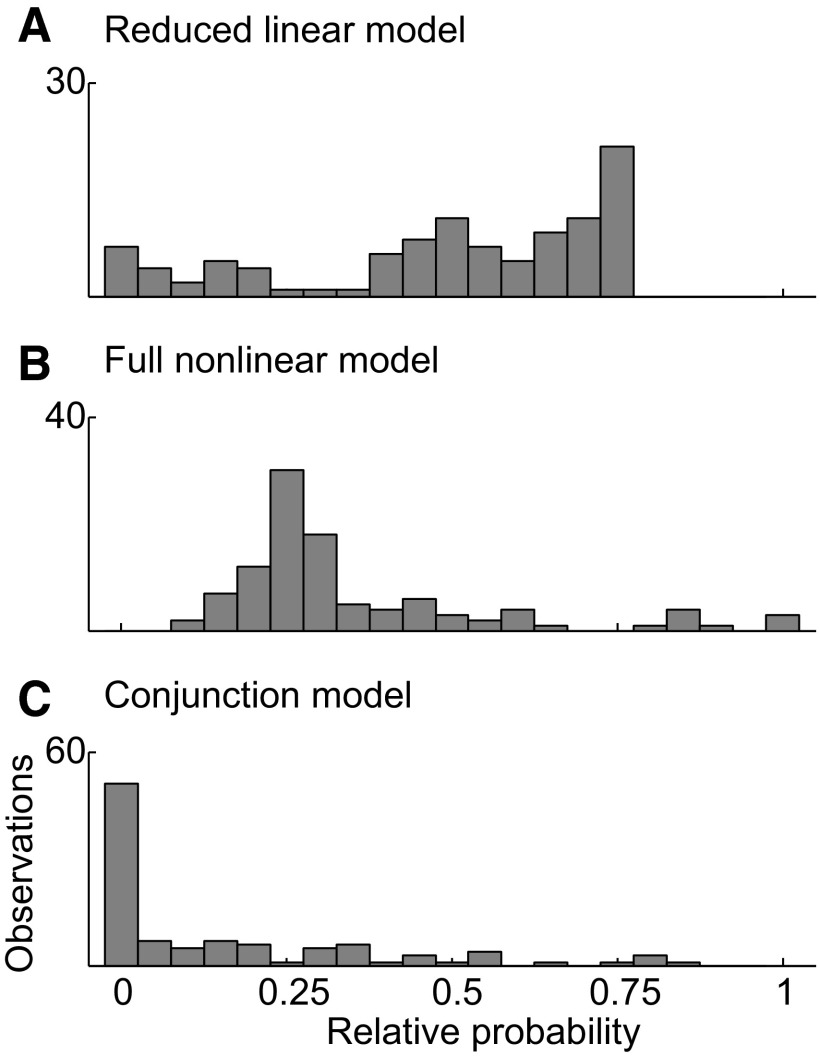
For a majority of neurons—those exhibiting a main effect of color and/or shape but not an interaction effect—we can conclude that no nonlinear model afforded a significantly better fit to the data than a linear model, although this outcome in itself does not provide a basis for ranking possible models by efficacy. To explore this issue, we carried out a comparison based on the Akaike information criterion. For any set of models, this approach provides an estimate of the relative probability that each model affords the best fit to the data (Motulsky and Christopoulos 2004). We included in the comparison set not only the full nonlinear and reduced linear models embodied in the ANOVA but also a simple conjunction model based on the assumption that one of four stimuli elicited a strong response and the three other stimuli elicited a uniform weak response. The distribution of relative probabilities for the linear model was much greater than that for the other two models (Fig. 5). Across 103 neurons exhibiting significant stimulus selectivity, the median probability weights (and interquartile ranges) were 0.54 (0.38–0.70) for the reduced linear model, 0.28 (0.23–0.42) for the full nonlinear model, and 0.031 (0.0001–0.27) for the conjunction model. There was no correlation between the neurons' mean visual responses and the Akaike weights for any of the models we tested (Pearson's correlation, P > 0.05 in all three cases). Thus the linear model was most likely to provide the best fit regardless of stimulus strength. In all, there were 71 neurons for which the reduced linear model gave the most likely fit, compared with 15 for the full nonlinear model and 17 for the multiplicative model.

FIG. 5.

Distribution across 103 significantly stimulus-selective neurons of the Akaike probability weights attaching to 3 models, each of which expresses firing rate as a function of shape and color.

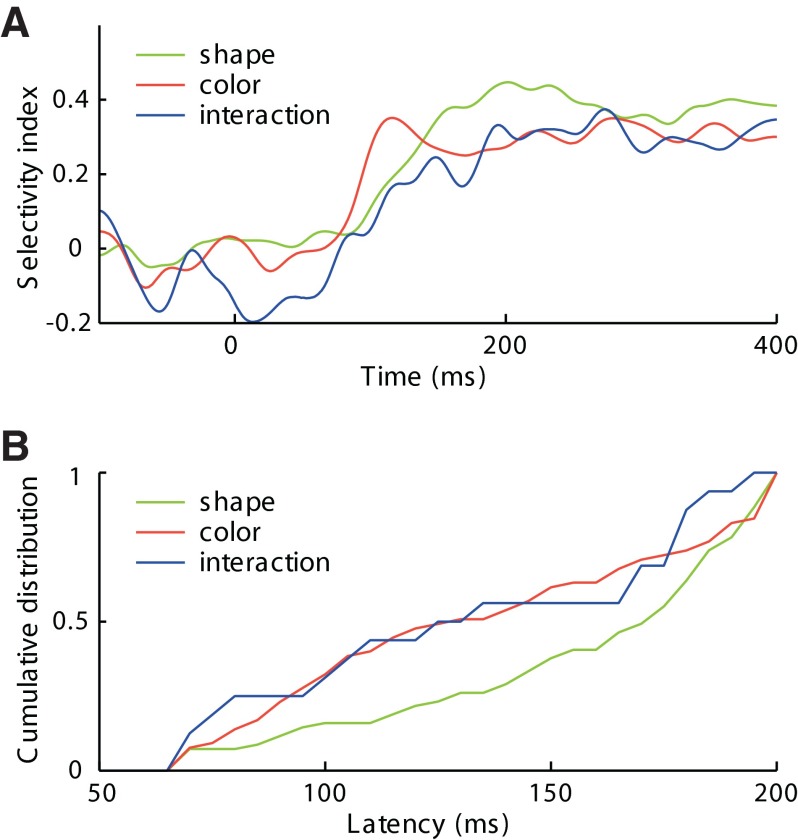
To determine whether interaction signals appeared later than shape and color signals, we constructed population plots representing the discriminative signals carried by three populations of neurons: those exhibiting a significant main effect of shape (n = 67), those exhibiting a significant main effect of color (n = 63), and those exhibiting a significant interaction effect (n = 16). We defined the discriminative signal as (P − N)/(P + N), where P and N are respectively the mean firing rates elicited by the preferred and nonpreferred shapes (in shape-selective neurons), colors (in color-selective neurons), and diagonals of the shape–color matrix (in neurons with interaction effects). We identified the preferred and nonpreferred conditions on the basis of neuronal activity late in the response period (200–400 ms after stimulus onset) to avoid circularity in the analysis of timing during the early phase of the response. The plots make clear that the three signals appeared at roughly the same time following stimulus onset (Fig. 6A).

FIG. 6.

Timing of shape, color, and interaction signals. A: time course following stimulus onset of population activity discriminating between 2 shapes (among 67 significantly shape-selective neurons), between 2 colors (among 63 color-selective neurons), and between 2 diagonals of the shape–color matrix (among 16 neurons with a significant shape–color interaction effect). The signal was computed as the instantaneous mean across the population of (P − N)/(P + N), where P and N are firing rates associated with the preferred and non-preferred conditions, respectively. Each curve was smoothed by convolution with a 10 ms Gaussian kernel. B: cumulative plots represent the distribution of latencies of the shape signal (for all 67 shape-selective neurons), of the color signal (for all 63 color-selective neurons), and of the interaction signal (for all 16 neurons with significant interaction effects).

To analyze whether the slight apparent differences in timing were significant, we calculated, for each neuron belonging to each class, the latency of its discriminative signal. We calculated latency by identifying the time window within which the discriminative signal was maximal and taking its leading edge as the time of onset of the response. The resulting cumulative distributions of latencies make clear that the color and interaction signals developed earlier than the shape signal (Fig. 6B). The mean of the latencies was 154 ms for the shape signal, 133 ms for the color signal, and 138 ms for the interaction signal. Only the difference between shape and color achieved significance (Kolmogorov–Smirnov [K-S] test, P = 0.008). The shape–color latency difference (also observed by Edwards et al. 2003) was present (154 ms for shape and 117 ms for color) and remained significant (P = 0.0046), even with consideration restricted to 30 neurons exhibiting main effects of both shape and color. Thus it reflected a difference between the signals as distinct from a difference between the neurons carrying them. Measurements of latency based on identifying the time window in which the discriminative signal was maximal might have been sensitive to the size of the window. This was not significantly different for shape, color, and interaction signals. Nevertheless, to be sure that window size played no role in the outcome, we repeated the analysis using a window of fixed 50-ms duration. The results were the same. We conclude that nonlinear interactions between shape and color occur early in the visual response. They are not delayed relative to signals reflecting shape alone and color alone.

The results described thus far are based on the analysis of data combined across two monkeys. We followed up on this analysis by considering whether trends evident in the combined data were present in the monkeys considered individually; in all key respects they were. 1) Shape and color main effects were distributed independently across neurons in both monkeys (χ² test, P = 0.54 in m1 and P = 0.90 in m2). 2) Interaction effects occurred at a frequency greater than expected by chance in both monkeys and the effect was significant in one of them (χ² test, P < 0.0001 in m1 and P = 0.39 in m2). 3) Shape indices were significantly greater in magnitude than interaction indices in both monkeys (paired t-test, P < 0.0001 in m1 and P < 0.0001 in m2). 4) Color indices were greater in magnitude than interaction indices in both monkeys and the effect achieved significance in one (paired t-test, P < 0.0001 in m1 and P = 0.25 in m2). 5) In neither monkey were the observed interaction indices significantly greater than control indices obtained after shuffling the data (paired t-test, P = 0.25 in m1 and P = 0.40 in m2). 6) Peg effects exceeded hole effects among neurons with two significant main effects and a significant interaction effect in both monkeys (4 pegs vs. 1 hole in m1 and 3 pegs vs. 0 hole in m2). 7) A linear model gave the best fit to firing rates in a majority of neurons (75% in m1 and 59% in m2) as indicated by AIC analysis. 8) The mean latency of color signals was significantly shorter than the mean latency of shape signals in both monkeys (Kolmogorov–Smirnov test, P = 0.009 in m1 and P = 0.016 in m2). 9) The mean latencies of the color and interaction signals were not significantly different in either monkey (Kolmogorov–Smirnov test, P > 0.05). The tendency for interaction signals to emerge at shorter latency than shape signals attained significance in m2 (Kolmogorov–Smirnov test, P = 0.012) but not in m1 (P > 0.05).

DISCUSSION

On analyzing neuronal responses to a small set of stimuli in which shape and color varied orthogonally, we found that the two signals sum linearly for the most part. We found no evidence of a specialized mechanism for representing conjunctions either in the form of widespread conjunction selectivity or in the form of a time-consuming binding process. It seems reasonable to expect that the principle of linear summation will apply to more complex stimulus sets created by fine gradation along multiple feature dimensions, although confirming this expectation will require further experiments. We consider the implications of these findings in the following text.

The influences of independent features combine linearly in most neurons.

We have shown that the influences of shape and color commonly sum linearly in IT. Previous studies of neuronal selectivity for shape and color in IT (Edwards et al. 2003; Komatsu and Ideura 1993; Tompa et al. 2005) did not address this issue. However, a recent study of shape and texture did address it and arrived at a conclusion parallel to ours: selectivity for shape and texture features predominantly takes the form of main effects rather than interaction effects (Köteles et al. 2008). Our findings appear to be discordant with reports indicating that part–part interactions within a shape frequently are nonlinear (Brincat and Connor 2004, 2006). However, the approach used in the shape studies was to manipulate parts that were adjacent to and merged smoothly into one another. Nonlinear interactions could have arisen if neighboring parts combined to produce at their borders juxtapositional features to which IT neurons were sensitive. To take a simple example: a neuron selective for a V presented over some range of orientations might exhibit not only main effects for right-arm and left-arm orientations but also an interaction effect arising from sensitivity to the angle at the vertex. This interpretation fits with the fact that nonlinear interactions are rare when the manipulated parts, isolated at the ends of a baton, are discrete and relatively distant from each other (Baker et al. 2002; De Baene et al. 2006).

Nonlinear interactions, when present, favor conjunction selectivity.

The impact of the majority of nonlinear interactions in the present study was to move the response profile of the neuron toward conjunction selectivity. The fact that nonlinear interactions, although rare and weak, assume a consistent pattern when present suggests that they are functionally significant. Their effect is to add a degree of sparseness to the otherwise highly distributed neuronal representation of visual images. The argument for functional significance is strengthened by the fact that discrimination training induces a small but significant increase (from 9 to 18%) in the frequency of conjunctive interaction effects (Baker et al. 2002).

Conjunction signals appear early in the visual response.

Interaction signals, although infrequent and weak, appear no later than shape and color signals following onset of the stimulus. This indicates that forming a neuronal representation of a conjunction of shape and color does not require extra time as would be expected if it depended on a specialized binding process (Bodelón et al. 2007; Treisman 1996, 2006). The only other study to measure the latency of conjunction signals in IT focused on how the influences of parts in a shape combine (Brincat and Connor 2006). In that study, nonlinear signals representing combinations of parts appeared at longer latency and grew more slowly than linear signals representing individual parts. The significance of the discrepancy is not clear. It could reflect a genuine difference between shape–color interactions and part–part interactions or could be related to the fact that the recording sites were different: in posterior TE/TEO in the former study as distinct from anterior TE in this study.

There is no need for conjunction selectivity or a specialized binding process.

A shape–color conjunction might in principle be represented by conjunction-selective neurons (Ghose and Maunsell 1999; Shadlen and Movshon 1999) or by synchronous spiking of shape-selective and color-selective visual cortical neurons (Gray 1999; Singer 1999; von der Marlsburg 1999) in some area of visual cortex. However, the detection of a conjunction does not require either mechanism. Among a population of neurons in all of which shape and color influences sum linearly, a red mortise will elicit the strongest activity in neurons with a main effect of shape favoring mortise and a main effect of color favoring red. It would be a simple matter for a dynamic post-visual winner-take-all decision process acting on the output of IT to categorize the stimulus as a red tenon.

Population activity in IT can explain the inefficiency of conjunction search.

The time required to find a conjunction target (let us say a red mortise among intermingled green mortises and red tenons) commonly increases linearly with the number of items in the display as if subjects found the target through serial item-by-item attentional scanning. This observation led to the notion, central to feature integration theory (Treisman and Gelade 1980), that the visual system does not explicitly represent a collection of features as a conjunction until attention has been focused on the object that contains them. However, it can be explained without recourse to such an idea. Conjunction search may be slower than feature search simply because 1) the target is more similar to the distracters and 2) the distracters are more different from each other than in feature search (Duncan and Humphreys 1989, 1992). This view is supported by the fact that the time required even for a simple form of feature search—finding an oddball of one color among distracters of a similar color—increases with the number of items in the display, with the time per item becoming greater as the colors become more similar (Nagy and Cone 1996; Nagy and Sanchez 1990).

The similarity-based model of Duncan and Humphreys (1989, 1992) allows an explicit formulation in terms of neuronal activity in IT: search will proceed relatively quickly if 1) the target and distracters elicit relatively dissimilar patterns of population activity and 2) the distracters elicit relatively similar patterns of population activity. The idea that representations in high-order visual cortex guide visual search is not new (Hochstein and Ahissar 2002). Moreover, it fits with the observation that neurons in extrastriate visual cortex are active during visual search, firing with increasing strength as attention constricts around a target that is a preferred stimulus (Bichot et al. 2005; Chelazzi et al. 1993; Sheinberg and Logothetis 2001).

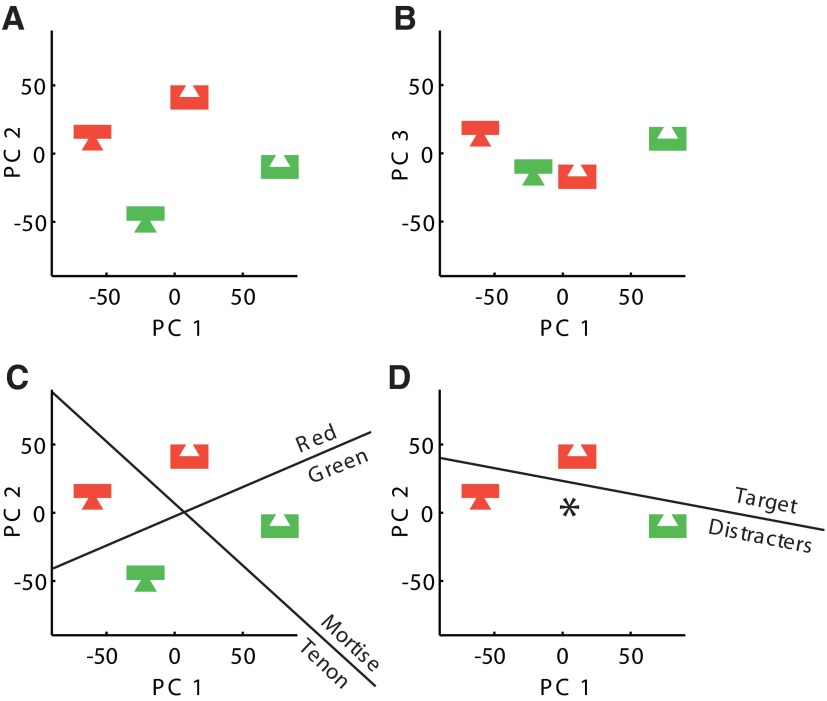
To explore this idea, we represented the four stimuli used in the present study as points in a neuronal activation space with 119 dimensions corresponding to the 119 recorded neurons. The arrangement of the points in the plane containing the first and second principal components (which together account for 95% of the variance) is shown in Fig. 7A. Their arrangement in the plane containing the first and third principal components (the latter of which accounts for the residual 5% of variance) is shown in Fig. 7B. We took as a measure of similarity between two stimuli the inverse of the Euclidean distance between the corresponding points. For eight possible cases of feature search (e.g., red mortise as target among distracters consisting of green mortises and green tenons; Fig. 7C) the mean distance between the target and the centroid of the distracters was 95 spikes/s and the mean distance between the distracters was 90 spikes/s. For four possible cases of conjunction search (e.g., red mortise as target among distracters consisting of green mortises and red tenons; Fig. 7D) the mean distance between the target and the centroid of the distracters was 66 spikes/s and the mean distance between the distracters was 118 spikes/s. The fact that target–distracter similarity was less and distracter–distracter similarity was greater in the case of feature search, when interpreted in the framework of Duncan and Humphreys (1989, 1992), leads to the valid prediction that feature search should be faster than conjunction search.

FIG. 7.

A: points representing the 4 stimuli are here projected from neuronal activation space onto a plane containing the first and second principal components of the distribution. The principal component analysis was performed on a 4 × 119 matrix of mean visual responses (responses of 119 neurons to the 4 stimuli). B: the same points projected onto a plane containing the first and third principal components. C: for a stimulus set allowing feature search (one example shown here) the distance of a target from the centroid of the distracters was relatively large and the distance between the distracters was relatively small. D: for a stimulus set requiring conjunction search (one example shown here) the distance of a target from the centroid of the distracters was relatively small and the distance between the distracters was relatively large.

It might be argued that neuronal responses elicited by presenting one stimulus at a time, as in the present study, are not relevant to understanding neuronal activity elicited by presentation of a search array. However, it is generally believed that responses to an array are directly predictable from responses to individual items according to two principles embodied in the biased competition model (Desimone and Duncan 1995). First, the response to a multi-item array during diffuse attention is, all other things being equal, the average of the responses to the individual items (Reynolds et al. 1999; Rolls and Tovee 1995; Zoccolan et al. 2005). Second, directing attention to a given item increases its relative weight at the stage of averaging (Chelazzi et al. 1993; Reynolds et al. 2000). Neither principle involves any change in the pattern of stimulus selectivity of the neuron. Thus stimuli eliciting similar or different patterns of population activity on individual presentation should do likewise when embedded in an array.

GRANTS

This research was supported by National Institutes of Health Grants EY-018620 to C. R. Olson and F31 NS-043876 to D.B.T. McMahon and the Pennsylvania Department of Health through the Commonwealth Universal Research Enhancement Program. The collection of magnetic resonance images was supported by National Center for Research Resources Grant P41RR-03631.