Partial molecular volumes of lipids and cholesterol

Abstract

Volumetric measurements are reported for fully hydrated lipid/cholesterol bilayer mixtures using the neutral flotation method. Apparent specific volume data were obtained with the lipids DOPC, POPC and DMPC at T = 30 °C, DPPC at 50 °C, and brain sphingomyelin (BSM) at 45 and 24 °C for mole fractions of cholesterol x from 0 to 0.5. Unlike previous cholesterol mixture studies, we converted our raw data to partial molecular volume V_L of the lipid and V_C of the cholesterol. The partial molecular volumes were constant for POPC and DOPC as x was varied, but had sharp breaks for the other lipids at values of x_C near 0.25 ± 0.05. Results for x < x_C clearly exhibit the condensation effect of cholesterol on DPPC, DMPC and BSM when measured at temperatures above their main transition temperatures T_M. The break points at x_C are compared to phase diagrams in the literature. For x > x_C the values of the partial molecular volumes of cholesterol clustered near 630 ± 10 ų in all the lipids when measured for T > T_M; we suggest that this is the most appropriate measure of the bare volume of cholesterol in lipid bilayers.

1. Introduction

The volume V_L per lipid for lipid bilayers immersed in water is perhaps the most accurate physical datum pertaining to bilayer structure. Results are routinely accurate to the 0.1% level with very good agreement obtained by different researchers and with different measurement methods (Nagle and Tristram-Nagle, 2000; Koenig and Gawrisch, 2005). This is a very important datum that supplements neutron (Kucerka et al., 2004) and X-ray structural data (Kucerka et al., 2006). V_L is also easily obtained from molecular dynamics (MD) simulations and the comparison with measurement provides an important test of the potentials used in the simulations (Armen et al., 1998).

Volume measurements in our lab use the neutral flotation method (Nagle and Wilkinson, 1978; Wiener et al., 1998). Recently Koenig and Gawrisch (2005) have employed this method to study a variety of unsaturated lipids and they have proposed a formula to predict the volume of phosphatidylcholines as a function of the chain composition and the temperature. The measurements we report in this paper, as well as our earlier measurement, provide additional tests that demonstrate the accuracy of the proposed formula. One may generally conclude that measurements of volumes for lipid bilayers consisting of just one lipid are now firmly established.

The major thrust of this paper is the volumetric study of lipid bilayers containing mixtures of cholesterol and lipids. We were motivated to do this by a recent paper that interpreted MD simulations of cholesterol in DPPC bilayers (Edholm and Nagle, 2005). Although that paper focused on the molecular areas A, it also obtained simulated volumes. To compare to that paper, in this paper it was only necessary to measure at one temperature in the fluid phase. However, when the lipid is DMPC or DPPC, our results suggest some kind of phase transition as a function of cholesterol mole fraction x. Although our results are restricted to one temperature, this provides an additional datum to the still controversial phase diagrams of cholesterol/lipid mixtures (McMullen and McElhaney, 1995).

In mixtures, the only well defined and unique measure of the volumes of the individual molecular components necessarily involves the classical physical chemical concept of partial molar volumes, which, equivalently, are partial molecular volumes when divided by Avogadro’s number. (In contrast, for a fully hydrated single component lipid, even though water is another component, the partial molecular volume of the lipid is trivially constant when water is in excess, as it is for our measurements. We will not classify water as a separate component in this paper.) Partial molecular volumes do not correspond to dividing space into local volumes surrounding the molecules. It is well known that partial molecular volumes of ions in water can even be negative due to electrostriction of the solvent. And the recent results for partial molecular areas are strongly negative for cholesterol at low concentration and therefore do not represent the local area occupied by each molecule (Edholm and Nagle, 2005). Even given a complete set of coordinates in an MD simulation, there is an arbitrary choice of how to partition either area or the volume to the different molecules, which makes any such definition non-unique. In contrast, canonical partial molecular volumes are uniquely measurable and thermodynamically precisely defined.

An extensive set of volumetric data for mixtures of cholesterol and DPPC was presented by Melchior et al. (1980) as a function of cholesterol concentration and over a wide temperature range that included the gel phase. These data clearly showed the main chain melting phase transition as well as a region of likely phase coexistence for temperatures below the main transition. However, only ‘apparent partial specific volumes’ were reported. No attempt was made to obtain the true partial molecular volume of cholesterol in the fluid L_α phase, and the data were too noisy to address the phase diagram at temperatures where fluid–fluid phase coexistence might occur. The data in the present study permits us to address this issue. A very recent study of cholesterol and POPC (Heerklotz and Tsamaloukas, in press) uses pressure perturbation calorimetry that obtains the coefficient of thermal expansion that is complementary to our volume data. Our study also obtains results for mixtures of cholesterol with several other lipids and this yields a common value for the volume of cholesterol in lipid bilayers above the chain melting temperature.

2. Experimental

2.1. Materials

1,2-Dipalmitoyl-sn-glycero-3-phosphocholine (DP-PC, Lot 160PC-267), 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC, Lot 140PC-222), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC, Lot 181PC-53), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC, Lot 160-181PC-154), brain sphingomyelin (BSM, Lot BSM-92), and cholesterol (Lot CH-55) were purchased from Avanti Polar Lipids (Alabaster, AL) in the lyophilized form and used without further purification. Thin layer chromatography (TLC) using chloroform:methanol:7N NH₄OH (46:18:3, v/v) revealed <0.1% lysolipid when stained with molybdic acid stain. D₂O/H₂O mixtures were made with Barnstead nanopure water and deuterium oxide (99.9 atom% D) (Aldrich, Milwaukee, WI). HPLC grade chloroform was purchased from Aldrich.

2.2. Preparation of cholesterol mixtures

For a given mole fraction x, on the order of 1 mg of dry cholesterol was weighed using an analytical balance (Mettler, model AE163, Hightstown, NJ), and then the appropriate weight of dry lipid was added. The dry mixture was dissolved in chloroform and divided into four 3 ml nalgene vials. The chloroform was then evaporated under nitrogen, and the vials were left in a fume hood for about ten hours to assure chloroform removal. Estimated errors in x due to weighing are ~0.01. It was also likely that a small amount of water remained firmly bound to the nominally dry lipid; one water per lipid and none per cholesterol would increase the reported mole fractions x by only a factor of 1.03.

2.3. Preparation of D₂O/H₂O mixtures

The mass fraction of D₂O in the solvent is defined as φ= m_D2O/(m_D2O + m_H2O), where m_D2O is the mass of the D₂O and m_H2O is the mass of the H2O. The inverse density of the solvent (in ml/g) is then υ_sol =φυ_D2O + (1 − φ)υ _H2O where υ_D2O and υ_H2O are the inverse densities obtained from tables (CRC Handbook of Chemistry and Physics, 52nd ed., pp. F-4, F-5). For each lipid/cholesterol mixture, four solvent mixtures were made by weighing D₂O and H₂O directly into the four nalgene vials containing the sample. Each solvent mixture had a value of υ_sol that was Δυ_sol ml/g larger than the previous one, and such that these four υ_sol spanned the expected volume υ_sample of the sample at the specified temperature. Weighing errors in the value of υ_sol were of the order of ±0.00005 ml/g. After sealing the vials, the lipid was hydrated by cycling three times between 50 and −20 °C and vortexing at each temperature.

2.4. Determination of lipid volumes

Multilamellar vesicles sink when suspended in a solution with a lower density than the lipid and float if the solution has a higher density, and this process is facilitated by centrifugation. The four vials were placed in centrifuge tubes and, together with two water filled tubes, were spun at 1000 rpm in a desktop centrifuge. For coarse determinations when Δυ_sol of the solvent between vials was large, determination of sinking or floating took approximately 5 min. For the final fine determination, Δυ_sol was set to 0.001 ml/g and the samples were spun for approximately 30 min. A successful determination of sample volume was obtained when the MLVs floated in vial A and sank in vial B and the difference in solvent volumes was υ_B − υ_A = 0.001 ml/g, thereby determining υ_sample to within ±0.0005 ml/g.

The centrifuge was situated in a home-built chamber and the temperature was maintained by a YSI model 72 proportional temperature controller (Yellow Springs, OH). The temperature of the two water filled tubes was read immediately after spinning using a Barnant platinum resistance thermometer (Barrington, IL) which had been calibrated by comparing to a NIST-calibrated thermometer (Taylor Inst. Co., Rochester, NY). Data were only recorded when the readout temperature was well within ±0.5 °C of the target temperature.

2.5. Data analysis

Data analysis was performed with Origin 6.0 software (OriginLab, Northampton, MA).

3. Results

3.1. Apparent specific volumes

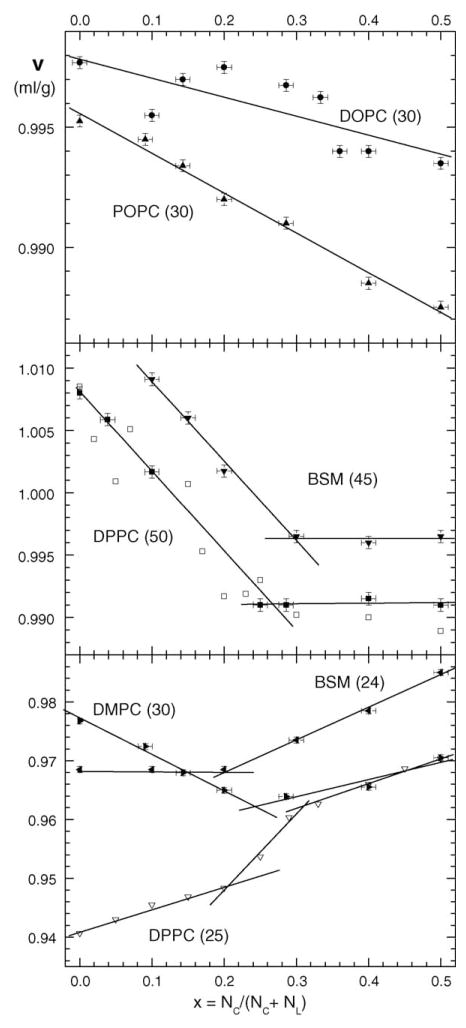
Fig. 1 shows the raw data for the apparent specific volumes υ of mixtures of cholesterol with several different lipids as a function of cholesterol mole fraction x. For most of the samples, the pure lipid bilayers were in the fluid Lα phase, T > T_M, where the chain melting temperature T_M is 41.4 °C for DPPC (Nagle and Wilkinson, 1978), 24.0 °C for DMPC (Nagle and Wilkinson, 1978), 39°C for BSM (McIntosh et al., 1992), −5 °C for POPC (Perly et al., 1985) and −15.5 °C for DOPC (Webb et al., 1993). Employing the convention that the temperature will be placed in parentheses after the acronym for the lipid, these samples were DOPC(30), POPC(30), DPPC(50), DMPC(30) and BSM(45). The two exceptions were gel phase DPPC(25) and BSM(24). The top panel suggests that υ can be represented by a single linear function of x for both DOPC(30) and POPC(30). In striking contrast, the middle panel shows that υ undergoes considerable changes in slope for DPPC(50) and BSM(45). The data for DPPC(50) includes our data (solid symbols) and also data (open symbols) taken from Fig. 3 of Melchior et al. (1980). The latter data are clearly noisier than our data, but the numerical values are in good agreement and they exhibit the same trend with x. There is no data point for BSM(45) at x = 0 because the pure lipid floats even in pure H₂O. The data for DPPC(50) and BSM(45) can each be reasonably represented by two straight lines, as can the data for DMPC(30) and BSM(24) shown in the bottom panel. In yet additional contrast, the gel phase data for DPPC(25) in the bottom panel that were taken from Fig. 3 of Melchior et al. (1980) clearly exhibit three regions that are even more obvious from their Fig. 3. It may be noted that their data were less noisy in the gel phase, perhaps because the high temperature υ were obtained by adding the volume change measured with a differential dilatometer to the υ obtained at lower temperature by the neutral flotation method, so we did not repeat their gel phase measurements. While these raw data for the apparent specific volumes of mixtures are suggestive, Fig. 1 does not lend itself readily to quantitative analysis.

Fig. 1.

Apparent specific volumes υ (ml/g) vs. cholesterol mole fraction x for five lipids at the temperatures indicated in parentheses in °C beside the names of the lipids. Our data are shown as solid symbols; the ±0.01 uncertainties shown for x are from weighing errors and the ±0.0005 ml/g uncertainties for υ are due to the resolution in the neutral buoyancy refinement. DPPC data from Fig. 3 of Melchior et al. (1980) are shown as open symbols.

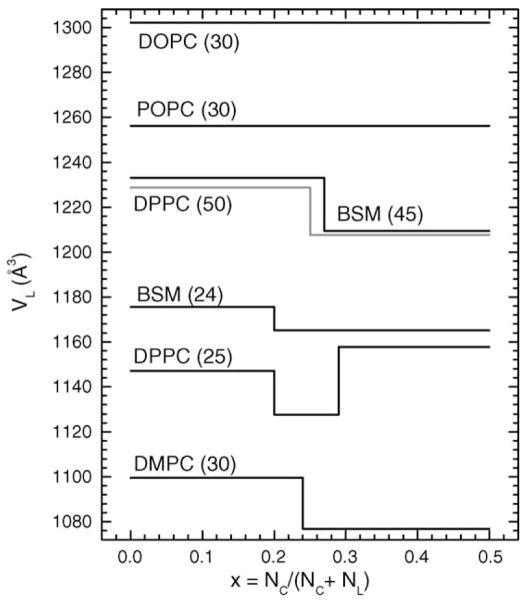
Fig. 3.

Partial molecular volumes V_L in ų of lipids as a function of cholesterol mole fraction x obtained from the x = 0 intercept of the linear fits in Fig. 2. Temperatures (°C) are shown in parentheses.

3.2. Partial molecular volumes

To proceed further, we calculate the true partial molecular, i.e. molecular, volumes of cholesterol and the lipid. One way to do this first converts the apparent specific volumes υ to volume per molecule V, where NV is the total volume of the MLV sample and N = N_C + N_L is the sum of N_C cholesterol molecules and N_L lipid molecules. The conversion employs the definition:

$$\upsilon =(\text{NV})N_{\text{A}}/(N_{\text{C}}{M}_{\text{C}}+N_{\text{L}}{M}_{\text{L}}),$$ (1)

where N_A is Avogadro’s number, M_C the molecular weight of cholesterol, and M_L is the molecular weight of the lipid. Dividing by N and rearranging gives

$$V(x)=[x{M}_{\text{C}}+(1-x)M_{\text{L}}]\upsilon (x)/N_{\text{A}}.$$ (2)

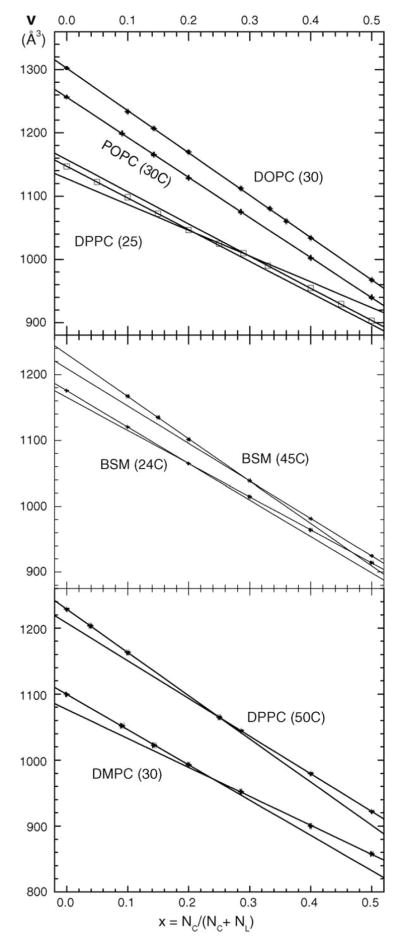
Fig. 2 shows V(x) obtained from the υ(x) data in Fig. 1.

Fig. 2.

Volume per molecule V in ų vs. mole fraction of cholesterol x derived from the measured υ(x) shown in Fig. 1.

The partial molecular volumes are defined for cholesterol V_C as

$$\begin{array}{l}{V}_{\text{C}}(x)={(\partial (\text{NV})/\partial N_{\text{C}})}_{\text{NL}}\text{and}\\ V_{\text{L}}(x)={(\partial \text{NV}/\partial N_{\text{L}})}_{\text{NC}}\end{array}$$ (3)

for lipid V_L. Then, as is well known from physical chemistry textbooks:

$$V(x)=x{V}_{\text{C}}(x)+(1-x)V_{\text{L}}(x).$$ (4)

Denoting derivatives with respect to x by primes, it may be shown that

$$\begin{array}{l}{V}_{\text{C}}(x)=V(x)+(1-x)V^{\prime }(x)\text{and}\\ V_{\text{L}}(x)=V(x)-x{V}^{\prime }(x).\end{array}$$ (5)

Therefore, the partial molecular volumes for each value of x may be obtained by first drawing the tangent to the V(x) plot. The x = 0 intercept is the partial molecular volume of lipid V_L and the intercept at x = 1 is the partial molecular volume of cholesterol V_C. If the V(x) plot is linear over a range of x values, then V_L and V_C are constants in that range. Fig. 2 suggests that DOPC(30) and POPC(30) have just one linear range, whereas DPPC(50), BSM(45) and DMPC(30) have two linear ranges with different intercepts and slopes, one range for low cholesterol concentrations, x < x_C and another range for high cholesterol concentrations x > x_C, where x_C is the intersection of the straight lines. (It may be noted that Eq. (2) shows that linearity in either the υ(x) or the V(x) plot generally implies that the other plot is non-linear, but the deviations from linearity are usually small.)

For DOPC(30) and POPC(30) the straight lines shown in Fig. 2 were fitted to the data at all values of x. For DPPC(50), BSM(45) and DMPC(30) straight lines were fitted separately to the small x and to the large x ranges of data as indicated in Fig. 2. For DPPC(25), three ranges of x are required. Fig. 3 shows the x-dependence of the partial molecular volumes V_L of the lipids and Fig. 4 shows the corresponding partial molecular volumes of cholesterol V_C in the different lipid bilayers. Numerical values of the partial molecular volumes are given in Table 1 for the mixtures in the figures and also for DOPC(24). Column 3 of Table 1 gives our directly measured volumes V_L(x = 0) of the fully hydrated pure lipid bilayer; estimated errors are ±0.3 ų. Column 4 shows the values predicted by the recent formula of Koenig and Gawrisch (2005). For those mixtures that appear to undergo a phase transition, the column 5 gives the value of the cholesterol mole fraction at the intersection of the linear portions shown in Fig. 2. The remaining columns give the values of the partial molecular volumes of lipid and cholesterol in the small x and large x ranges that were obtained by fitting all the data points in each range. Therefore, the values V_L(x < x_C) need not be identical to the V_L(x = 0) values. The close agreement between columns 3 and 6 is further indication that the data are quite linear in the small x regime.

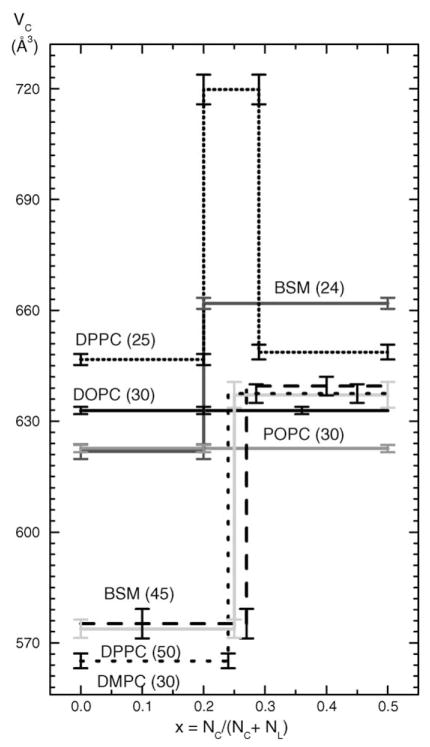
Fig. 4.

Partial molecular volumes V_C in ų of cholesterol in the same bilayers as Fig. 3 as a function of cholesterol mole fraction x obtained from the x = 1 intercept of the straight line fits in Fig. 2.

Table 1.

MW is molecular weight, T is temperature in °C, V is partial molecular volume of the lipid and V is the partial molecular volume of cholesterol

Lipid	MW	T (°C)	VL (x = 0)	VL (calc)	xC	VL (x < xC)	VC (x < xC)	VL (x > xC)	VC (x > xC)
DPPC	734.05	50	1228.5	1228.8	0.249	1228.6	573.8	1207.6	637.1
DMPC	677.94	30	1099.4	1099.4	0.240	1099.6	565.1	1076.8	637.5
POPC	760.10	30	1256.5	1255.5	None	1256.2	622.6
DOPC	786.15	30	1302.3	1300.1	None	1302.2	632.9
DOPC	786.15	24	1294.2	1294.2	None	1289.1	632.1
SM	731.09	45			0.269	1233.1	575.2	1209.4	639.5
SM	731.09	24	1175.6		0.200	1175.6	621.8	1165.2	661.9
DOPCBr4	1105.60	30	1346.7
di-22:1PC	898.34	30	1522.2	1523.0

For mixtures that have the same value at all measured mole fractions x, the values of the partial molecular volumes are given in columns 6 and 7.

For mixtures that have two different volumes, the values are shown for regions x < x_C (columns 6 and 7) and x > x_C (columns 8 and 9).

Table 1 also presents results for lipid bilayers composed of di-22:1PC, which floats even in H₂O, and for brominated DOPC, which sinks even in pure D₂O. The results for both lipids were obtained by mixing them with a sequence of concentrations of another similar lipid, DOPC with brominated DOPC and POPC with di-22:1PC. The apparent specific volumes of the two lipids were then obtained by extrapolation to zero concentration of the added lipid.

4. Discussion

4.1. Volumes of lipids in pure lipid bilayers

The excellent agreement in Table 1 of our directly measured lipid volumes V_L(x = 0) in column 3 with the recent formula of Koenig and Gawrisch (2005) V_L(calc) in column 4 strongly supports their formula for phosphatidylcholine lipid bilayers. Results for DPPC(50), DPPC(25), DMPC(30) and DOPC(30) agree well with earlier reports from this lab (Nagle and Wilkinson, 1978; Tristram-Nagle et al., 1998; Nagle and Tristram-Nagle, 2000), although the more recent value of 1232 ų for DPPC(50) (Wiener et al., 1998) appears now to be a few ų too large.

4.2. Dependence of partial molecular volumes on cholesterol mole fraction

For DOPC(30) and POPC(30) the V(x) plots are quite linear for the entire range of cholesterol mole fraction x as shown in Fig. 2. For POPC(30) we have one data point at x = 0.6 (not shown) which appears to deviate from linearity, but we chose not to focus on the very high cholesterol range x > 0.5 because of the well known complication that cholesterol crystallizes out of lipid bilayers thereby requiring special precautions to obtain reliable equilibrium results (Huang et al., 1999). The linearity of the V(x) plots gives constant values for the partial molecular volume V_L of the lipids DOPC(30) and POPC(30) and of the cholesterol V_C in these lipids as shown in Figs. 3 and 4. DOPC(30) and POPC(30) at the temperature T = 30 °C of our measurements can be characterized as lipids that are far from any gel phase transition T_M. For the lipids DMPC(30), DPPC(50) and BSM(45) that have saturated chains that form gel phases only a few degrees below the measured temperatures, there is a small, but distinctive break at x = x_C in the linearity of the V(x) plots in Fig. 2.

4.3. Condensation effect of cholesterol

Focusing first on the small x < x_C regime for DMPC(30), DPPC(50) and BSM(45), the partial molecular volumes of cholesterol V_C in Fig. 4 are considerably smaller than for DOPC(30) and POPC(30). The interpretation is clear. For small x, the partial molecular volume of cholesterol V_C accounts not only for the ‘bare’ volume of cholesterol, but also for its effect on neighboring lipid molecules. This condensation effect cannot be taken into account by a decrease in the partial molecular volume of the lipid because the insertion of another lipid molecule to a mixture with a small concentration of cholesterol does not alter the number of lipid molecules that are proximal to and strongly interacting with the few cholesterol molecules. Such an addition increases the total volume as if there were no cholesterol; therefore, by the definition in Eq. (3), V_L cannot account for the condensation of those lipid molecules close to the few cholesterol molecules. Instead, that condensation is included in V_C. This is analogous to the partial molecular volume of water being the same as its bulk value when it is present in excess with lipid bilayers. The difference in the value of V_C for DOPC(30) versus DPPC(50) therefore implies that saturated hydrocarbon chains on the lipids in contact with cholesterol straighten into more gel-phase-like conformations that occupy less volume whereas unsaturated DOPC(30) chains are much less affected. This condensation effect is consistent with the chains in DMPC(30), DPPC(50) and BSM(45) being close to their chain ordering phase transition temperatures so that the perturbation on the chains by cholesterol, with its flat, rigid face on the aromatic rings, can induce ordering whereas the unsaturated chains on DOPC(30) are thermodynamically too far from their conformational ordering transition for this perturbation to have significant effect.

This interpretation also suggests that when cholesterol is added to a gel phase, there should be no condensation effect. Instead, one would expect that cholesterol would disrupt the chain packing of the gel phase, which would lead to an increase in V_C, i.e., an expansion effect. Fig. 4 shows that for gel phase DPPC(25) there is a small increase in the V_C value compared to DOPC(30) and POPC(30). For gel phase BSM(24) V_C is close to the value for POPC(30) and DOPC(30), although it is considerably larger than the value for BSM(45).

POPC(30) is an especially interesting case because it has one saturated and one unsaturated chain, so one might predict that its behavior would be halfway between that of DOPC(30) and DPPC(50). Instead, it is apparently the thermodynamic distance from its transition temperature that makes its V_C closer to DOPC(30) than to DPPC(50) or DMPC(30). This is consistent with recent results from this lab that report the area per molecule A of POPC(30) to be closer to DOPC(30) than to DPPC extrapolated to the same temperature (Kucerka et al., 2006). Also, the difference in the value of V_C for POPC(30) compared to DOPC(30), while small, is consistent with the condensation effect recently reported by Heerklotz and Tsamaloukas (in press).

4.4. Phase behavior of cholesterol mixtures

The inadequacy of a single straight line fit to V(x) in Fig. 2 or to υ(x) in Fig. 1 for DPPC(50), DMPC(30) and BSM(45) suggests that some sort of phase transition takes place at x = x_C. Although our measurements were only performed for a few select temperatures, it may be of interest to compare our data with the phase diagrams proposed for bilayers composed of lipids and cholesterol. To facilitate such comparison, a generic phase diagram is sketched in Fig. 5. This phase diagram is topologically the same as the one presented by Vist and Davis (1990) for DPPC/cholesterol or the one by Almeida et al. (1992) for DMPC/cholesterol. Neither phase diagram shows a ripple phase; for that one may consider the phase diagrams of Lentz et al. (1980) or McMullen and McElhaney (1995), which present much more fine structure for temperatures below the pure lipid chain melting temperature T_M. Our Fig. 5 shows a somewhat narrow phase coexistence region between gel and liquid ordered phases that reflects the volumetric results of Melchior et al. (1980), reproduced for T = 25 °C in our Figs. 1 and 2, that strongly indicate a transition region 0.20 < x < 0.29 for DPPC for all temperatures below T_M.

Fig. 5.

A generic temperature-composition phase diagram for discussion purposes only and not necessarily supported by the data in this paper. The region designated F is meant to be a fluid (L_α) phase and the region designated G contains the gel, ripple and subgel phases, without showing their individual detailed locations. Regions of two-phase coexistence are contained within the bold lines within which the light dotted horizontal lines show the coexisting states at the ends of the lines, such as states A and B. State CP is a critical point where the distinction between the F phase and the so-called liquid ordered phase L_o disappears.

Our x = x_C datum for DPPC(50) could be pertinent to the boundary of the fluid–fluid coexistence region for temperatures above T_M, so we focus on that part of the phase diagram in Fig. 5. The phase diagram for DPPC/cholesterol of Vist and Davis (1990) was for deuterated lipid for which T_M is about 4° lower. Even adding this temperature difference, their phase diagram does not extend to T = 50 °C, but rough extrapolation suggests a narrow phase coexistence region, perhaps ending in a critical point, labeled CP in Fig. 5, near x = 0.25. While this value is consistent with our x_C = 0.25, near a critical point the two phases become identical, so one does not expect that the partial molecular volumes would exhibit the jumps shown in Figs. 3 and 4. A better explanation is that our x_C locates either the point labeled A or the point labeled B in Fig. 5. As is shown in Appendix A, one expects a discontinuity in the partial molecular volumes at such points. Comparing our numerical value x_C = 0.25 to the phase diagrams of Vist and Davis (1990), Sankaram and Thompson (1991), and Recktenwald and McConnell (1981) suggests that x_C locates the point B on the liquid ordered side of their coexistence regions. Our concern with this is that we do not observe a discontinuity at lower values of x corresponding to point A on the liquid disordered side of the phase diagram. While perhaps not impossible, this would require special cancellations in order that the partial molecular volumes not jump at x_A (see Appendix A). Instead, our rendering of Fig. 5 suggests that our x_C corresponds to point A and point B would then occur at larger values of x than could be observed.

The phase diagram of Vist and Davis (1990) has been strongly criticized by McMullen and McElhaney (1995) who presented a rather different picture for DPPC/cholesterol mixtures. Their ‘phase diagram’ has three phases coexisting over a non-zero temperature range in violation of Gibbs phase rule and, indeed, they describe their picture as “perhaps more accurately a temperature/composition diagram”. Our value of x_C = 0.25 at T = 50 °C compares reasonably well with their fluid–fluid phase transition line which has a value x = 0.19 at this temperature, especially considering that their method was thermodynamically orthogonal to ours. They employed DSC taken as temperature was varied at fixed composition x, whereas we took data at fixed temperature and varied the composition. Also, their fluid–fluid transition line was determined by taking the high temperature end of their broadest Gaussian obtained by fitting the DSC traces; having an excess heat capacity at temperatures below their fluid–fluid transition line would suggest phase coexistence toward lower temperatures as in Fig. 5, although such excess heat capacity would most likely not be best modeled by a Gaussian.

It may also be significant that the value of x_C is nearly the same ~0.25 for all the lipids we studied that have such a break at temperatures above T_M. This would not be expected if the break occurs at a point such as A in Fig. 5 because it is unlikely that all the phase lines occur at the same value of x for the various temperatures of our measurements. Our value x_C ~0.25 corresponds to one cholesterol to three lipids. Special packing ratios have been previously suggested, especially one cholesterol to two lipids (Engelman and Rothman, 1972), as well as many ratios that would correspond to superlattice packing (Chong, 1994). We also note that our single break at x_C might not be as sharp as required for either a phase transition or rigid stoichiometry. A more conservative picture is that x_C is a higher order transition line or the center of a narrow, but continuous transition region. Such a picture would not have a two-phase coexistence region and a second break point, such as at x_B in Fig. 5. Rather, x_C would locate the maximum mole fraction below which the condensing effect of cholesterol occurs. This interpretation is not inconsistent with the strongly contrasting behavior of gel phase DPPC(25) which clearly has two break points. The large value of V_C in the two-phase region between the two break points is quantitatively accounted for by the conversion of the small x phase into the large x phase and a small difference of V_C between those two phases, as shown in Appendix A.

4.5. Most appropriate volume for cholesterol in lipid bilayers

We turn next to the values of the partial molecular volume of cholesterol V_C for x > x_C. Fig. 4 shows that V_C = 630 ± 10 ų is nearly the same when measured at temperatures above the T_M of the host lipid. This surprising result first suggests that DOPC(30) and POPC(30) do not undergo volume condensation for any of our measured values of x. Second, it suggests that DPPC(50), BSM(45) and DMPC(30) undergo no further condensation when x > x_C because each lipid molecule is already close to a cholesterol and has been condensed as much as it can be by cholesterol. Then, the addition of another cholesterol would increase the total volume NV just due to the bare steric volume of the cholesterol. This would make this common value of V_C ~ 630 ± 10 ų the most appropriate value for the volume of cholesterol.

There is another interesting comparison regarding the volume of cholesterol. Measurements of the molecular volume of pure cholesterol in water give 627 ų for a form (band 2) that was identified as anhydrous cholesterol and 606 ų for a form (band 3) that was identified as the monohydrate (Renshaw et al., 1983). The existence of two different forms and different volumes at low water content and with no lipid suggests that the closely similar value of band 2 with our partial molecular volumes is merely coincidental.

Finally, we return to our initial goal of comparing the partial molecular volume of cholesterol with simulations. The recent value obtained from a composite of simulations from three groups was V_C = 541 ų (Edholm and Nagle, 2005). This is rather smaller than our measured value for x < x_C. The simulations did not indicate non-linear behavior in the molecular volume V(x) (designated υ(x) in Fig. 2), although the composite results were rather too noisy to discern any breaks. The simulations did show strongly non-linear behavior in the molecular area a(x) which is more sensitive to cholesterol addition than is the volume. Due to the high noise level, the favored way of analyzing the simulated a(x) was with smooth functions of x. However, it was also noted that there was a possible break near x = 0.3, which would be consistent with the x_C obtained experimentally in this paper.

We suggest that volumetric measurements, when analyzed as a function of mole fraction of cholesterol provide valuable information about molecular packing in bilayers and, when extended to additional temperatures, may continue to be a fruitful probe of the phase behavior of lipid cholesterol mixtures.

Appendix A. Equations for partial molecular volumes in a two-phase coexistence region

Let the subscripts LA refer to lipids in phase A, LB to lipids in phase B, CA to cholesterol in phase A and CB to cholesterol in phase B. Then

$$\text{NV}=N_{\text{LA}}{V}_{\text{LA}}+N_{\text{LB}}{V}_{\text{LB}}+N_{\text{CA}}{V}_{\text{CA}}+N_{\text{CB}}{V}_{\text{CB}}.$$ (6)

Let x_A < x < x_B be the coexistence region, so x_A is the cholesterol mole fraction for pure phase A and x_B is the cholesterol mole fraction for pure phase B. Then, using the definitions of partial molecular volumes in Eq. (3) and some algebra yields

$$\begin{array}{l}(V_{\text{C}}-V_{\text{CA}})/(1-x_{\text{A}})=-(V_{\text{L}}-V_{\text{LA}})/x_{\text{A}}\\ =[(V_{\text{CB}}-V_{\text{CA}})x_{\text{B}}+(V_{\text{LB}}-V_{\text{LA}})(1-x_{\text{B}})]/(x_{\text{B}}-x_{\text{A}}).\end{array}$$ (7)

The first part of Eq. (7) shows that the difference in cholesterol partial volume V_C – V_CA at point A in Fig. 5 is simply related to the difference in lipid partial volume V_L – V_LA by a lever rule with point A as the fulcrum, as can be visualized in Fig. 2 using the geometric definitions of partial molecular volumes embodied in Eq. (5). The latter part of Eq. (7) shows that small differences in the volumes V_CB – V_CA and V_LB – V_LA of the pure phases A and B are greatly magnified by the x_B – x_A denominator; this accounts for the large value of V_C in the region 0.20 = x_A < x < x_B = 0.29 for gel phase DPPC in Fig. 4. Although it is possible that V_C – V_CA is zero at point A, thereby yielding a volumetrically silent transition, this would require special, accidental cancellation of terms.