Neurovascular Modeling: Small-Batch Manufacturing of Silicone Vascular Replicas

Abstract

BACKGROUND AND PURPOSE: Realistic, population based cerebrovascular replicas are required for the development of neuroendovascular devices. The objective of this work was to develop an efficient methodology for manufacturing realistic cerebrovascular replicas.

MATERIALS AND METHODS: Brain MR angiography data from 20 patients were acquired. The centerline of the vasculature was calculated, and geometric parameters were measured to describe quantitatively the internal carotid artery (ICA) siphon. A representative model was created on the basis of the quantitative measurements. Using this virtual model, we designed a mold with core-shell structure and converted it into a physical object by fused-deposit manufacturing. Vascular replicas were created by injection molding of different silicones. Mechanical properties, including the stiffness and luminal coefficient of friction, were measured.

RESULTS: The average diameter, length, and curvature of the ICA siphon were 4.15 ± 0.09 mm, 22.60 ± 0.79 mm, and 0.34 ± 0.02 mm⁻¹ (average ± standard error of the mean), respectively. From these image datasets, we created a median virtual model, which was transformed into a physical replica by an efficient batch-manufacturing process. The coefficient of friction of the luminal surface of the replica was reduced by up to 55% by using liquid silicone rubber coatings. The modulus ranged from 0.67 to 1.15 MPa compared with 0.42 MPa from human postmortem studies, depending on the material used to make the replica.

CONCLUSIONS: Population-representative, smooth, and true-to-scale silicone arterial replicas with uniform wall thickness were successfully built for in vitro neurointerventional device-testing by using a batch-manufacturing process.

Recent advances in minimally invasive neuroendovascular interventions have been applied in the treatment of cerebrovascular diseases.^1–3 For the successful development of new devices designed for the intracranial circulation, in vitro evaluation in realistic vascular replicas is an important part of the design phase.^4–7 Of particular importance is the internal carotid artery (ICA) siphon, which offers challenging tortuosity for endovascular access. Several different manufacturing processes for fabrication of vascular replicas have been described previously^8–15; however, some limitations of these manufacturing processes cannot be ignored. First, the high-friction resistance on the surface of silicone impedes the deliverability and deployment of endovascular devices in the silicone replicas.¹⁶ Second, achieving the desired wall thickness by repeated painting or dip-spin steps is time-consuming and not precise. Most important, each model is essentially made by hand and, therefore, with limited reproducibility and large time expenditure.

The goal of the earlier studies was to make patient-specific silicone models instead of a model capable of representing the geometry of a population of patients. Vessel characterization is essential to prepare the latter model.^17,18 Various methods are available for vessel characterization,^19–21 and among them, tortuosity is generally used to summarize curvature information along the centerline of a blood vessel.^22–24 In this study, the median length, average curvature (AC), and diameter of the ICA siphon from 20 patients were used to build a true-to-scale batch-manufactured transparent silicone replica of a population-representative model. Furthermore, the inner wall of the silicone replica was modified by the liquid silicone rubber (LSR) topcoat to provide lubricity for the delivery of endovascular devices.

Materials and Methods

Patient Selection and MR Imaging

Twenty anonymized brain MR angiography (MRA) datasets were acquired from a retrospective review between December 30, 2007, and January 23, 2008, of patients having no pathologic findings. MR imaging was performed by using a 1.5T system (Signa Excite; GE Healthcare, Waukesha, Wis) and a receiving 8-channel head coil. Brain 3D time-of-flight MRA data were acquired (TR, 33.3 ms; TE 6.9 ms; flip angle, 20°; FOV, 200 × 200 mm; matrix, 512 × 512; section thickness, 1.4 mm with a 0.7-mm gap).

Vessel Segmentation and Centerline Generation

MRA images were imported section by section in Mimics (Materialise, Leuven, Belgium) and stacked to formulate a 3D model. The target vasculature was extracted from the neighboring tissue by thresholding. To generate a segmentation mask, we set minimum and maximum threshold values, and segmentation was further restricted by cropping the mask.

The selected pixels in each section were connected, resulting in a clean mask for the use of 3D model construction. The 3D segmentation object was fixed to assure that there were no shells, holes, noise, or bad edges and was smoothed before skeletonizing. The resulting centerline was composed of control points equally spaced at a constant 0.4-mm interval.

Vessel Characterization and Model Selection

The path length of the extracted centerline and the diameter of the best-fit circle to the vessel cross-section at each control point were recorded and averaged. The results were presented as average ± SD.

The AC of left and right ICA siphons of 20 patients was calculated. The vessel centerline r(s) = [x(s), y(s), z(s)] was first parameterized by arc length (s) and then fitted with a 10th-order polynomial for smoothing. To evaluate the goodness of fit, we applied the degree of polynomial varying from 2 to 22 to the original dataset, respectively, and the root mean square error (RMSE) was calculated.²⁵

The smoothed centerline was resampled to give control points at constant 0.05-mm intervals for curvature evaluation. The curvature (k) at each control point and the AC were given by^23,24:

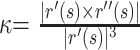1)

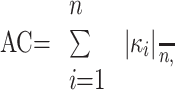2)

where r′(s) and r‴(s) denote the first and second derivatives of the centerline, and n indicates the total number of points.

The nonparametric Wilcoxon signed rank test was performed (Prism 5; GraphPad Software, La Jolla, Calif) to compare the median of each vessel feature against a hypothetic median, which was every single geometric parameter for the left and right ICA siphons in each patient. In this test, a P value > .05 indicated that there was no statistically significant difference between the median of a group of samples and the hypothesized median.

Generation of the Vascular Replica

A mold with a core-shell structure was created for silicone injection (Magics; Materialise). The inner core, representing the geometry of the vasculature, was encapsulated by the outer shell, which was created on the basis of the geometry of the core. The distance between the core and shell was the thickness of the silicone replica, which can be precisely controlled. In this study, the wall thickness was 1 mm.

The virtual design was transformed into a physical object (Prodigy Plus; Stratasys, Eden Prairie, Minn) by using fused-deposit manufacturing²⁶ to build the model in a layer-by-layer manner, with a layer thickness of 0.178 mm. The production capacity per batch was determined by the size of the target vasculature. For instance, 6 ICA-middle cerebral artery (MCA) core-shell models with a dimension of 47 × 41 × 81 mm³ each can be built in 1 batch and completed in 30 hours. The extrusion tips in the heated build envelop deposited the model (copolymer of acrylonitrile, butadiene, and styrene [ABS]) and support materials along the designated tool path. Both materials fused together to form a solid model. The soluble support material was removed in the sodium hydroxide solution at 70°C, which required approximately 24 hours.

Xylene and 2-propanol were infused into the mold alternately to smooth the core and the inner wall of the shell. Repeating the alternate rinse procedure 5 times, each time for 1 minute, achieved an adequate smoothing result. The rinsed mold was dried in the ventilation system before silicone infusion.

Sylgard 184 silicone kit (Dow Corning, Midland, Mich) and an injection molding-grade silicone, LIM 6030 pail kit (Momentive, New Milford, Conn), were infused into the core-shell mold. The Sylgard 184 replica was found to be optically clear and had a higher Shore A hardness. Compared with Sylgard 184, LIM 6030 had higher elongation at break, tensile strength, and viscosity. The amount of thinner, SF 96–5 (GES Waterford Plant, Waterford, NY), added to the LIM 6030 mixture accounted for 7% of total mixture weight. The silicone solution was mixed and degassed in a vacuum oven at room temperature under 76 cm Hg vacuum. Higher injection pressure, at least 1200 mm Hg, was required for the delivery of the viscous LIM 6030 compared with 55 mm Hg to infuse the Sylgard 184 into the mold. The silicones were cured at 60°C for 12 hours. The whole mold was immersed in xylene for mold dissolution overnight.

LSR Topcoat Modification

LSR topcoat (Momentive Performance Materials, Albany, NY), a 2-component translucent matte coating with a Brookfield viscosity of 1600 centipoise, was infused into smoothed open-ended straight silicone tubes (11 cm in length and 4 mm in diameter) by using a peristaltic pump and then was cured at 110°C in a ventilated oven for 30 minutes. This procedure was repeated from zero to 3 times. The effect of multiple coatings on the coefficient of friction (COF) was evaluated by using a customized friction rig (TA-265A; Texture Technologies, Hamilton, Mass), which was designed according to American Standard Test Method (ASTM) D1894.

During the friction test, the inner lumen of the replica slid 20 mm over a flat surface at a sliding speed of 5 mm/s 25 times. All tribological tests were conducted under ambient conditions with a constant temperature of 21°C. Five specimens were tested for each silicone material, and the average force was obtained to determine the static and dynamic COF of silicone material before and after LSR coating. The static COF was obtained from the averaged maximum force initiating motion between test material and surface, whereas, the dynamic COF was from the average force measured for the duration of sliding. The Student t test was performed to determine the statistical difference in friction before and after surface modification.

Tensile Test for Silicone Strips

The stress-stretch relationship (S-S relationship) was obtained by using an Instron machine (model 5542; Norwood, Mass) equipped with 0.5-kN-load cell, having 651-mm vertical test space. The 5-mm-wide 50-mm-long Sylgard 184 and LIM 6030 silicone strips with an average thickness of 0.54 ± 0.06 and 0.51 ± 0.02 mm were prepared for the tensile test. All the specimens (3 specimens for each group) were subjected to the test at a cross-speed rate of 30 mm/min, and the S-S relationship of the silicone strips was compared with that of the human MCA from postmortem examination, which was performed quasi-statically at a strain rate of approximately 0.05 seconds⁻¹.²⁷

Results

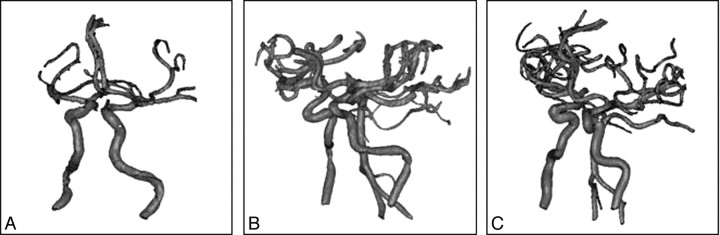
The anatomy of the 3 cerebral vessels from patients 1, 2, and 3 are shown in Fig 1A–C, having siphons with an AC ranging from 0.23 to 0.64 mm⁻¹. Patients 1, 2, and 3 were selected to illustrate mild, moderate, and severe curvature, respectively, of the ICA siphon in our patient population.

Fig 1.

Virtual cerebrovascular models show ICA siphons with mild (A), medium (B), and severe (C) curvature.

In the vessel characterization, the best-fit polynomial to smooth the original centerline data was determined by minimizing the error between the polynomial curve and original centerline. The results showed that the total error decreases significantly up to the 10th-order polynomial fit, followed by a more gradual decline. The smoothed centerline was re-sampled before curvature calculation. The AC tends to increase with the decrease of the distance between control points and becomes stable when the distance is <0.1 mm. This change is significant in the measurement of an ICA siphon with severe tortuosity, whose AC increases from 0.45 to 0.65 mm⁻¹ when the distance decreases from 0.4 to 0.01 mm. In this study, the polynomial curve was re-sampled to have points at constant 0.05-mm intervals for curvature calculation. With the 10th-order polynomial to smooth the original centerline and having control points with constant 0.05-mm intervals, the AC, arc length, and diameter from 20 patients were 0.34 ± 0.12 mm⁻¹, 21.86 ± 4.24 mm, and 4.17 ± 0.64 mm for the left ICA siphon, respectively. For the right siphon, the AC, arc length, and diameter were 0.34 ± 0.13 mm⁻¹, 23.31 ± 5.72 mm, and 4.12 ± 0.44 mm, respectively. In patient 18, the P values resulting from the Wilcoxon signed rank test for comparisons in AC, length, and diameter were all >.05, indicating each measured parameter of patient 18 had no significant difference compared with the corresponding median. The P values were .24, .37, and .96 for the comparisons of AC, arc length, and diameter, respectively, of the left ICA siphon, and 0.72, 0.29, and 0.49, respectively, for those of the right ICA siphon. This finding was only observed in patient 18 and led us to select patient 18 as a representative model of the chosen patient population in this study.

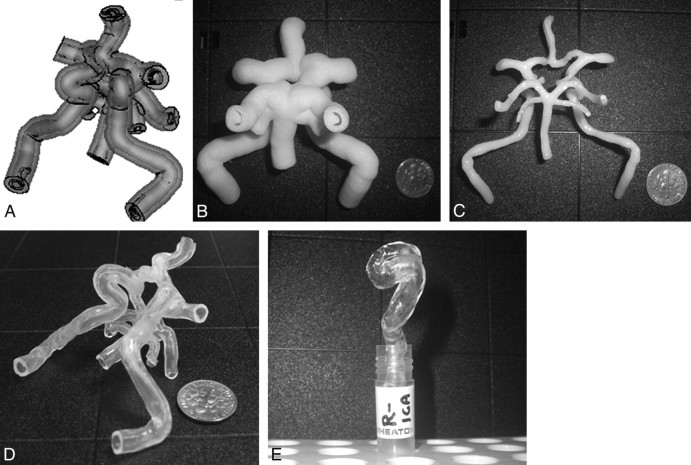
A computer mold consisting of a core-shell structure for silicone injection is shown in Fig 2A. Silicone was infused into a mold (Fig 2B), which contained the vasculature of the circle of Willis (CoW) from patient 2 as the core (Fig 2C). Figure 2D, -E shows silicone replicas of the CoW from patient 2 and the representative right ICA from patient 18, respectively. Using this batch-manufacturing process, we made 6 vascular replicas from the virtual model in 92 hours at a material cost of $250. The capital equipment and software used in this study were quite expensive; however, these tools are available at most universities and medical device companies.

Fig 2.

The virtual core-shell structure (A) is designed for the preparation of the physical ABS model (B), which contains the CoW (C) as the core. After the silicone is cured, the ABS model (B) is dissolved in xylene, resulting in a transparent CoW silicone replica (D). E, With the same manufacturing process, a representative right ICA siphon is built from patient 18.

The static and dynamic COF of Sylgard 184 and LIM 6030 with various numbers of LSR coatings are given in the Table. The best values were obtained with a single coating for Sylgard 184: COF reduced by 55%, with a minimum static COF of 0.334 ± 0.169 and a dynamic COF of 0.312 ± 0.174. For LIM 6030, a 47% reduction in COF was achieved with 3 layers of LSR topcoat, resulting in a static COF of 0.719 ± 0.121 and a dynamic COF of 0.683 ± 0.120. The S-S relationship of LIM 6030 and Sylgard 184 are shown and compared with that of the human MCA from postmortem examination obtained from the quasi-static test conducted by Monson et al²⁷ in Fig 3. Like human blood vessels, silicone rubber exhibits a nonlinear S-S relationship. Moreover, at low stretch, the slope of the S-S curve of LIM 6030 is 0.67 MPa, similar to that of the MCA from a postmortem examination (0.41 MPa).

Static and dynamic COFs of Sylgard 184 and LIM 6030 samples for different numbers of coatings after 25 runs^*

Coating No.	Sylgard 184		LIM 6030
	Static COF	Dynamic COF	Static COF	Dynamic COF
0	0.738 ± 0.093	0.707 ± 0.089	1.346 ± 0.113	1.298 ± 0.113
1	0.334 ± 0.169 (P = .0016)	0.312 ± 0.174 (P = .0019)	1.052 ± 0.216 (P = .0273)	1.026 ± 0.222 (P = .0435)
2	0.366 ± 0.114 (P = .0005)	0.312 ± 0.108 (P = .0002)	0.815 ± 0.114 (P < .0001)	0.765 ± 0.098 (P < .0001)
3	0.471 ± 0.091 (P = .0018)	0.416 ± 0.090 (P = .0009)	0.719 ± 0.121 (P < .0001)	0.683 ± 0.120 (P < .0001)

Note:—COF indicates coefficient of friction.

^*The COF is presented as mean ± SD. The Student t test compares the mean COF of the coated and uncoated groups. The 2-tailed P value < .05 indicates a statistically significant difference.

Fig 3.

The S-S curves of Sylgard 184, LIM 6030, and a human MCA from postmortem examination are compared. At low stretch, the elastic property of LIM 6030 is close to that of the MCA from postmortem examination. Short solid line indicates the MCA from a postmortem examination; dark dashed line, LIM 0.49 mm in thickness; light dashed line, LIM 0.52 mm in thickness; dotted line, LIM 0.53 mm in thickness; diamond, Sylgard 0.49 mm in thickness; square, Sylgard 0.53 mm in thickness; triangle, 0.61 mm in thickness.

Discussion

A great deal of effort has been used to create polymeric vascular models for surgical simulation, interventional practice, and hemodynamic research in vitro. Quantitating anatomic features of the arterial structures for disease or lesion prediction and diagnosis have also been widely investigated. On the basis of our literature search, no studies have yet to apply the vessel characterization results to the replica manufacturing process. In this article, the disclosed manufacturing process of replicas is based on a model extracted from a characterized population of imaging datasets. This could be an even more powerful technique in the future as image data bases grow, allowing an investigator to search for anatomy specific to a precise patient population for whom a given endovascular device is intended.

Arterial lumen replicas can be obtained from human cadavers.^10,14 Postmortem alterations, including the shrinkage of arterial trees, produce dimensional errors of the in vitro model. Using MRA data to acquire the geometry of the target vessels in our proposed manufacturing method avoids this problem and provides flexibility during the postprocessing. Stock et al²⁸ mentioned that the noninvasive non-contrast-enhanced 3D time-of-flight MRA is highly accurate in depicting the arterial segments of the CoW, except the posterior communicating arteries (PcomA), and the same observation also applies to this study. The poor depiction of PcomA could be attributed to the saturation effect of slow flow and the flow parallel to the acquired section plane in addition to the normal anatomic variations in which these vessels are not present.

To smooth the centerline generated from the MRA reconstruction, the RMSE describes how well the fitted curve matches the original dataset. In this study, the RMSE tends to decrease at a higher than 10th-order polynomial fit. However, a higher polynomial order does not guarantee better fitting results and can lead to oscillations between the data points. The 10th-order polynomial had a RMSE of 0.1 for patients 1 and 2 and 0.16 for patient 3 and was chosen as a smoothed centerline. To take minor changes along the vessel centerline into consideration, we measured and averaged the curvature of every 0.05-mm segment. The median of each vascular feature was used to select a representative model in this study.

Other methods of replica construction have been used, such as that described by Knox et al,¹¹ in which they created a reusable master mold of a lumen replica based on the CT scan data from a live patient to reproduce wax lumen models. The major difficulty of this technique is the fabrication of the master mold, which requires an experienced mold maker and is a time-consuming and expensive process, and the resulting mold is not easily modifiable to change the replica anatomy. Compared with the method of Knox et al, the construction of our core-shell structure is straightforward and efficient. On average, a virtual core-shell mold can be completed in 20 minutes after receiving the scanning data, enabling reproducible manufacturing of replicas of any selected configuration.

Sugiu et al¹⁴ used 4–6 thin layers of silicone liquid manually painted onto the wax lumen cast to simulate the vessel wall; however, the thickness and uniformity of the coating were not stated. Seong et al¹³ fabricated rabbit aneurysm replicas by using the dip-spin method. The lumen cast polished with sandpaper was dipped into the silicone mixture and then mounted on a spinning shaft to obtain a layer of uniform silicone coating. The repeated coating procedure is time-consuming and not reproducible. Our described methodology serves to improve these limitations. The core-shell mold keeps the consistency of the replica dimensions and saves time via the batch manufacturing. Due to the structural constraint, the sandpaper polish is not applicable to our core-shell mold. To smooth the lumen surface, the mold is rinsed with xylene and 2-propanol alternately. This procedure allows xylene to gradually dissolve model material and effectively prevents the core-shell structure from collapsing.

Besides the soft replica described above, the rigid-block model provides another option for in vitro use. Wetzel et al¹⁵ used the 3D printer with a resolution of the build layer of 0.076 mm to form the wax copies of the vascular trees based on rotational angiography data. The wax model is embedded in clear silicone, which is then cured to form a solid block. The holes drilled in the silicone block drain the melted wax. After evacuation of the wax, a transparent rigid model containing the vascular lumen inside is prepared. The major concern of this lost-wax technique is the fragility of the wax, which results in the breakage of the vessel branches <1 mm. With the method reported in our study, silicone vascular replicas with branches <0.5 mm were made.

A common concern for selecting silicone as a material for vascular replica fabrication is its high friction. Surprisingly few attempts have been made to minimize the resistance between silicone replicas and medical devices. So far, an alternative material used to prepare a vascular replica in the application of neurovascular modeling is polyvinyl alcohol (PVA).¹⁶ The high water content of PVA hydrogel gives the vascular replica a naturally lubricated surface; however, the life of PVA replicas is limited, depending on the rate of water evaporation. Aside from using PVA as a substitute for silicone, Parylene coating successfully reduces the COF of elastomers by forming a thin layer of Parylene film, which closely conforms to the substrate. The restriction of this coating method is the requirement of the coating system for vapor deposition during the process, which may increase the cost and restrain the popularity of this technique. Compared with the aforesaid methods, LSR topcoat offers an easy and efficient option for smoothing the inner wall of the silicone vascular model. The low viscosity allows the LSR topcoat to flow easily through the long and tortuous model; furthermore, it only takes 10–30 minutes to cure 1 layer of coating.

Rubber, like silicone, is generally amorphous, with few strong interactions between molecules. When the tensile force is applied, the tangled molecules are pulled to become stretched. Additional force is needed on the stretched oriented molecules to maintain the constant strain rate. When a vessel is subjected to a tensile force, the elastin and collagen fibers significantly contribute to the low and high stiffness in the S-S curve.²⁹ The results from the tensile test in this study show that the S-S relationship of LIM 6030 is similar to that of human MCA from postmortem examination at low stretch. To make this conclusion, one must clarify and discuss the potential differences between in vivo and in vitro test conditions. The blood vessel wall is an anisotropic composite material in general and receives multidirectional stress in the physiologic environment. All specimens described herein are subjected to uniaxial tensile strength and stretched longitudinally until breakage. Therefore, the results may not represent the mechanical response in vivo. Furthermore, the contribution from the surrounding tissue to the mechanical response of the vessels to the load is not taken into consideration in the in vitro and ex vivo studies. Last, factors such as age, sex, and disease history of donor; type of vessel; and strain rate may cause large variations in the S-S behavior for biologic materials. The cerebral arteries are significantly stiffer and less stretchable before failure compared with systemic arteries.³⁰

The described technique provides an efficient method for representative replica construction. However, there are technical difficulties that might be encountered while preparing the silicone models. Bubble formation during silicone injection may cause defects of the silicone replicas. The high pressure required to infuse silicone liquid with high viscosity into the mold may cause core structure motion, resulting in variation in wall thickness. Finally, more imaging data should be reviewed to create a more realistic environment for medical device testing, endovascular training, and in vitro hemodynamic studies.

Conclusions

Population-representative, smooth, and true-to-scale silicone arterial replicas with uniform wall thickness were successfully built for in vitro neurointerventional device testing by using a batch-manufacturing process.