Progenitor cell self‐renewal and cyclic neutropenia

Abstract

Objectives: Cyclic neutropenia (CN) is a rare genetic disorder where patients experience regular cycling of numbers of neutrophils and various other haematopoietic lineages. The nadir in neutrophil count is the main source of problems due to risk of life‐threatening infections. Patients with CN benefit from granulocyte colony stimulating factor therapy, although cycling persists. Mutations in neutrophil elastase gene (ELA2) have been found in more than half of patients with CN. However, neither connection between phenotypic expression of ELA2 and CN nor the mechanism of cycling is known.

Materials and methods:  Recently, a multicompartment model of haematopoiesis that couples stem cell replication with marrow output has been proposed. In the following, we couple this model of haematopoiesis with a linear feedback mechanism via G‐CSF.

Results:  We propose that the phenotypic effect of ELA2 mutations leads to reduction in self‐renewal of granulocytic progenitors. The body responds by overall relative increase of G‐CSF and increasing progenitor cell self‐renewal, leading to cell count cycling.

Conclusion:  The model is compatible with available experimental data and makes testable predictions.

Introduction

Cyclic neutropenia (CN) is a rare haematological disorder characterized by periodic severe neutropenia interspersed with normal or near‐normal neutrophil counts, that repeats every 19–21 days (1, 2). Although neutrophil nadir is the cause of the symptoms in this disorder, almost all other cellular elements in the blood may also cycle, being usually out of phase with neutrophils (2). Mutations in the gene coding for neutrophil elastase 2 (ELA2) have been identified in almost half of patients with this disorder, but the exact mechanisms of how these mutations cause the disease remain unclear (3, 4). Therefore, it is not surprising that some scepticism about the role of ELA2 mutation in aetiology of CN persists in the field (5). The majority of mutations in the ELA2 gene are base substitutions leading to loss of splice donor site in exon 4. This forces use of an upstream cryptic splice donor site, that results in loss of 30 nucleotides during RNA processing (3). Patients with CN benefit from pharmacological doses of granulocyte colony stimulating factor (G‐CSF) with rapid recovery of neutrophil count, although cycling of haematopoiesis persists (6, 7).

Several observations are pertinent to set the stage for modelling dynamics of this disorder. ELA2 expression is restricted to cells of granulocyte and monocyte lineage, with highest levels of expression being in promyelocytes and myelocytes. Promonocytes express the gene although at levels significantly lower than granulocyte precursors (8, 9). In addition, myeloblasts also express low levels of the enzyme (8). Many mutations in ELA2 identified in patients with CN often result in aberrant localization of the enzyme in subcellular compartments (4). G‐CSF is the main cytokine that controls proliferation, survival and differentiation of myeloid precursors (10) and accelerates neutrophil maturation (11). Granulocyte progenitors, isolated from patients with CN, are less sensitive to G‐CSF compared to normal controls (12). Neutrophils from grey collies (canine variant of the disease) with CN express normal numbers of G‐CSF receptors that appear to signal normally (13), although similar studies on myeloid progenitor and committed cells in which neutrophil elastase expression is maximal, have not been performed (8). In vitro, neutrophil elastase antagonizes action of G‐CSF by enzymatic cleavage of the cytokine (14), but there is no evidence of release of neutrophil elastase in bone marrow of patients with CN. In vivo studies show that levels of endogenous colony‐stimulating factors are highest with nadir of the neutrophil count (15) and reach a peak concomitant with monocyte count. Endogenous G‐CSF and other cytokines are produced by many cells, including endothelial cells, fibroblasts and monocytes (16, 17). In the grey collie variant of the disease, phlebotomy has no impact on cycling of reticulocytes or neutrophils. However, erythrocyte hypertransfusion stops reticulocyte but not neutrophil cycling (18). Neutrophils and their precursors express G‐CSF receptors and play an important role in clearance of the cytokine from the circulation (19). Finally, apart from being the most important cytokine controlling granulocyte production, G‐CSF is a growth and survival factor for haematopoietic stem cells (HSC) and granulocyte, erythroid, monocyte and megakaryocyte colony‐forming units (CFU‐GEMM) (17) and may increase peripheral blood lymphocyte counts (20).

Despite such a wealth of knowledge about this disorder, an all‐encompassing framework to understand its aetiology has not been provided. It has been postulated that the defect must reside in the stem cell compartment (2, 21). However, this is unlikely, since 19‐ to 21‐day cycling is not compatible with estimated rate of replication of the active stem cell pool (22, 23). Moreover, studies suggest that the effect of the mutated enzyme is restricted to cells that express the gene (i.e. myeloblasts and further cells downstream) (24). Other investigators have proposed models to explain CN on the basis of a multicompartment model of haematopoiesis (25, 26, 27). Haematopoiesis is divided into compartments that harbour stem cells, progenitor cells, more differentiated cells and mature cells that are linked together by cytokine feedback loops. The model specifically considers feedback loops with G‐CSF, Granulocyte‐macrophage colony stimulating factor (GM‐CSF) and erythropoietin, influencing dynamics of all compartments downstream of the HSC pool (25, 28). Schmitz et al. proposed that the main defect in CN is narrowing of variance in transit times of neutrophil precursors, but the authors did not provide a biological basis for such a reduction in the variance. However, this model could be used to study effects of therapy with these cytokines (26, 27).

Recently, a hierarchical model of haematopoiesis based on steady‐state fluxes between successive compartments has been proposed. The process is maintained by replication of HSC that can feed downstream compartments, which metaphorically represent cell lineages at different stages of differentiation (29). The model postulates that cells in a given compartment j divide at a rate r_j that is characteristic of that compartment. During each replication, cells may differentiate (with probability ε) so that the two daughter cells shift to compartment j + 1; with probability 1 – ε daughter cells retain the properties of their parent cell and remain in compartment j (Fig. 1). Under stationary conditions, the size of each compartment is constant and cells lost from one compartment due to differentiation are replaced by cells from the upstream compartment j – 1 (29). Using this model, it is possible to estimate the size of each haematopoietic compartment, rate of replication of cells and average time that a given cell type contributes to haematopoiesis (29). We have shown that in this model, the expected number of cell divisions or ‘compartments’ that link the HSC with circulating blood (K = 32, Fig. 2) is similar to that predicted in other models (30, 31, 32), as well as experimentally inferred from serial telomere shortening (30). It is important to point out that the notion of ‘compartment’ in this model should not be considered as a quantized image of haematopoiesis where various ‘compartments’ represent abrupt transitions, but rather a continuum between HSC and circulating blood with the ‘compartments’ simply being a tool to keep track of the number of cell divisions. Cells may divide and move from one compartment to the next (‘differentiate’), yet morphologically and perhaps functionally may appear to be the same. For example, the CFU‐GEMM cells can be accommodated in compartments 5–8. This is based on experimental evidence of PIG‐A mutations in neutrophils, monocytes and erythrocytes of healthy adults (33). Clearly, these individuals must have at least 1 mutated CFU‐GEMM cell and given the ratio of mutated to normal neutrophils, one can estimate maximum and minimum number of CFU‐GEMM cells at risk of mutation. CFU‐GM cells span compartments 9–11 while CFU‐G span compartments 12–16 based on current estimates of size of the population of cells (32, 34, 35, 36).

Figure 1.

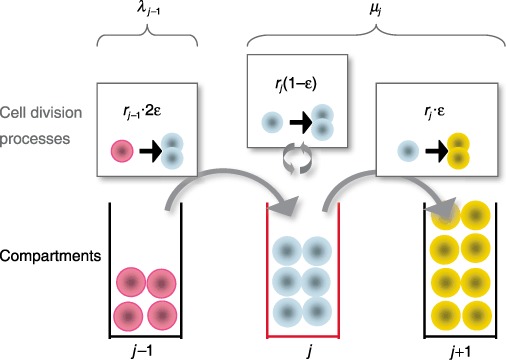
Haematopoietic cell behaviour and dynamics across three adjacent compartments in haematopoiesis. Three cell division processes affect population size in the focal compartment j (lower part of the figure, middle): (i) differentiation of one cell in compartment j – 1 at rate r_{j –1} leads to two new cells in compartment j– upper left; (ii) during self‐renewal at rate r_j, a cell divides and produces an identical daughter cell – upper middle; (iii) differentiation at rate r_j into the downstream compartment j+ 1 implies loss of one cell – upper right. The model parameters are fixed assuming that any compartment maintains constant population of cells, so that net cell loss µ from one compartment is replaced by cells from the upstream compartment, λ. The parameter ε governing intensity of self‐renewal is estimated as ε ≈ 0.85.

Figure 2.

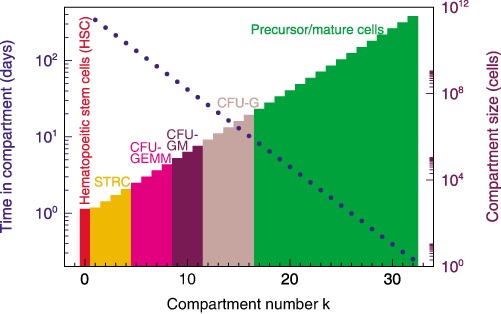
Compartmental architecture and dynamics during normal haematopoiesis. The scheme provides a summary of number of cells at various stages of differentiation from stem cells to the postmitotic pool. Cells in adjacent compartments may be morphologically and functionally similar but require a cell division to move from one compartment to the next as they become more differentiated. In the process they replicate faster and remain in subsequent compartments for shorter time intervals (y‐axes on the left). Blue dots represent average time that a cell will remain in that compartment.

Here, we develop a model of CN based on this framework of haematopoiesis, which (i) proposes a mechanism that explains origin and dynamics of the disease; (ii) is compatible with the most salient molecular biological features known to date; and, perhaps most importantly, (iii) proposes hypotheses that can be tested experimentally.

The model

Let us focus on dynamics of a specific compartment j and investigate time dependence of number of cells in that compartment, N_j. In keeping with the model of haematopoiesis referred to before (29), we consider two elementary processes: differentiation, → , which occurs with probability ε, and self‐renewal, → , which occurs with probability 1 – ε. Symbol  denotes a cell that stays in compartment j while symbol  describes a cell that moves to compartment j + 1 (Fig. 1). Therefore, behaviour of each cell during any division is stochastic in nature (37, 38), although net effect is that cells tend to differentiate rather than to self‐renew (1 > ε > 0.5), compatible with the view of haematopoiesis as a linear process with net cell flow from HSC to the circulating compartment (34, 35, 36). Within compartment j, rate of cell differentiation and transfer into compartment j + 1 is µ_j = r_j(2ε – 1) (29). This loss of cells is compensated for by injection of cells from the upstream compartment, taking place at a rate λ_j–1 = r_{j –1} 2ε (Fig. 1). Consequently, we may readily write down the equation for time dependence of the number of cells in compartment j:

(1)

The stationary solution for eqn (1) is given by

(2)

(1), (2) hold for all compartments with 1 ≤ j ≤ K = 31. In the multicompartment model, N ₀ ∼ 400 cells and represents the active HSC pool that remains constant during adult life (29, 39, 40). We have previously shown that the values of ε and r are robust with respect to changes in number of active stem cells (N ₀) across four orders of magnitude and can be considered as characteristics of normal haematopoiesis (29).

The ELA2 gene is expressed during some stages of myeloid differentiation; therefore, it has no effect on cell compartments where it is not expressed. However, once it is expressed, the mutated gene alters sensitivity of the progenitors to G‐CSF (12). Indeed, the cells need higher amounts of the cytokine to respond. One of the major effects of G‐CSF is to enhance self‐renewal of haematopoietic progenitors (10). We hypothesize that expression of mutant ELA2 reduces self‐renewal of cells in some compartments (due to reduced sensitivity to G‐CSF), with the result that total number of cells will decrease due to efflux to the next compartment. Hence, the given compartment will be depleted of cells with the effect slowly transmitted to downstream compartments. The neutrophil count, hence, will drop.

In order to model cyclic neutropenia, we investigate how small deviations in the number of cells in a given compartment (N_j) alter flux of cells into and out of that compartment, restricting analysis to two adjacent compartments. We introduce a linear feedback function so that depletion of cells from compartment j leads to additional influx of cells from compartment j – 1. In this way, we define a quantity for compartment j, probability of self‐renewal (ε) and replication rate of the cells (r) that is defined by

(3)

Under defined circumstances, it can be shown that oscillations in number of cells within a given compartment will occur and persist without damping, at a frequency given by

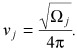(4)

In other words, eqn (4) captures the relationship between frequency of oscillations and the compartment j where they start, due to mutation or other insult. A detailed explanation of the model is provided in the Appendix.

Results

Where does the defect first appear?

In the multicompartment model of haematopoiesis, stem cells replicate at a rate r ₁ = 1/365 days (22, 23) and it was assumed that r and ε would be the same for all compartments (29). The free parameters of the model are fixed using data from expansion during polymorphonuclear leucocyte production, the number of active stem cells and daily output of the blood system, and cell division rates of stem cells and granulocyte precursors. This leads to r = 1.26 (cf. eqn 2) and ε = 0.85 (34, 35, 36). Given that period of the cycles in most patients with CN is between 19 and 21 days, using (3), (4), we can estimate the earliest compartment j where the defect has to be active to give the required frequency of oscillations. Our model suggests that j ≈ 21 (for both values of the period) which localizes the defect downstream of the CFU‐G compartment (cf. Fig. 2) (29). For the rare patient with longer cycles (< 52 days) (41), the model predicts that j > 17, which again places the defect downstream of the CFU‐G compartment. In other words, for a period of 19–21 days, compartment 20 will be the earliest compartment with a normal ε(ε = 0.85) and we predict that 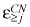 > 0.85 in cells of the granulocyte lineage.

Progenitor cell self‐renewal and cycling

The above calculations for compartment j assume that r = 1.26 remains constant even in CN. The rationale for this proposition is the observation that therapy with G‐CSF mainly shortens maturation time of cells in the postmitotic compartment rather than to increase the rate at which cells divide upstream in the haematopoietic cascade (26, 27). Moreover, progenitors from patients with CN are less sensitive to G‐CSF (12), and this cytokine is essential for self‐renewal of myeloid progenitors and their progeny cells (17, 42). Hence, reduction in sensitivity to G‐CSF will reduce self‐renewal of cells that express ELA2. Consequently, we propose that the variable affected in the disorder is ε. If we accept this conjecture, the model suggests that defect in CN phenotypically results in 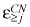 > 0.85, leading to decrease in self‐renewal of the progenitor cells and, ultimately, to a fall in neutrophil production (Fig. 3). Consequently, we expect decrease in cell output due to rapid cell transit of neutrophil precursors during haematopoiesis, a prediction that can be tested. Elevated ε means that neutrophils from patients with CN will have longer telomeres compared to normal controls, since their progenitors undergo less divisions compared to normal. Therapy with G‐CSF reduces ε and ε^CN and enhanced progenitor cell renewal results in increase of neutrophil production, although with a delay since upstream compartments must themselves expand before they can replenish downstream compartments (Fig. 3). If this scenario is correct, G‐CSF therapy should lead to shortening of neutrophil telomeres. Although G‐CSF shortens period of the oscillations, our model is not in conflict with this fact since the major effect of G‐CSF is to shorten transit time of cells in the postmitotic pool (26). In Fig. 4, we superimpose serial neutrophil counts observed in a patient with CN on cycling predicted by the model. The model captures overall behaviour without delving into detailed self‐regulatory mechanisms of haematopoiesis. Finally, note that eqn (2) can be rewritten as C = (1/r)[1 – (1/2ε)]⁻¹; if  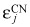> 0.85, then the equilibrium value, 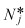, is reduced and compatible with the observation that neutrophil count in patients with CN typically oscillates around a value lower than the average in normal individuals.

Figure 3.

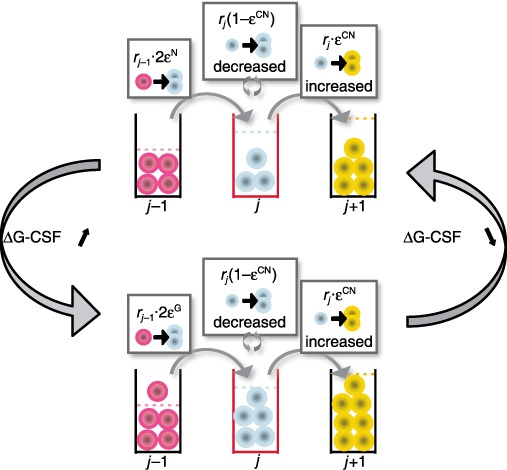
Schematic representation of the mechanism of cyclic neutropenia. Myeloid precursors that express mutated ELA2 have a higher ε (ε^CN > ε, upper panel); their self‐renewal capability is therefore reduced and downstream compartments have less cells, due to decreased net output from the compartment where the defect is phenotypically present. The lower neutrophil count increases G‐CSF level. The organism responds to this increase of G‐CSF by reducing ε in progenitor cells (ε^G < ε, lower panel). Downstream compartments are replenished and neutrophil output increases. This higher neutrophil count will decrease levels of G‐CSF; progenitor cell self‐renewal decreases and the cycle repeats itself. Therapy with G‐CSF ensures that neutrophil counts do not fall beneath a critical level.

Figure 4.

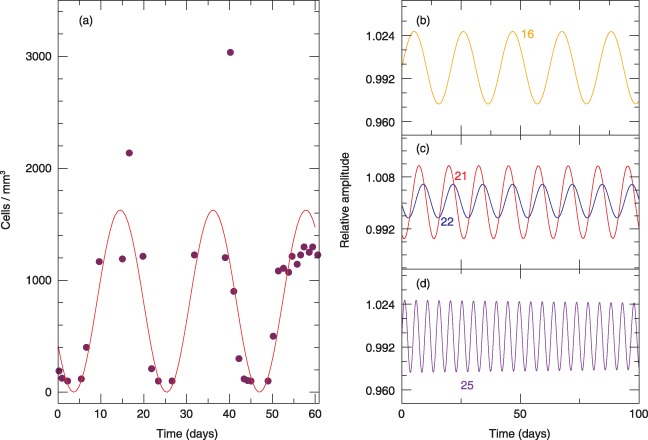
Superimposition of neutrophil cycling (solid curve) as predicted by the model, with experimental data taken from Hammond et al. ( 6 ) (solid circles). Normal range for neutrophils is 1.9–7.0 × 10³/mm³. (a) Simulation is for a mutation that appears in compartment j = 21 with a period T = 21 days. In (b) to (d), we show simulations of cycling frequency due to hypothetical mutations that occur in upstream (j = 16) or downstream compartments (j = 25).

We performed numerical simulations to couple additional compartments downstream of compartment j where the phenotypic effect is first observed in neutrophil lineage. All downstream compartments also oscillate at the same frequency but with a delay so that a ‘travelling wave’ appears down the compartments. In other words, the compartments oscillate out of phase. However, overall frequency of the oscillations is determined by location of the compartment where the defect initially appears. If the mutation appears in compartment j < 21 or j > 21, frequency of the oscillations will decrease and increase, respectively (Fig. 4b–d).

Discussion

Despite significant progress in elucidating the molecular biology of CN, aetiology of cycling in this disease has not been adequately explained (43). Here, we built on a recent multicompartment model of haematopoiesis to propose a mechanism for explaining cycling behaviour, and a testable hypothesis for this disorder (29). The underlying premise is feedback regulation between consecutive compartments, a process that is widespread in physiological systems (44, 45, 46). We postulate that the underlying defect in CN leads to reduction in the self‐renewal capability of cells immediately downstream of CFU‐G cells (that is, myeloblasts). Reduction in self‐renewal that starts in a particular compartment leads to loss of cells from that compartment that ultimately transfers fewer cells to downstream compartments with associated reduction in granulocyte output. The body responds to low neutrophil count with a relative increase of G‐CSF (and GM‐CSF). These cytokines in turn increase self‐renewal capacity of the CFU‐GM, CFU‐G (17, 42) and downstream compartments, leading to overall reduction in ε with associated increase in neutrophil output. However, neutrophils express G‐CSF receptors that act as sinks for the cytokine (19). Hence, as the neutrophil count recovers, cytokine concentrations decrease and the process repeats itself, given the incapacity of ε in the original compartment to return to normal values.

It is clear that although haematopoiesis is scattered in multiple sites of red bone marrow, there must be significant synchronization of cell replication for cycling to be observed. Synchronization of function in the body occurs if cells are coupled together either structurally or functionally via ion channels, or chemically. Separation of haematopoiesis in space excludes both structural and electrical cellular coupling, leaving chemical coupling as the only alternative. Both G‐CSF and GM‐CSF could provide such coupling from their known biology. The reader may wonder why oscillations are not seen in healthy adults if these inter‐compartment feedback loops are present. The explanation for this is that in normal haematopoiesis, there is no compartment with an abrupt loss of cells, as occurs due to mutations in ELA2. It is this loss of cells that amplifies the feedback signal (G‐CSF) leading to the oscillations. Under normal physiological conditions, changes in G‐CSF are small enough that the system is essentially always in a steady state. Interestingly, some patients with myelodysplastic syndrome (47) or myeloproliferative disorders, develop cycling haematopoiesis as an acquired phenomenon, the latter typically after starting therapy with cytoreductive agents such as hydroxyurea (48). These observations can be rationalized by our model, since patients with myelodysplasia can have defective differentiation of cells (altered ε) with depletion of specific differentiation compartments in haematopoiesis. Hydroxyurea can reduce neutrophils and their precursors, effectively increasing the half‐life of G‐CSF with amplification of its circulating concentration and onset of cycling. It would be of great interest to study sensitivity of myeloid precursors to G‐CSF in such patients.

Our model and the literature

The current model is consistent with observations that granulocyte‐committed progenitor cells have reduced responsiveness to both G‐CSF and GM‐CSF (12). Both cytokines are known to play important roles in growth, survival and self‐renewal of progenitor cells (17, 42). In the canine variant of the disease (grey collie syndrome), neutrophil progenitors express normal levels of G‐CSF receptors and perhaps the same is true for the human disorder (13). However, both G‐CSF and GM‐CSF share downstream mediators that could be the target of abnormal elastase produced in patients with this disease (17). Indeed, many mutations in ELA2 found in patients with CN lead to abnormal cytoplasmic accumulation of the enzyme where it may interact with second messengers involved in signalling from activated type 1 cytokine receptors (4, 49).

Our model predicts that the disorder cannot arise in progenitor cells earlier than CFU‐GM and contradicts other suggestions that the disorder is due to a defect at the stem cell level (2, 21). The current model fits with observation that mutations in ELA2 have a local effect in cells where it is expressed (24). In particular, eqn (7) allows one to identify the compartment in which the coupling leads to undamped oscillations. Moreover, ELA2 is known to be expressed in cells at the myeloblast stage, which are the closest cells to CFU‐GM in the haematopoietic cascade (8). The model is also compatible with the observation that progenitor cells can also cycle in this disorder (50, 51). Cycling at the level of the CFU‐GM can also explain monocyte oscillations that are observed in the disease. Monocytes are also an important source of G‐CSF that can provide necessary feedback to increase CFU‐GM self‐renewal with repopulation of compartments and increased output of neutrophils (17). However, one may question whether our model could explain cycling in other lineages, such as reticulocytes and lymphocytes. Cycling of G‐CSF and GM‐CSF do not only influence cells at the CFU‐GM stage, but can also increase self‐renewal and proliferation of CFU‐GEMM, which can lead to cells of the erythroid and megakaryocytic lineage with cycling in these cell lineages as well (17). Finally, G‐CSF can also increase lymphocyte counts and cycling of the cytokine could lead to cycling of lymphocytes (20).

In grey collie syndrome, neutrophils cycle with a shorter period than typical in the human illness. Rate of HSC replication scales allometrically with mass of the mammal as R(M) ~ M ^−1/4 (40). If human and canine illnesses are both due to a similar genetic problem, and architecture of haematopoiesis is conserved across mammals, allometric scaling allows us to estimate period (T) of the canine illness from that of humans (29). This is simply given by

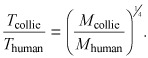Given that M _collie ∼ 13 kg, T _human ∼ 20 days, and M _human∼ 70 kg, it follows that T _collie ∼ 14 days, as observed in these animals (2).

The proposed model is purposefully kept simple. We consider dynamic interactions between two adjacent compartments: a normal compartment (j) where cells do not express ELA2 and an adjacent one (j + 1) where cells start to express and be affected by the mutated gene. A linear feedback mechanism between the two compartments is assumed, acting via cytokines such as G‐CSF (and others), although their concentrations are not explicitly modelled. Therefore, the model in its present format cannot be used to evaluate impact of therapies or potential interaction between cytokines that can act together on various compartments, as proposed by other investigators (26, 27). Moreover, it is possible that more complex behaviour, including intermittent peaks (as observed in some patients), may be due to stochastic fluctuations between multiple compartments. These details cannot be captured by our model at its current level of complexity. We also consider that the main effect of G‐CSF is to enhance self‐renewal of progenitor cells (17, 42), leaving replication rate (r) of cells constant. Although we cannot exclude an impact of G‐CSF on ‘r’, clinical and experimental observations suggest that rapid release of neutrophils by G‐CSF is due to shortening of transit time of cells in the postmitotic compartment rather than by accelerating rate of replication of progenitors (26, 27), implying that the effect on ε is more important than that on r. Despite its simplicity, our model makes a testable prediction: Neutrophils from patients with CN (before therapy with G‐CSF) should have longer telomeres compared to age matched controls. As a corollary, therapy with G‐CSF should lead to telomere shortening due to higher self‐renewal of progenitors during granulopoiesis.

In summary, our linear response model suggests that one potential mechanism to explain phenotypic effect of mutations in ELA2 in patients with CN is by decrease in self‐renewal of late granulocyte–monocyte progenitors and myeloblasts. The effect of G‐CSF feedback (in response to low neutrophil counts) is to increase progenitor cell self‐renewal and, hence, output of neutrophils. Scavenging of G‐CSF by increasing neutrophil count decreases the progenitor pool leading to reduction of neutrophil output. Pharmacological (therapeutic) doses of G‐CSF increase self‐renewal of CFU‐GM and downstream progenitors and increase neutrophil output. Cycling persists due to scavenging of the cytokine by neutrophils, blunted sensitivity of progenitors to this growth factor, and persistence of mutated ELA2 and its effect on ε in the cell compartments where it is expressed.

Appendix

Haematopoiesis is a multistep process whereby cells derived from haematopoietic stem cells (HSC) progressively expand and differentiate into all the circulating blood cells. Conceptually, each cell replication event is considered to be associated with a decision by progeny cells to either remain in a given compartment or move to the next where they become more specialized. However, during normal haematopoiesis, number of cells within each compartment remains constant. Let us consider dynamics of a specific compartment j and investigate time dependence of number of cells in that compartment, N_j. In keeping with the multicompartment model of haematopoiesis previously described (29), we consider two elementary processes: differentiation, → , which occurs with probability ε, and self‐renewal, → , which occurs with probability 1 – ε. Symbol  denotes a cell that stays in compartment j while symbol  describes a cell that moves to compartment j + 1 (Fig. 1). Behaviour of each cell during any division is stochastic in nature (37, 38), although the net effect is such that cells tend to differentiate rather than to self‐renew (1 > ε > 0.5), compatible with the view of haematopoiesis as a linear process with net cell flow from HSC to the circulating compartment (34, 35, 36). Within compartment j, rate of cell differentiation and transfer into compartment j + 1 is µ_j = r_j(2ε – 1) (29). This loss of cells is compensated for by injection of cells from the upstream compartment, taking place at a rate λ_j–1 = r_{j –1}2ε (Fig. 1). Consequently, we may readily write down the equation for the time dependence of the number of cells in compartment j:

(1)

The stationary solution for eqn (1) is given by

(2)

(1), (2) hold for all compartments with 1 ≤ j ≤ K = 31. In the multicompartment model, N ₀ ∼ 400 cells and represents the active HSC pool that remains constant during adult life (29, 39, 40). We have previously shown that values of ε and r are robust with respect to changes in number of active stem cells (N ₀) across four orders of magnitude, and can be considered as characteristics of normal haematopoiesis (29).

Let us investigate how time dependence of N_j is affected by small deviations from its stationary value. Dependence of both coefficients of eqn (1) on ε make it natural to expect that ε may be involved in the response of the haematopoietic system to external perturbations. Let us assume that due to a mutation in ELA2, there is a small deviation of size of the cell population N_j in a specific compartment j with respect to its stationary value (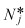) (eqn 2). To first order we may write for the changes in the rate coefficients

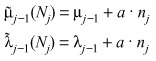(3)

where n_j = 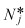 – N_j, and a > 0 is a parameter that describes strength of the response (Fig. 3). Such response mechanisms can in principle alter either r_j or ε but the effect is such that whenever N_j decreases, there is an increase in transfer of cells from compartment j – 1 to j. This is based on the well‐established principle of feedback that occurs in many physiological processes, including haematopoiesis (44, 45, 46). In the absence of data suggesting a more complex feedback process, we consider a linear mechanism since it is the simplest. For two consecutive compartments, we may write

(4)

where 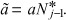Depending on the nature of the eigenvalues of the matrix in eqn (4), several types of behaviour are possible. Here we are interested in exploring the possibility of sustained (undamped) oscillations. These will be present whenever the eigenvalues x _1,2 are purely imaginary. They can be readily computed as

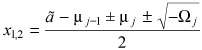(5)

with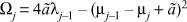 

Whenever 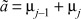, the real parts of the eigenvalues vanish, with Ω_j reading

(6)

Hence, oscillations will persist without damping at a frequency given by

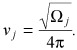(7)

In other words, we have established a relationship between frequency of oscillations and compartment location. For convenience of the readers, a summary description of all parameters used in the model is provided in Table 1.

Table 1.

Summary of the parameters used to describe the model of haematopoiesis and cyclic neutropenia

Parameter	Description
ε	Self‐renewal probability of haematopoietic cells
r	Ratio of cell division rates in adjacent compartments
rj	The rate of replication of cells in compartment j
Nj	The number of cells in compartment j
µj	The rate of net loss of cells from compartment j to j + 1
λj−1	The rate of cell gain from compartment j ‐ 1 to j
a	Factor by which compartment j – 1 increases input to compartment j in response to a decrease in Nj
vj	Frequency of the oscillations as a function of the compartment where they arise
Ωj	Summary variable that is a function of r, ε and j