Unmasking the CA1 Ensemble Place Code by Exposures to Small and Large Environments: More Place Cells and Multiple, Irregularly Arranged, and Expanded Place Fields in the Larger Space

Abstract

In standard experimental environments, a constant proportion of CA1 principal cells are place cells, each with a spatial receptive field called a place field. Although the properties of place cells are a basis for understanding the mammalian representation of spatial knowledge, there is no consensus on which of the two fundamental neural-coding hypotheses correctly accounts for how place cells encode spatial information. Within the dedicated-coding hypothesis, the current activity of each cell is an independent estimate of the location with respect to its place field. The average of the location estimates from many cells represents current location, so a dedicated place code would degrade if single cells had multiple place fields. Within the alternative, ensemble-coding hypothesis, the concurrent discharge of many place cells is a vector that represents current location. An ensemble place code is not degraded if single cells have multiple place fields as long as the discharge vector at each location is unique. Place cells with multiple place fields might be required to represent the substantially larger space in more natural environments. To distinguish between the dedicated-coding and ensemble-coding hypotheses, we compared the characteristics of CA1 place fields in a standard cylinder and an approximately six times larger chamber. Compared with the cylinder, in the chamber, more CA1 neurons were place cells, each with multiple, irregularly arranged, and enlarged place fields. The results indicate that multiple place fields is a fundamental feature of CA1 place cell activity and that, consequently, an ensemble place code is required for CA1 discharge to accurately signal location.

Introduction

The theory that the hippocampus is central to the neural representation of allocentric space (O'Keefe and Nadel, 1978) is based on the location-specific discharge of hippocampus place cells in freely moving rats (O'Keefe and Dostrovsky, 1971; O'Keefe, 1976), a signal subsequently demonstrated in freely moving monkeys, as well (Ludvig et al., 2004). Place cell spatial firing is routinely characterized by recording their discharge as rats move in two dimensions in cylinders, boxes, tracks, and mazes, most with maximal linear dimensions <1 m. In these conditions, most place cells have a single place field (for review, see Muller, 1996).

There are two major hypotheses of how neural activity codes information, and it remains unclear which of them better accounts for the hippocampus place code. According to local or dedicated-coding hypotheses, the discharge of an individual cardinal cell is an independent feature detector, selectively tuned to a complex stimulus or concept (Konorski, 1967; Barlow, 1972), like a face (Perrett et al., 1982) or a person (Quiroga et al., 2005). The spatial firing of individual place cells is routinely analyzed as exemplary cardinal cells for “place” (Muller et al., 1987; Shapiro et al., 1997; Fenton et al., 2000; Hollup et al., 2001; Lenck-Santini et al., 2001; Knierim, 2002; Huxter et al., 2003; Kentros et al., 2004). Even a form of phase-coding, the systematic shift of spiking relative to the theta local field oscillation, is still a dedicated code because it is the theta phase of the discharge of an individual place cell that may indicate the rat's location more accurately than the firing rate of the cell (Huxter et al., 2003). Within dedicated coding, position is signaled by an average location indicated by many place cells acting as independent feature detectors.

According to the major alternative, distributed or ensemble-coding hypotheses (Hebb, 1949; Abeles et al., 1993), the encoded information is distributed between cells. Each cell is active in multiple representations, and therefore cannot independently signal information unambiguously. A unique across-cell ensemble pattern of discharge defines a specific representation. Ensemble coding is commonly used to describe the hippocampal representation of whole environments because place cells are active in multiple environments, and ensemble activity is unique for each (Muller and Kubie, 1987). However, other work suggests that position within an environment is also represented by a place cell ensemble code (Samsonovich and McNaughton, 1997; Redish et al., 2000; Harris et al., 2003).

The dedicated-coding and ensemble-coding hypotheses predict different place codes in natural habits because such spaces are immensely larger than place cell recording setups. Compared with small environments, place fields may be enlarged (Muller and Kubie, 1987) and/or more pyramidal cells may be recruited to be place cells. Importantly, dedicated coding predicts cells with single place fields but ensemble coding predicts multiple place fields. Although technical barriers prevent recordings within natural habitats, we created a laboratory environment to determine whether place cells respond like cardinal cells or ensemble elements for “place” as rats move in three dimensions through an uncommonly large recording chamber (Fig. 1).

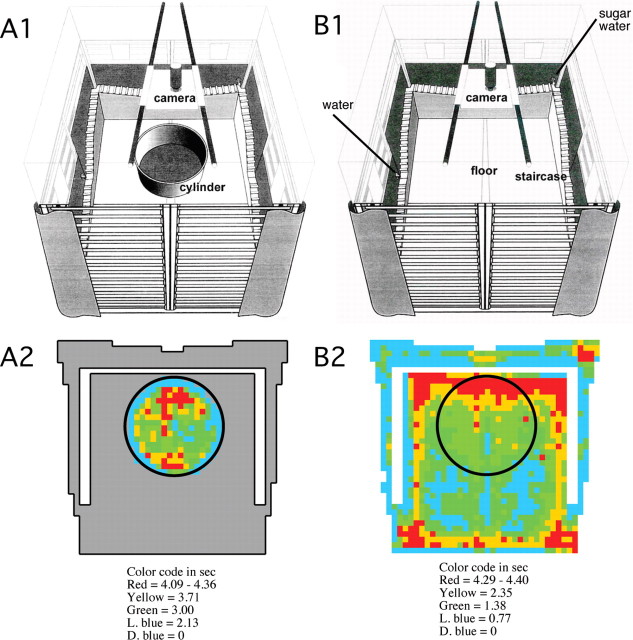
Figure 1.

Schemes of the 68-cm-diameter cylinder (A1) and the 150 × 140 cm chamber (B1). A2, B2, The corresponding time-in-location (“dwell”) maps averaged across rats and sessions illustrate that rats visited all parts of both the cylinder and chamber and that sampling of the cylinder and chamber floors were similar. Rats preferred to spend time at the periphery of the environment. The region of low dwell at the periphery of the environments is attributable to rats rearing on occasion. This can make it appear the rat is beyond the enclosing wall.

Some of these data were reported in abstract form (Ludvig et al., 2006).

Materials and Methods

Subjects.

Adult male Long–Evans hooded rats were obtained from a commercial breeder (Taconic Farms). The rats were 350–400 g at the start of training. All procedures received Institutional Animal Care and Use Committee approval and were in accordance with institutional and National Institutes of Health guidelines.

Recording environments.

Two recording environments were used (Fig. 1). One was a standard apparatus for place cell recordings. It was a 68-cm-diameter gray cylinder with a polarizing card on the wall that occupied 90° of arc. The other apparatus was a monkey chamber (Ludvig et al., 2004) that was adapted for this study. The chamber had a 150 × 140 cm footprint. It was equipped with stairs on three sides. The rat could traverse the stairs to access two drinking spouts. One spout provided plain water and the other contained a sucrose drinking solution. Access to fluid motivated the rat to traverse the stairs and to continuously forage for scattered food for >1 h. The rat could look through the chamber bars on the side without stairs and see into the surrounding room. The cylinder was positioned within the chamber for cylinder recordings and it was removed for chamber recordings.

Behavioral training.

The rats were trained in five consecutive phases. In phase 1, the rats were trained to forage for food on the floor of the chamber. First, the rats were handled for several days and exposed to 20 mg food pellets (Bioserve) in their home cages. Then the animals were placed in the chamber, with the floor of this chamber separated from the staircase by a cardboard barrier. In 15–30 min daily sessions over 5 d, the rats were allowed to forage for scattered food pellets triggered by an automatic overhead pellet feeder. The rats were mildly food-deprived, because no more than 12 g of conventional Purina food pellets were provided to them for the night before each of the training sessions. In phase 2, the rats were trained to traverse the staircase for something to drink, with the cardboard barrier still separating the stairs from the floor. The sucrose concentration gradually decreased from 10 to 2% by the end of this training phase. The rats were placed onto the staircase for two 15 min daily sessions over 5 d, each followed by a 5 min foraging session on the floor. They were given 2 ml of water and 12 g Purina pellets for the night before such sessions, and ad libitum access to water for 1 h after each session. In phase 3, the cardboard barrier was removed and the rats were allowed to both forage for food pellets on the floor and traverse the staircase for water and sucrose, in five consecutive daily sessions, 15–30 min each. In phase 4, the rats were trained to forage for the 20 mg food pellets scattered on the floor of a 68-cm-diameter cylinder placed inside the recording chamber. Finally, in phase 5, the rats received cylinder and chamber training screening sessions, at least once per week, to keep the experience of the two environments familiar, while the electrodes were advanced to record CA1 single units. The exact number of these screening sessions varied from rat to rat.

Electrophysiology.

Once the rats were foraging continuously, they were prepared for place cell recordings. Tetrodes (O'Keefe and Recce, 1993; Quirk and Wilson, 1999) made by twisting four strands of 25 μm nichrome, were used to aid unitary waveform discrimination. Eight tetrodes were loaded into a custom machined microdrive assembly (Bio-Signal Group). The assembly was surgically implanted under pentobarbital anesthesia (50 mg/kg) to position the tetrodes above the pyramidal cell layer in the dorsal hippocampus (centered at anteroposterior, 3.8 mm; lateral, 2.5 mm; dorsoventral, 2 mm relative to bregma) (Paxinos and Watson, 1986). The rats were allowed to recover for at least 1 week before the tetrodes were individually advanced in ≤50 μm steps during the course of 1–2 weeks. The goal was to position as many of the eight tetrodes in the dorsal CA1 pyramidal layer at the same time.

Extracellular potentials were buffered by unitary gain amplifiers plugged into the microdrive connector on the rat's head. The buffered signals were transmitted to main amplifiers (AM Systems) along wires. Action potential (AP) (300–10,000 Hz) bandpass-filtered signals were digitized (32 kHz), time-stamped (100 μs resolution), and 2 ms tetrode waveforms were recorded with the rat's position at 60 Hz to create a spike-at-position time series using custom data acquisition software (AcX; A. A. Fenton) synchronized to the tracking software (iTrack; Bio-Signal Group). Local field potentials were bandpass filtered (0.1–300 Hz) and digitized at 2 kHz.

Single-unit isolation.

Unitary spike waveforms were discriminated off-line using manual, custom waveform feature clustering software (Wclust). The quality of isolation for each cell was estimated by a measure called isolation information (I_iso). I_iso was computed as a symmetric distance between the action potential waveform feature probability distribution of a putative cell {P_j } and a waveform feature probability distribution of action potentials that were not in the cluster {Q_j}. Each waveform feature probability distribution was defined in the multidimensional waveform feature space and I_iso was the resistor average of the pair of Kullback–Leibler divergences (d_PQ, d_QP) computed between them (Kullback and Leibler, 1951):

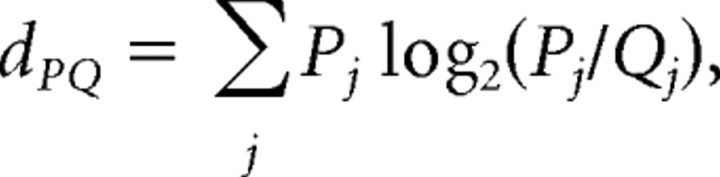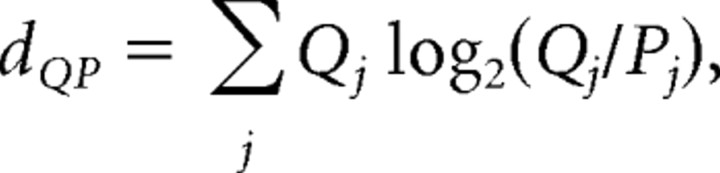and

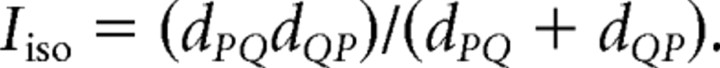I_iso quantifies the isolation quality and compactness in units of information (bits) of a unitary waveform. This provides a straightforward interpretation, independently of which features were used to define the single unit. Each bit of information about waveform features gained by knowing which single-unit cluster the features are from, approximately means a 50% reduction of the volume of the total feature space occupied by these cluster-specific features. The waveform feature probability distributions were defined in the eight-dimensional hyperspace created by the eight waveform parameters that contributed most to isolating the unit. Two versions of I_iso were computed. I_iso(background) estimates how well the cluster of features was isolated from all other action potentials that were recorded by the tetrode. I_iso(background) was computed by comparing the waveform feature probability distribution of a unit to the waveform feature probability distribution of action potentials not in the cluster of the unit. I_iso(neighbor) estimates the uniqueness of the waveform features of the unit. I_iso(neighbor) was computed by measuring I_iso between the waveform feature probability distribution of a unit and the waveform feature probability distribution of each other unit. The lowest I_iso was taken as I_iso(neighbor).

Analyses of place cell firing.

Data were collected from four rats, during cylinder and chamber recording sessions in the sequence cylinder–chamber–cylinder. Cylinder sessions lasted 15 min and chamber sessions lasted 60 min, which yielded similar sampling of the available space (Fig. 1). Sometimes the rat was not willing to move sufficiently in the second cylinder session and recording was aborted. Between recording sessions, the rat was disconnected from the recording system and placed in its home cage for 5–10 min while preparing for the next recording. Each rat was recorded on several days but data from only 1 d were analyzed unless the electrodes were advanced to sample a different ensemble of cells.

Single units with long duration action potentials (>350 μs), low (<5 AP/s) firing rates, and a tendency to fire in bursts (peak interspike interval, ≤10 ms) were distinguished from those with brief action potentials (<350 μs), high (>5 AP/s) firing rates and low tendency to burst, criteria corresponding to the putative classification of hippocampal pyramidal cells and interneurons, respectively (Ranck, 1973). Only putative pyramidal cells were studied. Conventional firing rate analyses, which average spike counts in 4.7 × 4.7 cm pixel locations across the entire recording session were performed to characterize location-specific firing in the cylinder and chamber (Fenton et al., 2000).

Place cell classification.

To objectively classify a cell as a place cell, we computed its firing rate map and, from that, its information content (Skaggs et al., 1993) and coherence (Muller and Kubie, 1989). Information content (bits/AP) measures the extent to which the discharge of an action potential reduces the uncertainty of the rat's position. Coherence is a nearest-neighbor two-dimensional positional autocorrelation that measures the local smoothness of the firing pattern. The correlation coefficient is z-transformed to standard units (Bostock et al., 1991). A cell was considered a place cell if coherence was >0.25 and information content was >0.5 bits/AP and if the cell had at least one place field.

Place field classification.

A place field was identified as a region of the firing rate map in which at least nine contiguous pixels had a rate >0 AP/s. All pixels in a place field shared at least one side with another pixel in the place field. The “in-field rate” was defined as the total number of action potentials emitted in the place field divided by the total time the rat was detected in the place field. The “out-of-field rate” was defined as the total number of action potentials that occurred in pixels that were not in any place field divided by the total time the rat was detected in the corresponding places. The proportion of the space in which a place cell fired was estimated as “the proportion of active pixels.” It is the number of pixels in which one or more action potentials was detected divided by the total number of pixels the rat visited.

Firing rate map similarity.

The similarity of two firing rate maps was estimated by computing Pearson's correlation between the firing rates in corresponding pixels in the two maps. Only pixels that were visited by the rat in the two recordings were used for the correlation. The correlation is reported, but for statistical comparisons, the correlation coefficient was z-transformed to standard units (Bostock et al., 1991). We also computed the rate map similarity after shrinking the chamber firing rate pattern so that the length of a side matched the diameter of the cylinder firing rate pattern.

Spatial autocorrelation analyses.

We looked for a characteristic spatial arrangement of the multiple place fields by computing the spatial autocorrelation of the firing rate map (Hafting et al., 2005). The firing rate map was systematically shifted against itself by a specific pixel offset, and then Pearson's correlation was calculated between the firing rates in all the overlapping pixels. The correlation was calculated at each of all the shifts that resulted in sufficient overlap to calculate the correlation. The correlation at the center of the autocorrelation map represents no shift and is therefore exactly 1. Each value in the spatial autocorrelation map represents the correlation after shifting the map the corresponding amount from the center. To look for periodicity, we first defined peaks in the autocorrelation map. Visual inspection failed to reveal a characteristic periodicity in the autocorrelation maps, which typically did not have noncentral regions with significant correlations. In an effort to characterize the pattern, we defined correlation peaks by first setting a threshold to only consider pixels with a correlation >0.06. (Substantially higher thresholds produced very few peaks.) A peak was defined as a set of at least 16 adjacent locations that each shared a side with at least one other location in the peak. The centroid of the peak was taken as the location of the peak. We then defined the characteristic central angle in the autocorrelation map as the angle between the nearest neighbor peak (NN), the central peak (CP), and a third peak (TP). TP was chosen to satisfy two criteria. First, if possible, it was not collinear with CP and NN. Second, it maximized the following ratio:

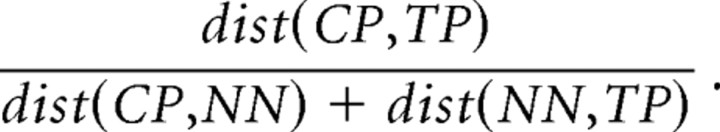The distance to the nearest neighbor peak, dist(CP,NN), was used to estimate the spatial scale of the autocorrelation.

Population vector analyses.

CA1 population activity characterized as a firing rate vector was used to estimate the rat's location during a short period of time (Wilson and McNaughton, 1993; Fenton and Muller, 1998). The activity of simultaneously recorded cells was characterized as a population vector at each time step. The duration of time steps was varied from 0.17 to 5 s. The rat's position was decoded from the activity of ensembles comprised of 5–25 cells using a simple template-matching method (Wilson and McNaughton, 1993; Fenton and Muller, 1998). At each location, the average firing rate of each cell in the ensemble was used to construct a location-specific template firing rate vector. The decoded position was the location that maximized the projection of the current firing rate vector onto one of the location-specific template vectors. If there was no activity during a time step, the current vector was null, and no attempt to decode position was made for the time step. This method was chosen because it is an explicit test of how well location-specific firing rate itself predicts the rat's location (Wilson and McNaughton, 1993; Fenton and Muller, 1998). Note that the method makes no assumptions about the importance of previous or subsequent discharge and therefore does not attempt to optimize the decoding of position from spike trains (Brown et al., 1998).

We used simulated place cell spike trains to estimate how well position could be decoded if we had recorded more cells simultaneously. A simulated Poisson spike train for each place cell was derived from the average firing rate map of the cell by generating a spike if a random number exceeded the probability of observing a spike during the time step at the rat's current location (Fenton and Muller, 1998). This common but oversimplified inhomogeneous Poisson model was used because our goal was to reproduce place cell positional firing patterns in a straightforward manner rather than estimate the complex temporal dynamics of these spike trains (Barbieri et al., 2001). The positional firing patterns of the 322 place cells in the chamber were used to generate 322 location-specific simulated spike trains for a single position time series taken from a real recording. This simulated a 322 place cell ensemble recording in which temporal coordination beyond location specificity was ignored. The same was done for the cylinder, in which case a randomly selected subset of 322 place cell recordings from the two cylinder sessions was used. The rat's position was then decoded from the simulated 322 cell ensemble spike trains.

Histology.

After recordings, the locations of the implanted tetrodes were verified with histological studies. The rats were killed with urethane (2 g/kg, i.p.). This was followed by the successive transcardial perfusions of PBS and a 10% formalin solution. The formalin-fixed brain was removed, postfixed in the same formalin solution for a week, embedded in paraffin, and sectioned. Twenty micrometer sections were prepared, stained with cresyl violet, and examined with a light microscope. As shown in Figure 4C, the tracks of the tetrodes were located in the CA1 region.

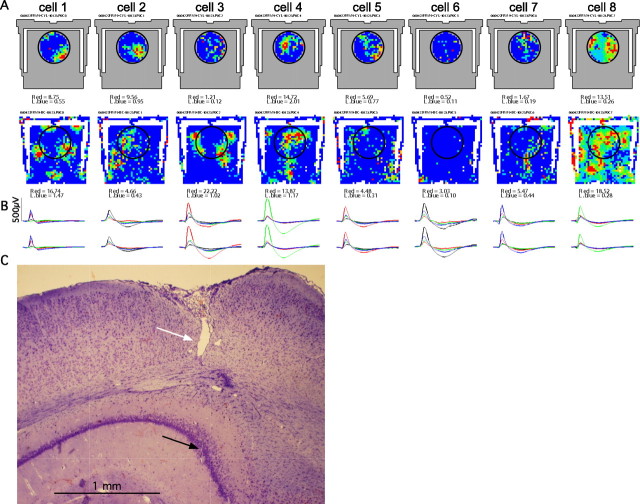
Figure 4.

A, Firing rate maps in the cylinder and chamber from eight place cells that were recorded simultaneously on the same tetrode. Cell 1 is unusual because its discharge was organized in a hexagonal grid that is characteristic for grid cells in the medial entorhinal cortex. The hexagonal pattern appears to be projected onto the two-dimensional plane of the floor, such that firing is at the appropriate parts of the stairs, although these are elevated positions in the chamber. It is as if the hexagonal pattern extends in the z-dimension. In the cylinder, this cell had a main field and opposite it, a smaller secondary field. It is noteworthy that the spatial organization of discharge could not be appreciated in the small standard cylinder. Cells 2–7 illustrate that cells in the same ensemble have multiple enlarged place fields, as well as increased recruitment of silent pyramidal cells to active place cells. Cell 8 is a putative interneuron. Except for cell 1, none of the others has a hexagonal grid-like firing pattern. B, Tetrode waveforms (2 ms) of the cells. The waveform of cell 1 is very narrow, even narrower than the interneuron, making it likely this is a recording from an entorhinal cortical fiber projecting to CA1 (Leutgeb et al., 2007). C, The cells were recorded in the dorsal CA1 region. The lesion caused by the guide cannula (white arrow) and the tetrode wires (black arrow) are indicated.

Results

Multiple place fields

CA1 positional firing patterns in the cylinder and chamber appeared to be independent, suggesting that a complete remapping occurred in all four examined rats (Fig. 2A). Indeed, the spatial similarity of the firing rate maps obtained in the prechamber and postchamber cylinder sessions was far higher than the near-chance similarity of the maps from the cylinder and chamber sessions (Fig. 2B) (p < 0.001). The same result was obtained if the firing pattern in the chamber was scaled to match the diameter of the cylinder before calculating the similarity (average ± SEM correlation, 0.06 ± 0.01). Of the pyramidal cells we recorded in both environments, 222 were place cells in at least one of the environments. Of these 222, 39% were place cells in only one environment and 61% were place cells in both. It was more likely to observe place cell firing in the chamber (84%) than the cylinder (77%; z = 2.1; p < 0.02). Thus, CA1 positional firing patterns in the cylinder and chamber were independent, and more cells expressed place fields in the chamber.

Figure 2.

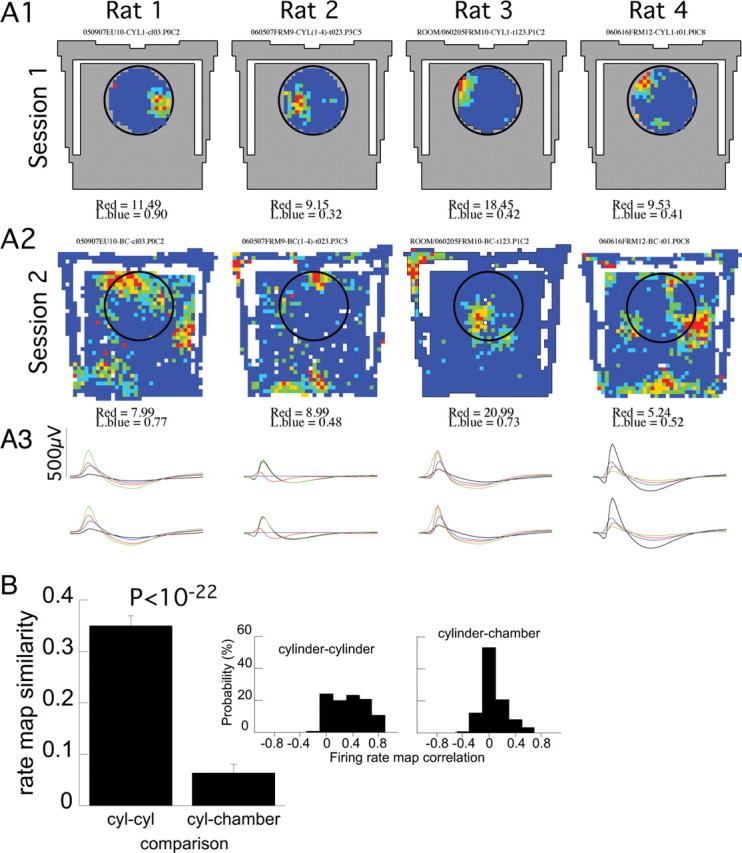
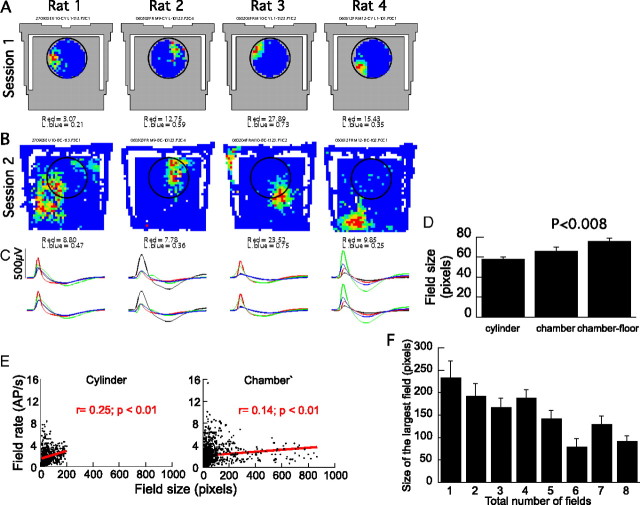
Multiple place fields in the chamber were independent of the single place fields in the cylinder. A, Single-cell examples of color-coded firing rate maps in the cylinder (A1) and chamber (A2). An example is given from each of the four studied rats. The chamber area is indicated by gray, and the previous location of the cylinder is indicated by a circle in the chamber recordings. The firing patterns were independent (i.e., remapped) in the two conditions. Cells with a single place field in the cylinder had multiple place fields in the chamber. The blue-to-red color code is as follows: dark blue, 0 AP/s. The minimum rate in the lowest nonzero rate category (light blue) and the highest rate category (red) are given for each map. A3, The average action potential waveforms for each place cell in the cylinder (top) and chamber (bottom) sessions were very similar. The average 2 ms waveform on each of the four-tetrode wires is shown. The black, red, green, and blue waveforms correspond to the average waveforms on tetrode wires 1 through 4, respectively. B, Average and (inset) distribution of similarity between positional firing rate patterns recorded in the cylinder and chamber. The patterns were very similar in the pair of cylinder sessions, but the cylinder and chamber patterns were unrelated. Error bars indicate SEM.

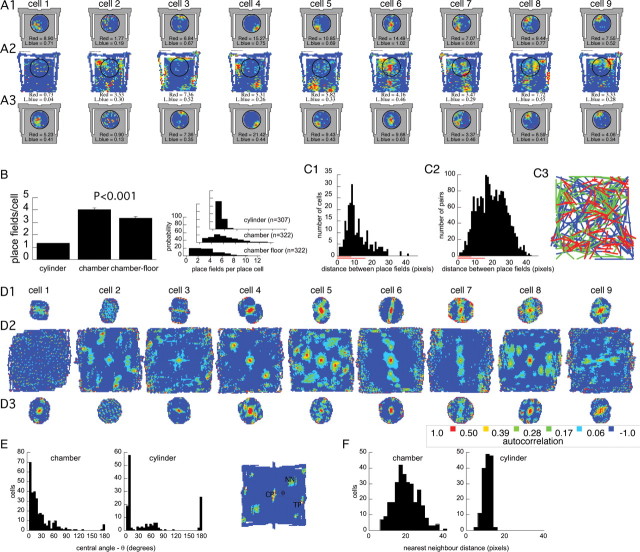
Beyond remapping, it was also immediately apparent that the positional firing patterns of the place cells recorded in the cylinder (n = 307) and chamber (n = 322) were fundamentally different. Most (72%) place cells had single place fields in the cylinder, whereas in the chamber, this dropped to 11%. The vast majority (89%) of place cells had multiple place fields on the chamber floor (Fig. 3A). Whereas in the cylinder each place cell had on average 1.3 ± 0.03 place fields, each place cell had 3.4 ± 0.11 place fields on the chamber floor (p < 0.001) (Fig. 3B). In fact, the number of place fields was even greater in the chamber, 4.05 ± 0.10, when firing on the chamber stairs was also considered.

Figure 3.

Place cells with single place fields in the cylinder had multiple place fields in the chamber. An example of color-coded firing rate maps from nine simultaneously recorded cells during the recording sequence cylinder (A1), chamber (A2), cylinder (A3). B, Average and (inset) distribution of number of place fields per place cell in the cylinder and chamber. Analyzing only discharge on the chamber floor, confirmed that the larger number of place fields in the chamber was not attributable to fields being fractionated by the stairs. Error bars indicate SEM. C, Distribution of the distance between nearest neighbor (C1) and all (C2) pairs of place fields from each single cell that had multiple place fields in the chamber. Only the distances between place fields of single cells contributed to the distributions. The short and long red lines on the x-axis indicate the radius of the cylinder (34 cm) and half-width (75 cm) of the chamber, respectively. C3, Spatial distribution of nearest neighboring place fields. The lines connect the centers of nearest neighbor place fields of each place cell with more than one place field in the chamber. The place field pairs were divided into three groups. The third with the closest nearest neighbors are shown in red. The next third of moderately separated nearest neighbors is green, and the third with the most distant nearest neighbor is blue. There is no obvious clustering or arrangement of near or far cell pairs. The distributions of the thirds with closest and farthest neighbors did not differ (Kolmogorov–Smirnov two-dimensional test, p = 0.17). D, Spatial autocorrelation plots corresponding to the firing rate maps in A do not reveal a characteristic spatial arrangement of place fields. The color code that is indicated was used for all the plots. E, F, Inset, The spatial autocorrelations were quantified by defining the distance from the central peak (CP) to the nearest neighbor (NN) and the central angle between the NN, CP, and the nearby third peak (TP). E, The distribution of the central angles are widely distributed and do not center on 60° for recordings in the chamber anymore than they do for recordings in the cylinder. F, The nearest neighbor distances in the chamber are also broadly distributed.

The spacing of multiple place fields

The locations of the place fields of a cell in the chamber were completely unrelated to the location of the place field if the cell expressed one in the cylinder (Fig. 3). Not only did this indicate independence of the cylinder and chamber positional firing patterns, but the change from a single place field to multiple place fields is difficult to explain as a simple dissection, stretching, or compression of place fields from one environment to the other (Muller and Kubie, 1987; O'Keefe and Burgess, 1996).

A more parsimonious account might be that CA1 place cells have multiple place fields but the field spacing is too great for more than one place field to commonly appear in the cylinder. Consistent with this possibility, the average distance between the nearest neighboring place fields was 11.5 ± 0.43 pixels, which was >8 pixels, the radius of the cylinder (Fig. 3C1). We determined an upper estimate of the likelihood of observing more than one place field within the cylinder as the product of two proportions (P1 and P2). An estimate of P1 is the proportion of cells in the chamber with a place field in a circle the size of the cylinder (0.36) and P2 is the proportion of cells that had a pair of place fields within one cylinder diameter (0.74). P1 was estimated by assuming that place fields were homogeneously distributed on the chamber floor. We then counted the proportion of cells with a place field center in a circle the size of the cylinder. The circle was centered at coordinates of the average place field center. This turned out to be the center of the chamber floor. In the chamber, the likelihood of multiple place fields occurring within an area the size of the cylinder (27%) was essentially the same as was observed in the cylinder (28%). This is consistent with the possibility that the place cells we recorded had multiple place fields with the same spacing between fields in both the chamber and cylinder. It is also possible that the hippocampus representation of the chamber had in fact been parceled out into discrete subregions and that the appearance of multiple place fields reflects remapping between the different parcels. This possibility predicts that, within a parcel, a cell is unlikely to have multiple fields. We did not find support for this possibility by inspecting the topographic arrangement of lines that were drawn between the centers of the nearest neighboring place fields of each cell with multiple place fields in the chamber (Fig. 3C3). According to the parcel hypothesis, multiple nearby place fields will predominantly occur only near a parcel border that separates the place fields. This predicts that, if we examine the locations of nearest neighbor place fields of each cell, the nearby place field pairs will be less homogeneously distributed throughout the chamber than the place field pairs that are more distant. This prediction was not supported because the spatial distribution of place field centers (n = 86) with the third of nearest neighbors did not differ from the spatial distribution of the place field centers with the third of farthest neighbors (Kolmogorov–Smirnov two-dimensional test, p = 0.17).

Irregular spatial arrangement of multiple place fields

It was apparent from visual inspection of the chamber firing rate maps (Fig. 3A2) that the place field locations of a place cell were arranged irregularly. The distribution of distances between nearest-neighbor place fields (Fig. 3C1) and all of the place fields of a cell (Fig. 3C2) started at 1 pixel. We expect that a population of cells with regularly spaced place fields would tend to have a null in the distribution that corresponded to the minimum spacing between place fields in the population. If cells had a regular arrangement of place fields like grid cells, that minimum spacing would have been 7–9 pixels (30–39 cm), which is the tightest steady-state spacing reported for grid cells close to the postrhinal cortex (Hafting et al., 2005). A substantial number of cells we observed had multiple fields with centers that were within just a few pixels of each other (Fig. 3C). Furthermore, if those cells had regularly arranged place fields, they would have discharged throughout most of the chamber instead of <35% of the space as was observed (Tables 1, 2). This lack of a characteristic spatial organization of the place fields was confirmed quantitatively by analyzing the spatial autocorrelation of the firing rate maps (Fig. 3D,E), a procedure that revealed the geometric organization of medial entorhinal grid cells with a central angle of 60° (Hafting et al., 2005). Most (301 of 322) place cells in the chamber had at least three significant peaks in their spatial autocorrelation pattern, reflecting the presence of multiple place fields. However, we could not detect a characteristic organization of the autocorrelation peaks. The distribution of the central angles formed by these peaks decreased monotonically from a peak near 0° (Fig. 3E). The average ± variance of the distribution was 15.4 ± 8.2° (Rayleigh's statistic, r = 0.93; p < 0.001). Only 7.6% of these cells had a central angle between 50 and 70°, which is a range that spans the characteristic grid cell angle by >2 SDs. Many fewer place cells in the cylinder (152 of 307) had three or more peaks in their spatial autocorrelation, consistent with the predominance of single place fields. The average central angle in these spatial autocorrelations was 30.4 ± 25.6° (Rayleigh's statistic, r = 0.78; p < 0.001) and 11.8% of these cells had a central angle between 50 and 70°. The distributions of central angles in the cylinder and chamber spatial autocorrelograms were different (Watson–Williams test, F_(1,422) = 23.9; p = 10⁻⁵) and the trend approached significance for the fraction of cells with a grid cell-like central angle to be greater in the cylinder than the chamber (z = 1.95; p > 0.05). The distance from the central peak in the spatial autocorrelation to the nearest neighboring peak was greater in the chamber (21.4 ± 0.5 pixels) than it was in the cylinder (10.1 ± 0.2 pixels; t₍₃₇₃₎ = 21.5; p < 0.0001) (Fig. 3F). Because only cells with multiple peaks in the autocorrelogram were considered for this comparison, the significant difference corroborates the previous analyses that suggested the spacing between multiple place fields in the chamber was, on average, greater than might be detected within the dimensions of the cylinder (Fig. 3C1). Comparing the results from the nearest-neighbor analysis of place fields and the nearest-neighbor analysis of peaks in the spatial autocorrelation also corroborates our impression that place fields were arranged irregularly. If the arrangement of place fields had been regular, we expect similar estimates of nearest-neighbor distance between place fields (11.5 pixels) and the nearest-neighbor distance between peaks in the spatial autocorrelation (21.4 pixels). However, these estimates were quite different (t₍₅₃₃₎ = 15.3; p < 0.0001). This occurred because, unlike grid cells, the irregular arrangement of place fields does not produce a significant peak in the spatial autocorrelation whenever the spatial firing rate maps are superimposed at a pair of place field peaks. In summary, CA1 place cells had multiple place fields in the chamber, but we could not detect a characteristic periodic spatial arrangement of the firing rate peaks.

Table 1.

Properties of place cells in the cylinder and chamber

Property	Cylinder	Chamber	Chamber floor	Chamber compared with cylinder	Chamber floor compared with cylinder
Firing rate (AP/s)	1.01 ± 0.04	0.91 ± 0.04	0.94 ± 0.05	t(627) = 1.6; p > 0.1	t(627) = 1.2; p > 0.2
In-field rate (AP/s)	2.0 ± 0.07	2.5 ± 0.09	2.2 ± 0.05	t(1703) = 3.3; p < 0.001	t(1484) = 2.4; p < 0.02
Out-of-field rate (AP/s)	0.10 ± 0.05	0.18 ± 0.08	0.14 ± 0.06	t(627) = 8.2; p < 0.001	t(627) = 5.1; p < 0.001
Information content (bits/AP)	1.8 ± 0.04	2.1 ± 0.05	1.9 ± 0.05	t(627) = 5.3; p < 0.001	t(627) = 1.6; p > 0.1
Coherence (std units)	0.61 ± 0.01	0.57 ± 0.009	0.61 ± 0.009	t(627) = 3.5; p < 0.001	t(627) = 0.18; p > 0.8
No. of place fields	1.3 ± 0.03	4.05 ± 0.12	3.4 ± 0.11	t(627) = 21; p < 0.001	t(627) = 17; p < 0.001
Place field size (pixels)	57.8 ± 2.4	66.2 ± 3.5	75.0 ± 3.9	t(1703) = 1.3; p > 0.2	t(1484) = 2.6; p < 0.009
Probability of place cell discharge	0.64	0.72	0.72	z = 3.3; p < 0.001	z = 3.3; p < 0.001
Place field size (proportion of space)	0.27 ± 0.01	0.055 ± 0.003	0.073 ± 0.004	t(1703) = 26; p < 0.001	t(1484) = 21; p < 0.001
Proportion of active pixels	0.41 ± 0.01	0.29 ± 0.01	0.31 ± 0.01	t(627) = 7.3; p < 0.001	t(627) = 6.1; p < 0.001

Only the data from the first cylinder recording of an ensemble were used for the characterization in the cylinder. Significant differences between discharge on the cylinder and chamber floors are highlighted in bold.

Table 2.

Properties of the same place cells recorded in both the cylinder and chamber

Property	Cylinder	Chamber floor	Chamber floor compared with cylinder
Firing rate (AP/s)	1.00 ± 0.07	0.96 ± 0.004	t(221) = 0.8; p > 0.4
In-field rate (AP/s)	2.1 ± 0.1	1.9 ± 0.08	t(479) = 2.1; p < 0.04
Out-of-field rate (AP/s)	0.09 ± 0.009	0.10 ± 0.008	t(221) = 1.0; p > 0.3
Information content (bits/AP)	2.0 ± 0.08	1.8 ± 0.07	t(221) = 1.8; p > 0.07
Coherence (std units)	0.63 ± 0.02	0.68 ± 0.01	t(221) = 2.2; p < 0.03
No. of place fields	1.3 ± 0.05	3.2 ± 0.18	t(221) = 10.6; p < 0.001
Place field size (pixels)	52.4 ± 3.5	94.6 ± 8.9	t(479) = 3.3; p < 0.001
Place field size (proportion of space)	0.24 ± 0.02	0.092 ± 0.009	t(479) = 9.5; p < 0.001
Proportion of active pixels	0.38 ± 0.02	0.35 ± 0.02	t(221) = 1.34; p > 0.17

Only the data from the cylinder recording before the chamber session are considered. Significant differences are highlighted in bold.

Although CA1 place cells had multiple place fields, their spatial discharge was distinct from the grid cell pattern, because the irregular arrangement CA1 place fields did not resemble the hexagonal array of grid cell place fields. This distinction could be directly observed in an ensemble recording that included a cell with a grid cell pattern, the only one we detected (Fig. 4). The waveform of this cell was so narrow that it did not qualify as a pyramidal cell, and the firing rate was too low to be classified as an interneuron. The cell is most likely a fiber projecting to CA1 from the medial entorhinal cortex (Leutgeb et al., 2007).

Quality of the multiple place field recordings

The basic electrophysiological properties of the recorded place cells, that is, their action potential waveforms, firing rates, spatial firing rate coherence and information content, as well as other characteristics were maintained across the chamber and the cylinder sessions, making it unlikely that the observation of multiple place fields was the result of technical shortcomings (Table 1, Fig. 5). Both qualitative and quantitative observations make it unlikely that poor quality of single-unit waveform discrimination accounts for the multiple place fields in the chamber. Single place fields were observed in the cylinder both before the rat was put in the chamber and afterward, when the rat was returned to the cylinder (Fig. 3A). This is the classic empirical method of demonstrating recording stability (Muller and Kubie, 1987). We note that all findings were confirmed when the cylinder–chamber comparisons were restricted to the 222 cells that had stable positional firing patterns in the cylinder sessions immediately before and after the chamber recordings (Table 2).

Figure 5.

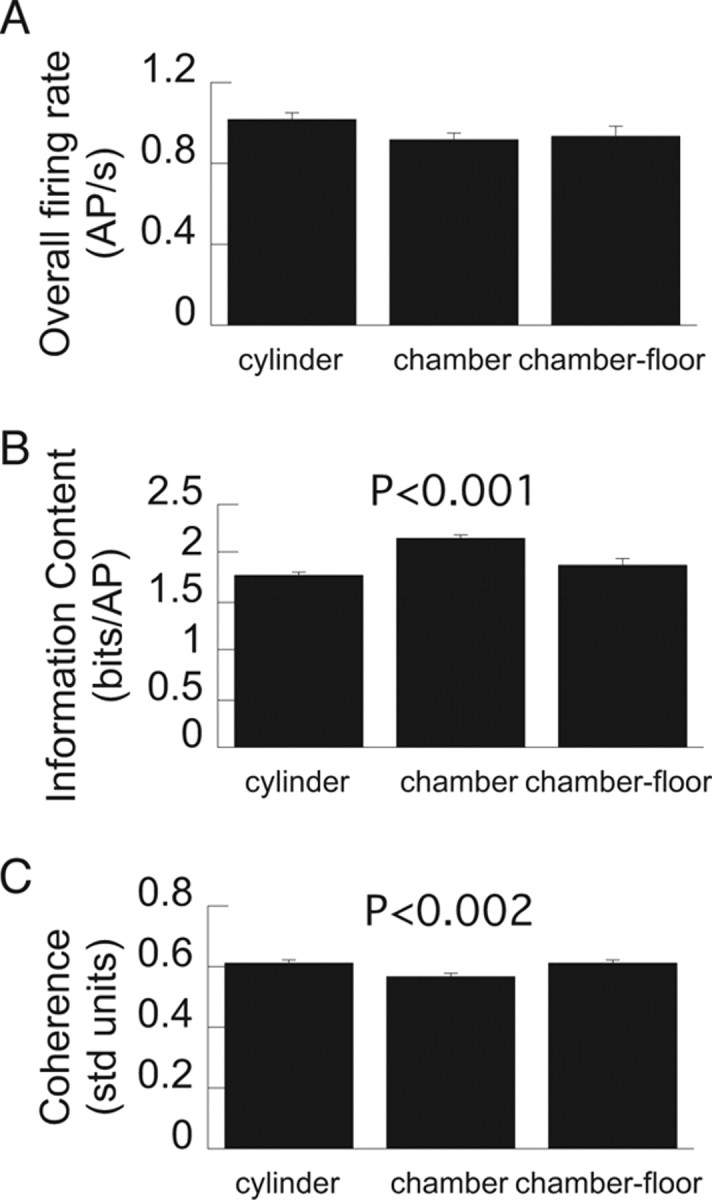
Basic place cell characteristics were similar on the chamber and cylinder floors. A–C, Overall firing rate (A), spatial information content (B), and local smoothness (coherence) (C) of place cell firing in the cylinder and chamber. Probabilities are given for significant differences relative to the cylinder condition. The significant differences arise because discharge on the narrow stairs in the chamber was different from discharge on the cylinder or chamber floors. Error bars indicate SEM.

It was unlikely, but nonetheless possible, that the appearance of multiple place fields in the chamber was the result of three conjunctive events: (1) cells were silent in the cylinder, (2) the silent cells recruited to be active in the chamber had action potential waveforms that were similar to each other, and (3) they also had similar waveforms to a cell that was active in the cylinder because the waveforms of most cells were stable across the cylinder and chamber sessions. If this constellation of events occurred, we would have had to misclassify approximately three single-unit waveforms as a unitary waveform in the chamber sessions. This possibility was deemed unlikely after visual inspection confirmed essentially complete overlap of the waveforms that contributed to the place fields of a single unit. Two examples are shown in Figure 6.

Figure 6.

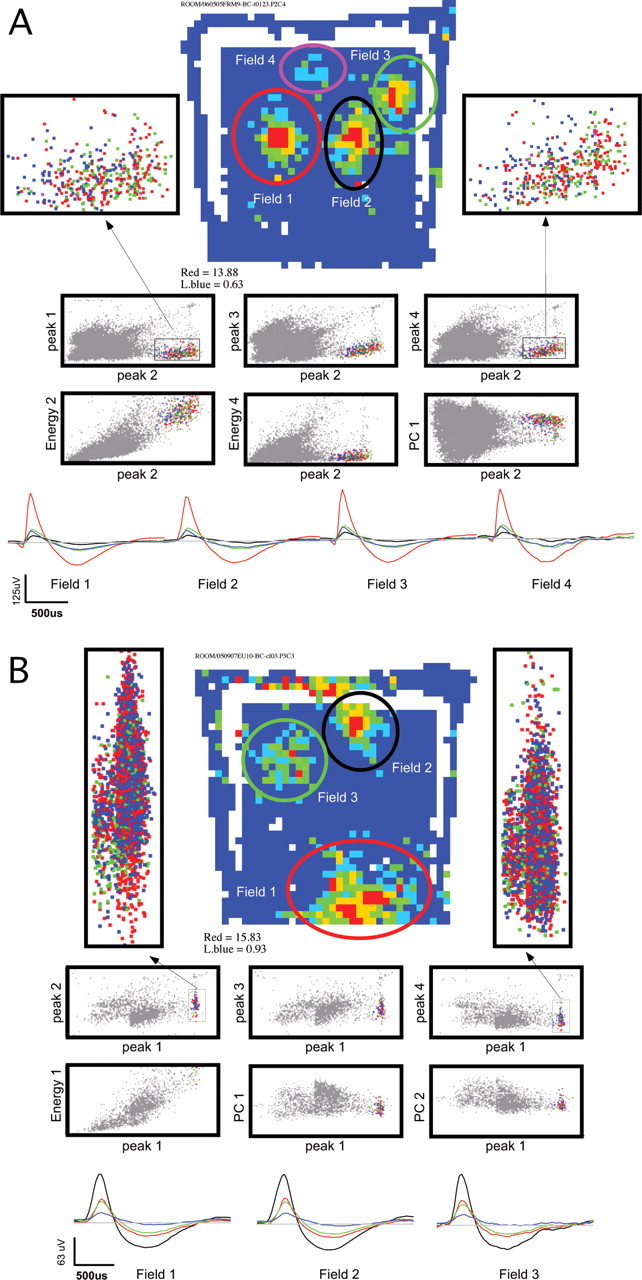
The action potential waveforms from the multiple place fields of a single unit could not be discriminated in the multidimensional waveform parameter space used for single-unit isolation. Examples from two cells are shown in A and B. These cells fired clear complex spikes. They were chosen because they also had three or four clear place fields on the chamber floor, which was the average for the population. The firing rate map of each unit is shown with the locations of the fields on the chamber floor indicated by ellipses. Action potentials in the different fields were discriminated using the location of the rat when the spike was emitted. Below the rate map, a set of six waveform parameter two-dimensional projections are shown. This is only a subset of the projections that were used to isolate the unitary waveform. The action potentials at the different field positions are indicated in colors that correspond to the ellipse color that marks the field location (the black ellipse corresponds to blue events). All other events recorded by the tetrode are indicated in gray. Two blowups of a waveform parameter projection are given to the left and right of each rate map. The blowups only show the isolated waveform events. This depicts that the waveforms strongly overlap in waveform parameter space. The average waveforms of the action potentials in each field are given in the bottom row. The waveforms on tetrode wires 1 through 4 are drawn in black, red, green, and blue, respectively. The cell in A discharged 1100 action potentials during the recording. The isolation quality measures for the highlighted single unit are as follows: I_iso(background) = 12.6; I_iso(neighbor) = 14.9. The cell depicted in B discharged 3580 action potentials during the recording. The isolation quality measures are as follows: I_iso(background) = 7.9; I_iso(neighbor) = 7.1, which is approximately the average isolation quality of the single units that were analyzed for this study.

Nonetheless, we quantitatively analyzed the quality of single-unit isolation to estimate the likelihood that poor single-unit waveform isolation accounts for observing multiple place fields in the chamber sessions (Table 3). Isolation quality was similar in the cylinder and chamber sessions. The average isolation quality was slightly worse for sessions with more isolated single units. Consistent with this and the finding of more active units in the chamber, single-unit isolation tended to be worse for cells with more place fields. However, this relationship only accounted for ∼6% of the variance in the number of place fields. We conclude that, in the chamber, the characteristic multiple place fields of CA1 pyramidal cells is unlikely to be an artifact of poor single-unit isolation.

Table 3.

Analysis of single-unit isolation

Property	Cylinder	Chamber
Iiso(background) (in bits), average ± SEM	7.9 ± 0.12	7.9 ± 0.11
Iiso(neighbor) (in bits), average ± SEM	6.6 ± 0.17	7.2 ± 0.19
Correlation: no. of units and Iiso(background)	−0.32	−0.22
Correlation: no. of units and Iiso(neighbor)	−0.26	−0.46
Correlation: no. place fields and Iiso(background)	−0.16	−0.25
Correlation: no. place fields and Iiso(neighbor)	−0.09	−0.22

Significant correlations are given in bold.

Place coding with multiple place fields

The ensemble-coding hypothesis predicts that across-cell ensemble firing of the multiple place field positional firing patterns can accurately signal the rat's location at least as well as the activity of place cells with single place fields (Fyhn et al., 2004). To examine this prediction, the rat's location in the cylinder and chamber was estimated from the concurrent activity of the CA1 population (Wilson and McNaughton, 1993; Fenton and Muller, 1998). The activity of simultaneously recorded cells was characterized as a firing rate vector at each time step. The duration of time steps was varied from 0.17 to 5 s. The rat's position was decoded from the activity of ensembles comprised of 5–25 cells.

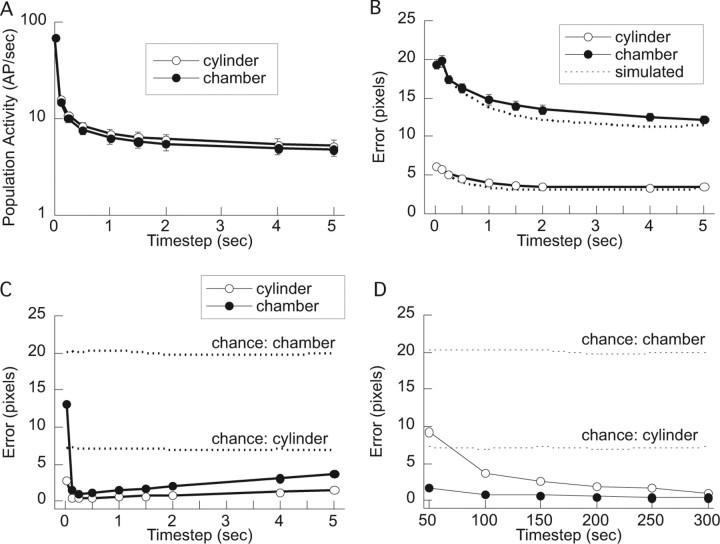
The population firing rates in the cylinder and chamber were similar, consistent with the notion that there is homeostasis of the hippocampal population firing rate (Fig. 7A) (Buzsáki et al., 2002). Decoding with the simulated location-specific spike trains resembled decoding with real spike trains (Fenton and Muller, 1998) (Fig. 7B). We therefore took advantage of this fact to estimate how well position could be decoded if we had recorded more cells simultaneously.

Figure 7.

Place cell ensemble activity in the cylinder and chamber. A, The amount of ensemble activity (magnitude of the ensemble firing rate vector) was similar in the two conditions across a broad range of timescales. B, Decoding the rat's position in the cylinder was much better than in the chamber for modestly sized (5–25 cells) place cell ensembles. Decoding position from simulated spike trains was similar (slightly better) than using the real spike trains. C, Decoding with a simulated ensemble of 322 spike trains was similar in the cylinder and chamber (cylinder slightly better). Decoding was optimal at 250 ms resolution. D, Decoding at 250 ms resolution improved with the size of the simulated ensemble. Decoding in the chamber was worse than the cylinder until ensembles of ∼200 cells or greater were used. Chance in C and D was determined by randomly selecting an estimate of the rat's location for each time step that the population vector was not null.

The location-specific activity of a 322 cell ensemble was simulated from the positional firing patterns of the 322 place cells that were recorded in the chamber and a 322 sample of the place cells that were recorded in the cylinder. We estimated the accuracy of the place cell positional signal in the population firing rates by decoding the rat's position from the simulated population firing rate patterns that were derived from the cylinder and chamber recordings (Fig. 7C). In both cases, the optimal decoding interval was 250 ms (Fig. 7C) and the decoding error at this optimum decreased as the number of cells in the ensemble increased (Fig. 7D). Importantly, the decoding error was similarly small (<5 cm) in the cylinder and chamber when the ensemble was ∼200 cells or more. Because many >200 place cells are active during exploration, we conclude that a CA1 ensemble place code based on a multiple place field firing pattern can accurately signal the rat's location.

Place field enlargement and place cell recruitment

Two additional place cell firing properties also differed between the cylinder and chamber. The size of each place field was larger in the chamber recordings, on average by 30% (Table 1, Fig. 8). As mentioned above, in the context of remapping, the second change occurred at the level of the place cell network. Namely, within the population of pyramidal cells that were active in at least one of the two environments, a cell was more likely to have place cell properties in the chamber than in the cylinder (Table 1, Fig. 9). Thus, although 64% (307 of 477) of the active CA1 pyramidal cells were recruited into the place cell ensemble during movement in the cylinder, a significantly (p < 0.001) higher percentage, 72% (322 of 448) of the active pyramidal cell population was recruited to act as place cells in the chamber. We underestimated the number of recordable pyramidal cells by not recording during sleep when the most pyramidal cells are active. Based on published values of the proportion of pyramidal cells that are active in environments like the cylinder (Wilson and McNaughton, 1993; Guzowski et al., 1999), we expect that the cells that were active in the cylinder represent 25–40% of the total pyramidal cell population. According to this assumption, the larger proportion of cells that were active in the chamber would therefore represent 28–45% of the pyramidal cell population. It was also unlikely that these estimates of the active subset (Kubie and Ranck, 1983) in the cylinder and chamber were equivalent according to the test of proportions, which confirmed that the active place cell subset increased in the larger environment (values of z ≥ 2.1; values of p ≤ 0.02).

Figure 8.

Place fields in the chamber were larger than place fields in the cylinder. A–C, Firing rate maps (A, B) and tetrode waveforms (C) for an example cell from each of four rats. Each set of four waveforms indicate the average waveform for a single unit on the four tetrode wires (black, red, green, blue). D, Place fields were larger in the chamber than the cylinder. A pixel is 22 cm². The chamber floor occupied approximately five times more area, so in terms of the proportion of the environment that a place field occupied, place fields in the chamber were more focused. Whereas the average place field occupied 27% of the cylinder floor, it occupied only 7% of the chamber floor (p < 0.001). E, The firing rate within a place field was greater for larger fields. This modest but significant relationship was similar in the cylinder and the chamber. F, There was a nonsignificant trend for a place field to be larger if the cell had a small number of place fields. The average size of the largest place field is plotted as a function of the number of place fields. These data are only from chamber recordings.

Figure 9.

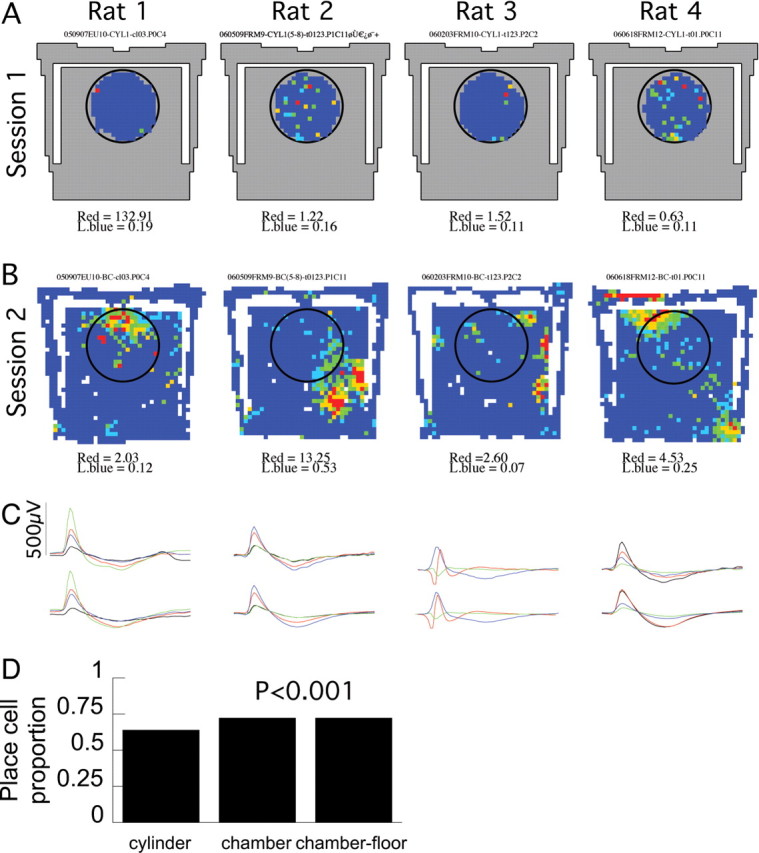
More pyramidal cells were recruited to be place cells in the chamber than the cylinder. A–C, An example cell from each rat. These cells rarely fired and did not have place fields in the cylinder. D, Proportion of pyramidal cells that were place cells in the two environments. Probabilities are given for comparisons to the cylinder recordings.

We also examined the conclusion that place cells were more likely to be observed in the chamber than the cylinder by examining the subset of place cells that were identified by the same single-unit waveform parameter definitions in both a cylinder and a chamber recording. Of these 227 cells, the majority (n = 138; 61%) were place cells in both the cylinder and chamber sessions; 37 (16%) were place cells in the cylinder session alone, and 52 (23%) were place cells only in the chamber recordings. This analysis also confirmed that it was significantly more likely to observe a place cell in the chamber (190 of 227) than the cylinder (175 of 227; z = 2.3; p = 0.01). Note that, unlike the observation of multiple place fields in the chamber, neither the place field enlargement nor the increased place cell recruitment in the chamber is sufficient to distinguish between the predictions of the dedicated-coding and ensemble-coding hypotheses.

Discussion

The fundamental CA1 place cell positional firing pattern

CA1 place cells with single place fields in the cylinder, had multiple place fields in the six times larger chamber. There was no evidence the place cell representation had parceled the chamber into multiple, effectively separate environments, with most place cells having only one place field within each parcel (Fig. 3C). Nonetheless, this possibility cannot be excluded. In previous work, adding a barrier to a familiar small environment induced a transient multiplication of place fields, prompting Lever et al. (2002) to state: “If place cells provide the rat's signal of its allocentric location within an environment, it might plausibly be reasoned that the hippocampal network will not tolerate too many cells firing in two distinct positions.” We found, in stable familiar conditions, that 89% of CA1 place cells discharged in multiple distinct locations. This requires revising the view that a hippocampal place cell signals a single location within an environment by firing rapidly only when the animal visits the place. Multiple, irregularly arranged place fields may be the fundamental discharge pattern because it is expressed during three-dimensional movement in a relatively large environment, a condition that has more features of a natural habitat than the standard cylinder.

Most (89%) CA1 place cells had multiple place fields. In fact, we probably underestimated the number of place fields because the conventional place field may actually be composed of multiple overlapping fields, each defined by a specific temporal rather than positional discharge pattern (Maurer et al., 2006). Scaling the size of the recording enclosure changes the size of place fields in hippocampus (Muller and Kubie, 1987; Maurer et al., 2005; Blair et al., 2007). However, it has also been reported that nonisomorphic scaling may cause place cell and grid cell place fields to merge or separate because of compressing or stretching described by simple rules (O'Keefe and Burgess, 1996; Barry et al., 2007). Unlike the steady-state multiple place fields in the present study, these previously characterized changes of hippocampal place cells occurred without global remapping, indicating that discharge patterns in the two environments remained related. In contrast, remapping occurred in our conditions (Fig. 2), and the positional discharge pattern in the chamber was therefore unconstrained by the pattern in the cylinder.

The multiple place fields in the chamber are unlikely to be an artifact of poor single-unit isolation. It is possible, but unlikely, that many of the cells that were silent in the cylinder could have become active in the chamber, creating the appearance of multiple place fields. Contradicting this possibility, there were three times more place fields in the chamber than the cylinder, yet the overall firing rates of individual cells and the moment-to-moment firing rate of the whole ensemble were constant across the two environments. Finally, we only detected a weak relationship between the quality of waveform isolation and the number of place fields. We therefore reject the possibility that multiple place fields in the chamber are technical artifacts, and instead conclude that multiple, irregularly arranged place fields is the fundamental CA1 place cell spatial discharge pattern.

CA1 place cells were also recorded from freely moving monkeys in the same chamber (Ludvig et al., 2004), allowing a direct comparison of rat and primate spatial firing patterns. The rats walked along the stairs and floor, but in the primate study there were no stairs; instead, the monkeys climbed the chamber walls. Unlike the rat, multiple place fields were never observed in the monkey; instead, each primate place cell produced a single, large place field. The simplest interpretation of this difference is that place fields in the monkey are larger than in the rat, and multiple primate place fields may emerge only in larger environments.

A recent study by Kjelstrup et al. (2008) recorded dorsal and ventral CA3 place cells as rats ran along an 18 m track. Similar to the field expansion we observed in the chamber, dorsal CA3 cells also had expanded place fields on the 18 m track. Whether or not the CA3 active subset was larger on the track was not reported. An undisclosed proportion of CA3 cells also had multiple place fields on the track. Some of these presumably had three or more place fields because an irregular arrangement was reported, like the CA1 cells in our chamber. In contrast to the dorsal CA1 cells we recorded in the chamber, the majority of CA3 cells had only a single place field on the 18 m track, with the ventral CA3 place fields extending several meters. CA3 and CA1 receive inputs from distinct layers of the medial entorhinal cortex, each of which may be sufficient to account for location-specific firing in Ammon's horn (Brun et al., 2002, 2008). It will be important in future work to determine whether CA3 and CA1 place fields are indeed fundamentally different by recording from both CA3 and CA1 in the same expansive environment. We note that, in agreement with the present finding, multiple place field firing patterns were observed during preliminary recordings of CA1 place cells as rats moved in two dimensions across a 13 × 2 m space (Gerrard et al., 2001). It is therefore unclear which findings from recording in the chamber and the 18 m track can be considered general to the hippocampus. A consensus may only emerge after recording place cell firing in different expansive environments that vary in geometry, size, and the rat's ability to move through the space in two and three dimensions. Furthermore, because remaining in an environment for long periods like a day can modulate place cell firing (Ludvig, 1999), it is also critical to study these cells while a rat inhabits a large space for extended times.

The CA1 ensemble place code

The multiple place field positional firing pattern of CA1 place cells strongly supports the hypothesis that the hippocampus place code is an ensemble code. This ensemble viewpoint is most often used to describe the place cell representation of a whole environment (Wilson and McNaughton, 1993; Lee et al., 2004; Leutgeb et al., 2005; Wills et al., 2005), whereas the alternative, dedicated-coding viewpoint is most often used to account for the representation of single locations within an environment (Muller et al., 1987; Shapiro et al., 1997; Fenton et al., 2000; Hollup et al., 2001; Lenck-Santini et al., 2001; Knierim, 2002; Huxter et al., 2003; Kentros et al., 2004). Although this dedicated-coding view is a parsimonious account for cells with single place fields, it is problematic for cells with multiple, dispersed place fields. In this case, it is ambiguous which of multiple locations an active cell might signal. This ambiguity is in fact similar to remapping, when a place cell may be active in two distinct environments. The ambiguity of two environments is easily resolved because the across-cell ensemble activity is unique for each environment. Cells with overlapping place fields in one environment may discharge together, but in the second environment, coactivity will be rare if their place fields remap to mutually distant locations. Similarly, when cells have multiple place fields, the ambiguity between positions within one environment is also easily resolved because ensemble activity is typically unique at each position (Fig. 7). Given that CA1 cells have multiple place fields, the parsimonious conclusion is that the hippocampus uses an ensemble place code for locations as well as whole small and large environments (Samsonovich and McNaughton, 1997; Redish et al., 2000; Harris et al., 2003).

Implications for understanding the neural computations of spatial knowledge

A key advance in understanding the neural computations underlying spatial knowledge was the discovery of grid cells. These medial entorhinal cortical cells discharge in a hexagonal array of place fields that repeat at regularly spaced intervals and extend across all known environments (Hafting et al., 2005; Fyhn et al., 2007). Another important advance was the demonstration that the monosynaptic entorhinal projection to CA1 is sufficient to maintain CA1 place fields (McNaughton et al., 1989; Brun et al., 2002) and it is necessary for high-quality CA1 place fields (Brun et al., 2008).

Building on these observations, various models were designed to explain how multiple place field grid cell activity transforms into hippocampal place cell activity with a single place field. Most models posit that place cell firing patterns are a thresholded sum of grid cell inputs. The summation, however, produces multiple place fields, which is consistent with the present data, but contrasted with the established notion that place cells have a single place field. Additional constraints were introduced to generate single place fields in the models (O'Keefe and Burgess, 2005; McNaughton et al., 2006; Rolls et al., 2006; Solstad et al., 2006; Franzius et al., 2007). In light of the present data that most place cells have multiple, irregularly arranged place fields, it may be profitable to remove the constraints that limited firing patterns to a single place field. Interestingly, one linear summation model did not limit the resulting multiple place fields. The authors report that increasing the number and variety of grid cell inputs to each place cell increased the randomness of the place field locations and, importantly, increased the uniqueness of the ensemble place code at each location within the environment (Fuhs and Touretzky, 2006). Although this model focused on the grid cells, it appears to be in agreement with multiple place fields in the chamber.

Our findings suggest CA1 place cells fundamentally discharge in multiple, irregularly arranged place fields. The ensemble discharge of such place cells contains at least as much positional information as the ensemble firing of cells with single place fields (Fig. 7) (Fyhn et al., 2004). The present findings are at odds with a dedicated-coding understanding of hippocampal place cells, but they are in excellent agreement with the ensemble-coding hypothesis. Unlike dedicated-coding views of hippocampal place codes, ensemble coding hypotheses are compatible with the characteristically unreliable spatial signal of place cells that has been characterized as overdispersion (Fenton and Muller, 1998; Olypher et al., 2002) and may be a consequence of the cell assembly dynamics that are characteristic of ensemble but not single cell firing (Harris et al., 2003; Jackson and Redish, 2007). Recent advances in conceptualizing, recording, and analyzing ensemble neural activity seem to provide a unified framework for understanding the information content in the activity of sets of hippocampal neurons with both selective and ambiguous spatial tuning.