Abstract
Mammals use two distinct gallops referred to as the transverse (where landing and take-off are contralateral) and rotary (where landing and take-off are ipsilateral). These two gallops are used by a variety of mammals, but the transverse gallop is epitomized by the horse and the rotary gallop by the cheetah. In this paper, we argue that the fundamental difference between these gaits is determined by which set of limbs, fore or hind, initiates the transition of the centre of mass from a downward–forward to upward–forward trajectory that occurs between the main ballistic (non-contact) portions of the stride when the animal makes contact with the ground. The impulse-mediated directional transition is a key feature of locomotion on limbs and is one of the major sources of momentum and kinetic energy loss, and a main reason why active work must be added to maintain speed in locomotion. Our analysis shows that the equine gallop transition is initiated by a hindlimb contact and occurs in a manner in some ways analogous to the skipping of a stone on a water surface. By contrast, the cheetah gallop transition is initiated by a forelimb contact, and the mechanics appear to have much in common with the human bipedal run. Many mammals use both types of gallop, and the transition strategies that we describe form points on a continuum linked even to functionally symmetrical running gaits such as the tölt and amble.
Keywords: gallop, locomotion, energetics
1. Introduction
Understanding the function of mammalian gaits is important to interpreting the structure of the locomotory apparatus in each species. The galloping gaits, as both the fastest and the most complex asymmetrical gaits, have attracted much interest in this regard. Early studies (Marey 1874; Muybridge 1887; Magne de la Croix 1936) identified two fundamental types of gallop variously called the diagonal or transverse gallop and the lateral or rotary gallop. These were fully described in detail in the classic paper by Hildebrand (1959), ‘Motions of the running cheetah and horse’, where the transverse gallop was epitomized by the horse and the rotary gallop by the cheetah. Yet, in spite of a great deal of often highly technical investigation into the galloping gait over the intervening half century (Alexander et al. 1977; Hildebrand 1977; Jayes & Alexander 1978; Hoyt & Taylor 1981; Heglund & Taylor 1988; Pandy et al. 1988; Minetti et al. 1999; Pfau et al. 2006; Walter & Carrier 2007; Maes et al. 2008), very little is understood about why these particular footfall patterns are used by galloping quadrupeds. Understanding these forms of the gallop requires knowing what is being accomplished by the motions of both the individual limbs and the centre of mass (CoM). The objective of this paper is to identify and explain one fundamental concept of the dynamics of the interaction of the animal's mass with the ground that distinguishes the mechanics of these two forms of gallop.
2. What is galloping and why?
A gait is a pattern of movement employed in locomotion. This simple definition applies well beyond the terrestrial gaits of mammals (Nauwelaerts & Aerts 2001; Hedrick et al. 2002; Young et al. 2004). The objective of a gait, including the complex gaits of terrestrial mammals, is to move the organism, as represented by its CoM, through its environment in a controlled and energetically effective manner. The highest speed locomotion of the horse, though only sustainable for relatively brief periods, represents a metabolically cost-effective way of generating high speeds using legs: even though substantial energy is needed for a horse to gallop, alternative ways of running at such speeds will be much less metabolically cost effective (Hoyt & Taylor 1981).
Although the galloping gait of the horse has been well described in the scientific literature for more than a century (Marey 1874; Muybridge 1887), it was not until recently that a functional explanation for the leg sequencing pattern of the horse gallop was proposed (Ruina et al. 2005). During the non-contact flight phase of the stride cycle, the mass of the animal travels forward ballistically with little work done by the legs. The ballistic portions of the gait are interspersed with brief ground contact periods used to reorient the CoM velocity vector and change the animal's trajectory (Ruina et al. 2005). Although muscles are called on to stiffen the joints and generate positive and negative work, the geometry of the transition itself determines that a substantial portion of the available momentum and, hence, kinetic energy is lost (even if some portion can be recovered later in the stride through other passive—e.g. elastic energy storage and return—or active—e.g. muscle work—means; Srinivasan & Ruina 2006). Therefore, during ground contact the majority of leg work is done to redirect the CoM trajectory from downward and forward at the end of the non-contact phase to upward and forward at the beginning of the next non-contact phase. Thus, though largely neglected in analyses of locomotion energetics until recently (McGeer 1990; Garcia et al. 1998; Donelan et al. 2002; Ruina et al. 2005; Kuo 2007), the contact-mediated transition, and the kinetic energy loss associated, may be one of the main reasons why mechanical work must be performed to maintain speed.
A change from downward to upward of the velocity vector of an animal's CoM during locomotion ultimately results from one or more mechanical collisions that occur as the forces transmitted through the limbs during ground contact alter the path of the CoM. For real animals, low forces act over a relatively extended time period to produce a smooth, non-impulsive transition during a collision-like event (where ‘impulsive’ is a dynamic term that implies extremely high forces applied over a very short, approaching instantaneous, period of time). However, certain essential features of such an event can be well modelled by rigid body mechanics, where high forces act instantaneously to produce a sudden impulsive transition (a true rigid body collision). This is because the same impulse-momentum balance between the before-collision and after-collision states must be maintained for both the smooth collision-like transitions of real animals and the impulsive collisions of the rigid body model. In the rigid body model, the galloping animal is represented as a point mass body with rigid, massless legs that act as struts (i.e. transfer force only along their long axis). When an animal lands, the momentum perpendicular to the limb remains unaffected by the contact, since no impulse can be transmitted in this direction. However, momentum oriented in line with the supporting limb is affected by the collision (figure 1a). In all real circumstances at least some momentum, and consequently kinetic energy, will be lost to the in-line collision interaction. Under almost all theoretical circumstances substantial energy could be lost, and it is only under very specific circumstances of well-tuned energy storage and return that such losses along the limb can be largely recovered. One way to minimize the potential for energy loss in some walking and running gaits is to manage the geometry of the support strut relative to the CoM velocity vector during contact to reduce the momentum component in line with the support limb (Garcia et al. 1998; Kuo 2002; Ruina et al. 2005).
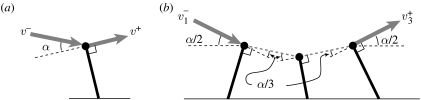
Figure 1.
Simple models illustrating how geometry dictates energy loss for (a) single and (b) multiple collision gaits. The velocity of the CoM is v, the body mass is m, the kinetic energy is E, the total angle of deflection (i.e. the angle between the incoming and outgoing velocity vectors) is α and the total number of collisions is n. The ‘minus’ and ‘plus’ superscripts indicate before collision and after collision values, respectively. The subscript i indicates the ith collision in a sequence involving multiple collisions. (a) For a single limb, the fraction of energy lost during a collision transition is given by ΔE/E−≈α2 for small angles; v+=v− cos α, E−=(1/2)m(v+)2, E+=E− cos2α, ΔE=E−−E+=E−(1−cos2α), ΔE/E−=sin2α≈α2. (b) For three legs in which the transition is evenly distributed between the legs, the fraction of energy lost for each collision is given by , because the angle for each collision is α/3. But there are three times as many collisions, so the total fraction of energy lost during the entire transition is (ΔE/E−)tot≈3(α/3)2=α2/3 or 1/3 of that lost for a transition mediated by a single limb. This can be extended to n legs where the total energy lost during a transition is given by (ΔE/E−)tot≈α2/n; , , , , , .
Any losses incurred through the transition collision correspond to a decrease in kinetic energy. However, kinetic energy must be held constant over the stride cycle in order to maintain constant speed. Thus, the kinetic energy that is lost during a collision must be replaced during steady-state locomotion and becomes, therefore, one of the main sources of mechanical cost associated with legged locomotion (Garcia et al. 1998; Kuo et al. 2005; Ruina et al. 2005). This holds even for gaits that on the surface appear substantially different from galloping—for instance, brachiation where the mass hangs from a superstrate and the deflection of the CoM path involves tensile rather than compressive loads (Bertram et al. 1999; Usherwood & Bertram 2003). Consequently, it is of value to limit energy loss to achieve economical gait. This can be done by passively storing and returning some portion of the kinetic energy lost during a collision, so only a fraction of the kinetic energy needs to be replaced by muscular work. But it is also possible to limit this loss by reducing the amount of kinetic energy involved in the collision in the first place.
The fraction of energy lost by a strut-like limb redirecting a moving body is a quadratic function of the deflection angle (figure 1a), so decreasing the deflection angle substantially reduces energetic loss for any given collision. The leg sequencing of the equine gallop allows the complete transition from downward–forward to upward–forward to be distributed over a sequence of near-equivalent angular changes, each associated with an individual foot contact and accompanying collision (figures 1b and 2b; Ruina et al. 2005). Even though distributing the complete transition between multiple contacts results in a greater number of collision-like events, the deflection angle for each is reduced so that substantially less total momentum (and, therefore, kinetic energy) is lost (figure 1). Although we recognize that many details of limb function influence equine gait, reducing momentum loss during transition of the CoM trajectory appears to be the main purpose of the distributed footfall pattern of the asymmetrical gallop as displayed by the horse (Ruina et al. 2005). This probably also explains why this gait is used only at high speeds: the greater the horizontal component of the CoM velocity, the smaller the deflection angle required of each contact and consequently the smaller the proportion of momentum loss.
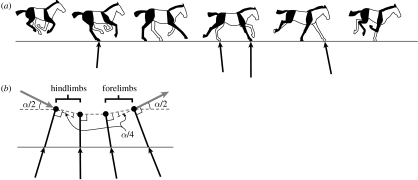
Figure 2.
(a) A sketch of the key points of the equine transverse gallop. The near side (right side of the horse) forelimb and hindlimb are indicated in black and the far side (left side of the horse) in white. Beginning with the aerial phase of the gait (the collected phase) at left, the animal lands on its right hindlimb and progresses through from rear to front alternating right and left sides. The animal eventually takes off from the final (lead) forelimb. The net impulse applied by each limb is indicated by the black vector arrow (horse image after Gray (1953), impulse vector calculated from Merkens et al. (1993)). The initial hindlimb contact results in a net acceleration because the CoM is located forward of the contact, while the final forelimb contact results in a net deceleration because the CoM lies behind the contact. (b) In order to clarify the mechanics of the transition, the horse is modelled as a point mass attached to a massless limb strut. The CoM velocity vector (grey vector arrow) is progressively deflected by the impulse (black vector arrow) that is transmitted through the limb strut at each footfall. The angle of the massless limb strut determines the direction of the impulse vector and, consequently, the direction in which momentum is lost. The CoM velocity vector undergoes a total angular deflection of α as it transitions from downward–forward to upward–forward. But, by dividing α into four equal parts (an idealization of the distribution used by horses) the energy lost in the transition is reduced from that lost in a single collision by a factor of four (Ruina et al. 2005).
The simple two-dimensional models depicted in figures 1 and 2b do not explicitly imply which limbs contact first in the sequence, but simply show the geometrical relationship between the limb strut and the CoM velocity vector that allows a limited loss transition. In order for the effective strut (the line from the foot contact point to CoM) to match those indicated in the model, taking into consideration that the mass distribution of mammals places the CoM between the shoulder and hip joints, figures 1 and 2b imply that the hindlimbs of galloping mammals should contact first with the remaining limbs continuing the sequence until the flight phase is again achieved through an impulse applied by a forelimb. Recent analysis of high-speed galloping in horses is consistent with this interpretation of the function of the limb contact pattern in the gallop (Pfau et al. 2006). Surprisingly, this includes an apparently modest reliance on elastic energy recovery, where it has previously been presumed that such strain energy recovery is a key feature of all gallops including that of the horse.
3. Motion of the horse and cheetah gallop
The transverse gallop of the horse is sketched in figure 2a (modified from Gray 1953). Although it might seem arbitrary to select an initial point in a cyclical gait, the first footfall following non-contact is chosen as the initiation of the stride, since the function of the footfalls is to cause the vertical direction transition and intervene between the low-work ballistic portions of the cycle. Thus, in the horse the stride is initiated with a hindlimb contact. This results in a net applied impulse for this limb oriented upward and forward, i.e. it accelerates the CoM in the horizontal direction. Although it might be expected that the initial contact should decelerate the animal, the observed net horizontal acceleration (figure 3a) simply indicates that the CoM is deflected more forward in its downward path as predicted by the strut model (figures 1b and 2b). In the horse, much of this is mediated by muscular activity within the limb and the initial hindlimb contact results in immediate horizontal deceleration followed by subsequent acceleration as the orientation of the limb changes. However, as the simple geometric model predicts, the initial hindlimb contact provides net horizontal acceleration during steady speed galloping (figures 2a and 3a; Merkens et al. 1993).
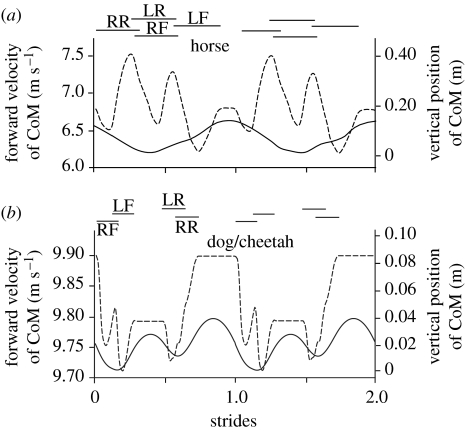
Figure 3.
Comparison of forward velocity (dashed) and vertical position of the CoM (solid) over the course of two strides for (a) the horse and (b) the dog using a cheetah-like gallop. In both cases, the vertical position shows a net decrease during the first part of the transition and a net increase during the second part of the transition. Although the shape of the forward velocity curve is complicated by horizontal deceleration and acceleration that occurs with the contact of each individual limb, the major difference between the equine and cheetah gallop is evident from the net effect of each limb. For the cheetah-like gallop, the major non-contact portion of the stride cycle comes when the forward velocity of the CoM is the greatest, while for the horse-like gallop the non-contact portion occurs when forward velocity of the CoM is relatively low. Data for (a) are adapted from Minetti et al. (1999); curves in (b) are constructed based on force data from Walter & Carrier (2007) and timings from data collected for dogs using a rotary gallop at 9.3 m s−1 (Maes et al. 2008) as well as timing trends extrapolated from several greyhound dogs galloping at speeds between 14 and 19 m s−1 (courtesy J. R. Usherwood). Values for forces and timings were adjusted so that the impulse due to the ground reaction force balanced gravity over one complete stride, and average vertical velocity and vertical position over one complete stride were zero. This generated position and velocity curves that were both biologically and physically reasonable despite the fact that a complete force and timing dataset was not available for a single dog or group of dogs.
Initial hindlimb footfall in the horse is followed by contralateral hindlimb contact and then ipsilateral forelimb contact. At slow speeds these ‘middle’ limb contacts can be almost coincident, and the gallop has the three-beat footfall pattern traditionally referred to as a ‘canter’ (although the total ‘transition’ from downward to upward is still mediated by the four limb contacts). At higher speeds these contacts are distributed in time to give the four-beat footfall of the full gallop (Pfau et al. 2006; Robilliard et al. 2007). At extremely high speeds these middle contacts can be far enough apart that a brief secondary period of extended-limb non-contact occurs (Howell 1944), and the timings between the four contacts of the gait approach equivalence.
The impulse provided by the second and third limb contacts continues the sequential deflection of the CoM but has only a limited net effect on horizontal velocity (Minetti et al. 1999; Pfau et al. 2006). These contacts reverse the vertical motion of the animal (i.e. the CoM vector is deflected from slightly downward and forward to slightly upward and forward).
The final limb to contact is the remaining forelimb, traditionally referred to as the ‘lead’ limb where convention emphasizes spatial position over temporal sequence. Thus, in the transverse gallop, contact alternates between limbs from each side as they progress from rear to fore. The lead forelimb (final limb to contact) provides an impulse that has a net orientation rearward that acts to decelerate the animal in the horizontal direction (figures 2 and 3a). This may appear contrary to the function of the gallop as a high-speed gait, but is required in order to complete the downward to upward transition, and to deflect the CoM from a near horizontal trajectory as it passes over the middle contacts to one with sufficient vertical velocity to allow the non-contact ballistic phase of the cycle. That is, this limb converts some forward kinetic energy to vertical (but in doing so some momentum is lost). Although the lead limb imparts active acceleration during the latter portion of its contact, its net effect is to slow progression in the horizontal direction. Surprisingly, and as a direct consequence, the CoM of the horse is travelling at a reduced horizontal speed relative to other times of the gait cycle as it initiates the non-contact phase when horizontal velocity of the CoM must remain constant (figure 3a; Minetti et al. 1999).
There are a number of easily observed differences between the cheetah gallop and that of the horse. The back of the cheetah undergoes substantial flexion and extension. Some extension and flexion occurs in the spine of the horse but it is of much lesser degree and is confined largely to the lumbosacral junction (Haussler et al. 2001). In the cheetah gallop, as with many other mammals employing the rotary gallop particularly at high speeds, there are regularly two non-contact phases in each stride. In the horse, the main non-contact phase occurs while the limbs are ‘collected’ under the animal (this is what Magne de la Croix (1936) referred to as ‘centrifugal’ flight). In the cheetah gallop, a similar collected flight occurs following contact of the front limbs prior to the next contact of the hindlimbs, but there is generally a more substantial extended non-contact phase (what Magne de la Croix referred to as ‘centripetal’ flight) following contact of the hindlimbs. Hildebrand (1959) observed that the high degree of back flexion–extension increased the length of the cheetah gallop stride; the footfall sequence depicted therein shows the collected flight phase of the cheetah as roughly three-quarters of the duration of the extended flight phase. Since running speed is the product of stride length and stride frequency, the back flexion–extension and lengthened stride were interpreted as adaptations to allow high speed. But for extended stride length to increase running speed, it is necessary to assume that adding extra length to each stride does not impede stride frequency.
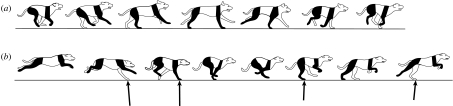
A more subtle difference between the rotary gallop of the cheetah and the transverse gallop of the horse lies in the pattern of footfalls. It is the particular left–right sequence of footfalls that has been used to define these two variants of the gallop (Hildebrand 1959). In the transverse gallop, the foot contacts alternate between sides as they progress from landing in the rear to take-off in the front (in the illustration depicted in figure 2a the sequence is near side rear, far side rear, near side fore and far side fore). Thus, the animal lands on a rear limb on one side and takes off to the collected non-contact phase of the cycle from the contralateral forelimb. In the rotary gallop of the cheetah, landing and take-off are from ipsilateral limbs of each pair. In figure 4a the cheetah lands on its near side forelimb (following the extended non-contact phase), progresses to its far side forelimb then far side rear limb, and takes off from its near side rear limb. The horse is capable of a footfall pattern equivalent to that of the rotary gallop of the cheetah, usually occurring when the lead of the forelimb pair changes relative to the hindlimbs. This is relatively common in turns. However, in spite of the superficial similarity in footfall sequence, the gallop of the horse remains fundamentally different from that of the cheetah, as explained below.
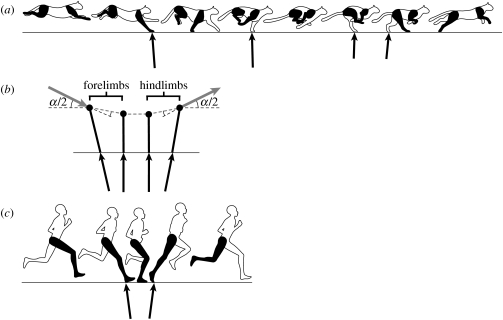
Figure 4.
(a) A sketch of the key points of the cheetah rotary gallop. Following the major flight phase of the gait (the extended phase), the animal lands on its nearside (right side of the cheetah) forelimb and progresses to the opposite side (left side of the cheetah) forelimb. At high speeds, there will be a brief intervening collected flight phase between lifting off from the last forelimb and landing on the hindlimb on the same side of the body. This is followed by the opposite side hindlimb making contact and the animal vaulting into the extended flight phase of the cycle. Net impulse vectors of each limb (indicated by black arrows) are estimated from canine galloping records (Walter & Carrier 2007). (b) Again, a point mass attached to a massless limb strut is used as a model to simplify the mechanics. As with the horse, the CoM velocity vector (grey vector arrow) is progressively deflected by the impulse (black vector arrow) that is transmitted through the limb strut at each footfall, but in the cheetah gallop the transition is initiated with the forelimbs and completed by the hindlimbs. Consequently, the component of the momentum of the CoM aligned with the limb is greater and more momentum is lost in the cheetah gallop than the equine gallop (strategies available to limit this loss are discussed in the text). Although four limbs are used instead of two, the impulse vectors show that the cheetah gallop may be mechanically similar to (c) a human run, where the forelimb contacts of the cheetah serve the same role as the first half of the contact while the hindlimbs operate as the second half.
The transverse and rotary gallops are asymmetric gaits that clearly have features in common but also exhibit important differences. Can we identify fundamental features that place these gait variants in a functional perspective? Such an understanding is necessary if the constraints and opportunities of each gait are to be evaluated and the morphology on which each depends is eventually to be analysed.
4. Interpreting ground reaction forces for hindlimb-initiated (horse-like) and forelimb-initiated (cheetah-like) gallops
The strut deflection model for a galloping animal (figure 1) predicts some general features of CoM motion (both position and velocity) over the course of the impulsive contacts of the limbs. An initial test of the model can be conducted by evaluating these predictions against observations of mammalian galloping. Vertical position and velocity changes over the sequence of contact can be determined via integration of ground reaction forces since the measured force results in the acceleration of the mass of the animal (F=ma). Direct measurement of ground reaction forces from a complete stride in a fast moving, large animal such as the horse is difficult. Composite ground reaction force records (where a single force plate was used and the complete stride force profile was estimated from records from different strides) exist from one study at the slower speed three-beat transverse gallop referred to as the canter (Merkens et al. 1993). CoM motion can also be calculated through three-dimensional motion analysis if care is taken to account for the motion and acceleration of all the segments. Such a calculation was performed by Minetti et al. (1999) for a horse cantering on a motorized treadmill. Estimates of CoM motion of freely moving horses carrying a rider at extremely high speeds are recently available from complex analysis of accelerometer data calibrated with global positioning instrumentation (Pfau et al. 2006). Together, such data allow a reasonable estimate of CoM vertical and horizontal position changes for the galloping horse (figure 3a). Currently, no direct ground reaction force measurements are available for the cheetah. However, ground reaction forces of larger dogs using a similar high-speed rotary gallop are available (Bryant et al. 1987; Walter & Carrier 2007). Although some details will differ between the species, the fundamental features of the rotary gallop will be equivalent for both the cheetah and fast galloping dogs. In figure 3b, the CoM vertical position and velocity are reconstructed based on force recordings of a Weimaraner galloping at 9.9 m s−1 (Walter & Carrier 2007), combined with footfall timings based on the data from dogs using a rotary gallop at 9.3 m s−1 (Maes et al. 2008), and several greyhounds galloping at speeds between 14 and 19 m s−1 (courtesy J. R. Usherwood). Values for forces and timings were adjusted (within physiological bounds based on the data from Walter & Carrier (2007), Maes et al. (2008) and J. R. Usherwood (2008, personal communication)) so that the impulse due to the ground reaction force balanced gravity over one complete stride and so that average vertical velocity and vertical position over one complete stride were zero. This allowed us to generate position and velocity curves that were both biologically and physically reasonable despite the paucity of the available data (but see Cavagna et al. (1977) for equivalent records from a single galloping dog).
In both the horse and high-speed dog/cheetah gallop, the CoM motion transitions from downward to upward over the course of the sequential foot contacts, but the sequence that accomplishes this transition is fundamentally different. The net action of the final limb to contact the ground—a forelimb in the horse and a hindlimb in the dog or cheetah at high speed—plays a particularly important role in distinguishing these two forms of galloping. Owing to the position of the limbs relative to the CoM, the horse must impart a substantial net deceleration with its final forelimb contact in order to complete the deflection of the CoM velocity vector to an upward direction (figures 2b and 3a). This means that the horizontal velocity of the horse CoM is relatively modest as its feet leave the ground and the horizontal velocity must remain constant during the ballistic flight phase of the gait cycle. This is also the case in the slow gallop of the dog. Cavagna et al. (1977) calculated forward velocity (represented by kinetic energy) and CoM position (gravitational potential energy) over the course of 17.2 km h−1 (4.8 m s−1) hindlimb-initiated, single flight phase gallop (their fig. 14) that shows virtually the identical pattern to the equine gallop of figure 3a.
By contrast, by initiating the downward to upward transition of the high-speed gallop with a forelimb, the cheetah or dog at speed is positioned to impart substantial net horizontal acceleration with its hindlimbs (the last limbs to contact the ground; figure 4a) as the upward deflection into the next flight phase is completed (and this acceleration may well be supplemented through axial extension of the back). Thus, the dog/cheetah enters the main ballistic portion of its fast gallop stride with the greatest horizontal velocity of the gait cycle (figure 3b) and relatively high forward speed is maintained until the next limb contact. This probably contributes to the speed capability of the carnivoran cursors such as the cheetah and dog. Indeed, although the dog regularly employs the horse-like hindlimb-initiated transition gallop, it does so only where great speed is not required. Our depiction in figure 3b of the putative fast canine/cheetah gallop is identical to that determined by Cavagna et al. (1977) for a higher speed 31 km h−1 (8.6 m s−1) double flight phase canine gallop (their fig. 14), though their interpretation of the mechanics of the gait differs substantially from ours.
5. Managing vertical direction changes during the galloping stride
As described above, the limb sequencing of the equine gallop functions to distribute the angular deflections of the CoM as the animal transitions from a downward and forward path at the end of the previous ballistic flight to an upward and forward path in the beginning of the following ballistic phase of the stride. In both the transverse and rotary gallops, potential energy is the highest during the main non-contact phase of the gait; in the case of the horse it is during the collected non-contact phase prior to touch down by the first rear limb (figures 2a and 3a), and for the cheetah it is during the extended non-contact phase prior to touch down of the first forelimb (figures 3a and 4a). The fundamental difference between these two variations of the gallop is in which limbs initiate the impulsive transition from downward to upward: in the horse gallop the transition is initiated following the main non-contact phase by a rear limb and take-off is from a forelimb while in the high speed cheetah gallop the transition is initiated by a forelimb and the animal takes off from a hindlimb. As mentioned, horses can use a rotary-like footfall pattern on occasion, yet the mechanics of their rotary gallop is not equivalent to that of the rotary gallop of the cheetah because the mechanics of transition initiation and take-off remain unchanged in spite of the difference in left–right footfall pattern. Likewise, cats, dogs and many other rotary galloping forms can employ the footfall pattern of a transverse gallop. The footfall pattern of a cat, for instance, may alternate between the customary rotary gallop and a transverse gallop or take an intermediate form where the hindlimbs move together as a bound or half bound (Smith et al. 1993). However, in these cases the difference is simply due to foot position and not any major difference in the mechanics of the transition. Thus, even though the footfall pattern of the cat gallop can match the classification of a rotary gallop, a transverse gallop, a bound or half bound, we propose that all of these ‘gaits’ involve a mechanically equivalent transition initiated by forelimb contact. Conversely, many running mammals can use both an equine-like hindlimb-initiated transition and a cheetah-like forelimb-initiated transition gallop. The dog is a good example. Under most high-speed running conditions, the dog will use a gait remarkably similar to that of the cheetah where the transition is initiated by forelimb contact (figure 5a; Muybridge 1887, plate 119). However, dogs regularly use an equine-like stiff back gallop, particularly at modest running speeds where the transition is initiated by hindlimb contact (figure 5b; Muybridge 1887, plate 118).
Figure 5.
Both (a) the hindlimb-initiated horse-like gallop and (b) the forelimb-initiated cheetah-like gallop are used by the dog. It is interesting to note that the dog can use the rotary footfall pattern for both types of gallop. This suggests that the type of downward to upward transition used does not depend on the rotary versus transverse distinction. Drawings of dogs are based on photos from Muybridge (1887). Net impulse vectors of each limb (black arrows) of the forelimb-initiated canine gallop are estimated from Walter & Carrier (2007). Net impulse vectors for (a) the hindlimb-initiated horse-like gallop are expected to parallel those of the horse (figure 2a).
Given the range of possibilities of footfall sequence and the variability of specific sequence within the mechanical context of the gait, it is preferable to categorize these two forms of gallop based on whether the transition is initiated with a hindlimb, as in the equine transverse gallop, or a forelimb, as in the cheetah rotary gallop. It will be seen that the mechanical differences between these two forms of asymmetric gallop persist regardless of left–right footfall sequence employed, or indeed whether there even is a lateral separation in forelimb and hindlimb contact.
6. Centre of mass motion not footfall pattern defines the mechanics of the ‘gallop’ gaits
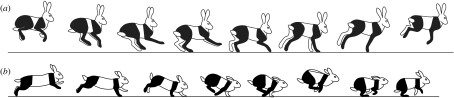
Although the rotary–transverse dichotomy is well established in the lexicon of gait analysis, the mechanics of galloping are remarkably independent of this distinction and it is possible to use a horse-like hindlimb-initiated transition or cheetah-like forelimb-initiated transition with either footfall sequence or with a sequence that does not match either. For instance, the North American jackrabbit (Lepus townsendii) generally gallops using a bound or half bound, where the hindlimbs contact in near unison while the forelimbs can contact together or slightly separated in time and position. However, in spite of using the same footfall pattern, the jackrabbit can employ both the hindlimb-initiated (horse-like) and forelimb-initiated (cheetah-like) gallop. The similarity of the bound and half bound and gallop has been well recognized (Hildebrand 1977). The cheetah-like, flexed back half bound is used by rabbits and hares during high-speed running when the animals are evading an immediate threat. In this gait, the spine displays a substantial arch as in the cheetah gallop and is the gait commonly identified with the rabbits and hares (figure 6b; Alexander 1988; Simons 1999). Although the flexed-back half bound is the common high-speed gait, the jackrabbit also performs an alternative slower speed, stiff backed half bound. This slower gallop-like gait clearly shows the horse-like initiation of the CoM transition via hindlimb contact and subsequent deflection of the CoM path through contacts progressing from rear to front (figure 6a). The fact that the jackrabbit can perform both styles of gallop using a virtually identical footfall pattern demonstrates that the key mechanical determinant of each gait is not the left–right sequence of foot contacts, but rather the role played by the front and rear limbs in the downward-to-upward transition of the CoM.
Figure 6.
A comparison of (a) the hindlimb-initiated half bound used at slow speeds (jackrabbit) and (b) the forelimb-initiated half bound used at high speeds (domestic rabbit). The transition mechanics of the hindlimb-initiated half bound are similar to those of the transverse gallop of the horse, while those of the forelimb-initiated half bound resemble those of the rotary gallop of the cheetah and dog. The fact that the jackrabbit can perform both styles of gallop using an apparently identical footfall pattern (hindlimbs contact nearly simultaneously while the forelimbs contact either in unison or at slightly different times) further demonstrates that it is not the sequence of left and right foot contacts that determines the mechanical distinction between these gaits, but rather the front–rear sequence and its relation to the downward-to-upward transition of the CoM. Drawings for the slow-speed bound are based on video footage of jackrabbits filmed by J. E. A. Bertram, and drawings of the high-speed half bound are based on fig. 4 of Simons (1999).
The horse-like hindlimb-initiated gallop, whether in the horse, dog or jackrabbit (at slower galloping speeds in the latter two species), distributes the transition so that a large portion of the available momentum is not involved in the impulsive contact of the limbs, but remains to contribute to the next stride. Although muscular action and some elastic energy storage and return doubtlessly contribute to the effectiveness of the gait, the gait does not appear to depend fundamentally on this (see, for instance, elastic recovery calculations of Pfau et al. (2006) for the horse distal limb). The transition of the CoM from downward–forward to upward–forward occurs in a manner grossly analogous to a stone skipping on the surface of water. Although the stone appears to bounce along the surface, it does so inelastically (the water is unable to store and return elastic strain energy). The ‘bounce’ occurs with the same geometry of the strut model in figure 1, except in this case the ‘strut’ is simply the line of action between the surface and the CoM of the stone. Provided the angle of deflection is within a boundary that allows sufficient kinetic energy to remain perpendicular to this line of action following contact, the stone will become airborne again (Rosellini et al. 2005). In the horse gallop, the bounce also need not be elastic. But unlike the vertical impulse produced on the stone, the transition of the hindlimb-initiated gallop is performed by multiple legs, allowing for a relatively smooth transition by distributing the individual contacts. Also unlike the stone, which dissipates energy with each skip, the legs perform work in each stride to maintain total mechanical energy in spite of some inevitable loss as a result of foot contact.
The configuration of the strut model of the cheetah-like gallop (figure 4b) indicates that it should result in large momentum losses due to the direction of the momentum vector relative to the ground contact points (i.e. a substantial component of the momentum vector is oriented parallel to the limb strut, so should be ‘lost’ to the collision). Alexander (1988) suggested that the front limb contact and flexion of the back following the extended flight in this type of gallop allow storage of strain potential energy in the spine and associated tissues that could then be transferred to the rear for hindlimb take-off following the collected flight phase. This may be the fundamental explanation of the highly arched back in this gait, which has coincident advantages of extending stride length and having the highest forward speed during the ballistic portion of the gait cycle. Such energy storage and return requires that net deceleration occurs on the forelimbs and net acceleration in the hindlimbs. This is consistent with the currently available evidence (Bryant et al. 1987; Walter & Carrier 2007), but no ground reaction force measurements are available from truly high-speed galloping in cheetahs or fast running dogs such as greyhounds. If there is no net difference in acceleration from the forelimb and hindlimb then transfer of energy through elastic structures in the back would not be possible. High-speed video of greyhounds at their highest running speeds suggests that if energy storage and return exists (i.e. if there is a speed change from forelimb to hindlimb contacts), it may not be very great (J. R. Usherwood 2008, personal communication).
Although the high-speed dog/cheetah gallop employs four contacts, the transition process and relationship of the CoM to the contact point of the limb struts is reminiscent of that of bipedal humans in running (figure 4b). Similar to the interpretation of the cheetah gallop above, human running has also been considered dependent on elastic energy storage and return and is routinely modelled as a classic spring–mass system (Cavagna et al. 1977; Blickhan 1989; Dalleau et al. 1998). Although strain energy storage and return certainly plays a substantial role in the action and efficiency of the human leg in running, the gait may not be fundamentally dependent on this. In running, the downward to upward CoM transition occurs while the contact limb changes its effective length (distance between ground contact and CoM). This length change provides an opportunity to manage the momentum loss of the transition. By changing limb length, the CoM transition is smoothed in the same way sequential limb contacts reduce momentum losses in the horse-like gallop. A single limb that changes length in a manner that minimizes impulse along its axis could have much the same effect as a large number of limbs, each of a different length, acting in a sequence (Ruina et al. 2005). To exploit this strategy, the limb muscles must follow the same force–length relation as a passive spring–mass system, so this form of transition ‘management’ has been termed ‘pseudo-elasticity’ (Ruina et al. 2005). Although the passive strain energy storage and return and pseudo-elastic momentum retention have the same action (a linear force–extension relation) and effect (kinetic energy saving), the mechanism responsible for the retention of energy is fundamentally different, where one stores and returns available energy while the other avoids energy loss in the first place. These two mechanisms for conserving energy are not mutually exclusive, so both are probably employed during running in bipeds and quadrupeds.
To some degree it is inconvenient that the predictions of the spring–mass and pseudo-elastic models of transition dynamics are identical, since this makes the design of an experiment that distinguishes the potential contribution of each factor exceedingly difficult in human running. However, if the bipedal run and high-speed canine gallop are indeed functionally parallel, the canine gallop may offer a unique opportunity to evaluate the relative contribution of these two mechanisms for increasing running efficiency. The complexity of the elastic storage system in the galloping canine, which potentially involves not only energy storage in the muscles and tendons surrounding the spine but also energy transfer between the limbs, provides an opportunity to selectively evaluate the contribution of each component to the recovery of energy. Likewise, because the forelimb-initiated transition involves coordination of two sets of limbs and the trunk to manage the CoM position relative to the limb strut contact point, this may provide an opportunity to evaluate the role of specific components in determining the pseudo-elastic transition that are unavailable in the bipedal human model.
7. Focused versus distributed transitions: towards a continuum of asymmetric and symmetric running
Although the above discussion has emphasized the differences between forelimb- and hindlimb-initiated transition gallops, and such a distinction suggests a fundamental difference between these two versions of the gallop gait, the differences may actually be subtler than these arguments portray. The angle of incidence of the CoM velocity vector (which determines the angle of deflection, given a specifically oriented strut) must be small as transition is initiated in the equine-like gallop or substantial momentum loss will occur (figure 1). This probably explains why this gait is only used at relatively high speeds (i.e. faster than most walk or trot speeds)—for any given ballistic flight higher horizontal speed produces a lower deflection angle. In theory, the minimum angle of incidence is achieved if the ballistic phase of the gait is minimized. Such a gait would distribute the impulse throughout the stride with each limb performing almost exactly the same mechanical role (M. Srinivasan 2007, personal communication). Gaits do exist that match this prediction, where the animal has evenly distributed foot contacts while moving at relatively high speeds. For instance, the tölt has been described as a ‘running walk’ (Biknevicius et al. 2006), in that it is a quadrupedal running gait but the footfall pattern is symmetrical. The tölt has the characteristics of the evenly distributed ‘gallop’ (where we recognize that gallop has traditionally been restricted to asymmetric gaits) and may indeed be an expression of the equine gallop taken to the limit of even contact distribution and the elimination of an intervening ballistic phase. The amble as displayed by the elephant may also have a similar function, and should possibly be considered a form of ‘symmetrical gallop’ (Ren & Hutchinson 2008). Such even distributions in contacts at speed in the elephant may play a role in limiting vertical force by optimally distributing the impulse required for support. Small mammals tend towards much less even contact distributions. The exaggerated bound of a squirrel is one that can commonly be observed but bounding gaits are the norm in small mammals (Hildebrand 1989).
The symmetric and evenly distributed CoM transition described above appears to have some advantages over the focused transition that occurs in most mammals (i.e. where an asymmetric transition event occurs in between relatively large ballistic, non-contact portions of the gait). The advantage of the focused transition is not currently understood, but it is more apparent at modest speeds or for smaller mammals. As speed increases to its limit in either the equine-like hindlimb-initiated or the dog/cheetah-like forelimb-initiated gallops, the ballistic portion of the stride is reduced to extremely small intervals (figure 7) even though asymmetry of the limb contact can remain, as in dogs (Maes et al. 2008). It is fairly obvious that there is a trade-off between the advantages of a low power ballistic phase and the higher power transition that allows such ballistic flight. The apparent size and speed scaling of the ballistic emphasis suggests that force capacity of the support limb may be the limitation, but this has not currently been fully evaluated. However, the trend towards distributing the support role between the limbs as speed increases, as opportunity to provide vertical impulse to generate the downward to upward transition decreases, suggests an important role for the collision-like interaction of the foot contact to determine the dynamics of the galloping gaits.
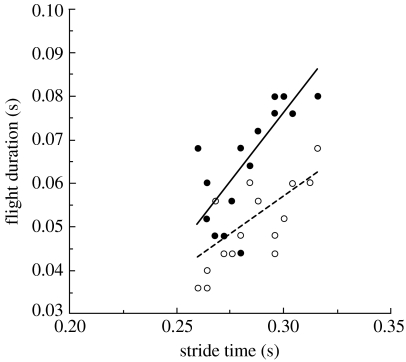
Figure 7.
Comparison of extended flight (filled circles, solid line) and collected flight (open circles, dashed line) duration from 17 racing greyhounds galloping between 14 and 19 m s−1. Extended flight is usually the main ballistic portion of the dog/cheetah gallop as indicated by the dominance of the extended duration, but the difference becomes indistinguishable for the most rapid strides (shortest total duration of non-contact). This indicates that at the highest galloping speeds greyhound galloping approaches a flat trajectory. Extended flight duration, R2=0.644; collected flight duration, R2=0.38 (data courtesy of J. R. Usherwood).
8. Conclusions
The two well-recognized galloping gaits—that of the horse and the cheetah—are functionally distinguished based on which limb pair, fore or hind, initiates the transition of the CoM from downward–forward to upward–forward during the ground contact periods interspersed between the main ballistic (non-contact) portions of the stride. It is during this transition that substantial momentum can be lost if the dynamics of the ground interaction are not managed effectively. Different strategies for managing the transition are employed in the two forms of galloping. The horse-like gallop reduces loss primarily by using the limbs as struts and distributing the CoM deflection. This strategy has the disadvantage that the primary ballistic phase of the gait occurs at a relatively slow forward velocity. The cheetah-like gallop does not appear to have the same geometric relationship between the CoM velocity vector and the supporting strut-like limbs. We suspect that the body and contact strut (limb and back in coordination) actively change length in a manner that requires muscle work but may limit the momentum lost due to the ground contact for this transition geometry by allowing the CoM to follow a smooth, pseudo-elastic path. This probably works in concert with elastic energy storage and return mechanisms and appears to be analogous to the strategy used in the bipedal (human) run.
It is currently not known why many ungulates appear restricted in their capacity to employ the forelimb-initiated gallop. It is difficult to contend that the horse is not functionally capable of a forelimb-initiated gallop since horses are observed to initiate transition from downward to forward using forelimbs when landing from a jump (Muybridge 1887, plates 74–78) and accelerate from hindlimbs when initiating a run. Since the hindlimb–forelimb-initiated transition dichotomy has not previously been recognized, currently there is no survey documenting which species employ the hindlimb-initiated gallop. Some plates from Muybridge (1887) indicate that deer may use a forelimb-initiated transition gallop (plates 148–153). It is likely that the prevalence of one type of gallop within a species is determined by the energetic cost of the gait and this is influenced by the dynamics of the downward to upward transition of each stride. This must be considered when evaluating function in running gaits such as the gallop.
Acknowledgments
We would like to thank Dr Rebecca Walter for graciously sharing ground force recordings of canine galloping and Dr Jim Usherwood for data on greyhound gallop kinematics. The manuscript has been improved by discussions with J. R. Usherwood, A. Wilson and the patient efforts of three anonymous reviewers. This study was funded through a Discovery Grant (J.E.A.B.) from the Natural Sciences and Engineering Research Council of Canada.
References
- Alexander R.M. Why mammals gallop. Am. Zool. 1988;28:237–245. doi: 10.1093/icb/28.1.237. [DOI] [Google Scholar]
- Alexander R.M., Langman V.A., Jayes A.S. Fast locomotion of some African ungulates. J. Zool. Lond. 1977;183:291–300. [Google Scholar]
- Bertram J.E.A., Ruina A., Cannon C.E., Chang Y.H., Coleman M.J. A point-mass model of gibbon locomotion. J. Exp. Biol. 1999;202:2609–2617. doi: 10.1242/jeb.202.19.2609. [DOI] [PubMed] [Google Scholar]
- Biknevicius A., Mullineaux D.R., Clayton H.M. Locomotor mechanics of the tolt in Icelandic horses. Am. J. Vet. Res. 2006;67:1505–1510. doi: 10.2460/ajvr.67.9.1505. [DOI] [PubMed] [Google Scholar]
- Blickhan R. The spring-mass model for running and hopping. J. Biomech. 1989;22:1217–1227. doi: 10.1016/0021-9290(89)90224-8. [DOI] [PubMed] [Google Scholar]
- Bryant J.D., Bennett M.B., Brust J., Alexander R.M. Forces exerted on the ground by galloping dogs (Canis familiaris) J. Zool. Lond. 1987;213:193–203. doi: 10.1111/j.1469-7998.1987.tb03693.x. [DOI] [Google Scholar]
- Cavagna G.A., Heglund N.C., Taylor C.R. Mechanical work in terrestrial locomotion: two basic mechanisms for minimizing energy expenditure. Am. J. Physiol. 1977;233:R243–R261. doi: 10.1152/ajpregu.1977.233.5.R243. [DOI] [PubMed] [Google Scholar]
- Dalleau G., Belli A., Bourdin M., Lacour J.R. The spring-mass model and the energy cost of treadmill running. Eur. J. Appl. Physiol. Occup. Physiol. 1998;77:257–263. doi: 10.1007/s004210050330. [DOI] [PubMed] [Google Scholar]
- Donelan M.J., Kram R., Kuo A.D. Simultaneous positive and negative external work in human walking. J. Biomech. 2002;35:117–124. doi: 10.1016/S0021-9290(01)00169-5. [DOI] [PubMed] [Google Scholar]
- Garcia M., Chatterjee A., Ruina A., Coleman M. The simplest walking model: stability, complexity and scaling. J. Biomech. Eng. 1998;120:281–288. doi: 10.1115/1.2798313. [DOI] [PubMed] [Google Scholar]
- Gray J. Cambridge University Press; Cambridge, UK: 1953. How animals move. [Google Scholar]
- Haussler K.K., Bertram J.E., Gellman K., Hermanson J.W. Segmental in vivo vertebral kinematics at the walk, trot and canter: a preliminary study. Equine Vet. J. Suppl. 2001;33:160–164. doi: 10.1111/j.2042-3306.2001.tb05381.x. [DOI] [PubMed] [Google Scholar]
- Hedrick T.L., Tobalske B.W., Biewener A.A. Estimated circulation and gait change based on three-dimensional kinematic analysis of flight in cockatiels (Nymphicus hollandicus) and ringed turtle-doves (Stretopelia risoria) J. Exp. Biol. 2002;205:1389–1409. doi: 10.1242/jeb.205.10.1389. [DOI] [PubMed] [Google Scholar]
- Heglund N.C., Taylor C.R. Speed, stride frequency and energy cost per stride: how do they change with body size and gait? J. Exp. Biol. 1988;138:301–318. doi: 10.1242/jeb.138.1.301. [DOI] [PubMed] [Google Scholar]
- Hildebrand M. Motions of the running cheetah and horse. J. Mammal. 1959;40:481–495. doi: 10.2307/1376265. [DOI] [Google Scholar]
- Hildebrand M. Analysis of asymmetrical gaits. J. Mammal. 1977;58:131–156. doi: 10.2307/1379571. [DOI] [Google Scholar]
- Hildebrand M. The quadrupedal gaits of vertebrates. BioScience. 1989;39:766–775. doi: 10.2307/1311182. [DOI] [Google Scholar]
- Howell A.B. University of Chicago Press; Chicago, IL: 1944. Speed in animals: their specialization for running and leaping. p. 270. [Google Scholar]
- Hoyt D.F., Taylor C.R. Gait and the energetics of locomotion in horses. Nature. 1981;292:239–240. doi: 10.1038/292239a0. [DOI] [Google Scholar]
- Jayes A.S., Alexander R.M. Mechanics of locomotion of dogs (Canis familiaris) and sheep (Ovis aries) J. Zool. (Lond.) 1978;185:289–308. doi: 10.1111/j.1469-7998.1978.tb03334.x. [DOI] [PubMed] [Google Scholar]
- Kuo A.D. Energetics of actively powered locomotion using the simplest walking model. J. Biomech. Eng. 2002;124:113–120. doi: 10.1115/1.1427703. [DOI] [PubMed] [Google Scholar]
- Kuo A.D. The six determinants of gait and the inverted pendulum analogy: a dynamic walking perspective. Hum. Mov. Sci. 2007;26:617–656. doi: 10.1016/j.humov.2007.04.003. [DOI] [PubMed] [Google Scholar]
- Kuo A.D., Donelan J.M., Ruina A. Energetic consequences of walking like an inverted pendulum: step-to-step transitions. Exerc. Sport Sci. Rev. 2005;33:88–97. doi: 10.1097/00003677-200504000-00006. [DOI] [PubMed] [Google Scholar]
- Maes L.D., Herbin M., Hackert R., Bels V.L., Abourachid A. Steady locomotion in dogs: temporal and associated spatial coordination patterns and the effect of speed. J Exp. Biol. 2008;211:136–149. doi: 10.1242/jeb.008243. [DOI] [PubMed] [Google Scholar]
- Magne de la Croix P. Evolution of locomotion in mammals. J. Mammol. 1936;17:51–54. doi: 10.2307/1374551. [DOI] [Google Scholar]
- Marey J.-E. Appleton and Co; New York, NY: 1874. Animal mechanism: a treatise on terrestrial and aerial locomotion. [Google Scholar]
- McGeer T. Passive dynamic walking. Int. J. Robot. Res. 1990;9:68–82. doi: 10.1177/027836499000900206. [DOI] [Google Scholar]
- Merkens H.W., Schamhart H.C., van Osch G.J., Hartman W. Ground reaction force patterns of Dutch warmbloods at the canter. Am. J. Vet. Res. 1993;54:670–674. [PubMed] [Google Scholar]
- Minetti A.E., Ardigo L.P., Reinach E., Saibene F. The relationship between mechanical work and energy expenditure of locomotion in horses. J. Exp. Biol. 1999;202:2329–2338. doi: 10.1242/jeb.202.17.2329. [DOI] [PubMed] [Google Scholar]
- Muybridge, E. 1887 Animals in motion. New York, NY: Dover Publications, Inc. (Dover Publications edition (ed. L. S. Brown) 1957.)
- Nauwelaerts S., Aerts P. Two distinct gait types in swimming frogs. J. Zool. Lond. 2001;258:183–188. doi: 10.1017/S0952836902001292. [DOI] [Google Scholar]
- Pandy M.G., Kumar V., Berme N., Waldron K.J. The dynamics of quadrupedal locomotion. J. Biomech. Eng. 1988;110:230–237. doi: 10.1115/1.3108436. [DOI] [PubMed] [Google Scholar]
- Pfau T., Witte T.H., Wilson A.M. Centre of mass movement and mechanical energy fluctuation during gallop locomotion in the thoroughbred racehorse. J. Exp. Biol. 2006;209:3742–3757. doi: 10.1242/jeb.02439. [DOI] [PubMed] [Google Scholar]
- Ren L., Hutchinson J.R. The three-dimensional locomotor dynamics of African (Loxodonta africana) and Asian (Elephas maximus) elephants reveal a smooth gait transition at moderate speed. J. R. Soc. Interface. 2008;5:195–211. doi: 10.1098/rsif.2007.1095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robilliard J.J., Pfau T., Wilson A.M. Gait characterization and classification in horses. J. Exp. Biol. 2007;210:187–197. doi: 10.1242/jeb.02611. [DOI] [PubMed] [Google Scholar]
- Rosellini L., Hersen F., Clanet C., Bocquet L. Skipping stones. J. Fluid Mech. 2005;543:137–146. doi: 10.1017/S0022112005006373. [DOI] [Google Scholar]
- Ruina A., Bertram J.E.A., Srinivasan M. A collisional model of the energetic cost of support work qualitatively explains leg sequencing in walking and galloping, pseudo-elastic leg behavior in running and the walk-to-run transition. J. Theor. Biol. 2005;237:170–192. doi: 10.1016/j.jtbi.2005.04.004. [DOI] [PubMed] [Google Scholar]
- Simons R. Running, breathing and visceral motion in the domestic rabbit (Oryctolagus cuniculus): testing visceral displacement hypotheses. J. Exp. Biol. 1999;202:563–577. doi: 10.1242/jeb.202.5.563. [DOI] [PubMed] [Google Scholar]
- Smith J.L., Chung S.H., Zernicke R.F. Gait-related motor patterns and hindlimb kinetics for the cat trot and gallop. Exp. Brain Res. 1993;94:308–322. doi: 10.1007/BF00230301. [DOI] [PubMed] [Google Scholar]
- Srinivasan M., Ruina A. Computer optimization of a minimal biped discovers walking and running. Nature. 2006;439:72–75. doi: 10.1038/nature04113. [DOI] [PubMed] [Google Scholar]
- Usherwood J.R., Bertram J.E.A. Understanding brachiation: insight from a collision perspective. J. Exp. Biol. 2003;206:1631–1642. doi: 10.1242/jeb.00306. [DOI] [PubMed] [Google Scholar]
- Walter R.M., Carrier D.R. Ground forces applied by galloping dogs. J. Exp. Biol. 2007;210:208–216. doi: 10.1242/jeb.02645. [DOI] [PubMed] [Google Scholar]
- Young P.S., Swanson C., Cech J.J., Jr Photophase and illumination effects on the swimming performance and behavior of five California estuarine fishes. Copeia. 2004;2004:479–487. doi: 10.1643/CP-03-061R1. [DOI] [Google Scholar]