Elastic coupling of limb joints enables faster bipedal walking

Abstract

The passive dynamics of bipedal limbs alone are sufficient to produce a walking motion, without need for control. Humans augment these dynamics with muscles, actively coordinated to produce stable and economical walking. Present robots using passive dynamics walk much slower, perhaps because they lack elastic muscles that couple the joints. Elastic properties are well known to enhance running gaits, but their effect on walking has yet to be explored. Here we use a computational model of dynamic walking to show that elastic joint coupling can help to coordinate faster walking. In walking powered by trailing leg push-off, the model's speed is normally limited by a swing leg that moves too slowly to avoid stumbling. A uni-articular spring about the knee allows faster but uneconomical walking. A combination of uni-articular hip and knee springs can speed the legs for improved speed and economy, but not without the swing foot scuffing the ground. Bi-articular springs coupling the hips and knees can yield high economy and good ground clearance similar to humans. An important parameter is the knee-to-hip moment arm that greatly affects the existence and stability of gaits, and when selected appropriately can allow for a wide range of speeds. Elastic joint coupling may contribute to the economy and stability of human gait.

1. Introduction

Human walking requires the coordination of multiple muscles and joints to simultaneously move the legs in a periodic pattern, support body weight and maintain dynamic stability. Coordination may be simplified by taking advantage of the passive dynamics of the legs (McGeer 1990a), which can perform all of these functions automatically. For example, passive dynamic walking robots can descend a gentle slope with no energy input other than gravity, and have no active control. These abilities may be extended to walking on level ground by adding minimal energy input and allowing passive dynamics to still account for most of the motion. Active dynamic walking is often quite economical, because no effort is expended to force the limbs through predetermined trajectories (Kuo 2007a). Passive stability also makes walking easy to control. There are, however, two important issues for dynamic walking. The first is the appropriate means of powering stable walking on level ground, and the second is the modulation of speed, step length and step frequency to match human gait. Here, we consider the coordination of the joints to achieve these two aims, using the contrasting abilities of robots and humans as the basis for study.

Level walking can in principle be powered with simple, single-joint actions such as ankle push-off. Powering is necessary because mechanical energy is dissipated at the end of each step when the leading leg strikes the ground (Kuo 2002). This may be regarded as a mechanical collision (Garcia et al. 1998), because the dissipation occurs over a relatively brief duration and with little displacement of the body centre of mass. Ankle push-off can offset the energy loss; if initiated just prior to heelstrike as with humans (Donelan et al. 2001, 2002a,b), it can reduce the ensuing collision and therefore the amount of push-off work needed (Kuo 2002). The work of the step-to-step transition—comprising both push-off and collision—accounts for much of the energy expended during human walking (Kuo et al. 2005; Kuo 2007b). An alternative is to perform work about the hip, which also produces stable dynamic walking but with lower economy. The differences are demonstrated empirically by recent robots that use ankle or hip actuation (Collins et al. 2005; Wisse 2005). Their gaits bear considerable resemblance to that of humans, but their simple actuation schemes are clearly different from the complex joint torque patterns employed by humans. The minimal requirements for active dynamic walking may nonetheless provide insight regarding how humans coordinate multiple joints.

One potential advantage of multi-joint coordination is faster walking. Dynamic walking machines (e.g. McGeer 1990b; Collins et al. 2005; Wisse 2005) are currently limited to speeds equivalent to approximately one-third of a relaxed human's typical 1.25 m s⁻¹. Faster gaits may be produced in a straight-legged dynamic walking model, simply by applying spring-like hip torques acting between the legs (Kuo 2002). The spring stiffness effectively modulates step frequency, whereas push-off mostly modulates step length. For the same push-off, faster speeds may be achieved at no additional energetic cost merely by increasing the stiffness of the hip spring. This, however, appears insufficient for legs with passive knees. A hip-powered robot (Wisse 2005) could walk only with an additional knee spring, without which knee extension at the end of swing could not be guaranteed. Although the effect of the spring was not explored parametrically, its necessity suggests that springs may provide a simple means to achieve human-like walking speeds. Human muscles, although capable of many behaviours, are well-suited to act as springs due to the elasticity of tendon. They must produce active force to support tendon force, and therefore must also expend energy if only to act elastically (Doke et al. 2005; Doke & Kuo 2007), but springs may nevertheless improve the overall economy (Kuo 2001). Robots and humans alike may therefore benefit from multi-joint coordination for gait modulation.

The purpose of the present study was to examine how joint springs can modulate gait for faster walking. We considered multiple configurations for springs about the knee and hip to provide different combinations of joint coupling. We began with a kneed model of dynamic walking and considered the limitations of push-off actuation, not previously studied systematically. With this model, we examined how uni-articular hip and knee springs, alone or in combination, can modulate gait. We also examined a bi-articular spring configuration, and found it to be best suited for faster walking. Optimizing its parameters, based purely on mechanical criteria, yields a faster gait quite similar to that employed by humans.

2. Kneed walking model

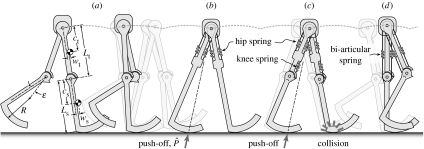
We examined the behaviour of a model of walking in the sagittal plane, with passive knee and hip joints (figure 1). The model is nearly identical to the gravity-powered mechanism with knees (figure 1a) studied by McGeer (1990b), except with the addition of push-off impulses to power level walking, and springs about the joints to modulate the gait. As with McGeer (1990b), the model comprises four rigid segments connected by hinge joints, with anthropomorphically distributed mass, a point mass representing the upper body at the hip and curved feet offset forward of the legs. Unlike humans, the model has no torso; recent dynamic walking machines have added a torso with minimal effect on the passive dynamics of the legs (Wisse 2005). All dimensions, mass parameters and other variables are described in non-dimensional terms, with the model's total mass M, leg length L and gravity g serving as base units (table 1). For reference, comparisons are made with a typical human with mass 70 kg and leg length 0.98 m. One addition to McGeer's (1990b) model is a latching mechanism that keeps the knee extended until the end of the ipsilateral stance phase. Although passive forces can theoretically keep the knee fully extended, a latch improves robustness and is included in several robots (Collins et al. 2005).

Figure 1.

Four dynamic walking models. (a) McGeer (1990b) demonstrated gravity-powered walking with knees. The model walks down a gentle slope, with a gait generated entirely by the passive dynamics of the limbs. The knee provides automatic ground clearance for the swing leg's foot. (b) Kuo (2002) showed that a push-off impulse could power straight-legged gait on level ground, with a hip spring modulating step frequency for faster, economical walking. Here we consider (c) a powered kneed model with uni-articular hip and/or knee springs, as well as (d) bi-articular springs acting across both knee and hip. Separate models are depicted with a common hip trajectory. See table 1 for dimensions in (a).

Table 1.

Geometric and mass distribution parameters for kneed walking model (after McGeer 1990b). (Length parameters are presented as a fraction of total leg length L and mass parameters as fraction of total body mass M. Length parameters are depicted in figure 1.)

parameter	symbol	value
mass of pelvis	mp	0.676
mass of thigh	mt	0.1
mass of shank	ms	0.062
length of thigh	Lt	0.46
length of shank	Ls	0.54
moment of inertia of thigh	It	0.00182
moment of inertia of shank	Is	0.00214
location of thigh COM relative to hip	ct	0.26
location of shank COM relative to knee	cs	0.3
forward offset of thigh COM	wt	0
forward offset of shank COM	ws	0.01
radius of curvature of foot	R	0.3
angular offset of foot COM relative to shank	ϵ	0.2

We added the push-off impulse to provide an economical means of powering gait (figure 1b). The impulse $\hat{P}$ (expressed as fraction of Mg^−0.5L^0.5) is applied at the ground contact (GC) point of the stance leg immediately prior to heelstrike, directed towards the hip. This impulse performs positive work as it redirects the COM velocity. The positive work offsets energy losses, which can occur only in two instances. The first is the knee stop collision that occurs as the knee reaches full extension, as the shank's motion relative to the thigh is arrested inelastically by the passive knee stop. The second is the heelstrike collision of the swing foot with ground, accounting for a major proportion of the energy lost in human walking (Donelan et al. 2002a,b). The advantage of push-off over other means of performing work is that it reduces the COM velocity at heelstrike. When properly applied just before heelstrike, the push-off impulse actually decreases the negative work of the collision, so that less positive work must be performed compared to, say, powering about the hips (Kuo 2002).

The model's gait was modulated by the addition of passive springs. In the uni-articular spring model, we placed springs about the hip and/or knee joints (figure 1c), with the torque generated at the hip proportional to the angle between the legs, and the torque generated at the knees proportional to the angle of knee flexion. The springs' effects are summarized by torsional stiffness parameters K_hip and K_knee (as fraction of MgL), respectively, with the hip spring in equilibrium when the thighs are aligned (zero hip angle), and the knee spring when the knee is fully extended. In the bi-articular model (figure 1d), we added springs acting across both hips and knees, coupling knee flexion and hip extension, and vice versa, roughly analogous to the bi-articular hamstrings and rectus femoris muscles of humans. Each spring has a separate moment arm about hip and knee, with equilibrium occurring with both legs fully extended and parallel. In both uni- and bi-articular models, the legs react not against a torso but against each other. This is more restrictive than humans, who can also produce hip torques against the inertial mass of the torso. The simpler configuration was designed to reduce the number of parameters, rather than to explicitly model a given robot or human accurately. The result is that two parameters are sufficient to describe the springs' behaviour: the linear stiffness k_kh (as fraction of MgL⁻¹) and the ratio r_kh between the knee and hip moment arms. We arbitrarily set the hip moment arm to 0.01, which automatically assigns the knee a moment arm of 0.01r_kh.

We used standard procedures of dynamic walking models to determine periodic walking gaits (McGeer 1990a,b), briefly summarized as follows. Each step was simulated starting with a set of initial conditions for the configuration and velocities of the joints immediately following the heelstrike. The simulation was advanced forward in time until the swing knee reached full extension, at which point the knee stop collision produced a change in velocities. The simulation then continued with a straight swing leg, until just prior to GC, when an impulsive push-off was applied to the trailing leg, followed immediately by the leading leg's heelstrike collision. We used a first-order gradient search to find limit cycles where each step yielded repeating initial conditions for the next step, as is necessary for periodic motion. We also determined each gait's local asymptotic stability from the eigenvalues of the linearized step-to-step function. All eigenvalues were required to have magnitude less than one for a gait to be classified as stable, meaning automatic rejection of small perturbations without need for active control.

Gaits produced by this model could fail in several ways. We classified a gait as successful if it yielded a stable limit cycle in which heelstrike occurred after knee stop, with the knee fully extended. Humans can of course walk in an aperiodic manner, actively stabilize a passively unstable gait or actively prevent the knee from buckling. Rather than incorporating such active behaviours, we examined only gaits arising naturally from passive dynamics with minimal control. With many spring configurations, the kneed model passively flexes the knee at mid-stance, thereby gaining ground clearance for the swing leg. Some configurations caused knee stop to occur prior to mid-stance, causing the extended swing leg to briefly touch the floor at mid-swing. But we did not classify such ‘foot scuffing’ (Garcia et al. 2000) as a failure, because it can be avoided in several ways. For example, some straight-legged machines gain ground clearance by lifting the swing foot slightly (McGeer 1990a). Humans and some machines (Collins et al. 2001) can gain sufficient clearance simply by rocking laterally with each step, which otherwise has negligible effect on the sagittal plane motion (Kuo 1999). We nevertheless noted which gaits exhibited a tendency towards foot scuffing, based on the timing of knee stop relative to mid-stance, because humans appear to prefer knee stop to occur after the swing leg passes the stance leg. Aside from identifying the conditions that would lead to a fall or otherwise prevent a limit cycle, we did not simulate the actual falls that would occur in an aperiodic step or an unstable limit cycle.

3. Powered walking with push-off

Applying push-off impulses to the kneed walking model, we verified that the impulses can successfully power a stable gait on level ground (figure 2a). The magnitude of push-off simultaneously affects both step length and walking speed. A stronger push-off causes the stance leg to move at a higher velocity, traversing a larger angle before heelstrike occurs, with little effect on the timing of knee stop and heelstrike. The step length increases roughly with the square root of push-off magnitude (figure 2b), much as the straight-legged model (Kuo 2002). This is accompanied by a very slight increase in step frequency, so that overall walking speed—the product of step length and step frequency—also increases roughly with the square root of push-off magnitude. Comparing the gaits with those generated by a straight-legged model with the same human-like mass distribution and geometry (figure 2b), the kneed model walks with slightly shorter steps and slightly higher step frequencies. These effects cancel so that both models walk at very similar speeds. With small push-off impulses $(\hat{P}<0.085)$, the straight-legged model walks with a slightly higher speed, while with larger push-off impulses the kneed model is slightly faster.

Figure 2.

Powering the kneed walking model with push-off. (a) Kinematics are illustrated with the angle of each segment measured anticlockwise with respect to vertical, plotted for one step (heelstrike to opposite heelstrike). Stronger push-off produces longer steps, as heelstrike occurs with a larger angle between the swing and stance legs. The knee angle is equal to the difference between the swing thigh and shank angles, with knee stop occurring when these angles meet. (b) Gait parameters (step length, step frequency and walking speed) as a function of push-off impulse magnitude. A single vertical axis shows dimensionless values for all parameters; a separate dimensional scale for human legs is provided for each parameter. Greater push-off results in longer steps and faster walking speed, and slightly higher step frequency. These effects are roughly similar to those of a straight-legged model (dashed lines; Kuo 2002), but over a smaller range of speeds. All dimensionless quantities are determined using body mass, leg length and gravitational acceleration as base units for normalization. For example, one dimensionless unit in the vertical axis corresponds to a speed of 3.1 m s⁻¹, step length 1 m or step frequency 3.1 Hz for a typical human with 1 m leg length. The fastest speed of the kneed model (solid lines) is equivalent to 0.74 m s⁻¹ with step length 0.62 m and frequency 1.2 Hz. (c) Work per step as a function of push-off impulse. In the straight-legged model (dashed lines), the only energy loss is in heelstrike. In the model with knees (solid lines), energy is lost at knee stop as well as heelstrike, their sum equalling the energy gained at push-off. The overall collision losses of both straight-legged and kneed models are the same for a given push-off.

The kneed model differs from its straight-legged relative by having an additional means of losing energy, the knee stops collision. Its energetic cost per step, however, is not different (figure 2c), because push-off performs the same amount of positive work, as both models are in the same straight-legged configuration at that instant. The difference is in the apportionment of losses. The kneed model dissipates substantial energy at knee stop, exceeding that from heelstrike and accounting for the majority of the total energy lost per step. But heelstrike energy losses are reduced considerably when compared with the straight-legged model, because the additional degree of freedom of the trailing leg's shank allows less energy to be dissipated in the step-to-step transition. A collision performs negative work on a system because its velocities must suddenly change in order to conform to a new kinematic constraint (i.e. GC). Combined with the slightly shorter steps of the kneed model, the overall effect is for heelstrike losses to be considerably lower than for the straight-legged model. As with the straight-legged model, the energy added by push-off increases approximately with the square of impulse magnitude $\hat{P}$ (Kuo 2002). For the same push-off, overall collision losses per step are about the same with or without knees, as are the walking speeds (figure 2b).

The kneed model, however, can walk only for approximately half the range of push-off impulses as the straight-legged model (figure 2b). Stable limit cycles occur only for a range $0.054<\hat{P}<0.114$. Smaller push-off impulses cause a weak push-off (WP) failure (figure 3a), where there is insufficient energy input to drive an acceptable gait. This is because the knee stop collision dissipates substantial energy even at slow walking speeds. The straight-legged model has no such loss and can walk with lower push-off magnitude and thus slower speed compared to the kneed model. The kneed gaits actually deteriorate over a range of weakening push-off impulses $(0.042<\hat{P}<0.054)$, with the model initially producing an asymmetric or limping gait that alternates between steps with straight-legged swing and normal swing. Asymmetric gaits that repeat over two or more steps occur as push-off decreases, but we did not quantitatively evaluate them other than noting that no limit cycles exist for $\hat{P}<0.042$.

Figure 3.

Failure modes for powered walking with knees. (a) With WP, the stance leg moves too slowly to drive the swing leg through its normal pendulum motion, preventing a forward step from being taken (parameters: $\hat{P}=0.01$, no springs). (b) The model can also stumble (ST), where the swing foot lands while swinging forward with the knee flexed (parameters: $\hat{P}=0.12$, no springs). (c) Another failure is no knee stop (NKS), where the swing knee never reaches extension even if the leg otherwise completes a swing (parameters: $\hat{P}=0.10$; k_kh=100; r_kh=0.95). All steps end at GC, although some simulations (light grey lines in (a) and (b)) are depicted beyond this point to demonstrate the passive motions that would occur if the floor did not intervene.

The kneed model is also more limited in the upper range of push-off impulses. With stronger push-off $(\hat{P}>0.114)$, the stance leg moves more quickly, in fact too quickly for the swing leg to catch the body at heelstrike (termed stumble or ST; figure 3b). Large impulses produce more asymmetric gaits in the transition to instability. By contrast, the straight-legged model can walk with considerably larger push-off impulses before going unstable (up to $\hat{P}\approx 0.166$).

4. Uni-articular knee spring

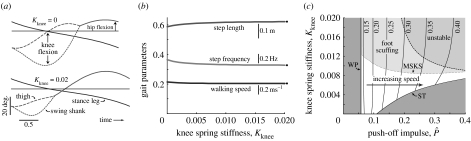
The addition of a spring about the knee joint is helpful for explaining the difference between walking with and without knees. A model with zero knee joint stiffness and no push-off impulse is identical to McGeer's (1990b) kneed model. At intermediate stiffnesses, the added spring leads to earlier knee stop, less knee flexion and greater hip flexion (figure 4a). As the stiffness increases, the knee motion becomes progressively shorter in duration and smaller in amplitude, eventually approaching the straight-legged gait (figure 4b). Despite its profound effect on knee joint motion, the torsional spring stiffness has much less influence on gait speed and other characteristics. With a constant push-off impulse, increasing spring stiffness leads to slightly increased step length and decreased step frequency, and practically no change in the walking speed. Changes mostly occur with relatively weak knee springs (K_knee<0.01), beyond which the system converges on the straight-legged model.

Figure 4.

Effect of a knee spring on dynamic walking gait. (a) A uni-articular knee spring results in earlier knee stop, less knee flexion and more hip flexion (parameter: $\hat{P}=0.10$). (b) Dimensionless gait parameters as a function of knee spring stiffness. Increasing knee spring stiffness causes small changes in gait characteristics; step length increases, step frequency decreases and walking speed decreases very slightly. As knee stiffness continues to increase, gaits asymptotically approach those of the straight-legged model (filled circles). (c) Contour plot of walking speed (labelled at top) as a function of push-off impulse and spring stiffness. There are two regions where there are no gaits (darker shaded areas): low push-off impulses result in the WP failure and low knee stiffnesses result in the stumbling (ST) failure. There are successful gaits for moderately high knee stiffness and push-off, with walking speed increasing with push-off. Increasing knee stiffness causes knee stop to occur earlier, eventually leading to foot scuffing, as delineated by the mid-stance knee stop (MSKS) boundary (where knee stop occurs as the two legs pass each other). Still faster gaits with high knee stiffness become unstable. Stable gaits without foot scuffing (unshaded areas) are nonetheless possible across a range of speeds, as long as knee stiffness is chosen appropriately. For reference, the limit cycles in (b) are roughly equivalent to a human walking at a relatively slow speed of 0.65 m s⁻¹, step frequency of 1.0 Hz and step length of 0.63 m.

The knee spring also greatly extends the range of push-off impulses and walking speeds achievable without stumbling. As with the model with push-off alone (figure 2), walking speed is determined primarily by the push-off impulse, increasing roughly with its square root (Kuo 2002). With low push-off impulse magnitudes, the model does not receive sufficient energy input to offset collision losses, regardless of knee joint stiffness, resulting in a WP failure. For intermediate magnitudes, greater push-off produces higher speeds with longer steps, normally limited by the stumbling failure (figure 3b). But the knee spring averts this failure, producing faster flexion and then extension of the swing leg, with earlier knee stop. This allows for stronger push-off and faster speeds, as long as spring stiffness is increased with push-off magnitude. There is, however, an upper limit to the knee joint stiffness that is helpful. With increasing push-off and knee stiffness comes an increasing tendency for knee stop to occur earlier in the step, leading to foot scuffing (delineated by mid-stance knee stop boundary; figure 4c). These gaits are stable for a range of values, but become unstable (figure 4c, unstable region) beyond an upper stiffness limit that gradually decreases with increasing push-off magnitude. The range of useful stiffnesses becomes narrow (K_knee range 0.0067–0.0089 for a push-off of $\hat{P}=0.4$), as the lower limit associated with stumbling approaches an upper limit associated with foot scuffing and instability. Between these limits, knee spring stiffness has little effect on walking velocity, with the highest speeds found at the lowest stiffness for which a gait cycle is produced. Low stiffness also means low force, making it advantageous to use the lowest stiffness that averts the stumbling failure, in terms of both maximal speed and minimal force production. With a knee spring within this narrow range, the model can walk with larger push-off impulses and walking speeds exceeding 0.4, equivalent to a human at 1.25 m s⁻¹.

5. Uni-articular hip spring

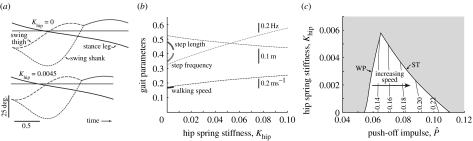
A hip joint spring by itself has a very modest effect on the gait limit cycles produced by the kneed walking model. The spring causes the stance and swing legs to move more quickly, producing earlier heelstrike (figure 5a). For a constant push-off impulse magnitude, increasing hip stiffness leads to a slight increase in step frequency and a decrease in step length, with a minimal effect on walking speed (figure 5b). But stable limit cycles are generated only for a limited range of stiffnesses, above which the unactuated knee prevents the shank from moving quickly enough to match the thigh. With a stiff hip spring (K_hip>0.005), the overall effect is a stumbling failure (as in figure 3b). This is in contrast to the effect of a hip spring on a straight-legged model, where a hip joint spring can greatly increase the step frequency, allowing for a wide range of step length and speed combinations (Kuo 2002). Here, the unactuated knees do not allow for such a range in the kneed model with hip spring alone.

Figure 5.

Effect of a uni-articular hip spring on gait. (a) Hip springs produce slightly faster steps, as the stance and swing leg both move faster (parameter: $\hat{P}=0.075$). (b) Dimensionless gait parameters as a function of hip spring stiffness. Limit cycles only exist for a narrow range of stiffnesses. Within this range, the hip spring causes shorter step lengths and higher step frequencies, with a minimal effect on walking speed. (c) Contour plot of walking speed as a function of hip spring stiffness and push-off impulse shows that the spring reduces the range of achievable gaits. Increasing stiffness leads to step failures either owing to WP or stumbling (ST).

These effects apply even with greater push-off magnitudes. In fact, only a limited range of push-off impulses and walking speeds are achievable with the hip spring alone (figure 5c). Compared with the push-off model without springs (figure 2), the hip spring actually restricts the lower bound on push-offs that are not too weak and reduces the upper limit on those that are not too strong. The failure boundaries converge with increasing hip joint stiffness, so that a stiffness of approximately 0.0061 yields no gait at all.

6. Combined uni-articular knee and hip springs

The combination of springs about both knee and hip can potentially reduce the limitations of either type of spring alone. The knee spring by itself allows for faster walking speeds and stronger push-off, but with low step frequencies and poor economy. The hip spring by itself has little of the step frequency-enhancing effect observed with the straight-legged model. The two springs together, however, would be expected to allow for greater step frequency and walking speed, because the knee spring makes the model behave more as if it has straight legs, so that the hip spring can successfully increase step frequency and improve economy (Kuo 2002).

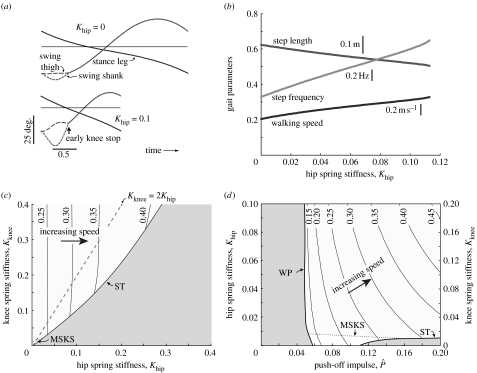
Model simulations verify that combining both can indeed speed leg motion. Adding a hip spring to the knee spring model causes both the stance leg and swing leg to move faster, so that heelstrike occurs earlier (figure 6a). The hip spring also causes increased knee flexion, because it speeds the thigh without affecting the shank. Parametrically increasing the hip stiffness leads to shorter steps, higher step frequencies and faster walking speeds (figure 6b), all changing approximately linearly. A particular choice of hip stiffness also requires a minimal knee stiffness to prevent stumbling (figure 6c), without which the thigh moves too fast for the shank and GC occurs with a flexed knee. We also found that the minimal knee stiffness to avoid stumbling also tends to cause knee extension to occur before mid-stance, resulting in foot scuffing. Excepting very low spring stiffnesses and walking speeds, foot scuffing is a typical characteristic of walking with uni-articular springs.

Figure 6.

Uni-articular knee and hip springs together produce faster walking. (a) For a model with a knee spring (figure 4), the addition of a hip spring causes a faster step with increased knee flexion (parameters: $\hat{P}=0.1$, K_knee=0.1). (b) Dimensionless gait parameters as a function of hip spring stiffness, keeping push-off impulse and knee stiffness fixed. Increasing hip stiffness produces higher step frequencies and lower step lengths, and overall faster walking speeds. (c) Contour plot of speed as a function of the two stiffnesses, showing that stumbling (ST) can occur with high hip stiffness, denoted by the grey region to the right of the stumbling (ST) boundary (parameter: $\hat{P}=0.1$). Stumbling can, however, be avoided if knee stiffness is increased concurrently, but most of these gaits are characterized by the knee reaching full extension before mid-stance, making them prone to foot scuffing. This can be avoided only with very low hip and knee stiffnesses, below the MSKS boundary. (d) Contour plot of speed as a function of push-off and both stiffnesses changing in proportion (K_knee=2K_hip as shown in (c)). Here stumbling can easily be avoided, and high walking speeds can be produced. Except at the lowest stiffnesses, most uni-articular spring combinations here (above the MSKS boundary) cause foot scuffing.

Higher speeds may be achieved by increasing the two stiffnesses together. With a higher knee stiffness, stronger hip springs are able to produce stable gaits without stumbling, achieving higher walking speeds (figure 6c) for the same push-off. For a given knee spring stiffness, the highest walking speed is produced with the strongest hip spring that still generates a stable limit cycle. Conversely, for a given hip spring stiffness, the highest speed occurs with the weakest knee spring that produces a stable limit cycle. This is because a weak spring yields low collision losses at knee stop. It is desirable to select a stiffness combination close to the stumbling boundary, because that will produce a gait with the lowest peak spring torques.

The stiffnesses should also be coordinated to increase with the push-off impulse. Overall walking speed is determined by the push-off impulse, knee spring stiffness and hip spring stiffness. As a demonstration, we constrained the stiffnesses to increase with a constant knee-to-hip proportionality of 2 (dashed line in figure 6c), thus roughly following the stumbling boundary. Walking speed increases with either stronger push-off impulses or stiffer springs (figure 6d). Increases in push-off impulse generate longer steps, while stiffer springs produce higher step frequencies. Only with strong push-off impulses and weak springs does the model stumble. It is therefore desirable to attain high speeds by increasing push-off while adjusting the two spring stiffnesses together.

7. Bi-articular spring

Considering that separate knee and hip springs are best combined with proportional stiffnesses, a spring spanning both joints might also be expected to produce faster walking speeds. Rather than producing knee and hip torques separately, a bi-articular spring could introduce a coupling torque between the two joints, which would be expected to cause a somewhat different gait from the uni-articular model. The bi-articular spring's two parameters, spring stiffness k_kh and moment arm ratio r_kh, determine the model's behaviour.

Simulations show that the bi-articular spring affords a wide range of walking speeds and step frequencies. It produces faster steps, roughly analogous to the hip spring in the straight-legged model. It also produces earlier knee stop (figure 7a) because it speeds motion of the knee. Much as with the two-spring, uni-articular model, increasing spring stiffness k_kh leads to higher frequency steps, slightly shorter step lengths and an overall increase in walking velocity (figure 7b).

Figure 7.

Effect of a bi-articular spring on kneed walking. (a) A bi-articular spring speeds the step, causing both knee stop and heelstrike to occur earlier (parameters: $\hat{P}=0.1$, r_kh=0.35). (b) Dimensionless gait parameters (step length, step frequency and walking speed) as a function of bi-articular spring stiffness. Increasing the spring stiffness results in higher step frequencies, shorter steps and greater walking speeds. (c) Contour plot of speed as a function of spring knee-to-hip moment arm ratio r_kh and stiffness k_kh. There is a minimum ratio needed to avoid stumbling (ST). Above that minimum, there are two regions with successful gaits that all walk faster with increasing stiffness. High ratios lead to foot scuffing, whereas intermediate ratios do not. These gaits are separated by a narrow range of ratios that yield no gaits due to the NKS failure. The gaits between the ST and NKS failures are most human-like, with knee stop occurring late in swing (parameter: $\hat{P}=0.1$). (d) Contour plot as a function of stiffness and push-off impulse, keeping moment arm ratio constant (r_kh=0.35). Here, walking speed can be increased by either stronger push-off impulses or stiffer springs, without causing foot scuffing. At higher speeds, the model stumbles with insufficient spring stiffness.

Although the bi-articular spring can increase walking speed, the existence of stable limit cycles is highly influenced by knee-to-hip moment arm ratio r_kh. Keeping the impulse magnitude fixed, the model can walk with practically any ratio of moment arms when the spring has low stiffness. But as stiffness is increased, there are two ranges of favourable moment arms. One range yields good clearance of the swing leg without foot scuffing, and is bounded below by the stumbling failure, and above by the no knee stop (NKS) failure, in which a strong knee flexion moment prevents the swing knee from ever reaching full extension (figure 3c). Increasing r_kh further leads to a second range of gaits that are susceptible to foot scuffing. For high spring stiffnesses and a fixed push-off, there is only a narrow range of moment arm ratios yielding limit cycles without foot scuffing (figure 7c), with r_kh range 0.33–0.38 for $\hat{P}=0.1$.

For a properly chosen moment arm ratio such as r_kh=0.35, walking velocity can be increased with stronger push-off impulse or stiffer bi-articular springs (figure 7d). As with other models, no stable limit cycle is found for WP impulses. As push-off is gradually increased, there is initially a wide range of allowable spring stiffnesses and moment arm ratios, with higher stiffnesses producing higher step frequencies and faster speeds. However, for a push-off magnitude of about $\hat{P}>0.114$, a minimum stiffness is required to avert stumbling. It is preferable to increase both push-off magnitude and bi-articular stiffness together to produce faster walking speeds.

8. Modulation of human-like gaits

The kneed walking models may also be compared against a nominal human gait. At a customary walking speed of 1.25 m s⁻¹, humans tend to walk with a preferred step frequency of 1.8 Hz (or equivalently a stride frequency of 0.9 Hz, defining a stride as two steps) and step length of 0.69 m (Donelan et al. 2002b), equivalent to dimensionless values 0.40, 0.57 and 0.70, respectively. Dynamic walking models without springs are unable to walk this fast or at such a high step frequency. The addition of springs in either the uni-articular or bi-articular model allows the production of these gaits through the appropriate choice of three parameter values. The push-off impulse effectively determines the step length, whereas the remaining two spring parameters (uni-articular K_knee and K_hip or bi-articular k_kh and r_kh) are available to determine the step frequency. Both models can therefore produce the nominal human gait with one extra parametric degree of freedom, which determines all possible gaits that have the same step length and frequency.

We generate human-like speeds with the uni-articular model, treating knee spring stiffness as the free parameter. For a particular choice of knee spring stiffness, only one combination of push-off impulse and hip spring stiffness yields the nominal human gait. Simulation results show that the push-off impulse remains nearly constant regardless of knee spring stiffness (figure 8a). This is because push-off occurs when both legs are straight, a configuration where the knee spring has no effect on the work performed by the push-off impulse. By contrast, the hip spring stiffness must be modulated with knee spring stiffness, over a limited range of values. There is little to distinguish the various combinations, except that it might be preferable to use the weakest spring combination that still yields a stable limit cycle, because it requires the lowest knee and hip joint torques.

Figure 8.

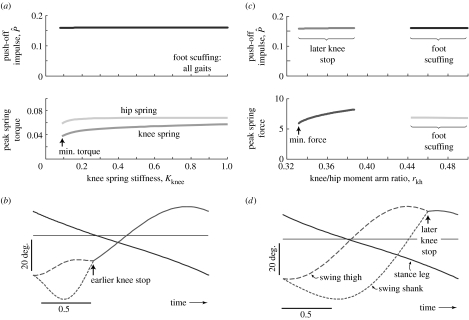
Two ways to walk as fast as a human at a typical speed of 1.25 m s⁻¹ and step frequency of 1.8 Hz. (a) The uni-articular hip and knee spring model (figure 6) produces this gait with push-off $\hat{P}=0.16$ and a range of spring combinations (knee spring stiffness is plotted on horizontal axis, with K_hip=0.082–0.093). The low extreme within this range results in the lowest peak torques. (b) Kinematics show that knee stop occurs relatively early in the step (prior to mid-stance), leading to foot scuffing. Knee stop may be delayed by reducing knee stiffness, but this causes the model to stumble. All successful limit cycles produce early knee stop in the uni-articular model. (c) The bi-articular model (figure 7) can also walk as a human, with $\hat{P}=0.16$ and k_kh=703–933, shown as a function of moment arm ratio r_kh. Larger values (above 0.44) yield earlier knee stop and are therefore prone to foot scuffing. A much narrower, lower range (0.33–0.39) leads to later knee stop. The lowest allowable ratio results in the minimum spring forces. (d) Kinematics illustrate a gait with later knee stop and no foot scuffing.

When producing these gaits, all uni-articular models cause knee stop to occur relatively early in the step, resulting in foot scuffing (figure 8b). No combination of hip and knee springs can avoid this tendency when walking at human-like step frequencies. High step frequency necessitates stiff springs to speed the legs and avoid stumbling. Stiff springs, especially at the knee, produce early knee stop. High speeds are possible with lower spring stiffnesses and hence lower step frequencies, but with longer steps that are uneconomical due to collision losses. At a typical human speed, a uni-articular model must either walk with poor economy and/or foot scuff.

In the bi-articular spring model, the same nominal speed, step length and step frequency may also be produced in a variety of ways (figure 8c). Here we treat the knee-to-hip moment arm ratio r_kh as the free parameter, and find two distinct ranges that conform to the gait requirements. One range contains higher ratios (r_kh>0.44) that produce early knee stop, but the other range, while relatively narrow (approx. 0.332–0.387), avoids foot scuffing with a later knee stop. There are no limit cycles between the two ranges due to the NKS failure mode. Focusing on the narrower range, we find that the necessary push-off magnitude varies little, but spring stiffness k_kh must increase nearly linearly with r_kh. All gaits are energetically similar, except that the weakest bi-articular spring possible has the advantage of producing the smallest spring forces and thus joint torques (figure 8d). The bi-articular spring allows the knee to move with much greater amplitude and duration without stumbling or scuffing the foot.

This model's kinematics may be compared with those of a human. For nearly all gaits that avoid foot scuffing, the model's knee reaches full flexion near mid-stance, with knee stop occurring very late in the swing phase (compare figure 9a,b), similar to humans. These qualitative similarities occur despite some notable differences between model and human. In the model, the stance leg is always fully extended and the knee stop passively provides the torque to support body weight, overriding the springs. By contrast, the human stance leg is never fully straight (figure 9a), and active torques support body weight and govern flexion and extension of the knee throughout stance. The model therefore cannot predict the human stance phase knee torque, and it also imposes somewhat different initial conditions for the swing phase.

Figure 9.

Comparison of the gaits produced by the bi-articular spring model and by humans. (a) Human kinematics, shown as angles of stance leg, swing thigh and swing shank measured anticlockwise with respect to vertical (data from Winter 1991). Stance leg angle (solid line) is defined as the average of the thigh and shank (dotted lines) for comparison with model. (b) Bi-articular model kinematics (from figure 8c, gait requiring minimum spring force). One difference with humans is that the model's stance leg is fully extended at double support, leading to different initial conditions for the swing phase and less swing phase knee flexion. (c) Knee torque versus hip torque for human and model, emphasizing swing phase. Human swing phase has joint torques covarying fairly linearly. In the model, linear covariation is a result of the bi-articular springs, although the average ratio of knee and hip torques is somewhat lower (−0.33 versus approximately −0.68 in humans). The dynamic walking model is powered by push-off, and bi-articular springs allow it to walk at the equivalent of a human's 1.25 m s⁻¹.

We next focus on the swing phase that is driven by joint torques at the knee and hip. In the model, the springs produce these passively and in linear proportion. Humans actively produce torques that also vary in roughly linear proportion (figure 9c). The ratio between knee and hip torques is approximately −0.33 in the model (minimum spring force gait from figure 8d), substantially less than an average ratio of approximately −0.68 in humans, from the data of Winter (1991). The model corresponds best with human early in swing, whereas after mid-stance, the human knee produces a greater proportion of knee torque. This might be attributable to the fact that the rectus femoris is most active before mid-stance and the hamstrings afterwards (Hof et al. 2002), and these muscles can have different moment arm ratios. It is, however, difficult to conclusively estimate ratios from the literature. For example, estimates for the rectus femoris knee-to-hip ratio vary between approximately 0.83 in one study (Hernandez et al. 2008; estimated for early swing phase) and 1.6 in another (Visser et al. 1990; estimated from regression equations). One report estimates a ratio of 0.78 for semimembranosus and semitendinosus (Arnold et al. 2000; estimated from 3.5 cm approximate moment arm at knee and 4.5 cm at hip) and another estimates 0.15 for biceps femoris (Visser et al. 1990). Even with more definite ratios, the model has a single moment arm ratio that would still be unable to model the four distinct bi-articular muscles of humans. Nor can the model's springs reproduce the antagonistic co-activation observed in parts of human gait (Hof et al. 2002). It is nevertheless interesting that a crude model with bi-articular springs alone can produce human-like walking speeds from passive dynamics, and that the multiple uni- and bi-articular muscles of the human produce a roughly linear proportion of joint torques during swing.

9. Discussion

We had sought to determine how walking with knees can be powered to achieve human-like speeds. We used a sagittal plane model with mass distribution similar to human to seek walking gaits driven mostly by the passive dynamics of the limbs. These dynamic walking gaits were powered by a combination of a push-off impulse from the trailing leg and spring-like torques about the hip and knee. We verified that push-off alone can power walking on the level, but only up to approximately half the speed that humans prefer, at the point in which the model stumbles. Stumbling may be averted with the addition of springs about the joints. A hip spring increases the step frequency for faster walking and a knee spring speeds the lower leg to avoid stumbling. A drawback of uni-articular springs is that knee stop typically occurs early in a step, causing foot scuffing. Bi-articular springs can produce a gait with better swing foot ground clearance and human-like speeds, although only for a narrow range of knee-to-hip moment arms. Walking modulated by such springs and powered by push-off can be both fast and economical. Below, we examine implications for walking robots and humans.

The model presents a straightforward means of improving the performance of walking robots. It demonstrates why dynamic walking robots to date, powered by push-off alone, walk slowly, and why kneed walking machines in general are prone to stumbling. One notable insight is that higher walking speeds may be produced through the simple installation of bi-articular springs acting about the joints, without needing additional energy input. Other robots have shown that similar springs can also improve stability in response to small perturbations for walking and running even at slow speeds (Iida et al. 2008). Optimization-based models also mimic human walking well with passive or nearly passive mechanical elements (Endo et al. 2006). Our model adds to these findings by indicating how the ratio of knee-to-hip moment arms is critical to faster walking. The particular range needed for a human-like gait is certainly specific to the model's geometry and configuration. Other configurations might have a different range, but we would nevertheless expect that too low a knee-to-hip ratio would still increase the propensity to stumble, because the hip will tend to move too quickly and GC will occur earlier than knee stop. Too high a ratio would still be expected to produce too much knee flexion torque during swing, either preventing knee stop from occurring at all or causing scuffing of the foot. The choice of bi-articular moment arms must therefore be performed with care. But with appropriate design, bi-articular springs could be incorporated in dynamic walking machines and potentially improve both walking speed and stability.

The bi-articular model's gait also bears some resemblance to that of humans. Ankle push-off provides much of the mechanical energy input of human walking, with a metabolic cost proportional to the work performed (Donelan et al. 2001, 2002a). The swing leg motion appears to be dictated largely by the coupled dynamics of the legs (Mochon & McMahon 1980). This motion is also actively modulated, with the most substantial muscle activity occurring at the beginning and end of swing (Hof et al. 2002), especially in bi-articular muscles (Prilutsky et al. 1998). For example, rectus femoris has a burst of activity at the beginning of swing, and the hamstrings at the end of swing (Hof et al. 2002). This could be modelled more realistically by adding slack to the springs or by varying the equilibrium points (as in Endo et al. 2006). Humans are not restricted to the production of spring-like muscle forces, and can also choose from a wider variety of uni- and bi-articular muscles, each with a unique action (Kuo 1994). Nor must their hip torques perfectly oppose each other as in the model, because the hip muscles can act against the human trunk as long as it is kept upright. Given these potential complexities, it is interesting to note that human joint torques nevertheless covary in a simple and approximately linear relationship (figure 9c), similar to the spring-driven model. The human bi-articular muscles seem well matched to the passive dynamics of the limbs.

Spring-like forces might allow human tendons to act elastically, storing and returning mechanical energy. Alexander (1990) previously proposed that compliance about the hip can aid running; the present model suggests a similar advantage for walking, where compliance can reduce the work performed within a cycle to move the legs back and forth (Kuo 2002). Compliance also allows the muscles to produce force with relatively low amplitude and bandwidth, with very simple control. Unlike actual springs, the muscles almost certainly do expend energy to speed leg motion (Doke et al. 2005), for the production of force as well as for work (Doke & Kuo 2007). But it might nonetheless be economical to do so, because active leg motion may trade off against the cost of collisions to yield a metabolic optimum (Kuo 2001). Humans might find it advantageous to harness the passive dynamics, applying spring-like torques to economically modulate the pendular motion.

This is not to imply that muscles and tendons need or should be perfectly elastic. Relatively stiff muscles, activated mainly at the extremes of leg motion, could accommodate a variety of stride frequencies, simply by changing the duration and amount of active force produced in series with a fixed mechanical stiffness (Kuo 2001). There are sparse data regarding the series compliance of bi-articular muscles crossing the hip and knee, but the tendons appear shorter than those of the triceps surae (ankle plantar flexors), suggesting relatively high stiffness. As stiffness increases and compliance approaches zero, higher forces for shorter durations are needed to reverse leg motion, but even pseudo-elasticity—an inelastic actuator acting with the same length–tension profile as a spring—can nonetheless be advantageous for minimizing work (Srinivasan & Ruina 2006). Spring-like forces may therefore aid leg motion regardless of the actual degree of compliance.

Spring-actuated models walk with very simple control and very little work. All of the springs act passively, and even inelastic actuators could mimic this behaviour with very simple feedback. The only net positive work necessary is at push-off that could be produced with a simple feedback trigger for the ankle. This corresponds roughly with the large burst of positive power humans perform during ankle push-off (Winter 1991). Humans also perform net negative work about the knee, with a burst at the end of swing corresponding with knee stop in the models, and another burst corresponding with the models' heelstrike collisions. One substantial difference is at the hip, where humans perform net positive work but the models, having only springs, perform no net work. Simple models do not favour hip work to power walking, because push-off reduces heelstrike collision losses for better economy (Kuo 2002). More complex models with knee stop collisions and other joints could potentially find advantage in positive work about the hip, but passive dynamics would still be expected to allow for relatively simple control.

The uni-articular model bears little resemblance to normal human walking, but may provide insight regarding pathologies such as ‘stiff-knee gait’. This pathology is associated with spastic paresis, and is often treated by surgical lengthening or transfer of the bi-articular rectus femoris (Waters et al. 1979). In the present study, the model with uni-articular knee springs exhibits limited knee flexion and early knee stop, whereas the bi-articular model does not. As modelled by others (Piazza & Delp 1996), the rectus femoris reduces flexion of the knee, but the comparable spring in our model does not produce a stiff-knee gait as a result of high spring stiffnesses. It is possible that spasticity of rectus femoris is only one of the multiple factors causing stiff-knee gait.

The model's application to normal and pathological gait is subjected to limitations, most notably in the stance phase. Humans actively produce extension torque as the knee flexes and extends during stance (Kuo et al. 2005). The model presented here captures none of this behaviour, because its knee is kept fully extended against the knee stop. Key events such as the collision following heelstrike and the push-off preceding swing phase are therefore modelled impulsively. Even though this leads to incorrect durations and displacements for these events, the model does predict how the energetics of the step-to-step transition will change as a function of step length, step width and foot shape (Donelan et al. 2001, 2002a; Adamczyk et al. 2006). These energetics also appear to compete with the cost of actively moving the legs (Doke et al. 2005; Doke & Kuo 2007) to determine the optimum combination of step length and frequency (Zarrugh et al. 1974; Kuo 2001). These features are not, however, restricted to impulsive events. An improved model might include both uni- and bi-articular springs to allow the knee to flex during stance. It might then retain the same energetics and swing phase behaviour as the present model while producing a more human-like stance phase.

Other simulation models already incorporate more complex musculoskeletal features, often to study pathological gait. One approach is to analyse a normal gait simulation, for example to infer the effects of chronic conditions such as muscle stiffness, spasticity or weakness (e.g. Arnold et al. 2005). Another is to perturb normal muscle forces during the step and then examine the resulting motions, for example in stiff-knee gait (Goldberg et al. 2004). Imposing a perturbation on an otherwise normal muscle activation pattern will typically cause the model to fall. But in chronic situations, humans usually adjust their control to yield a different and compensatory limit cycle. These compensations are difficult to predict, making it a challenge to model a gait that is both periodic and realistically pathological. The limit cycle approach employed here allows the mechanical system to compensate. Each parameter perturbation considered here is applied chronically, and predicts whether there is a limit cycle that is compatible with limb dynamics. Complex models are not usually amenable to limit cycle analysis. There may be an intermediate level of complexity that yields limit cycles and still captures relevant musculoskeletal features of pathological gait, yielding greater insight regarding human walking.

Supplementary Material

Dynamic walking simulations

Animations of walking model embedded in a PDF document (Windows Acrobat only The PDF format is not recommended for Mac users)