In situ observation of graphene sublimation and multi-layer edge reconstructions

Abstract

We induced sublimation of suspended few-layer graphene by in situ Joule-heating inside a transmission electron microscope. The graphene sublimation fronts consisted of mostly {1100} zigzag edges. Under appropriate conditions, a fractal-like “coastline” morphology was observed. Extensive multiple-layer reconstructions at the graphene edges led to the formation of unique carbon nanostructures, such as sp²-bonded bilayer edges (BLEs) and nanotubes connected to BLEs. Flat fullerenes/nanopods and nanotubes tunneling multiple layers of graphene sheets were also observed. Remarkably, >99% of the graphene edges observed during sublimation are BLEs rather than monolayer edges (MLEs), indicating that BLEs are the stable edges in graphene at high temperatures. We reproduced the “coastline” sublimation morphologies by kinetic Monte Carlo (kMC) simulations. The simulation revealed geometrical and topological features unique to quasi-2-dimensional (2D) graphene sublimation and reconstructions. These reconstructions were enabled by bending, which cannot occur in first-order phase transformations of 3D bulk materials. These results indicate that substrate of multiple-layer graphene can offer unique opportunities for tailoring carbon-based nanostructures and engineering novel nano-devices with complex topologies.

Imagine burning a piece of paper: The reaction front tends to be jagged. Furthermore, if one examines the ashes left behind, most are curved. This is because paper, being a thin 2-dimensional (2D) object, is easy to bend. Here, we report an analogous experiment, but on graphene instead of ordinary paper, and at the nanoscale inside a high-resolution transmission electron microscope (HRTEM). We induced the sublimation of suspended multilayer graphene by Joule-heating, so it becomes thermodynamically favorable for carbon atoms to escape into the gas phase, leaving freshly exposed (open) edges on the solid graphene. The remaining graphene edges curled up under observation, and often welded together. We attribute this behavior to the driving force to reduce dangling bonds on the edges (capillary energy), at the cost of bending energy. The sublimation of few-layer graphene, such as a 10-layer stack, is particularly interesting compared with the sublimation of monolayer graphene. In few-layer graphene, different layers often spontaneously fuse together, forming nanostructures in situ, on top of 1 or 2 electrically conductive, extended, graphene sheets. During Joule heating, both the flat graphene sheet and the self-wrapping nanostructures, like bilayer edges (BLEs) (1) and nanotubes (2, 3) interconnected to BLEs, have unique electronic properties important for device applications. However, the biggest obstacle to exploiting the extraordinary properties of graphene or carbon nanotubes etc., is to control their nanostructure and assembly. The in situ self-assembly process we observed leads to new understanding of carbon nanostructure formation and may eventually lead to a new paradigm for engineering integrated carbon-based devices (4–16).

Results and Discussion

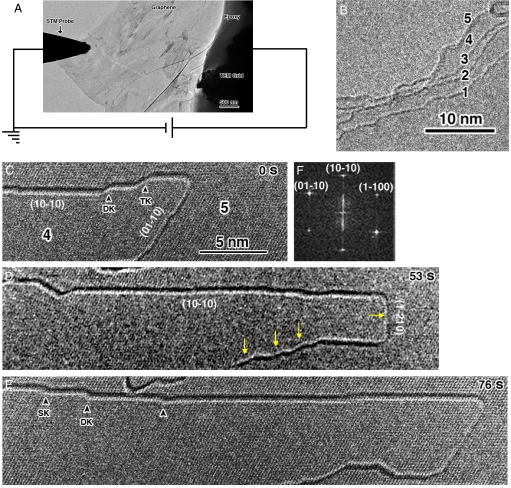
Graphene samples were prepared using a Scotch tape peeling method similar to that reported in the literature (4–7, 9, 10). (For details see Fig. S1) In brief, individual graphene was mounted on a TEM grid, and was connected by a scanning tunneling microscopy (STM) tip, using a Nanofactory TEM-STM platform (17, 18). TEM observations were conducted in a Tecnai F30 analytical electron microscope operated at 300 kV. A STM probe was manipulated to contact individual graphene with a layer thickness of ≈10 layers (Fig. 1A), followed by Joule-heating of the graphene to high temperatures by applying a bias voltage of ≈2.5 V. Once a high current was passed through the graphene layers, its crystalline quality and surface cleanness were improved. Fig. 1B shows a Joule-heated graphene with 10 layers. [Each fringe in fact corresponds to a bilayer (1); for details, see Figs. 3B, 4, and 5]. The surface was very clean and free of amorphous materials. The maximum current density flowing in a graphene layer was similar to that in a carbon nanotube, ≈10⁸ A/cm² (19–24). From this current density and the sublimation temperature of graphite in high vacuum (25), we estimated that the temperature in the Joule heated graphene is ≈2000 °C, which is similar to the temperatures in Joule-heated carbon nanotubes (26). At high temperatures and under electron beam irradiation, sublimation of graphene took place. The sublimation is predominantly caused by Joule-heating, but facilitated by electron beam irradiation. Without Joule-heating, few layer graphene turned into highly disordered or even amorphous structure.

Fig. 1.

In situ TEM images showing a graphene sublimation pattern. (A) A TEM image showing a graphene sheet mounted on a TEM grid connected with an STM probe. (B) A HRTEM image of a 10-layer (5-bilayer) graphene. The graphene was Joule-heated to high temperatures by applying a bias voltage of ≈2.5 V. (C–E) Sequential HRTEM images showing the propagation of one void created by atom sublimation. The numbers 4 and 5 indicate the layer thickness being 4 and 5 bilayers, respectively. The arrowheads and SK, DK, and TK pointed out single, double, and triple atomic-plane-thick kinks on the BLEs, respectively. Arrows in D point out armchair edges. (F) A Fast Fourier Transformation of the graphene shown in C–E.

Fig. 3.

Kinetic Monta Carlo simulation of fractal sublimination of graphene. (A) A graphene sublimation pattern obtained from a kMC calculation after 120,000 simulation steps. Only atoms on the graphene edges are shown. (B) schematic of a zigzag BLE of graphene (1).

Fig. 4.

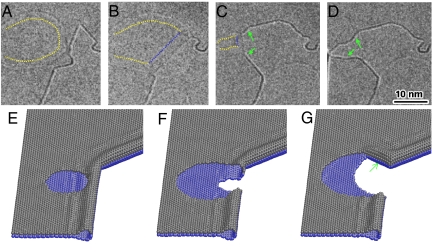
Experimental evidence of graphene BLEs. (A–D) Sequential HRTEM images proving the existence of BLEs of graphene (Movie S3). Yellow-dotted lines point out the edge of a monolayer vacancy hole on the top-layer. The blue-dotted lines pointed out the monolayer edge of the bottom layer. Green arrows denote the reconstructed BLEs. (E–G) Schematic drawings corresponding to (A–C), respectively, showing the zipping up of MLEs to BLEs.

Fig. 5.

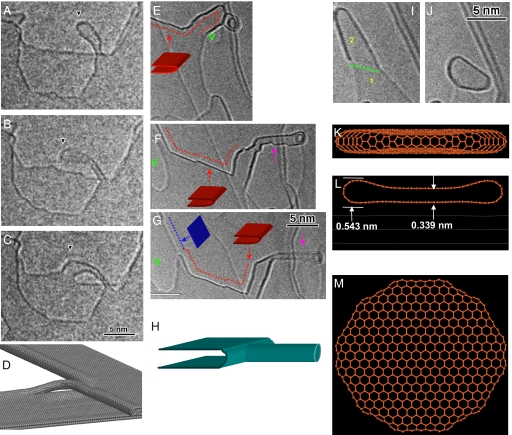
Carbon nanostructures formed in situ on graphene substrate by Joule-heating. (A–D) Two neighboring bilayer graphene interconnected by a carbon nanotube (pointed out by arrowheads in (A–C). (E–G) HRTEM images of interconnected graphene layers. The red- and blue-dotted lines point out BLEs and a MLE, respectively. Schematic drawing of BLEs and MLEs are shown in (E–G). The pink arrows in F and G point out carbon nanotubes connected to a bilayer graphene, a schematic drawing of which is shown in H. Note each dark fringe in (E–G) may represent either a BLE or a MLE. The determination of the structural configurations of each fringe is described in Fig. S3. (I and J) Sequential HRTEM images showing the formation of a nano-pod/flat fullerene. The numbers “1” and “2” indicate the layer thickness being 1 and 2 layers, respectively. A green-dotted line in I marks a MLE. The monolayer graphene sublimated and then reconstructed with a neighboring graphene edge, forming a nanopod/flat fullerene. Detailed formation process of the nanopod/flat fullerene is described in Fig. S4. (K–M) Structural models of a nanopod/flat fullerene in a side view (K), cross-section view (L), and top view (M), respectively.

The sublimation front consisted predominantly of zigzag edges, and very rarely of the armchair or other high-index-plane edges. Fig. 1 C–E and Movie S1 show sequential HRTEM images of the evolution of a sublimation edge. The graphene was close to the [0001] orientation, as seen from a Fast Fourier Transformation (Fig. 1F). The sublimation created a nano-hole or void with a 60°-angular-tip formed by 2 intersecting zigzag planes, and the void propagated along the (–10) and (01–10) zigzag edges (Fig. 1C). Occasionally, the void propagated along a (1–210) armchair edge (Fig. 1D), but this lasted for only a few seconds, and the void then propagated back to the zigzag edges (Fig. 1E). During the void propagation, kink motions along the zigzag edges occurred (pointed out by arrowheads in Fig. 1 C and E). The kink, marked as “SK” (Fig. 1E), “DK” (Fig. 1 C and 1E), and “TK” (Fig. 1C), is 1, 2, and 3 atomic rows high, respectively, which could nucleate from anywhere on the zigzag edges, then propagated along the same edges. After each kink swept through, 1 or a few zigzag atomic rows were eliminated. This rendered graphene with predominantly zigzag edges, connected by small armchair edge segments (e.g., the irregular edges pointed out by arrows in Fig. 1D).

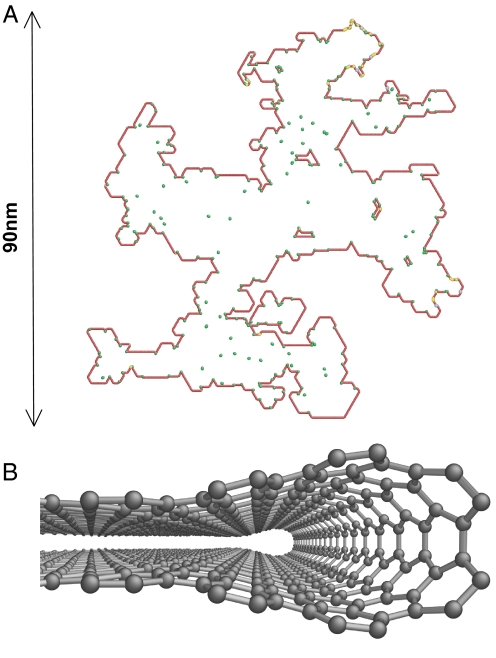
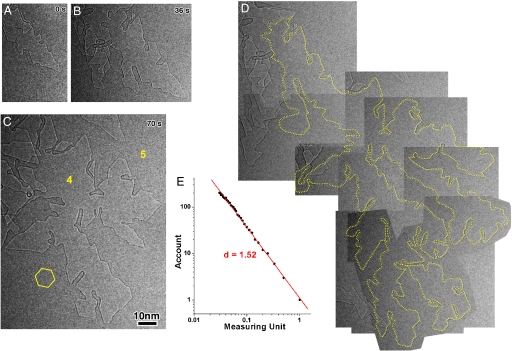
Fig. 2(Movie S2) shows a fractal-like overall sublimation pattern (27). There are 10 layers in this graphene, determined from the lattice fringes of the graphene edges (Fig. 1B). Initially, a main void (Fig. 2A) with some small secondary voids appeared in one of the 5 bilayers. The main void and its secondary voids all grew with the lapse of time (Fig. 2B). Simultaneously, new voids were nucleated on the side faces of existing ones and the propagation directions can change to new sets of zigzag planes. Similarly, the next generations of voids nucleated and grew, until a fractal-like pattern emerged (Fig. 2C). Most of the voids propagated along one of the 6 equivalent {1100} zigzag edges, and in a very rare occasion, a void propagated along a {1120} armchair edge. From the overlaid sequential images of the sublimation fronts (Fig. 2D), we calculated the fractal dimension of the “coastline” pattern (28) to be 1.52 (Fig. 2E, details of the fractal dimension calculation are in Fig. S2). In comparison, the well-known Sierpinski triangle sieve has fractal dimension 1.58; and the Sierpinski hexagon, which has hexagonal symmetry, has fractal dimension 1.63 (www.tgmdev.be/curvesierpinskiobj.htm).

Fig. 2.

Fractal sublimination of graphene. (A–C) Sequential HRTEM images showing a fractal sublimation pattern of graphene. The numbers 4 and 5 indicate the layer thickness is 4 and 5 bilayers, respectively. The hexagon in C marks the 6 sets of equivalent {1100} zigzag planes. The bias voltage applied to the graphene was 2.5 V. (D) An overlay of sequential images of the propagating void fronts with the void edges highlighted in yellow-dotted lines. (E) A fractal dimension estimation of the yellow-dotted fractal pattern. See Movie S2.

This intriguing local zigzag-edge preference and the resulting global “coastline” morphologies can be understood by performing kinetic Monte Carlo (kMC) simulations of the sublimation pattern and dynamics. Fig. 3A shows a kMC simulation with a minimal number of parameters, which reproduced the main experimental features. Details of the simulation methods are given in Materials and Methods. Briefly, a graphene bilayer with a small void and periodic boundaries were used as the initial configuration and the simulation was performed at k_BT = 0.2 eV. The activation energy Q^sub for the sublimation of carbon atom varies according to its local environment, determined by the nearest neighbor (NN) numbers within each single layer: Q^sub = 2.5 eV if NN = 1; Q^sub = 7.5 eV for atoms on zigzag edges, and 4.5 eV on other edges and void tips, if NN = 2. There is also an activation energy for bilayer-based reconstruction, Q^rec = 5.2 eV, which governs the probability of a freshly created monolayer edge (MLE) being stabilized in time against further sublimation. This may be attributed to sp²-based reconstruction that gives rise to BLEs (Fig. 3B) (1). These reconstructions eliminate dangling bonds and make subsequent sublimation more difficult. Of the 4 parameters, Q^rec was the most crucial to the kMC simulation. It led to the aging effect: Namely, it was easier for carbon atoms to escape from freshly created void tips and edges, but the sublimation became more sluggish with the lapse of time due to reconstructions into lower-energy, more stable BLE configurations. This explains the initial rapid advancement, then slowing down, and finally the completely stop of 60°-angular-void tips. The process repeated when another 60°-angular-void tip was nucleated on the well-aged, long-straight zigzag edges. Such stop-and-go and branching kinetics naturally led to a fractal-like “coastline” sublimation morphology.

Next, we examined the physical causes of aging. Under a high vacuum in a TEM, passivation by gaseous species such as H or O was unlikely. Sp²-based in-plane reconstructions of open monolayer graphene edges have been proposed theoretically (29), but the reconstructed edges still have 1 dangling bond per carbon atom, which does not produce the strong aging effect that we observed. Reactions of 2 MLEs to form one BLE eliminate all of the dangling bonds at the edges and is a much more stable configuration from our density functional theory calculations. The modeling also shows that the geometric shape of the BLE, which is essentially a “fractional single-walled carbon nanotubes” or a nanoarch, is controlled by the competition between out-of-plane bending energy of graphene, and van der Waals adhesion energy between the 2 adjacent layers of graphene.

The in situ-formed BLEs provide high-quality, covalent linkage between the top and bottom graphene layers, and should have peculiar transport properties of their own. From a practical perspective, the fact that these well-defined mono-disperse atomic structures are already connected to electrically conductive graphene substrates makes them attractive for device applications.

More than 99% of the graphene perimeters shown in Fig. 2 and Movies S1–S4 are in fact BLEs, with each lattice fringe in the HRTEM images representing an edge of a bilayer graphene, the structures of which were reported by Liu et al. (1). Fig. 4 and Movie S3 show direct evidence of the existence of a BLE. A void initially appeared on the top layer (Fig. 4 A and E), and migrated toward the edge of the bilayer (Fig. 4 B and F), then the bottom layer (shown in blue in Fig. 4) sublimated. As the bottom layer sublimated, its trailing edge bonded with the top layer (pointed out by green arrows in Fig. 4C, D, and G), forming BLEs in situ. Existence of similar bilayers was reported in heat-treated graphite (1), indicating that a BLE rather than a MLE is the more stable structural unit in a multiple-layer graphene. The results have important implications in the device applications of graphene: When one designs a graphene-based device, one must consider the possibility that the device operates with a BLE (Fig. 3B), rather than with a MLE. These BLEs may be misinterpreted as MLEs in a recent report (16).

In addition to BLEs that may serve as well-defined 1D device components, we have also found many other types of interconnected nanostructures. Fig. 5 A–C and Movie S4 show the in situ formation of a single-walled nanotube that bridges two BLEs. Fig. 5D illustrates the geometry of the final product, which is based entirely on sp² bonding. Such complex topology, formed in situ, is only possible in 2D layered materials, where bending is easy. Generally speaking, we interpret the spontaneous formation of various interconnected carbon nanostructures as pathways for graphene to reduce its capillary energy. Fig. 5 E–H and Fig. S3 show the in situ formation of a single-walled nanotube by the wrapping or rolling of a graphene ribbon, while still connecting to a bilayer graphene. The tube appears to be very flexible and can bend to large angles (Fig. S3). Again, these coherently interconnected carbon nanostructures with electrical leads in and out might be useful from device and processing considerations.

The stability of some of the interconnected carbon nanostructures is astonishing (Movie S4). Once formed, they maintained their nanostructures despite the flat graphene around them having lower carbon chemical potential (no bending elastic energy and no topological defects) and are in the process of sublimation. The extreme limits of this metastability are the fully encapsulated nanopods/flat fullerenes (Fig. 5 I–M, Fig. S4, and Movie S4) that formed in situ, which apparently made random walks (framed area in Movie S4) on the graphene surface without growing, shrinking, or changing their shape whereas the graphene matrix rapidly receded in front of it (Fig. S4E and Movie S4). We attribute such metastability to the elimination of free edges, making subsequent sublimation kinetically difficult. Therefore, the driving force for creating the interconnected carbon nanostructures, e.g., reduction of capillary energy by bending and curling enabled reconstructions, also protected them from further sublimation.

In summary, we observed the following sequence of salient features during graphene sublimation: (i) creation of open edges (high capillary energies) on 1 or 2 adjacent layers of graphene by external energy; (ii) large spontaneous conformational (30) and topological changes of the remaining graphene, which we attribute to bending to reduce the high capillary energy of open edges; and (iii) in situ formation of metastable nanostructures, interconnected to 1 or 2 or multiple layers of extended graphene via sp² carbon-carbon bonds with large out-of-plane curvature. The process of (ii) is unique to quasi-2D systems, which has a small bending modulus and bending gives rise to unique morphologies, kinetics and products fundamentally very different from the 3D bulk systems. Controlled fabrication of these carbon nanostructures on few-layer graphene substrates and in-depth studies of their electronic properties may lead to production of new carbon-based nanoelectronic devices.

Materials and Methods

TEM Sample Preparation Procedures.

Highly orientated pyrolytic graphite (HOPG) with a thickness of a few hundred μm was glued to a glass slide with a double-sided adhesive tape (Fig. S1A). The HOPG was thinned down to transparent under an optical microscope by repeated peeling using a Scotch tape (Fig. S1B). A 200-mesh transmission electron microscopy (TEM) grid was cut into half, painted with conducting silver epoxy on the grid bars, and then glued on the transparent graphene sheet on the glass slide. Once the silver epoxy was cured, the half grid was lifted off from the glass slide (Fig. S1C). Graphene was attached to the grid (sketched in dark) after lifting off from the glass slide (Fig. S1D). The half TEM grid was glued to an Au rod of 280 μm and inserted into a Nanofactory TEM–scanning tunneling microscopy (TEM-STM) platform (Fig. S1D), in which a full functional STM is integrated into a TEM sample holder, allowing for in situ manipulation and measurements of individual graphene. The as-prepared samples had many graphene sheets attached to the Cu grid bars. Graphene sheets up to 100 μm long by 50 μm wide and with a layer thickness from a single layer to ≈20 layers of graphene could be found.

Fractal Dimension Measurement.

The fractal dimension of the propagating front pattern was measured by the same method as that used to measure the fractal dimension of the coastline (28). First, a close loop was drawn by fitting the experimental propagating sublimation front (Fig. S2 A and B). Then the close loop was measured on a 2D square lattice. In the measurement, only those squares that intersect with the close loop were accounted (e.g., the gray squares in Fig. S2C). By varying the size of the squares, the number of accounted squares as a function of a square size (i.e., the measuring unit) was plotted (Fig. S2D). According to the definition of the fractal dimension, the fractal dimension of the loop or the propagating loop is calculated as:

where N is the number of the accounted squares and l is the size of the squares or the measuring unit. For the propagating front shown in Fig. S2A, the fitted fractal dimension is 1.52.

Kinetic Monte Carlo (KMC) Simulation Procedures.

In kinetic Monte Carlo (kMC) simulations, graphene bilayer with 1 small void (diameter <1 nm) and periodic boundary conditions were used as initial configurations. The kMC operations occurred only on graphene edge atoms, whose nearest neighbor (NN) atoms in a single layer are less than 3. In each sublimation step only 1 carbon atom is removed and its activation energy Q^sub varies according to the local environment (NN number and edge types): Q^sub = 2.5 eV when NN = 1; when NN = 2, Q^sub = 7.5 eV for zigzag edges and 4.5 eV for armchair edges and void tips. The type of edge is determined by the total summation number of nearest neighbors of nearest neighbors (NNNN) for the atoms on that edge: it is zigzag edges when NNNN = 6 and armchair edges when NNNN = 5. Because of this definition, a single step on a zigzag edge is considered as a small armchair edge and removed quickly in simulation. A void tip is defined as a 60° –angular-tip formed by 2 crossing zigzag edges or a zigzag edge with <3 edge atoms. In addition, there is some probability, with an activation energy Q^rec = 5.21 eV, for one atom on a freshly created less-stable edge (armchair, void tip or NN = 1) to reconstruct into a state as stable as those on a zigzag edge. Such a reconstruction may result from a sp³ junction with the bottom graphene layer, which exists in real experiments; and we assume that on a zigzag edge the similar reconstruction occurs immediately after an edge creation, which may be the reason that initially Q^sub of a zigzag edge is much larger than the other edges. After the catalog of reaction event i and the corresponding activation energy Q_i is built, a kMC simulation is performed with event probability p_i = υ_i ×exp(−Q_i/k_BT), where υ_i = 1.0 × 10¹³ s⁻¹ and k_BT = 0.2 eV.

HRTEM Image Simulation Methods.

HREM image simulations were performed by multislice calculation using JEMS software, using the following electron optical parameters: 300 KV acceleration voltage, spherical aberration of 1.2 mm, beam convergence angle of 0.5 mrad, defocus-spread 10 nm and under-defocus of 99 nm. The thermal vibration of the C atoms was included in the calculation by the Debye–Waller factor.

Note Added in Proof.

It was brought to our attention that the surface of graphite polyhedral crystal was terminated in nanoarches (30, 31), similar to the closed edges reported in ref. 1 and the BLEs reported in this paper. These observations further assert that BLEs or closed edges, rather than MLEs or open edges, are the stable edge configurations in general graphitic materials.