Abstract
Recent evidence suggests that performance of complex locomotor tasks such as walking may be accomplished using a simple underlying organization of co-active muscles, or “modules”, which have been assumed to be structured to perform task-specific biomechanical functions. However, no study has explicitly tested whether the modules would actually produce the biomechanical functions associated with them or even produce a well-coordinated movement. In this study, we generated muscle-actuated forward dynamics simulations of normal walking using muscle activation modules (identified using non-negative matrix factorization) as the muscle control inputs to identify the contributions of each module to the biomechanical sub-tasks of walking (i.e., body support, forward propulsion and leg swing). The simulation analysis showed a simple neural control strategy involving five muscle activation modules was sufficient to perform the basic sub-tasks of walking. Module 1 (gluteus medius, vasti and rectus femoris) primarily contributed to body support in early stance while Module 2 (soleus and gastrocnemius) contributed to both body support and propulsion in late stance. Module 3 (rectus femoris and tibialis anterior) acted to decelerate the leg in early and late swing while generating energy to the trunk throughout swing. Module 4 (hamstrings) acted to absorb leg energy (i.e., decelerate it) in late swing while increasing the leg energy in early stance. Post-hoc analysis revealed an additional module (Module 5: iliopsoas) acted to accelerate the leg forward in pre- and early swing. These results provide evidence that the identified modules can act as basic neural control elements that generate task-specific biomechanical functions to produce well-coordinated walking.
Keywords: modeling, simulation, non-negative matrix factorization, muscle activity, biomechanical function
Introduction
Coordination of purposeful movements requires the nervous system to coordinate multi-articular limbs with many degrees-of-freedom and highly non-linear redundant muscle actuators, while accounting for the complex dynamic coupling between body segments and the interaction with the environment. Walking in particular is a complex task with a number of biomechanical sub-tasks that must be successfully performed including body support, forward propulsion and leg swing (e.g., Neptune et al., 2001; Zajac et al., 2003; Neptune et al., 2004). Although highly complex patterns of muscle activation appear to be necessary to perform these subtasks, a number of studies have shown these patterns may be described by a more basic underlying organization of co-active muscles, or “modules”. Further, modular organization has been shown to explain muscle activity across a wide range of walking speeds, levels of body weight support and other combined movement tasks (d'Avella et al., 2003; Ivanenko et al., 2005; Cappellini et al., 2006). The timing and composition of muscle activity comprising each module have also been shown to be relatively consistent regardless of the factorization algorithm (e.g., factor analysis, independent component analysis or non-negative matrix factorization) used to identify the modules (Ivanenko et al., 2005; Cappellini et al., 2006; Tresch et al., 2006), providing confidence that the identified modules do indeed reflect basic elements of neural control.
We recently demonstrated that a small set of independently activated modules accounts for the complexity and cycle-by-cycle variability of muscle activity over a wide range of walking speeds in healthy adults (Clark et al., 2008). There were robust consistencies in the timing and composition of the modules across subjects, with each module corresponding to a key phase of the gait cycle and consistent with the biomechanical subtasks of walking. Module 1 consisted of activity in early stance primarily from the gluteus medius, vastus medialis and, to a lesser extent, rectus femoris. Module 2 consisted of soleus and medial gastrocnemius activity in late stance while Module 3 was composed primarily of activity in the tibialis anterior and rectus femoris with separate peaks of activity in early stance and early swing. Finally, Module 4 was mainly comprised of activation of the medial and lateral hamstrings in late stance and early swing.
Previous studies have hypothesized that the modular organization of muscle activation may represent the functional translation between sensorimotor control signals and biomechanical actions (Ting and Macpherson, 2005). Most factorization approaches are purely signal processing algorithms, and therefore there is no requirement that identified modules produce biomechanically relevant output. Nevertheless, a number of studies have shown correlations between the activity from muscle modules and functional outputs related to task performance (e.g., Ivanenko et al., 2005; Ting and Macpherson, 2005). However, no study has explicitly tested whether the modules would actually produce the biomechanical functions associated with them. Raasch and Zajac (1999) did use computer simulations of pedaling to show that three signals controlling six muscle groups (3 pairs of alternating antagonistic functions) were sufficient to generate a variety of pedaling tasks (e.g., one legged, two legged, smooth, and energy efficient pedaling) by adjusting the relative excitation among the muscle groups. However, walking is a more complex motor task as there are increased kinematic degrees-of-freedom and upright balance is difficult to control. In addition, their muscle groupings were not extracted from their data using a factorization approach. Thus, an open question remains as to whether the modular organization of motor activity identified in factor analyses corresponds to the production of specific biomechanical output to yield flexible yet robust control of walking sub-tasks.
Detailed neuromusculoskeletal models provide an ideal framework to investigate the biomechanical function of each module by identifying and quantifying their contributions to the critical walking sub-tasks of body support, forward propulsion and leg swing. In this study, we generated muscle-actuated forward dynamics simulations of normal healthy walking using the muscle activation modules identified in a subset of the subjects from Clark et al. (2008) as the muscle control inputs to a) assess whether the modules are sufficient to produce well-coordinated walking, and b) identify the contributions of each module to the necessary biomechanical walking sub-tasks. This approach will critically assess the functional output of the previously identified modular organization of muscle activity in walking and investigate whether it provides a foundation for the neuromotor control of human locomotion.
Methods
Neuromusculoskeletal Model
A previously described forward dynamics musculoskeletal model and simulation of sagittal plane walking (e.g., Neptune et al., 2008) was developed using SIMM (MusculoGraphics, Inc.) and consisted of rigid segments representing a trunk (head, torso and arms) and two legs, with each leg consisting of a thigh, shank, patella, rear-foot, mid-foot and toes (Fig.1). The model had 13 degrees of freedom including flexion/extension at the hip, knee, ankle, mid-foot and toe joints of each leg, and horizontal and vertical translation and rotation at the trunk. Foot-ground contact was modeled using 30 visco-elastic elements with coulomb friction (Neptune et al., 2000) distributed over the three foot segments. The dynamical equations-of-motion were generated using SD/FAST (PTC, Needham, MA) and a forward dynamics simulation were generated using Dynamics Pipeline (MusculoGraphics, Inc.) The model was driven by 25 Hill-type musculotendon actuators per leg that were combined into 13 functional groups based on anatomical classification (Fig. 1), with muscles within each group receiving the same excitation pattern.
Figure 1.
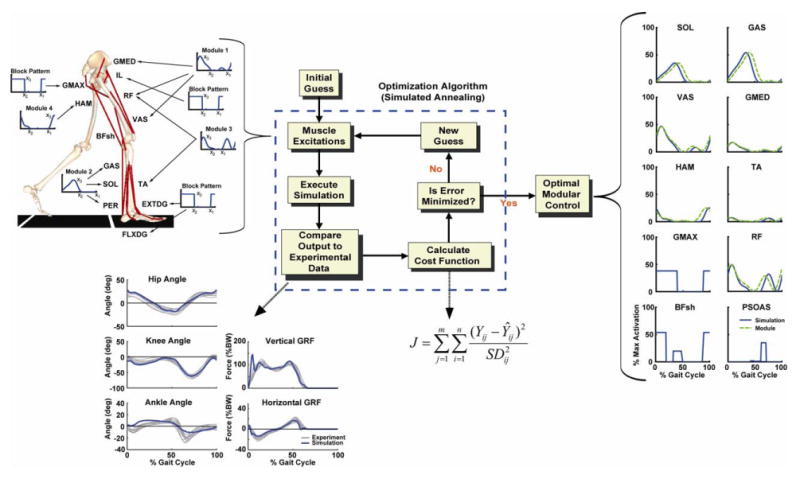
The 2D-sagittal plane musculoskeletal model and optimization framework. The model consistedof a trunk (head, arms, torso and pelvis) and left and right legs (femur, tibia, patella, rear-foot, mid-foot and toes). Only the 13 muscle groups for the right leg are shown, which included GMED (anterior and posterior portion of gluteus medius), IL (iliacus, psoas), RF (rectus femoris), VAS (3-component vastus), TA (tibialis anterior, peroneus tertius), PER (peroneus longus, peroneus brevis), FLXDG (flexor hallucis longus, flexor digitorum longus), EXTDG (extensor hallucis longus, extensor digitorum longus), SOL (soleus, tibialis posterior), GAS (medial and lateral gastrocnemius), BFsh (biceps femoris short head), HAM (medial hamstrings, biceps femoris long head) and GMAX (gluteus maximus, adductor magnus). The Optimization Algorithm fine-tuned the muscle excitation patterns for each muscle group to produce a well-coordinated walking pattern that emulated the experimental data. The excitation patterns were defined by the muscle modules or a block pattern if no EMG data were available. Each Muscle Excitation pattern was parameterized by three parameters, the excitation onset(x1), offset (x2) and magnitude (x3) that allowed the pattern to be scaled in magnitude and temporally shifted during the optimization. As seen in the resulting Optimal Modular Control patterns, the optimization shifted the timing very little. For comparison purposes, the experimental module patterns were normalized to the peak simulation excitation magnitude. Note, the RF excitation is the summed contribution from Modules 1 and 3. The muscle excitation patterns for the small muscles that primarily control the foot (PER, FLXDG, EXTDG) were omitted in the Optimal Module Control comparison. The Compare Output to Experimental Data shows how well the simulation emulated the experimental hip, knee and ankle joint angles, and vertical and horizontal GRFs over the gait cycle (i.e., from right heel-strike to right heel-strike).
Four muscle activation modules were identified using non-negative matrix factorization (NNMF, see below) and used as the muscle excitation control inputs. If the average muscle weighting across subjects was greater than 40%, we considered the module to contribute to the excitation of the muscle. With this criterion, Module 1 was used to excite GMED, VAS and RF, Module 2 excited SOL and GAS, Module 3 excited TA and RF while Module 4 excited HAM. All muscles within a module received the same excitation pattern and timing (defined by the NNMF), although the excitation magnitude was allowed to vary between muscles within a module. RF received excitation inputs from both Module 1 and Module 3. For those muscles for which we did not have EMG, and therefore were not associated with a specific module, their excitation patterns were block patterns defined by three parameters (an excitation onset, duration and magnitude). Activation-deactivation dynamics were modeled by a first-order differential equation (Raasch et al., 1997) with activation and deactivation time constants based on Winters and Stark (1988). For those muscles whose time constants were not available in Winters and Stark, nominal values of 12 and 48 ms were used.
Dynamic Optimization
A walking simulation of a complete gait cycle from right heel-strike to right heel-strike was generated using a simulated annealing algorithm (Goffe et al., 1994) that fine-tuned the muscle excitation patterns and initial joint velocities such that the difference between the simulated and experimentally measured walking data was minimized. The variables tracked included the left and right hip, knee and ankle angles, trunk translations (horizontal and vertical) and horizontal and vertical ground reaction forces. The optimization was run until the average errors were within two standard deviations of the group averaged experimental data.
Experimental Data
Kinematic, ground reaction force and muscle EMG data were collected from 14 healthy adults (2 male, 12 female, mean age 63.1 ± 9.1 years) as they walked for 30 second at 1.2 m/s on an ADAL split-belt treadmill (Techmachine, Andrezieux Boutheon, France). These subjects were a subset from Clark et al (2008) who walked at 1.2 m/sec and all subjects provided informed consent prior to data collection. Bipolar Ag-AgCl surface electrodes were used to record EMG from the tibialis anterior (TA), soleus (SOL), medial gastrocnemius (GAS), vastus medialis (VAS), rectus femoris (RF), medial hamstrings (MH), lateral hamstrings (LH) and gluteus medius (GMED) of each leg using a telemetered EMG acquisition system (Konigsberg Instruments, Pasadena, CA). All data were collected at 2000 Hz using Vicon Workstation v4.5 software. EMG signals were high-pass filtered (40 Hz), demeaned, rectified and low-pass filtered (4 Hz). The ground reaction forces were filtered at 20 Hz.
Non-Negative Matrix Factorization
To identify the muscle activation modules, a previously described (Clark et al., 2008) matrix factorization technique was used and will be reviewed briefly here. For each subject, the EMG were combined into an m × t matrix (EMGo), where m indicates the number of muscles and t is the time base (t = # of strides × 101). A non-negative matrix factorization algorithm (Lee and Seung 1999; Ting and Macpherson 2005) was applied to the m × t matrix. NNMF defines the muscle activation modules by populating two matrices: 1) an m × n matrix indicating the relative weighting of each muscle within each module, and 2) an n × t matrix reflecting the activation timing profile of the module across the gait cycle. EMG variability across all eight muscles in the majority of subjects was explained by four independent modules (Clark et al., 2008), which were used in the present study. NNMF assumes that the weightings remain fixed over the entire gait cycle, and that muscles may belong to more than one module. The two matrices were multiplied to produce an m × t matrix of reconstructed EMG (EMGr), which was then compared to the original EMG matrix (EMGo) and the agreement quantified by least squares error: (EMGo–EMGr) 2/EMGo2. NNMF then performed an iterative optimization procedure by adjusting the muscle weightings and activation profiles until they converged and minimized the error between EMGo and EMGr. For each subject, the identified modules were averaged across gait cycles and then across subjects to obtain a group average.
Assessing Biomechanical Function
To quantify the contributions of each module to the biomechanical subtasks of body support, forward propulsion and leg swing, individual muscle force contributions to the ground reaction forces and body segment mechanical energetics were quantified. Body support and forward propulsion were quantified by each muscle's contribution to the vertical and horizontal ground reaction force, respectively. Each muscle's contribution to leg swing was quantified by the mechanical power delivered to the leg during pre-swing (i.e., swing initiation) and over the swing phase. Details regarding the ground reaction force decomposition and body segment power analysis can be found in elsewhere (Neptune et al., 2004; Neptune et al., 2008). The contributions of each module to the biomechanical subtasks was found by summing individual muscle contributions to each sub-task from those muscles associated with each module. For RF, its contribution was scaled according to the relative contribution of each of the two modules to the muscle's total excitation.
Results
NNMF identified four modules, which were consistent across subjects in terms of module weightings and timing profiles and corresponded to specific regions of the gait cycle (Fig. 2). When the module profiles and weightings were used to reconstruct the EMG data, they were able to account for greater than 90% of the EMG variance for all muscles and regions in the gait cycle. When the modules were used as the inputs for the muscle excitation patterns in the musculoskeletal model, the simulation emulated well the group-averaged kinematic and ground reaction force walking data (see Compare Output to Experimental Data, Fig. 1). Surprisingly, to generate the walking motion the optimization altered the module timing very little (see Optimal Modular Control, Fig. 1). For those muscles not associated with a specific module, the excitation patterns had similar timing as previously published data (e.g., Perry, 1992). Thus, the muscle activation modules were sufficient to generate the necessary walking sub-tasks for a well-coordinated motion (Fig. 3). Module 1 (GMED, VAS and RF activity) primarily contributed to body support in early stance while Module 2 (SOL and GAS activity) contributed to both body support and trunk propulsion in late stance (Figs. 3, 4). Module 3 (RF and TA) activity acted to decelerate the leg in early and late swing while generating energy to the trunk throughout swing (Figs. 3, 4). Module 4 (HAM activity) acted to absorb energy from the leg (i.e., decelerate the leg) in late swing while increasing the energy of the leg in early stance (Figs. 3, 5). Muscles not associated with specific modules also contributed to walking sub-tasks. IL acted to deliver energy to the leg in pre-and early swing to facilitate leg swing while GMAX was active in early stance to provide body support. BFsh provided energy to the leg in early stance and swing. All other muscle contributions to the walking sub-tasks were negligible.
Figure 2.
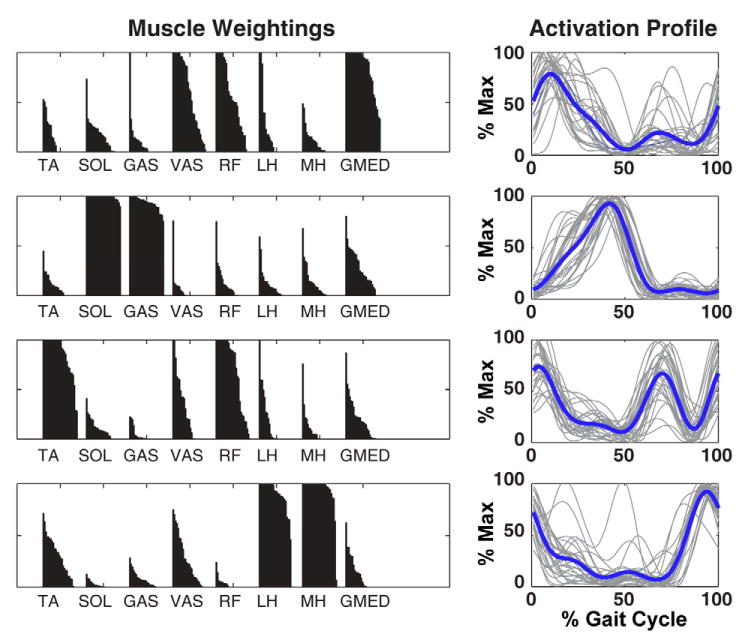
Muscle module weightings and activation timing profiles while control subjects walked at 1.2 m/s derived from NNMF. A) Muscle weightings indicate the representation of each muscle within the corresponding module. The black region over each muscle is composed of 28 separate bars (14 subjects × 2 legs) that would form a perfect rectangle if the muscle was maximally associated with that module for both legs in all subjects. B) Activation timing profiles indicate when a muscle module is active during the gait cycle. Gray lines indicate individual profiles for each leg of each subject (28 total, normalized to their maximum value). Thick black lines indicate the group average.
Figure 3.
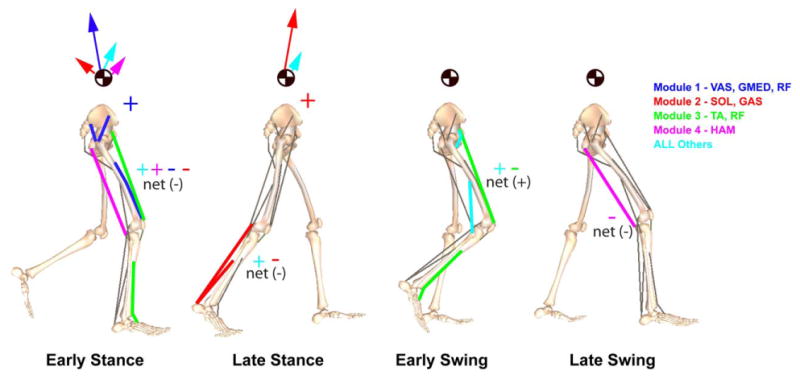
Module contributions to the walking subtasks of body support, forward propulsion and leg swing in the beginning of early stance (∼15% gait cycle), late stance (∼45% gait cycle), early swing (∼70 % gait cycle) and late swing (∼85% gait cycle). Arrows acting on the center-of-mass symbol indicate the resultant module contributions to the horizontal and vertical ground reactions forces that act to accelerate the body center-of-mass to provide body support and forward propulsion. Net energy flow by each individual module to the trunk or leg (“net” total of all modules also presented for leg) is denoted by a “+” (energy increase) or “-” (energy decrease). In early stance, Modules 1 and 2 provide body support while acting to decelerate forward motion while Module 4 and all Other muscles combined to provide a little body support and forward propulsion. In late stance, Module 2 provides both body support and forward propulsion. All Others includes the contributions by BFsh, IL, PER and GMAX.
Figure 4.
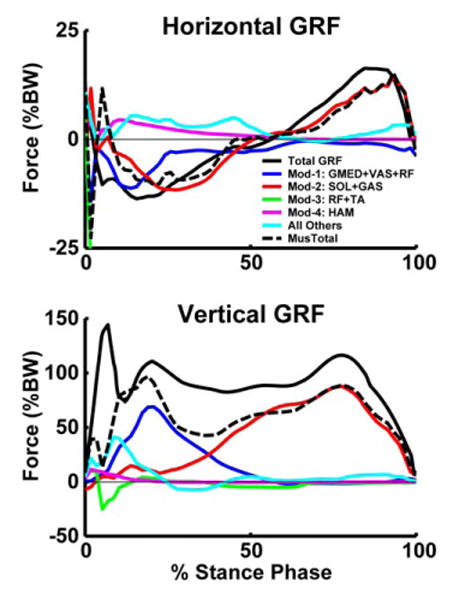
Module contributions to the horizontal and vertical ground reaction forces. All Others includes the contributions by BFsh, IL, PER and GMAX.
Figure 5.
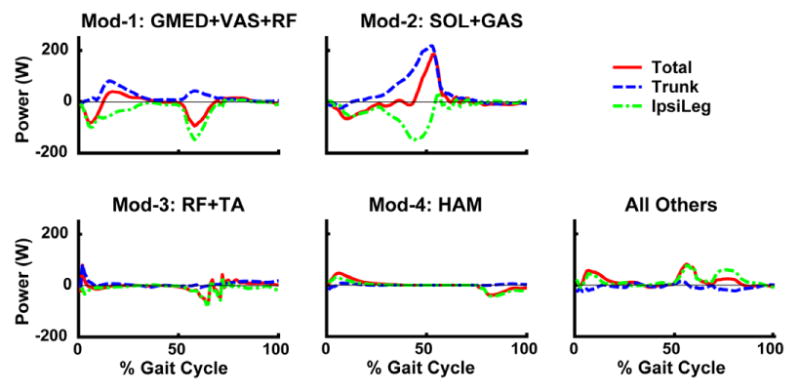
Mechanical power delivered to the trunk and ipsilateral leg by each module over the gait cycle. Total is the summed mechanical power delivered to the trunk, ipsilateral and contralateral leg (small and not shown). All Others includes the contributions by BFsh, IL, PER and GMAX. Positive (negative) power indicates the muscle acted to accelerate (decelerate) the leg in the direction of its motion.
Discussion
Accumulating evidence indicates that co-activity of muscles during common movements, such as that occurring from our locomotor modules, are organized around the performance of task-specific biomechanical functions. During kicking movements in intact frogs, three independent groupings of co-active muscles or “synergies” were found to account for the variable activation patterns required to kick in different directions. Further, the level of activation to each synergy was found to be associated with movement kinematics (d'Avella et al., 2003). Another study examining the response to postural perturbations in cats demonstrated that both hindlimb EMG and kinetic responses were described by four independent components, with each EMG component being associated with a different kinetic component (Ting and Macpherson, 2005). These findings suggest that modular organization of neural activation may represent a translation from high-dimensional sensorimotor signals to lower dimensional biomechanical functions that can be flexibly combined to meet task demands. This hierarchy from higher to lower dimensionality of control is further supported by evidence suggesting that limb kinematics during a variety of walking tasks may be encoded according to global parameters of limb length and orientation (Ivanenko et al., 2007).
Consistent with the hypothesis that modular neural organization drives biomechanical output, the modules derived from our experimental data contributed to task appropriate biomechanical responses in our model and successfully simulated forward walking. The NNMF identified four muscle activation modules that were used to control 7 of 13 muscle groups in the model and were found to be the primary contributors to the biomechanical sub-tasks of body support, forward propulsion and leg swing. The resulting well-coordinated walking kinematics and kinetics were consistent with our previous walking simulations that were driven with 13 independent muscle controllers (e.g., Neptune et al., 2008). Detailed analyses of previous muscle driven simulations have shown the hip (GMAX) and knee extensors (VAS) act in early stance to provide body support by contributing to the vertical ground reaction force (e.g., Anderson and Pandy, 2003; Neptune et al., 2004). However, while GMAX provides some forward propulsion after the loading response, VAS acts primarily to decelerate the body (e.g., Neptune et al., 2004; Liu et al., 2006). In addition, GMED also provides body support and forward propulsion in early stance (Anderson and Pandy, 2003; Liu et al., 2006). Both SOL and GAS provide body support and forward propulsion in late stance, although SOL primarily accelerates the trunk forward while GAS accelerates the leg into swing (Neptune et al., 2001). HAM acts to decelerate the leg in late swing in preparation for heel strike and then accelerates the body forward in early stance. RF acts to accelerate the trunk forward in pre-swing by transferring energy from the leg to the trunk to provide forward propulsion (Zajac et al., 2003; Neptune et al., 2004). When RF is active in early stance, it acts co-functional with VAS to provide body support.
The biomechanical functions produced by each module were consistent with superposition of the functions generated by the independent muscles associated with each module. Module 1 (GMED, VAS and RF) combined to provide body support and decelerate the body in early stance while Module 2 (SOL and GAS) provided body support and forward propulsion in late stance. Modules 3 (RF and TA) and 4 (HAM) were necessary to coordinate leg swing by acting to accelerate the leg into swing in early stance and decelerate the leg in late swing in preparation for foot contact. Thus, it appears using a simple neural control scheme based on controlling muscles with similar biomechanical functions is sufficient to satisfy the task demands of walking. Control schemes based on biomechanical function, with some muscles contributing to multiple functions, has been previously proposed (e.g., Raasch and Zajac, 1999; Ting et al., 1999; Neptune et al., 2000). An important note is that our model was constrained to the sagittal plane, and therefore some modules may have important frontal plane biomechanical functions yet to be identified. This remains an important area for future work.
The modules identified using NNMF were consistent in shape and timing with a number of previous studies (e.g., Ivanenko et al., 2004; Ivanenko et al., 2005). Ivanenko and colleagues identified five modules during normal walking, with four of the five being nearly identical to ours. The fifth module was associated primarily with IL and erector spinae muscle activity, which were not collected in our present study. Thus, had we collected IL activity, we most likely would have had a fifth module as normal IL muscle activity does not easily map into our existing modules. Similarly, we did not collect EMG data from GMAX or BFsh. Ivanenko also found that GMAX is strongly associated with Module 1, which is consistent with our previous studies showing GMAX acts co-functional with VAS in providing body support in early stance (Zajac et al., 2003; Neptune et al., 2004). Thus, GMAX most likely would have been included in the Module 1 factorization had the EMG data been available. Similarly, BFsh is often co-excited with HAM (e.g., Sutherland, 1984) and acts to decelerate the leg in late swing (Neptune et al., 2004; Neptune et al., 2008) and most likely would been included in Module 4.
To test these predictions, we performed an additional post-hoc simulation analysis to include GMAX in Module 1 (with GMED, VAS and RF), and BFsh in Module 4 (with HAM). IL still received its own excitation pattern (Module 5). The 5 modules now controlled 10 of the 13 muscles groups (with the remaining three small muscles controlling the foot). The excitation patterns were reoptimized and the analysis showed these new modules produced a nearly identical walking pattern. The GRF decomposition showed Module 1 continued to provide body support in early stance while Module 4 continued to decelerate the leg in late swing and accelerate the leg in early stance. The new Module 5 (IL activity) acted to accelerate the leg forward in pre- and early swing by generating energy directly to the leg while simultaneously transferring energy from the trunk to the leg to accelerate it forward (Fig. 6).
Figure 6.
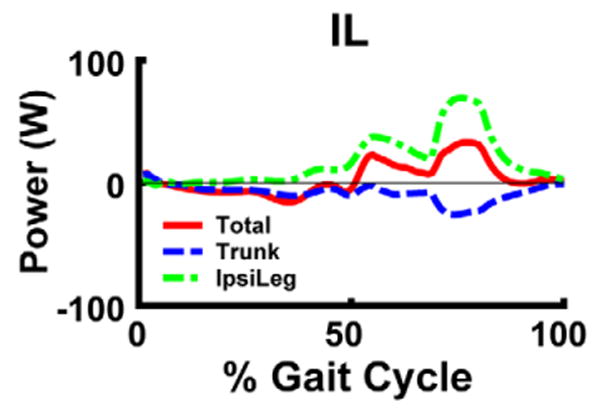
Mechanical power delivered to the trunk and ipsilateral leg by IL over the gait cycle. Positive (negative) power indicates the muscle acted to accelerate (decelerate) the leg in the direction of its motion.
Thus, well-coordinated walking can result from a simple neural control strategy involving 5 muscle activation modules to perform the basic sub-tasks of walking. It is generally accepted that the nervous system adopts neural strategies to reduce control complexity, and these results using a simple modular control strategy supports this idea. We have shown that the same modules can explain a wide range of walking speeds with modest changes in timing (Clark et al., 2009) and expect that simulation analyses would be consistent. Potential areas for future work include analyzing additional locomotor tasks (e.g., accelerated/decelerated and forward/backward walking) to see if simple changes in timing and magnitude for the muscle activation modules are sufficient to satisfy the new task requirements. This will provide insight into whether a task-dependent control strategy based on biomechanical functions is capable of performing a number of lower-limb walking tasks. In addition, since our goal in the present study was to assess the biomechanical function of the modules used by the majority of the subjects tested, we used fixed associations between specific muscles and corresponding modules. However, some subjects used different associations (Fig. 2). An area for future work would be to allow for flexibility between modules to see if other muscle-module associations are just as effective in producing a well-coordinated walking pattern, and if such associations do exist, identify the corresponding biomechanical functions.
Acknowledgments
The authors would like to thank Erin Carr, Mark Bowden, Bhavana Raja, Cameron Nott, Dr. Chitra Balasubramanian and Ryan Knight for help with the data collection and processing. This work was funded by NIH grant RO1 HD46820 and the Rehabilitation Research & Development Service of the VA.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson FC, Pandy MG. Individual muscle contributions to support in normal walking. Gait Posture. 2003;17(2):159–69. doi: 10.1016/s0966-6362(02)00073-5. [DOI] [PubMed] [Google Scholar]
- Cappellini G, Ivanenko YP, Poppele RE, Lacquaniti F. Motor patterns in human walking and running. J Neurophysiol. 2006;95(6):3426–37. doi: 10.1152/jn.00081.2006. [DOI] [PubMed] [Google Scholar]
- Clark DJ, Neptune RR, Zajac FE, Ting LH, Kautz SA. Modular organization of muscle activity underlying locomotor control complexity and recovery following stroke. Journal of Neuroscience. 2008 in review. [Google Scholar]
- d'Avella A, Saltiel P, Bizzi E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat Neurosci. 2003;6(3):300–8. doi: 10.1038/nn1010. [DOI] [PubMed] [Google Scholar]
- Goffe WL, Ferrier GD, Rogers J. Global optimization of statistical functions with simulated annealing. J Econometrics. 1994;60(12):65–99. [Google Scholar]
- Ivanenko YP, Cappellini G, Dominici N, Poppele RE, Lacquaniti F. Coordination of locomotion with voluntary movements in humans. J Neurosci. 2005;25(31):7238–53. doi: 10.1523/JNEUROSCI.1327-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP, Cappellini G, Dominici N, Poppele RE, Lacquaniti F. Modular control of limb movements during human locomotion. J Neurosci. 2007;27(41):11149–61. doi: 10.1523/JNEUROSCI.2644-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP, Poppele RE, Lacquaniti F. Five basic muscle activation patterns account for muscle activity during human locomotion. J Physiol. 2004;556(Pt 1):267–82. doi: 10.1113/jphysiol.2003.057174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu MQ, Anderson FC, Pandy MG, Delp SL. Muscles that support the body also modulate forward progression during walking. J Biomech. 2006;39(14):2623–30. doi: 10.1016/j.jbiomech.2005.08.017. [DOI] [PubMed] [Google Scholar]
- Neptune RR, Kautz SA, Zajac FE. Muscle contributions to specific biomechanical functions do not change in forward versus backward pedaling. J Biomech. 2000;33(2):155–64. doi: 10.1016/s0021-9290(99)00150-5. [DOI] [PubMed] [Google Scholar]
- Neptune RR, Kautz SA, Zajac FE. Contributions of the individual ankle plantar flexors to support, forward progression and swing initiation during walking. J Biomech. 2001;34(11):1387–98. doi: 10.1016/s0021-9290(01)00105-1. [DOI] [PubMed] [Google Scholar]
- Neptune RR, Sasaki K, Kautz SA. The effect of walking speed on muscle function and mechanical energetics. Gait Posture. 2008;28(1):135–43. doi: 10.1016/j.gaitpost.2007.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neptune RR, Wright IC, Van Den Bogert AJ. A method for numerical simulation of single limb ground contact events: application to heel-toe running. Comput Methods Biomech Biomed Engin. 2000;3(4):321–334. doi: 10.1080/10255840008915275. [DOI] [PubMed] [Google Scholar]
- Neptune RR, Zajac FE, Kautz SA. Muscle force redistributes segmental power for body progression during walking. Gait Posture. 2004;19(2):194–205. doi: 10.1016/S0966-6362(03)00062-6. [DOI] [PubMed] [Google Scholar]
- Perry J. Gait Analysis: Normal and Pathological Function. Thorofare, NJ: Slack, Inc.; 1992. [Google Scholar]
- Raasch CC, Zajac FE. Locomotor strategy for pedaling: muscle groups and biomechanical functions. J Neurophysiol. 1999;82(2):515–25. doi: 10.1152/jn.1999.82.2.515. [DOI] [PubMed] [Google Scholar]
- Raasch CC, Zajac FE, Ma B, Levine WS. Muscle coordination of maximum-speed pedaling. J Biomech. 1997;30(6):595–602. doi: 10.1016/s0021-9290(96)00188-1. [DOI] [PubMed] [Google Scholar]
- Sutherland DH. Gait Disorders in Childhood and Adolescence. Baltimore, MD: Williams and Wilkins; 1984. [Google Scholar]
- Ting LH, Kautz SA, Brown DA, Zajac FE. Phase reversal of biomechanical functions and muscle activity in backward pedaling. J Neurophysiol. 1999;81(2):544–51. doi: 10.1152/jn.1999.81.2.544. [DOI] [PubMed] [Google Scholar]
- Ting LH, Macpherson JM. A limited set of muscle synergies for force control during a postural task. J Neurophysiol. 2005;93(1):609–13. doi: 10.1152/jn.00681.2004. [DOI] [PubMed] [Google Scholar]
- Tresch MC, Cheung VC, d'Avella A. Matrix factorization algorithms for the identification of muscle synergies: evaluation on simulated and experimental data sets. J Neurophysiol. 2006;95(4):2199–212. doi: 10.1152/jn.00222.2005. [DOI] [PubMed] [Google Scholar]
- Winters JM, Stark L. Estimated mechanical properties of synergistic muscles involved in movements of a variety of human joints. J Biomech. 1988;21:1027–1041. doi: 10.1016/0021-9290(88)90249-7. [DOI] [PubMed] [Google Scholar]
- Zajac FE, Neptune RR, Kautz SA. Biomechanics and muscle coordination of human walking: part II: lessons from dynamical simulations and clinical implications. Gait Posture. 2003;17(1):1–17. doi: 10.1016/s0966-6362(02)00069-3. [DOI] [PubMed] [Google Scholar]


