Abstract
T cell receptors (TCRs) are proteins that recognize peptides from foreign proteins bound to the Major Histocompatibility Complex (MHC) on the surface of an antigen-presenting cell. This interaction enables the T cells to initiate a cell-mediated immune response to terminate cells displaying the foreign peptide on their MHC. Naturally occurring TCRs have high specificity but low affinity toward the peptide-MHC (pepMHC) complex. This prevents the usage of solubilized TCRs for diagnosis and treatment of viral infections or cancers. Efforts to enhance the binding affinity of several TCRs have been reported in recent years, through randomized libraries and in vitro selection. However, there have been no reported efforts to enhance the affinity via structure-based design, which allows more control and understanding of the mechanism of improvement. Here we have applied structure-based design to a human TCR to improve its pepMHC binding. Our design method evolved based on iterative steps of prediction, testing and generating more predictions based on the new data. The final design function, named ZAFFI, has a correlation of 0.77 and average error of 0.35 kcal/mol with the binding free energies of 26 point mutations for this system that we measured by surface plasmon resonance. Applying the filter we developed to remove non-binding predictions, this correlation increases to 0.85 and the average error decreases to 0.3 kcal/mol. Using this algorithm, we predicted and tested several point mutations that improved binding, with one giving over 6-fold binding improvement. Four of the point mutations that improved binding were then combined to give a mutant TCR that binds the pepMHC 99 times more strongly than the wild-type TCR.
Keywords: TCR, MHC, structure-based design, Rosetta, ZRANK, SPR
Introduction
T cell receptors (TCRs) are heterodimeric proteins that play a critical role in the cellular immune response. By binding to the complex of a foreign peptide and the Major Histocompatibility Complex protein (pepMHC), they initiate an immune response against this cell, protecting the host from foreign invasion.1 The interaction between TCR and pepMHC is highly specific, but of low affinity, making this system an attractive target for protein design. By utilizing protein engineering methods, the binding of TCRs can be increased while maintaining their specificity, thus making them useful agents for targeting cancers and pathogens. These designed TCRs should have immense therapeutic potential, for instance to detect and treat virally infected cells. This is complementary to and has distinct advantages over monoclonal antibody-based therapy, which recognizes the surface epitopes of intact virus. Viruses rapidly mutate the surfaces of their coat proteins to evade host immune response. Because TCRs target peptides, some of which are generated from the functional sites of viral proteins and hence cannot be easily mutated, TCRs may be more effective than antibodies in treating viral infection. Additionally, some TCRs recognize pepMHC complexes on cancerous cells and be applied to cancer therapy.
Efforts to improve protein-protein interactions by protein engineering have generally fallen into two categories: directed evolution and structure-based design. Directed evolution involves using randomized libraries of mutant proteins (displayed on the surface of phage or yeast, or directly attached to ribosome in a cell-free manner) to select strong-binding clones. In the context of TCR engineering, there have been several directed evolution efforts, improving binding by approximately 100 fold for a mouse TCR,2 and up to 1,000,000 fold for human TCRs.3-5 However, such technologies can have limitations, such as inadequate library size, and problems with displaying certain mutants due to inefficient protein folding in the expression system.6
Structure-based methods to enhance protein-protein interactions have become more widely used over recent years, with more crystal structures of protein complexes available, greater computational processing power, and more advanced algorithms to compute binding energy changes. Selzer et al. enhanced the association rate of the TEM-BLIP enzyme-inhibitor system by over 200-fold, by producing point mutations on the BLIP protein near the TEM interface predicted to enhance electrostatic attraction.7 While the association rate (kon) and dissociation equilibrium constant (KD) were significantly affected, the dissociation rate (koff) did not change significantly. Another study used several in silico methods to optimize the ICAM-1 protein to bind to LFA-1 protein, resulting in a mutant ICAM-1 with 22-fold binding affinity improvement over the wild-type.8 Structure-based design has also been used to alter the specificity of several protein-protein interactions.9,10 Structure-based design efforts to enhance the affinities of immunoglobulin proteins (the superfamily to which both antibodies and TCRs belong) have led to four times affinity improvement for a CD8-HLA complex11 and over seven times affinity improvement for an antibody-antigen system.12 A recent study performed computational redesign of two antibodies via point mutations; combining five of the tested point mutations led to a 140-fold improvement over wild-type affinity for an antibody to lysozyme.13 There are currently no studies that have utilized structure-based design to improve the TCR-pepMHC interaction.
We have chosen to engineer the human A6 TCR for enhanced affinity toward its in vivo binding partner, the Tax peptide/HLA-A2 MHC complex. HLA-A2 is the most abundant Class I MHC allele, possessed by nearly half of the human population. The peptide is a 9-mer from the Tax protein of the human T cell lymphotrophic virus (HTLV-1). In addition to being characterized biophysically,14,15 the wild-type structure for this complex has been crystallized.16 As with other TCR-pepMHC complexes, this system has a relatively low binding affinity (KD in the micromolar range).
In this study, we predicted point mutations of the TCR based on the crystal structure of the complex, and tested their binding affinities for pepMHC using surface plasmon resonance (SPR). We chose to focus on the A6 TCR alpha chain, as it has a large number of contacts with both peptide and MHC, and the beta chain has been engineered in another study using phage display.3 Based on our initial experimental results, we developed a new protein design algorithm named ZAFFI (Zlab AFFInity enhancement) that yielded point mutations with up to 6 times binding improvement. We then combined several point mutations with improved binding to create a single TCR with 99 times improved affinity for the tax/MHC, which was then tested for specificity with several other peptides bound to the HLA-A2 protein.
Materials and Methods
Modeling of Initial Point Mutations
Initial mutation predictions were produced using molecular modeling of the point mutations using CONGEN,17-19 followed by scoring using electrostatics and solvation, with a van der Waals filter. Mutations were tested if they exhibited improved electrostatics and solvation energies, and passed the van der Waals filter for no severe clashes.
Structural Modeling of Point Mutations Using Rosetta
For this study, structures of point mutations were simulated by Rosetta's interface mutagenesis module,20 using a fixed protein backbone, and the wild-type protein crystal structures as input. Only the mutant side chain was packed by Rosetta, except when exploring repacking neighboring residues. In that case the “-repack_neighbors” flag was passed to Rosetta, which caused residues in the vicinity of the mutation to be repacked. For side chain packing, standard rotamers were augmented with extra chi1, chi2, and chi3 rotamers for all residues with at least 12 neighbors within 10 Å.
Parameterization of ZAFFI Scoring Function
Based on the experimental results from this method, we proceeded to develop the ZAFFI function that ultimately performed the predictions of the mutations. Training of the energy function was performed using a dataset of systematic point mutations at 10 positions on the ovomucoid turkey inhibitor (OMTKY) molecule in four enzyme-inhibitor complexes (from Professor Michael Laskowski, personal communication to Zhiping Weng). Specifically, the OMTKY mutations were at positions p6, p5, p4, p2, p1, p1’, p2’, p3’, p14’ and p18’ on the protein, with wild-type residue identities lysine, proline, alanine, threonine, leucine, glutamic acid, tyrosine, arginine, glycine, and asparagine, respectively. For each OMTKY position, the binding affinities of all 19 amino acid variants were measured, giving 10*19*4 = 760 experimentally characterized point mutations. Thus this set provided a broad set of mutations, on a system different from the TCR, to train candidate scoring function weights.
To model these point mutations, the structures of the wild-type complexes (PDB IDs: 1CHO, 1PPF, 1YU6, and 3SGB) were used as input for Rosetta structural modeling, as described above. For each mutant, the score was obtained by subtracting the score of the wild-type complex from that of the mutant structure. We filtered some of the mutations prior to training due to excessive clash as measured by the van der Waals repulsive term, leaving 648 OMTKY mutations out of the original 760 for training. The 112 structural models that were removed before training most likely required further side chain or backbone packing to accommodate the clash and were considered false negatives, which were not of interest as we sought to reduce false positives. Inclusion of these mutations in the training set led to excessively low van der Waals repulsive weights (data not shown).
The scoring terms explored were:
van der Waals attractive (vdW_atr)
van der Waals repulsive (vdW_rep)
Lazaridis-Karplus solvation (solv)
hydrogen bonding (HB)
intra-residue clash (intra)
short-range electrostatics (SR elec)
long-range electrostatics (LR elec)
amino acid backbone probability (BB prob)
ACE
IFACE
DFIRE
Terms 1, 2, 6, 7, and 9 are from the ZRANK scoring function;21 as with the original ZRANK implementation, these terms are calculated across the interface, using all atoms except nonpolar hydrogens. The van der Waals and electrostatics terms are calculated based on the parameters in the CHARMM 19 potential.22 For the van der Waals terms, a short-range linearization is used (based on Gray et al.23), and the upper limit for inter-atom distances is 8.0 Å. The electrostatics terms are calculated using a dielectric that is directly proportional to the distance, and short-range and long-range electrostatics determined by the inter-atom distance: 0 Å < r < 5 Å (short-range) or 5 Å ≤ r < 12 Å (long-range). For inter-atom distances less than the sum of the atomic radii, the distance is approximated by the sum of the atomic radii to avoid large values due to clash. The ACE (Atomic Contact Energy) function is a statistical contact potential developed by Zhang et al.;24 for all (non-hydrogen) atom pairs less than 6 Å apart, the ACE score is incremented by a value based on the identity of the atom pair. It was originally parameterized based on intra-chain contact propensities seen in the Protein Data Bank (PDB),25 and has since been successfully utilized to analyze protein docking predictions.26,27
Terms 3, 4, 5, and 8 are from Rosetta; to obtain them, we modified the Rosetta code to set their weights to 1.0 and output the numbers with higher precision than the default. The Lazaridis-Karplus term uses Gaussian solvent exclusion between the (non-hydrogen) atoms to model the solvation free energy of the system.28
IFACE is a protein interface atomic level statistical potential,29, similar to ACE but parameterized using protein interfaces rather than protein monomers. DFIRE is a distance-dependent statistical potential,30 the numbers for which were obtained from the dcomplex program.
Using the above terms, we combined all possible sets of sizes 0 to 5 for terms 4−11 with terms 1, 2, and 3. This led to 219 candidate sets of scoring terms. For each set of scoring terms, multilinear regression was applied, using the GNU Scientific Library (http://www.gnu.org/software/gsl/) and the filtered mutations for the OMTKY data set described above. This determined a set of weights for the terms that was optimized to fit the energies of the OMTKY point mutants. Each weighted function from the multilinear regression was then tested using the data set of our measured point mutations for the T cell receptor (simulating the point mutants using Rosetta as described above), and evaluated based on correlation.
These are the optimal terms and weights obtained from training on the OMTKY data and then applied to our T cell receptor mutations:
van der Waals attractive: 0.24
van der Waals repulsive: 0.017
Lazaridis-Karplus solvation: 0.24
intra-residue clash: 0.073
ACE: 0.32
ZAFFI Energy Score = 0.24*vdW_atr + 0.017*vdW_rep + 0.24*solv + 0.073*intra + 0.32*ACE
Results for this weighted function applied to the OMTKY dataset (along with the results using the original Rosetta scores) are given in Figure S1.
Parameterization of ZAFFI Filter
We developed the ZAFFI filter to remove non-binding TCR mutants that were not detected by the ZAFFI scoring function. This function was developed using all point mutants described in Tables 1 and S1, except for the following, which were produced after filter development:
α chain: D26V, D26W, D26M, R27F, G28M, G28T, G28R, Q30M, Q30H, Q30E, S51M, K68H, T93Q, T98E, G102D, G102S
β chain: I54R, R95F, G100I
Table 1.
Binding kinetics and prediction method for measured A6 TCR point mutants.
| Mutation1 |
Pred.2 |
ka, ×104 M−1s-1 |
kd, ×10−1 s−1 |
KD_wt/KD_mut3 |
ΔΔG, kcal/mol4 |
|---|---|---|---|---|---|
| WT | 5.11 | 1.08 | 1.0 | 0.00 | |
|
alpha chain | |||||
| D26M | R | - | - | 0.7 | 0.19 ± 0.11 |
| D26V | Z | - | - | 0.1 | 1.45 ± 0.17 |
| D26W | Z | 2.44 | 0.08 | 6.2 | −1.08 ± 0.13 |
| R27F | Z | 8.03 | 1.18 | 1.4 | −0.22 ± 0.13 |
| G28A | I | 3.72 | 2.10 | 0.4 | 0.58 ± 0.13 |
| G28I | I | 4.27 | 0.58 | 1.6 | −0.27 ± 0.11 |
| G28L | I | 6.92 | 0.68 | 2.2 | −0.46 |
| G28M | R | 8.59 | 0.77 | 2.4 | −0.51 ± 0.21 |
| G28R | R | - | - | 0.02 | 2.43 ± 0.49 |
| G28T | Z | 6.76 | 0.39 | 3.6 | −0.76 ± 0.12 |
| G28V | I | 2.48 | 1.34 | 0.4 | 0.56 ± 0.16 |
| S29A | I | 3.91 | 1.45 | 0.6 | 0.33 ± 0.11 |
| Q30N | I | 2.88 | 2.09 | 0.3 | 0.73 ± 0.17 |
| Q30E | Z | - | - | 0.5 | 0.43 ± 0.14 |
| S51M | Z | 5.38 | 0.61 | 1.9 | −0.37 ± 0.22 |
| K68H | Z | - | - | 0.2 | 1.09 |
| S100A | I | 4.71 | 0.97 | 1.0 | −0.01 ± 0.14 |
| S100N | I | - | - | 0.04 | 1.92 ± 0.84 |
| S100T | I | 2.58 | 0.24 | 2.3 | −0.49 ± 0.10 |
| S100Y |
I |
- |
- |
0.02 |
2.34 ± 0.55 |
|
beta chain | |||||
| I54R | R | - | - | 0.1 | 1.28 ± 0.84 |
| A99M | L | 3.63 | 0.45 | 1.7 | −0.31 ± 0.11 |
| A99K | I | 2.08 | 0.52 | 0.9 | 0.10 ± 0.14 |
| G100S | L | 2.48 | 0.31 | 1.7 | −0.32 ± 0.10 |
| G101A | L | 1.86 | 0.06 | 6.3 | −1.09 ± 0.10 |
| R102Q | L | 2.27 | 1.03 | 0.5 | 0.45 ± 0.23 |
The point mutation tested. WT = wild-type A6 TCR. Mutations in bold are those from ZAFFI predictions which improved binding.
The prediction algorithm responsible for the mutation. I = our initial method; R = Rosetta (using Rosetta score); Z = ZAFFI; L = from Li et al. quadruple mutant {Li, 2005 #147}
Binding affinity improvement, calculated as KD of the wild-type A6 TCR (measured value = 2.11 μM) divided by KD of the specified mutant.
Binding energy change from the wild-type, with standard deviation calculated by separate analysis of three concentration gradients. For G28L and K68H, the uncertainty could not be calculated because only two gradients were used.
“−” kinetics not measurable, KD obtained by steady-state analysis of the sensorgram. Otherwise KD obtained by koff/kon
To train the ZAFFI filter, a Monte Carlo algorithm was used to generate candidate weights for pairs of scoring terms. All possible pairs of terms used in ZAFFI energy function development (described in the previous section) were tested. For each set of weighted terms, the function was judged based on the Area Under the Curve (AUC) of the Receiver Operating Characteristic (ROC) curve. This was computed using all mutants with ZAFFI energy score less than 0.0, separating the mutants found to bind form those that did not bind, thus separating true positives from false positives from the ZAFFI energy function.
Based on the above training, the ZAFFI filter function was determined, with these terms and weights:
ZAFFI Filter Score = 1.0*HB + 0.01*LR elec
This function had an AUC of 0.93 using the test data. A filter score cutoff of 0.05 was used to filter the predictions. Filter scores for all measured data points can be seen in Table 4.
Table 4.
ZAFFI Scores, Filter Scores, and measured binding for all measured TCR point mutants.
| Chain | Mutant | ZAFFI Score | ZAFFI Filter | Pass1 | ΔΔG2 |
|---|---|---|---|---|---|
| α | Q30W | −3.00 | 0.46 | N | NB |
| α | Q30F | −2.90 | 0.63 | N | NB |
| α | Q30Y | −2.37 | 0.66 | N | NB |
| α | G28M | −1.88 | 0.03 | Y | −0.51 |
| α | Q30M | −1.82 | 0.63 | N | NB |
| α | Q30H | −1.59 | 0.47 | N | NB |
| α | Q30L | −1.50 | 0.63 | N | NB |
| α | S100L | −1.49 | 0.08 | N | NB |
| α | R27F | −1.28 | 0.15 | N | −0.22 |
| α | S100I | −1.07 | 0.08 | N | NB |
| α | D26W | −1.05 | 0.03 | Y | −1.08 |
| β | G101A | −1.00 | 0.03 | Y | −1.09 |
| α | G28T | −0.97 | 0.01 | Y | −0.76 |
| α | S51M | −0.90 | 0.04 | Y | −0.37 |
| α | G28I | −0.89 | 0.03 | Y | −0.27 |
| α | G100I | −0.89 | 0.00 | Y | NB |
| α | K68H | −0.83 | 0.93 | N | 1.09 |
| β | A99M | −0.72 | 0.00 | Y | −0.31 |
| α | D26M | −0.49 | 0.03 | Y | 0.19 |
| α | G28A | −0.46 | 0.03 | Y | 0.58 |
| α | R95F | −0.46 | 0.33 | N | NB |
| α | S100T | −0.46 | 0.01 | Y | −0.49 |
| α | G28L | −0.43 | 0.03 | Y | −0.46 |
| α | Q30E | −0.42 | 0.50 | N | 0.43 |
| β | E30Y | −0.33 | 0.25 | N | NB |
| β | E30F | −0.33 | 0.25 | N | NB |
| β | E30W | −0.31 | 0.26 | N | NB |
| β | G100S | −0.25 | −0.02 | Y | −0.32 |
| α | S100A | −0.19 | 0.07 | N | −0.01 |
| β | E30M | −0.18 | 0.25 | N | NB |
| α | T93I | −0.17 | 0.04 | Y | NB |
| β | A99K | −0.14 | 0.05 | N | 0.1 |
| α | S100M | −0.14 | 0.10 | N | NB |
| α | S100F | −0.13 | 0.08 | N | NB |
| α | G102D | −0.12 | −0.11 | Y | NB |
| α | D26V | −0.11 | 0.04 | Y | 1.45 |
| β | A99D | −0.10 | −0.01 | Y | NB |
| α | G102S | −0.03 | −0.61 | Y | NB |
| β | R102Q | −0.03 | 0.14 | N | 0.45 |
| α | T98E | −0.01 | 0.62 | N | NB |
| α | S29A | 0.00 | 0.02 | Y | 0.33 |
| β | E30Q | 0.01 | 0.21 | N | NB |
| α | Q30N | 0.10 | −0.32 | Y | 0.73 |
| β | E30A | 0.10 | 0.25 | N | NB |
| β | L98F | 0.10 | 0.00 | Y | NB |
| α | T93Q | 0.22 | −1.49 | Y | NB |
| α | S100Y | 0.26 | 0.22 | N | 2.29 |
| β | L98I | 0.49 | 0.00 | Y | NB |
| β | G101V | 0.51 | 0.03 | Y | NB |
| α | G28V | 0.52 | 0.03 | Y | 0.56 |
| α | S100Q | 0.52 | 0.10 | N | NB |
| α | I54R | 0.54 | −0.74 | Y | 1.28 |
| α | D99N | 0.58 | 0.26 | N | NB |
| α | S100N | 0.58 | 0.11 | N | 1.92 |
| β | G101M | 0.61 | 0.02 | Y | NB |
| β | L98M | 0.96 | 0.01 | Y | NB |
| α | G28R | 1.65 | −0.51 | Y | 2.43 |
| β | A99Y | 1.92 | −0.01 | Y | NB |
| β | L98D | 2.48 | 0.09 | N | NB |
Whether the mutant passed the ZAFFI filter, defined by having a filter score less than 0.05.
Measured binding energy change (kcal/mol). NB = no binding detected or unmeasurable binding.
Application of ZAFFI Function to A6 TCR Dataset
For ZAFFI, the simulation of the point mutations was performed using Rosetta's interface mutagenesis module20 as described above and the crystal structure of the wild-type TCR complex.16 All 26 interface residues (within a 5 Å cutoff of pepMHC) were systematically mutated, generating structural models for 494 point mutations. Rosetta output included predicted energies of the mutations (using its own weighted energy function20), as well as structures of the mutants. The ZAFFI energetic and filter scores were then calculated from these models using the functions described above.
Protein Expression and Purification
Wild-type HLA-A2, β2M, TCRα and TCRβ, and mutant TCRα and TCRβ proteins were expressed separately as inclusion bodies in E. coli. Mutations were introduced to the constructs via site-directed mutagenesis using standard PCR protocols. The inclusion bodies were refolded using protocols based on those of Garboczi et al.31,32 However, fast protein liquid chromatography (FPLC) using a size exclusion column (rather than dialysis and ion exchange) was used to purify the refolded proteins from the aggregates; this resulted in much faster purification of the proteins than the previously published method.31
Measurement of Binding Kinetics
Binding of wild-type and mutant A6 TCR to the Tax-HLA-A2 complex was tested at 25°C using Biacore 3000 surface plasmon resonance (SPR) biosensor. Approximately 400 response units of each TCR were immobilized on the CM5 chip using the standard amine coupling procedure. The Tax-HLA-A2 complex was injected over the immobilized TCRs at a flow rate of 100 μl/min. In order to correct for non-specific binding of the Tax-HLA-A2 to the chip surface, Tax-HLA-A2 was also injected over a surface on which no TCR was bound; this signal was subtracted from those of the TCR-bound cells. After the binding dissociation phase, the baseline was regenerated with a 2 min injection of 0.01 M HEPES (pH 7.4) 1 M NaCl over all channels. HBS-EP (0.01 M HEPES (pH 7.4), 0.15 mM NaCl and 3 mM EDTA, 0.005% v/v Surfactant P20) was used as a running buffer during binding affinity measurements.
BIAevaluation (Biacore) was used to determine the kon and koff of the complex formation by simultaneous global fitting of the data to a 1:1 Langmuir model. When kinetics were not measurable, steady-state analysis was used to obtain the KD. Steady-state analysis was also used to verify the KD values obtained by kinetics analysis whenever possible, and the differences were within the range of uncertainty seen from the kinetics replicates (in the ΔΔG column in Table 1). For all mutants tested, three different Tax-HLA-A2 concentration gradients were used to compute the kinetic and equilibrium parameters.
Results
Identification of T Cell Receptor Point Mutations with Enhanced Binding to pepMHC
We used several prediction methods to generate point mutations to test experimentally. These included our original method using the CONGEN program 18, Rosetta's “interface” module,20 and ZAFFI. ZAFFI uses an optimized energy-based scoring function and Rosetta for side chain packing. These algorithms are described in more detail in the Materials and Methods section. In addition, four point mutations comprising the quadruple β chain mutant produced in the study of Li et al.3 were included in the training set for ZAFFI. All mutants were expressed, folded, and measured for binding using the protocol described in the Materials and Methods section. Kinetics and binding results for mutations with measurable binding to pepMHC are shown in Table 1.
In addition to the mutations that showed measurable binding, we also found that several mutations exhibited loss of binding or unmeasurable binding; these are listed in Table 2. These represent a large proportion of our initial data set and indicate that the A6 TCR is highly sensitive to interface point mutations. This was also seen in an alanine-scanning study of another human TCR, where 14 of the 39 tested mutations (36%) resulted in binding below the threshold of reliable surface plasmon resonance measurement.33 While such tendencies can help to modulate TCR cross-reactivity (and may be a result of the low wild-type binding affinity), it indicates that this system presents a major challenge for structure-based design, because a naïve algorithm would have little success in predicting affinity-enhancing mutations.
Table 2.
TCR point mutations that exhibited no measurable binding to pepMHC. The mutations produced during development of the ZAFFI filter are shown in italics.
| CDRα1 | CDRα3 | CDRβ1 | CDRβ3 |
|---|---|---|---|
| Q30M | T93Q | E30A | R95F |
| Q30H | T93I | E30F | L98D |
| Q30L | T98E | E30Q | L98F |
| Q30F | D99N | E30W | L98I |
| Q30W | S100M | E30Y | L98M |
| Q30Y | S100I | A99D | |
| S100L | A99Y | ||
| S100F | G100I | ||
| G102S | G101M | ||
| G102D | G101V |
Table 1 indicates improved performance in moving from our initial algorithm to Rosetta to our final ZAFFI algorithm. Our initial predictions (“I”) had three mutations with improved binding, seven worse, and one approximately the same (αS100A), while using Rosetta scoring to produce mutations (“R”), one improved binding and three became worse. When utilizing these results and developing the ZAFFI function (“Z”), our success improved so that we had four mutations with improved binding (in bold in Table 1) and three with worse binding. It should be noted that some of the points with worse binding were intentionally produced to verify the ZAFFI function during its development, so its success rate is in fact higher than indicated in Table 1 (its performance on all points is discussed in the next section). Among the mutations identified by ZAFFI were αD26W (the highest affinity point mutation identified by all three methods) and αG28T, which improved binding by 6.2 and 3.6 times, respectively.
ZAFFI Scoring Function
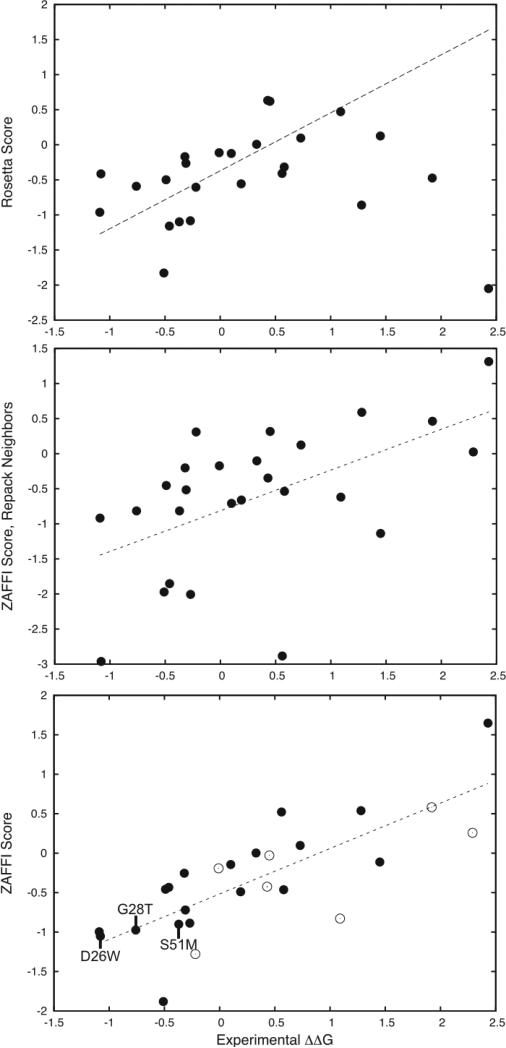
As shown above, ZAFFI was clearly able to identify mutations that improved binding. We then examined whether it was able to model the energetics of the measured mutations accurately. Figure 1 provides the predicted scores versus experimentally measured values for the 26 measured point mutation energies in Table 1, for Rosetta scoring (top) and ZAFFI scoring (bottom). For ZAFFI, the correlation coefficient is 0.77 (P-value < 10−5) and the average error from the fit is 0.35 kcal/mol, while for Rosetta the correlation is 0.42. We also tested repacking nearby interface residues to model the structures (Figure 1, middle); this was found to lead to a lower correlation than ZAFFI scoring without repacking (correlation = 0.55), due to increased outliers and false positives. It was suggested by Kortemme and Baker that repacking neighboring residues aided predictions for some systems but not others.20 Our results indicate that it is best not to repack for this T cell receptor system.
Figure 1.
Scores versus experimentally measured binding energy changes for three different modeling protocols for 26 measured point mutations of the A6 TCR/tax-MHC complex. Shown are: Rosetta scoring (top; correlation = 0.42), ZAFFI with repacking of neighbor residues (middle; correlation = 0.55), and ZAFFI (bottom; correlation = 0.77). The linear regression line is shown as a dotted line for each plot. For the Rosetta scoring, one outlier point is outside the range of the plot and is not shown. For the ZAFFI scoring (bottom plot), the points that did not pass the filter function are shown as empty circles, and identities of three ZAFFI predictions that improved binding are labeled.
As discussed in the Materials and Methods section, the ZAFFI scoring function contains five terms: van der Waals attractive and repulsive (calculated by the protein docking scoring function ZRANK21), Lazaridis-Karplus solvation,28 intra-residue clash (calculated by Rosetta20), and atomic contact energy (ACE, a statistical potential24). The weights for these terms were obtained using multilinear regression on a large set of measured enzyme-inhibitor mutations (Materials and Methods and Figure S1). Supplemental Table 1 provides the weighted values of these terms for all of the 26 TCR point mutations in this study. To explore the specific ZAFFI terms that contributed the most to the correlation and the binding improvements, we calculated the correlations of the individual terms alone with the measured binding energies; these are shown in Table 3. Also presented in Table 3 are the individual correlations for the other six terms utilized when testing candidate scoring functions.
Table 3.
Scoring terms, individual correlations with measured TCR binding energies, and change (loss) in correlation when removing term from ZAFFI scoring function (marked “−” for terms not in ZAFFI scoring function).
| Term | Correlation | Corr. Change |
|---|---|---|
| vdW_atr | −0.01 | 0.28 |
| vdW_rep | 0.12 | 0.19 |
| solv | 0.48 | 0.39 |
| HB | −0.12 | - |
| intra | 0.08 | 0.05 |
| SR elec | −0.09 | - |
| LR elec | 0.10 | - |
| BB prob | 0.20 | - |
| ACE | 0.42 | 0.10 |
| IFACE | 0.07 | - |
| DFIRE | 0.14 | - |
Although the scoring terms were ultimately utilized together in the ZAFFI weighted scoring function, the values in Table 3 provide insights into which terms are more valuable. It can be seen that the Lazaridis-Karplus solvation (“solv”) and ACE terms yield the highest correlations with the measured binding energies. In addition, although the van der Waals attractive term does not give a high correlation alone, removing this term from the ZAFFI scoring function causes a loss of 0.28 from the correlation. Therefore, the improvements in binding affinity are largely due to improved contacts, as measured by van der Waals, solvation, and contact energies. In contrast, other terms can be seen to provide less precise discrimination of binding affinities (as measured by the correlation), such as the hydrogen bonding and the electrostatics terms.
To further illustrate this point, plots of several terms (van der Waals attractive, ACE, hydrogen bonding, and short-range electrostatics) alone versus measured ΔΔG are given in Figure S2. Interestingly, the hydrogen bonding term plot (lower left) contains false positive predictions for point mutations βI54R and αG28R, as does the Rosetta scoring function (Figure 1, top). Therefore it seems that this term, which is part of the Rosetta scoring function, is at least partly responsible for those false positive predictions, and by removing it in the ZAFFI function those false positive predictions have been avoided.
ZAFFI Filter Function
The ZAFFI filter complements the energetic scores by removing non-binding false positive predictions. The filter uses a weighted sum of two energy terms: hydrogen bonding and long-range electrostatics, which are not utilized directly in the ZAFFI scoring function. The predictive improvements due to the ZAFFI filter can be seen by comparison of the binding mutations in Table 1 with the non-binding mutations in Table 2. Prior to developing the filter (corresponding to “I” in Table 1), 36 point mutations were tested, of which 26 (72%) ablated binding to the pepMHC (in Roman font in Table 2). During and after development of the filter (corresponding to “R” and “Z” in Table 1; in italics in Table 2), 19 point mutations were tested, of which 8 (42%) did not bind. It should be noted that as with the scoring function, while developing the filter several points were produced to test candidate filter functions. The final filter function has much higher success on the tested point mutations.
The scoring of all experimentally tested point mutations (binding and non-binding) from this filter function can be seen in Table 4, which is sorted by ZAFFI score. By ZAFFI scores alone, the top scoring mutations were mutations at residue αQ30 that did not bind; thus the filtering is necessary to remove such false-positives. Using a ZAFFI score cutoff of −0.4 to select predictions, 12 points pass the filter, 9 of which are better binders, out of a total of 11 found in this study (αS100A does not bind significantly better than the wild-type and is not counted as a better binder).
Even though the filter was trained only to remove non-binding mutations, it also removes false positive predictions for the mutations with measured binding. Using just the points that passed the filter (Figure 1, bottom, solid points) gives an even greater correlation of 0.85, and a lower average error of 0.30 kcal/mol (versus correlation of 0.77 and average error of 0.35 for all points). This indicates that the two terms in the filter prove useful as a binary classifier to indicate mutations that may lose crucial electrostatics contacts, thereby reducing binding below what is expected by the ZAFFI score.
Kinetics and Structures of A6 TCR Point Mutations
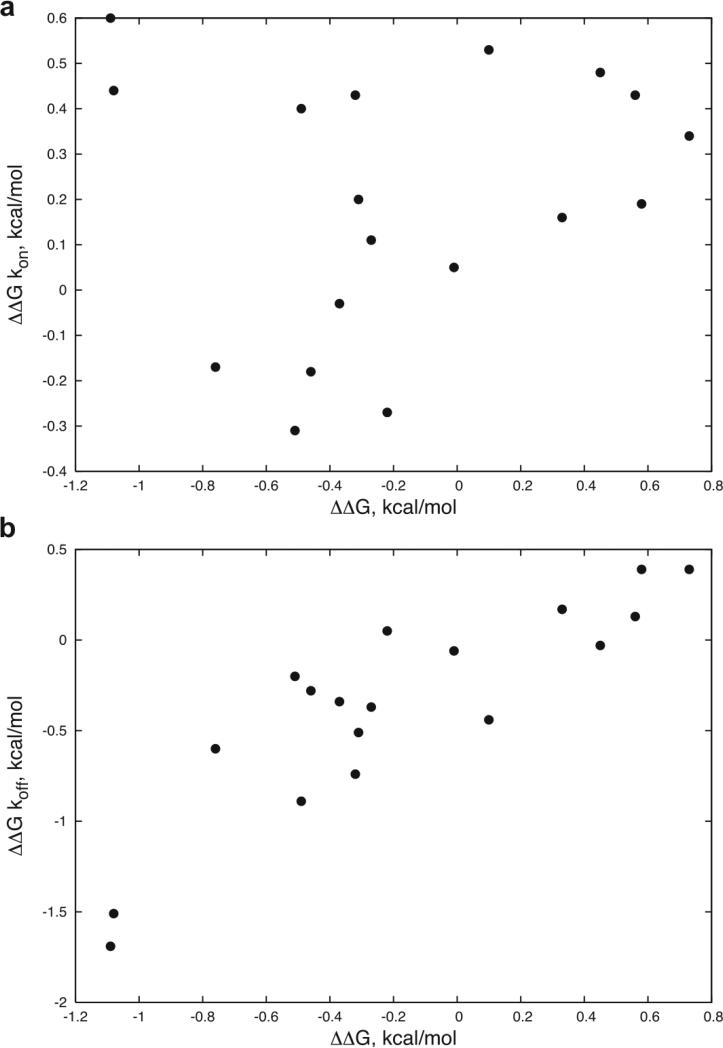
For the mutations that improved binding, it can be seen in Table 1 that the improvements are largely due to a decrease in the dissociation rates. This is further shown in Figure 2, which divides the ΔΔGs into kon and koff components and compares with the total ΔΔG. Exceptions include αR27F and αG28M, with the former showing significant kon improvement and the latter showing improvements in both kon and koff.
Figure 2.
ΔΔG kon (a) and ΔΔG koff (b) versus ΔΔG for the 18 measured point mutations with kinetics values in Table 1, with values defined as follows: ΔΔG kon = RT*ln(kon_wt/ kon_mut), ΔΔG koff = RT*ln(koff_mut/ koff_wt), and ΔΔG = RT*ln(KD_mut/ KD_wt) = RT*(ln(kon_wt/kon_mut) + ln(koff_mut/koff_wt)) = ΔΔG kon + ΔΔG koff. The correlations are: a) 0.15 and b) 0.87.
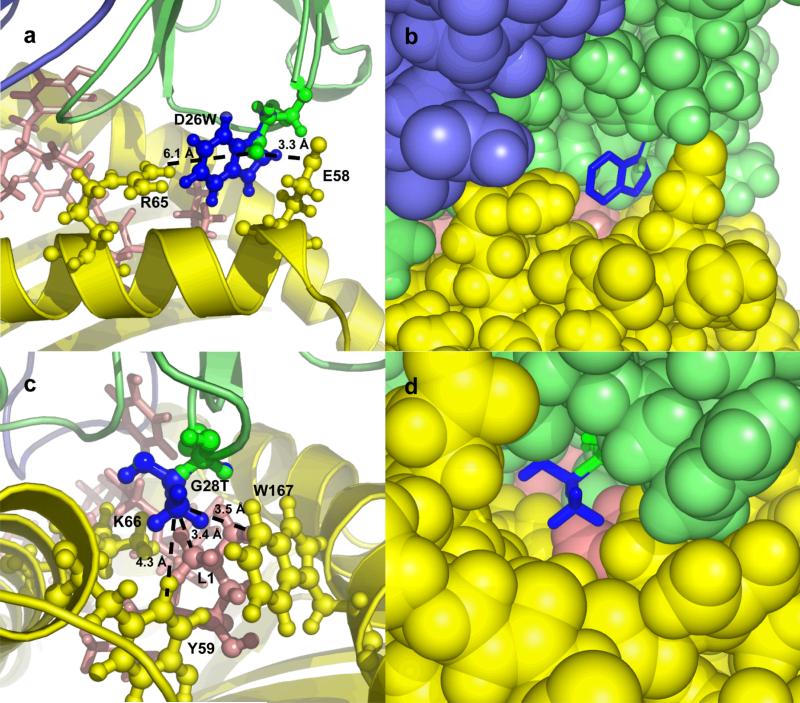
As examples of the structural mechanisms of binding affinity improvement, we show models for two of these mutations, αD26W and αG28T, in Figure 3. The mutation αD26W (Figure 3a and 3b) is on the periphery of the interface, near MHC residues E61 and R65. The substitution of a neutral residue (tryptophan; W) for a negatively charged one (D; aspartic acid) in this position of the TCR is electrostatically permitted because the position is closer to the negative E61 than to the positively charged R65 (3.3 Å versus 6.1 Å). Furthermore, the mutant tryptophan residue is predicted to make extensive hydrophobic contacts with the MHC, as can be seen in Figure 1b. The model for the mutation αG28T (Figure 3c and 3d) shows the contacts made by the T (threonine) residue with the peptide residue 1 (leucine) and several hydrophobic MHC residues. Although several mutations at this position bound the pepMHC, αG28T was the strongest binding mutation. These structural models give further evidence that the affinity gains are through improved contacts and desolvation, as seen earlier with the specific scoring terms in Table 3.
Figure 3.
Models of mutant complexes for point mutations D26W (a and b) and G28T (c and d) of the TCR α chain, using cartoon (a and c) and spacefill (b and d) to represent the molecules. Wild-type residues and TCR α chain are shown in green, mutant residues are shown in blue, MHC is colored yellow, peptide is colored pink, and TCR β chain is colored slate. In a and c, side chains of peptide and MHC residues in the vicinity of the mutation are labeled. In a, dotted lines indicate the distance from the TCR D26 OD2 atom to the MHC E58 OE1 atom (3.3 Å), and to the MHC R65 NH2 atom (6.1 Å). In c, dotted lines indicate the distances from the (modeled) TCR T28 CG2 atom to the peptide L1 CD1 atom (3.4 Å), to the MHC W167 CZ2 atom (3.5 Å), and to the MHC Y59 CD1 atom (4.3 Å). Images generated using Pymol (www.pymol.org).
Cooperativity of Multiple Point Mutations
Point mutations on the TCR α chain that improved binding to pepMHC were then combined to determine if it was possible to further improve the affinity beyond those of the single point mutations. By comparing with the results for the measured energies with the sums of the component single point mutants, we determined whether the combinations were additive, or exhibited positive or negative cooperativity. Results for binding kinetics and cooperativity are given in Table 5.
Table 5.
Binding kinetics of combinations of point mutants, and cooperativity of the energetics.
| Mutation1 | kon, ×104 M−1s−1 | koff, ×10−1 s−1 | KD, μM | ΔΔG, kcal/mol | Coop2 |
|---|---|---|---|---|---|
| WFTMT | 1.98 | 0.0481 | 0.240 | −1.28 ± 0.24 | 1.64 |
| WFGMT | 6.32 | 0.0135 | 0.0214 | −2.72 ± 0.10 | −0.56 |
Residue identities at positions 26, 27, 28, 51, and 100 on the TCRα chain. Mutant residues are in bold.
Cooperativity of the mutations, defined by ΔΔGmutant - Σ(ΔΔGindivdual point mutants)
The combination of the top binding mutations at five positions on the α chain (WFTMT) had significantly less binding than expected from additivity (negative cooperativity of 1.64 kcal/mol), suggesting that some of the mutations were interfering with one another. Based on analysis of the structural models of the mutations, we determined that interference between the αD26W and αG28T mutations was most likely the cause due to possible clash between their side chains. The mutations WFMMT, WFLMT, and WFIMT did not fold, indicating that mutations of αG28 to larger hydrophobic residues in combination with the other four mutations destabilize the folding of the TCR. We then restored α chain residue 28 to glycine to create the WFGMT mutant; this resulted in some positive cooperativity (−0.56 kcal/mol) and a 99 fold KD improvement over the wild-type TCR.
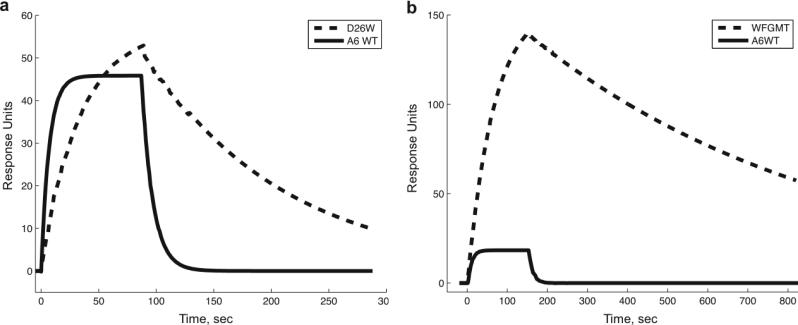
As with most of the single point mutations, the kinetics for the WFGMT mutant had a marked decrease in koff responsible for the majority of the affinity improvement. Figure 4 shows the sensorgram for this mutant, compared with the A6 wild-type and the αD26W point mutation. More detailed kinetics data for the wild-type and WFGMT TCRs are given in Figure S3.
Figure 4.
Biacore SPR sensorgrams for binding of Tax/HLA-A2 to designed and wild-type TCRs. In a), the binding for αD26W (dashed line) is compared with binding to wild-type (solid line) for Tax/HLA-A2 concentration of 40 μg/ml. In b), the binding of combined mutant αWFGMT (dashed line) is compared with wild-type (solid line), using Tax/HLA-A2 concentration of 10 μg/ml. Approximately 400 response units of TCR were immobilized for each experiment.
Mutant T Cell Receptor Specificity
To determine whether the engineered TCRs in this study have cross-reactivity with peptides other than Tax, we displayed three 9-mer peptides on HLA-A2 and tested the binding of these complexes to the wild-type A6 and WFGMT mutant TCR using Biacore. The peptides are known epitopes from the human immunodeficiency virus (HIV), with sequences SLYNTVATL, ILKEPVHGV, and VIYQYMDDL. None were found to bind either the wild-type or WFGMT TCR (sensorgrams not shown).
We additionally displayed the V7R point mutant of the Tax peptide (sequence, with mutation in bold, is LLFGYPRYV) on the HLA-A2 and tested its binding to the WFGMT TCR mutant using SPR (Table 6). The binding affinity of the wild-type A6 TCR for this peptide variant has already been characterized by SPR in another study, and found to be approximately 9.9-fold less than for the Tax peptide.34 Inspection of the crystal structure of the HLA-A2/TaxV7R/A6 TCR complex34 indicates that there are no significant changes in the interface of the TCR α chain with the MHC (though the TCR β chain has considerable movement on the CDR3 loop), thus the specificity for this peptide would not be expected to change significantly for the WFGMT mutant. Our measured specificity of the WFGMT mutant for the Tax peptide with respect to the V7R variant (Table 6) is 9.3-fold, close to that of the wild-type A6 TCR.
Table 6.
Binding kinetics and specificity of WFGMT TCR mutant for HLA-A2 with Tax peptide and V7R point mutant of Tax peptide.
| peptide | ka, ×104 M−1S-1 | kd, ×10−3 s−1 | KD, nM | ΔΔG, kcal/mol | Specificity1 |
|---|---|---|---|---|---|
| Tax | 6.32 | 1.35 | 21.4 | −2.72 ± 0.10 | NA |
| V7R | 1.14 | 2.28 | 200 | −1.40 ± 0.21 | 9.3 |
Fold change in KD with respect to Tax peptide.
Discussion
This study shows the use of structure-based design to significantly enhance the affinity of a T cell receptor for its peptide-MHC. The final design protocol, named ZAFFI, combines the structural modeling of Rosetta with a novel scoring function that includes shape complementarity and desolvation terms. These terms were found to be optimal after a systematic evaluation of many possible sets of terms, including electrostatics, hydrogen bonding, and several statistical potentials. We successfully utilized this function, which was selected based on initial data from this system, to predict new mutations that improved binding affinity.
To complement the scoring function, ZAFFI also uses a filter that includes hydrogen bonding and electrostatics terms to remove false positive non-binders. As with the scoring function terms, these terms were found to be optimal after systematic evaluation of possible filter terms on an initial of TCR mutations. An earlier protein design study also used satisfaction of hydrogen bonds as a filter, as part of a design function to engineer receptor proteins.35
We chose a conservative approach toward structural modeling of point mutations. We repacked the mutant side chain using Rosetta, without moving the backbone or neighboring side chains. It is possible that this led to some overlooked substitutions that improve binding (false negatives), of which the conformations require side chain and/or backbone rearrangement. However, the focus of this study was to limit false positive predictions while reliably predicting some true positives, and it can be seen in Table 1 that we were still able to identify many candidate mutations that improved binding.
The mutations that improved TCR binding affinity in this study were hydrophobic substitutions that increased interface complementarity without losing crucial electrostatic contacts. The improvement of complementarity and hydrophobic packing can be seen in Table 3, with the Lazaridis-Karplus solvation and ACE terms, which both reward hydrophobic packing, having the highest correlations with measured energies among all terms considered (including electrostatics). This is also seen when analyzing the individual energetic terms for the mutants (Supplemental Table 1); of 11 mutations with significant measured affinity improvements, all of them featured improvements in both the van der Waals attractive and ACE terms. To complement the scoring function, the filter function ensured no loss of significant electrostatic interactions, by including the hydrogen bonding and long-range electrostatics terms.
One recent study has found that the hydrophobic residues tryptophan, methionine, and phenylalanine (W, M, and F) are the most highly conserved of all residues in protein-protein binding sites,36 thus are key components in naturally evolved binding interfaces. A phage display-derived TCR mutant against another pepMHC also had hydrophobic substitutions, including a CDR2α substitution of QSS to PFW.4 These highlight the usefulness of hydrophobic substitutions in protein interfaces, in particular for T cell receptors where electrostatics may not the major contributor to the affinity (versus, for instance, the barnase-barstar complex which is highly electrostatic in nature37). In our structure-based design approach, we are able to select the hydrophobic substitutions that improve binding with a high specificity. For instance, αQ30W, αS100Y, and αG28V all bind with lower affinity than wild-type and are correctly identified by ZAFFI as poor binders by either the filter or scoring function.
In contrast with the ZAFFI scoring function, the study of Lippow et al. found that electrostatics was the most useful term in their computational design of antibodies.13 They additionally found that “problematic designs were at the binding site periphery”, in particular for large residue substitutions with favorable van der Waals. They explored a more advanced formulation of the solvation using a continuum van der Waals model38 reducing the “magnitude of favorable prediction” for some false positives but still yielding incorrect predictions. In our case, we identified two mutations of large residues, αD26W and αR27F, near the periphery that improved binding significantly (both are part of the quadruple mutation WFGMT). However, we failed to identify mutations that significantly improved the electrostatics (based on our scoring terms and also the relative lack of experimental association rate changes). The differences between the successful residue substitutions seen in these two studies may reflect the computational accuracies of their scoring functions for the terms of interest, or the structural and physicochemical differences between the systems being designed (antibodies and the T cell receptor).
Interestingly, during preparation of this manuscript, another structure-based design study was published that focused on substitutions from polar to nonpolar residues while not losing electrostatics contacts.39 This protocol was utilized to predict single residue substitutions for two (non-immunoglobulin) systems, Gαi1-RGS14 and UBCH7-E6AP, with successful results when tested experimentally. Our scoring function, developed for optimization of a very different interface, employs a similar overall scoring strategy; the independent development of such strategies for such different systems highlights the effectiveness of such a design method. However, clear differences in the studies exist: our current study, for instance, uses the statistical potential ACE, and estimates the ΔΔG (resulting in a strong correlation with measured values) rather than making binary predictions for whether the mutation will improve binding.
Consistent with the hydrophobic substitutions, the binding improvements seen in this study are largely due to decreases in the off-rate. The correlation between the energy contribution from off-rate and total energy change is 0.87, while this correlation for the on-rate is 0.15 (Figure 2). Decreased off-rate has also been seen as the means of TCR affinity improvement via randomized libraries.3,4 The off-rate, which is directly related to the half life of the TCR binding, is known to be related to the functional importance of the TCR signaling.40
The results from combining point mutations indicate the complex nature of affinity improvement and protein binding energetics. We observed dramatic negative cooperativity in the case of WFTMT (likely due to intra-chain van der Waals clash), and some positive cooperativity in the case of WFGMT. Another study noted significant cooperativity when mutating another TCR (based on a phage display mutant), both within and between clusters of residues (referred to as “hot regions”).41 We also observed that the β chain point mutations that we tested indicate that the phage display derived mutations for the A6 TCR from Li et al. have significant positive cooperativity. In our case, it is unclear whether the cooperativity of −0.56 kcal/mol for the WFGMT mutant arises from within a hot region (residues 26−27) or between regions (involving the more distant residues 51 and 100) on the alpha chain. Although the structural modeling indicated possible clash leading to the WFTMT negative cooperativity, the modeling protocol did not predict the positive cooperativity of WFGMT (it predicted energetic additivity). It should be noted that the cooperativity of −0.56 kcal/mol is less than the cutoff for being labeled “cooperative” in other studies,13,41 thus, given that its magnitude is relatively small, the structural and energetic factors underlying this may be somewhat subtle. Further experimental testing of combinations of mutations at these positions should provide more insight and can aid in adapting the modeling procedure to explain these mutants.
To complement our testing of affinity improvement for the Tax peptide, we also tested whether the structure-based design against the Tax peptide structure would reduce or eliminate specificity for several HLA-A2 binding peptides. As the mutants D26W, R27F, and S51M primarily contact the MHC in the structural models, it was important to confirm that the WFGMT mutant would still preferentially bind the Tax peptide over peptide variants. Notably, the specificity of the WFGMT TCR for the V7R Tax variant was found to be approximately the same as what is measured for the A6 wild-type, and there was no binding to other peptides tested for either wild-type or WFGMT TCRs. TCR mutants that have been optimized by phage display have been shown to maintain some peptide specificity as well.5 This includes the A6 TCR CDR3β variant from Li et al.3 which was tested for binding two HLA-A2/peptide complexes known to cross-react with the A6 TCR and found to have somewhat greater specificity than the wild-type.42 Based on the crystal structure of the wild-type A6 TCR complex with HLA-A2/Tax,16 the specificity increase in that case may have been due to contacts between mutant CDR3β residues and the peptide at positions where peptide residues varied from Tax.
Future work includes application of the ZAFFI algorithm for specificity enhancement and application to other systems. This includes designing the A6 TCR against other peptides bound to the HLA-A2 MHC, using either crystal structures (e.g. the complexes with Tax mutants described by Ding et al.34) or in silico modeling of peptides based on existing structures. Additionally, crystallization of the complexes of the TCR combination mutants described in Table 5 would yield information on detailed structural changes in these high affinity mutations (as has been performed for in vitro matured TCRs4,43,44), and could explain the basis of the cooperativity and noncooperativity observed in our tested mutations. Structure-based design of other protein receptors using approaches similar to our study can yield more effective therapeutics than the wild-type molecules, and can also be used to further improve interfaces that have been optimized using in vitro selection methods.
Supplementary Material
Figure S1. Scores versus experimentally measured ΔΔG values for Rosetta (top) and ZAFFI (bottom) for the set of 648 OMTKY point mutations used in ZAFFI training. For the top plot, two outlier points with high scores are not shown in the figure. Dotted lines representing linear fits are shown; correlations are 0.31 for Rosetta and 0.58 for ZAFFI.
Figure S2. Scoring term value versus measured ΔΔG for the 26 measured TCR point mutations presented in this study. The scoring terms are: van der Waals attractive (upper left), ACE (upper right), hydrogen bonding (lower left), and long-range electrostatics (lower right).
Figure S3. Sensorgrams for the (a) A6 wild-type and (b) WFGMT TCRs binding to the tax/HLA-A2 complex. Fit residuals are shown below the sensorgrams. Fits were produced using BIAevaluation software with a Langmuir 1:1 binding model. Approximately 400 RUs of TCR were immobilized for each experiment, and tax/HLAA2 concentrations of (a) 0.9 μM, 0.84 μM, 0.785 μM, 0.45 μM, 0.42 μM, 0.3925 μM, 0.225 μM, 0.21 μM, 0.192625 μM and (b) 0.45 μM, 0.42 μM, 0.225 μM, 0.21 μM, 0.1125 μM, 0.105 μM, 0.098125 μM were injected over the surface.
Acknowledgements
The authors would like to thank Professor Michael Laskowski for generously providing the dataset of affinities for the mutant OMTKY molecules and Professor Brian Baker for the T cell receptor constructs. Additionally, Julian Mintseris, Kevin Wiehe, and Howook Hwang provided the authors with helpful discussions. We are grateful to the Scientific Computing Facilities at Boston University and the Advanced Biomedical Computing Center at NCI, NIH for computing resources, and Mary Ellen Fitzpatrick for computing support. This work was funded by NSF grants DBI-0078194, DBI-0133834 and DBI-0116574.
References
- 1.Immunobiology 5 : the immune system in health and disease. xviii. Garland Pub.; Janeway C. New York: 2001. p. 732. [Google Scholar]
- 2.Holler PD, Holman PO, Shusta EV, O'Herrin S, Wittrup KD, Kranz DM. In vitro evolution of a T cell receptor with high affinity for peptide/MHC. Proc Natl Acad Sci U S A. 2000;97(10):5387–5392. doi: 10.1073/pnas.080078297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Li Y, Moysey R, Molloy PE, Vuidepot AL, Mahon T, Baston E, Dunn S, Liddy N, Jacob J, Jakobsen BK, Boulter JM. Directed evolution of human T-cell receptors with picomolar affinities by phage display. Nat Biotechnol. 2005;23(3):349–354. doi: 10.1038/nbt1070. [DOI] [PubMed] [Google Scholar]
- 4.Dunn SM, Rizkallah PJ, Baston E, Mahon T, Cameron B, Moysey R, Gao F, Sami M, Boulter J, Li Y, Jakobsen BK. Directed evolution of human T cell receptor CDR2 residues by phage display dramatically enhances affinity for cognate peptide-MHC without increasing apparent cross-reactivity. Protein Sci. 2006;15(4):710–721. doi: 10.1110/ps.051936406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chlewicki LK, Holler PD, Monti BC, Clutter MR, Kranz DM. High-affinity, peptide-specific T cell receptors can be generated by mutations in CDR1, CDR2 or CDR3. J Mol Biol. 2005;346(1):223–239. doi: 10.1016/j.jmb.2004.11.057. [DOI] [PubMed] [Google Scholar]
- 6.Dufner P, Jermutus L, Minter RR. Harnessing phage and ribosome display for antibody optimisation. Trends Biotechnol. 2006;24(11):523–529. doi: 10.1016/j.tibtech.2006.09.004. [DOI] [PubMed] [Google Scholar]
- 7.Selzer T, Albeck S, Schreiber G. Rational design of faster associating and tighter binding protein complexes. Nat Struct Biol. 2000;7(7):537–541. doi: 10.1038/76744. [DOI] [PubMed] [Google Scholar]
- 8.Song G, Lazar GA, Kortemme T, Shimaoka M, Desjarlais JR, Baker D, Springer TA. Rational design of intercellular adhesion molecule-1 (ICAM-1) variants for antagonizing integrin lymphocyte function-associated antigen-1-dependent adhesion. J Biol Chem. 2006;281(8):5042–5049. doi: 10.1074/jbc.M510454200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Joachimiak LA, Kortemme T, Stoddard BL, Baker D. Computational design of a new hydrogen bond network and at least a 300-fold specificity switch at a protein-protein interface. J Mol Biol. 2006;361(1):195–208. doi: 10.1016/j.jmb.2006.05.022. [DOI] [PubMed] [Google Scholar]
- 10.Kortemme T, Joachimiak LA, Bullock AN, Schuler AD, Stoddard BL, Baker D. Computational redesign of protein-protein interaction specificity. Nat Struct Mol Biol. 2004;11(4):371–379. doi: 10.1038/nsmb749. [DOI] [PubMed] [Google Scholar]
- 11.Cole DK, Rizkallah PJ, Boulter JM, Sami M, Vuidepot AL, Glick M, Gao F, Bell JI, Jakobsen BK, Gao GF. Computational design and crystal structure of an enhanced affinity mutant human CD8 alphaalpha coreceptor. Proteins. 2007;67(1):65–74. doi: 10.1002/prot.21176. [DOI] [PubMed] [Google Scholar]
- 12.Clark LA, Boriack-Sjodin PA, Eldredge J, Fitch C, Friedman B, Hanf KJ, Jarpe M, Liparoto SF, Li Y, Lugovskoy A, Miller S, Rushe M, Sherman W, Simon K, Van Vlijmen H. Affinity enhancement of an in vivo matured therapeutic antibody using structure-based computational design. Protein Sci. 2006;15(5):949–960. doi: 10.1110/ps.052030506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lippow SM, Wittrup KD, Tidor B. Computational design of antibody-affinity improvement beyond in vivo maturation. Nat Biotechnol. 2007;25(10):1171–1176. doi: 10.1038/nbt1336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Baker BM, Ding YH, Garboczi DN, Biddison WE, Wiley DC. Structural, biochemical, and biophysical studies of HLA-A2/altered peptide ligands binding to viral-peptide-specific human T-cell receptors. Cold Spring Harb Symp Quant Biol. 1999;64:235–241. doi: 10.1101/sqb.1999.64.235. [DOI] [PubMed] [Google Scholar]
- 15.Davis-Harrison RL, Insaidoo FK, Baker BM. T cell receptor binding transition states and recognition of peptide/MHC. Biochemistry. 2007;46(7):1840–1850. doi: 10.1021/bi061702p. [DOI] [PubMed] [Google Scholar]
- 16.Garboczi DN, Ghosh P, Utz U, Fan QR, Biddison WE, Wiley DC. Structure of the complex between human T-cell receptor, viral peptide and HLA-A2. Nature. 1996;384(6605):134–141. doi: 10.1038/384134a0. [DOI] [PubMed] [Google Scholar]
- 17.Bruccoleri RE. Application of Systematic Conformational Search to Protein Modeling. Molecular Simulation. 1993;10(2):151–174. [Google Scholar]
- 18.Bruccoleri RE, Karplus M. Prediction of the folding of short polypeptide segments by uniform conformational sampling. Biopolymers. 1987;26(1):137–168. doi: 10.1002/bip.360260114. [DOI] [PubMed] [Google Scholar]
- 19.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. Journal of Computational Chemistry. 1983;4:187–217. [Google Scholar]
- 20.Kortemme T, Baker D. A simple physical model for binding energy hot spots in protein-protein complexes. Proc Natl Acad Sci U S A. 2002;99(22):14116–14121. doi: 10.1073/pnas.202485799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pierce B, Weng Z. ZRANK: reranking protein docking predictions with an optimized energy function. Proteins. 2007;67(4):1078–1086. doi: 10.1002/prot.21373. [DOI] [PubMed] [Google Scholar]
- 22.Neria E, Fischer S, Karplus M. Simulation of activation free energies in molecular systems. The Journal of Chemical Physics. 1996;105(5):1902–1921. [Google Scholar]
- 23.Gray JJ, Moughon S, Wang C, Schueler-Furman O, Kuhlman B, Rohl CA, Baker D. Protein-protein docking with simultaneous optimization of rigid-body displacement and side-chain conformations. J Mol Biol. 2003;331(1):281–299. doi: 10.1016/s0022-2836(03)00670-3. [DOI] [PubMed] [Google Scholar]
- 24.Zhang C, Vasmatzis G, Cornette JL, DeLisi C. Determination of atomic desolvation energies from the structures of crystallized proteins. J Mol Biol. 1997;267(3):707–726. doi: 10.1006/jmbi.1996.0859. [DOI] [PubMed] [Google Scholar]
- 25.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucleic Acids Res. 2000;28(1):235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Li L, Chen R, Weng Z. RDOCK: refinement of rigid-body protein docking predictions. Proteins. 2003;53(3):693–707. doi: 10.1002/prot.10460. [DOI] [PubMed] [Google Scholar]
- 27.Murphy J, Gatchell DW, Prasad JC, Vajda S. Combination of scoring functions improves discrimination in protein-protein docking. Proteins. 2003;53(4):840–854. doi: 10.1002/prot.10473. [DOI] [PubMed] [Google Scholar]
- 28.Lazaridis T, Karplus M. Effective energy function for proteins in solution. Proteins-Structure Function and Genetics. 1999;35(2):133–152. doi: 10.1002/(sici)1097-0134(19990501)35:2<133::aid-prot1>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 29.Mintseris J, Pierce B, Wiehe K, Anderson R, Chen R, Weng Z. Integrating statistical pair potentials into protein complex prediction. Proteins. 2007 doi: 10.1002/prot.21502. [DOI] [PubMed] [Google Scholar]
- 30.Zhou H, Zhou Y. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci. 2002;11(11):2714–2726. doi: 10.1110/ps.0217002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Garboczi DN, Utz U, Ghosh P, Seth A, Kim J, VanTienhoven EA, Biddison WE, Wiley DC. Assembly, specific binding, and crystallization of a human TCR-alphabeta with an antigenic Tax peptide from human T lymphotropic virus type 1 and the class I MHC molecule HLA-A2. J Immunol. 1996;157(12):5403–5410. [PubMed] [Google Scholar]
- 32.Garboczi DN, Hung DT, Wiley DC. HLA-A2-peptide complexes: refolding and crystallization of molecules expressed in Escherichia coli and complexed with single antigenic peptides. Proc Natl Acad Sci U S A. 1992;89(8):3429–3433. doi: 10.1073/pnas.89.8.3429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Borg NA, Ely LK, Beddoe T, Macdonald WA, Reid HH, Clements CS, Purcell AW, Kjer-Nielsen L, Miles JJ, Burrows SR, McCluskey J, Rossjohn J. The CDR3 regions of an immunodominant T cell receptor dictate the ‘energetic landscape’ of peptide-MHC recognition. Nat Immunol. 2005;6(2):171–180. doi: 10.1038/ni1155. [DOI] [PubMed] [Google Scholar]
- 34.Ding YH, Baker BM, Garboczi DN, Biddison WE, Wiley DC. Four A6-TCR/peptide/HLA-A2 structures that generate very different T cell signals are nearly identical. Immunity. 1999;11(1):45–56. doi: 10.1016/s1074-7613(00)80080-1. [DOI] [PubMed] [Google Scholar]
- 35.Looger LL, Dwyer MA, Smith JJ, Hellinga HW. Computational design of receptor and sensor proteins with novel functions. Nature. 2003;423(6936):185–190. doi: 10.1038/nature01556. [DOI] [PubMed] [Google Scholar]
- 36.Ma B, Nussinov R. Trp/Met/Phe hot spots in protein-protein interactions: potential targets in drug design. Curr Top Med Chem. 2007;7(10):999–1005. doi: 10.2174/156802607780906717. [DOI] [PubMed] [Google Scholar]
- 37.Lee LP, Tidor B. Barstar is electrostatically optimized for tight binding to barnase. Nat Struct Biol. 2001;8(1):73–76. doi: 10.1038/83082. [DOI] [PubMed] [Google Scholar]
- 38.Levy RM, Zhang LY, Gallicchio E, Felts AK. On the nonpolar hydration free energy of proteins: surface area and continuum solvent models for the solute-solvent interaction energy. J Am Chem Soc. 2003;125(31):9523–9530. doi: 10.1021/ja029833a. [DOI] [PubMed] [Google Scholar]
- 39.Sammond DW, Eletr ZM, Purbeck C, Kimple RJ, Siderovski DP, Kuhlman B. Structure-based protocol for identifying mutations that enhance protein-protein binding affinities. J Mol Biol. 2007;371(5):1392–1404. doi: 10.1016/j.jmb.2007.05.096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cole DK, Pumphrey NJ, Boulter JM, Sami M, Bell JI, Gostick E, Price DA, Gao GF, Sewell AK, Jakobsen BK. Human TCR-binding affinity is governed by MHC class restriction. J Immunol. 2007;178(9):5727–5734. doi: 10.4049/jimmunol.178.9.5727. [DOI] [PubMed] [Google Scholar]
- 41.Moza B, Buonpane RA, Zhu P, Herfst CA, Rahman AK, McCormick JK, Kranz DM, Sundberg EJ. Long-range cooperative binding effects in a T cell receptor variable domain. Proc Natl Acad Sci U S A. 2006;103(26):9867–9872. doi: 10.1073/pnas.0600220103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Laugel B, Boulter JM, Lissin N, Vuidepot A, Li Y, Gostick E, Crotty LE, Douek DC, Hemelaar J, Price DA, Jakobsen BK, Sewell AK. Design of soluble recombinant T cell receptors for antigen targeting and T cell inhibition. J Biol Chem. 2005;280(3):1882–1892. doi: 10.1074/jbc.M409427200. [DOI] [PubMed] [Google Scholar]
- 43.Cho S, Swaminathan CP, Yang J, Kerzic MC, Guan R, Kieke MC, Kranz DM, Mariuzza RA, Sundberg EJ. Structural basis of affinity maturation and intramolecular cooperativity in a protein-protein interaction. Structure. 2005;13(12):1775–1787. doi: 10.1016/j.str.2005.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sami M, Rizkallah PJ, Dunn S, Molloy P, Moysey R, Vuidepot A, Baston E, Todorov P, Li Y, Gao F, Boulter JM, Jakobsen BK. Crystal structures of high affinity human T-cell receptors bound to peptide major histocompatibility complex reveal native diagonal binding geometry. Protein Eng Des Sel. 2007;20(8):397–403. doi: 10.1093/protein/gzm033. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Scores versus experimentally measured ΔΔG values for Rosetta (top) and ZAFFI (bottom) for the set of 648 OMTKY point mutations used in ZAFFI training. For the top plot, two outlier points with high scores are not shown in the figure. Dotted lines representing linear fits are shown; correlations are 0.31 for Rosetta and 0.58 for ZAFFI.
Figure S2. Scoring term value versus measured ΔΔG for the 26 measured TCR point mutations presented in this study. The scoring terms are: van der Waals attractive (upper left), ACE (upper right), hydrogen bonding (lower left), and long-range electrostatics (lower right).
Figure S3. Sensorgrams for the (a) A6 wild-type and (b) WFGMT TCRs binding to the tax/HLA-A2 complex. Fit residuals are shown below the sensorgrams. Fits were produced using BIAevaluation software with a Langmuir 1:1 binding model. Approximately 400 RUs of TCR were immobilized for each experiment, and tax/HLAA2 concentrations of (a) 0.9 μM, 0.84 μM, 0.785 μM, 0.45 μM, 0.42 μM, 0.3925 μM, 0.225 μM, 0.21 μM, 0.192625 μM and (b) 0.45 μM, 0.42 μM, 0.225 μM, 0.21 μM, 0.1125 μM, 0.105 μM, 0.098125 μM were injected over the surface.