An Evaluation of Psychophysical Models of Auditory Change Perception

Abstract

In many psychophysical experiments, the participant's task is to detect small changes along a given stimulus dimension, or to identify the direction (e.g., upward vs. downward) of such changes. The results of these experiments are traditionally analyzed using a constant-variance Gaussian (CVG) model or a high-threshold (HT) model. Here, the authors demonstrate that for changes along three basic sound dimensions (frequency, intensity, and amplitude-modulation rate), such models cannot account for the observed relationship between detection thresholds and direction-identification thresholds. It is shown that two alternative models can account for this relationship. One of them is based on the idea of sensory “quanta”; the other assumes that small changes are detected on the basis of Poisson processes with low means. The predictions of these two models are then compared against receiver operating characteristics (ROCs) for the detection of changes in sound intensity. It is concluded that human listeners' perception of small and unidimensional acoustic changes is better described by a discrete-state Poisson model than by the more commonly used CVG model or by the less favored HT and quantum models.

An Evaluation of Psychophysical Models of Auditory Change Perception

Detecting simple differences or “unidimensional changes” between sensory stimuli (e.g., changes in brightness or loudness) and identifying the direction of these changes (e.g., upward vs. downward) are two fundamental perceptual abilities. How these abilities are related to one another is an important question for psychophysicists. The answer has both theoretical and practical implications. An important practical implication relates to the choice of psychophysical paradigm for measuring just-noticeable differences (JNDs) between stimuli. In auditory psychophysics, for instance, the two-interval two-alternative forced-choice (2I2AFC) paradigm has been commonly used to measure JNDs for various sound dimensions. However, JNDs are usually defined as the smallest stimulus differences that an individual can detect with a certain level of accuracy (e.g., 70% correct). In contrast, the 2I2AFC paradigm requires from the participant that he/she identifies the relative positions of the two presented stimuli along some sensory dimension, or equivalently, that he/she identifies the direction of the stimulus change. Thus, interpretations of 2I2AFC thresholds in terms of “JNDs” rest (in most cases, implicitly) on the assumption that thresholds for the identification of the direction of sensory changes are closely related to thresholds for the detection of those changes. Specifically, it is commonly assumed that an individual's ability to identify the direction of simple sensory changes is limited solely by that individual's ability to detect those changes, or that as soon as a change has been detected, its direction can be identified.

Clearly, this assumption is not always warranted. For instance, Semal and Demany (2006) recently identified listeners who could detect relatively small changes in frequency (subjectively, pitch) between consecutive tones, but required changes approximately one order of magnitude larger in order to correctly identify their direction. Similar findings were obtained by Johnsrude et al. (2000) in individuals with auditory-cortex lesions. Another example of dissociation between change detection and change-direction identification was provided by experiments concerning the perception of transient intensity changes in a continuous sound (Macmillan, 1971, 1973; Hafter et al., 1998; Gallun, 2003). These experiments revealed that listeners are able to detect transient intensity changes using a cue which provides no information regarding change direction.

Although these findings show that, in some cases, detecting a change is not sufficient for the identification of its direction, they represent exceptions. More generally, experimental data in the auditory perception¹ literature are consistent with the view that the ability to identify the direction of changes in sound frequency or sound intensity is limited only by the ability to detect these changes. Some information relevant to that issue comes from studies in which frequency and/or intensity discrimination thresholds measured using a 2I2AFC task (which required from participants that they identify the direction of stimulus change) were compared with thresholds measured in the same participants using a “same-different” (or AX)² task (which required the detection of a change but not the identification of its direction). The authors of such experiments (Creelman & Macmillan, 1979; Jesteadt & Bilger, 1974; Jesteadt & Sims, 1975) intended to determine whether this relationship was consistent with the predictions of the standard constant-variance Gaussian (CVG) psychophysical model from signal detection theory (Green & Swets, 1966; Macmillan & Creelman, 2005; Wickens, 2001). In this model, the presentation of a stimulus is assumed to evoke a sensory observation contaminated by Gaussian internal noise with zero mean and constant variance. Under the assumption that performance in the 2I2AFC and AX tasks is limited by the same internal noise, and that the listener's decision strategy is optimal in the likelihood-ratio sense, the model predicts that the paradigm-independent index of sensitivity d′, defined as the standardized distance between the means of the probability density functions corresponding to the two stimulus classes that must be discriminated, should be the same in the two tasks. As it turns out, the mean d′ ratio (d′ in the AX task over d′ in the 2I2AFC task) measured across several studies (Creelman & Macmillan, 1979; Jesteadt & Bilger, 1974; Jesteadt & Sims, 1975; see also the compact summary of these studies in Macmillan and Creelman, 2005, p. 182) is approximately equal to 0.8. This ratio, smaller than 1, is obviously consistent with the idea that the ability to identify the direction of sensory changes is limited only by the ability to detect these changes. On the other hand, the reason why the ratio differs from 1 is not clear. One possibility is that listeners had difficulties in using a stable response criterion in the AX task. Another possibility, which is more interesting, is that the CVG model does not describe adequately how human listeners detect simple auditory changes.

The theoretical work reported here used detailed measurements of auditory change-detection and change-direction-identification thresholds in order to test several psychophysical models of auditory change detection. The considered acoustic changes were unidimensional and it was reasonable to assume that, as soon as they were detectable, their direction could be identified; for these changes, in other words, a warranted assumption was that detection and direction identification merely represented different decision rules applied to the same sensory information (Thomas, 1985; Thomas, Gille, & Barker, 1982). The analyzed data were collected using a “dual-pair” psychophysical paradigm. This paradigm allowed change-detection and change-direction-identification thresholds to be measured using the same stimulus design, and it had the advantage of alleviating some of the concerns usually associated with the two-interval same-different (AX) design.

The outline of this note is as follows. First, the dual-pair psychophysical paradigm that was used to collect the experimental data is briefly described. Then, the predictions of two “classic” psychophysical models (the CVG model and the high-threshold model) regarding the relationship between change-detection thresholds and change-direction-identification thresholds in the considered paradigm are derived. In the third section, these predictions are compared to the experimental data. In the fourth section, ways in which the CVG model may be reconciled with the data are explored. The fifth section is devoted to exploring alternative models, and it shows that two models, respectively assuming quantized-Gaussian (Stevens, 1972; Stevens, Morgan, & Volkmann, 1941; Stevens & Volkmann, 1940) and Poisson-distributed (Kaernbach, 1991a) decision variables, can account for the experimental data. Finally, the relative merits of the two latter models are discussed.

The Dual-Pair Paradigm

The experimental data that provide the empirical basis for this note were collected using a four-interval stimulus design, also known as “dual pair”. As the name indicates, in this design, two pairs of stimuli are presented on each trial. In one of the two pairs the stimuli are identical, in the other they are different; for brevity, we will refer to these pairs as the “same” pair and the “different” pair. The order of presentation of the two pairs is randomized, each of the two possible orderings being as likely (a priori) as the other. In the “different” pair, the change between the first and second stimulus can be either “upward” (e.g., the second tone has a higher intensity than the first) or “downward”, with equal probability. This dual-pair stimulus design can be used to measure change detection and change-direction identification, the only difference being in the instructions given to the subject. In the change-detection (D) task, the subject is asked to indicate which of the two pairs contained different stimuli. In the change-direction-identification (I) task, the subject must report in which direction the stimuli in the “different” pair changed.

The dual pair design makes it possible to measure both change detection and change-direction identification using the same stimulus design while avoiding (or at least, alleviating) concerns regarding the influence of bias on performance. In this respect, this four-interval design is superior to the more popular two-interval AX paradigm for measuring change detection, because the two-interval AX is notoriously susceptible to bias. In fact, the dual-pair design can be thought as a two-interval AX design “embedded into” a 2I2AFC design (Noreen, 1981).

In addition to these general features, the model predictions derived below take the following methodological features into account. Firstly, the frequency (or AM rate) of the first stimulus in each pair was randomized independently from that in the other pair. This technique, known as “roving” in the auditory psychophysics literature, is frequently used in order to discourage participants from comparing individual stimuli across the two pairs. When, as was the case here, the roving range is large compared to the measured thresholds, listeners are forced to rely on perceived differences between the stimuli in each pair, rather than on comparisons of individual stimuli across pairs, across trials, or with a fixed internal reference in memory. Secondly, thresholds in the D and I tasks were measured using an adaptive procedure, which tracked the 75%-correct point on the psychometric function (Kaernbach, 1991b). Finally, in order to avoid some of the difficulties inherent to double-judgment psychophysics (Klein, 1985), the D and I thresholds were not tested simultaneously, but in separate blocks of trials, intermingled within each test session.

Under those methodological circumstances, what do “classic” psychophysical models predict regarding the relationship between thresholds in the D and I tasks?

Predictions of the CVG Model and the High-Threshold Model

The CVG Model

Gaussian signal-detection theory posits the existence of a continuum of sensory observations, contaminated by normally distributed internal noise (Green & Swets, 1966). The most common instantiation of this theory, the CVG model, further assumes that the variance of the internal noise is constant, i.e., that it is the same for all observations and does not vary over time. In addition, the Gaussian internal noises added to the observations are assumed to be uncorrelated, i.e., statistically independent.

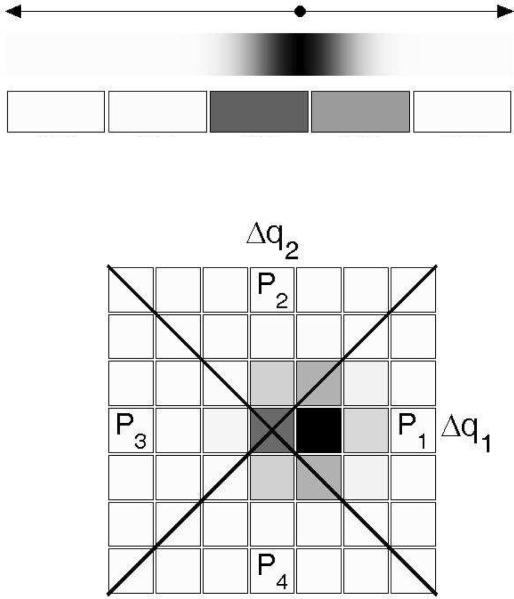
Since the dual-pair design described above involves the presentation of four stimuli on each trial, each stimulus yielding one observation, the decision space for this paradigm is four-dimensional. However, in the experiments considered here, wide across-pair roving was used in order to prevent listeners from taking advantage of comparisons between individual observations across the two pairs. With such roving, we can assume that the observer derives no significant information from the absolute positions of the observations, or from comparisons between single observations in different pairs; only the relative positions of, or the differences between the observations within each pair are relevant (Dai, Versfeld, & Green, 1996; Macmillan, Kaplan, & Creelman, 1977; Noreen, 1981; Macmillan & Creelman, 2005). Therefore, there is no significant loss of information in reducing the decision space to two axes corresponding to the signed differences between the observations in each pair. Denoting the four observations made consecutively on each trial by y₁₁, y₁₂, y₂₁, and y₂₂, in that order, we can plot the difference Δy₁ = y₁₂^- y₁₁ (first pair) along the X-axis, and the difference Δy₂ = y₂₂^- y₂₁ (second pair) along the Y-axis of a Cartesian plane.

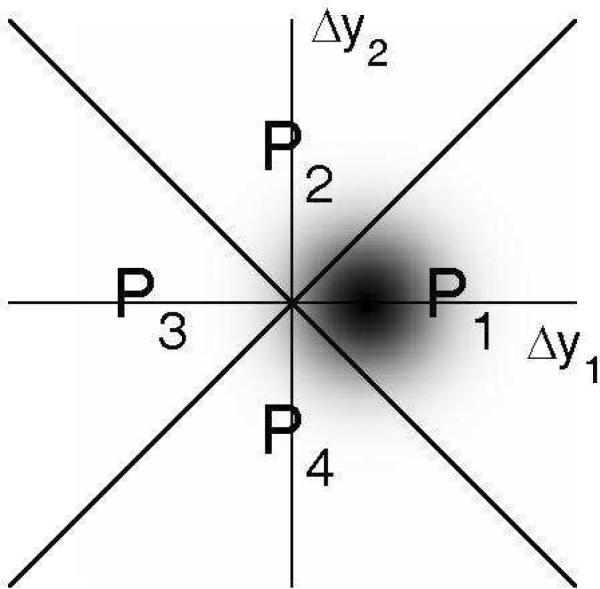
Figure 1 provides a schematic illustration, in this decision space, of the two-dimensional conditional probability density function (PDF) of the difference variables, Δy₁ and Δy₂, conditioned on the “different” pair being presented first, and on the change being “upward”; accordingly, the bi-dimensional Gaussian PDF has a positive mean along axis Δy₁ and a zero mean along axis Δy₂.³ It is easy to imagine what the conditional PDFs for the other three possible stimulus configurations look like.

Figure 1.

Schematic illustration of the decision space for the dual-pair detection and identification tasks, according to the CVG model. Differences between the two observations from the first pair, y₁₂ - y₁₁, are plotted along the Δy₁ axis. Differences between the two observations from the second pair, y₂₂ - y₂₁, are plotted along the Δy₂ axis. The four quadrants (labeled P1 to P4) delimited by the major and minor diagonals correspond to different decision regions, as explained in the text. The fuzzy patch represents the two-dimensional probability density function (PDF) of the decision variables (with darker areas corresponding to regions of higher probability density) for trials in which the first pair contained an upward change; accordingly, the mean is positive along the Δy₁ axis and zero along the Δy₂ axis. In this example, the mean of the PDF along the Δy₁ axis was chosen so that the probability mass over quadrants P1 and P3 was equal to 0.75, the targeted probability of a correct response in the detection (D) task in the psychophysical experiments described in the text.

The correct-response probabilities in the D and I tasks can be found by integrating the conditional PDFs of the decision variables over regions of the decision space that correspond to a correct response. These regions depend on the decision rule used by the observer for task performance. An ideal observer uses optimal decision rules, i.e., rules that maximize the probability of a correct response, given the constraints. For the D task with wide across-pair roving, the optimal decision rule consists in selecting the pair for which the magnitude (i.e., absolute value) of the difference between the observations is largest (Macmillan, Kaplan, & Creelman, 1977; Noreen, 1981; Rousseau & Ennis, 2001). According to this rule, the observer chooses pair 1 if the point defined by the differences between the observations in each pair falls inside quadrant P1 or P3, and pair 2 if it falls inside quadrant P2 or P4. Therefore, under the CVG model, the probability of a correct response in the D task can be calculated as the integral, over the region corresponding to quadrants P1 and P3, of the joint PDF shown in Figure 1, which corresponds to the case in which an upward change occurred in the first pair.⁴ Macmillan et al. (1977; see also Micheyl & Messing, 2006) provided a formula for this integral as a function of d′; this equation is:

$$P{C}_{DCVG}={\left[\varphi \left(\frac{d^{\prime }}{2}\right)\right]}^2+{\left[1-\varphi \left(\frac{d^{\prime }}{2}\right)\right]}^2$$ (1)

where PC_DCVG denotes the proportion of correct responses in the detection task under the CVG model, and Φ(x) denotes the cumulative standard normal function, defined as the integral from -∞ to x of the Gaussian function with zero mean and unit variance. The converse equation, which gives d′ as a function of PC_DCVG is:

$$d^{\prime }2{\varphi }^{-1}\left(\frac{1}{2}+\sqrt{\frac{P{C}_{DCVG}}{2}-\frac{1}{4}}\right)$$ (2)

where Φ^-1 denotes the inverse cumulative standard normal function. According to this equation, when PC_DVG equals 0.75 (the probability of correct responses corresponding to threshold in the experimental data used here), d′ in the D task equals approximately 2.10.

For the I task, an intuitive strategy is to select the pair in which the magnitude of the difference between the two observations is largest, and to respond “up” if the signed difference between these observations is positive, and “down” otherwise. Going through the four quadrants of Figure 1, which illustrates the PDF of the decision variables for the case of an upward change in the first pair, we find that correct responses will occur in this case whenever the point (Δy₁, Δy₂) falls in the half-plane formed by the quadrants P1 and P2. Thus, the decision rule may be reformulated as follows: respond “up” if Δy₁ > -Δy₂; otherwise, respond “down”. Note that this can be rewritten as: respond “up” if Δy₁ + Δy₂ > 0, providing another description of the same decision rule. As it turns out, this decision rule is optimal in a likelihood-ratio sense. Using this decision rule, we can derive the probability of responding correctly in the I task under the CVG model; it is

$$P{C}_{ICVG}=\varphi \left(\frac{d^{\prime }}{2}\right)$$ (3)

Note that this equation is identical to that defining the relation between d′ and the probability of a correct response of an unbiased observer in the single-interval (Yes/No) task (Green & Swets, 1966; Macmillan & Creelman, 2005). Equation 3 can be used to determine that the value of d′ corresponding to a correct-response probability of 0.75 in the I task is approximately 1.34. This is roughly 1.56 times smaller than the value found for the D task using equation 2. Thus, according to the CVG model, thresholds should be approximately 56% larger in the D task than in the I task.

The HT Model

HT theory posits the existence of a sensory threshold, which can never be exceeded in the absence of a signal (for a review of the theory, see Green and Swets, 1966; Wickens, 2001; Macmillan and Creelman, 2005). In the case of discrimination, the “signal” is defined as the physical difference, Δ, between the two stimuli to be discriminated. The theory further posits the existence of two internal states: a “non detect” state, which occurs whenever the signal does not exceed the threshold, and a “detect” state, which occurs whenever the signal exceeds the threshold. Subjects left in the non-detect state take a guess, which in the absence of bias is equally likely to be either response alternative.

A slight complication arises from the fact that, with the experimental design considered in this note, Δ can be either positive or negative. While the sign of Δ is irrelevant for the D task, it is crucial for the I task. Therefore, we must assume two types of detect states: a “detect+” state, which corresponds to the detection of an upward change, and a “detect-” state, which corresponds to the detection of a downward change. The three internal states, “detect-”, “non detect”, and “detect+” are separated by two thresholds. For simplicity, these thresholds are assumed to be positioned symmetrically around zero along the relevant physical axis.

The HT model assumes that the threshold will never be exceeded in the absence of a change. If an upward change is never registered in a “same” pair, i.e., a pair of identical stimuli, it is logical to assume that such a change is also never registered in presence of a downward change. Thus, according to this model, whenever a change has been detected, the direction of that change should be readily identified.

In order to account for the probabilistic nature of detection or discrimination, HT theory posits that thresholds fluctuate over time. Thus, associated with each Δ, there is a certain probability, P_D(Δ), that the observer is in one of the two “detect” states, and a probability of 1-P_D(Δ) that he/she is in the “non-detect” state. Since for the “same” pair, Δ=0, and according to the theory the threshold can never be exceeded in the absence of the signal, the “same” pair can never leave the observer in the “detect” state. Therefore, at the end of a trial in the dual-pair paradigm, the HT observer can find him/herself in one of the following three situations: a) he/she detected an upward change in one of the two pairs; b) he/she detected a downward change in one of the two pairs; c) he/she failed to detect a change. In cases a and b, the response of the listener in the D task should obviously correspond to the pair in which a change was detected; in those cases, the probability of a correct response is 1. In case c, the listener is forced to guess and the probability of a correct response is 0.5. For the I task, the response of the listener should, according to the model, correspond to the perceived direction of the change in cases a and b; in case c, the listener should, again, guess. It follows that under this model the predicted probability of a correct response in the I task is the same as that for the D task.⁵ Thus, unlike the CVG model, the HT model predicts that the threshold in the I task should be the same as the threshold in the D task, i.e., a D/I threshold ratio of 1.

Comparison between Model Predictions and Experimental Data

In order to test the predictions of the two above-described models, we reanalyzed data collected in a series of experiments concerning the detection and direction-identification of changes in frequency, intensity, and AM rate. The vast majority of these data were reported in an earlier article (Semal & Demany, 2006). Although that article is entitled “Individual differences in the sensitivity to pitch direction”, it contains data on intensity and AM-rate discrimination in addition to frequency discrimination, and we strongly encourage readers to look into it for details regarding how the discrimination thresholds on which the D/I threshold ratios reported here are based were measured. Importantly, Semal and Demany's article was primarily focused on listeners who exhibited unusually large thresholds in the discrimination of the direction of frequency changes (i.e., the I task); these listeners were recruited especially for the purpose of that study, and are not representative of those tested in the vast majority of earlier studies on frequency discrimination. In contrast, here, we were interested specifically in listeners who did not exhibit a conspicuous deficit in the identification of the direction of frequency changes, and whose thresholds in this task are “normal”, in the sense that they are in line with those typically reported in the psychoacoustical literature.⁶ Additional data on frequency discrimination, which were collected by the same authors using the same paradigm as in their original study, but were not reported in the 2006 article, were also included into the present analysis; these supplementary data are, as of yet, unpublished. Overall, the data analyzed here represent a total of 1210 threshold measurements (460 for frequency discrimination, 630 for intensity discrimination, and 120 for AM-rate discrimination), from 11 different listeners.

The geometric means and ranges of the D and I thresholds for frequency, intensity, and AM-rate discrimination that were used in the analyses described below are indicated in Table I. For frequency discrimination, the mean D and I thresholds (expressed in musical cents; 1 cent = 1/100 semitone = 1/1200 octave) correspond to frequency differences of less than 1 %. For AM-rate discrimination, the thresholds (also expressed in cents) are very much larger, as expected from previous studies on AM perception (Formby, 1985; Hanna, 1992). For intensity discrimination, the thresholds were around 2 dB. In comparing these thresholds with those obtained in earlier studies, it is important to note that the thresholds reported here were measured using a wide roving range, which explains why they are somewhat larger than those reported in earlier studies using no (or smaller) roving. The frequency and intensity discrimination thresholds reported here are generally consistent with those measured in other studies using roving (e.g., Berliner & Durlach, 1973; Demany & Semal, 2005). Importantly, note that for each of the three dimensions considered, thresholds in the D task were larger on average than thresholds in the I task.

Table I.

Geometric means and ranges (across participants) of the thresholds measured in the D task and the I task.

	Frequency discrimination (cents)	Intensity discrimination (dB)	AM-rate discrimination (cents)
D task	13.7 (10.3-14.8)	2.2 (1.2-4.2)	184.3 (152.0-223.4)
I task	9.9 (8.8-11.0)	1.8 (0.9-3.9)	155.2 (110.7-208.4)

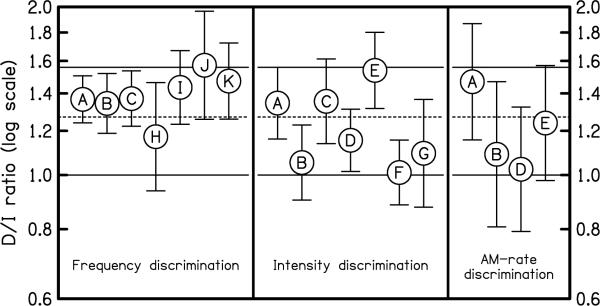
For each listener, we computed the mean ratio between the thresholds measured in the D task and the thresholds measured in the I task.⁷ Statistical bootstrap (Efron & Tibshirani, 1993) was used in order to estimate the 95% confidence intervals around these mean D/I threshold ratios.⁸ Figure 2 shows the mean D/I ratios. Each circle corresponds to the estimated D/I ratio for a given listener (identified by a specific letter) and a given acoustic dimension, along with the associated 95% confidence intervals. The predictions of the CVG and HT models, which correspond to D/I ratios of 1.56 and 1.00, are indicated by horizontal solid lines. It can be seen that 17 of the 18 D/I ratios displayed in Figure 2 fall between 1.0 (the prediction of HT theory) and 1.56 (the prediction of the CVG model); the exception (subject J, frequency discrimination) is a D/I ratio of 1.57. In view of their confidence intervals, eight D/I ratios are statistically consistent with the CVG model and not the HT model, six go in the opposite direction, and the remaining four are inconsistent with both models. Further statistical evidence that the data do not agree with the prediction of either model is provided by a simple sign test: If the CVG model were correct, the mean D/I ratios should fluctuate around 1.56, with roughly half of them below that value, and the other half above it. Instead, 17 out of the 18 measured mean D/I ratios were lower than 1.56, an outcome which has a negligible probability of occurring (p<0.0001) under the hypothesis that the underlying mean D/I ratio is 1.56. For the HT model, the outcome is even clearer: none of the mean D/I ratios is lower than 1.

Figure 2.

Mean individual D/I threshold ratios measured in 11 listeners (A, B, C, … K) for three sound attributes (frequency, intensity,, and AM-rate). Values greater than 1.0 indicate that the threshold for detection of a change is higher than the threshold for the identification of the direction of the change. Note that only two listeners (A and B) were tested on all three attributes. Error bars indicate the 95% confidence intervals around the mean ratios, estimated using statistical resampling (bootstrap). The two solid horizontal lines indicate the predictions of the CVG model (a ratio of 1.56) and of the HT model (a ratio of 1.00). The geometric mean of the 18 plotted D/I ratios is indicated by a dashed line.

Although a trend is apparent for D/I ratios to be higher (and closer to the prediction of the CVG model) for frequency discrimination than for the other two acoustic dimensions tested, the mean difference between the D/I ratios for frequency discrimination and intensity discrimination failed to reach statistical significance; t(12) = 1.99, P = 0.069. Thus, it is not clear that the relationship between D and I thresholds really differs across auditory domains; this is a question for future studies. Assuming for now that the fluctuations in the mean D/I ratios across acoustic dimensions merely reflect random variability across and/or within listeners, it is interesting to pool the data in order to compute the “grand average” (geometric mean) D/I ratio, across all acoustic dimensions and listeners. The result is a D/I ratio of 1.27. This value, which is indicated by the horizontal dashed line in Figure 2, falls almost exactly halfway between the predictions of the HT and CVG models, making it difficult to favor one model over the other. Judging from the confidence-interval bars in Figure 2, a model that would be able to predict a D/I ratio of 1.27 would be statistically consistent with the vast majority of the data points shown in this figure: 16 out of the 18 confidence intervals encompass this value.

In summary, neither the HT model nor the CVG model provides a satisfactory account of the observed relationship between the measured D and I thresholds. While the HT model predicts a D/I ratio of 1.00, which is significantly lower than more than half of the measured mean D/I ratios, the CVG model predicts a ratio of 1.56, which is significantly higher than more than half of the measured mean D/I ratios. Overall, the mean measured D/I ratio falls almost exactly in-between the predictions of these two models. This makes it difficult to favor one model over the other, and it suggests that, in fact, neither of these two models based on widespread assumptions is consistent with the experimental data.

Can the CVG Model be Reconciled with the Data?

In this section, we explore whether and how the CVG model can be modified to yield predicted D/I ratios between 1.00 and 1.56, consistent with the empirical data. The CVG model is characterized by several assumptions. In particular, it assumes that the sensory observations on a trial are contaminated by additive Gaussian noises, which are uncorrelated and have a constant variance. Moreover, the relationships between d′ and the probability of a correct response for the D and I tasks, as given in equations 1 and 3, are based on the assumption that the observer is unbiased, i.e., has no a priori preference for either response alternative. Departures from these assumptions affect the predictions of the model and can, in some cases, yield smaller predicted D/I threshold ratios.

Some intuition into which changes in model assumptions are likely to yield predicted D/I ratios lower than 1.56 can be gained by considering the geometry of the decision space illustrated in Figure 1. Any geometric transformation of the PDF or decision axes that increases the probability mass in quadrant P1 or P3 relative to that in quadrants P2 or P4 contributes to lower the predicted threshold in the D task relative to that in the I task. In order to limit the number of possible transformations, we considered only linear transformations (i.e., stretchings and/or rotations of the PDF or decision axis) that had a relatively simple interpretation. For instance, horizontal stretching of the PDF corresponds to an increase in the variance of the internal noise associated with the sensory trace evoked by the first pair, which might be due to memory noise (as discussed below); a stretch and 45° rotation of the PDF reflects correlation between the decision variables, due possibly to fluctuating bias (as discussed below).

In order to compute how such modifications affected the predicted D/I ratios, we ran a series of computer experiments simulating the behavior of a virtual listener in the D and I tasks using modified versions of the original CVG model. Our main findings are summarized below.

Non-Constant Internal-Noise Variance?

The CVG model assumes that the variance of the internal noise that contaminates the sensory observations remains constant over time. There are at least two reasons why this assumption might not hold. The first relates to the possible influence of memory on sensory representations. According to the CVG model, correct performance in the D and I tasks requires comparing a quantity derived from the two observations in the first pair with one derived from the two observations in the second pair. Thus, it requires that the observer hold in memory the first quantity, or the original observations from which it derives, until the second quantity can be computed. Retention in memory is not perfect. Stochastic diffusion models of memory assume that sensory traces undergo a “random walk”, which may be modeled as a linear increase in internal noise variance as a function of time (Kinchla & Smyzer, 1967). According to this type of model, the variance of the internal noise associated with the difference between the observations in the first pair should be larger than that associated with the difference between the observations in the second pair. Monte-Carlo simulations showed that systematic differences in internal noise magnitude between the first and the second pairs could produce D/I threshold ratios lower than 1.56. However, these simulations also revealed that, in order for the predicted D/I ratio to equal 1.27 (the mean D/I ratio measured based on the experimental data), the standard deviation of the internal noise had to change (increase or decrease) by a factor of approximately four between the first and the second pair.⁹ Assuming that such a difference in internal-noise magnitude between the sensory representations of the differences in the two pairs was due entirely do sensory-trace diffusion occurring between the offset of the first pair and that of the second (i.e., an interval of 1.45 s), and that trace variance increases linearly as a function of time, this should translate into an approximately four-fold decrease in d′ in a 2I2AFC task as the delay between the two stimuli is increased from 0.55 to 2 s. Clément, Demany, & Semal (1999) found that d′ decreased by a factor of about two as the delay between the two sounds that listeners had to discriminate increased from 0.5 to 2 s. Thus, memory noise does not provide a plausible explanation for why thresholds in the D task are only 27% larger than thresholds in the I task, on average.

A second reason why the magnitude of the internal noise added to the observations could differ between the two pairs relates to the use of across-pair roving. As mentioned earlier, the data in Figure 2 were obtained in experiments in which the frequency (or AM rate) of the stimuli was roved over a relatively wide range across pairs in order to discourage listeners from comparing individual observations between the two pairs on a trial. Although data in the literature (Buus & Florentine, 1991; Jesteadt & Bilger, 1974; Nelson & Freyman, 1986) indicate that frequency and intensity JNDs do not vary markedly over the frequency range used as roving range here (400-2400 Hz), it is possible that even small or moderate differences in internal-noise variance across pairs due to roving contributed to significantly reduce D/I ratios. In order to investigate this possibility, we ran Monte-Carlo simulations in which the standard deviation of the noise added to the sensory observations varied randomly across pairs, being drawn from a probability distribution that was uniform on a logarithmic axis (consistent with the use of uniform roving on a semitone frequency scale in the experiments). The simulation results revealed that such across-pair fluctuations in internal-noise magnitude could indeed produce smaller predicted D/I ratios.¹⁰ However, they also revealed that for this effect to explain D/I ratios as small as 1.27, it was necessary to assume that the standard deviation of the internal-noise varied by a factor of more than 100 across the roving range. Such a large variation in internal-noise magnitude would lead to wide variations in frequency or intensity JNDs across the considered frequency range (400-2400 Hz), inconsistent with psychophysical data in the literature (Buus & Florentine, 1991; Jesteadt & Bilger, 1974; Nelson & Freyman, 1986). Thus, roving-related fluctuations in internal-noise magnitude cannot plausibly explain the finding of smaller than expected D/I ratios.

Response Bias?

Another way in which the CVG model can be altered to yield lower D/I ratios involves introducing bias into the decision. In general, the proportion of correct responses achieved by a biased observer is lower than that achieved by an unbiased observer. Thus, a simple way to reduce the D/I ratio predicted by the CVG model is to assume that listeners are not unbiased, and that the bias affects only the I task, or at least, that its influence on thresholds is larger in this task than in the D task. The simplest form of bias corresponds to a constant a priori preference for one of the two response alternatives. For instance, some listeners may be more inclined to choose the “upward” direction than the “downward” direction; for other listeners, the converse may be true. In fact, an analysis of the trial-by-trial data collected in some of the listeners whose data are shown in Figure 2 showed no such bias. Instead, the listeners' responses were equally distributed between “upward” and “downward”, as they should given that these stimulus alternatives were equally likely a priori. Thus, this simple form of bias can be ruled out.

A subtler form of bias, which cannot be ruled out so easily, consists of fluctuations in the position of the internal criterion across trials. Such bias may occur as a result of the observer's response to the current trial being influenced by his/her response to the previous trial or, if feedback is given (as was the case in the experiments considered here), by the outcome of that trial, i.e., whether the response was correct or incorrect (Treisman & Williams, 1984). For example, the participant may be inclined to choose the same response as that given on the previous trial if that preceding response turned out to be correct. While the precise generating mechanisms of this “fluctuating bias” cannot be determined based on the data currently available, the fact that the stimulus alternative presented on a given trial did not depend on that presented on the previous trial makes it possible to model this type of bias as a random variation of the decision criterion. Moreover, although variable across trials, the direction and magnitude of the shift may to a first approximation be regarded as constant within a trial. As a result, this form of fluctuating bias introduces some correlation between the decision variables derived from the different observations or pairs of observations on a trial; the assumption of statistical independence, which was made in the original CVG model, is violated.

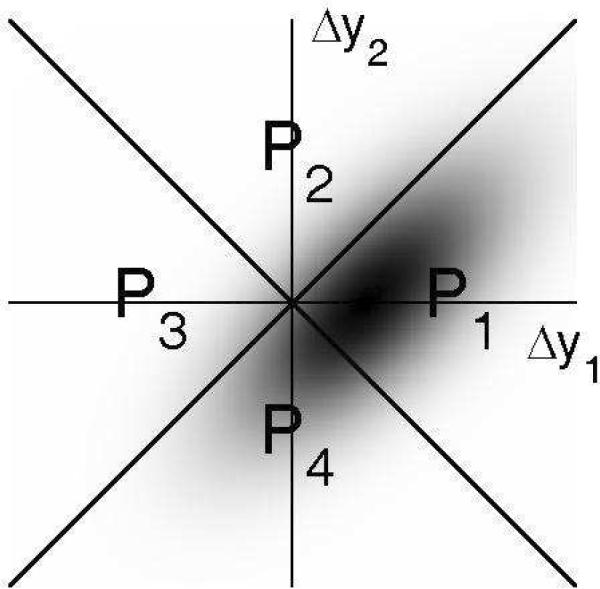
A schematic illustration of this effect is provided in Figure 3. The situation illustrated in this figure is that in which an upward change occurred in the first pair, and the task is to identify the direction of the change. For this task, a random shift of the criterion is mathematically equivalent to an addition of the same random value to the two decision variables, Δy₁ and Δy₂. Figure 3 shows how this modifies the joint PDF. The contour of the PDF, which was circular in Figure 1, is now elongated along the major diagonal of the decision plane, reflecting a positive correlation between the two decision variables. This transformation affects the way in which the mass of the PDF is shared among the four quadrants. The effect may be depicted schematically as an increase in the proportion of the mass in the half-plane formed by P4 and P3 at the expense of that in the half-plane formed by P1 and P2. Assuming that the observer is unable to adjust his/her decision strategy to take into account the correlation between the decision variables, the predicted proportion of correct responses in the I task is still given, as in Figure 1, by the proportion of the probability mass contained in quadrants P1 and P2, relative to that contained in quadrants P3 and P4. An increase in the mass in P3 at the expense of P2 translates into a decrease of the predicted proportion-correct for the I task, and therefore, in a smaller predicted D/I ratio.

Figure 3.

Decision space for the CVG model with fluctuating bias added to the decision variables, Δy₁ and Δy₂ In this example, the bias-related noise has a normal distribution with a standard deviation twice as large as that of the sensory noise. As manifested by the elliptical shape of the PDF, and its diagonal orientation, this type of bias introduces a correlation between the two decision variables. This correlation contributes to reduce the proportion of correct responses, compared to the case where no such bias is present (Figure 1).

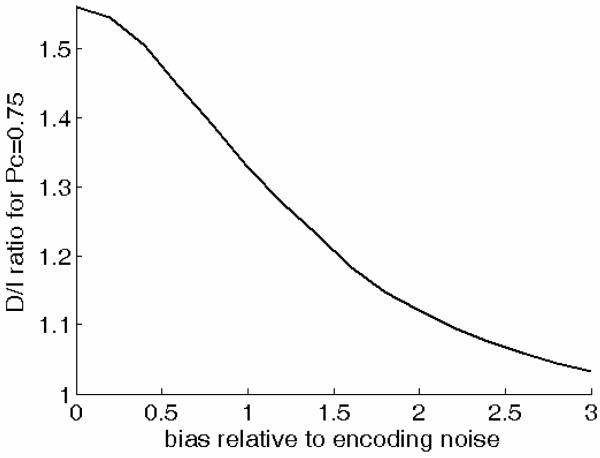
Figure 4 shows how the D/I ratio predicted by a modified CVG model based on this assumption of fluctuating bias in the I task only depends on the standard deviation of the bias-related noise relative to that of the sensory noise. As the relative magnitude of the fluctuating bias increases from zero to infinity, the predicted D/I ratio decreases from 1.56 to 1.00. In order for the D/I ratio predicted by the model to equal the mean measured D/I ratio (1.27), the bias-related noise must have approximately the same standard deviation as the sensory noise.

Figure 4.

Influence of the magnitude of the bias toward one of the two response alternatives in the D task on the D/I threshold ratios predictions of the CVG model. The magnitude (i.e., standard deviation) of the bias is expressed relative to that of the sensory noise.

To summarize, D/I ratios lower than 1.56 can be accounted for by assuming a CVG observer with a fluctuating bias toward the “upward” or “downward” response in the I task. However, it is important to note that this is an ad hoc assumption. The data presented in this note provide no evidence for or against such fluctuating bias, affecting selectively the decision between the “upward” and “downward” responses. One might equally well assume that a similar fluctuating bias also affected the decision between the first and second pairs in the D task, leading the listener to favor the first interval on some trials, and the second interval on other trials. Such bias would reduce the proportion of correct responses in the D task, thereby contributing to bring the D/I ratio back toward its original value of 1.56. Thus, an explanation of the results in Figure 2 in terms of fluctuating bias remains largely speculative.

Non-Linear Psychometric Functions?

A third way in which D/I ratios lower than 1.56 might be explained without completely abandoning the CVG model involves violating the assumption of linear psychometric functions. So far, we have assumed in all mathematical derivations and simulations that d′ was proportional to the physical difference (in cents, or in dB) between the stimuli to be compared. This assumption is supported by results in the psychoacoustical literature (Buus & Florentine, 1991; Nelson & Freyman, 1986; Turner & Nelson, 1982).¹¹ However, due to variability in the psychophysical measures, the experimental evidence is necessarily limited, and it cannot be used to rule out moderate deviations from linearity. Therefore, one may wonder how deviations from the assumption of linear psychometric functions influence the D/I ratio predictions of the CVG model, and more specifically, whether moderate deviations may in fact result in substantially lower predicted values, consistent with those shown in Figure 2.

In order to investigate this possibility, we ran additional Monte-Carlo simulations using the basic CVG model, but this time assuming that the relationship between d′ and the stimulus difference, Δ, followed a power-law (d′ = Δ^k) instead of a linear relationship. The power law is often used to model psychometric functions (Gescheider, 1997; Hartmann, 1998). It presents the advantage over other elementary mathematical functions, such as the logarithmic and exponential, that it can assume either convex or concave shapes, depending on whether the value of the exponent, k, is larger or smaller than unity. In the simulations, this value was varied systematically until the D/I ratio predicted by the simulated CVG model was consistent with the mean ratio measured in the psychophysical experiments: 1.27. The results revealed that for this to be the case, the exponent in the power-law function had to be about 1.85. Such an exponent results in a substantial deviation from linearity in the shape of the psychometric function. This outcome is inconsistent with the psychophysical results reported by Turner & Nelson (1982) or Nelson & Freyman (1986) for frequency discrimination, and by Buus and Florentine (1991) for intensity discrimination. (We are not aware of relevant experimental data in the case of AM-rate discrimination.)

Alternative Models

The observation that the CVG model cannot easily be reconciled with the experimental data leads us to consider other types of psychophysical models. The observation that all but one of the mean D/I ratios shown in Figure 2 fall in-between the predictions of the HT and CVG models suggests that listeners' behavior in the D and I tasks might be adequately captured by a model that combines some of the features of these two types of models. In this section, we briefly describe two such models. The first was obtained by appending a quantization stage to the CVG model; the resulting model is referred to as the “quantized Gaussian” (QG) model. The second model is a pure discrete-state model, inspired by neurophysiological observations, which suggest that the perception of stimulus changes may be mediated, at the neural level, by the relative activations of neurons that are selectively sensitive to increments or decrements, and whose spike-count output follows a Poisson distribution.

A Quantized-Gaussian Model

The idea of quantized sensory representations is not new. Following Boring (Boring, 1926), Stevens and colleagues (Stevens, 1972; Stevens et al., 1941; Stevens & Volkmann, 1940) and others (Miller & Garner, 1944; Larkin and Norman, 1964) argued for a “quantum” model of sensory discrimination. The “quantized-Gaussian” model, which we consider here, assumes an initial stage in which, as in the CVG model, the sensory activity evoked by the stimuli is modeled as a Gaussian-distributed random quantity along a continuous axis. This first stage is followed by a second one, in which the continuous sensory activity from the first stage is “quantized”. It is assumed that the subject only has access to the output of the latter stage; therefore, his/her decisions are based on an imperfect, quantized representation of the stimuli. This idea is represented schematically in Figure 5. Due to the quantization operation, the decision space for this model is a discrete version of that for the CVG model shown in Figure 1.

Figure 5.

Schematic illustration of the sensory-observation process and decision space for the quantized-Gaussian (QG) model. Top panel: Schematic representation of the physical and sensory scales. A stimulus with a certain value on a physical scale, x, evokes a sensory response on a continuous sensory scale, y As in the CVG model, this sensory response is contaminated by Gaussian noise. However, in the QG model, the observer only has access to a quantized representation of the sensory activity, as represented by the discrete scale, q In this example, the size of the quanta was chosen to equal three times the standard deviation of the Gaussian sensory noise. In addition, we purposefully chose a case where sensory activity on the continuous scale, y, falls close to the border between two quanta, to illustrate the fact that a given stimulus value does not always result in the activation of the same quantum. Bottom panel: Two-dimensional decision space for the QG model. This can be compared to the decision space for the CVG model illustrated in Figure 1. As in that figure, the situation illustrated is one in which an upward change occurred in the first pair. Here, the probability of a correct response is computed as a sum over quadrants P1 and P3 for the D task, and P1 and P2 for the I task. For quanta that are cut through by one or two diagonals, decisions are determined by guessing. In this example, the physical difference, Δ, between the two stimuli was set to 2.1 times the standard deviation of the Gaussian sensory noise, so that the proportion-correct in the D task equals approximately 0.75.

By varying the size of the quantization steps relative to the magnitude of the internal Gaussian noise, one can generate predicted D/I ratios that range from 1 to 1.56, as shown in Figure 6. This can be understood by considering that, when the size of the quantization steps is large relative to the magnitude of the internal Gaussian noise, the quantized-Gaussian model is essentially equivalent to a two-state HT model. On the other hand, if the quantization steps are made infinitely small, the quantized-Gaussian model becomes equivalent to the CVG model.

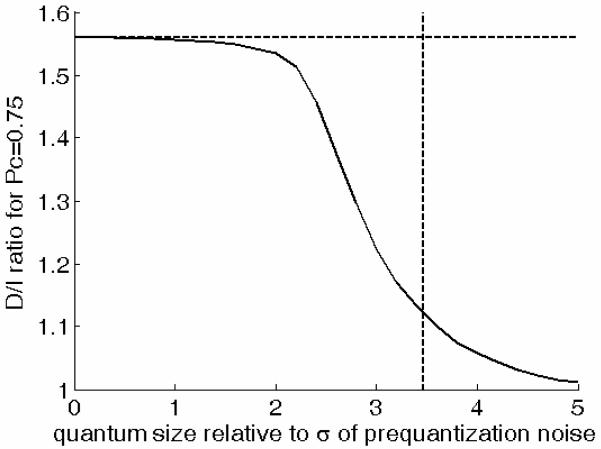
Figure 6.

D/I ratio predicted by the quantum model as a function of the quantum size relative to the standard deviation of the pre-quantization noise. The vertical dotted line shows the relative quantum size corresponding to the case of a quantization noise with a standard deviation equal to that of the pre-quantization noise, as discussed in the text.

From this point of view, the HT and CVG models described in earlier sections can be thought of as extreme cases on a continuum going from two to an infinitely large number of possible internal states. The results shown in Figure 2 suggest that human observers stand in-between these two extremes: they behave as if their decisions were based on a finite number of states, although more than assumed by the HT model. The simulation results shown in Figure 6 indicate that in order for the QG model to predict a D/I ratio equal to the mean D/I ratio measured experimentally (1.27), the size of the quantization step (or “quantum”) must be between two and three times larger than the standard deviation of the internal Gaussian noise. (Figure 5 was produced assuming a quantum size equal to three times the standard deviation of the internal Gaussian noise.)

It is worth noting that Stevens and Volkmann (1940) and Stevens (1972) reached a different conclusion regarding the relative size of the quantum, compared to other sources of noise affecting the observer's responses in sensory discrimination experiments. These authors concluded that the quantum size was probably smaller than that of the other sources of noise, explaining why quantization effects are usually difficult to observe. Following this line of reasoning, one might object that if, as indicated by our simulation results, the quantum size is several times the standard deviation of the pre-quantization noise, this should produce visible steps in psychometric functions for frequency and intensity discrimination, whereas in most published reports of such functions, such steps are not clearly apparent.¹² A possible explanation for this lack of evidence for a quantization operation in psychometric data is that the standard deviation of the additional sensory noise introduced by the quantization operation is only 1/√12 of the quantum size. This means that even if the size of the quanta is up to 3.5 times the standard deviation of the Gaussian sensory noise, the quantization operation will contribute less noise than there already is in the system. Thus, a quantum size between two and three times larger than the standard deviation of the pre-quantization noise, as indicated by our results, might not produce detectable steps in psychometric functions, at least under usual testing conditions.

To summarize, the simulation results indicate that D/I threshold ratios comprised between 1.00 and 1.56 can be predicted by a model based on the assumption that listeners only have access to a quantized representation of Gaussian sensory observations. From this point of view, the experimental data are consistent with the general idea behind the psychophysical “quantum” theory (Stevens & Volkmann, 1940).

A Neurophysiologically Inspired Poisson Model

The second model considered here is based on the idea (supported by experimental data, in the auditory domain as well as the visual domain) that some neurons in the central nervous system respond with an increased firing rate when a stimulus changes in a given direction. Psychophysical observations reported by Demany & Ramos (2005) provide strong evidence for the existence of automatic and direction-sensitive “frequency-shift detectors” in the human auditory system. This study showed that a sequence of two pure tones differing in frequency and separated by a 500-ms silent delay can elicit a percept of directional pitch shift even when the pitch of the first tone is not consciously audible.

The model that we propose here involves a neural “increment detector”, which compares the two stimuli in a pair, and whose mean firing rate increases monotonically with the difference in intensity or frequency, Δ, between these stimuli, but only if this difference is positive (i.e., Δ>0). For simplicity, we assume that when Δ is relatively small, as is typically the case near discrimination threshold, the mean firing rate of the detector increases linearly with Δ. For negative physical differences (i.e., Δ<0), the output of this detector is distributed following the same distribution as for physically identical stimuli (i.e., Δ=0), reflecting the fact that the detector is insensitive to decrements. Furthermore, it is assumed that the output of this detector can be modeled as a Poisson process with a driving rate μ₀ for identical stimuli or decrements, and μ=μ₀+αΔ for increments (with α a constant). Poisson processes are frequently used as an approximate model of neural spiking, and accordingly the Poisson distribution is commonly used as an approximate model of the distribution of spike counts (Rieke, Warland, de Ruyter van Steveninck, & Bialek, 1997).

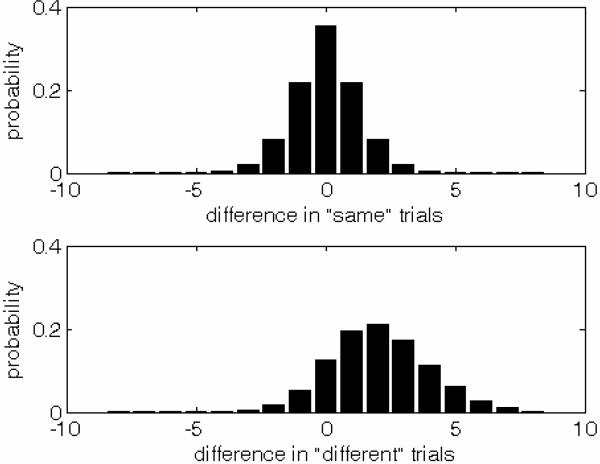
In addition to this “increment” detector, the model contains a “decrement” detector, which produces a Poisson-distributed output with mean rate μ₀ for Δ≥0, and mean rate μ=μ₀+α|Δ| for Δ<0. The difference between the outputs of these increment and decrement detectors is used in order to decide whether or not a change occurred, and if a change did occur, in which direction it was. Accordingly, the decision space for this model resembles that for the Gaussian and QG models, in that the decision variables are differences between random variables derived from the first and second pairs; however, instead of having a Gaussian or quantized-Gaussian distribution, here, the decision variables have a distribution given by the difference between two Poisson-distributed random variables. Examples of such Poisson-difference distributions are shown in Figure 7. The two panels in this figure show how the decision variables are distributed for “same” trials (upper panel) and “different” trials (lower panel), assuming a Poisson process with a mean spontaneous rate, μ₀, of 0.8 spikes per second and a mean evoked rate of 2.9 spikes per second. As can be seen, the two distributions have different spreads; this results from the fact that the variance of a Poisson-distributed random variable increases with the mean.

Figure 7.

Example probability distributions for the “difference between observations” decision variable in the Poisson model. The two panels in this figure show how the decision variables are distributed on “same” trials (upper panel) and on “different” trials (lower panel). These distributions are for a Poisson process with a mean spontaneous rate, μ₀, of 0.8 spikes per second and a mean evoked rate of 2.9 spikes per second.

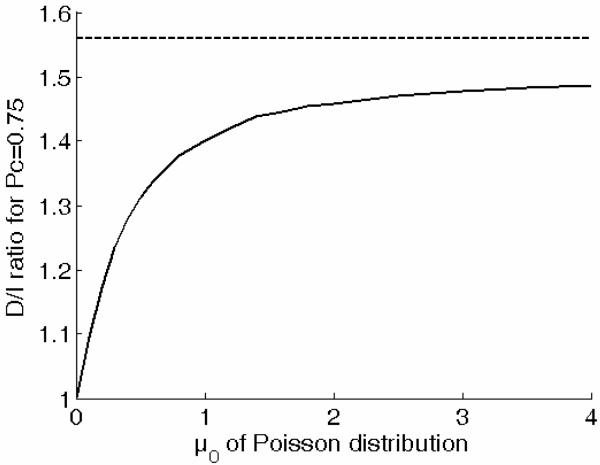
The critical variable, in this model, is the mean spontaneous rate, μ₀, of the increment and decrement detectors; for simplicity, this rate is assumed to be the same for the two types of detectors. As the mean spontaneous rate increases, and the mean evoked rate increases beyond it, the probability distribution of the difference between the output of the two types of detectors tends toward a Gaussian distribution, and the D/I predicted by this Poisson model tends toward that of the CVG model. In Figure 8, we show how the D/I threshold ratio predicted by the Poisson model depends on the mean spontaneous rate, μ₀. For each value of μ₀ we determined the value of the evoked rate, μ_D, that yielded a predicted proportion of correct responses of 0.75 in the D task, and the value of evoked rate, μ_I, corresponding to the same proportion correct in the I task. The D/I ratio was then calculated as (μ_D - μ₀)/(μI - μ₀). These results confirm that this Poisson model can predict D/I ratios lower than 1.56, and they reveal that such ratios result from relatively low spontaneous rates: D/I ratios below 1.4 require a mean spontaneous rate of approximately 1 or less.

Figure 8.

D/I ratios for decisions based on Poisson increment and decrement detectors as a function of the mean spontaneous rate at the output of the detector.

Receiver Operating Characteristics for Change Detection: A Further Test of the Models

The above simulation results reveal that a discrete Poisson model, or a “hybrid” (continuous-discrete) quantized-Gaussian model, provide a more satisfactory account of the empirical D/I threshold ratio data shown in Figure 2 than the HT and CVG models. However, it may be argued that the former two models are ad hoc, and that although they originate in earlier work independent from the present one (e.g., Green and Swets, 1966; Egan, 1975; Kaernbach, 1991a), they were only invoked here because it was suspected that they would resolve the particular problem under consideration. Therefore, it was desirable to consider additional experimental data, besides D/I ratios, in order to further evaluate whether the Poisson and quantized-Gaussian models provide more adequate models of how sensory changes are perceived.

Receiver operating characteristics (ROCs), which represent the probability of a false alarm as a function of the probability of a hit for different values of the criterion (Green & Swets, 1966; Egan, 1975), provide such data. A landmark of the Poisson model is that it can account for experimental findings of asymmetric ROCs in Yes-No signal-detection tasks (Egan, 1975; Kaernbach, 1991a; Swets, Tanner & Birdsall, 1961). This stems from the Poisson distribution being asymmetric, and from its variance increasing with its mean. In contrast to the Poisson model, the CVG model predicts symmetric ROC curves, at least for the Yes-No detection task. Therefore, ROCs provide a way of distinguishing the Poisson model from the CVG model.

One complication, which must be taken into account here, stems from the fact that we are not dealing simply with detection, but with change detection. More precisely, we are dealing with the detection of discrete sensory changes. The paradigm of choice for measuring this ability is not the Yes-No paradigm, for which the above distinction between the CVG and Poisson models has been established, but rather the Same-Different (2IAX) paradigm. For that paradigm, the CVG model can actually predict asymmetric ROCs in some situations (see, e.g., Dai et al., 1996; Hautus, Irwin & Sutherland, 1994). This is the case, in particular, for experiments in which the stimuli are roved over a relatively wide range across trials, as commonly done to force listeners to compare the two stimuli presented on each trial, rather than rely on a long-term memory trace. In this situation, the ROCs predicted by the CVG model are slightly asymmetric about the minor diagonal (Dai et al., 1996).¹³ This makes the task of distinguishing between the CVG and Poisson models less straightforward, since asymmetric ROCs are now expected for both models (Kaernbach, in preparation). Fortunately, there is a simple way to overcome this problem. The CVG model only predicts asymmetric ROCs in the 2IAX paradigm if the direction of the change is not known in advance by the observer. If the observer knows the direction of the change in advance the asymmetry is eliminated. This is because knowing the direction of the change eliminates the need for an optimal CVG observer to base his decisions on the absolute value (or any other non-monotonic transformation) of the difference between the sensory observations evoked by the two stimuli presented on a trial. Instead, the CVG observer can now decide between “same” and “different” on the basis of the signed (as opposed to the unsigned) difference between the two observations. This decision strategy is formally equivalent to the differencing strategy for the 2I2AFC paradigm, which we mentioned earlier, except for the placement of the criterion: Assuming a balanced design (with equal a priori probabilities and symmetric payoffs), the optimal placement of the criterion in the 2I2AFC paradigm corresponds to the origin (zero) of the decision axis; in contrast, in the direction-known 2IAX paradigm, the optimal placement of the criterion corresponds to a positive value for trials on which the direction of the change is “upward”, and to a negative value for trials on which the direction is “downward”. In both cases, the criterion should be positioned halfway between the means of the difference distributions corresponding to “same” and “different” trials. Therefore, if in a 2IAX experiment the change between the two stimuli in the different pairs always has the same direction, and listeners are aware of this fact, ROCs should be symmetric under the CVG model. Since, on the other hand, the Poisson model still predicts asymmetric ROCs, this provides a way of distinguishing between the CVG and Poisson models in a change-detection setting.

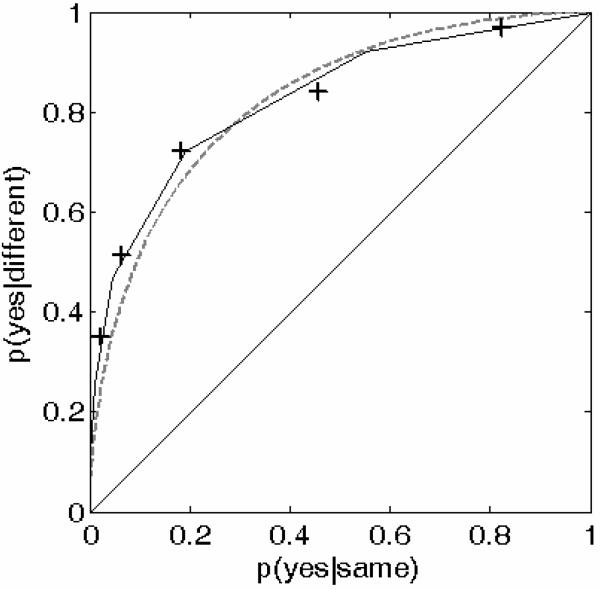
The above rationale led us to analyze ROC data obtained in a 2IAX intensity-discrimination experiment where the change in intensity between the two tones presented on “different” trials could only be downward. Note that intensity is the dimension for which we previously found D/I ratios to be the lowest on average (Figure 2), consistent with a Poisson process having a relatively low mean. Therefore, it is for this dimension that one should expect the most asymmetric ROC curves, if the Poisson model accurately describes the change-detection process. This provides ideal conditions for testing which of the two rival models, CVG and Poisson, is most consistent with empirical ROCs.

Listeners rated their certitude regarding the occurrence of a change between the stimuli using six response categories: “very sure yes”, “sure yes”, “maybe yes”, “maybe no”, “sure no”, and “very sure no”. A multiple-response monetary payoff matrix was used in order to entice listeners to vary their criteria for deciding between the different response categories over a relatively broad range, going from most conservative (i.e., trying to limit the number of false alarms) to most liberal (i.e., trying to achieve a high hit rate). The ROC data measured across five listeners using this technique are shown as symbols in Figure 9. The best-fitting predictions of the CVG model and Poisson model are shown as dashed and solid curves, respectively. As can be seen, the best-fitting asymmetric ROC produced by the Poisson model provides a better fit to the empirical data than the best-fitting symmetric ROC produced by the CVG model (model comparison: log of Poisson/CVG likelihood ratio = 75.5; p<0.0001).¹⁴ Interestingly, the best-fitting Poisson model had a mean spontaneous rate, m0, of approximately 0.8, and an evoked mean rate of approximately 2.6. Based on the data shown in Figure 8, which illustrate how the mean D/I ratio predicted by the Poisson model depends on the mean spontaneous rate, a mean spontaneous rate of 0.8 corresponds to a mean D/I ratio slightly below 1.4. This value is somewhat larger than the mean empirical D/I ratio computed from the data displayed in Figure 2, which was 1.27. However, in view of the inter- and intra-individual variability in the psychophysical data, our estimates of the Poisson-model parameters derived from the D/I data are in reasonably good agreement with those derived from the ROC data.

Figure 9.

ROCs predicted by the CVG and Poisson models compared to human data. The crosses show mean hit and false-alarm probabilities measured in five human listeners performing a 2IAX intensity-discrimination task where the direction of intensity changes (downward) was constant and known to the listener (see text for details). The dashed curve shows the best-fitting ROC curve produced by the CVG model, which under such testing conditions can only yield symmetric ROCs. The solid lines indicate the best-fitting ROC obtained using the Poisson model described in the text. As can be seen, the latter predicts an asymmetric ROC, which more accurately fits the data than the symmetric ROC produced by the CVG model.

So far, this section has focused exclusively on the Poisson and CVG models. One remaining question is whether the ROC data can also be used to distinguish the Poisson model from the other two models that were shown earlier to account for the empirical threshold-ratio data, namely the modified Gaussian model with fluctuating bias, and the quantized-Gaussian model. The former is easy to rule out because it assumed that a fluctuating bias was present only in the I task. For the D task, the predictions of that model are exactly the same as those of the CVG model. Consequently, we turn our attention to the quantized-Gaussian model. In order to investigate whether and how well this model could explain the ROC data, we ran simulations using different quantum sizes (relative to the magnitude of the pre-quantization internal noise), until the best possible match between the measured and predicted ROCs was achieved. The results of this analysis revealed that the quantized-Gaussian model could produce asymmetric ROCs, if the quantum size was sufficiently large. This can be understood by considering that, as the quantum size increases, the Gaussian internal-noise distribution is sampled more and more coarsely. For very large quantum sizes, the number of relevant internal states in the quantized-Gaussian model is relatively small, yielding ROCs with visible edges. Occasionally, depending on the exact relationship between the quanta and the pre-quantization noise, the main edge in the predicted ROC falls below the minor diagonal, as observed in the empirical ROC data. However, this requires a specific relationship between the quanta and the pre-quantization noise; in practice, this requirement is unlikely to be met consistently. Moreover, we found that in order to account for a substantial departure from symmetry in the predicted ROCs, the quantum size must be very large compared to the standard deviation of the pre-quantization noise. Specifically, our simulation results revealed that in order to account for the asymmetry observed in the empirical ROC data in Figure 9, the quantum size must be roughly eight times larger than the standard deviation of the pre-quantization noise. This factor of 8 is considerably larger than the factor that we arrived at earlier on the basis of empirical D/I ratios, which indicated an average quantum size at most three times larger than the pre-quantization noise. A quantum size eight times larger than the pre-quantization noise is inconsistent, not only with this earlier result, but also with other data in the literature (cf. our earlier discussion of the consequences of a large quantum size on psychometric functions).

To summarize the results and arguments presented in this section, the Poisson model correctly predicts that ROCs for the detection of sensory changes having a fixed and known direction are asymmetric. In addition to being qualitatively consistent with empirical ROC data, the predictions of this model are in better quantitative agreement with the data than those of the various other models considered in this work. Further study is required in order to determine whether these findings, which concern changes in sound intensity, hold for other dimensions of auditory perception, and for other sensory modalities. However, combined with our previous demonstration that the Poisson model can account for the observed relationship between D and I thresholds, these results pinpoint this model as a more adequate description of the perceptual and/or neural processes involved in the perception of simple sensory changes than the HT, CVG, or quantized-Gaussian model.

Conclusions

A statistical analysis of detailed measurements of thresholds for the detection of simple changes in auditory stimuli, and thresholds for the identification of the direction of these changes measured under identical stimulus conditions in the same listeners, revealed that the relationship between these thresholds departed significantly from the predictions of two common psychophysical models, the CVG model and the HT model. However, remarkably, for the three acoustic dimensions studied (intensity, frequency, and AM rate) and all but one of the 11 listeners tested, the mean measured D/I threshold ratios fell in-between the predictions of these two models. This led us to consider the possibility that a hybrid model combining early Gaussian sensory observations with a later quantization stage (the “quantized-Gaussian” model), or a discrete-state model with a larger number of internal states than the basic HT model (the “Poisson” model), might adequately capture the behavior of human listeners in the D and I tasks. This possibility was confirmed by simulation results: both the quantized-Gaussian and Poisson model were able to produce D/I threshold ratios between 1.00 and 1.56, as observed in humans. In order to further evaluate the different models, we analyzed ROC data collected under conditions in which the direction of the sensory change was fixed, and known to the listener. These ROC data were best accounted for (both qualitatively and quantitatively) by the Poisson model.

Gaussian models have usually been favored over discrete-state models, because of their ability to fit empirical ROC curves better than their historic competitor, the dual-state HT model. However, as noted by Green and Swets (1966), ROCs typically contain a handful of data points, and discrete-state models with at least as many internal states as the number of data points can fit such empirical ROCs as well as the Gaussian model. The quantized-Gaussian model and the Poisson model described in this note fall into this category. The Poisson model presents the advantage that it can accommodate asymmetric empirical ROCs (Kaernbach, 1991a). Future studies involving detailed measurements of ROCs for the detection of changes in sound intensity or frequency under stimulus conditions similar to those considered here may provide further arguments for or against this model.

Another argument that is often used to justify the Gaussian assumption is that, by the central-limit theorem, the distribution of the sum of a large number of random variables tends toward a Gaussian. However, this statistical theorem applies specifically to large numbers of statistically independent sources of variability combined additively. Research on the neural underpinnings of perception conducted during the past decades indicates that the neural responses that are combined in order to arrive at a perceptual decision are usually correlated rather than independent (Averbeck, Latham, & Pouget, 2006; Zohary, Shadlen, & Newsome, 1994). Moreover, neural responses may be combined in complex non-linear ways rather than additively. The view that perception ultimately relies on discrete quantities is consistent with a wealth of neurophysiological observations, including in particular findings indicating that perceptual decisions may be based on the correlated spike counts of a relatively limited number of neurons (Shadlen & Newsome, 1998). In this respect, the Poisson model of change-detection and change-direction-identification described here is particularly attractive, because of its neurophysiological plausibility and simplicity.

Another argument in support of the quantized-Gaussian and Poisson models stems from the introspective fact that physically identical sounds are often perceived as identical. According to a model in which sensory observations are continuous and contaminated by Gaussian internal noise, the sensory observations evoked by two physically identical stimuli have an infinitely small probability of being exactly identical, due to the influence of internal noise. By contrast, in discrete-state models, the probability that two physically identical stimuli evoke strictly identical percepts is not negligible. In order to reconcile the CVG model with introspection, one would have to assume that the subject does not have conscious access to the “true” sensory observations, but only to the decisions that were reached after comparing these observations with an internal criterion. This is tantamount to assuming that the decisions of the subject rest on a quantized (discrete) representation of the stimuli.

Based on these results and considerations, we suggest that discrete-state models, and in particular a Poisson model, describe more adequately than the CVG model the processes involved in the perception of simple changes in auditory stimuli. Of course, it would be interesting to know if such a conclusion is valid for auditory dimensions not considered here (for instance sound localization) and to see if a similar conclusion can be drawn for other sensory modalities. It is therefore hoped that the analysis described in this note will spark further empirical studies, concerning especially the relationship between change detection and change-direction identification.