A simulation–approximation approach to sample size planning for high-dimensional classification studies

Abstract

Classification studies with high-dimensional measurements and relatively small sample sizes are increasingly common. Prospective analysis of the role of sample sizes in the performance of such studies is important for study design and interpretation of results, but the complexity of typical pattern discovery methods makes this problem challenging. The approach developed here combines Monte Carlo methods and new approximations for linear discriminant analysis, assuming multivariate normal distributions. Monte Carlo methods are used to sample the distribution of which features are selected for a classifier and the mean and variance of features given that they are selected. Given selected features, the linear discriminant problem involves different distributions of training data and generalization data, for which 2 approximations are compared: one based on Taylor series approximation of the generalization error and the other on approximating the discriminant scores as normally distributed. Combining the Monte Carlo and approximation approaches to different aspects of the problem allows efficient estimation of expected generalization error without full simulations of the entire sampling and analysis process. To evaluate the method and investigate realistic study design questions, full simulations are used to ask how validation error rate depends on the strength and number of informative features, the number of noninformative features, the sample size, and the number of features allowed into the pattern. Both approximation methods perform well for most cases but only the normal discriminant score approximation performs well for cases of very many weakly informative or uninformative dimensions. The simulated cases show that many realistic study designs will typically estimate substantially suboptimal patterns and may have low probability of statistically significant validation results.

1. INTRODUCTION

Recent years have seen an explosion of work on classification problems where the number of measured features per sample is vastly greater than the number of samples. For biological classification problems, such data arise from genomic DNA microarrays and proteomic mass spectrometry assays, from which investigators try to classify disease categories, tumor types, response to drugs, or other categories (Ludwig and Weinstein, 2005). Most of the efforts in method development have appropriately focused on what to do with real data sets (Wang and Shen, 2006, Adam and others, 2002). Generally speaking, various methods must select features (sometimes called biomarkers) to be used for classification and estimate a classifier without over-fitting to the many available data dimensions.

Because of the complexity of the algorithms involved, it is not straightforward to answer questions about study design. For example, if there are 10 informative and 5000 noninformative features and the best possible classification error rate is 5%, how many samples are necessary to have an 80% chance of estimating a classifier with less than 10% error rate for independent validation samples? Or, how many samples are necessary so that with probability 95%, the estimated classifier will perform statistically significantly better than a 50% error rate for independent validation samples, that is, conclude the study has at least found something nonrandom? Investigators planning studies have access to sound statistical principles but few specifics to serve as guideposts in evaluating sample sizes relative to hypothesized outcomes. Analysis of study design for high-dimensional classification studies has been identified as an important problem for genomics and proteomics because significant resources are required to execute such studies (Dobbin and Simon, 2007, Allison and others, 2006, Pusztai and Hess, 2004, Hwang and others, 2002).

Issues of sample size for genomic and proteomic pattern discovery studies are potentially quite important. Over 60 proteomics discovery studies have been published in recent years (Coombes and others, 2005, Baker, 2005). Many have sample sizes in the approximately 10–20 range; some notable cases with higher sample sizes (e.g. Adam and others, 2002, Petricoin, Ardekani, and others, 2002, Petricoin, Ornstein, and others, 2002, Zhang and others, 2004, Rogers and others, 2003) reveal that in broad terms, sample sizes of ∼50 per group are rare and of ∼100 per group are very rare. Implicit in some rationales for biomarker discovery studies is the possibility that multiple, individually weak biomarkers could combine to form a collectively strong diagnostic pattern. The observation that discovery studies often find nonspecific markers (Baker, 2005) also suggests that disease-specific patterns may require multiple, individually weak biomarkers. Detecting patterns of multiple weak biomarkers amid many noninformative data dimensions may require substantially greater sample sizes than detecting individually strong biomarkers.

In proteomics, early biomarker discovery and validation studies (Petricoin, Ardekani, and others, 2002, Petricoin, Ornstein, and others, 2002, Petricoin and Liotta, 2003, Rogers and others, 2003, Adam and others, 2002, Li and others, 2002, Adam and others, 2001) led to renewed attention toward potential pitfalls of design and analysis methods. These include low discovery and validation sample sizes, uncertainty about data preprocessing and statistical methods, low sample processing and measurement reproducibility within and between study sites, uncertainty about the biological nature and consistency of patterns, and lack of independent validation studies (Sorace and Zhan, 2003, Diamandis, 2004a, Diamandis, 2004b, Listgarten and Emili, 2005, Coombes and others, 2005, Ebert and others, 2006, Wilkins and others, 2006). Similar issues have been raised for genomic studies (e.g. Pusztai and Hess, 2004, Ludwig and Weinstein, 2005). Two important studies notable for their independent validation trials highlight the possibility—among many possible reasons for low validation success—that small sample sizes have been fundamentally limiting. Rogers and others (2003) saw sensitivity for renal cancer decline from ∼100% in discovery to ∼40% in validation, and Zhang and others (2004) saw specificity decline from ∼90% in discovery to ∼65% in validation.

For prospective analysis of pattern discovery study designs, purely simulation approaches quickly become cumbersome because there are many scenarios of interest, but purely analytical results are not easy to obtain. We take a middle road between simulations and approximations, with Monte Carlo methods for the feature-selection step and approximations for generalization error rates given each feature set. We use multivariate normal data and linear discriminant classification of features selected by univariate tests. While biologically simplistic, this framework captures the key impacts of both inaccurate feature selection and inaccurate classifier estimation. Related studies that use multivariate normal models include Pepe and others (2003), Hu and others (2005), Jung (2005), and Dobbin and Simon (2007), among others. Our approach gives order-of-magnitude faster estimation of generalization error compared to direct simulations, which are given for comparison. Both full simulation and simulation–approximation results are useful, but the latter can facilitate more practical exploration of study designs. Our approach also gives insight into which sources of variation are most important and suggests directions for future improvements.

We evaluate the simulation–approximation approach by comparing it to complete simulations that address meaningful study design questions (supplementary material available at Biostatistics online, http://www.biostatistics.oxfordjournals.org). We ask how validation error rate depends on the strength and number of informative features (and hence the minimum possible error rate), the number of noninformative features, the patient sample size, and the number of features allowed into the pattern. We find that typical sample sizes may perform poorly when there is a true pattern composed of many individually weak features. This result is not surprising based on general principles, but moving from principles to specific examples as guideposts is important for design of real studies.

We also give 2 approximations of the generalization (or test, or validation) error of a linear discriminant classifier when the training and validation samples do not follow the same distributions. The first is a delta approximation, from Taylor expansions of generalization error around the expected discriminant boundary. The second, and more successful, approximates the discriminant scores as normally distributed. Approximations of linear discriminant analysis with training and generalization samples from the same distributions have been reviewed by McLachlan (1992) and Wyman and others (1990). According to Wyman and others (1990) and Viollaz and others (1995), normal approximations of discriminant scores seem to be more accurate than other approaches, consistent with our results.

A related approach was given by Dobbin and Simon (2007), but ours appears to be more general and accurate (at the expense of being more computational). Theoretical bounds on generalization error from machine learning theory give another path of investigation (Hastie and others, 2001). For the related goal of identifying individually significant data dimensions (features), much study design work has built on feature-by-feature false discovery rate ideas (Benjamini and Hochberg, 1995, Storey, 2002, Efron, 2007). Feature-by-feature metrics of study design efficacy include the expected discovery rate (Gadbury and others 2004), anticipated average power (Pounds and Cheng, 2005), expected number of false discoveries (Tsai and others, 2005), and probability of informative features ranking highly (Pepe and others, 2003). Numerous recent studies give methods for feature selection or estimation of generalization error given real data, as opposed to prospective study design (e.g. Mukherjee and others (2003), Fu and others (2005), Wang and Shen (2006).

2. PROBLEM DEFINITION

Consider samples of size n_j for each of J classes ($j\in \{1,\dots ,J\}$), with each sample having M dimensions. By a high-dimensional classification problem, we mean $M\gg n$, where $n={\sum }_{j=1}^J{n}_j$ is the total sample size. For the training samples, from which the classifier will be estimated, let be the data vector for the ith sample of class j. Let X_j be all the data for class j and X be all the training data.

Let the number of dimensions of the data distributions that are truly informative (i.e. differ between classes) be M_I and those that are truly uninformative be M_U, with M = M_I + M_U. In the examples below, we will for simplicity use J = 2 and group means centered around 0 with all variances equal to 1. Let Δ be the vector of differences between class means for the informative dimensions, so the means from group 1 are (−0.5 Δ, 0_MU) and the means from group 2 are (0.5 Δ, 0_MU), where 0_MU is a length M_U vector of zeros. In this notation, a true pattern is defined by (Δ, M_U) and a study design scenario is defined by (Δ, M_U, n), where n = (n₁, n₂).

A classifier $\psi ({\mathbf{x}}_G\left|\mathbf{X}\right)$ predicts the class, $j\in 1,\dots ,J$, of a new (generalization or validation) sample x_G based on the training data, X. The generalization sample comes from one of the same distributions (for its unknown class) as the training samples. Define the conditional generalization error for class j as the expected fraction of incorrect classifications for a new sample, x_Gj, from class j given a training sample X,

(2.1)

where the expectation is over x_Gj sampled from true distribution j and the indicator function I() is 1 if is true and 0 otherwise.

Define the conditional generalization error across all classes as

(2.2)

where P(j) is the probability that a new sample is from class j.

The generalization error for a new sample from group j is the conditional generalization error averaged over training samples:

(2.3)

where E_T denotes expectation over training samples, X, with sample sizes n. Finally, the overall generalization error is

(2.4)

Given a generalization sample X_G, with replicate data x_Gj from groups $j=1,2$, and a classification procedure $\psi ({\mathbf{x}}_G\left|\mathbf{X}\right)$, define the “pattern discovery power” as the expected probability of rejecting the null hypothesis that the predictions $\psi ({\mathbf{x}}_{Gj}\left|\mathbf{X}\right)$ are independent of the true class labels, using an appropriate statistical test, with expectations over both the training and generalization samples. This is the probability that the independent validation step of an entire study concludes that the estimated classifier is at least better than random. This paper focuses on calculating generalization error rather than pattern discovery power, but the latter relates to one of the ultimate judgments about a study—whether something nonrandom has been independently validated—and is represented graphically with the simulation results.

3. SIMULATION–APPROXIMATION OF GENERALIZATION ERROR

Next, we give a joint simulation and approximation approach to estimate efficiently the generalization error rates CGj and G_j for multivariate normal data analyzed with linear discriminant analysis. Define a partition of the space of X samples into R nonoverlapping regions, ${\Omega }_1,\dots ,{\Omega }_R$, that determine which dimensions of X are selected to estimate the classifier, that is, the feature selection. Define δ = (δ₁, …, δ_M) to be a vector of 0s and 1s, with ${\delta }_k=1$ if dimension k will be used for classification and 0 if not. For all $\mathbf{X}\in {\Omega }_r$, the same dimensions of X are used by the classifier (so $R\ge 2^M$), so it makes sense to write δ as a function of ${\Omega }_r$: δ_r ≡ δ(Ω_r).

The generalization error for class j can be factored as

(3.1)

where $P(·)$ is the probability indicated by its argument.

We develop approximations for $E_{\text{T}}[{\text{CG}}_j(\mathbf{\Delta },M_{\text{U}}\left|\mathbf{X}\right)|\mathbf{X}\in {\Omega }_r]$ based on the first 2 moments of $P\left(\mathbf{X}\right|\mathbf{X}\in {\Omega }_r)$, the probability density of training data sets given that they lead to feature selection δ_r. This is an expected generalization error given that the training and generalization samples do not come from the same distributions. We use Monte Carlo samples to estimate $P(\mathbf{X}\in {\Omega }_r)$ and the first 2 moments of $P\left(\mathbf{X}\right|\mathbf{X}\in {\Omega }_r)$, which can be generated efficiently. In what follows, $\Omega \in \{{\Omega }_1,\dots ,{\Omega }_R\}$.

In a real analysis, feature selection is intertwined with the problem of how many features to include, which is one type of regularization parameter that may be optimized over data-based estimates of generalization error, such as cross-validation. From the study design point of view, the goal is to provide insight into typical study outcomes under various scenarios. Instead of trying to include optimization of the number of features within each approximation, we calculate the approximation across a range of the feature-selection thresholds. This does not include variation or suboptimality in the feature-selection threshold in our estimates of generalization error distributions, but it does offer insight about the sensitivity of generalization error to the feature-selection threshold, which provides context and builds intuition for interpreting results with real data.

3.1. Monte Carlo approximation of feature selection

Next, we show how $P(\mathbf{X}\in \Omega )$ and the mean and variance of $P\left(\mathbf{X}\right|\mathbf{X}\in \Omega )$ can be estimated with Monte Carlo methods. In the examples here, we assume feature selection is based on feature-by-feature univariate t-tests, which, when the data dimensions really are independent, makes the analysis optimistic because it “knows” this aspect of the “truth.” It is common to use feature-by-feature hypothesis tests to estimate false discovery rates as part of analyzing a high-dimensional study, so this simplification allows our results to stand side-by-side with expected false discovery rates and related ideas in considering study designs.

Consider a single data dimension, k, which may or may not be truly informative, for which δ_k will be 1 if the dimension is selected for the pattern and 0 if not. Let $x_{ijk}$ be the kth dimension of sample i from class j. Let the n₁ and n₂ samples from groups j = 1 and j = 2, respectively, be normally distributed in dimension k: . Suppose the decision to include feature k in classification is based on the P-value of a t-test. One calculates for $j=1,2$; , where ${\text{df}}_s=n_1+n_2-2$ are the degrees of freedom of s_k²; and . The feature is included if $|t_k|\hspace{0.17em}>\hspace{0.17em}{t}_{1-P_{\text{c}}/2,{\text{df}}_s}$, where $P_{\text{c}}$ is a threshold significance level for choosing ${\delta }_k=1$ and $t_{1-P_{\text{c}}/2,{\text{df}}_s}$ is the inverse cumulative t-density at $1-P_{\text{c}}/2$ with ${\text{df}}_s$ degrees of freedom.

It is equivalent to consider the 2 independent random variables

(3.2)

and . Then,

(3.3)

and

(3.4)

Using or $g(z,e^2)={\sigma }^2{e}^2/{\text{df}}_s$ in (3.4) gives an estimate of the mean difference between groups 1 and 2 or the within-group variance, respectively, given that the t-test is significant.

Working with the densities of z and e² allows more efficient numerical methods to estimate (3.3) and (3.4) than if one worked with the densities of $x_{ijk}$ directly. Next, 2 possible Monte Carlo implementations are given, but a variety of numerical methods could be used. For the case of a t-test, (3.3) is simply a cumulative density of a noncentral t-distribution with noncentrality parameter and ${\text{df}}_s$ degrees of freedom. For a Monte Carlo estimate of (3.4), define $\{z^{\left(l\right)},e^{2,\left(l\right)}\},l=1,\dots ,m$, to be a simulated sample from , which can be generated efficiently with a Markov chain Monte Carlo (MCMC) algorithm. Then, a Monte Carlo estimate of (3.4) is

(3.5)

Even a small sample (by MCMC standards) of say $m=100$ can be reasonable for (3.5).

If one chose to extend the basic idea here for a test for which values of (3.3) are not as easily available as a noncentral t-distribution, then both (3.3) and (3.4) could be estimated by Monte Carlo. For that case, redefine $\{z^{\left(l\right)},e^{2,\left(l\right)}\},l=1,\dots ,m$, to be a Monte Carlo sample of size m from $P(z,e^2)$. Then, the natural estimates of (3.3) and (3.4) are

(3.6)

and

(3.7)

Extensions based on other Monte Carlo numerical integration techniques (such as importance sampling) are straightforward and not our focus here.

3.2. Approximations for generalization error

Let be the parameter vector of the classification function ψ, a linear discriminant function in the examples here. An estimated classifier $\psi ({\mathbf{x}}_{Gj}\left|\mathbf{X}\right)$ is defined by estimated parameters = (X). For more concise notation, we view generalization error as a function of , that is, CG_j(Δ, M_U|X) = CG_j().

Delta approximation. A delta approximation for the class generalization error given $\mathbf{X}\in \Omega$ is

(3.8)

where is the second derivative of CG_j with respect to _r and _s evaluated at is the covariance between the r and the s dimensions of |X ∈ Ω, and p is the number of features selected due to $\mathbf{X}\in \Omega$. The delta approximation is derived by Taylor series expansion of the expectation integral around . Note that although the dimensions (or features) are assumed to be independent for feature selection, after they are selected they are approximated as multivariate normal, so the covariances in (3.8) are not necessarily zero.

Normal score approximation. Classifiers typically involve a continuous score function, , with prediction of group 1, $\psi ({\mathbf{x}}_{Gj}\left|\mathbf{X}\right)=1$, if < 0 (by convention here) and prediction of group 2, $\psi ({\mathbf{x}}_{Gj}\left|\mathbf{X}\right)=2$, if > 0. The normal score approximation is to treat as normally distributed with mean E[] and variance V[]. Then,

(3.9)

where $u_1=+1$, $u_2=-1$, and $\Phi (·)$ is the standard normal cumulative density function.

Relation to linear discriminant theory. For the case that ψ is a linear discriminant function, we need to calculate and 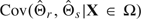for the delta approximation and E[] and V[] for the normal score approximation. Define ${\mathbf{x}}_{Fij}$ to be the selected training features (i.e. given $\mathbf{X}\in \Omega$) of the ith sample from class j. It is convenient to arrange the signs of the data in a consistent manner, so we assume (without loss of generality) that whenever dimension k is included in the classifier, (i.e. if , reverse the signs of the data). Then, define μ_Fj and Σ_F to be the mean vector and covariance matrix of ${\mathbf{x}}_{Fij}$, respectively. The difference between means is ${\mathbf{\Delta }}_F={\mathbf{\mu }}_{F2}-{\mathbf{\mu }}_{F1}$. By symmetry, ${\mathbf{\mu }}_{F1}+{\mathbf{\mu }}_{F2}=0$. The distributions of the ${\mathbf{x}}_{Fij}$ will not typically be normal because they are conditioned on a significant difference between normal sample means, but the approximation below uses exact expressions (see supplementary material available at Biostatistics online) for , and V[] under the assumption that the distributions are normal. The expressions use results of Siskind (1972) on the second moments of inverse Wishart distributions, which are related to the sampling distribution of . This allows full incorporation of multivariate sampling variability in estimating the linear discriminant classifier and uses the principle that second moment–based approximations derived from normal theory are often reasonable. Thus, there are really 2 approximations happening: an approximation of training features (given they have been selected) as multivariate normally distributed and either the delta approximation or normal score approximation of generalization error.

3.3. Linear discriminant analysis when the training and validation samples follow different distributions

As above, define a training sample of , $i=1,\dots ,n_1$, from class 1 and , $i=1,\dots ,n_2$, from class 2. Define ${\mathbf{\Delta }}_F={\mathbf{\mu }}_{F2}-{\mathbf{\mu }}_{F1}$, with ${\mathbf{\Delta }}_F\hspace{0.17em}>\hspace{0.17em}0$ in every dimension. Define the “true” parameters of ψ in the linear discriminant case as =(w, a), where and $\mathbf{a}=0.5({\mathbf{\mu }}_{F1}+{\mathbf{\mu }}_{F2})=0$. These are estimated by , where

(3.10)

is the pooled unbiased estimate of , and . This is the setup of standard linear discriminant analysis (McLachlan, 1992).

Define a validation sample from class j as . The discriminant score for a value x_G is

(3.11)

with prediction of class 1 for < 0 and class 2 for > 0. If the training and validation samples came from the same distributions, then w and a would give the optimal discriminant function.

We maintain the generality of the prior log-odds ratio, $\text{log}\left(P\right(1)/P(2\left)\right)$, in the derivations. In the simulations below, we assume $P\left(1\right)=P\left(2\right)$. These values may be very different for a population screening test, where only a very small fraction is expected to have a disease condition, compared to a problem such as disease classification given disease presence. Consideration of $P\left(1\right)\ne P\left(2\right)$ is standard in balancing sensitivity and specificity of medical tests.

To use the delta approximation (3.8), we need the first 2 moments of and and the derivatives of the generalization error with respect to the elements of and . To use the normal score approximation (3.9), we need the first 2 moments of . These are given exactly in the supplementary material available at Biostatistics online for the approximation that the training samples are normally distributed given that the selected dimensions were individually significant.

3.4. Summation over feature spaces

It remains to complete the calculation (3.1) efficiently by combining the Monte Carlo estimates of (3.3) and (3.4) and the approximations (3.8) or (3.9). If the space of features that might be selected is relatively simple, then one might directly enumerate cases where $P(\mathbf{X}\in \Omega )$ is appreciably greater than zero; this is not stated mathematically here. More generally, one can use a Monte Carlo sample from the space of selected features to approximate (3.1).

Let $\left\{{\Omega }^{\left(l\right)}\right\},l=1,\dots ,m$, be a sample from $P(\Omega )\equiv P(\mathbf{X}\in \Omega )$. Corresponding to each partition piece Ω, there is a distribution $P\left(\mathbf{X}\right|\mathbf{X}\in \Omega )$. Since this is characterized by ${\mathbf{\Delta }}_F$ and ${\mathbf{\Sigma }}_F$ (estimated by (3.5)), we denote . Then, the Monte Carlo approximation of (3.1) is

(3.12)

For feature-by-feature selection as discussed above, the relationship ${\mathbf{\delta }}_r=\mathbf{\delta }({\Omega }_r),r=1,\dots ,R,$ is one-to-one, so we can identify $P({\mathbf{\delta }}_r)\equiv P({\Omega }_r)$. Then, sampling from $P(\Omega )$ in practice amounts to simulating on a feature-by-feature basis whether each feature is selected.

3.5. Choice of feature-selection thresholds

The above simulation and approximation steps require a choice for the P-value cutoff, P_c, used for feature selection. In practice, one can consider a range of P_c-values based on heuristic considerations to encompass the value of P_c that minimizes the expected validation error. In the simulation results here (supplementary material available at Biostatistics online, summarized below), the following heuristics perform well. The lower bound P_L of P_c is set to the value at which the probability of zero true discoveries is 30% because excluding most or all informative features will not lead to good patterns. The upper bound P_U of P_c is the minimum of 2 values. The first is the P_c level at which the probability of including all informative features equals 80%, on the rationale that after including most or all informative features, error rates will only get worse as false features are added. The second is the P_c such that the expected number of uninformative features is $N/2-M_{\text{I}}$, that is, the expected total number of features if all truly informative features are included should not exceed $N/2$. In scenarios where the second bound was lower than the first, higher P_c would lead to worse validation error rates due to many uninformative features.

3.6. Summary of simulation–approximation method

In summary, the simulation–approximation procedure uses the following steps:

• 1. Choose Δ, $M_{\text{U}}$, and n to define a study scenario.

• 2. Choose a useful range of feature-selection thresholds, P_c, which influence how many features are chosen in the feature-selection stage.

• 3. For each (unique) dimension of Δ and each P_c, use the noncentral t-distribution and/or Monte Carlo methods to estimate

  • a) the probability that the feature will be selected,
  • b) the expected within-group variances and difference between group means given that the feature is selected.

• 4. For the Monte Carlo approximation (3.12), generate a sample of training feature combinations, $\left\{{\Omega }^{\left(l\right)}\right\}$, for which the generalization error will be approximated.

• 5. For each training feature combination, use the variances and mean differences given that the features are selected to approximate the generalization error using either (3.8) or (3.9) with the calculations in the supplementary material available at Biostatistics online.

• 6. Sum the terms in (3.12).

4. SIMULATION STUDY

Results of simulations of 7 realistic study designs are detailed in the supplementary material available at Biostatistics online. The first 6 scenarios consider optimal (i.e. Bayes) error rates of 0.05, 0.10, and 0.20 with either 3 (few strong) or 12 (many weak) truly informative dimensions, while the seventh considers optimal error of 0.05 from 46 (very many, very weak) dimensions. All scenarios use equal discovery sample sizes for control and disease groups, $n_1=n_2$, with the same mean difference for all informative dimensions and 10 patients per group for validation power. The simulation–approximation is accurate with the normal score approximation in all scenarios and with the delta approximation in all scenarios except for very many, very weak true features. Both methods are most accurate when most of the variation in generalization error is due to variation in which features are selected rather than in discriminant parameters given the feature space. Much larger numbers of truly informative dimensions would render the approximations inaccurate, and, moreover, suggest methods beyond basic linear discriminant analysis (LDA), such as shrinkage methods to constrain high variances in estimated patterns.

Several realistic scenarios have limited statistical power for validation and lead to substantially suboptimal patterns. With 12 informative and 2000 uninformative features and optimal error rate of 20%, sample sizes of 20, 50, and 100 give median validation error rates around 48%, 40%, and 30–35%, respectively, with only sample sizes of 100 giving better than 50% power for validation. If the features give optimal error rate of 10%, then 50 patients per group give high validation power but with median error rates of roughly 18–22% for 1000–5000 uninformative dimensions. With an optimal error rate of 5%, 20 samples would give roughly 50–80% validation power at 5% significance for 1000–5000 uninformative dimensions.

For a given optimal error rate, it is much harder to find patterns from many weak than from few strong informative features. Given optimal error rate of 20%, 50 patients per group for 3 strong features give better results than 100 patients per group with 12 weak features. For optimal error rate of 10% or 5%, 20 patients per group for 3 strong features give roughly comparable performance to 50 patients per group for 12 weak features. In summary, by far the strongest factors in pattern discovery power are sample size and individual feature strength. Some of these results are sobering in light of sample sizes in typical studies. It is plausible that some real studies to discover diagnostic patterns from high-dimensional assays could have low power for independent validation and find patterns far from the best true pattern.

5. DISCUSSION

Prospective analysis of study design for high-dimensional pattern discovery is important to plan studies with reasonable expectations of success based on scientific guesswork about the types of real patterns that might exist. The complexity of feature selection and pattern analysis methods raises many challenges for prospective study design. Here, we have explored a middle road between simulation and approximation, with simulations to handle variability in the selected features and an approximation of linear discriminant analysis given that the selected features appear to be informative in training data.

One of the most complicated ways in which the scenarios here may be optimistic is their lack of multivariate patterns and pattern recognition methods. Multivariate patterns could include correlated features that appear to be individually weak but are collectively strong or even harder possibilities such as the classic “XOR” (checkerboard) problem, where each marginal distribution has no information and only more complicated models than LDA can represent the pattern. In such problems, the hazard of over-fitting is greater than for the simulations here and would likely produce less favorable results. Other directions for further exploration of the relationships between sample size, numbers of informative and noninformative features, true optimal error rate, and discovery and generalization error rates include the following: generation of data from distributions that are unknown to the learning method (i.e. non-normal), further development of the relationship between false discovery rates and pattern discovery power, and further theoretical development of accurate approximations and/or efficient simulations.