Abstract
RNA internal loops are often important sites for folding and function. Residues in internal loops can have pKa values shifted close to neutral pH because of the local structural environment. A series of RNA internal loops were studied at different pH by UV absorbance versus temperature melting experiments and imino proton nuclear magnetic resonance (NMR). A stabilizing CA pair forms at pH 7 in the 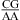 and
and 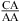 nearest neighbors when the CA pair is the first noncanonical pair (loop-terminal pair) in 3 × 3 nucleotide and larger size-symmetric internal loops. These
nearest neighbors when the CA pair is the first noncanonical pair (loop-terminal pair) in 3 × 3 nucleotide and larger size-symmetric internal loops. These  and
and 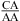 nearest neighbors, with CA adjacent to a closing Watson−Crick pair, are further stabilized when the pH is lowered from 7 to 5.5. The results are consistent with a significantly larger fraction (from ∼20% at pH 7 to ∼90% at pH 5.5) of adenines being protonated at the N1 position to form stabilizing wobble CA+ pairs adjacent to a sheared GA or AA pair. The noncanonical pair adjacent to the GA pair in
nearest neighbors, with CA adjacent to a closing Watson−Crick pair, are further stabilized when the pH is lowered from 7 to 5.5. The results are consistent with a significantly larger fraction (from ∼20% at pH 7 to ∼90% at pH 5.5) of adenines being protonated at the N1 position to form stabilizing wobble CA+ pairs adjacent to a sheared GA or AA pair. The noncanonical pair adjacent to the GA pair in 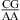 can either stabilize or destabilize the loop, consistent with the sequence-dependent thermodynamics of GA pairs. No significant pH-dependent stabilization is found for most of the other nearest neighbor combinations involving CA pairs (e.g.,
can either stabilize or destabilize the loop, consistent with the sequence-dependent thermodynamics of GA pairs. No significant pH-dependent stabilization is found for most of the other nearest neighbor combinations involving CA pairs (e.g., 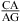 and
and 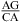 ), which is consistent with the formation of various nonwobble pairs observed in different local sequence contexts in crystal and NMR structures. A revised free-energy model, including stabilization by wobble CA+ pairs, is derived for predicting stabilities of medium-size RNA internal loops.
), which is consistent with the formation of various nonwobble pairs observed in different local sequence contexts in crystal and NMR structures. A revised free-energy model, including stabilization by wobble CA+ pairs, is derived for predicting stabilities of medium-size RNA internal loops.
The N1 nitrogen of adenine and N3 nitrogen of cytosine normally have pKa values of 3.5 and 4.2, respectively, but the pKa values (1−3) and thermodynamic contributions (4−7) of noncanonical pairs involving A and C in folded DNA and RNA are sequence- and context-dependent.
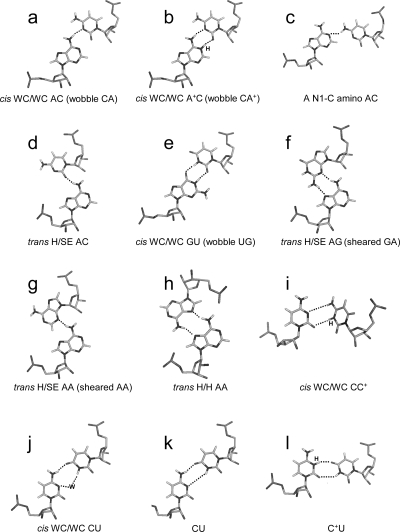
General acid−base catalysis, involving protonation and deprotonation of nucleobases at physiological pH, has been found for ribozyme catalysis of cleavage and ligation of specific phosphodiester bonds (2,6). The formation of wobble CA+ (cis Watson−Crick/Watson−Crick) pairs (Figure 1b) causes local and global conformational changes in RNA (8−13). Understanding the sequence-dependent driving force of a pKa shift of nucleobases within noncanonical pairs is needed to provide insight into RNA folding and catalytic mechanisms (6,7). It may also facilitate better understanding of the pH-dependent assembly of RNA viruses (14).
Figure 1.
Structures of several base pairs discussed in the paper. The hydrogen atoms in phosphate−sugar backbones are not shown. Only the base−base hydrogen bonds are shown. The proton from protonation and the bridging water are labeled with H and W, respectively. Most of the structures are taken from the BGSU Basepair Catalogue (http://rna.bgsu.edu/FR3D/basepair/). See ref (43) for notations.
The thermodynamics of CA pairs is also important for bioinformatic approaches that reveal structure−function relationships for RNA. For example, an approach for identifying which strand of complementary RNAs is most likely to rely on structure for function depends upon the different thermodynamic stabilities of CA and GU pairs (15).
Here, thermodynamic stabilities of a variety of RNA internal loops were measured in 1 M NaCl at pH 7 and 5.5. At pH 7, a nearest neighbor of 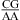 or
or 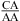 , with the CA adjacent to a closing canonical pair, can stabilize 3 × 3 nucleotide and larger size-symmetric (n1 = n2)1 internal loops on average by about 1 kcal/mol at 37 °C. Such nearest neighbors with the CA adjacent to a closing Watson−Crick pair are further stabilized on average by 1 kcal/mol at 37 °C when the pH is lowered from 7 to 5.5. Dependent upon the sequence, the noncanonical pair adjacent to the GA pair in
, with the CA adjacent to a closing canonical pair, can stabilize 3 × 3 nucleotide and larger size-symmetric (n1 = n2)1 internal loops on average by about 1 kcal/mol at 37 °C. Such nearest neighbors with the CA adjacent to a closing Watson−Crick pair are further stabilized on average by 1 kcal/mol at 37 °C when the pH is lowered from 7 to 5.5. Dependent upon the sequence, the noncanonical pair adjacent to the GA pair in 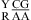 or
or 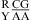 can either stabilize or destabilize the medium-size internal loops, consistent with the previous thermodynamic model (16). A better understanding of the protonation effects should help improve the prediction of the RNA internal loop structure and stability and provide a deeper insight into folding and function of large RNA.
can either stabilize or destabilize the medium-size internal loops, consistent with the previous thermodynamic model (16). A better understanding of the protonation effects should help improve the prediction of the RNA internal loop structure and stability and provide a deeper insight into folding and function of large RNA.
Materials and Methods
Oligonucleotide Synthesis and Purification
Oligonucleotides were synthesized on an Applied Biosystems 392 DNA/RNA synthesizer using the phosphoramidite method (17,18), deprotected, and purified, as described previously (19,20). Controlled pore glass (CPG) supports and phosphoramidites were purchased from Proligo, AZCO, Glen Research, or ChemGenes. The mass of all oligonucleotides was verified by electrospray ionization mass spectrometry (ESI−MS). Purities were checked by reverse-phase high-performance liquid chromatography (HPLC) or analytical thin-layer chromatography (TLC), and all were greater than 95% pure.
UV Absorbance Versus Temperature Melting Experiments and Thermodynamics
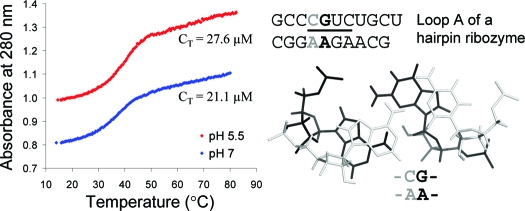
Concentrations of single-stranded oligonucleotides were approximated from the absorbance at 280 nm and 80 °C, and extinction coefficients were predicted from those of dinucleotide monophosphates and nucleosides (21,22) with RNAcalc (http://www.meltwin.com) (23). The extinction coefficients were estimated by replacing purine riboside with adenosine. Although extinction coefficients differ upon functional group substitutions, individual nucleotides contribute only a small portion of the oligomer extinction and, thus, do not significantly affect thermodynamic measurements. UV melting buffer conditions were 1 M NaCl, 20 mM sodium cacodylate, and 0.5 mM sodium ethylenediaminetetraacetic acid (EDTA) at pH 7 and 5.5 or 1 M NaCl, 20 mM 4-(2-hydroxyethyl)-1-piperazinepropanesulfonic acid) (HEPPS), 0.5 mM sodium EDTA at pH 8. Cacodylate and HEPPS were used because their pKa values are essentially temperature-independent. Curves of absorbance at 280 nm versus temperature were acquired using a heating rate of 1 °C/min with a Beckman Coulter DU640C spectrophotometer, having a Peltier temperature controller cooled with a water bath.
Melting curves were first fit to a two-state model with MeltWin (http://www.meltwin.com) (23), assuming linear sloping baselines and temperature-independent ΔH° and ΔS° (23−25). Presumably, the pKa values do not change until the RNA duplex melts; i.e., pKa values exhibit a two-state manner (with zero-sloping baselines) coupled with the melting of an RNA structure (7). This is a reasonable assumption because nucleobase protonation/deprotonation is linked with the two-state folding/unfolding of the RNA duplex. The temperature at which half the strands are in duplex, TM, at total strand concentration, CT, was used to calculate thermodynamic parameters for duplex formation according to (26)
Here, R is the gas constant, 1.987 cal mol−1 K−1, and a is 1 for self-complementary duplexes and 4 for non-self-complementary duplexes. All of the ΔH° values from TM−1 versus ln(CT/a) plots (eq 1) and from the average of the fits of melting curves to two-state transitions agree within 15%, suggesting that the two-state model is a reasonable approximation for these transitions. The equation ΔG°37 = ΔH° − (310.15)ΔS° was used to calculate the free-energy change at 37 °C (310.15 K).
Exchangeable Proton NMR Spectroscopy
All exchangeable proton spectra (27) were acquired on a Varian Inova 500 MHz (1H) spectrometer. One-dimensional imino proton spectra were acquired with an S pulse sequence (28) at temperatures ranging from −5 to 40 °C in 80 mM NaCl, 10 mM sodium phosphate, and 0.5 mM sodium EDTA. SNOESY spectra (28) were recorded with an 150 ms mixing time from −5 to 10 °C. The Felix (2000) software package (Molecular Simulations, Inc.) was used to process 2D spectra. Proton spectra were referenced to H2O or HDO at a known temperature-dependent chemical shift relative to 3-(trimethylsilyl)tetradeutero sodium propionate (TSP).
Results
Thermodynamics at Different pH
An RNA secondary-structure prediction and analysis program, RNAstructure 4.2 (http://rna.urmc.rochester.edu/rnastructure.html) (29), was used to design sequences that form heteroduplexes without competing homoduplexes. Thermal melting studies of the individual single strands (16,19) (see ) confirmed the absence of competing homoduplexes. Measured thermodynamic parameters at 1 M NaCl for duplexes and internal loops (calculated by eq 3a shown below) are listed in Tables 1 and 2, respectively. For a given duplex or internal loop, the values from bottom to top are for pH values 5.5, 7, and 8, respectively. In Tables 1 and 2, most sequences are ordered from the most negative to the most positive values of ΔΔG°37,pH, which is defined as
For several duplexes with two loop-terminal CA pairs, ΔΔG°37,pH is half the value given by eq 2 (see the footnotes of Tables 1 and 2). Measured thermodynamic parameters for the formation of the internal loops (Table 2 and ) are calculated according to the following equation (30):
For example,
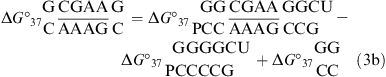 |
Here, ΔG°37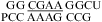 is the measured value of the duplex containing the internal loop (Table 1); ΔG°37
is the measured value of the duplex containing the internal loop (Table 1); ΔG°37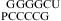 is calculated from the measured value of the duplex
is calculated from the measured value of the duplex 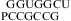 (20) by a nearest neighbor model (25,31) (ΔG°37
(20) by a nearest neighbor model (25,31) (ΔG°37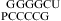 = ΔG°37
= ΔG°37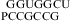 − ΔG°37
− ΔG°37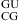 − ΔG°37
− ΔG°37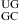 + ΔG°37
+ ΔG°37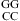 ); and ΔG°37
); and ΔG°37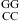 is the free-energy increment for the nearest neighbor base stack interaction interrupted by the internal loop. Values for ΔH°loop and ΔS°loop are calculated similarly. Whenever available, measured thermodynamic values of canonical stems are used for the calculation of measured thermodynamic parameters of loops. All of the thermodynamic parameters used in this calculation are derived from TM−1 versus ln(CT/a) plots (eq 1).
is the free-energy increment for the nearest neighbor base stack interaction interrupted by the internal loop. Values for ΔH°loop and ΔS°loop are calculated similarly. Whenever available, measured thermodynamic values of canonical stems are used for the calculation of measured thermodynamic parameters of loops. All of the thermodynamic parameters used in this calculation are derived from TM−1 versus ln(CT/a) plots (eq 1).
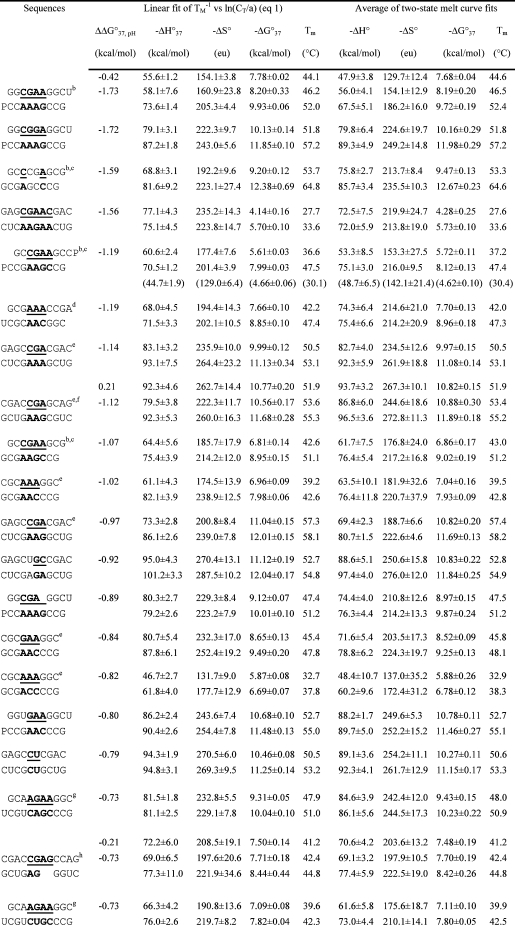
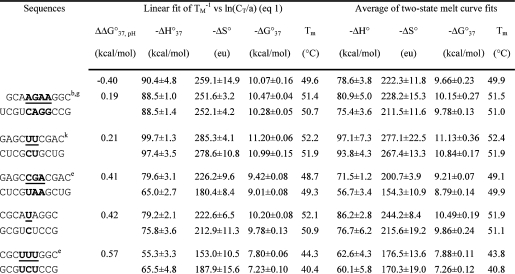
Table 1. Measured Thermodynamic Parameters for RNA Duplex Formation in 1 M NaCl.
|
For each duplex, the values from bottom to top are measured at pH 5.5, 7, and 8, respectively. Sequences are ordered from the most negative to the most positive values of ΔΔG°37,pH = ΔG°37,pH5.5 − ΔG°37,pH7, unless noted in footnote . Tm values were calculated from eq 1 at CT = 0.1 mM. Data in parentheses were measured in NMR buffer with 80 mM NaCl at pH 7.
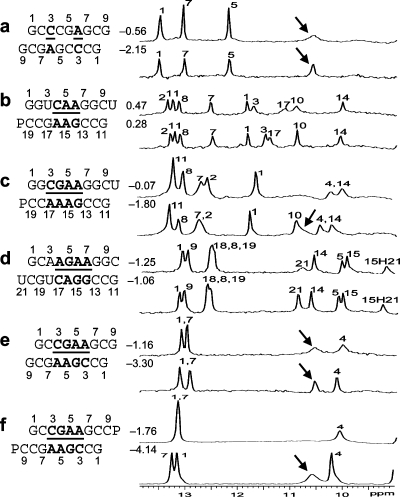
Imino proton NMR spectra were measured (Figure 2).
ΔΔG°37,pH is per CA pair.
Loop sequence from a J4/5 loop of a group I intron (36).
Data at pH 7 are from ref (19).
Loop sequence derived from the loop A of hairpin ribozyme (3).
Loop sequence from the Alu domain of human SRP RNA (71).
The pH-independent thermodynamics is consistent with the NMR structure without the formation of the C+U pair (61).
The pH-independent thermodynamics is consistent with the NMR structure without the formation of the UC+ pair (62).
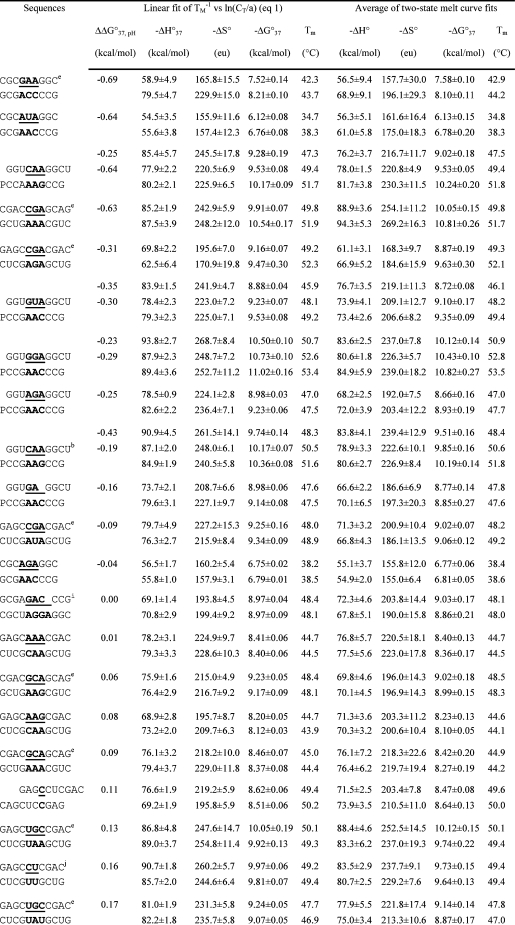
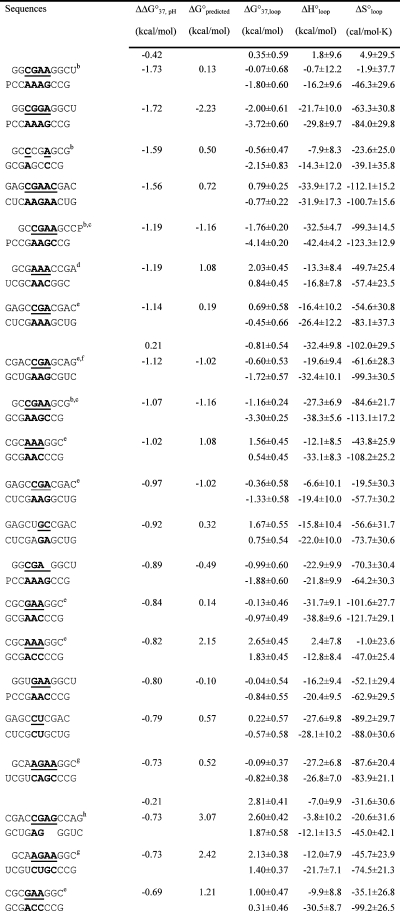
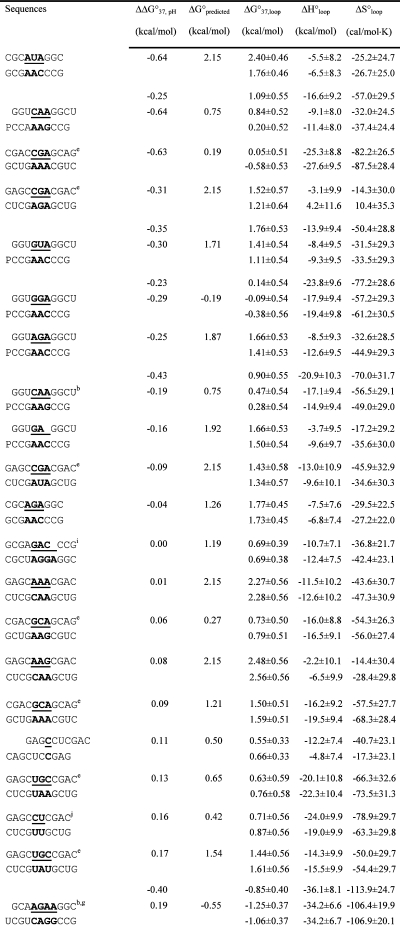
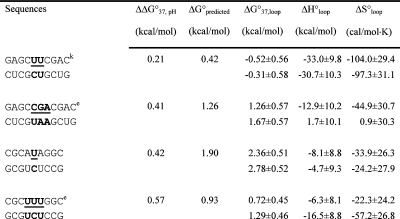
Table 2. Measured and Predicted Thermodynamic Parameters for RNA Internal Loop Formation in 1 M NaCl.
|
Calculated from eq 3a and data in Table 1 unless noted otherwise. Experimental errors for ΔG°37, ΔH°, and ΔS° for the canonical stems are estimated as 4, 12, and 13.5%, respectively, according to ref (25). These errors were propagated to estimate errors in loop thermodynamics. For each duplex, the values from the bottom to the top are measured at pH 5.5, 7, and 8, respectively. Sequences are ordered from the most negative to the most positive values of ΔΔG°37,pH = ΔG°37,pH5.5 − ΔG°37,pH7, except for (GCCCGAGCG)2 and those noted in footnote , where ΔΔG°37,pH is divided by 2. ΔG°predicted values are calculated according to eq 4. Loops smaller than 3 × 3 nucleotides are predicted according to refs (16, 29, and 31).
Imino proton NMR spectra were measured (Figure 2).
ΔG°5′CR/3′AA bonus is applied twice to predict the free energy for loop formation.
Loop sequence from a J4/5 loop of a group I intron (36).
Data at pH 7 are from ref (19).
Loop sequence derived from the loop A of hairpin ribozyme (8).
Loop sequence from the Alu domain of human SRP RNA (71).
The pH-independent thermodynamics is consistent with the NMR structure without the formation of the C+U pair (61).
The pH-independent thermodynamics is consistent with the NMR structure without the formation of the UC+ pair (62).
The thermodynamics of canonical stems is calculated for pH 7 and assumed to be independent of the pH between 5.5 and 8, as shown for other stems (32,33). This is a reasonable assumption because the N1 of adenine and N3 of cytosine normally have pKa values of 3.5 and 4.2, respectively, and the pKa values shift further down in forming Watson−Crick pairs in canonical stems (1−3,7). In addition, most of the duplexes do not form wobble CA+ or CC+ pairs (panels b and i of Figure 1) and do not show a pH effect, consistent with the assumption of pH-independent thermodynamics in the absence of CA+ or CC+ pairs (Table 1 and ).
Thermodynamic Model Including Stabilization Effects of CA and CA+ Pairs in Medium-Size RNA Internal Loops
Measured free energies of RNA internal loops with 6−10 nucleotides, ΔG°37, loop, reported here and previously (16,19,20) for 1 M NaCl at pH 7 and 37 °C were combined for linear regression to the equation
 |
Here, n1 and n2 are the number of nucleotides on each side of the loop; m1−m8 can be 0, 1, or 2; and the definitions of free-energy parameters are given in Table 3. Multiple linear regression on 168 loop free energies () gives the free-energy parameters listed in Table 3, with an R2 = 0.87 and standard deviation of 0.55 kcal/mol, which averages less than 0.07 kcal/mol for each nucleotide contributing to ΔG°predicted at 37 °C. The last term (ΔG°5′CR/3′AA bonus = −1.07 kcal/mol) in eq 4 represents the only difference with the equation derived previously (16). Without the last term, R2 = 0.82 and the standard deviation is 0.65 kcal/mol. Aside from the last term, the parameters in Table 3 are essentially the same as previously derived (16). Note that the bonus and penalty parameters have negative and positive values, respectively.
Table 3. Free-Energy Parameters (kcal/mol) at 37 °C for Predicting 3 × 3 Nucleotide and Larger RNA Internal Loops.
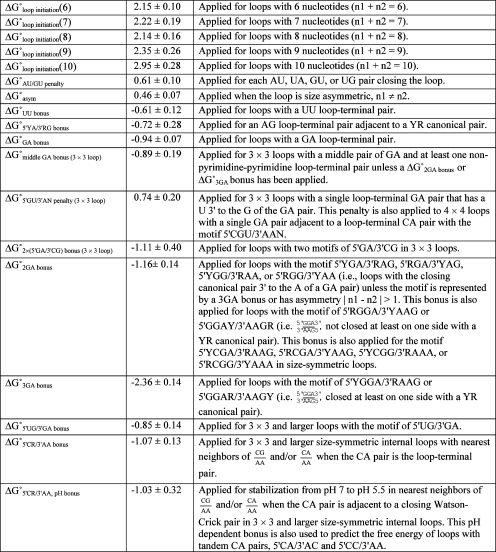 |
These parameters are used to predict the free energy of the 3 × 3 nucleotide and larger internal loops in 1 M NaCl according to eq 4. Except for the new parameters, ΔG°5′CR/3′AA bonus and ΔG°5′CR/3′AA, pH bonus, the parameters derived here are similar to those in ref (16). YR is a canonical pair of CG, UA, or UG, with the pyrimidine Y on the 5′ side of the internal loop. In general, Y and R are defined, respectively, as U or C and A or G in the UG, UA, or CG pair.
Size-symmetric internal loops with 5′CR/3′AA nearest neighbors with the CA adjacent to a closing Watson–Crick pair, are further stabilized on average by 1.03 ± 0.32 kcal/mol when the pH is lowered from 7 to 5.5 (see ). Thus, a bonus, ΔG°5′CR/3′AA, pH bonus = −1.03 ± 0.32 kcal/mol, is used to account for the pH stabilization at pH 5.5 compared to pH 7 (Table 3). At this stage, we do not apply ΔG°5′CR/3′AA, pH bonus for the size-symmetric internal loops with 5′CR/3′AA nearest neighbors with the CA adjacent to a closing UG or GU pair. Loops with tandem CA pairs are also further stabilized when the pH is lowered from 7 to 5.5 (see ).
Dependent upon the sequence, the noncanonical pair adjacent to the GA pair in 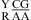 or
or 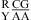 can either stabilize or destabilize the medium-size internal loops, consistent with the previous thermodynamic model (e.g., ΔG°2GA bonus and ΔG°5′GU/3′AN penalty (3 × 3 loop)) (16). No significant stabilization at pH 7 and 5.5 is found for most of the other nearest neighbor combinations involving CA pairs, which is consistent with wobble CA+ pairs (Figure 1b) not forming in different local sequence contexts in crystal and NMR structures (3,34−40). Thermodynamics of several duplexes were measured at pH 8, and no significant differences were observed compared to those at pH 7.
can either stabilize or destabilize the medium-size internal loops, consistent with the previous thermodynamic model (e.g., ΔG°2GA bonus and ΔG°5′GU/3′AN penalty (3 × 3 loop)) (16). No significant stabilization at pH 7 and 5.5 is found for most of the other nearest neighbor combinations involving CA pairs, which is consistent with wobble CA+ pairs (Figure 1b) not forming in different local sequence contexts in crystal and NMR structures (3,34−40). Thermodynamics of several duplexes were measured at pH 8, and no significant differences were observed compared to those at pH 7.
Exchangeable Proton NMR Spectra at Different pH
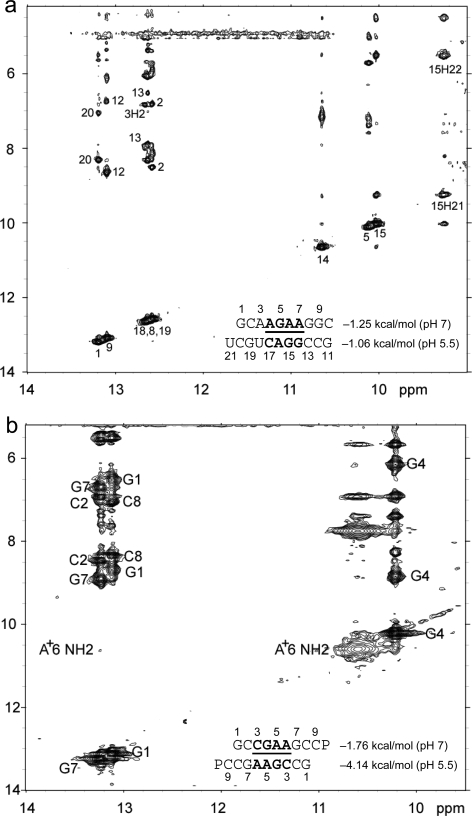
Figure 2 shows 1D imino proton NMR spectra for selected sequences. The resonances observed are consistent with the expected canonical and sheared GA base pairs. Figure 3 shows 2D SNOESY spectra for 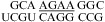 and
and 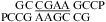 . The spectra contain the typical cross-peak patterns expected for the imino protons in the duplexes, although in some cases, definitive assignment is not made. In Figure 3a, four of the five imino protons between 12 and 14 ppm exhibit cross-peak patterns typical of a Watson−Crick GC pair (two strong cross-peaks to resonances that show a very strong cross-peak to each other and to a likely H5 resonance, as expected for the C amino protons of a GC pair). The fifth imino proton shows a strong cross-peak to a narrow resonance, as expected for a U imino proton close to the AH2 in a Watson−Crick AU pair. There is a very weak cross-peak between the imino protons of two of the GC pairs, which are assigned to G1 and G19. Three other resonances between 9.5 and 11 ppm have chemical shifts and cross-peaks typical of G imino protons in sheared GA pairs, including those observed in a duplex with the same sequence of three GA pairs (20). In Figure 3b, the two imino proton resonances between 13.0 and 13.5 ppm show typical GC pair characteristics. A cross-peak between the equivalent imino protons in the similar sequence,
. The spectra contain the typical cross-peak patterns expected for the imino protons in the duplexes, although in some cases, definitive assignment is not made. In Figure 3a, four of the five imino protons between 12 and 14 ppm exhibit cross-peak patterns typical of a Watson−Crick GC pair (two strong cross-peaks to resonances that show a very strong cross-peak to each other and to a likely H5 resonance, as expected for the C amino protons of a GC pair). The fifth imino proton shows a strong cross-peak to a narrow resonance, as expected for a U imino proton close to the AH2 in a Watson−Crick AU pair. There is a very weak cross-peak between the imino protons of two of the GC pairs, which are assigned to G1 and G19. Three other resonances between 9.5 and 11 ppm have chemical shifts and cross-peaks typical of G imino protons in sheared GA pairs, including those observed in a duplex with the same sequence of three GA pairs (20). In Figure 3b, the two imino proton resonances between 13.0 and 13.5 ppm show typical GC pair characteristics. A cross-peak between the equivalent imino protons in the similar sequence, 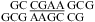 , confirms that these protons are in adjacent pairs (see ).
, confirms that these protons are in adjacent pairs (see ).
Figure 2.
One-dimensional imino proton NMR spectra in 80 mM NaCl, 10 mM sodium phosphate, and 0.5 mM sodium EDTA at 0 °C unless otherwise noted at different pH values, with the top spectrum of each RNA sequence acquired at near pH 7 and the bottom spectrum at lower pH. Assignments are preliminary and largely based on assignments for similar sequences. Values between sequence and spectra are ΔG°37,loop in kcal/mol measured in 1 M NaCl at pH 5.5 (bottom) and pH 7 (top). Resonances labeled with arrows are consistent with a previous assignment to the adenine amino protons in a CA+ pair (12). No resonances were observed between 14 and 16 ppm. (a) CT = 0.5 mM, pH 6.9 and 5.4; (b) CT = 0.3 mM, pH 6.9 and 5.0; (c) CT = 1.8 mM, pH 6.8 and 5.1; (d) CT = 0.5 mM, pH 6.9 and 5.3 (see Figure 3a for 2D spectrum); (e) CT = 0.5 mM, pH 6.9 and 5.9; and (f) CT = 1.5 mM, pH 6.6 and 5.1 (5 °C, see Figure 3b for the 2D spectrum).
Figure 3.
Two-dimensional exchangeable proton SNOESY spectra (150 ms mixing time in 80 mM NaCl, 10 mM sodium phosphate, and 0.5 mM sodium EDTA). The NOE cross-peaks of G imino protons to C amino and G amino protons are labeled with corresponding residues. Values beside the sequence are ΔG°37,loop in kcal/mol measured in 1 M NaCl at pH 5.5 (bottom) and pH 7 (top). (a) 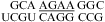 (CT = 0.5 mM, pH 5.3, 0 °C, see Figure 2d for 1D spectrum). There is a very weak cross-peak of G1H1−G19H1 (not shown). The imino protons of G5, G14, and G15 have chemical shifts and cross-peaks typical of consecutive sheared GA pairs (16,20,72). The G15 amino protons resonate at 9.2 and 5.5 ppm, respectively, suggesting the formation of sheared GA pairs with G5 and G15 in the C2′-endo sugar pucker (73,74). There is no indication of the formation of A+C pair in this loop. (b)
(CT = 0.5 mM, pH 5.3, 0 °C, see Figure 2d for 1D spectrum). There is a very weak cross-peak of G1H1−G19H1 (not shown). The imino protons of G5, G14, and G15 have chemical shifts and cross-peaks typical of consecutive sheared GA pairs (16,20,72). The G15 amino protons resonate at 9.2 and 5.5 ppm, respectively, suggesting the formation of sheared GA pairs with G5 and G15 in the C2′-endo sugar pucker (73,74). There is no indication of the formation of A+C pair in this loop. (b) 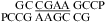 (CT = 1.5 mM, pH 5.1, −5 °C, see Figure 2f for 1D spectrum). The cross-peak of G1H1−G7H1 is unresolved because of overlap but is observed in
(CT = 1.5 mM, pH 5.1, −5 °C, see Figure 2f for 1D spectrum). The cross-peak of G1H1−G7H1 is unresolved because of overlap but is observed in 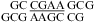 (see and Figure 2e for 1D spectrum). The broad peak at ∼10.6 ppm is likely due to the amino protons of A+6, which shows a strong cross-peak to the other amino proton and a weak cross-peak to the G7 imino proton. Adenine amino protons with similar chemical shift have been observed in other cases of CA+ pairs (12). The G4 amino protons resonate at 8.8 and 6.2 ppm, respectively, suggesting the formation of sheared GA pairs with G4 in the C2′-endo sugar pucker (73,74).
(see and Figure 2e for 1D spectrum). The broad peak at ∼10.6 ppm is likely due to the amino protons of A+6, which shows a strong cross-peak to the other amino proton and a weak cross-peak to the G7 imino proton. Adenine amino protons with similar chemical shift have been observed in other cases of CA+ pairs (12). The G4 amino protons resonate at 8.8 and 6.2 ppm, respectively, suggesting the formation of sheared GA pairs with G4 in the C2′-endo sugar pucker (73,74).
The 1D imino proton spectra of several duplexes in Figure 2 reveal a similar peak near ∼10.6 ppm that increases in intensity at lower pH. These peaks are likely due to adenine amino protons in CA+ pairs, as observed in other cases of CA+ pairs (12). The broad peak in Figure 3b at ∼10.6 ppm assigned to the A6 amino group has a strong cross-peak to the other amino proton and a weak cross-peak to the G7 imino proton.
Discussion
The pKa of N1 nitrogen of adenine is about 3.5 and shifted by less than 0.3 pK unit when incorporated into unpaired single strands (7). Small pKa shifts were also observed for other nucleobases when incorporated in unpaired single strands (7,41). When incorporated into double helices, however, the pKa of A shifts down in Watson−Crick pairs but up by as much as 3 pK units in some noncanonical pairs (1,7). For example, the pKa of the A in a 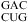 sequence is ≤3.1, whereas the two A’s in
sequence is ≤3.1, whereas the two A’s in 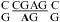 (loop sequence of a leadzyme) have pKa values of 6.5 (shown in bold) and 4.3, respectively (1).
(loop sequence of a leadzyme) have pKa values of 6.5 (shown in bold) and 4.3, respectively (1).
In addition to local context effects, pKa values may also be shifted by global context. For example, the local dielectric constant in the middle of large structures, such as the ribosome and viral RNA encapsidated in virion, may differ from that in bulk water. Thus, it is important to know the possible effects of protonation on thermodynamic stability of RNA structures.
Dependent upon the sequence context and pH, a CA+ pair can form with A protonated at the N1 position (Figure 1b). The CA+ pair can form two hydrogen bonds and easily fit into an A-form helix. Thus, it has the potential to stabilize a helix. Protonation will also affect base stacking and other interactions, however, so that effects of protonation will be sequence-dependent. The thermodynamic studies of short oligonucleotides at pH 7 and 5.5 provide insight into the sequence- and context-dependent stabilization effects of CA pairs. Many of the sequences studied were chosen because three-dimensional structures are available to allow stability−structure correlations (1,3,8,9,12,34−40,42).
Single CA+ Pairs Stabilize Watson−Crick Stems
The CA+ wobble pair is isosteric with a UG wobble pair (panels b and e of Figure 1) and can fit in an A- or B-form structure without large backbone distortion (see ) (12,42,43). Consistent with formation of a CA+ wobble pair, the measured loop free energy of 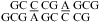 (ΔG°37,pH7,loop = −0.56 kcal/mol for each CA pair) is about 1 kcal/mol more stable than that predicted by a previous thermodynamic model (29,44), without considering a stabilization effect for the CA pair (Table 2). In addition, a stabilization of ΔΔG°37,pH = −1.59 kcal/mol was found per
(ΔG°37,pH7,loop = −0.56 kcal/mol for each CA pair) is about 1 kcal/mol more stable than that predicted by a previous thermodynamic model (29,44), without considering a stabilization effect for the CA pair (Table 2). In addition, a stabilization of ΔΔG°37,pH = −1.59 kcal/mol was found per 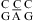 nearest neighbor combination at pH 5.5 compared to that at pH 7 (Table 2). The resonance at ∼10.6 ppm in
nearest neighbor combination at pH 5.5 compared to that at pH 7 (Table 2). The resonance at ∼10.6 ppm in 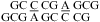 (Figure 2a) is consistent with a previous assignment to A amino protons in a CA+ pair (12). Thus, both UV thermal melting and NMR results are consistent with the formation of the hydrogen bonds in a wobble CA+ pair (Figure 1b).
(Figure 2a) is consistent with a previous assignment to A amino protons in a CA+ pair (12). Thus, both UV thermal melting and NMR results are consistent with the formation of the hydrogen bonds in a wobble CA+ pair (Figure 1b).
A similar pH effect on thermodynamics was found for single CA mismatches in DNA (4,7). The A+ imino proton was not observed by NMR (4), probably because of broadening by solvent exchange. The pKa of the N1 of adenine in the DNA nearest neighbor combination, 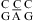 , is about 6.6, as measured with a pH profile of the chemical shifts of the N1 nitrogen (45).
, is about 6.6, as measured with a pH profile of the chemical shifts of the N1 nitrogen (45).
Detailed understanding of the stabilization effect of CA or CA+ wobble pairs within different Watson−Crick stems will provide insight into RNA structure and function. For example, a single CA mismatch has been shown to be preferred for efficient A to I editing by adenosine deaminases acting on RNA (ADAR) (46). Understanding the sequence-dependent thermodynamics of CA (44) and CI mismatches and the pH effect might facilitate better understanding of the editing specificity and mechanism (46).
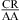 Nearest Neighbor with CA Adjacent to a Closing Canonical Pair Stabilizes 3 × 3 and Larger Size-Symmetric Internal Loops at pH 7
Nearest Neighbor with CA Adjacent to a Closing Canonical Pair Stabilizes 3 × 3 and Larger Size-Symmetric Internal Loops at pH 7
When the CA is the first noncanonical (loop-terminal) pair, most of the size-symmetric internal loops with nearest neighbors of 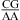 and/or
and/or 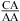 are more stable than predicted by a recently proposed thermodynamic model (16,19). A bonus parameter, ΔG°5′CR/3′AA bonus = −1.07 ± 0.13 kcal/mol at pH 7, is derived here for such nearest neighbor combinations with a loop-terminal CA pair followed by a GA or AA pair (Table 3). These nearest neighbor combinations occur in several internal loops within catalytic ribozymes, e.g., the VS ribozyme substrate loop (8,9),
are more stable than predicted by a recently proposed thermodynamic model (16,19). A bonus parameter, ΔG°5′CR/3′AA bonus = −1.07 ± 0.13 kcal/mol at pH 7, is derived here for such nearest neighbor combinations with a loop-terminal CA pair followed by a GA or AA pair (Table 3). These nearest neighbor combinations occur in several internal loops within catalytic ribozymes, e.g., the VS ribozyme substrate loop (8,9), 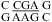 (ΔG°37,pH7,loop = −0.60 kcal/mol), the loop A of hairpin ribozyme (3),
(ΔG°37,pH7,loop = −0.60 kcal/mol), the loop A of hairpin ribozyme (3), 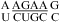 (ΔG°37,pH7,loop = 2.13 kcal/mol), and the J4/5 loop of a group I intron (36),
(ΔG°37,pH7,loop = 2.13 kcal/mol), and the J4/5 loop of a group I intron (36), 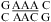 (ΔG°37,pH7,loop = 2.03 kcal/mol).
(ΔG°37,pH7,loop = 2.03 kcal/mol).
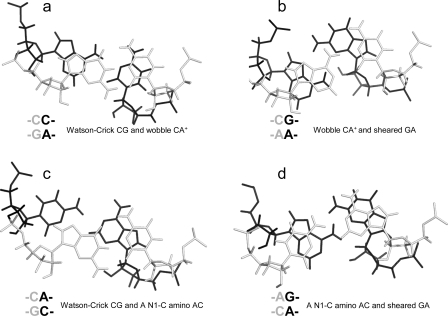
The thermodynamic stabilization is consistent with the geometric compatibility of 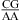 and
and 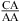 nearest neighbors if the CA pair is protonated and the purine−purine pair is sheared (panels f and g of Figure 1) (3,8,9,36). Solution NMR reveals a protonated wobble CA+ pair adjacent to a sheared GA pair (
nearest neighbors if the CA pair is protonated and the purine−purine pair is sheared (panels f and g of Figure 1) (3,8,9,36). Solution NMR reveals a protonated wobble CA+ pair adjacent to a sheared GA pair (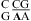 , sequence in a hairpin ribozyme and VS ribozyme) (see Figure 4 and ), and the pKa of the A (in bold) is about 6.3, according to the pH profile of the chemical shifts of the C2 carbon in adenine (3,8,9). Consistently, the amino protons of A+ (shown in bold) for the symmetric loop
, sequence in a hairpin ribozyme and VS ribozyme) (see Figure 4 and ), and the pKa of the A (in bold) is about 6.3, according to the pH profile of the chemical shifts of the C2 carbon in adenine (3,8,9). Consistently, the amino protons of A+ (shown in bold) for the symmetric loop 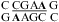 resonate at 10.6 ppm at neutral and lower pH (panels e and f of Figure 2 and Figure 3b). In addition, a wobble CA pair forms adjacent to a sheared AA pair (shown in bold) within the J4/5 loop,
resonate at 10.6 ppm at neutral and lower pH (panels e and f of Figure 2 and Figure 3b). In addition, a wobble CA pair forms adjacent to a sheared AA pair (shown in bold) within the J4/5 loop, 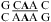 , in the crystal structure of a group I intron (see ) (36).
, in the crystal structure of a group I intron (see ) (36).
Figure 4.
Base stacking and base pairing involving CA. Base pairs shown in gray lines are closer to the viewer. The Watson−Crick CG, wobble CA+ (the proton from protonation is not shown), and sheared GA pairs shown in a and b are taken from the 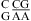 segment of the NMR structure of the substrate loop of VS ribozyme (9). The Watson−Crick CG, A N1−C amino single hydrogen-bond AC pair, and sheared GA shown in c and d are taken from
segment of the NMR structure of the substrate loop of VS ribozyme (9). The Watson−Crick CG, A N1−C amino single hydrogen-bond AC pair, and sheared GA shown in c and d are taken from 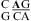 segment of the NMR structure of loop B of a hairpin ribozyme (37). The stacking figures are generated by the 3DNA program (75).
segment of the NMR structure of loop B of a hairpin ribozyme (37). The stacking figures are generated by the 3DNA program (75).
The noncanonical pair adjacent to a loop-terminal GA pair was previously found to either stabilize (e.g., ΔG°2GA bonus) or destabilize (e.g., ΔG°5′GU/3′AN penalty (3 × 3 loop)) the loop (16,19). Here, the noncanonical pair adjacent to the GA pair in the nearest neighbor combinations 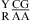 and
and 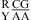 was also found to be stabilizing or destabilizing, although the CA but not GA pair is a loop-terminal pair. Thus, when the parameters in Table 3 were derived, the CA pair in the nearest neighbor combinations
was also found to be stabilizing or destabilizing, although the CA but not GA pair is a loop-terminal pair. Thus, when the parameters in Table 3 were derived, the CA pair in the nearest neighbor combinations 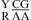 and
and 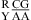 was treated in a way similar to a canonical wobble UG pair; i.e., the thermodynamic effect of the GA pair was modeled as a first noncanonical (loop-terminal) pair. For example, a penalty of ΔG°5′GU/3′AN penalty (3 × 3 loop) = 0.74 kcal/mol was applied for
was treated in a way similar to a canonical wobble UG pair; i.e., the thermodynamic effect of the GA pair was modeled as a first noncanonical (loop-terminal) pair. For example, a penalty of ΔG°5′GU/3′AN penalty (3 × 3 loop) = 0.74 kcal/mol was applied for 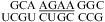 (ΔG°37,pH7,loop = 2.13 kcal/mol), although this parameter was proposed only for 3 × 3 nucleotide internal loops (16,19). This is suggested by NMR data for this loop, which shows the formation of a stabilizing CA+ wobble pair, isosteric to a canonical wobble UG pair and adjacent to a sheared GA pair, even at nearly neutral pH (3). Consistent with the penalty of ΔG°5′GU/3′AN penalty (3 × 3 loop), the U is flipped out in an NMR structure of the
(ΔG°37,pH7,loop = 2.13 kcal/mol), although this parameter was proposed only for 3 × 3 nucleotide internal loops (16,19). This is suggested by NMR data for this loop, which shows the formation of a stabilizing CA+ wobble pair, isosteric to a canonical wobble UG pair and adjacent to a sheared GA pair, even at nearly neutral pH (3). Consistent with the penalty of ΔG°5′GU/3′AN penalty (3 × 3 loop), the U is flipped out in an NMR structure of the 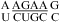 loop, which is from a hairpin ribozyme (3).
loop, which is from a hairpin ribozyme (3).
Similarly, a bonus of ΔG°2GA bonus = −1.16 kcal/mol (Table 3) was applied for 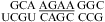 (ΔG°37,pH7,loop = −0.09 kcal/mol),
(ΔG°37,pH7,loop = −0.09 kcal/mol), 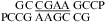 (ΔG°37,pH7,loop = −1.76 kcal/mol), and
(ΔG°37,pH7,loop = −1.76 kcal/mol), and 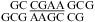 (ΔG°37,pH7,loop = −1.16 kcal/mol), although the two consecutive GA pairs are not adjacent to a canonical pair on either side. Note that, for the latter two sequences, the ΔG°5′CR/3′AA bonus was applied twice.
(ΔG°37,pH7,loop = −1.16 kcal/mol), although the two consecutive GA pairs are not adjacent to a canonical pair on either side. Note that, for the latter two sequences, the ΔG°5′CR/3′AA bonus was applied twice.
CA pairs are not treated exactly as canonical UG closing pairs, however. Only one thermodynamic parameter, ΔG°5′CR/3′AA bonus, is applied for the nearest neighbor combinations of 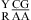 or
or 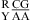 , but for
, but for 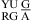 or
or 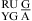 , three parameters of ΔG°
, three parameters of ΔG°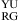 (or ΔG°
(or ΔG°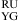 ), ΔG°5′UG/3′GA bonus, and ΔG°GA are applied (16).
), ΔG°5′UG/3′GA bonus, and ΔG°GA are applied (16).
 Nearest Neighbors with the CA Adjacent to a Watson−Crick Pair in Size-Symmetric Internal Loops Are More Stabilizing When the pH Is Lowered from 7 to 5.5
Nearest Neighbors with the CA Adjacent to a Watson−Crick Pair in Size-Symmetric Internal Loops Are More Stabilizing When the pH Is Lowered from 7 to 5.5
If a wobble CA+ pair is responsible for the extra stabilities observed for 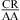 nearest neighbors, then lowering the pH should further enhance stability because a larger fraction of A is protonated for the formation of CA+ pairs. About 89 and 17% of adenine N1 residues are protonated at pH 5.5 and 7.0, respectively, with a pKa of 6.3, as shown for the A (in bold) in
nearest neighbors, then lowering the pH should further enhance stability because a larger fraction of A is protonated for the formation of CA+ pairs. About 89 and 17% of adenine N1 residues are protonated at pH 5.5 and 7.0, respectively, with a pKa of 6.3, as shown for the A (in bold) in 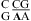 (3,8,9). We observed an enhanced stabilization of 1.03 ± 0.32 kcal/mol on average per nearest neighbor
(3,8,9). We observed an enhanced stabilization of 1.03 ± 0.32 kcal/mol on average per nearest neighbor 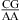 or
or 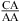 with the CA adjacent to a Watson−Crick pair when lowering pH from 7 to 5.5, e.g., the VS ribozyme substrate loop (8,9),
with the CA adjacent to a Watson−Crick pair when lowering pH from 7 to 5.5, e.g., the VS ribozyme substrate loop (8,9), 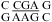 (ΔΔG°37,pH = −1.12 kcal/mol), and the J4/5 loop of a group I intron (36),
(ΔΔG°37,pH = −1.12 kcal/mol), and the J4/5 loop of a group I intron (36), 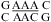 (ΔΔG°37,pH = −1.19 kcal/mol). Note that two CA+ pairs can form in the symmetric loop
(ΔΔG°37,pH = −1.19 kcal/mol). Note that two CA+ pairs can form in the symmetric loop 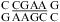 (ΔΔG°37,pH = −1.19 and −1.07 kcal/mol per CA pair for the two duplexes measured).
(ΔΔG°37,pH = −1.19 and −1.07 kcal/mol per CA pair for the two duplexes measured).
Only one pH-dependent bonus parameter, ΔG°5′CR/3′AA, pH bonus = −1.03 ± 0.32 kcal/mol, is derived here for 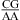 or
or 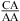 with CA adjacent to a Watson−Crick pair (Table 3). The sequence dependence is likely more complicated, however. For example, the thermodynamic stabilities of
with CA adjacent to a Watson−Crick pair (Table 3). The sequence dependence is likely more complicated, however. For example, the thermodynamic stabilities of 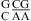 and
and 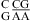 may be significantly different. A stabilization effect of ΔΔG°37,pH = −1.67 ± 0.10 kcal/mol per
may be significantly different. A stabilization effect of ΔΔG°37,pH = −1.67 ± 0.10 kcal/mol per 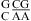 nearest neighbor combination was observed when lowering pH from 7 to 5.5, e.g.,
nearest neighbor combination was observed when lowering pH from 7 to 5.5, e.g., 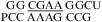 (ΔΔG°37,pH = −1.73 kcal/mol) and
(ΔΔG°37,pH = −1.73 kcal/mol) and 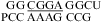 (ΔΔG°37,pH = −1.72 kcal/mol). This contrasts with the average of ΔΔG°37,pH = −0.98 ± 0.21 kcal/mol for loops with a
(ΔΔG°37,pH = −1.72 kcal/mol). This contrasts with the average of ΔΔG°37,pH = −0.98 ± 0.21 kcal/mol for loops with a 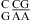 combination (see Table 2 and ). The pKa of A N1 in the CA pair of
combination (see Table 2 and ). The pKa of A N1 in the CA pair of 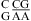 (sequence found in a hairpin ribozyme and VS ribozyme) is about 6.3 with a wobble CA pair adjacent to a sheared GA pair (3,8,9). Presumably, the same noncanonical base pairs form in
(sequence found in a hairpin ribozyme and VS ribozyme) is about 6.3 with a wobble CA pair adjacent to a sheared GA pair (3,8,9). Presumably, the same noncanonical base pairs form in 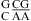 , although the pKa of A N1 in the CA pair is not known. Further detailed experimental (e.g., measurement of pKa) and computational studies (47,48) are needed to understand the different pH effect on the thermodynamics of
, although the pKa of A N1 in the CA pair is not known. Further detailed experimental (e.g., measurement of pKa) and computational studies (47,48) are needed to understand the different pH effect on the thermodynamics of 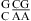 and
and 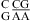 .
.
No Significant Stabilizing Effect Was Observed for CA Pairs within Other Sequence Contexts in Size-Symmetric Internal Loops
No significant thermodynamic stabilization (i.e., free-energy stabilization of 1 kcal/mol or more) at either pH 7 or 5.5 was found for size-symmetric loops with the A of a potential AC pair 3′ to the adjacent Watson−Crick pair, e.g., 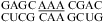 (ΔG°37,pH7,loop = 2.27 kcal/mol, ΔΔG°37,pH = 0.01 kcal/mol),
(ΔG°37,pH7,loop = 2.27 kcal/mol, ΔΔG°37,pH = 0.01 kcal/mol), 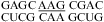 (ΔG°37,pH7,loop = 2.48 kcal/mol, ΔΔG°37,pH = 0.08 kcal/mol),
(ΔG°37,pH7,loop = 2.48 kcal/mol, ΔΔG°37,pH = 0.08 kcal/mol), 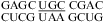 (ΔG°37,pH7,loop = 0.63 kcal/mol, ΔΔG°37,pH = 0.13 kcal/mol), and
(ΔG°37,pH7,loop = 0.63 kcal/mol, ΔΔG°37,pH = 0.13 kcal/mol), and 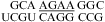 (ΔG°37,pH7,loop = −1.25 kcal/mol, ΔΔG°37,pH = 0.19 kcal/mol). The pH stabilization for
(ΔG°37,pH7,loop = −1.25 kcal/mol, ΔΔG°37,pH = 0.19 kcal/mol). The pH stabilization for 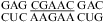 (ΔΔG°37,pH = −1.56 kcal/mol) and
(ΔΔG°37,pH = −1.56 kcal/mol) and 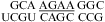 (ΔΔG°37,pH = −0.73 kcal/mol) can be attributed to the
(ΔΔG°37,pH = −0.73 kcal/mol) can be attributed to the 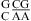 and
and 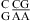 segments (see the discussion above for different pH stabilization observed for
segments (see the discussion above for different pH stabilization observed for 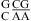 and
and 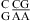 when lowering pH from 7 to 5.5), respectively, with no contribution from the
when lowering pH from 7 to 5.5), respectively, with no contribution from the 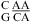 and
and 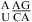 segments.
segments.
The lack of extra stability when the A of an AC pair is 3′ of a Watson−Crick pair is probably general. For example, on the basis of NMR spectra of a 7 × 9 nucleotide loop B domain of a hairpin ribozyme, the apparent pKa of the N1 position of the bold A in a 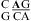 segment is 5.4, and, at pH 6.8, the AC has a single hydrogen-bond, A N1−C amino pair (Figure 1c). The GA is a sheared pair (37). Here, the single hydrogen-bond (A N1−C amino) AC pair has A and C shifted to major and minor grooves, respectively, which is opposite to a wobble AC pair. A sheared GA pair has G and A shifted to major and minor grooves, respectively, which favors base stacking between the single hydrogen-bond (A N1−C amino) AC and sheared GA pairs (see Figure 4d and ).
segment is 5.4, and, at pH 6.8, the AC has a single hydrogen-bond, A N1−C amino pair (Figure 1c). The GA is a sheared pair (37). Here, the single hydrogen-bond (A N1−C amino) AC pair has A and C shifted to major and minor grooves, respectively, which is opposite to a wobble AC pair. A sheared GA pair has G and A shifted to major and minor grooves, respectively, which favors base stacking between the single hydrogen-bond (A N1−C amino) AC and sheared GA pairs (see Figure 4d and ).
The enhanced stability of a CA pair with the C on the 3′ side of a Watson−Crick pair relative to one with the A on the 3′ side of a Watson−Crick pair may be related to stacking on the adjacent helix. As with the G of a UG pair (49), the A of a CA+ pair stacks to its 3′ side by shifting to the minor groove. Thus, having the Watson−Crick pair 3′ of the A provides more favorable stacking by increasing the base overlap (see Figure 4a and ). Interestingly, the U in 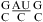 (loop sequence in a U6 RNA intramolecular stem loop), which is stacked within the helix at pH 7.0, is flipped out at pH 5.7 to favor a stacking interaction between wobble A+C and Watson−Crick GC pairs flanking the U bulge (10). Evidently, the stabilization effect of CA and/or CA+ pairs and the pKa of A in a CA pair is sequence-context-dependent.
(loop sequence in a U6 RNA intramolecular stem loop), which is stacked within the helix at pH 7.0, is flipped out at pH 5.7 to favor a stacking interaction between wobble A+C and Watson−Crick GC pairs flanking the U bulge (10). Evidently, the stabilization effect of CA and/or CA+ pairs and the pKa of A in a CA pair is sequence-context-dependent.
No significant stabilization was observed for 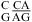 at either pH 7 or 5.5 in
at either pH 7 or 5.5 in 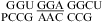 (ΔG°37,pH7,loop = −0.09 kcal/mol, ΔΔG°37,pH = −0.29 kcal/mol),
(ΔG°37,pH7,loop = −0.09 kcal/mol, ΔΔG°37,pH = −0.29 kcal/mol), 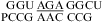 (ΔG°37,pH7,loop = 1.66 kcal/mol, ΔΔG°37,pH = −0.25 kcal/mol),
(ΔG°37,pH7,loop = 1.66 kcal/mol, ΔΔG°37,pH = −0.25 kcal/mol), 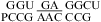 (ΔG°37,pH7,loop = 1.66 kcal/mol, ΔΔG°37,pH = −0.16 kcal/mol), and
(ΔG°37,pH7,loop = 1.66 kcal/mol, ΔΔG°37,pH = −0.16 kcal/mol), and 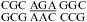 (ΔG°37,pH7,loop = 1.77 kcal/mol, ΔΔG°37,pH = −0.04 kcal/mol). This is consistent with sheared-type CA and GA pairs (trans Hoogsteen/sugar-edge AC and AG) (panels d and f of Figure 1) forming in the loop
(ΔG°37,pH7,loop = 1.77 kcal/mol, ΔΔG°37,pH = −0.04 kcal/mol). This is consistent with sheared-type CA and GA pairs (trans Hoogsteen/sugar-edge AC and AG) (panels d and f of Figure 1) forming in the loop 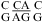 in helix 41a of the crystal structure of Thermus thermophilus 16S rRNA (39). It is possible, however, that a
in helix 41a of the crystal structure of Thermus thermophilus 16S rRNA (39). It is possible, however, that a 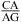 nearest neighbor may provide enhanced stability in other contexts. A wobble CA pair adjacent to a sheared GA pair was observed by NMR for the internal loop
nearest neighbor may provide enhanced stability in other contexts. A wobble CA pair adjacent to a sheared GA pair was observed by NMR for the internal loop 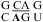 (sequence of a VS ribozyme active site loop), where the pKa of N1 of the bold A is 6.2 at 30 °C (50). Evidently, the formation of a stabilizing wobble AC or CA pair adjacent to a GA, AG, or AA pair is sequence-context-dependent.
(sequence of a VS ribozyme active site loop), where the pKa of N1 of the bold A is 6.2 at 30 °C (50). Evidently, the formation of a stabilizing wobble AC or CA pair adjacent to a GA, AG, or AA pair is sequence-context-dependent.
Adjacent CA Pairs Provide No Significant Stabilization at pH 7 But Are Stabilized by 0.8 kcal/mol on Average at pH 5.5
The 3 × 3 loops in duplexes, 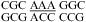 (ΔG°37,pH7,loop = 2.65 kcal/mol, ΔΔG°37,pH = −0.82 kcal/mol) and
(ΔG°37,pH7,loop = 2.65 kcal/mol, ΔΔG°37,pH = −0.82 kcal/mol) and 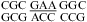 (ΔG°37,pH7,loop = 1.00 kcal/mol, ΔΔG°37,pH = −0.69 kcal/mol), are predicted well without a bonus parameter at pH 7 but have enhanced stabilities at pH 5.5. A similar pH-dependent effect was observed for the 2 × 2 loops in duplexes,
(ΔG°37,pH7,loop = 1.00 kcal/mol, ΔΔG°37,pH = −0.69 kcal/mol), are predicted well without a bonus parameter at pH 7 but have enhanced stabilities at pH 5.5. A similar pH-dependent effect was observed for the 2 × 2 loops in duplexes, 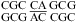 (ΔΔG°37,pH = −0.87 kcal/mol) and
(ΔΔG°37,pH = −0.87 kcal/mol) and 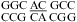 (ΔΔG°37,pH = −0.77 kcal/mol) (5). Perhaps adjacent protonated pairs are not electrostatically favorable and, thus, result in a lower pKa and stabilized only when pH is as low as 5.5. Tandem wobble CA pairs were observed in
(ΔΔG°37,pH = −0.77 kcal/mol) (5). Perhaps adjacent protonated pairs are not electrostatically favorable and, thus, result in a lower pKa and stabilized only when pH is as low as 5.5. Tandem wobble CA pairs were observed in 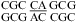 by X-ray crystallography at pH 5.5 (see ) (51). An average ΔG°37,pH bonus = −1.03 ± 0.32 kcal/mol (Table 3) is used to predict pH stabilization for both tandem CA pairs and single CA pairs in appropriate contexts, as described above.
by X-ray crystallography at pH 5.5 (see ) (51). An average ΔG°37,pH bonus = −1.03 ± 0.32 kcal/mol (Table 3) is used to predict pH stabilization for both tandem CA pairs and single CA pairs in appropriate contexts, as described above.
No Significant pH-Dependent Thermodynamic Effect Was Found for Nearest Neighbors with CA Adjacent to UG
For the three duplexes, 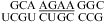 (ΔG°37,pH7,loop = 2.13 kcal/mol, ΔΔG°37,pH = −0.73 kcal/mol, but the pH effect is presumably only due to
(ΔG°37,pH7,loop = 2.13 kcal/mol, ΔΔG°37,pH = −0.73 kcal/mol, but the pH effect is presumably only due to 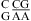 because no noncanonical pairs form in
because no noncanonical pairs form in 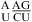 (3)),
(3)), 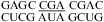 (ΔG°37,pH7,loop = 1.43 kcal/mol, ΔΔG°37,pH = −0.09 kcal/mol), and
(ΔG°37,pH7,loop = 1.43 kcal/mol, ΔΔG°37,pH = −0.09 kcal/mol), and 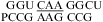 (ΔG°37,pH7,loop = 0.47 kcal/mol, ΔΔG°37,pH = −0.19 kcal/mol), no significant pH effect could be attributed to a CA pair adjacent to a UG pair. With the exception of
(ΔG°37,pH7,loop = 0.47 kcal/mol, ΔΔG°37,pH = −0.19 kcal/mol), no significant pH effect could be attributed to a CA pair adjacent to a UG pair. With the exception of 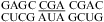 (ΔG°37,pH7,loop = 1.43 kcal/mol versus ΔG°predicted = 2.15 kcal/mol at pH 7, ΔΔG°37,pH = −0.09 kcal/mol), all of the loop free energies are well-predicted at pH 7 for the loops with a CA adjacent to a UG pair. Thus, it is unlikely that in these loops a wobble CA+ pair is formed adjacent to a wobble UG pair, with the pKa significantly above 7 for the adenine N1.
(ΔG°37,pH7,loop = 1.43 kcal/mol versus ΔG°predicted = 2.15 kcal/mol at pH 7, ΔΔG°37,pH = −0.09 kcal/mol), all of the loop free energies are well-predicted at pH 7 for the loops with a CA adjacent to a UG pair. Thus, it is unlikely that in these loops a wobble CA+ pair is formed adjacent to a wobble UG pair, with the pKa significantly above 7 for the adenine N1.
Note that there is also no significant thermodynamic difference between pH 8 and 7 for the loop 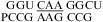 (ΔG°37,pH8,loop = 0.90 kcal/mol). We applied the bonus parameter of ΔG°5′CR/3′AA bonus for
(ΔG°37,pH8,loop = 0.90 kcal/mol). We applied the bonus parameter of ΔG°5′CR/3′AA bonus for 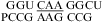 at pH 7, although there is no further stabilization at pH 5.5. The pH-dependent shifting of the imino proton resonances from the UG pair suggests a pH-dependent conformational change within the loop, however (Figure 2b). This may be another example of the idiosyncratic behavior of UG pairs. For example, thermodynamic and NMR studies suggest that adjacent UG pairs do not always form canonical wobble pairs (52,53).
at pH 7, although there is no further stabilization at pH 5.5. The pH-dependent shifting of the imino proton resonances from the UG pair suggests a pH-dependent conformational change within the loop, however (Figure 2b). This may be another example of the idiosyncratic behavior of UG pairs. For example, thermodynamic and NMR studies suggest that adjacent UG pairs do not always form canonical wobble pairs (52,53).
Context-Dependent pH Effect of CC Pairs
CC can form a cis Watson−Crick/Watson−Crick CC+ pair (Figure 1i). A pH-dependent stabilization was observed in 2 × 2 loops 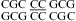 (ΔΔG°37,pH = −2.48 kcal/mol for two CC pairs) (5) and in
(ΔΔG°37,pH = −2.48 kcal/mol for two CC pairs) (5) and in 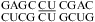 (ΔΔG°37,pH = −0.79 kcal/mol) (Table 2). In contrast, the stability of a single CC mismatch is essentially pH-independent and well-predicted,
(ΔΔG°37,pH = −0.79 kcal/mol) (Table 2). In contrast, the stability of a single CC mismatch is essentially pH-independent and well-predicted, 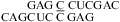 (ΔG°37,pH7,loop = 0.55 kcal/mol, ΔΔG°37,pH = 0.11 kcal/mol). The thermodynamic effect of GAC 3′ dangling ends are assumed to be the same as GA 3′ dangling ends (54,55) to calculate the measured thermodynamic parameters of the 1 × 1 loop with a single CC mismatch.
(ΔG°37,pH7,loop = 0.55 kcal/mol, ΔΔG°37,pH = 0.11 kcal/mol). The thermodynamic effect of GAC 3′ dangling ends are assumed to be the same as GA 3′ dangling ends (54,55) to calculate the measured thermodynamic parameters of the 1 × 1 loop with a single CC mismatch.
UC Pairs Are Not More Stable at Lower pH
No significant pH effect was found for 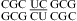 (ΔΔG°37,pH = −0.10 kcal/mol) and
(ΔΔG°37,pH = −0.10 kcal/mol) and 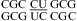 (ΔΔG°37,pH = −0.06 kcal/mol) (5). This is consistent with crystal structures of
(ΔΔG°37,pH = −0.06 kcal/mol) (5). This is consistent with crystal structures of 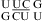 that reveal cis Watson−Crick/Watson−Crick UC pairs with a water-mediated hydrogen bond between the U imino proton and C N3 but without protonated nucleobases (Figure 1j) (56,57). Quantum chemical calculations show that a water-mediated UC pair is energetically preferred over a UC pair with two direct hydrogen bonds (U O4 to C amino and U H3 to C N3) (Figure 1k) (58). Molecular dynamics simulations of the loops
that reveal cis Watson−Crick/Watson−Crick UC pairs with a water-mediated hydrogen bond between the U imino proton and C N3 but without protonated nucleobases (Figure 1j) (56,57). Quantum chemical calculations show that a water-mediated UC pair is energetically preferred over a UC pair with two direct hydrogen bonds (U O4 to C amino and U H3 to C N3) (Figure 1k) (58). Molecular dynamics simulations of the loops 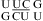 (59) and
(59) and 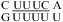 (sequence found in human telomerase RNA) (60) reveal dynamics of the water-mediated UC pairs. No significant pH effect is observed for
(sequence found in human telomerase RNA) (60) reveal dynamics of the water-mediated UC pairs. No significant pH effect is observed for 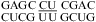 (ΔΔG°37,pH = 0.16 kcal/mol) and
(ΔΔG°37,pH = 0.16 kcal/mol) and 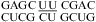 (ΔΔG°37,pH = 0.21 kcal/mol), which is consistent with the NMR structures of
(ΔΔG°37,pH = 0.21 kcal/mol), which is consistent with the NMR structures of 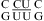 (sequence found in a poliovirus 3′-UTR) (61) and
(sequence found in a poliovirus 3′-UTR) (61) and 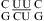 (sequence found in HCV IRES domain II) (62), which contain no protonated C+U and UC+ pairs (Figure 1l), respectively.
(sequence found in HCV IRES domain II) (62), which contain no protonated C+U and UC+ pairs (Figure 1l), respectively.
A Watson−Crick-type UC pair with two direct hydrogen bonds (U O4 to C amino and U H3 to C N3) (Figure 1k) was observed in  (loop found in several RNA viruses) by NMR (63,64), which is consistent with the small pH-dependent thermodynamics observed for
(loop found in several RNA viruses) by NMR (63,64), which is consistent with the small pH-dependent thermodynamics observed for 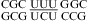 (ΔG°37,pH7,loop = 0.72 kcal/mol, ΔΔG°37,pH = 0.57 kcal/mol). The loop free energies at pH 7 are well-predicted, and no pH stabilization is observed for loops in the duplexes,
(ΔG°37,pH7,loop = 0.72 kcal/mol, ΔΔG°37,pH = 0.57 kcal/mol). The loop free energies at pH 7 are well-predicted, and no pH stabilization is observed for loops in the duplexes, 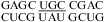 (ΔG°37,pH7,loop = 1.54 kcal/mol, ΔΔG°37,pH = 0.17 kcal/mol),
(ΔG°37,pH7,loop = 1.54 kcal/mol, ΔΔG°37,pH = 0.17 kcal/mol), 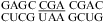 (ΔG°37,pH7,loop = 1.26 kcal/mol, ΔΔG°37,pH = 0.41 kcal/mol), or
(ΔG°37,pH7,loop = 1.26 kcal/mol, ΔΔG°37,pH = 0.41 kcal/mol), or 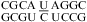 (ΔG°37,pH7,loop = 2.36 kcal/mol, ΔΔG°37,pH = 0.42 kcal/mol).
(ΔG°37,pH7,loop = 2.36 kcal/mol, ΔΔG°37,pH = 0.42 kcal/mol).
No pH Bonus Is Applied to Size-Asymmetric Internal Loops
The duplex, 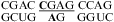 (ΔG°37,pH7,loop = 2.60 kcal/mol, ΔΔG°37,pH = −0.73 kcal/mol), has the 2 × 4 internal loop from the leadzyme (1,65−67) and is 0.73 kcal/mol more stable at pH 5.5 than pH 7. This stabilization is consistent with the formation of a wobble CA+ pair in the NMR structure without multivalent metal ions (1,65) but not with the crystal structure with multivalent ions (66) and a molecular modeling study of the active conformation (67). The molecular model of the active conformation is consistent with kinetic studies, in which different loop G’s are forced to be in syn glycosidic conformation (68).
(ΔG°37,pH7,loop = 2.60 kcal/mol, ΔΔG°37,pH = −0.73 kcal/mol), has the 2 × 4 internal loop from the leadzyme (1,65−67) and is 0.73 kcal/mol more stable at pH 5.5 than pH 7. This stabilization is consistent with the formation of a wobble CA+ pair in the NMR structure without multivalent metal ions (1,65) but not with the crystal structure with multivalent ions (66) and a molecular modeling study of the active conformation (67). The molecular model of the active conformation is consistent with kinetic studies, in which different loop G’s are forced to be in syn glycosidic conformation (68).
In helix 58 of the large ribosomal subunit of Haloarcula marismortui(40), trans Hoogsteen/sugar AC (Figure 1d) and trans Hoogsteen/Hoogsteen AA pairs (Figure 1h) (43) form in 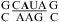 . The A in bold is in a syn glycosidic conformation, and the U is bulged out. Apparently, this conformation is more stable in this 3 × 4 internal loop than a wobble CA+ pair adjacent to a sheared AA pair. Further thermodynamic and structural studies are needed to see whether the loop structure is preformed or induced by tertiary and protein binding in the ribosome.
. The A in bold is in a syn glycosidic conformation, and the U is bulged out. Apparently, this conformation is more stable in this 3 × 4 internal loop than a wobble CA+ pair adjacent to a sheared AA pair. Further thermodynamic and structural studies are needed to see whether the loop structure is preformed or induced by tertiary and protein binding in the ribosome.
Moderate pH effects were found for the 1 × 2 loop in 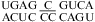 (ΔΔG°37,pH = −1.04 kcal/mol) and the 2 × 3 loop in
(ΔΔG°37,pH = −1.04 kcal/mol) and the 2 × 3 loop in 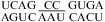 (ΔΔG°37,pH = −0.63 kcal/mol) (69). Pairings within the loop that are sensitive to pH and context are likely in size-asymmetric internal loops, because they provide flexibility (1,65−68). This will make it difficult to determine sequence- and pH-dependent rules for size-asymmetric internal loops and other flexible loops.
(ΔΔG°37,pH = −0.63 kcal/mol) (69). Pairings within the loop that are sensitive to pH and context are likely in size-asymmetric internal loops, because they provide flexibility (1,65−68). This will make it difficult to determine sequence- and pH-dependent rules for size-asymmetric internal loops and other flexible loops.
Thermodynamics of Internal Loops May Be Useful for Predicting Kinetics
The internal loops of 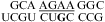 (ΔG°37,pH7,loop = 2.13 kcal/mol),
(ΔG°37,pH7,loop = 2.13 kcal/mol), 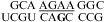 (ΔG°37,pH7,loop = −0.09 kcal/mol), and
(ΔG°37,pH7,loop = −0.09 kcal/mol), and 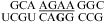 (ΔG°37,pH7,loop = −1.25 kcal/mol) belong to proposed consensus sequences in loop A of the hairpin ribozymes (3). The bold G has to flip out and dock with the loop B domain to form the functional hairpin ribozyme conformation (70). On the basis of loop A stability and structure, this step is predicted to be slowest at pH 7 for the
(ΔG°37,pH7,loop = −1.25 kcal/mol) belong to proposed consensus sequences in loop A of the hairpin ribozymes (3). The bold G has to flip out and dock with the loop B domain to form the functional hairpin ribozyme conformation (70). On the basis of loop A stability and structure, this step is predicted to be slowest at pH 7 for the 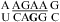 loop (Figure 3a) if the transition states for all of the sequences have similar free energies.
loop (Figure 3a) if the transition states for all of the sequences have similar free energies.
Conclusion
The pKa of the A N1 nitrogen in a CA pair depends upon local sequence context, as evidenced by thermodynamic and structural results shown here and previously (1,3,8,9,12,34−40,42). In a nearest neighbor of 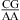 or
or 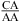 with the CA adjacent to a closing canonical pair (including wobble UG pairs), the formation of a wobble CA+ adjacent to a sheared GA or AA pair stabilizes 3 × 3 nucleotide and larger size-symmetric internal loops on average by about 1 kcal/mol at 37 °C, pH 7, and 1 M NaCl. Such nearest neighbors with the CA adjacent to a closing Watson−Crick pair are further stabilized on average by 1 kcal/mol at 37 °C when the pH is lowered from 7 to 5.5. Other stabilizing nearest neighbor combinations can exist to shift pKa. The pKa may also depend upon global context; e.g., pKa could be shifted in the middle of a large structure, such as the ribosome. The results presented here along with published NMR and crystal structures provide benchmarks to test free-energy and structural calculations by computational chemists.
with the CA adjacent to a closing canonical pair (including wobble UG pairs), the formation of a wobble CA+ adjacent to a sheared GA or AA pair stabilizes 3 × 3 nucleotide and larger size-symmetric internal loops on average by about 1 kcal/mol at 37 °C, pH 7, and 1 M NaCl. Such nearest neighbors with the CA adjacent to a closing Watson−Crick pair are further stabilized on average by 1 kcal/mol at 37 °C when the pH is lowered from 7 to 5.5. Other stabilizing nearest neighbor combinations can exist to shift pKa. The pKa may also depend upon global context; e.g., pKa could be shifted in the middle of a large structure, such as the ribosome. The results presented here along with published NMR and crystal structures provide benchmarks to test free-energy and structural calculations by computational chemists.
Acknowledgments
G.C. thanks Prof. C. C. Kao for discussions on viral RNA encapsidation.
Supporting Information Available
Tables of single-strand UV melting results, linear regression data, figures of base stacking and base pairing involving CA pairs, and an exchangeable proton SNOESY spectrum. This material is available free of charge via the Internet at http://pubs.acs.org.
This work was supported by National Institutes of Health (NIH) Grant GM22939.
Funding Statement
National Institutes of Health, United States
Footnotes
Abbreviations: CT, total concentration of all strands of oligonucleotides in solution; eu, entropy units in cal mol−1 K−1; n1 × n2, an internal loop with n1 nucleotides on one side and n2 nucleotides on the opposite side; P, purine riboside; RY, canonical pair of GC, AU, or GU, with R on the 5′ side and Y on the 3′ side of the internal loop; size-symmetric internal loops, a n1 × n2 nucleotide internal loop with n1 = n2; TM, melting temperature in kelvins; Tm, melting temperature in degrees Celsius; YR, canonical pair of CG, UA, or UG, with Y on the 5′ side and R on the 3′ side of the internal loop; ΔG°5′CR/3′AA bonus, a free-energy bonus derived to account for stabilization in the 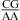 and/or
and/or 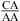 nearest neighbors when the CA pair is the first noncanonical pair (loop-terminal pair) in 3 × 3 nucleotide and larger size-symmetric internal loops at pH 7, 1 M NaCl, and 37 °C; ΔG°5′CR/3′AA, pH bonus, the free-energy bonus derived to account for stabilization from pH 7 to 5.5 in the
nearest neighbors when the CA pair is the first noncanonical pair (loop-terminal pair) in 3 × 3 nucleotide and larger size-symmetric internal loops at pH 7, 1 M NaCl, and 37 °C; ΔG°5′CR/3′AA, pH bonus, the free-energy bonus derived to account for stabilization from pH 7 to 5.5 in the 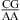 and/or
and/or 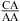 nearest neighbors when the CA pair is adjacent to a closing Watson−Crick pair in 3 × 3 nucleotide and larger size-symmetric internal loops (ΔG°5′CR/3′AA, pH bonus is also applied for loops with tandem CA pairs); ΔG°37,pH7,loop, the measured loop free energy at 37 °C and pH 7; ΔΔG°37,pH, the measured loop free-energy difference between pH 5.5 and 7, unless otherwise noted (see the footnotes of the tables).
nearest neighbors when the CA pair is adjacent to a closing Watson−Crick pair in 3 × 3 nucleotide and larger size-symmetric internal loops (ΔG°5′CR/3′AA, pH bonus is also applied for loops with tandem CA pairs); ΔG°37,pH7,loop, the measured loop free energy at 37 °C and pH 7; ΔΔG°37,pH, the measured loop free-energy difference between pH 5.5 and 7, unless otherwise noted (see the footnotes of the tables).
Supplementary Material
References
- Legault P.; Pardi A. (1997) Unusual dynamics and pKa shift at the active site of a lead-dependent ribozyme. J. Am. Chem. Soc. 119, 6621–6628. [Google Scholar]
- Bevilacqua P. C. (2003) Mechanistic considerations for general acid−base catalysis by RNA: Revisiting the mechanism of the hairpin ribozyme. Biochemistry 42, 2259–2265. [DOI] [PubMed] [Google Scholar]
- Cai Z.; Tinoco I. Jr. (1996) Solution structure of loop A from the hairpin ribozyme from tobacco ringspot virus satellite. Biochemistry 35, 6026–6036. [DOI] [PubMed] [Google Scholar]
- Allawi H. T.; SantaLucia J. Jr. (1998) Nearest-neighbor thermodynamics of internal AC mismatches in DNA: Sequence dependence and pH effects. Biochemistry 37, 9435–9444. [DOI] [PubMed] [Google Scholar]
- SantaLucia J. Jr.; Kierzek R.; Turner D. H. (1991) Stabilities of consecutive A·C, C·C, G·G, U·C, and U·U mismatches in RNA internal loops: Evidence for stable hydrogen bonded U·U and C·C+ pairs. Biochemistry 30, 8242–8251. [DOI] [PubMed] [Google Scholar]
- Bevilacqua P. C.; Brown T. S.; Chadalavada D.; Lecomte J.; Moody E.; Nakano S. (2005) Linkage between proton binding and folding in RNA: Implications for RNA catalysis. Biochem. Soc. Trans. 33, 466–470. [DOI] [PubMed] [Google Scholar]
- Moody E. M.; Lecomte J. T. J.; Bevilacqua P. C. (2005) Linkage between proton binding and folding in RNA: A thermodynamic framework and its experimental application for investigating pKa shifting. RNA 11, 157–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flinders J.; Dieckmann T. (2001) A pH controlled conformational switch in the cleavage site of the VS ribozyme substrate RNA. J. Mol. Biol. 308, 665–679. [DOI] [PubMed] [Google Scholar]
- Michiels P. J. A.; Schouten C. H. J.; Hilbers C. W.; Heus H. A. (2000) Structure of the ribozyme substrate hairpin of Neurospora VS RNA: A close look at the cleavage site. RNA 6, 1821–1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiter N. J.; Blad H.; Abildgaard F.; Butcher S. E. (2004) Dynamics in the U6 RNA intramolecular stem-loop: A base flipping conformational change. Biochemistry 43, 13739–13747. [DOI] [PubMed] [Google Scholar]
- Zimmermann G. R.; Shields T. P.; Jenison R. D.; Wick C. L.; Pardi A. (1998) A semiconserved residue inhibits complex formation by stabilizing interactions in the free state of a theophylline-binding RNA. Biochemistry 37, 9186–9192. [DOI] [PubMed] [Google Scholar]
- Puglisi J. D.; Wyatt J. R.; Tinoco I. Jr. (1990) Solution conformation of an RNA hairpin loop. Biochemistry 29, 4215–4226. [DOI] [PubMed] [Google Scholar]
- Durant P. C.; Bajji A. C.; Sundaram M.; Kumar R. K.; Davis D. R. (2005) Structural effects of hypermodified nucleosides in the Escherichia coli and human tRNALys anticodon loop: The effect of nucleosides s2U, mcm5U, mcm5s2U, mnm5s2U, t6A, and ms2t6A. Biochemistry 44, 8078–8089. [DOI] [PubMed] [Google Scholar]
- Bink H. H.; Hellendoorn K.; van der Meulen J.; Pleij C. W. (2002) Protonation of non-Watson−Crick base pairs and encapsidation of turnip yellow mosaic virus RNA. Proc. Natl. Acad. Sci. U.S.A. 99, 13465–13470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiche K.; Stadler P. F. (2007) RNAstrand: Reading direction of structured RNAs in multiple sequence alignments. Algorithms Mol. Biol. 2, 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G.; Turner D. H. (2006) Consecutive GA pairs stabilize medium-size RNA internal loops. Biochemistry 45, 4025–4043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Usman N.; Ogilvie K. K.; Jiang M. Y.; Cedergren R. J. (1987) Automated chemical synthesis of long oligoribonucleotides using 2'-O-silylated ribonucleoside 3′-O-phosphoramidites on a controlled-pore glass support: Synthesis of a 43-nucleotide sequence similar to the 3′-half molecule of an Escherichia coli formylmethionine tRNA. J. Am. Chem. Soc. 109, 7845–7854. [Google Scholar]
- Wincott F.; Direnzo A.; Shaffer C.; Grimm S.; Tracz D.; Workman C.; Sweedler D.; Gonzalez C.; Scaringe S.; Usman N. (1995) Synthesis, deprotection, analysis and purification of RNA and ribozymes. Nucleic Acids Res. 23, 2677–2684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G.; Znosko B. M.; Jiao X. Q.; Turner D. H. (2004) Factors affecting thermodynamic stabilities of RNA 3 × 3 internal loops. Biochemistry 43, 12865–12876. [DOI] [PubMed] [Google Scholar]
- Chen G.; Znosko B. M.; Kennedy S. D.; Krugh T. R.; Turner D. H. (2005) Solution structure of an RNA internal loop with three consecutive sheared GA pairs. Biochemistry 44, 2845–2856. [DOI] [PubMed] [Google Scholar]
- Borer P. N.1975Optical properties of nucleic acids, absorption and circular dichroism spectra, in Handbook of Biochemistry and Molecular Biology: Nucleic Acids, 3rd ed. (Fasman G. D., Ed.) pp 589−595, CRC Press, Cleveland, OH [Google Scholar]
- Richards E. G.1975Use of tables in calculation of absorption, optical rotatory dispersion and circular dichroism of polyribonucleotides, in Handbook of Biochemistry and Molecular Biology: Nucleic Acids, 3rd ed. (Fasman G. D., Ed.) pp 596−603, CRC Press, Cleveland, OH [Google Scholar]
- McDowell J. A.; Turner D. H. (1996) Investigation of the structural basis for thermodynamic stabilities of tandem GU mismatches: Solution structure of (rGAGGUCUC)2 by two-dimensional NMR and simulated annealing. Biochemistry 35, 14077–14089. [DOI] [PubMed] [Google Scholar]
- Petersheim M.; Turner D. H. (1983) Base-stacking and base-pairing contributions to helix stability: Thermodynamics of double-helix formation with CCGG, CCGGp, CCGGAp, ACCGGp, CCGGUp, and ACCGGUp. Biochemistry 22, 256–263. [DOI] [PubMed] [Google Scholar]
- Xia T.; SantaLucia J. Jr.; Burkard M. E.; Kierzek R.; Schroeder S. J.; Jiao X.; Cox C.; Turner D. H. (1998) Thermodynamic parameters for an expanded nearest-neighbor model for formation of RNA duplexes with Watson−Crick base pairs. Biochemistry 37, 14719–14735. [DOI] [PubMed] [Google Scholar]
- Borer P. N.; Dengler B.; Tinoco I. Jr.; Uhlenbeck O. C. (1974) Stability of ribonucleic acid double-stranded helices. J. Mol. Biol. 86, 843–853. [DOI] [PubMed] [Google Scholar]
- Lukavsky P. J.; Puglisi J. D. (2001) RNAPack: An integrated NMR approach to RNA structure determination. Methods 25, 316–332. [DOI] [PubMed] [Google Scholar]
- Smallcombe S. H. (1993) Solvent suppression with symmetrically shifted pulses. J. Am. Chem. Soc. 115, 4776–4785. [Google Scholar]
- Mathews D. H.; Disney M. D.; Childs J. L.; Schroeder S. J.; Zuker M.; Turner D. H. (2004) Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc. Natl. Acad. Sci. U.S.A. 101, 7287–7292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gralla J.; Crothers D. M. (1973) Free energy of imperfect nucleic acid helices: III. Small internal loops resulting from mismatches. J. Mol. Biol. 78, 301–319. [DOI] [PubMed] [Google Scholar]
- Mathews D. H.; Sabina J.; Zuker M.; Turner D. H. (1999) Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J. Mol. Biol. 288, 911–940. [DOI] [PubMed] [Google Scholar]
- Blake R. D.1996Denaturation of DNA, in Encyclopedia of Molecular Biology and Molecular Medicine (Meyers R. A., Ed.) pp 1−19, VCH, New York [Google Scholar]
- Record M. T. Jr. (1967) Electrostatic effects on polynucleotide transitions. II. Behavior of titrated systems. Biopolymers 5, 993–1008. [DOI] [PubMed] [Google Scholar]
- Nagaswamy U.; Larios-Sanz M.; Hury J.; Collins S.; Zhang Z. D.; Zhao Q.; Fox G. E. (2002) NCIR: A database of non-canonical interactions in known RNA structures. Nucleic Acids Res. 30, 395–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamura M.; Hendrix D. K.; Klosterman P. S.; Schimmelman N. R.; Brenner S. E.; Holbrook S. R. (2004) SCOR: Structural classification of RNA, version 2.0. Nucleic Acids Res. 32, D182–D184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adams P. L.; Stahley M. R.; Kosek A. B.; Wang J. M.; Strobel S. A. (2004) Crystal structure of a self-splicing group I intron with both exons. Nature 430, 45–50. [DOI] [PubMed] [Google Scholar]
- Butcher S. E.; Allain F. H. T.; Feigon J. (1999) Solution structure of the loop B domain from the hairpin ribozyme. Nat. Struct. Biol. 6, 212–216. [DOI] [PubMed] [Google Scholar]
- Schuwirth B. S.; Borovinskaya M. A.; Hau C. W.; Zhang W.; Vila-Sanjurjo A.; Holton J. M.; Cate J. H. D. (2005) Structures of the bacterial ribosome at 3.5 Å resolution. Science 310, 827–834. [DOI] [PubMed] [Google Scholar]
- Wimberly B. T.; Brodersen D. E.; Clemons W. M.; Morgan-Warren R. J.; Carter A. P.; Vonrhein C.; Hartsch T.; Ramakrishnan V. (2000) Structure of the 30S ribosomal subunit. Nature 407, 327–339. [DOI] [PubMed] [Google Scholar]
- Ban N.; Nissen P.; Hansen J.; Moore P. B.; Steitz T. A. (2000) The complete atomic structure of the large ribosomal subunit at 2.4 Å resolution. Science 289, 905–920. [DOI] [PubMed] [Google Scholar]
- Acharya S.; Barman J.; Cheruku P.; Chatterjee S.; Acharya P.; Isaksson J.; Chattopadhyaya J. (2004) Significant pKa perturbation of nucleobases is an intrinsic property of the sequence context in DNA and RNA. J. Am. Chem. Soc. 126, 8674–8681. [DOI] [PubMed] [Google Scholar]
- Pan B.; Mitra S. N.; Sundaralingam M. (1998) Structure of a 16-mer RNA duplex r(GCAGACUUAAAUCUGC)2 with wobble CA+ mismatches. J. Mol. Biol. 283, 977–984. [DOI] [PubMed] [Google Scholar]
- Leontis N. B.; Stombaugh J.; Westhof E. (2002) The non-Watson−Crick base pairs and their associated isostericity matrices. Nucleic Acids Res. 30, 3497–3531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kierzek R.; Burkard M. E.; Turner D. H. (1999) Thermodynamics of single mismatches in RNA duplexes. Biochemistry 38, 14214–14223. [DOI] [PubMed] [Google Scholar]
- Wang C.; Gao H.; Gaffney B. L.; Jones R. A. (1991) Nitrogen-15-labeled oligodeoxynucleotides. 3. Protonation of the adenine N1 in the AC and AG mispairs of the duplexes {d[CG(15N1)AGAATTCCCG]}2 and {d[CGGGAATTC(15N1)ACG]}2. J. Am. Chem. Soc. 113, 5486–5488. [Google Scholar]
- Wong S. K.; Sato S.; Lazinski D. W. (2001) Substrate recognition by ADAR1 and ADAR2. RNA 7, 846–858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yildirim I.; Turner D. H. (2005) RNA challenges for computational chemists. Biochemistry 44, 13225–13234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang C. L.; Alexov E.; Pyle A. M.; Honig B. (2007) Calculation of pKas in RNA: On the structural origins and functional roles of protonated nucleotides. J. Mol. Biol. 366, 1475–1496. [DOI] [PubMed] [Google Scholar]
- Mizuno H.; Sundaralingam M. (1978) Stacking of Crick wobble pair and Watson−Crick pair: Stability rules of G−U pairs at ends of helical stems in tRNAs and the relation to codon−-anticodon wobble interaction. Nucleic Acids Res. 5, 4451–4461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flinders J.; Dieckmann T. (2004) The solution structure of the VS ribozyme active site loop reveals a dynamic “hot-spot”. J. Mol. Biol. 341, 935–949. [DOI] [PubMed] [Google Scholar]
- Jang S. B.; Hung L. W.; Chi Y. I.; Holbrook E. L.; Carter R. J.; Holbrook S. R. (1998) Structure of an RNA internal loop consisting of tandem CA+ base pairs. Biochemistry 37, 11726–11731. [DOI] [PubMed] [Google Scholar]
- Znosko B. M.; Kennedy S. D.; Wille P. C.; Krugh T. R.; Turner D. H. (2004) Structural features and thermodynamics of the J4/5 loop from the Candida albicans and Candida dubliniensis group I introns. Biochemistry 43, 15822–15837. [DOI] [PubMed] [Google Scholar]
- Chen X.; McDowell J. A.; Kierzek R.; Krugh T. R.; Turner D. H. (2000) Nuclear magnetic resonance spectroscopy and molecular modeling reveal that different hydrogen bonding patterns are possible for G·U pairs: One hydrogen bond for each G·U pair in r(GGCGUGCC)2 and two for each G·U pair in r(GAGUGCUC)2. Biochemistry 39, 8970–8982. [PubMed] [Google Scholar]
- O'Toole A. S.; Miller S.; Haines N.; Zink M. C.; Serra M. J. (2006) Comprehensive thermodynamic analysis of 3′ double-nucleotide overhangs neighboring Watson−Crick terminal base pairs. Nucleic Acids Res. 34, 3338–3344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohmichi T.; Nakano S.; Miyoshi D.; Sugimoto N. (2002) Long RNA dangling end has large energetic contribution to duplex stability. J. Am. Chem. Soc. 124, 10367–10372. [DOI] [PubMed] [Google Scholar]
- Holbrook S. R.; Cheong C. J.; Tinoco I. Jr.; Kim S. H. (1991) Crystal structure of an RNA double helix incorporating a track of non-Watson−Crick base pairs. Nature 353, 579–581. [DOI] [PubMed] [Google Scholar]
- Cruse W. B. T.; Saludjian P.; Biala E.; Strazewski P.; Prange T.; Kennard O. (1994) Structure of a mispaired RNA double helix at 1.6 Å resolution and implications for the prediction of RNA secondary structure. Proc. Natl. Acad. Sci. U.S.A. 91, 4160–4164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandl M.; Meyer M.; Suhnel J. (1999) Quantum−chemical study of a water-mediated uracil−cytosine base pair. J. Am. Chem. Soc. 121, 2605–2606. [Google Scholar]
- Schneider C.; Brandl M.; Suhnel J. (2001) Molecular dynamics simulation reveals conformational switching of water-mediated uracil−cytosine base-pairs in an RNA duplex. J. Mol. Biol. 305, 659–667. [DOI] [PubMed] [Google Scholar]
- Yingling Y. G.; Shapiro B. A. (2005) Dynamic behavior of the telomerase RNA hairpin structure and its relationship to Dyskeratosis congenita. J. Mol. Biol. 348, 27–42. [DOI] [PubMed] [Google Scholar]
- Lescrinier E.; Tessari M.; van Kuppeveld F. J. M.; Melchers W. J. G.; Hilbers C. W.; Heus H. A. (2003) Structure of the pyrimidine-rich internal loop in the poliovirus 3′-UTR: The importance of maintaining pseudo-2-fold symmetry in RNA helices containing two adjacent non-canonical base-pairs. J. Mol. Biol. 331, 759–769. [DOI] [PubMed] [Google Scholar]
- Lukavsky P. J.; Kim I.; Otto G. A.; Puglisi J. D. (2003) Structure of HCV IRES domain II determined by NMR. Nat. Struct. Biol. 10, 1033–1038. [DOI] [PubMed] [Google Scholar]
- Du Z. H.; Yu J. H.; Ulyanov N. B.; Andino R.; James T. L. (2004) Solution structure of a consensus stem-loop D RNA domain that plays important roles in regulating translation and replication in enteroviruses and rhinoviruses. Biochemistry 43, 11959–11972. [DOI] [PubMed] [Google Scholar]
- Ohlenschlager O.; Wohnert J.; Bucci E.; Seitz S.; Hafner S.; Ramachandran R.; Zell R.; Gorlach M. (2004) The structure of the stemloop D subdomain of coxsackievirus B3 cloverleaf RNA and its interaction with the proteinase 3C. Structure 12, 237–248. [DOI] [PubMed] [Google Scholar]
- Hoogstraten C. G.; Legault P.; Pardi A. (1998) NMR solution structure of the lead-dependent ribozyme: Evidence for dynamics in RNA catalysis. J. Mol. Biol. 284, 337–350. [DOI] [PubMed] [Google Scholar]
- Wedekind J. E.; McKay D. B. (2003) Crystal structure of the leadzyme at 1.8 Å resolution: Metal ion binding and the implications for catalytic mechanism and allo site ion regulation. Biochemistry 42, 9554–9563. [DOI] [PubMed] [Google Scholar]
- Lemieux S.; Chartrand P.; Cedergren R.; Major F. (1998) Modeling active RNA structures using the intersection of conformational space: Application to the lead-activated ribozyme. RNA 4, 739–749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yajima R.; Proctor D. J.; Kierzek R.; Kierzek E.; Bevilacqua P. C. (2007) A conformationally restricted guanosine analog reveals the catalytic relevance of three structures of an RNA enzyme. Chem. Biol. 14, 23–30. [DOI] [PubMed] [Google Scholar]
- Schroeder S. J.; Turner D. H. (2000) Factors affecting the thermodynamic stability of small asymmetric internal loops in RNA. Biochemistry 39, 9257–9274. [DOI] [PubMed] [Google Scholar]
- Ferre-D'Amare A. R. (2004) The hairpin ribozyme. Biopolymers 73, 71–78. [DOI] [PubMed] [Google Scholar]
- Weichenrieder O.; Wild K.; Strub K.; Cusack S. (2000) Structure and assembly of the Alu domain of the mammalian signal recognition particle. Nature 408, 167–173. [DOI] [PubMed] [Google Scholar]
- Chen G.; Kennedy S. D.; Qiao J.; Krugh T. R.; Turner D. H. (2006) An alternating sheared AA pair and elements of stability for a single sheared purine−purine pair flanked by sheared GA pairs in RNA. Biochemistry 45, 6889–6903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heus H. A.; Wijmenga S. S.; Hoppe H.; Hilbers C. W. (1997) The detailed structure of tandem G·A mismatched base-pair motifs in RNA duplexes is context dependent. J. Mol. Biol. 271, 147–158. [DOI] [PubMed] [Google Scholar]
- Tolbert B. S.; Kennedy S. D.; Schroeder S. J.; Krugh T. R.; Turner D. H. (2007) NMR structures of (rGCUGAGGCU)2 and (rGCGGAUGCU)2: Probing the structural features that shape the thermodynamic stability of GA pairs. Biochemistry 46, 1511–1522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu X. J.; Olson W. K. (2003) 3DNA: A software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 31, 5108–5121. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.