Variable Selection for Partially Linear Models with Measurement Errors

Abstract

This article focuses on variable selection for partially linear models when the covariates are measured with additive errors. We propose two classes of variable selection procedures, penalized least squares and penalized quantile regression, using the nonconvex penalized principle. The first procedure corrects the bias in the loss function caused by the measurement error by applying the so-called correction-for-attenuation approach, whereas the second procedure corrects the bias by using orthogonal regression. The sampling properties for the two procedures are investigated. The rate of convergence and the asymptotic normality of the resulting estimates are established. We further demonstrate that, with proper choices of the penalty functions and the regularization parameter, the resulting estimates perform asymptotically as well as an oracle procedure (Fan and Li 2001). Choice of smoothing parameters is also discussed. Finite sample performance of the proposed variable selection procedures is assessed by Monte Carlo simulation studies. We further illustrate the proposed procedures by an application.

1 INTRODUCTION

Various linear and nonlinear parametric models have been proposed for statistical modeling in the literature. However, these statistical parametric models and methods may not be flexible enough when dealing with real, high-dimensional data, which are frequently encountered in biological research. A variety of semiparametric regression models have been proposed for a partial remedy to the “curse of dimensionality” termed by Bellman (1961) to describe the exponential growth of volume as a function of dimensionality. In this article, we focus on partially linear models, a class of commonly-used and -studied semiparametric regression models, which can retain the flexibility of nonparametric models and ease of interpretation of linear regression models while avoiding the “curse of dimensionality”. Specifically, we shall propose variable selection procedures for partially linear models when the linear covariates are measured with errors.

In practice, many explanatory variables are generally collected and need to be assessed during the initial analysis. Deciding which covariates to keep in the final statistical model and which variables are non-informative is practically interesting, but is always a tricky task for data analysis. Variable selection is therefore of fundamental interest in statistical modeling and analysis of data, and has become an integral part in most of the widely used statistics packages. No doubt variable selection will continue to be an important basic strategy for data analysis particularly as high throughout technologies bring us larger data sets with greater number of exploratory variables. The development of variable selection procedures has progressed rapidly since the 1970s. Akaike (1973) proposed the Akaike information criterion (AIC). Hocking (1976) gave a comprehensive review on the early developments of variable selection procedure for linear models. Schwarz (1978) developed the Bayesian information criterion (BIC), and Foster and George (1994) developed the risk inflation criterion (RIC). With these criteria, stepwise regression or the best subset selection are frequently used in practice, but these procedures suffer from several drawbacks such as the lack of stability as noted by Breiman (1996) and lack of incorporating stochastic errors inherited in the stage of variable selection. In an attempt to overcome these drawbacks, Fan and Li (2001) proposed a class of variable selection procedures for parametric models via a nonconcave-penalized-likelihood approach, which simultaneously selects significant variables and estimates unknown regression coefficients. Starting with the seminal work by Mitchell and Beauchamp (1988), Bayesian variable selection has become a very active research topic during the last two decades. Pioneer work includes Mitchell and Beauchamp (1988), George and McCulloch (1993), and Berger and Percchi (1996). See Raftery, Madigan, and Hoeting (1997), Hoeting, Madigan, Raftery, and Volinsky (1999), and Jiang (2007) for more recent developments.

Some variable selection procedures for partially linear models include Bunea (2004), and Bunea and Wegkamp (2004), which developed model selection criteria for partially linear models with independent and identically distributed data. Bunea (2004) proposed a covariate selection procedure, which estimates the parametric and nonparametric components simultaneously, for partially linear models via penalized least squares with a L₀ penalty. Bunea and Wegkamp (2004) proposed a two-stage model selection procedure that first estimates the nonparametric component, and then selects the significant variables in the parametric component. Their procedure is similar to a one-step backfitting algorithm with a good initial estimate for the nonparametric component. In addition, Fan and Li (2004) proposed a profile least squares approach for partially linear models for longitudinal data.

Measurement error data are often encountered in many fields, including engineering, economics, physics, biology, biomedical sciences and epidemiology. For example, in AIDS studies, virologic and immunologic markers, such as plasma concentrations of HIV-1 RNA and CD4+ cell counts, are measured with errors. Statistical inference methods for various parametric measurement error models have been well established over the past several decades. Fuller (1987) and Carroll, Ruppert, Stefanski, and Crainiceanu (2006) gave a systematic survey on this research topic and present many applications of measurement error data. Partially linear models have been used to study measurements with errors (Wang, Lin, Gutierrez, and Carroll 1998; Liang, Härdle, and Carroll 1999; Ma and Carroll 2006; Liang, Wang, and Carroll 2007; Pan, Zeng, and Lin 2008).

To the best of our knowledge, most existing variable selection procedures are limited to directly observed predictors. Variable selection for measurement error data imposes challenges for statisticians. For linear regression models containing more than two covariates, some of which are measured with error and others are error-free, it can be shown that the ordinary least squares method, which directly substitutes the observed surrogates for the unobserved error-prone variables, yields an inconsistent estimate for the regression coefficients because the loss function contains the error-prone covariates and the expected value of the corresponding estimating function does not equal zero. The inconsistency nullifies the theoretic property of the ordinary penalized least squares estimate without accounting for the measurement error. Note that most variable selection procedures are equivalent or asymptotically equivalent to minimizing a penalized least squares function. Thus, in the presence of measurement error, the existing penalized least squares variable selection procedures ignoring measurement errors may not work properly. Extension of the existing methods of variable selection accounting for measurement error is therefore by no means straightforward. Thus, we are motivated to develop variable selection procedures for measurement error data. The proposed procedures result models with a parsimonious and well-fitting subset of observed covariates. We will consider the situation in which the covariates are measured with additive errors. Hence, selection of observed covariates with measurement error is equivalent to selection of the corresponding latent covariates. The coefficients of the observed surrogates and the associated latent covariates have the same meaning.

In this article, we propose two classes of variable selection procedures for partially linear measurement error models: one based on penalized least squares, and the other based on penalized quantile regression. The former is more familiar and computationally easier, while the latter is more robust to outliers. Our proposed strategy to correct the estimation bias due to measurement error for the penalized least squares is quite different from that for the penalized quantile regression. For the penalized least squares method, we correct the bias by subtracting a bias correction term from the least squares function. For the penalized quantile regression, we correct the bias by using orthogonal regression (Cheng and Van Ness 1999). To investigate the sample properties of the proposed procedures, we first demonstrate how the rate of convergence of the resulting estimates depends on the tuning parameter in the penalized models. With proper choice of the penalty function and the tuning parameter, we show that the resulting estimates of the proposed procedures asymptotically perform as well as an oracle procedure, in the terminology of Fan and Li (2001). Practical implementation issues, including smoothing parameter selection and tuning parameter selection, are addressed. We conduct Monte Carlo simulation experiments to examine the performance of the proposed procedures with moderate sample sizes, and compare the performance of the proposed penalized least squares and penalized quantile regression with various penalties. We also compare the performance of the proposed procedures with naive extension of the best subset variable selection from the ordinary linear regression models. Our simulation results demonstrate that the proposed procedures perform with moderate sample sizes almost as well as the oracle estimator.

The rest of this article is organized as follows. In Section 2, we propose a class of variable selection procedures for partially linear measurement error models via penalized least squares. In Section 3, we develop a penalized quantile regression procedure for selecting significant variables in the partially linear measurement error models when considering the effects of outliers. Simulation results are presented in Section 4, and we also illustrate the proposed procedures by an empirical analysis of a real data set. Regularity conditions and technical proofs are given in the Appendix.

2 PENALIZED LEAST SQUARED METHOD

Suppose that {(W_i, Z_i, Y_i), i = 1,…, n} is a random sample from the partially linear measurement error model (PLMeM),

$$\{\begin{array}{l}Y={\mathbf{X}}^{\text{T}}\mathit{\beta }+\nu (Z)+\epsilon ,\hfill \\ \mathbf{W}=\mathbf{X}+\mathbf{U},\hfill \end{array}$$ (2.1)

where Z is a univariate observed error-free covariate, X is a d-dimensional vector of unobserved latent covariates which is measured in an error-prone way, W is the observed surrogate of X, ε is the model error with E(ε|X, Z) = 0, U is the measurement error with mean zero and (possibly singular) covariance matrix Σ_uu. Thus, X may consist of some error-free variables. In this section, it is assumed that U is independent of (X, Z, Y). For example, Z could be measurement time, X could be a vector of biomarkers like T-cell count or blood pressure, W could be the measured values for the quantities X, and U is the difference between the observed W and unknown X. In this article, we only consider univariate Z. The proposed method is applicable for multivariate Z. The extension to the multivariate Z might be practically less useful due to the “curse of dimensionality”.

To get insights into the penalized least squares procedure, we first consider the situation in which Σ_uu is known. We will study the case of unknown Σ_uu later on. Define a least squares function to be

$$\frac{1}{2}\sum _{i=1}^n{\{Y_i-{\mathbf{W}}_i^{\text{T}}\mathit{\beta }-\nu (Z_i)\}}^2-\frac{n}{2}{\mathit{\beta }}^{\text{T}}{\mathrm{\sum }}_{uu}\mathit{\beta }.$$

The second term is included to correct the bias in the squared loss function due to measurement error. Since E(U|Z) = 0, ν(Z) = E (Y|Z) − E(W|Z)^Tβ. Then the least squares function can be rewritten as

$$\frac{1}{2}\sum _{i=1}^n{[\{Y_i-E(Y_i\mid Z_i)\}-{\{{\mathbf{W}}_i-E({\mathbf{W}}_i\mid Z_i)\}}^{\text{T}}\mathit{\beta }]}^2-\frac{n}{2}{\mathit{\beta }}^{\text{T}}{\mathrm{\sum }}_{uu}\mathit{\beta }.$$

This motivates us to consider a penalized least squares method based on partial residuals. Denote m_w(Z) = E(W|Z) and m_y(Z) = E(Y|Z). Let m̂_w(·) and m̂_y(·) be estimates of m_w(·) and m_y(·), respectively. In this article, we employ local linear regression (Fan and Gijbels 1996) to estimate both m_w(·) and m_y(·). The bandwidth selection for the local linear regression is discussed in Section 4.1. The penalized least squares function based on partial residuals is defined as

$${\mathcal{L}}_P({\mathrm{\sum }}_{uu},\mathit{\beta })=\frac{1}{2}\sum _{i=1}^n{[\{Y_i-{\widehat{m}}_y(Z_i)\}-{\{{\mathbf{W}}_i-{\widehat{\mathbf{m}}}_w(Z_i)\}}^{\text{T}}\mathit{\beta }]}^2-\frac{n}{2}{\mathit{\beta }}^T{\mathrm{\sum }}_{uu}\mathit{\beta }+n\sum _{j=1}^d{p}_{{\lambda }_{jn}}(\mid {\beta }_j\mid ).$$

where p_λjn (·) is a penalty function with a tuning parameter λ_jn, which may be chosen by a data-driven method. For the sake of simplicity of notation, we use λ_j to stand for λ_jn throughout this paper. We will discuss the selection of the tuning parameter in Section 4.1. Denote Ŷ_i = Y_i − m̂_y(Z_i) and Ŵ_i = W_i − m̂_w(Z_i). Thus, ℒ_P (Σ_uu, β) can be written as

$${\mathcal{L}}_P({\mathrm{\sum }}_{uu},\mathit{\beta })=\frac{1}{2}\sum _{i=1}^n{({\widehat{Y}}_i-{\widehat{\mathbf{W}}}_i^{\text{T}}\mathit{\beta })}^2-\frac{n}{2}{\mathit{\beta }}^{\text{T}}{\mathrm{\sum }}_{uu}\mathit{\beta }+n\sum _{j=1}^d{p}_{{\lambda }_j}(\mid {\beta }_j\mid ).$$ (2.2)

Minimizing ℒ_P (Σ_uu, β) with respect to β results in a penalized least squares estimator β̂. It is worth noting that the penalty functions and the tuning parameters are not necessarily the same for all coefficients. For instance, we want to keep important variables in the final model, and therefore we should not penalize their coefficients.

The penalized least squares function (2.2) provides a general framework of variable selection for PLMeM. Taking the penalty function to be the L₀-penalty (also called the entropy penalty in the literature), namely, $p_{{\lambda }_j}(\mid {\beta }_j\mid )=0.5{\lambda }_j^{2}I\{\mid {\beta }_j\mid \ne 0\}$, where I{·} is an indicator function, we may extend the traditional variable selection criteria, including the AIC (Akaike 1973), BIC (Schwarz 1978) and RIC (Foster and George 1994), for the PLMeM:

$$\frac{1}{2}\sum _{i=1}^n{({\widehat{Y}}_i-{\widehat{\mathbf{W}}}_i^{\text{T}}\mathit{\beta })}^2-\frac{n}{2}{\mathit{\beta }}^{\text{T}}{\mathrm{\sum }}_{uu}\mathit{\beta }+\frac{n}{2}\sum _{j=1}^d{\lambda }_j^{2}I\{\mid {\beta }_j\mid \ne 0\}$$ (2.3)

as ${\sum }_{j=1}^{d}I\{\mid {\beta }_j\mid \ne 0\}$ equals the size of the selected model. Specifically, the AIC, BIC and RIC correspond to ${\lambda }_j\equiv \sigma \sqrt{2/n},\sigma \sqrt{log(n)/n}$ and $\sigma \sqrt{log(d)/n}$, respectively.

Note that the L₀-penalty is discontinuous, and therefore optimizing (2.3) requires exhaustive search over 2^d possible subsets. This search poses great computational challenges. Furthermore, as noted by Breiman (1996), the best subset variable selection suffers from several drawbacks, including its lack of stability. In the recent literature of variable selection for linear regression model without measurement error, many authors advocated the use of continuous and smooth penalty functions, for example, Bridge regression (Frank and Friedman 1993) corresponding to the L_q-penalty p_λ (|β_j|) = q⁻¹λ|β_j|^q; the LASSO (Tibshirani 1996) corresponding to the L₁-penalty. Fan and Li (2001) studied the choice of penalty functions in depth. They advocated the use of the SCAD penalty, defined by

$$p_{\lambda }(\mid \beta \mid )=\{\begin{array}{ll}\lambda \mid \beta \mid ,\hfill & \text{if}0\le \mid \beta \mid <\lambda ;\hfill \\ \frac{(a^2-1){\lambda }^2-{(\mid \beta \mid -a\lambda )}^2}{2(a-1)},\hfill & \text{if}\lambda \le \mid \beta \mid <a\lambda ;\hfill \\ \frac{(a+1){\lambda }^2}{2},\hfill & \text{if}\mid \beta \mid \ge a\lambda .\hfill \end{array}$$

where a = 3.7. For simplicity of presentation, we will use the name “SCAD” for all procedures using the SCAD penalty. As demonstrated in Fan and Li (2001), the SCAD is an improvement of the LASSO in terms of modeling bias and of the bridge regression with q < 1 in terms of stability.

We next study the sampling property of the resulting penalized least squares estimate. Let ${\mathit{\beta }}_0={({\beta }_{10},\dots ,{\beta }_{d0})}^{\text{T}}={({\mathit{\beta }}_{10}^{\text{T}},{\mathit{\beta }}_{20}^{\text{T}})}^{\text{T}}$ be the true value of β. Without loss of generality, assume that β₁₀ consists of all nonzero components of β₀, and β₂₀ = 0. Let s denote the dimension of β₁₀. Denote

$$a_n=\underset{1\le j\le d}{max}\{\mid p_{{\lambda }_j}^{\prime }(\mid {\beta }_{j0}\mid )\mid ,{\beta }_{j0}\ne 0\},\text{and}{b}_n=\underset{1\le j\le d}{max}\{\mid p_{{\lambda }_j}^{″}(\mid {\beta }_{j0}\mid )\mid ,{\beta }_{j0}\ne 0\},$$ (2.4)

$$\begin{array}{l}\mathbf{b}={\{p_{{\lambda }_1}^{\prime }(\mid {\beta }_{10}\mid )sgn({\beta }_{10}),\dots ,p_{{\lambda }_s}^{\prime }(\mid {\beta }_{s0}\mid )sgn({\beta }_{s0})\}}^{\text{T}},\\ \text{and}{\mathrm{\sum }}_{\lambda }=\text{diag}\{p_{{\lambda }_1}^{″}(\mid {\beta }_{10}\mid ),\dots ,p_{{\lambda }_s}^{″}(\mid {\beta }_{s0}\mid )\}.\end{array}$$ (2.5)

In what follows, A^⊗2 = AA^T for any vector or matrix A. Let ς̃ = ς − E(ς|Z) for any random variable/vector ς. For example, X̃ = X − E(X|Z). Denote by S_*1 the elements of S_* with respect to β₁₀ for any random/function vector S_*. For example, U₁₁ and X̃₁₁ are the vectors comprised by the first s elements of U₁ and X̃₁, respectively. Let Σ_uu1 be the (s, s) − left upper submatrix of Σ_uu, and Σ_X|Z = cov{X₁₁ − E(X₁₁|Z₁)}. ||v|| denotes the Euclidean norm for the vector v. We have the following theorem, whose proof is given in the Appendix.

Theorem 1

Suppose that a_n = O(n^−1/2), b_n → 0 and the regularity conditions (a)–(e) in the Appendix hold. Then we have the following conclusions.

1. With probability approaching one, there exists a local minimizer β̂ of ℒ_P (Σ_uu, β) such that ||β̂ − β|| = O_P(n^−1/2).

   Further assume that all λ_j → 0, n^1/2 λ_j → ∞, and

$$\underset{n\to \infty }{liminf}\{\underset{u\to 0^{+}}{liminf}{p}_{{\lambda }_j}^{\prime }(u)/{\lambda }_j\}>0.$$ (2.6)

With probability approaching one, the root n consistent estimator β̂ in (I) satisfies (a) β̂₂ = 0, and (b) β̂₁ has an asymptotic normal distribution

$$\sqrt{n}({\mathrm{\sum }}_{\text{X}\mid \text{Z}}+{\mathrm{\sum }}_{\lambda })\{{\widehat{\mathit{\beta }}}_1-{\mathit{\beta }}_{10}+{({\mathrm{\sum }}_{\text{X}\mid \text{Z}}+{\mathrm{\sum }}_{\lambda })}^{-1}\mathbf{b}\}\stackrel{D}{\to }N(0,\mathrm{\Gamma }),$$

where $\mathrm{\Gamma }=E{\left\{{\stackrel{\sim }{\mathbf{X}}}_{11}(\epsilon -{\mathbf{U}}_{11}^{\text{T}}{\mathit{\beta }}_{10})+\epsilon {\mathbf{U}}_{11}+({\mathbf{U}}_{11}{\mathbf{U}}_{11}^{\text{T}}-{\mathrm{\sum }}_{uu1}){\mathit{\beta }}_{10}\right\}}^{\otimes 2}$.

To make statistical inference on β₁₀, we need to estimate the standard error of the estimator β̂₁. From Theorem 1, the asymptotic covariance matrix of β̂₁ is

$$\frac{1}{n}{({\mathrm{\sum }}_{\text{X}\mid \text{Z}}+{\mathrm{\sum }}_{\lambda })}^{-1}\mathrm{\Gamma }{({\mathrm{\sum }}_{\text{X}\mid \text{Z}}+{\mathrm{\sum }}_{\lambda })}^{-1}.$$

A consistent estimate of Σ_X|Z is defined as

$${(n-s)}^{-1}\sum _{i=1}^n{\widehat{\mathbf{W}}}_{i1}^{\otimes 2}-{\mathrm{\sum }}_{uu1}\stackrel{\text{def}}{=}{\widehat{\mathrm{\sum }}}_{\text{X}\mid \text{Z}}.$$

Furthermore, Γ can be estimated by

$${\widehat{\mathrm{\Gamma }}}_n=n^{-1}\sum _{i=1}^n{\left\{{\widehat{\mathbf{W}}}_{i1}({\widehat{Y}}_i-{\widehat{\mathbf{W}}}_{i1}^{\text{T}}{\widehat{\mathit{\beta }}}_1)+{\mathrm{\sum }}_{uu1}{\widehat{\mathit{\beta }}}_1\right\}}^{\otimes 2}.$$

The covariance matrix of the estimates β̂₁, the nonvanishing component of β̂, can be estimated by

$$n^{-1}{\left\{{\widehat{\mathrm{\sum }}}_{\text{X}\mid \text{Z}}+{\mathrm{\sum }}_{\lambda }({\widehat{\mathit{\beta }}}_1)\right\}}^{-1}{\widehat{\mathrm{\Gamma }}}_n{\left\{{\widehat{\mathrm{\sum }}}_{\text{X}\mid \text{Z}}+{\mathrm{\sum }}_{\lambda }({\widehat{\mathit{\beta }}}_1)\right\}}^{-1},$$ (2.7)

where Σ_λ (β̂₁) is obtained by replacing β₁ by β̂₁ in Σ_λ.

Remark 1

The proposed penalized least squares procedure can directly be applied for a linear measurement error model, which can be regarded as a PLMeM in the absence of the nonparametric component ν(Z). Thus, under the conditions of Theorem 1, the resulting estimate obtained from the penalized least squares function (2.3) is $\sqrt{n}$ consistent, and satisfies β̂₂ = 0, and

$$\sqrt{n}\{cov({\mathbf{X}}_{11})+{\mathrm{\sum }}_{\lambda }\}[{\widehat{\mathit{\beta }}}_1-{\mathit{\beta }}_{10}+{\{cov({\mathbf{X}}_{11})+{\mathrm{\sum }}_{\lambda }\}}^{-1}\mathbf{b}]\stackrel{D}{\to }N(0,{\mathrm{\Gamma }}_0),$$

where ${\mathrm{\Gamma }}_0=E{\{{\mathbf{X}}_{11}(\epsilon -{\mathbf{U}}_{11}^{\text{T}}{\mathit{\beta }}_{10})+\epsilon {\mathbf{U}}_{11}+({\mathbf{U}}_{11}{\mathbf{U}}_{11}^{\text{T}}-{\mathrm{\sum }}_{uu1}){\mathit{\beta }}_{10}\}}^{\otimes 2}$.

We now consider the situation in which Σ_uu is unknown. To estimate Σ_uu, it is common to assume that there are partially replicated observations, so that we observe W_ij = X_i + U_ij for j = 1, …, J_i (Carroll, Ruppert, Stefanski, Crainiceanu 2006, Chapter 3). Let ${\overline{\mathbf{W}}}_i=J_i^{-1}{\sum }_{j=1}^{J_i}{\mathbf{W}}_{ij}$ be the sample mean of the replicates. Then a consistent, unbiased method of moments estimate for Σ_uu is

$${\widehat{\mathrm{\sum }}}_{uu}=\sum _{i=1}^n\sum _{j=1}^{J_i}{({\mathbf{W}}_{ij}-{\overline{\mathbf{W}}}_i)}^{\otimes 2}/\sum _{i=1}^n(J_i-1).$$

Let ${\overline{\mathbf{U}}}_i=J_i^{-1}{\sum }_{j=1}^{J_i}{\mathbf{U}}_{ij}$. Note that cov $({\overline{\mathbf{U}}}_i)=J_i^{-1}{\mathrm{\sum }}_{uu}$. Thus, the penalized least squares function is defined as

$${\mathcal{L}}_P({\widehat{\mathrm{\sum }}}_{uu},\mathit{\beta })=\frac{1}{2}\sum _{i=1}^n\{{({\widehat{Y}}_i-{\widehat{\overline{\mathbf{W}}}}_i^{\text{T}}\mathit{\beta })}^2-J_i^{-1}{\mathit{\beta }}^{\text{T}}{\widehat{\mathrm{\sum }}}_{uu}\mathit{\beta }\}+n\sum _{j=1}^d{p}_{{\lambda }_j}(\mid {\beta }_j\mid ),$$ (2.8)

where ${\widehat{\overline{\mathbf{W}}}}_i={\overline{\mathbf{W}}}_i-{\widehat{\mathbf{m}}}_{\overline{w}}(Z_i)$ and m̂_w̄(z) is local linear estimate of E(W̄_i|Z_i = z). Throughout this section, we assume that $\frac{1}{n}{\sum }_{i=1}^n{J}_i^{-1}$ converges to a finite constant as n → ∞.

Theorem 2

Under the conditions of Theorem 1, we still have the following conclusions:

1. With probability approaching one, there exists a local minimizer β̂ of ℒ_P (Σ̂_uu, β) defined in (2.8) such that ||β̂ − β|| = O_p(n^−1/2).

   Further assume that all λ_j → 0, $\sqrt{n}{\lambda }_j\to \infty$, and (2.6) holds. With probability approaching one, the root n consistent estimate β̂ in (I) satisfies β̂₂ = 0, and

$$\sqrt{n}({\mathrm{\sum }}_{\text{X}\mid \text{Z}}+{\mathrm{\sum }}_{\lambda })\{{\widehat{\mathit{\beta }}}_1-{\mathit{\beta }}_{10}+{({\mathrm{\sum }}_{\text{X}\mid \text{Z}}+{\mathrm{\sum }}_{\lambda })}^{-1}\mathbf{b}\}\stackrel{D}{\to }N(0,{\mathrm{\Gamma }}^{\ast }),$$

where ${\mathrm{\Gamma }}^{\ast }=\underset{n\to \infty }{lim}\frac{1}{n}{\displaystyle \sum _{i=1}^n}E{\left\{{\stackrel{\sim }{\mathbf{X}}}_{i1}({\epsilon }_i-{\overline{\mathbf{U}}}_{i1}^{\text{T}}{\mathit{\beta }}_{10})+{\epsilon }_i{\overline{\mathbf{U}}}_{i1}+({\overline{\mathbf{U}}}_{i1}{\overline{\mathbf{U}}}_{i1}^{\text{T}}-J_i^{-1}{\mathrm{\sum }}_{uu1}){\mathit{\beta }}_{10}\right\}}^{\otimes 2}$. and Ū_i1 is the average of {U_ij1, j = 1,…, J_i}.

As a special case, if J_i ≡ J₀ > 1, then it follows

$${\mathrm{\Gamma }}^{\ast }=E{\left\{{\stackrel{\sim }{\mathbf{X}}}_{11}(\epsilon -{\overline{\mathbf{U}}}_{11}^{\text{T}}{\mathit{\beta }}_{10})+\epsilon {\overline{\mathbf{U}}}_{11}+({\overline{\mathbf{U}}}_{11}{\overline{\mathbf{U}}}_{11}^{\text{T}}-J_0^{-1}{\mathrm{\sum }}_{uu1}){\mathit{\beta }}_{10}\right\}}^{\otimes 2}.$$

Because Σ̂_uu is a consistent, unbiased estimator of Σ_uu, Theorem 2 can be proved in a similar way to Theorem 1 by replacing ℒ_P (Σ_uu, β) by ℒ_P (Σ̂_uu, β). To save space, we omit the details.

We next derive an estimate of the standard error of β̂₁. A consistent estimator of Σ_X|Z is defined as

$${(n-s)}^{-1}\sum _{i=1}^n\left[{\left\{{\overline{\mathbf{W}}}_{i1}-\widehat{E}({\overline{\mathbf{W}}}_{i1}\mid Z_i)\right\}}^{\otimes 2}-\frac{1}{J_i}{\widehat{\mathrm{\sum }}}_{uu1}\right],$$

where Σ̂_uu1 is the (s, s) − left upper submatrix of Σ̂_uu. Estimates of Γ^* can be also easily obtained. Let

$$R_i={\widehat{\overline{\mathbf{W}}}}_{i1}({\widehat{Y}}_i-{\widehat{\overline{\mathbf{W}}}}_{i1}^{\text{T}}{\widehat{\mathit{\beta }}}_1)+{\widehat{\mathrm{\sum }}}_{uu1}{\widehat{\mathit{\beta }}}_1/J_i.$$

Then a consistent estimate of Γ^* is the sample covariance matrix of the R_i’s. See Liang, Härdle, and Carroll (1999) for a detailed discussion.

3 PENALIZED QUANTILE REGRESSION

In the presence of outliers, the least squares method may perform badly. Quantile regression is taken as a useful alternative and has been popular in both the statistical and econometric literature. Koenker (2005) provides a comprehensive review on quantile regression techniques. In this section, we explore robust variable selection, and propose a class of penalized quantile-regression variable selection procedures for PLMeM in the presence of contaminated response observations.

In the penalized least squares procedure discussed in the last section, the term −nβ^TΣ_uuβ was included in the loss function (2.2) to correct the estimation bias due to measurement error of the ordinary least squares estimate. However, this approach cannot be extended to quantile-regression for correcting the estimation bias because a direct subtraction cannot correct the bias. We now propose a penalized quantile function based on the orthogonal regression. That is, the objective function is defined as the sum of squares of the orthogonal distances from the data points to the straight line of regression function, instead of the residuals obtained from the classical regression (Cheng and Van Ness 1999). The orthogonal regression has been used to correct estimation bias due to measurement error of the least squares estimate of regression coefficients in linear measurement error models (Lindley 1947; Madansky 1959). He and Liang (2000) applied the idea of orthogonal regression for quantile regression for both linear models and partially linear models with measurement errors. However, they did not consider variable selection problem. Partly motivated by the work of He and Liang (2000), we further used the orthogonal regression method to develop a penalized quantile regression procedure to select significant variables in the partially linear models.

To define orthogonal regression for quantile regression with measurement error data, it is assumed that the random vector (ε, U^T) follows an elliptical distribution with mean zero and covariance matrix σ²Σ, where σ² is unknown, while Σ is a block diagonal matrix with (1,1)-element being 1 and the last d × d diagonal block matrix being C_uu. Readers are referred to Fang, Kotz, and Ng (1990) for details about elliptical distributions and Li, Fang, and Zhu (1997) for tests of spherical and elliptical symmetry. The matrix C_uu is proportional to Σ_uu and is assumed to be known in this section. As discussed in the last section, it can be estimated with partially replicated observations in practice.

Denote ρ_τ the τ-th quantile objective function,

$${\rho }_{\tau }(r)=\tau max(r,0)+(1-\tau )max(-r,0).$$ (3.1)

Note that the solution to minimizing Eρ_τ (ε − u) over u ∈ R is the τ-th quantile of ε. Define penalized quantile function to be of the form:

$${\mathcal{L}}_{\tau }(\mathit{\beta })\stackrel{\text{def}}{=}\sum _{i=1}^n{\rho }_{\tau }\left(\frac{{\widehat{Y}}_i-{\widehat{\mathbf{W}}}_i^{\text{T}}\mathit{\beta }}{\sqrt{1+{\mathit{\beta }}^{\text{T}}{\mathbf{C}}_{uu}\mathit{\beta }}}\right)+n\sum _{j=1}^d{p}_{{\lambda }_j}(\mid {\beta }_j\mid ).$$ (3.2)

He and Liang (2000) proposed the quantile regression estimate for β by minimizing the first term in (3.2). However, it was assumed in He and Liang (2000) that (ε, U^T) follows a spherical distribution, i.e., C_uu = I_d. The sphericity assumption implies that the elements of U are uncorrelated. Here we relax the sphericity assumption. He and Liang (2000) also provided insights into why to use the first term in (3.2). Because ε_i and $({\epsilon }_i-{\mathbf{U}}_i^{\text{T}}\mathit{\beta })/\sqrt{1+{\mathit{\beta }}^{\text{T}}{\mathbf{C}}_{uu}\mathit{\beta }}$ have the same distribution on the basis of the fact given in (A.8) in Appendix A.2, we can establish the consistency for the resulting estimate by using similar arguments to those in He and Liang (2000). Compared with the penalized least squares function in (2.3), the penalized quantile function uses the factor $\sqrt{1+{\mathit{\beta }}^{\text{T}}{\mathbf{C}}_{uu}\mathit{\beta }}$ to correct the bias in the quantile loss function due to the presence of the error-prone variables.

Let f(·) be the density function of ε, a_n = O(n^−1/2) and b_n → 0

Theorem 3

Suppose that (ε_i, U_i) follows an elliptical distribution with mean zero and the covariance structure aforementioned for i = 1,…, n. Assume that the equation Eρ_τ (ε _i − q) = 0 has the unique solution, which is denoted by q_τ, and that f(ω+ q_τ) − f (q_τ) = O(ω^1/2) as ω → 0. Then,

1. With probability tending to one, there exists a local minimizer β̂_τ of ℒ_τ (β) defined in (3.2) such that its rate of convergence is O_P(n^−1/2).

   Further assume (2.6) holds. If all λ_j → 0, $\sqrt{n}{\lambda }_j\to \infty$, then with probability tending to one, the root n consistent estimator ${\widehat{\mathit{\beta }}}_{\tau }={({\widehat{\mathit{\beta }}}_{\tau 1}^{\text{T}},{\widehat{\mathit{\beta }}}_{\tau 2}^{\text{T}})}^{\text{T}}$ in (I) must satisfy (a) β̂_τ2 = 0; and (b) $\sqrt{n}f(q_{\tau }){(1+{\mathit{\beta }}_{10}^{\text{T}}{\mathbf{C}}_{11}{\mathit{\beta }}_{10})}^{1/2}{\mathrm{\sum }}_{\text{X}\mid \text{Z}}({\widehat{\mathit{\beta }}}_{\tau 1}-{\mathit{\beta }}_{10})+n\mathbf{b}{(1+{\mathit{\beta }}_{10}^{\text{T}}{\mathbf{C}}_{11}{\mathit{\beta }}_{10})}^{1/2}\stackrel{D}{\to }N(0,{\mathcal{J}}_q)$, where C₁₁ is the first s × s diagonal submatrix of C_uu, and

$${\mathcal{J}}_q=\tau (1-\tau ){\mathrm{\sum }}_{\text{X}\mid \text{Z}}+cov\left\{{\psi }_{\tau }(\xi )\left({\mathbf{U}}_{11}+\frac{\xi {\mathit{\beta }}_{10}}{\sqrt{1+{\mathit{\beta }}_{10}^{\text{T}}{\mathbf{C}}_{11}{\mathit{\beta }}_{10}}}\right)\right\}$$ (3.3)

with $\xi =(\epsilon -{\mathbf{U}}_{11}^{\text{T}}{\mathit{\beta }}_{10})/\sqrt{1+{\mathit{\beta }}_{10}^{\text{T}}{\mathbf{C}}_{11}{\mathit{\beta }}_{10}}-q_{\tau }$ and ψ_τ being the derivative of ρ_τ.

It is worth pointing out that when C_uu = I_d and b = 0, which corresponds to no penalty term in (3.2), the asymptotic normality is the same as that in He and Liang (2000). However, the conditions imposed in Theorem 3 are weaker than those in He and Liang (2000).

4 SIMULATION STUDY AND APPLICATION

We now investigate the finite sample performance of the proposed procedures by Monte Carlo simulation, and illustrate the proposed methodology by an analysis of a real data set. In our numerical examples, we use local linear regression to estimate m_w(z) and m_y(z) with the kernel function K(u) = 0.75(1 − u²)I_(|u|≤1).

4.1 Issues Related to Practical Implementation

In this section, we address practical implementation issues of the proposed procedures.

Bandwidth selection

Condition (b) in the Appendix requires that the bandwidths in estimating m_w(·) and m_y(·) are of order n^−1/5. Any bandwidths with this rate lead to the same limiting distribution for β̂. Therefore the bandwidth selection can be done in a standard routine. In our implementation, we use the plug-in bandwidth selector proposed in Ruppert, Sheather, and Wand (1995) to select bandwidths for the estimation of m_w(·) and m_y(·). In our empirical study, we have experimented shifting bandwidths around the selected values, and found that the results are stable.

Local quadratic approximation

Since the penalty functions such as the SCAD penalty and the L_q penalty with 0 < q ≤ 1 are singular at the origin, it is challenging to minimize the penalized least squares or quantile loss functions. Hunter and Li (2005) proposed a perturbed version of the local quadratic approximation of Fan and Li (2001); that is,

$$p_{{\lambda }_j}(\mid {\beta }_j\mid )\approx p_{{\lambda }_j}(\mid {\beta }_j^{(0)}\mid )+\frac{1}{2}\{p_{{\lambda }_j}^{\prime }(\mid {\beta }_j^{(0)}\mid )/(\mid {\beta }_j^{(0)}\mid +\eta )\}({\beta }_j^2-{\beta }_j^{(0)2})\stackrel{\text{def}}{=}{q}_{{\lambda }_j}(\mid {\beta }_j\mid ),$$

where η is a small positive number. Hunter and Li (2005) discussed how to determine the value of η in detail. In our implementation, we adopt their strategy to choose η. With the aid of the perturbed local quadratic approximation, the Newton-Raphson algorithm can be applied to minimize the penalized least squares or quantile loss function. We set the unpenalized estimate β̂^u as the initial value of β.

Choice of regularization parameters

Here we describe the regularization parameter selection procedure for the penalized least square function in (2.8) in detail. The idea can be directly applied for the penalized least square function in (2.2) and the penalized quantile regression. For the penalized least squares function in (2.8), let

$$\ell (\mathit{\beta })=\frac{1}{2}\sum _{i=1}^n\left[{\{Y_i-{\widehat{m}}_y(Z_i)-{({\overline{\mathbf{W}}}_i-{\widehat{m}}_{\overline{\mathbf{w}}}(Z))}^{\text{T}}\mathit{\beta }\}}^2-J_i^{-1}{\mathit{\beta }}^{\text{T}}{\widehat{\mathrm{\sum }}}_{uu}\mathit{\beta }\right].$$

Then

$${\mathcal{L}}_P({\widehat{\mathrm{\sum }}}_{uu},\mathit{\beta })=\ell (\mathit{\beta })+n\sum _{j=1}^d{q}_{{\lambda }_j}(\mid {\beta }_j\mid ).$$

Following Fan and Li (2001), we define the effective number of parameters

$$e(\mathbf{\lambda })=\text{tr}[{\{{\mathcal{L}}_P^{″}({\widehat{\mathrm{\sum }}}_{uu},\widehat{\mathit{\beta }})\}}^{-1}{\ell }^{″}(\widehat{\mathit{\beta }})],$$

where λ = (λ₁,…, λ_d), and, for any function g(β), g″(β) = ∂²g(β)/∂β∂β^T, the Hessian matrix of g(β). Following Wang, Li, and Tsai (2007), we define the BIC score to be

$$\text{BIC}(\mathbf{\lambda })=log{\text{RSS}}_{\mathbf{\lambda }}+e(\mathbf{\lambda })\ast log(n)/n,$$

where RSS_λ is the residual sum of squares corresponding to the model selected by the penalized least squares with the tuning parameters λ. Minimizing BIC(λ) with respect to λ over a d-dimensional space is difficult. Fan and Li (2004) advocated that the magnitude of λ_j should be proportional to the standard error of the unpenalized least squares estimator of β_j, denoted by ${\widehat{\beta }}_j^u$. Following Fan and Li (2004), we take ${\lambda }_j=\lambda \ast \text{SE}({\widehat{\beta }}_j^u)$, where SE( ${\widehat{\beta }}_j^u$) is the estimated standard error of ${\widehat{\beta }}_j^u$. Such a choice of λ_j works well from our simulation experience. Thus, the minimization problem over λ will reduce to a one-dimensional minimization problem concerning, and the tuning parameter λ, and the minimum can be obtained by a grid search. In our simulation, the range of λ is selected to be wide enough so that the BIC score reaches its minimum approximately in the middle of the range, and 50 grid points are set to be evenly distributed over the range of λ.

For the penalized quantile regression, ρ_τ (·) is not differentiable at the origin. We use the MM algorithm proposed by Hunter and Lange (2000) to minimize the penalized quantile function. In other words, we approximate ρ_τ(·) by a local quadratic function at each step during the course of iteration. This idea is similar to that of the perturbed local quadratic approximation algorithm.

4.2 Simulation Studies

In our simulation study, we will compare the underlying procedures with respect to estimation accuracy and model complexity for the penalized least squares and the penalized quantile regression procedures. It is worth noting that the best method for achieving the most accurate estimate (i.e. minimizing the squared error in Examples 1 and 2) need not coincide with the best method for having the sparsest model (i.e., maximizing the expected number ‘C’ of correctly deleted variables and minimizing the expected number ‘I’ of incorrectly deleted variables in Examples 1 and 2).

Example 1

In this example we simulate 1000 data sets, each consisting of n = 100, 200 random samples from PLMeM (2.1), in which ν(z) = 2 sin (2πz³). The covariates and random error are generated as follows. The covariate vector X is generated from a 12-dimensional normal distribution with mean 0 and variance 1. To study the effect of correlation among covariates on the performance of variable selection procedures, the off-diagonal elements of covariance matrix of X are set to be cov(X_i, X_j) = 0.2 for i = 1, 2 and j = 1,…, 12, cov(X_i, X_j) = 0.5 for i, j = 3, …, 6, cov(X_i, X_j) = 0.8 for i, j = 7,…, 10, and cov(X_i, X_j) = 0.99 for i, j = 11, 12. Thus, X₁ and X₂ are weakly correlated with the other X-variables, X₃,…, X₆ are moderately correlated, while X₇,…, X₁₀ are strongly correlated. X₁₁ and X₁₂ are nearly collinear. In this example, we set β₀ = c₁(1.5, 0, 0.75, 0, 0, 0, 1.25, 0, 0, 0, 1, 0)^T with c₁ = 0.5, 1 and 2 so that one of weakly, moderately, strongly correlated or nearly collinear covariates has nonzero coefficient, and the other covariates have zero coefficients. The covariate $Z=\mathrm{\Phi }\{(X_1+\sqrt{3}{Z}_0)/2\}$, where Z₀ ~ N (0, 1) and Φ(·) is the cumulative distribution of the standard normal distribution. Thus, Z ~ uniform(0, 1), but is correlated with the X-variables. The correlation between Z and X₁ is about 0.5, while the correlation between Z and X_j (j = 2,…, 12) is about 0.1. In this example, we consider two scenarios to generate the random error: (i) ε follows N(0, 1), i.e., homogeneous error; and (ii) ε follows $\mid sin\{2\pi {({\mathbf{X}}^{\text{T}}\mathit{\beta })}^2+0.2Z\}\mid ({\mathcal{X}}_2^2-2)$, where ${\mathcal{X}}_2^2$ denotes the chi-squared distribution with 2 degrees of freedom. This case is designed to investigate the effect of asymmetric and heteroscedastic error on the estimators. The first 2 components of X are measured with errors U_j which follow a normal distribution with mean 0, variance c₂0.5² and correlation between U₁ and U₂ being 0.5. The last 10 components of X are error free. To estimate Σ_uu, two replicates of W are generated, i.e., J_i ≡ 2. To study the effect of the level of measurement error, we take c₂ = 1 and 2. A direct calculation indicates that the naive estimator of β will be consistent to c₁(1.12, −0.10, 0.77, 0.02, 0.02, 0.02, 1.26, 0.01, 0.02, 0.02, 1.04, 0.01) for c₂ = 1 and c₁(0.91, −0.13, 0.78, 0.03, 0.04, 0.03, 1.26, 0.02, 0.02, 0.03, 1.06, 0.01) for c₂ = 2. The magnitude of all elements but the second of these two vectors is the same as that of the corresponding elements of β. This point was justified by Gleser (pp 690, 1992) that separate reliability studies of each component of X generally cannot substitute for reliability studies of the vector X treated as a unit. We therefore anticipate that if one ignores measurement errors, any appropriate variable selection procedures may falsely classify the second element of X as a significant one. Consequently, the number of zero coefficients decreases to 7 from 8. Our simulation results below exactly demonstrate this point, and further indicate that ignoring measurement error may cause errors in variable selection procedures. To save space, we present results for n = 200 only. The results for other values of n are referred to Liang and Li (2008).

We first compare estimation accuracy for the penalized least squares procedures with and without considering measurement errors. Table 1 depicts the median of squared error (MedSE), ||β̂ − β₀||², over the 1000 simulations. In Table 1, the top panel is the MedSE of the penalized least squares procedures which take account of measurement error, while the bottom panel is the MedSEs of the penalized least procedures ignoring measurement error. As a benchmark, we include the oracle estimate, the estimate for just the nonzero subset of slope β, if this subset were known and specified in advance. The column with ‘Full’ stands for the estimator based on the loss function modified to correct bias due to measurement error, but not penalized for complexity. The columns with ‘SCAD’, ‘Hard’ and ‘L_0.5’ stand for the penalized least squares with the SCAD penalty, the hard-thresholding penalty (Fan and Li 2001) and the L_0.5 penalty, respectively, and the columns with AIC, BIC, and RIC stand for the penalized least squares procedures with AIC, BIC and RIC penalties, as defined in Section 2, respectively, and ‘Oracle’ for the oracle procedure. Since the entropy penalty is discontinuous, the solutions for AIC, BIC, and RIC are obtained by exhaustively searching over all possible subsets. Thus, the resulting subsets are the best subsets for the corresponding criterion, and the computational cost for these procedures is much more expensive than that for the proposed penalized least squares methods with the continuous penalties. Rows with ‘Homo’ stand for the error ε is a homogenous error, corresponding to scenario (i), while rows with ‘Hete’ stand for the error ε is a heteroscedastic error, corresponding to scenario (ii). From Table 1, all variable selection procedures significantly improve the MedSE over the full model no matter whether the measurement error is considered or not. Furthermore, the MedSE with heteroscedastic error is slightly larger than that with homogeneous error. Weighted penalized least squares might be used to improve the penalized least squares in the presence of heteroscedastic error. The level of measurement error certainly affects the performance of the procedures compared in Table 1. That is, with an increase of either c₁ or c₂, MedSEs of all procedures increase no matter the procedures account the measurement errors or not. As expected, the MedSE of a procedure taking into account the measurement error is dramatically less than that of the corresponding procedure without considering measurement error. As shown in Table 1, the MedSEs of the penalized least squares procedures with SCAD, Hard and L_0.5 penalties are much smaller than those of the best subset variable selection procedures with AIC, BIC and RIC. Although the penalized least squares with SCAD, Hard and L_0.5 penalties share the asymptotic oracle property in Theorem 2, the SCAD procedure was advocated by Fan and Li (2001) due to its continuity property, which is shared by the Hard procedure and L_0.5 procedures. Readers are referred to Fan and Li (2001) for the definition of continuity property. The continuity property of the SCAD procedure may increase estimation accuracy and avoid variable selection instability. As seen from Table 1, the SCAD procedure performs the best in terms of estimation accuracy among the penalized least squares procedures with SCAD, Hard and L_0.5 penalties. The MedSE of the SCAD procedure is quite close to that of the oracle procedure.

Table 1.

MedSEs for example 1

(c1, c2)	Error	Full	SCAD	Hard	L0.5	AIC	BIC	RIC	Oracle
Incorporating measurement error
(1,1)	Homo	20.942	2.542	2.897	3.279	9.172	5.223	5.437	2.289
(1,1)	Hete	25.891	3.517	3.930	4.404	12.236	6.346	6.906	2.960
(.5,1)	Homo	8.894	1.267	1.633	1.745	3.830	1.590	1.699	1.022
(.5,1)	Hete	14.970	2.316	2.553	2.929	6.378	2.576	2.670	1.619
(2,1)	Homo	64.328	7.920	8.493	9.754	30.595	25.215	25.810	7.178
(2,1)	Hete	72.853	9.639	10.540	11.376	34.005	25.554	26.818	8.630
(1,2)	Homo	40.720	5.676	5.803	6.350	14.154	11.150	11.468	4.807
(1,2)	Hete	48.275	7.684	7.733	8.193	19.918	13.710	14.146	5.561
(.5,2)	Homo	14.834	2.517	2.577	2.929	5.338	3.454	3.547	1.649
(.5,2)	Hete	21.411	4.818	4.346	4.607	10.046	5.748	6.026	2.469
(2,2)	Homo	143.042	19.360	19.923	21.784	50.469	44.969	45.026	16.562
(2,2)	Hete	161.537	23.477	23.225	24.811	58.215	51.068	51.276	18.830
Ignoring measurement error
(c1, c2)	Error	Full	SCAD	Hard	L0.5	AIC	BIC	RIC	Oracle
(1,1)	Homo	30.287	17.986	18.951	18.709	23.471	19.024	19.177	17.678
(1,1)	Hete	35.886	18.389	19.421	19.377	25.862	19.697	19.926	17.736
(.5,1)	Homo	11.415	5.038	5.435	5.383	7.704	5.328	5.350	4.841
(.5,1)	Hete	16.476	5.890	6.488	6.267	9.807	6.245	6.325	5.215
(2,1)	Homo	104.607	69.747	71.926	71.266	86.555	72.440	72.877	68.755
(2,1)	Hete	109.518	68.572	70.725	70.430	87.481	71.914	72.201	66.599
(1,2)	Homo	57.374	41.940	42.690	42.757	48.899	43.640	43.865	42.201
(1,2)	Hete	63.135	42.379	43.246	43.474	51.292	44.710	45.167	42.562
(.5,2)	Homo	18.130	11.078	11.573	11.628	14.039	11.733	11.801	10.947
(.5,2)	Hete	23.262	12.114	12.521	12.472	16.328	12.465	12.667	11.354
(2,2)	Homo	212.973	165.423	168.211	167.338	187.880	171.567	172.710	166.359
(2,2)	Hete	214.813	162.558	165.597	164.413	187.594	168.685	168.607	163.999

Values in table equal 100*MedSE

Now we compare the model complexity of models selected by the proposed procedures. Overall, results for homogeneous error and heteroscedastic error are similar in terms of model complexity. To save space, Tables 2 and 3 depict the results with homogeneous error only. Results for heteroscedastic error can be found in Liang and Li (2008). In Tables 2 and 3, the column labeled ‘C’ denotes the average number of the eight true zero coefficients that were correctly set to zero, and the column labeled ‘I’ denotes the average number of the four truly nonzero coefficients incorrectly set to zero. These two tables also report the proportions of models underfitted, correctly fitted and overfitted. In the case of overfitting, the columns labeled ‘1’, ‘2’ and ‘≥ 3’ are the proportions of models including 1, 2 and more than 2 irrelevant covariates, respectively. From Table 2, it can been seen that when measurement errors are taken into account, the proportion of correctly fitted model increases and the number of true zero coefficients identified is closer to 8 as c₁ gets large, whereas a converse trend is observable as c₂ gets large. This may be not surprised since when c₁ becomes large, the nonzero coefficients are further away from zero, and zero coefficients may be easier to be identified. While c₂ gets large, the measurement error may be more involved in attenuating non-zero coefficients, and it is more difficult to correctly identify the zero coefficients. An inverse pattern can be observed for the proportion of underfitted or overfitted models, and the number of false zero coefficients. However, a similar conclusion is not available when measurement errors are ignored. In particular, the number of correctly set zero coefficients closes to seven instead of eight, as expected from our theoretic calculation above. Comparing Table 2 with Table 3, we can see that the proposed penalized least squares can dramatically reduce model complexity. In terms of model complexity, the SCAD, the Hard and the L_0.5 procedures considering measurement error outperform the ones that do not consider measurement error by further reducing model complexity, and increasing the proportion of correctly fitted models. The gain in the proportion of correctly fitted models by incorporating measurement error can be 10%, 20% and 30% for c₂ = 1 and c₁ = 0.5, 1 and 2, respectively. The gain can be even more for c₂ = 2. This is expected since ignoring measurement error may lead to an inconsistent estimate. Thus, ignoring measurement error, the bias of the estimates of the zero coefficients can be large, thus increasing the chance of identifying the corresponding variables as significant ones. As to the best subset variable selection procedures, it seems that a variable selection procedure ignoring measurement error yields a sparser model than the corresponding one incorporating measurement error, although the latter has much smaller MedSEs, as shown in Table 1. From Tables 2 and 3, the SCAD and the L_0.5 procedures that consider measurement error outperform other procedures in terms of model complexity. It is somewhat surprising that the L_0.5 procedure performs slightly better than the SCAD procedure in terms of the number of zero coefficients, and outperforms the SCAD procedure in terms of the proportion of correctly fitted models, although the SCAD procedure has smaller MedSE than the L_0.5 procedure. By a closer look at the output, we find that the SCAD estimate may contain some very small, but non-zero coefficient estimate to gain the model stability and estimation accuracy. It pays a price at reduction of the proportion of correctly fitted models. This explains why L_0.5 has better proportion of correctly fitted models, but has larger MedSE than the SCAD procedures. Increasing the level of measurement error does not really affect the average number of the eight true zero coefficients that are correctly set to zero, but does slightly increase the average number of the four truly nonzero coefficients incorrectly set to zero. This yields an increase in the proportion of under-fitted models. By a closer look at the output, we find that most underfitted models selected by the SCAD, the Hard and the L_0.5 procedures including X₁₂ while exclude X₁₁. However, in the presence of high-level measurement error, the best subset variable selection procedures that account for measurement error have quite large proportions of under-fitted models. This is certainly undesirable. From our simulation experience, it is found that these procedures tend to fail identifying X₁ as a significant variable.

Table 2.

Comparison of model complexity using the studying procedure for example 1 when considering measurement error.

(c1, c2)	Method	Under-fitted(%)	Correctly fitted(%)	Overfitted(%)			No. of Zeros
				1	2	≥ 3	C	I
(.5,1)	SCAD	7.1	56.3	27.6	8.1	0.9	7.428	0.071
	Hard	7.3	25.0	41.6	20.7	5.4	6.853	0.073
	L0.5	6.8	80.7	10.6	1.7	0.2	7.780	0.068
	AIC	2.6	14.5	29.5	28.7	24.7	6.226	0.026
	BIC	5.0	57.9	27.5	8.2	1.4	7.451	0.050
	RIC	5.0	54.0	29.7	9.5	1.8	7.387	0.050
(1,1)	SCAD	2.4	69.1	22.6	5.7	0.2	7.622	0.024
	Hard	2.2	54.4	35.6	7.1	0.7	7.445	0.022
	L0.5	2.7	85.4	10.9	0.9	0.1	7.842	0.030
	AIC	0	5.3	18.8	29.0	46.9	5.543	0
	BIC	0.1	26.0	36.5	24.8	12.6	6.701	0.001
	RIC	0.1	23.8	36.1	25.9	14.1	6.631	0.001
(2,1)	SCAD	0.8	71.8	23.2	3.8	0.4	7.667	0.008
	Hard	0.7	74.4	22.0	2.7	0.2	7.711	0.007
	L0.5	0.9	78.9	18.3	1.8	0.1	7.763	0.009
	AIC	0	1.6	9.4	21.6	67.4	4.763	0
	BIC	0	8.0	20.4	26.0	45.6	5.361	0
	RIC	0	7.4	19.3	26.1	47.2	5.315	0
(.5,2)	SCAD	15.0	46.9	28.1	9.0	1.0	7.338	0.207
	Hard	12.8	39.4	33.1	11.2	3.5	7.138	0.129
	L0.5	11.8	81.1	6.2	0.9	0	7.797	0.119
	AIC	22.4	8.3	22.8	24.0	22.5	5.751	0.230
	BIC	25.1	31.9	28.8	11.8	2.4	6.925	0.264
	RIC	24.9	29.9	28.6	13.7	2.9	6.850	0.261
(1,2)	SCAD	9.8	57.8	26.6	4.7	1.1	7.514	0.143
	Hard	7.3	68.4	20.7	3.1	0.5	7.622	0.075
	L0.5	6.3	84.0	8.8	0.7	0.2	7.821	0.063
	AIC	20.4	3.3	14.7	26.6	35.0	4.781	0.205
	BIC	20.6	13.2	27.6	22.1	16.5	5.560	0.207
	RIC	20.5	12.3	27.4	22.2	17.6	5.521	0.206
(2,2)	SCAD	8.3	62.2	23.6	5.2	0.7	7.565	0.118
	Hard	5.5	76.7	15.3	2.4	0.1	7.740	0.057
	L0.5	5.1	75.1	18.4	1.4	0	7.717	0.051
	AIC	20.8	2.3	9.7	21.3	45.9	4.192	0.208
	BIC	20.9	4.7	17.5	21.4	35.5	4.497	0.209
	RIC	20.9	4.6	17.2	21.5	35.8	4.493	0.209

Table 3.

Comparison of model complexity for example 1 when we ignore measurement error.

(c1, c2)	Method	Under-fitted(%)	Correctly fitted(%)	Overfitted(%)			No. of Zeros
				1	2	≥ 3	C	I
(.5,1)	SCAD	5.7	45.6	37.8	9.7	1.2	7.306	0.057
	Hard	5.4	8.9	33.8	37.1	14.8	6.324	0.054
	L0.5	5.1	67.9	22.6	4.0	0.4	7.617	0.051
	AIC	2.9	19.6	32.0	28.4	17.1	6.465	0.029
	BIC	6.0	72.9	17.8	3.1	0.2	7.682	0.060
	RIC	5.8	70.4	19.7	3.7	0.4	7.648	0.058
(1,1)	SCAD	1.2	44.9	40.4	11.2	2.3	7.281	0.012
	Hard	0.8	10.9	47.8	32.6	7.9	6.608	0.008
	L0.5	0.7	56.7	31.0	9.7	1.9	7.431	0.007
	AIC	0	12.3	31.8	32.8	23.1	6.240	0
	BIC	1.1	63.3	29.5	5.4	0.7	7.561	0.011
	RIC	1.1	59.0	32.3	6.7	0.9	7.501	0.011
(2,1)	SCAD	0.3	36.3	44.4	15.4	3.6	7.131	0.003
	Hard	0.2	19.6	55.7	21.8	2.7	6.920	0.002
	L0.5	0.3	43.1	39.6	13.5	3.5	7.219	0.006
	AIC	0	8.0	28.7	35.0	28.3	6.052	0
	BIC	0.2	52.5	37.6	8.5	1.2	7.414	0.002
	RIC	0.2	49.8	38.0	10.6	1.4	7.362	0.002
(.5,2)	SCAD	6.8	28.3	48.0	14.6	2.3	7.041	0.068
	Hard	6.5	4.5	34.0	39.5	15.5	6.210	0.065
	L0.5	6.3	58.6	26.9	6.7	1.5	7.469	0.063
	AIC	3.8	12.4	31.4	30.5	21.9	6.242	0.038
	BIC	6.7	63.7	24.8	4.1	0.7	7.562	0.067
	RIC	6.8	59.2	27.5	5.6	0.9	7.496	0.068
(1,2)	SCAD	2.6	24.7	52.9	16.2	3.6	6.983	0.026
	Hard	2.2	5.4	51.6	34.4	6.4	6.537	0.022
	L0.5	2.0	42.0	37.4	15.1	3.5	7.184	0.020
	AIC	0.4	6.7	26.5	35.9	30.5	5.977	0.004
	BIC	2.1	48.6	39.4	8.5	1.4	7.359	0.021
	RIC	2.0	43.9	42.0	10.5	1.6	7.288	0.020
(2,2)	SCAD	0.6	20.4	52.8	20.1	6.1	6.869	0.006
	Hard	0.4	12.9	58.1	24.6	4.0	6.796	0.004
	L0.5	0.6	27.3	43.4	22.2	6.5	6.911	0.012
	AIC	0	4.4	24.2	37.4	34.0	5.851	0
	BIC	0.5	39.0	43.6	15.1	1.8	7.199	0.005
	RIC	0.5	36.3	43.5	17.1	2.6	7.136	0.005

With respect to estimation accuracy and model complexity, Tables 1, 2 and 3 suggest that the SCAD procedure performs the best. We have also tested the accuracy of the standard error formula proposed in Section 2. From our simulation, we found that the sandwich formula (2.7) gives us accurate estimates of standard errors, and the coverage probability of the confidence interval β̂_j ± z_αSE(β̂_j) is close to the nominal level, where z_α is the 100(1 – α/2)th percentile of the standard normal distribution. To save space, we do not to present the results here.

Example 2

We generate 1000 data sets, each consisting of n = 200 random observations from model (2.1), in which the covariates X, Z, and the baseline function ν(Z) are exactly the same as those in Example 1. The regression coefficient vector β₀ is taken to be the same as the one with c₁ = 1 in Example 1. The first two components of X are measured with the error U, while (ε, U^T) follows a contaminated normal distributions, (1 − π)N₃(0, σ²I₃) + πN₃(0, (10σ)²I₃) with π being the expected proportion of contaminated data. Thus, (ε, U^T) follows an elliptical distribution, which satisfies the assumptions of Theorem 3. This contaminated model yields outlying data in a more regular and predictable fashion than the one including some outliers arbitrarily. To simultaneously examine the impact of contamination proportion and the level of measurement error, we consider π = 0.05, 0.1 and σ = 0.1 and 0.2.

The MedSE, ||β̂ – β₀||², over 1000 simulations for τ = 0.1, 0.25, 0.5, 0.75 and 0.9 are displayed in Table 4, whose caption is the same as that of Table 1. In this example, we also investigate the impact of the outliers on the performance of penalized least squares procedures. The row with ‘LS’ in Table 4 is the simulation results for the penalized least squares procedures. It can be seen from Table 4 that the penalized quantile regression procedure outperforms the corresponding penalized least squares procedure in terms of MedSE. The gain in the penalized quantile regression over the penalized least squares is considerable. The MedSEs for different τ are similar for each combination of π and σ. Table 4 shows that the SCAD procedure performs the best among the penalized quantile regression procedures in terms of MedSE. The MedSE of the SCAD procedure is very close to that of the oracle estimate.

Table 4.

MedSEs for example 2

σ	π	τ	Full	SCAD	Hard	L0.5	AIC	BIC	RIC	Oracle
.1	.05	LS	5.2505	0.7579	0.7696	1.0262	3.5733	1.8216	1.9568	0.7479
.1	.05	.10	2.9625	0.3609	0.3669	0.3934	0.3839	0.3654	0.3654	0.3098
.1	.05	.25	2.8904	0.3500	0.3615	0.3871	0.3872	0.3755	0.3755	0.3046
.1	.05	.50	2.7860	0.3537	0.3525	0.3954	0.3777	0.3682	0.3682	0.3084
.1	.05	.75	2.7805	0.3515	0.3551	0.4055	0.3876	0.3658	0.3658	0.3072
.1	.05	.90	2.9248	0.3593	0.3640	0.4160	0.4038	0.3942	0.3942	0.3197
.1	.1	LS	9.1360	1.4144	1.3989	1.9219	6.1702	3.6743	3.8031	1.3557
.1	.1	.10	3.6928	0.4495	0.4643	0.5144	0.4690	0.4675	0.4675	0.4123
.1	.1	.25	3.5604	0.4413	0.4668	0.5082	0.4759	0.4702	0.4702	0.4198
.1	.1	.50	3.6038	0.4485	0.4523	0.5132	0.4743	0.4702	0.4702	0.4244
.1	.1	.75	3.5173	0.4508	0.4685	0.5270	0.4930	0.4918	0.4918	0.4190
.1	.1	.90	3.5477	0.4685	0.4817	0.5455	0.5140	0.5066	0.5066	0.4360
.2	.05	LS	26.1258	16.3923	6.6318	7.4031	15.6449	11.9190	12.2234	4.7687
.2	.05	.10	7.1712	1.0638	1.1981	1.2334	1.2848	1.2942	1.2942	1.0974
.2	.05	.25	6.9312	1.0568	1.1707	1.2592	1.2891	1.2905	1.2905	1.1057
.2	.05	.50	6.7713	1.0910	1.2136	1.2808	1.3142	1.3094	1.3094	1.1157
.2	.05	.75	7.1882	1.1091	1.3154	1.3082	1.3569	1.3569	1.3552	1.1480
.2	.05	.90	7.1637	1.1574	1.2728	1.3477	1.4036	1.4085	1.4036	1.1573
.2	.1	LS	52.0506	72.4912	127.1681	13.9245	24.0957	18.9553	19.1162	9.1986
.2	.1	.10	9.8230	1.7160	1.9919	1.9998	2.1483	2.4303	2.3086	1.7300
.2	.1	.25	9.5495	1.6977	1.9183	1.9743	2.1899	2.4234	2.2989	1.7625
.2	.1	.50	9.5487	1.7500	2.0045	2.0589	2.2897	2.5340	2.4321	1.7535
.2	.1	.75	9.6995	1.7806	1.9767	2.0562	2.2263	2.4990	2.4066	1.8252
.2	.1	.90	9.8581	1.8075	1.9991	2.0678	2.1863	2.4859	2.4025	1.8757

Values in table equal 100*MedSE

Since overall pattern for the model complexity of the penalized quantile regression with different values of τ is similar. To save space, Table 5 depicts the model complexity of the penalized least squares and penalized quantile regression with τ = 0.5 only. Because the model complexity of the penalized quantile regression with the BIC and RIC is similar, we present the results with BIC only in Table 5. Results for other values of τ and for RIC can be found in Liang and Li (2008). The caption is the same as that in Table 2. From Table 5, it can be seen that the model complexity of the penalized least squares is significantly affected by the proportion of contaminated data (π) and the noise level (σ), which also indicates the level of measurement error in this example. When σ = 0.1, the penalized least squares can outperform the penalized quantile regression in terms of model complexity. However, when σ = 0.2, the penalized least squares procedures performs badly. In this example, the penalized quantile regression with AIC, BIC and RIC penalties has a large portion of under-fitted models. This is undesirable, and therefore they are not recommended. The model complexity for different τ is similar for each combination of π and σ. The SCAD and L_0.5 procedures have almost the same average number of zero coefficients in the selected models. Both the SCAD and the L_0.5 procedures perform better than the Hard procedure in this example. The L_0.5 procedure has a higher proportion of correctly fitted models than the SCAD procedure. This is consistent with the observation in Example 1.

Table 5.

Model complexity for example 2.

(σ, π)		Method	Under-fitted(%)	Correctly fitted(%)	Overfitted(%)			No. of Zeros
					1	2	≥ 3	C	I
(.1,.05)	LS	SCAD	0	92.3	7.3	0.3	0.1	7.918	0
		Hard	0	86.3	12.3	1.3	0.1	7.848	0
		L0.5	0	89.2	9.8	0.7	0.3	7.879	0
		AIC	0	7.6	16.5	26.0	49.9	5.286	0
		BIC	0	42.0	29.1	13.3	15.6	6.716	0
(.1,.05)	τ = .5	SCAD	0	39.1	22.4	16.8	21.7	6.687	0
		Hard	0	39.4	20.3	8.0	32.3	5.835	0
		L0.5	0	53.6	14.0	8.7	23.7	6.674	0
		AIC	11.4	85.7	2.8	0.1	0	7.970	0.342
		BIC	11.4	88.6	0	0	0	8.000	0.342
(.1,.1)	LS	SCAD	0	89.2	10.2	0.6	0	7.886	0
		Hard	0.1	89.6	10.1	0.2	0	7.893	0.001
		L0.5	0.1	89.8	8.9	1.2	0	7.886	0.001
		AIC	0	6.2	16.3	22.4	55.1	5.070	0
		BIC	0	33.6	30.3	14.2	21.9	6.365	0
(.1,.1)	τ = .5	SCAD	0	42.9	21.3	14.8	21.0	6.736	0
		Hard	0	43.4	18.4	11.0	27.2	6.170	0
		L0.5	0	58.2	11.7	9.5	20.6	6.793	0
		AIC	11.3	88.0	0.7	0	0	7.993	0.339
		BIC	11.3	88.5	0.2	0	0	7.998	0.339
(.2,.05)	LS	SCAD	5.0	81.8	12.2	1.0	0	7.817	0.056
		Hard	16.9	81.1	2.0	0	0	7.923	0.172
		L0.5	1.1	92.5	6.2	0.2	0	7.921	0.011
		AIC	0.1	4.7	14.8	22.0	58.4	4.956	0.001
		BIC	0.5	23.3	26.4	16.0	33.8	5.638	0.005
(.2,.05)	τ = .5	SCAD	0	58.8	18.8	11.6	10.8	7.200	0
		Hard	0	45.5	19.2	9.1	26.2	6.175	0
		L0.5	0	69.1	9.2	6.5	15.2	7.067	0
		AIC	18.3	81.1	0.6	0	0	7.994	0.549
		BIC	19.1	80.7	0.2	0	0	7.994	0.563
(.2,.1)	LS	SCAD	25.1	62.9	10.7	1.1	0.2	7.744	0.359
		Hard	75.0	24.6	0.4	0	0	7.923	0.978
		L0.5	5.6	88.3	5.9	0.2	0	7.880	0.056
		AIC	12.2	6.9	20.9	23.9	36.1	5.152	0.122
		BIC	13.1	27.2	25.8	14.8	19.1	5.818	0.131
(.2,.1)	τ = .5	SCAD	0.2	64.0	19.2	7.3	9.3	7.324	0.002
		Hard	0.1	46.8	19.7	9.0	24.4	6.300	0.001
		L0.5	0	75.2	9.2	4.7	10.9	7.322	0
		AIC	19.8	79.4	0.8	0	0	7.989	0.588
		BIC	28.3	71.6	0.1	0	0	7.991	0.791

4.3 An Application

Now we illustrate the proposed procedures by an analysis of a real data set from a nutritional epidemiology study. In nutrition research, the assessment of an individual’s usual intake diet is difficult but important in studying the relation between diet and cancer as well as in monitoring dietary behavior. Food Frequency Questionnaires (FFQ) are frequently administered. FFQ’s are thought to often involve a systematic bias (i.e., under-or over-reporting at the level of the individual). Two commonly used instruments are the 24-hour food recall and the multiple-day food record (FR). Each of these FR’s is more work-intensive and more costly, but is thought to involve considerably less bias than a FFQ.

We consider the data from the Nurses’ Health Study (NHS), which is a calibration study of size n = 168 women, all of whom completed a single FFQ, y, and four multiple-day food diaries (J_i = 4 in our notation), x₁. Other variables from this study include 4-day energy and Vitamin A (VA), x₂, the energy intake, x₃, body mass index (BMI), x₄, and age, z. A subset of this data set has been analyzed in Carroll, Freedman, Kipnis, and Li (1998).

Because of measurement errors, x₁ is not directly observable. Four replicates of x₁, denoted by w₁, …, w₄, are collected for each subject. Of interest here is to investigate the relation between FFQ and FR, and the other four factors. As an illustration, the following PLMeM is considered:

$$y=\nu (z)+\sum _{k=1}^4{\beta }_k{x}_k+\sum _{u=2}^4\sum _{v=u}^4{\beta }_{uv}{x}_u{x}_v+\epsilon ,$$ (4.1)

and for each subject,

$$w_j=x_1+u_j,j=1,\cdots ,4,$$

are observed. We apply the SCAD variable selection procedure to the model. Since the linear component in (4.1) is quadratic in the X-variables, we do not penalize the linear effects β_j, j = 1, …, 4, but penalize all other β’s in the SCAD procedure. The selected λ is 6.9857 by minimizing the BIC score. With the selected λ, the estimated coefficients for the selected model by SCAD are presented in the 3rd column of Table 6. For the purpose of comparison, the estimated coefficients and their standard errors are listed in the 2nd column of Table 6. We further apply the penalized quantile regression procedure with τ =0.1, 0.25, 0.5, 0.75 and 0.9. The resulting estimates are given in the columns of 4th to 8th in Table 6, respectively. From Table 6, the estimates of regression for different values of τ are almost the same. This implies that the error likely is homogeneous error. Furthermore, the selected model by the SCAD indicates that all interactions and quadratic terms are not significant. To further confirm this, we construct a Wald’s test based on the asymptotic normality in Theorem 2 without involving the penalty for hypothesis:

$$H_0:{\beta }_{uv}=0,\text{for}2\le u\le v\le 4\text{versus}{H}_1:{\beta }_{uv}\ne 0,\text{for}2\le u\le v\le 4.$$

Table 6.

NHS study: Estimated coefficients and standard errors for the full model, the models selected by penalized least squares method and quantile regression method using the SCAD procedure.

Variable	Full Model	SCAD LS	SCAD τ = 0.1	SCAD τ = 0.25	SCAD τ = 0.5	SCAD τ = 0.75	SCAD τ = 0.9
x1	−0.0200(0.0162)	−0.0231(0.0175)	0.0217	0.0181	0.0207	0.0192	0.0219
x2	0.2694(0.0248)	0.2659(0.0257)	0.2741	0.2685	0.2599	0.2576	0.2523
x3	−0.0551(0.0232)	−0.0483(0.0244)	−0.0184	−0.0190	−0.0229	−0.0232	−0.0244
x4	0.0420(0.0284)	0.0016(0.0212)	−0.0137	−0.0161	−0.0086	−0.0133	−0.0110
$x_2^2$	−0.0264(0.0170)	0(0.0000)	0	0	0	0	0
x2x3	0.0060(0.0227)	0(0.0000)	0	0	0	0	0
x2x4	0.0298(0.0285)	0(0.0000)	0	0	0	0	0
$x_3^2$	−0.0203(0.0134)	0(0.0000)	0	0	0	0	0
x3x4	0.0297(0.0324)	0(0.0000)	0	0	0	0	0
$x_4^2$	−0.0216(0.0103)	0(0.0000)	0	0	0	0	0

From Theorem 2, the limiting distribution of the Wald test follows a chi-square distribution with 6 degrees of freedom. The resulting Wald’s test is 12.4969 with P-value 0.0518, which is in favor of H₀ at significance level 0.05. Thus, we would conclude the following selected model

$$\widehat{y}=\widehat{\nu }(z)-0.0230x_1+0.2705x_2-0.0497x_3+0.0158x_4,$$

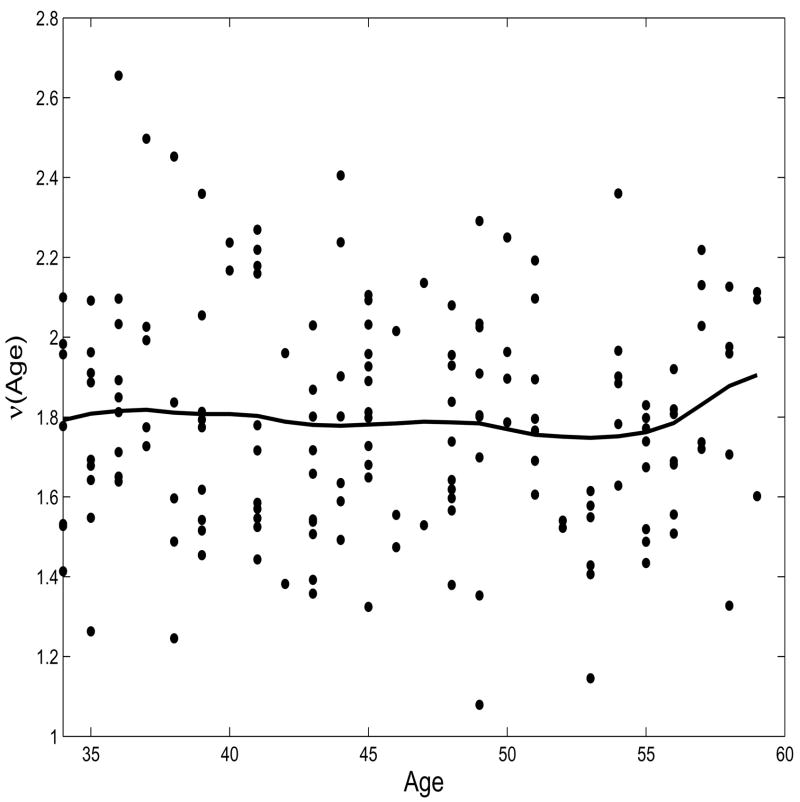
where ν̂ (z) equals m̂ (z) − m̂_w(z)^Tβ̂ and is depicted in Figure 1.

Figure 1.

Estimated curve of ν (·) with a consideration of measurement error for the NHS data. The dots are the partial residuals $r_i=y_i-{\mathbf{W}}_i^{\text{T}}\widehat{\mathit{\beta }}$ with β̂ obtained under the full model. The solid curve is the estimated ν (·).

5 DISCUSSION

Variable selection for statistical models with measurement errors seems to be overlooked in the literature. In this article, we have developed two classes of variable selection procedures, the penalized least squares and the penalized quantile regression with nonconvex penalty, for partially linear models with error-prone linear covariates and possibly contaminated response variable. The sampling properties of the proposed procedures are studied, the finite sample performance of the proposed methodology is empirically examined, the effects of ignoring measurement errors on variable selection are also studied by Monte Carlo simulation, and numerical comparisons between the proposed method and direct extension of traditional variable selection criteria, such as AIC, BIC and RIC, are conducted. From our simulation study, the nonconvex penalized least squares and penalized quantile regression methods outperform direct extension of the traditional variable selection criteria.

As a referee pointed out, in the corrected least squares function, the first two terms in (2.2) may take on negative values. In particular, one may run into such problems frequently under the low-information conditions. If this occurs, one might consider correcting the bias in the least squares loss by using the orthogonal regression method, as in (3.2). Further study is needed in this area.

As demonstrated in our simulation, the proposed procedures perform reasonably well with moderate sample sizes. As a referee noted, it is of interest to study variable selection for large dimension, small sample size measurement error data. We have conducted some empirical study via Monte Carlo simulation. From our limited experience, one should be cautious in applying our methods when the number of predictors is close to the sample size. In such situations, the proposed procedures likely result in an under-fitted model excluding some significant predictors. There are some recent developments on variable selection for linear regression models with large dimension and small sample size data (Candes and Tao 2007; Fan and Lv 2008). Further research is needed for measurement error data.

APPENDIX

The following regularity conditions are needed for Theorems 1–3. They may not be the weakest ones.

Regularity Conditions

1. Σ_X|Z is a positive-definite matrix, E(ε|X, Z) = 0, and E(|ε|³|X, Z) < ∞;

2. The bandwidths in estimating m_w(z) and m_y(z) are of order n^−1/5;

3. K(·) is a bounded symmetric density function with compact support and satisfies ∫K(u)du = 1, ∫K(u)udu = 0 and ∫u²K(u)du = 1;

4. The density function of Z, f_Z(z), and the density function of (Y, Z) are bounded away from 0 and have bounded continuous second derivative;

5. m_y(z) and m_w(z) have bounded and continuous second derivatives;

We first point out a fact, which is assured by Conditions (b)–(e), that the local polynomial estimates of m_y(·) and m_w(·) satisfy

$$\underset{z}{sup}\mid {\widehat{m}}_y(z)-m_y(z)\mid =o_p(n^{-1/4}),\text{and}\underset{z}{sup}\mid {\widehat{m}}_{w,j}(z)-m_{w,j}(z)\mid =o_p(n^{-1/4})$$ (A.1)

for j = 1, …, d, where m_w,j(·) and m̂_w,j(·) are the j-th components of m_w(·) and m̂_w(·), respectively. See Mack and Silverman (1982) for a detailed discussion of the proof of (A.1), which will repeatedly be used in our proof. Let |ξ| = max_i |ξ| for any sequence {ξ_i}.

Lemma 1

Assume that random variables a_i(W_i, Z_i, Y_i) and c_i(W_i, Z_i, Y_i), denoted by a_i and c_i, satisfy a_i(W_i,Z_i,Y_i) ≡ 1 or Ea_i = 0 and |c_i| = o_p(n^−1/4). Then

$$\sum _{i=1}^n{a}_i{c}_i{\varpi }_i=o_p(\sqrt{n}),$$

where ϖ_i are independent variables with mean zero and finite variance.

The lemma can be shown along the same lines as those of Lemma A.5 of Liang, Härdle, and Carroll (1999). We omit the details.

A.1 Proof of Theorem 1

The strategy to prove Theorem 1 is similar to those of Theorems 1 and 2 of Fan and Li (2001). Only the key ideas are outlined below.

Let α_n = n^−1/2. We show that, for any given ζ > 0, there exists a large constant C such that

$$P\left\{\underset{\mid \mid \mathbf{v}\mid \mid =C}{inf}{\mathcal{L}}_P({\mathrm{\sum }}_{uu},{\mathit{\beta }}_0+{\alpha }_n\mathbf{v})>{\mathcal{L}}_P({\mathrm{\sum }}_{uu},{\mathit{\beta }}_0)\right\}\ge 1-\zeta .$$ (A.2)

Denote

$$\begin{array}{l}{J}_n(\mathbf{v})=\sum _{i=1}^n\left[{\left\{{\widehat{Y}}_i-{\stackrel{\sim }{\mathbf{W}}}_i^{\text{T}}({\mathit{\beta }}_0+{\alpha }_n\mathbf{v}\right\}}^2-{\left({\widehat{Y}}_i-{\widehat{\mathbf{W}}}_i^{\text{T}}{\mathit{\beta }}_0\right)}^2\right]\\ -n\{{({\mathit{\beta }}_0+{\alpha }_n\mathbf{v})}^{\text{T}}{\mathrm{\sum }}_u({\mathit{\beta }}_0+{\alpha }_n\mathbf{v})-{\mathit{\beta }}_0^{\text{T}}{\mathrm{\sum }}_u{\mathit{\beta }}_0\}.\end{array}$$

Then, J_n(v) can be represented as

$$J_n(\mathbf{v})=-2{\alpha }_n\sum _{i=1}^n\left({\widehat{Y}}_i{\widehat{\mathbf{W}}}_i^{\text{T}}-{\widehat{\mathbf{W}}}_i^{\text{T}}{\mathit{\beta }}_0{\widehat{\mathbf{W}}}_i^{\text{T}}+{\mathit{\beta }}_0^{\text{T}}{\mathrm{\sum }}_u\right)\mathbf{v}+n{\alpha }_n^2{\mathbf{v}}^{\text{T}}(n^{-1}{\widehat{\mathbf{W}}}_i{\widehat{\mathbf{W}}}_i^{\text{T}}-{\mathrm{\sum }}_u)\mathbf{v}.$$ (A.3)

We next calculate the order of the first term. Note that

$$\begin{array}{l}\sum _{i=1}^n({\widehat{Y}}_i{\widehat{\mathbf{W}}}_i^{\text{T}}-{\widehat{\mathbf{W}}}_i^{\text{T}}{\mathit{\beta }}_0{\widehat{\mathbf{W}}}_i^{\text{T}}+{\mathit{\beta }}_0^{\text{T}}{\mathrm{\sum }}_u)\\ =\sum _{i=1}^n({\widehat{Y}}_i-{\stackrel{\sim }{Y}}_i){({\widehat{\mathbf{W}}}_i-{\stackrel{\sim }{\mathbf{W}}}_i)}^{\text{T}}+\sum _{i=1}^n({\widehat{Y}}_i-{\stackrel{\sim }{Y}}_i){\stackrel{\sim }{\mathbf{W}}}_i^{\text{T}}+\sum _{i=1}^n{\stackrel{\sim }{Y}}_i{({\widehat{\mathbf{W}}}_i-{\stackrel{\sim }{\mathbf{W}}}_i)}^{\text{T}}\\ +\sum _{i=1}^n({\stackrel{\sim }{Y}}_i-{\stackrel{\sim }{\mathbf{W}}}_i^{\text{T}}{\mathit{\beta }}_0{\stackrel{\sim }{\mathbf{W}}}_i^{\text{T}}+{\mathit{\beta }}_0^{\text{T}}{\mathrm{\sum }}_u)-\sum _{i=1}^n{({\widehat{\mathbf{W}}}_i-{\stackrel{\sim }{\mathbf{W}}}_i)}^{\text{T}}{\mathit{\beta }}_0{({\widehat{\mathbf{W}}}_i-{\stackrel{\sim }{\mathbf{W}}}_i)}^{\text{T}}\\ -\sum _{i=1}^n{\stackrel{\sim }{\mathbf{W}}}_i^{\text{T}}{\mathit{\beta }}_0{({\widehat{\mathbf{W}}}_i-{\stackrel{\sim }{\mathbf{W}}}_i)}^{\text{T}}-\sum _{i=1}^n{({\widehat{\mathbf{W}}}_i-{\stackrel{\sim }{\mathbf{W}}}_i)}^{\text{T}}{\mathit{\beta }}_0{\stackrel{\sim }{\mathbf{W}}}_i^{\text{T}}.\end{array}$$

It is seen that the first and fifth terms are o_p(n^1/2) by (A.1). Using Lemma 1 yields that the second, third, sixth and seventh terms are O_p(n^1/2). Furthermore, EỸ_i = 0, EW̃_i = 0. It follows from the central limit theorem that the fourth term is O_p(n^1/2). Therefore, the first term in (A.3) is of the order $O_p(\sqrt{n}{\alpha }_n)=O_p(1)$ as α_n = O(n^−1/2). Taking C large enough, the first term in (A.3) is dominated by the second term in (A.3) as $n^{-1}{\widehat{\mathbf{W}}}_i{\widehat{\mathbf{W}}}_i^{\text{T}}-{\mathrm{\sum }}_u\to E{\stackrel{\sim }{\mathbf{X}}}^{\text{T}}\stackrel{\sim }{\mathbf{X}}$ in probability.

Note that

$$\begin{array}{l}{D}_n(\mathbf{v})\equiv {\mathcal{L}}_P({\mathrm{\sum }}_{uu},{\mathit{\beta }}_0+{\alpha }_n\mathbf{v})-{\mathcal{L}}_P({\mathrm{\sum }}_{uu},{\mathit{\beta }}_0)\\ \ge J_n(\mathbf{v})+n\sum _{j=1}^s\{p_{{\lambda }_n}(\mid {\beta }_{j0}+{\alpha }_n{v}_j\mid )-p_{{\lambda }_n}(\mid {\beta }_{j0}\mid )\},\end{array}$$ (A.4)

where s is the dimension of β₁₀.

As shown in Fan and Li (2001), the second term of (A.4) is bounded by the second term in (A.3) under the assumption of a_n = O_p(n^−1/2) and b_n → 0. Thus, by taking C large enough, the second term in (A.3) dominates both the first term in (A.3) and the second term in (A.4). This proves Part I.

We now prove the sparsity. It suffices to show that for any given β₁ satisfying ||β₁ −β₁₀||= O_p(n^−1/2) and j = s + 1, …, d, such that $\frac{\partial {\mathcal{L}}_P({\mathrm{\sum }}_{uu},\beta )}{\partial {\beta }_j}>0$ for 0 < β_j < ε_n = Cn^−1/2, and $\frac{\partial {\mathcal{L}}_P({\mathrm{\sum }}_{uu},\beta )}{\partial {\beta }_j}<0$ for −ε_n < β_j < 0.

By the Taylor expansion, we have

$$\begin{array}{c}\frac{\partial {\mathcal{L}}_P({\mathrm{\sum }}_{uu},\beta )}{\partial {\beta }_j}=-2[Y_i-{\widehat{m}}_y(Z_i)-{\{{\mathbf{W}}_i-{\widehat{\mathbf{m}}}_w(Z_i)\}}^{\text{T}}\beta ]\\ {\{{\mathbf{W}}_i-{\widehat{\mathbf{m}}}_w(Z_i)\}}_j+n{p}_{{\lambda }_j}^{\prime }(\mid {\beta }_j\mid )sgn({\beta }_j).\end{array}$$

The first term can be shown to be O_p(n^−1/2) by (A.1) and that β₁ − β₁₀ = O_p(n^−1/2). Recall that n^1/2λ→∞, and lim inf_n→∞ lim inf_{u→0 +} p′ _λ(u)/λ>0. We know that the sign of $\frac{\partial {\mathcal{L}}_P({\mathrm{\sum }}_{uu},\beta )}{\partial {\beta }_j}$ is determined by that of β_j, and is negative for 0 < β_j < ε_n and positive for −ε_n > β_j > 0. It follows that β̂₂ = 0.

We now prove II(b) by using the results of Newey (1994) to show the asymptotic normality of β̂₁. Note that the estimators β̂₁ based on the penalized likelihood function given in (2.2) is equivalent to the solution of the estimating equation:

$$\sum _{i=1}^n\mathrm{\Phi }({\widehat{\mathbf{m}}}_{w1},{\widehat{m}}_y,{\mathit{\beta }}_1,Y_i,{\mathbf{W}}_{i1},Z_i)-n{\mathit{\zeta }}_1=0,$$ (A.5)

where Φ(m_w1,m_y,β₁, Y, W₁, Z) = {W₁ − m_w1(Z)} [Y − m_y(Z) − {W₁ − m_w1(Z)}^T β₁] Σ_uu1β₁ and ${\mathit{\zeta }}_1={\{p_{\lambda }^{\prime }(\mid {\mathit{\beta }}_1\mid )sgn({\mathit{\beta }}_1),\dots ,p_{\lambda }^{\prime }(\mid {\mathit{\beta }}_s\mid )sgn({\mathit{\beta }}_s)\}}^{\text{T}}$.

It follows from (A.1) that |m̂_w1(Z) − m̂_w1(Z)| = o_p(n^−1/4) and m̂_y(Z) − m_y(Z) = O_p(n^−1/4). Thus, Assumption 5.1(ii) in Newey (1994) holds. Let

$$D({\mathbf{m}}_{w1}^{\ast }-{\mathbf{m}}_{w1},m_y^{\ast }-m_y)=\frac{\partial \mathrm{\Phi }}{\partial {\mathbf{m}}_{w1}}({\mathbf{m}}_{w1}^{\ast }-{\mathbf{m}}_{w1})+\frac{\partial \mathrm{\Phi }}{\partial m_y}(m_y^{\ast }-m_y).$$

where $\frac{\partial \mathrm{\Phi }}{\partial {\mathbf{m}}_{w1}}$ and $\frac{\partial \mathrm{\Phi }}{\partial m_y}$ are the Frechet derivatives. A direct but cumbersome calculation derives that $E\left(\frac{\partial \mathrm{\Phi }}{\partial {\mathbf{m}}_{w1}}\right)=0$ and $E\left(\frac{\partial \mathrm{\Phi }}{\partial m_y}\right)=0$. Furthermore,

$$\begin{array}{l}\mid \mathrm{\Phi }({\mathbf{m}}_{w1}^{\ast },m_y^{\ast },{\mathit{\beta }}_1,Y,{\mathbf{W}}_1,Z)-\mathrm{\Phi }({\mathbf{m}}_{w1},m_y,{\mathit{\beta }}_1,Y,{\mathbf{W}}_1,Z)-D({\mathbf{m}}_{w1}^{\ast }-{\mathbf{m}}_{w1},m_y^{\ast }-m_y)\mid \\ =O_p\left(\mid {\mathbf{m}}_{w1}^{\ast }-{\mathbf{m}}_{w1}{\mid }^2+\mid m_y^{\ast }-m_y{\mid }^2\right).\end{array}$$ (A.6)

This indicates that Assumption 5.1(i) in Newey (1994) is valid. Furthermore, it can be seen by noting the expression of D(·, ·) that Assumption 5.2 of Newey (1994) is also valid. In addition, it follows from the above statements that for any ( ${\mathbf{m}}_{w1}^{\ast },m_y^{\ast }$),

$$E\left\{D({\mathbf{m}}_{w1}^{\ast }-{\mathbf{m}}_{w1},m_y^{\ast }-m_y)\right\}=0,$$

and Newey’s Assumption 5.3, α(T) = 0, holds. By Lemma 5.1 in Newey (1994), it follows that β̂₁ has the same distribution as the solution to the equation

$$0=\sum _{i=1}^n\mathrm{\Phi }({\mathbf{m}}_{w1},m_y,{\mathit{\beta }}_1,Y_i,{\mathbf{W}}_{i1},Z_i)-n{\mathit{\zeta }}_1.$$ (A.7)

A direct simplification yields that

$${\stackrel{\sim }{\mathbf{X}}}_{11}{\stackrel{\sim }{\mathbf{X}}}_{11}^{\text{T}}\sqrt{n}({\widehat{\mathit{\beta }}}_1-{\mathit{\beta }}_{01})+n^{1/2}\mathbf{b}=n^{-1/2}\sum _{i=1}^n\{{\stackrel{\sim }{\mathbf{X}}}_{i1}({\epsilon }_i-{\mathbf{U}}_i^{\text{T}}{\mathit{\beta }}_{10})+{\mathbf{U}}_i{\epsilon }_i+({\mathbf{U}}_i{\mathbf{U}}_i^{\text{T}}-{\mathrm{\sum }}_{uu1}){\mathit{\beta }}_{10}\}+o_p(1).$$

This completes the proof.

A.2 Proof of Theorem 3

To prove Theorem 3, we need a fact regarding elliptical distributions. Let ϑ be a random vector. It is said that ϑ follows an elliptical distribution if its characteristic function is of the form

$$E\{exp(i{\mathbf{t}}^{\text{T}}\mathit{\vartheta })\}=exp(i{\mu }^{\text{T}}\mathbf{t})\phi ({\mathbf{t}}^{\text{T}}\mathrm{\Lambda }\mathbf{t}).$$

It is known that E(ϑ) = μ and cov(ϑ) = {−2φ′(0)} Λ (Fang, Kotz, and Ng 1990). Furthermore, we have that if μ = 0, then for any constant vector b ≠ 0,

$${\vartheta }_1\stackrel{d}{=}\frac{{\mathbf{b}}^{\text{T}}\mathit{\vartheta }}{\sqrt{{\mathbf{b}}^{\text{T}}\mathrm{\Lambda }\mathbf{b}/{\mathrm{\Lambda }}_{11}}},$$ (A.8)

where ϑ₁ is the first element of ϑ, and Λ₁₁ is the (1,1)-element of Λ, and $R_1\stackrel{d}{=}{R}_2$ means R₁ and R₂ have the same distribution. (A.8) can be easily shown by calculating the characteristic functions of the random variables on each side of (A.8).

Now we prove Theorem 3. We can use the arguments similar to those for Theorem 1 to prove Part I and II(a), and omit the details. We now finish the proof of Part II(b) in three steps. For notational simplicity, write ${\widehat{a}}_i={\widehat{\mathbf{W}}}_i+\frac{{\widehat{Y}}_i-{\widehat{\mathbf{W}}}_i^{\text{T}}\mathit{\beta }}{1+{\mathit{\beta }}^{\text{T}}{\mathbf{C}}_{uu}\mathit{\beta }}·\mathit{\beta },{\widehat{c}}_i={\psi }_{\tau }\left(\frac{{\widehat{Y}}_i-{\widehat{\mathbf{W}}}_i^{\text{T}}\mathit{\beta }}{\sqrt{1+{\mathit{\beta }}^{\text{T}}{\mathbf{C}}_{uu}\mathit{\beta }}}\right),a_i={\stackrel{\sim }{\mathbf{W}}}_i+\frac{{\epsilon }_i-{\mathbf{U}}_i^{\text{T}}\mathit{\beta }}{1+{\mathit{\beta }}^{\text{T}}{\mathbf{C}}_{uu}\mathit{\beta }}·\mathit{\beta }$, and $c_i={\psi }_{\tau }(\frac{{\epsilon }_i-{\mathbf{U}}_i^{\text{T}}\mathit{\beta }}{\sqrt{1+{\mathit{\beta }}^{\text{T}}{\mathbf{C}}_{uu}\mathit{\beta }}})$, where ψ_τ is the derivative of ρ_τ.

Step 1

It is straightforward to verify that

$$\underset{1\le i\le n}{max}\mid {\widehat{a}}_i-a_i\mid =o_p(n^{-1/4}),\underset{1\le i\le n}{max}\mid {\widehat{c}}_i-c_i\mid =o_p(n^{-1/4}).$$ (A.9)

Note that both a_i and c_i are sequences of i.i.d. variables with mean zero and finite variances. It follows from (A.9) and Lemma 1 that

$$\begin{array}{l}\sum _i{\widehat{a}}_i{\widehat{c}}_i-\sum _i{a}_i{c}_i=\sum _i({\widehat{c}}_i-c_i)({\widehat{a}}_i-a_i)+\sum _i({\widehat{c}}_i-c_i)a_i-\sum ({\widehat{a}}_i-a_i)c_i\\ =o_p(n^{1/2}).\end{array}$$

This argument indicates that the estimator β̂_τ has the same asymptotic distribution as that of the estimators constructed by minimizing the objective function:

$$\sum _{i=1}^n{\rho }_{\tau }\left(\frac{{\stackrel{\sim }{Y}}_i-{\stackrel{\sim }{\mathbf{W}}}_i^{\text{T}}\mathit{\beta }}{\sqrt{1+{\mathit{\beta }}^{\text{T}}{\mathbf{C}}_{uu}\mathit{\beta }}}\right)+n\sum _{j=1}^d{p}_{{\lambda }_j}(\mid {\beta }_j\mid )\stackrel{\text{def}}{=}Q(\mathit{\beta })+n\sum _{j=1}^d{p}_{{\lambda }_j}(\mid {\beta }_j\mid )$$

with respect to β.

Step 2

Note that the loss function ρ_τ is differentiable everywhere except at the point of zero. The directional derivatives of Q(β) at the solution β̂_τ are all non-negative, which implies that

$$\begin{array}{l}\sum _i\left({\stackrel{\sim }{W}}_{i1}+\frac{{\stackrel{\sim }{Y}}_i-{\stackrel{\sim }{\mathbf{W}}}_{i1}^{\text{T}}{\mathit{\beta }}_1}{1+{\mathit{\beta }}_1^{\text{T}}{\mathbf{C}}_{11}{\mathit{\beta }}_1}{\mathit{\beta }}_1\right){\psi }_{\tau }\left(\frac{{\stackrel{\sim }{Y}}_i-{\stackrel{\sim }{\mathbf{W}}}_{i1}^{\text{T}}{\mathit{\beta }}_1}{\sqrt{1+{\mathit{\beta }}_1^{\text{T}}{\mathbf{C}}_{11}{\mathit{\beta }}_1}}\right)-n{\mathit{\zeta }}_1\sqrt{1+{\mathit{\beta }}_1^{\text{T}}{\mathbf{C}}_{11}{\mathit{\beta }}_1}\\ =O_p(\sum {\stackrel{\sim }{\mathbf{W}}}_{i1})\end{array}$$ (A.10)

at β₁ = β̂_τ1.

Step 3

We apply a similar idea to Corollary 2.2 of He and Shao (1996) for M-estimators to complete the proof by verifying the assumptions needed for the Corollary and setting r = 1, A_n = λ_max( _q)n, and ${\mathbf{D}}_n=nf(q_{\tau }){(1+{\mathit{\beta }}_{10}^{\text{T}}{\mathbf{C}}_{11}{\mathit{\beta }}_{10})}^{-1/2}{\mathrm{\sum }}_{\text{X}\mid \text{Z}}$. Here λ_max( _q) denotes the maximum eigenvalue of _q, which is equal to

$$E\{{\psi }_{\tau }^2(\xi ){\stackrel{\sim }{\mathbf{X}}}_1^{\otimes 2}\}+cov\left\{\left({\mathbf{U}}_{11}+\frac{\xi {\mathit{\beta }}_{10}}{\sqrt{1+{\mathit{\beta }}_{10}^{\text{T}}{\mathbf{C}}_{11}{\mathit{\beta }}_{10}}}\right){\psi }_{\tau }(\xi )\right\}.$$

Furthermore, let ${\xi }_i=({\epsilon }_i-{\mathbf{U}}_{i1}^{\text{T}}{\mathit{\beta }}_{10})/\sqrt{1+{\mathit{\beta }}_{10}^{\text{T}}{\mathbf{C}}_{11}{\mathit{\beta }}_{10}}-q_{\tau }$. With the assumption of elliptical symmetry on (ε, U^T) and by (A.8), ξ_i and ε_i − q_τ have the same distribution. It then follows from an argument similar to that for Corollary 2.2 of He and Shao (1996) that

$$\begin{array}{l}\sqrt{n}f(q_{\tau }){(1+{\mathit{\beta }}_{10}^{\text{T}}{\mathbf{C}}_{11}{\mathit{\beta }}_{10})}^{1/2}{\mathrm{\sum }}_{\text{X}\mid \text{Z}}({\widehat{\mathit{\beta }}}_{\tau 1}-{\mathit{\beta }}_{10})+n\mathbf{b}\sqrt{1+{\mathit{\beta }}_{10}^{\text{T}}{\mathbf{C}}_{11}{\mathit{\beta }}_{10}}\\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n\left({\stackrel{\sim }{\mathbf{X}}}_{i1}+{\mathbf{U}}_{i1}+\frac{{\xi }_i{\mathit{\beta }}_{10}}{\sqrt{1+{\mathit{\beta }}_{10}^{\text{T}}{\mathbf{C}}_{11}{\mathit{\beta }}_{10}}}\right){\psi }_{\tau }({\xi }_i)+o_p(1).\end{array}$$

The proof of Theorem 3 is completed by using the central limit theorem with a direct calculation.