ABC/2 for rapid clinical estimate of infarct, perfusion, and mismatch volumes

Abstract

Background:

Rapid and easy clinical assessments for volumes of infarction and perfusion mismatch are needed. We tested whether simple geometric models generated accurate estimates of these volumes.

Methods:

Acute diffusion-weighted image (DWI) and perfusion (mean transit time [MTT]) in 63 strokes and established infarct volumes in 50 subacute strokes were measured by computerized planimetry. Mismatch was defined as MTT/DWI ≥ 1.2. Observers, blinded to planimetric values, measured lesions in three perpendicular axes A, B, and C. Geometric estimates of sphere, ellipsoid, bicone, and cylinder were compared to planimetric volume by least-squares linear regression.

Results:

The ABC/2 formula (ellipsoid) was superior to other geometries for estimating volume of DWI (slope 1.16, 95% confidence interval [CI] 0.94 to 1.38; R² = 0.91, p = 0.001) and MTT (slope 1.11, 95% CI 0.99 to 1.23; R² = 0.89, p = 0.001). The intrarater and interrater reliability for ABC/2 was high for both DWI (0.992 and 0.965) and MTT (0.881 and 0.712). For subacute infarct, the ABC/2 formula also best estimated planimetric volume (slope 1.00, 95% CI 0.98 to 1.19; R² = 0.74, p = 0.001). In general, sphere and cylinder geometries overestimated all volumes and bicone underestimated all volumes. The positive predictive value for mismatch was 92% and negative predictive value was 33%.

Conclusions:

Of the models tested, ABC/2 is reproducible, is accurate, and provides the best simple geometric estimate of infarction and mean transit time volumes. ABC/2 has a high positive predictive value for identifying mismatch greater than 20% and might be a useful tool for rapid determination of acute stroke treatment.

GLOSSARY

CBF

= cerebral blood flow;

CBV

= cerebral blood volume;

CI

= confidence interval;

DWI

= diffusion-weighted image;

FOV

= field of view;

ICH

= intracerebral hemorrhage;

MCA

= middle cerebral artery;

MTT

= mean transit time;

PWI

= perfusion-weighted imaging;

ROI

= region of interest;

TE

= echo time;

TR

= repetition time.

Recent thrombolytic trials for cerebral infarction have used inclusion criteria of stroke volume less than 1/3 the middle cerebral artery (MCA) territory or mismatch of diffusion-weighted image (DWI) and perfusion volumes.^1,2 However, these criteria are often derived by clinical gestalt, rather than true measurements. A rapid, easy, and accurate means to assess stroke volume is needed if this criterion is to be uniformly applied. Furthermore, stroke volume can be a clinically relevant prognostic variable for counseling patients and their families on outcomes.^3–11 Stroke volume can also predict those patients who are likely to have post-thrombolysis hemorrhage or malignant edema.^12–16 Thus, outside of the research setting in which stroke volumes are measured using computer planimetry in a post hoc fashion, clinicians do not have this information at hand for patient selection for acute treatment,¹⁷ counseling patients,¹⁸ anticipating complications, or enrolling patients in trials.

A simple, fast, clinically relevant method has been devised for assessing intracerebral hemorrhage (ICH) volume.^19,20 For ICH, the validated ABC/2 method assumes an ellipsoid shape but makes adjustments to slices based on their proportional representation to the largest volume.²⁰ Validation of this ABC/2 formula has been applied to other intracranial hemorrhages,^21,22 but not to ischemic stroke volume. Without making an assumption as to the best geometric model, we tested several Euclidean geometric shapes to assess which simple model produced the most reliable ischemic volume compared to computer planimetry.

METHODS

Patient selection.

Review of our stroke and radiology database was approved by our human institutional review board. This retrospective study did not require patient consent. We identified 87 patients with acute MCA infarctions who underwent MR diffusion-weighted imaging (DWI) and perfusion-weighted imaging (PWI) within 9 hours of symptom onset between September 2005 and June 2006. Twenty patients were excluded from analysis: 9 with poor image quality, 3 with PWI not covering the infarcted territory, 3 with chronic infarctions that alter perfusion, 3 with critical ICA stenoses, 2 with reperfusion, and 4 with either no DWI lesion or numerous small punctate lesions. Thus, acute image analysis was performed on 63 patients. For subacute analysis, a separate consecutive subgroup of 50 patients was selected with CT or MRI infarcts present at least 20 hours after ischemic onset. There was no selection of scans based on pathophysiology, regularity of lesion, or location of lesion.

Image acquisition and processing.

MRI was performed on a 1.5-Tesla Signa scanner (GE Medical Systems, Milwaukee, WI) with echoplanar capabilities. CT imaging was performed with a High Speed Advantage helical CT scanner (GE Medical Systems). DWI was obtained using single shot, spin echoplanar imaging with sampling of the entire diffusion tensor. Six high-b-value images corresponding to diffusion measurements in different gradient directions were acquired, in addition to a single low-b-value image. Double inversion pulses were used to help reduce eddy current effects. The high b-value was 1,000 s/mm² and the low b-value was 0 s/mm². Other parameters were as follows: repetition time (TR) of 5,000 msec, time to echo (TE) of 90–100 msec, field of view (FOV) of 22 cm by 22 cm, image matrix of 128 by 128 pixels, slice thickness of 5 mm with a 1 or 2 mm gap, and five signal averages. Isotropic DWI images and ADC maps were reviewed.

PWI was performed using a dynamic susceptibility contrast technique. Serial echoplanar gradient echo images were acquired with TR of 1,500 msec, TE of 40 msec, and same FOV and thickness as DWI. A complete volume of 16 slices was acquired every 1.5 s, and 46 complete volumes were acquired. Total imaging time was 1 minute, 9 seconds. Ten seconds after the beginning of image acquisition, 20 mL of gadopentetate dimeglumine (0.5 mmol/mL) was injected via a peripheral IV catheter at a rate of 5 mL/s. This injection was immediately followed by injection of 20 mL of normal saline, at the same injection rate. The nonhelical CT scanning technique was 120 kV, 170 mA, 2-s scan time, and 5-mm section thickness with no gap.

For MRI, dynamic susceptibility contrast images were used to generate signal intensity-vs-time curves for each pixel in the imaged volume. These curves were integrated to yield maps of cerebral blood volume (CBV) for each pixel. Cerebral blood flow (CBF) was calculated for each pixel by deconvolution, using the singular value decomposition technique.^23,24 Software used for deconvolution was the Siemens PWI task card performed on a Leonardo workstation (Syngo Leonardo VD 10B). A global arterial input function was derived manually from the middle cerebral artery ipsilateral to each patient's infarction by technologists placing four to five regions of interest (ROIs) at the edge of the blossoming middle cerebral artery. Mean vascular transit time (MTT) was calculated by dividing CBV by CBF.

Imaging analysis and measurements.

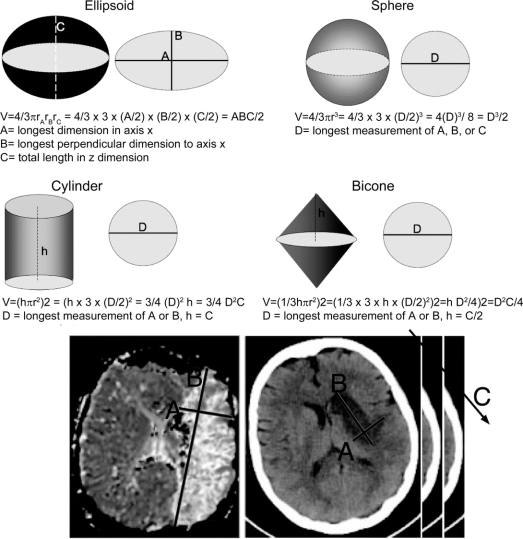
MRI lesions for acute or subacute volumes were measured on DWI or MTT images. Subacute infarcts on CT images were measured using windows/levels of 80/20 or 30/30 for Houndsfield units.² Absolute infarcts were measured by E.S.R. using Alice software (Parexel Corp.). DWI and MTT lesions volumes were measured by P.W.A. using Analyze 7.0 software (Analyze Direct, KS). The ischemic ROIs were visually segmented to determine the volume. Stroke volumes ranged over three orders of magnitude from 0.25 to 403 cm³ by computerized planimetry. Observers (J.R.S. and L.R.G.) blinded to planimetric data measured lesions in three perpendicular axes. The slice with the largest lesion was first selected by eye. The longest lesion axis on this slice was measured with the ruler tool on an AGFA R4 Workstation with Impax Select software (v5205.0.0.1). A second line was drawn perpendicular to the first at the widest dimension. These two measurements were called the x (A) and y (B) axes. A third axis, the z (C) axis, was computed by multiplying the number of slices by slice thickness (figure 1). The scan slice for CT was 5 mm. MRI thickness ranged from 6 to 7 mm. Time to perform these three measurements was less than 1 minute.

Figure 1 Classic Euclidean volumes and their formulas

Derivation of these formulas from simple radiologic measurements in three axes can be performed. Examples of A, B, and C axes selection on a MRI mean transit time map and CT are shown.

For analysis of DWI and MTT mismatch, mismatch was defined as MTT volume/DWI volume ≥1.2. A parameter of 20% mismatch was chosen based on trials using eyeball estimate of 20% mismatch and may not be the optimal mismatch.^1,25 Absolute volumes measured by planimetry were compared to estimates of ellipsoid ABC/2 (see below) for DWI volume and MTT volume.

Euclidean shapes.

Euclidean shapes are demonstrated in figure 1. We tested the ellipsoid model both unadjusted and the adjusted model used for ICH,²⁰ as well as sphere, cylinder, and bicone. For the hemorrhage-adjusted ellipsoid model according to Kothari et al.,²⁰ all slices with lesion volume less than 25% of the slice with the maximum lesion volume were not counted in the z axis. For slices in which the lesion volume was between 25 and 75%, the slice thickness was multiplied by 0.5, and for slices where the lesion volume was >75%, the slice thickness was multiplied by 1. For all geometric models, π was simplified to 3, for ease of clinical assessment. Formula simplifications for A, B, and C axes are as follows:

Ellipsoid model:

V =4/3π r_Ar_Br_C = 4/3 × 3 × (A/2) × (B/2) × (C/2) = ABC/2

where A = longest dimension in axis x, B = longest perpendicular dimension to axis x (y), and C = total length in z dimension.

Sphere model:

V = 4/3πr³ = 4/3×3×(D/2)³ = (D)³/2 = D³/2

where D = longest measurement of A, B, or C.

Cylinder model:

V =hπr² = h×3×(D/2)² =3/4(D)²h =3/4D²C

where D = longest measurement of A or B and h = C.

Bicone model:

V = (1/3hπr²)2 = (1/3 × 3×h ×(D/2)²)2 = (hD²/4)2 or D² C/4

where D = longest measurement of A or B and h = C/2.

Statistical analysis.

Geometric estimates were compared to planimetric volume by least-squares linear regression using the R statistical package (www.r-project.org, R Development Core Team, Vienna, Austria) or SPSS v16 for Macintosh (SPSS Inc., Chicago, IL). The following linear regression model was used to compare a single rater to a single set of planimetric volumes. Confidence intervals of slopes for the ABC/2 formula were tested for robustness of sample data by bootstrap analysis. Bootstrap used 30 samples to find optimal solution, typically after third or fifth iteration, stating a constant = 0 and slope = 1. Twenty random samples were used to calculate interrater and intrarater reliabilities (measurements by J.R.S. and L.R.G.) by a mixed-model intraclass correlation.²⁶ Representative values were determined by averaging, except when the distribution was highly asymmetric (e.g., DWI, MTT, and subacute infarct volumes), in which case the median was used as a robust alternative to the mean. All ± values represent SD. Absolute measurement error was compared by a two-tailed binomial test, using a 0.25 frequency for four model comparisons and a 0.5 frequency for two model comparisons for probability of success. Significance was considered at p ≤ 0.05.

RESULTS

Acute imaging volumes.

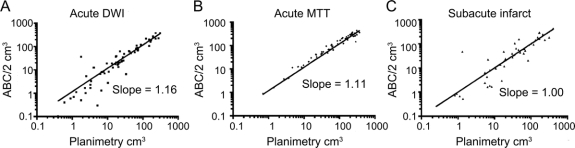
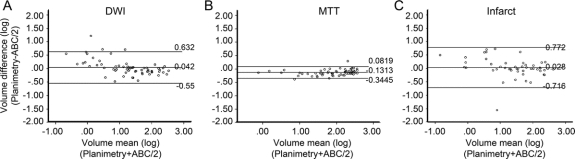
A total of 63 MRI scans for DWI and MTT were performed at a mean of 4.8 ± 2.0 hours (range 1.48 to 8.95 hours) from onset of ischemia. The average age of the patients was 71 ± 15 years (range 38 to 93), and 46% of these infarcts occurred in men. Median DWI volume measured by planimetry was 20.3 ± 72.8 cm³ (range 0.4 to 308.3 cm³). Of the four geometric volumes tested (table), the ellipsoid ABC/2 was the best fit with a slope that was not significantly different from a slope of 1 (figure 2). All regressions were significant at p = 0.001. The ellipsoid model also had significantly more values closest to the true planimetry value in 31 out of 63 measurements compared to the other three models (p = 0.00001) (table). The ellipsoid model, when compared to the second best model alone, the bicone, was closest in 40 out of 63 measurements (p = 0.01). The ellipsoid model also was extremely consistent when comparing intrarater (R = 0.992) and interrater reliability (R = 0.965). To demonstrate the performance of the ellipsoid model over the range of DWI measurements, a Bland-Altman plot (figure 3A) shows that the mean difference in log volumes between planimetry and ABC/2 was 0.042, an underestimate of planimetry by 10% (95% CI, underestimate by 328% or overestimate by 255%). The greatest estimation variability occurs at DWI volumes less than 10 cm³.

Table Linear regression models of diffusion-weighted imaging, mean transit time, and subacute volume estimation

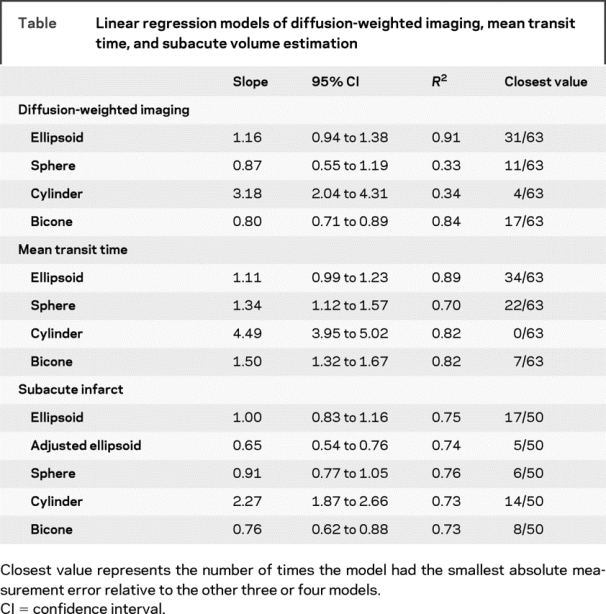
Figure 2 Linear regression of ABC/2 with computerized planimetry

Scatterplots of diffusion-weighted imaging, mean transit time, and subacute infarct volumes are shown along with their respective regression line. Each plot is on a logarithmic scale for ease of demonstrating the distribution of volumes.

Figure 3 Bland-Altman plots

The plots represent a graphical representation of the difference between the log volume of the planimetric measurement and the log volume of the ABC/2 measurement over the mean of these logs for diffusion-weighted imaging (A), mean transit time (B), and subacute infarcts (C). The middle horizontal line of each graph represents the average of the respective differences; the lines above and below represent the 95% confidence interval of the mean difference. The numbers to the right of the lines note the value of the line.

Median MTT volume measured by planimetry was 103.8 ± 106.9 cm³ (range 0.65 to 365.8 cm³). The ellipsoid model for MTT volume was also superior to the other three geometric estimates tested (table). The slope was not significantly different from a slope of 1 (figure 2). All regressions were significant at p = 0.001. As with DWI, the ellipsoid model for MTT volumes also had significantly more values closest to the true planimetry value in 34 out of 63 measurements compared to the other three models (p = 0.00001). The ellipsoid model when compared to the second best model alone, the sphere, was closest in 38 out of 63 measurements (p = 0.03). The intrarater (R = 0.881) and interrater (R = 0.712) reliability was somewhat less consistent than the DWI but still remained very good. To demonstrate the performance of the ellipsoid model over the range of MTT measurements, a Bland-Altman plot (figure 3B) shows that the mean difference in log volumes between planimetry and ABC/2 was −0.13, an overestimate of planimetry by 35% (95% CI, overestimate by 120% and underestimate by 20%). The estimate variability for MTT measurements was consistent across all volumes.

After determining that the ellipsoid, ABC/2, model was superior to other models for the best estimate of DWI and MTT volumes, we tested whether this model would accurately predict the presence of infarct and delayed perfusion mismatch. We chose an infarct/perfusion mismatch of 20% or greater, as this goal has served as a target for acute stroke trials.¹ We found that ABC/2 correctly classified mismatch present in 55 out of 57 cases (sensitivity 96%) and incorrectly classified 5 cases as mismatch present (positive predictive value 92%). ABC/2 correctly classified mismatch absent in 1 of 5 cases (specificity 17%) and incorrectly identified 2 cases as mismatch absent (negative predictive value 33%).

Subacute infarct.

A total of 50 subacute infarcts were analyzed (32 CTs and 18 MRIs) after an average of 45 ± 18 hours (range 20 to 104 hours) from onset of ischemia. The average age of the patients was 75 ± 10 years (range 36 to 90 years), and 56% of these infarcts occurred in men. In this analysis we also included an adjusted ellipsoid, which was has been validated for intracranial hemorrhage.²⁰ The median infarct volume measured by planimetry was 30.6 ± 86.2 cm³ (range 0.25 to 403.7 cm³). As with acute DWI and MTT volumes, the ellipsoid model had excellent concordance with subacute infarct volumes determined by planimetry (table). The slope was not significantly different from 1.0 (figure 2). Furthermore, the unadjusted ABC/2 model had a smaller absolute error of measurement compared to all other models (17 out of 50, p = 0.008). The ellipsoid model was closest in 35 out of 50 measurements when compared only to the cylinder model (p = 0.002). The ellipsoid model, when compared only to the hemorrhage-adjusted ellipsoid model, was better in 37 out of 50 cases (p = 0.001). The hemorrhage-adjusted model significantly underestimated infarct volumes due to the elimination of the smaller slice volumes. For subacute infarcts, the sphere model also performed well with a slope that did not differ from concordance of 1.0 and narrow CIs. However, the ellipsoid model had significantly smaller absolute error of measurement in 30 out of 50 cases when compared only to the sphere (p = 0.04). To demonstrate the performance of the ellipsoid model over the range of subacute infarct volume measurements, a Bland-Altman plot (figure 3C) shows that the mean difference in log volumes between planimetry and ABC/2 was 0.028, an underestimate of planimetry by 7% (95% CI, underestimate by 491% or overestimate by 420%). The greatest variability of estimates for subacute infarct measurements was at infarct volumes less than 10 cm³.

DISCUSSION

We tested four basic, Euclidean geometries to the estimation of stroke and perfusion volumes. Our stroke volumes by planimetry and geometry estimation spanned over three orders of magnitude in stroke volume. Our analysis suggests that the best geometric model for a rapid and accurate clinical estimation of stroke volume is the pure ellipsoid model of ABC/2. This model choice fits closely with previously published data on stroke lesion volumetric characteristics of lacunar infarcts²⁷ and middle cerebral artery infarcts performed by computerized analysis.²⁸ The agreement between the hemorrhage-adjusted ellipsoid model and other measurement techniques was also previously reported.²⁹ However, unlike the previous report,²⁹ we found better concordance with an unadjusted ellipsoid model, which had not been analyzed.

The average volume of MCA territory³⁰ is approximately 300 cm³. Future trials, with stroke >1/3 exclusion criterion, could rapidly assess with ABC/2 a stroke volume of 100 cm³ to more accurately and rapidly apply this exclusion. The ABC/2 model requires less than a minute to perform and has good intrarater and interrater reliability. Application of ABC/2 also allows for accurate stroke volume estimation in intensive care units for discussion of prognosis and planning interventions. It should be noted that we did not test ABC/2 on acute infarcts <9 hours on CT. A CT scan is the most common study in the acute stroke setting. While it is anticipated that ABC/2 is the best method for estimating acute infarct volumes, the method would likely have worse interrater reliability given the difficulty of defining infarct margins <3 hours on CT. Nevertheless, if a margin on CT can be seen, this method should provide as reasonable an estimate as planimetry given that planimetry still relies on an individual to define the ROI.

Our data also suggest that ABC/2 has a role in determining 20% mismatch. A rapidly calculated estimation would appear preferable to the current visual estimation. Such visual estimation inappropriately excludes 25% of patients from thrombolysis due to inaccurate guessing.³¹ Visual estimation overestimates infarct size and underestimates the amount of mismatch. Recently, attempts to provide better quantitative estimates of DWI volume and mismatch have used an ASPECTS rating of DWI.³² Unlike the ASPECTS rating, which is limited to MCA occlusions, ABC/2 is applicable to other arterial territories. Our results show that ABC/2 performs poorly on negative predictive value of mismatch; this is likely due to the low number of cases without mismatch, and the influence of case prevalence on both negative predictive value and positive predictive value. Performance on a much larger case series might determine a more representative negative predictive value. However, since the goal is to select those with mismatch and without large lesion volumes, ABC/2 should perform better (sensitivity 96%, positive predictive value 92%) than the current visual estimation system that most clinicians are currently using. We anticipate that the positive predictive value at times later than 9 hours would decrease as infarct grows into mismatch and the prevalence of mismatch would decrease. Analysis of our Bland-Altman plot for DWI shows that at small volumes ABC/2 deviates most from planimetric measurements and underestimates volume. Thus an underestimation of DWI volume would favor the presence of a mismatch when one is not present, which would decrease specificity. Indeed our specificity is poor at 17%. Analysis of the five cases with false positives, i.e., mismatch present, shows that three of five infarcts were less than 10 cm³ and four of five were less than 20 cm³. Thus the false positive rate is indeed at the small end of the infarct size and is thus less likely to impact clinical outcome, despite the poor specificity. It is unclear whether 20% mismatch is the appropriate cutoff²⁵; we anticipate that sensitivity would improve for larger cutoffs and be reduced for smaller cutoffs. The ease of applying ABC/2 in the acute stroke setting should allow for more uniform determination of stroke exclusion criteria for thrombolytic therapy and provide more accurate estimations of lesion volume to guide therapeutic choices and future trials.

AUTHOR CONTRIBUTIONS

Statistical analysis was performed by M.V. and J.R.S.

Address correspondence and reprint requests to Dr. John R. Sims, Massachusetts General Hospital, CNY149 Rm 6403, 13th Street, Charlestown, MA 02129 jsims@partners.org.

Supported by the American Heart Association, Scientist Development Grant 0535138N and NIH K08 NS049241.

Disclosure: The authors report no disclosures.

Medical Devices: High Speed Advantage helical CT scanner and Signa scanner (GE Medical Systems, Milwaukee, WI).

Received September 5, 2008. Accepted in final form March 30, 2009.