Permeability calculations in three-dimensional isotropic and oriented fiber networks

Abstract

Hydraulic permeabilities of fiber networks are of interest for many applications and have been studied extensively. There is little work, however, on permeability calculations in three-dimensional random networks. Computational power is now sufficient to calculate permeabilities directly by constructing artificial fiber networks and simulating flow through them. Even with today’s high-performance computers, however, such an approach would be infeasible for large simulations. It is therefore necessary to develop a correlation based on fiber volume fraction, radius, and orientation, preferably by incorporating previous studies on isotropic or structured networks. In this work, the direct calculations were performed, using the finite element method, on networks with varying degrees of orientation, and combinations of results for flows parallel and perpendicular to a single fiber or an array thereof, using a volume-averaging theory, were compared to the detailed analysis. The detailed model agreed well with existing analytical solutions for square arrays of fibers up to fiber volume fractions of 46% for parallel flow and 33% for transverse flow. Permeability calculations were then performed for isotropic and oriented fiber networks within the fiber volume fraction range of 0.3%–15%. When drag coefficients for spatially periodic arrays were used, the results of the volume-averaging method agreed well with the direct finite element calculations. On the contrary, the use of drag coefficients for isolated fibers overpredicted the permeability for the volume fraction range that was employed. We concluded that a weighted combination of drag coefficients for spatially periodic arrays of fibers could be used as a good approximation for fiber networks, which further implies that the effect of the fiber volume fraction and orientation on the permeability of fiber networks are more important than the effect of local network structure.

INTRODUCTION

The study of creeping flow in fibrous media is of considerable interest in a wide variety of applications such as paper production,^{1, 2, 3} filtration,⁴ fibrous beds for manufacturing processes,⁵ and transport in biological systems.^{6, 7, 8, 9, 10} The most common measure used to characterize such flows is the hydraulic permeability k, which for an isotropic medium is defined by Darcy’s law as¹¹

$$\mu U=-k\nabla P,$$ (1)

where μ is the fluid viscosity, U is the superficial fluid velocity, and ∇P is the mean pressure gradient. For a fibrous medium, the hydraulic permeability depends on the volume fraction, the fiber diameter, and the orientation of the fibers relative to the flow.

For fibers of uniform diameter, the drag force developed on them is inversely proportional to the permeability and is given by¹²

$$\frac{F}{\mu U}=\frac{\pi }{\varphi }\left(\frac{a^2}{k}\right),$$ (2)

where F is the force per unit length on the fiber, ϕ is the fiber volume fraction, and a is the fiber radius. In Eq. 2, the dimensionless force F∕μU is called the drag coefficient and the hydraulic permeability is nondimensionalized by a².

The first models developed for studying creeping flow in fibrous media were two dimensional and utilized a unit cell of a single fiber or a periodic array of fibers. The Stokes equations were solved for flow parallel or transverse to the fiber axis and expressions for the hydraulic permeability and∕or the drag coefficients were derived.^{13, 14, 15, 16, 17, 18} An excellent review of these models can be found in a review paper by Jackson and James.¹⁹

More recently, solutions for flow in two-dimensional random arrays of cylinders were provided. Sangani and Yao²⁰ used the periodic singular solution of the Laplace equation to calculate the stream function and vorticity fields, while Sangani and Mo²¹ employed a multipole expansion method to incorporate lubrication forces among particles and were able to deal with a larger number of fibers than in Ref. 20. Finite element²² (FE), lattice-Boltzmann,^{23, 24} and domain decomposition²⁵ methods have been also used, which further increased the number of the fibers. In another study,²⁶ Voronoi networks were employed and a methodology was described for low and high fiber volume fractions, and in Ref. 27 a two-scale method was developed for flow through oriented fiber tows. In addition, two-dimensional models for mixed fibrous materials with two distinct families of fibers have been developed.^{28, 29}

In three dimensions, rigorous solution of creeping flow past a fibrous system is more difficult. For spatially periodic media, Tsay and Weinbaum³⁰ solved the Stokes equations for flow past a square array of fibers confined between two parallel walls. Higdon and Ford¹² used a spectral boundary element method to calculate the permeability in simple cubic, body-centered cubic, and face-centered cubic structures, and Palassini and Remuzzi³¹ employed a finite element method to solve the Stokes equations for a tetrahedral periodic array of cylinders to model the glomerular basement membrane. In addition, there are two-scale models^{32, 33} in which the effective permeability is determined by first incorporating a spatially periodic microstructure and subsequently applying the microscopic information to a three-dimensional representation of the fibrous medium. Two-scale models have been also developed for calculating the relative permeability in fibrous materials consisting of two fluid phases.³⁴ A common characteristic of all these models is that they assume a periodic structure, and the calculations are performed in a relatively simple domain (unit cell). There are, however, relatively few studies for permeability calculations in random fibrous media.³⁵ Clague and Phillips³⁶ performed permeability calculations using a slender body theory and the Ewald summation technique, while in other studies^{2, 3, 37, 38} a lattice-Boltzmann method was employed, and in Ref. 39 the permeability of dilute fibrous media was derived based on a multiple-scattering hydrodynamic theory. More recently,⁴⁰ the three-dimensional structure of fibrous media was obtained via digital volumetric imaging and flow simulations were performed using a commercial computational fluid dynamics code. All of the studies listed above considered isotropic random fiber media; to our knowledge, no characterization has been done on anisotropic random networks with varying orientation.

In the present work, two methodologies for permeability calculations in three-dimensional isotropic and oriented fiber networks are presented. Even though we are primarily interested in polymeric hydrogels and hydrated biological tissues whose fiber volume fractions do not exceed 10% of the total volume,^{7, 8, 41} the methods described here are applicable to any fibrous medium. Fiber networks are generated stochastically and served as a basis of comparison for the two methods. In the first approach, finite element models of the networks are generated, and the Stokes equations are solved directly. The predictions of this direct-FE method are considered to be exact. Subsequently, a volume-averaging method is employed, and the permeability is determined by adding the contribution of each fiber to the total network drag. The formulation of this model requires a correlation to provide the drag coefficients for flows parallel and perpendicular to a fiber. Such correlations exist for the case of a long isolated fiber⁴² and for spatially periodic arrays of fibers,^{14, 15} but not for the general case of a random fiber network. Therefore, these equations provide only an approximation. Initial simulations to validate both approaches are performed for a square array of cylindrical fibers, for which analytical solutions exist. Then, the permeability of isotropic and oriented fiber networks is calculated, and the results of the two approaches are compared to each other and to results of other published theories. Finally, advantages and limitations of both methodologies are discussed.

METHODS

Generation of the fiber network

A detailed description of the network generation is presented elsewhere.^{43, 44} Nucleation sites were generated randomly within a cubic space and allowed to grow segmentally in opposite directions along a randomly chosen vector. The segments grew progressively by a unit length until they collided with the network boundary or with another segment. In the former case, a boundary cross-link was generated, and in the latter case, an interior cross-link was generated at the point of collision. Collision between two segments was defined when their distance was less than a prescribed fiber diameter. A fiber was defined as the line between two cross-links associated with the same segment. Aligned networks were generated by selecting the directional vectors from an anisotropic distribution. A random network generated by this procedure is shown in Fig. 1a.

Figure 1.

The four steps for the generation of the FE mesh from the fiber networks. (a) The initial network generated with the method described in Sec. 2A. (b) The parasolid model of the fibers. (c) The parasolid model of the surrounding fluid. (d) The final FE mesh.

Direct-FE method

The fiber networks [Fig. 1a] were converted into parasolid models in SolidWorks (SolidWorks Corp. Concord, MA) [Fig. 1b] and subtracted from the surrounding cubic space so that the remaining model represented only the fluid phase of the fibrous media [Fig. 1c]. Finally, the fluid model was imported into Simmetrix (Clifton Park, NY) for the generation of the FE mesh [Fig. 1d]. Under conditions of low Reynolds number flow, the governing equations were the Stokes equation

$$\nabla P+\mu {\nabla }^2\mathbf{V}=0$$ (3)

and the continuity equation

$$\nabla \cdot \mathbf{V}=0,$$ (4)

where P is the pressure and V is the velocity of the fluid.

For the boundary conditions, we applied a unit velocity normal to the inlet (z=−1), while at the outlet (z=1) the total normal stress was set to zero, and we allowed flow only normal to the surface. For the other four boundaries, the normal velocity and the shear forces were set to zero (symmetry). The no-slip boundary condition was applied at the surface of each fiber. Analytically, the boundary conditions were

$$V_x=0,{\sigma }_{xy}=0,{\sigma }_{xz}=0\text{on}x=\pm 1,$$$${\sigma }_{yx}=0,V_y=0,{\sigma }_{yz}=0\text{on}y=\pm 1,$$$$V_x=0,V_y=0,V_z=1\text{on}z=-1\left(\text{inlet}\right),$$$$V_x=0,V_y=0,{\sigma }_{zz}=0\text{on}z=+1\left(\text{outlet}\right),$$$$V_z=0,V_y=0,V_z=0\text{on}\text{fiber}\text{surface},$$ (5)

where σ is the total stress tensor, σ=−PI+μ[∇V+(∇V)^T].

Equations 3, 4, 5 describe the boundary value problem of our system, which we solved with the Galerkin finite element method. The code used a 15-node tetrahedral element with mixed basis functions. Velocity was represented by quadratic Lagrangian basis functions and pressure by linear discontinuous basis functions. This element was described in Ref. 45, where a similar element first developed in Ref. 46 was modified. Numerical integration was performed using a fifth-order, 15-point volume Gauss quadrature.⁴⁷ The equations were solved iteratively using GMRES with diagonal preconditioning,⁴⁸ based on a square root scaling introduced in Ref. 49. The code was implemented in parallel on 24 processors using domain decomposition and message passing interface.⁵⁰ The hydraulic permeability of the network was calculated by rewriting Eq. 1 as

$$k=\frac{\mu Q}{A(\Delta P∕\Delta L)},$$ (6)

where Q is the flow rate, ΔP is the pressure difference between the inlet and the outlet, A is the cross-sectional area of the inlet, and ΔL is the distance between inlet and outlet. The flow rate Q was calculated from the surface integral of the fluid velocity normal either at the inlet or the outlet,

$$Q=\int \mathbf{n}\cdot \mathbf{V}dS.$$ (7)

A limitation of this approach is that as the fiber volume fraction increases, the fibers come closer to each other and finally overlap, which distorts the initial network structure. Fiber overlapping was observed at volume fractions greater than 0.15, and thus our computations for the random networks were restricted to low volume fractions (ϕ<0.15), but still within the volume fraction range of hydrogels and biological tissues.^{7, 8} Another limitation of this approach is the inability of the mesh generator to mesh a cylinder exactly. Thus, the true volume fraction of the fibers in the FE model [Fig. 1d] was up to 3.5% lower than the apparent volume fraction calculated from the total fiber length in Fig. 1a and the fiber diameter. For the results presented here, we used the values of the true volume fractions.

Volume-averaging method

The fiber networks, as shown in Fig. 1a, were employed and the volume-averaged drag coefficient matrix of the network, D, was calculated as

$$\mathbf{D}=\frac{1}{V_{\mathrm{net}}}\sum \mathbf{d},$$ (8)

where V_net is the total volume of the network (fibers+interstitial space) and d is the drag coefficient matrix of the individual fiber. The network permeability k is proportional to the inverse of the network drag,

$$\mathbf{k}={\mathbf{D}}^{-1}.$$ (9)

The fiber drag coefficient matrix d can be calculated based on existing solutions of Stokes flow parallel and perpendicular to a cylindrical fiber, along with the proper orthogonal transformation of the fiber’s coordinate system to match the coordinate system of the flow,

$$\mathbf{d}={\mathbf{R}}^{\mathbf{T}}\mathbf{C}\mathbf{R},$$ (10)

where R is the direction cosines matrix of the fiber and C is the diagonal matrix of the principal drag coefficients.

As has been already mentioned, there are no explicit equations to provide C for a disordered fibrous medium. One option is to assume that there are no hydrodynamic interactions among fibers and use slender body theory, when the aspect ratio of the fibers is high enough. Cox⁴² solved this problem and found the drag coefficients parallel (C₁₁) and perpendicular (C₂₂ and C₃₃) to the fiber axis to be

$$C_{11}=\frac{2\pi l}{\ln \left(2e\right)-0.80685},$$$$C_{22}=C_{33}=\frac{4\pi l}{\ln \left(2e\right)+1-0.80685},$$ (11)

where e is the aspect ratio of the fiber and l is the fiber length. Notice that in a stochastic network like ours, the fibers do not have identical length and thus the drag coefficients of the fibers are not the same. Equation 11 is expected to be valid at very low volume fractions where hydrodynamic interactions among fibers are negligible.

An alternative approach²⁶ is to use equations that provide drag coefficients for spatially periodic arrays of fibers. For a square array of cylinders, Drummond and Tahir¹⁴ derived an expression of the drag force for parallel flow, and Sangani and Acrivos¹⁵ for transverse flow,

$$C_{11}=\frac{4\pi l}{-\ln \left(\varphi \right)-1.476+2\varphi -0.5{\varphi }^2-O\left({\varphi }^4\right)},$$$$C_{22}=C_{33}=\frac{8\pi l}{-\ln \left(\varphi \right)-1.476+2\varphi -1.774{\varphi }^2+4.078{\varphi }^3+O\left({\varphi }^4\right)}.$$ (12)

Equation 12 accounts for the effect of the fiber volume fraction and subsequently for hydrodynamic interactions between the fibers, but it is derived for periodic arrays and not for a network. In our analysis, Eqs. 11, 12 will be used and assessed for their accuracy.

RESULTS

Periodic arrays of fibers

Preliminary calculations to test the accuracy of both approaches were performed for a square array of fibers, and the model results were compared with analytical solutions of Drummond and Tahir¹⁴ for parallel flow,

$$\frac{k}{a^2}=\frac{-\ln \left(\varphi \right)-1.476+2\varphi -0.5{\varphi }^2-O\left({\varphi }^4\right)}{4\varphi },$$ (13)

and Sangani and Acrivos¹⁵ for transverse flow,

$$\frac{k}{a^2}=\frac{-\ln \left(\varphi \right)-1.476+2\varphi -1.774{\varphi }^2+4.078{\varphi }^3+O\left({\varphi }^4\right)}{8\varphi }.$$ (14)

The results are presented in Figs. 23. Figure 2 depicts the permeability calculations for flow parallel to a square array of fibers and Fig. 3 shows the calculations for transverse flow. The direct-FE calculations are in excellent agreement with Drummond and Tahir and with Sangani and Acrivos for volume fractions up to 0.2, encompassing the range of our interest (ϕ<0.15). For volume fraction of 0.33, the FE calculations are 20% higher than Drummond and Tahir and 25% higher than Sangani and Acrivos. However, Eqs. 13, 14 are asymptotic results and not expected to be accurate enough at high volume fractions (ϕ>0.3).

Figure 2.

Permeability calculations for parallel flow in a square array of fibers.

Figure 3.

Permeability calculations for transverse flow in a square array of fibers.

From Figs. 23 we also see that when no hydrodynamic interactions between the fibers were considered [Eq. 11], predictions were constantly off by a factor ranging from 1.5 at low volume fractions (ϕ=0.003) to 35 at high volume fractions (ϕ=0.64) as hydrodynamic interactions became stronger.

Isotropic and oriented fiber networks

For the characterization of the degree of alignment of fiber networks, the second-order fiber orientation tensor Ω, as described elsewhere,^{43, 44, 51} was employed

$$\mathbf{\Omega }=\frac{1}{l_{\mathrm{tot}}}\sum l_i\left[\begin{array}{ccc}{\sin }^2{\alpha }_i{\cos }^2\vartheta & {\sin }^2{\alpha }_i\sin {\vartheta }_i\cos {\vartheta }_i& \cos {\alpha }_i\sin {\alpha }_i\sin {\vartheta }_i\\ {\sin }^2{\alpha }_i\sin {\vartheta }_i\cos {\vartheta }_i& {\sin }^2{\alpha }_i{\sin }^2{\vartheta }_i& \cos {\alpha }_i\sin {\alpha }_i\sin {\vartheta }_i\\ \cos {\alpha }_i\sin {\alpha }_i\cos {\vartheta }_i& \cos {\alpha }_i\sin {\alpha }_i\sin {\vartheta }_i& {\cos }^2{\alpha }_i\end{array}\right],$$ (15)

where l_i is the length of the ith fiber, l_tot is the total fiber length, and the sum is over all fibers. α is the angle formed between the fiber axis and the z-axis and ϑ is the angle formed between the projection of the fiber on the x-y plane and the x-axis. The trace of Ω is always 1. For the isotropic case, Ω_xx=Ω_yy=Ω_zz=1∕3, while for aligned networks, the value of the diagonal components is a measure of fiber alignment in the coordinate directions. Off-diagonal components indicate significant alignment in a direction other than a coordinate direction.

Calculations were performed for three sets of fiber networks with different degrees of alignment. A set of nearly isotropic networks, a set of moderately aligned networks, and a set of strongly aligned networks were employed (Fig. 4). For the two sets of aligned networks, calculations were performed for flow parallel and transverse to the preferred fiber direction so that the effect of fiber alignment on network permeability can be examined. Each set consisted of five networks with similar alignment. The fiber volume fraction can be varied either by changing the fiber diameter or by increasing the number of the fibers. The dimensionless permeability by either variation should be the same. To justify our method we varied the number of the fibers (and subsequently the total fiber length) and adjusted the fiber diameter so that the networks will have similar volume fractions. Structural characteristics of the networks employed are shown in Table 1. The table presents the total fiber length, the number of the fibers and cross-links that comprise the fiber networks, and the diagonal components of the orientation tensor. For isotropic networks, the number of fibers varied from 22 to 51 and the total fiber length from 8.14 to 20.6. The aligned networks consisted of relatively fewer fibers because due to the network generation procedure is less likely for fibers that grow in similar directions to form cross-links. The percentage of interior cross-links was kept almost the same for all networks. The diagonal components of the orientation tensor of the isotropic networks were similar. The oriented networks had a preferred alignment in the z direction and the two other components had similar values. Off-diagonal components of the orientation tensor were minimal. Detailed results of the permeability calculations, including the fiber radii that were used for each of the simulations, can be found at the supplementary tables.⁵²

Figure 4.

The isotropic 4 (left), the moderately aligned 4 (center), and the highly aligned 4 (right) networks that were employed in the calculations. Structural properties of these networks are shown in Table 1.

Table 1.

The table presents structural characteristics of the isotropic, moderately aligned, and highly aligned networks employed in this study.

Network	Number offibers	Total fiberlength	Number ofx-links	Interior x-links(%)	Ωxx	Ωyy	Ωzz
Isotropic 1	22	8.14	26	9 (35%)	0.30	0.32	0.38
Isotropic 2	30	8.30	33	13 (39%)	0.34	0.28	0.38
Isotropic 3	41	12.42	44	19 (43%)	0.31	0.29	0.40
Isotropic 4	51	15.30	53	20 (38%)	0.38	0.34	0.28
Isotropic 5	51	20.60	61	24 (39%)	0.39	0.27	0.34
Mod. aligned 1	26	9.15	29	11 (38%)	0.19	0.17	0.64
Mod. aligned 2	29	12.86	34	12 (35%)	0.17	0.18	0.65
Mod. aligned 3	30	9.83	34	13 (38%)	0.15	0.12	0.73
Mod. aligned 4	41	15.51	48	17 (35%)	0.14	0.17	0.69
Mod. aligned 5	42	16.30	45	17 (38%)	0.16	0.13	0.71
Highly aligned 1	22	8.39	23	10 (43%)	0.07	0.04	0.89
Highly aligned 2	26	8.74	28	11 (39%)	0.07	0.10	0.83
Highly aligned 3	30	10.58	31	13 (42%)	0.06	0.08	0.86
Highly aligned 4	32	15.15	39	15 (38%)	0.07	0.07	0.86
Highly aligned 5	37	15.10	43	15 (35%)	0.06	0.09	0.85

Figure 5 shows streamlines for flow through the isotropic network 4. As expected, the flow paths are tortuous as the fluid passes through the fibers. Permeability calculations based on the flow solutions are shown in Fig. 6. In the same figure and for comparison, a formula derived in Ref. 19 for flow in isotropic three-dimensional fibrous media based on two-dimensional solutions is plotted,

$$\frac{k}{a^2}=\frac{3}{20\varphi }[-\ln \left(\varphi \right)-0.931],$$ (16)

along with numerical results by Clague and Phillips³⁶ for a random fibrous medium and by Higdon and Ford¹² for fcc and cc lattices. The permeability values for the five networks are similar, which further justifies our computational approach. Because of the discrepancy between true and apparent volume fraction, it was not possible to predict from the beginning of the network generation procedure the final volume fraction of the FE model. For that reason we did not calculate average permeabilities but preferred to plot all values together. For the volume-averaging approach, however, we plotted the average of the five network permeability. The standard deviations were undistinguishable in the scale of the plot and were omitted. At low volume fractions, the averaging approach using drag coefficients for spatially periodic fibers [Eq. 12] overpredicts the permeability, and for ϕ=0.007 its prediction is 38% higher than the value of the direct-FE calculations. At higher volume fractions (ϕ>0.05), however, the two models agree very well. The use of drag coefficients ignoring fiber hydrodynamic interactions [Eq. 11] overpredicts the permeability as it did for the spatially periodic arrays. The values of either Eq. 16 or the numerical results by Clague and Phillips³⁶ and by Higdon and Ford¹² are similar to direct FE calculations, and any deviations are presumed to be due either to the accuracy of Eq. 16 or to the different network structures considered here compared to Clague and Phillips³⁶ and Higdon and Ford.¹²

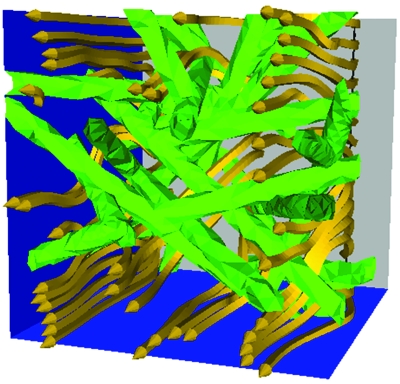
Figure 5.

The streamlines for flow through the isotropic fiber network 4.

Figure 6.

Permeability calculations for isotropic fiber networks. The permeability calculated using Eqs. 11, 12 is the average over the five isotropic networks.

Figures 7a, 7b present the permeability calculations for flow parallel [Fig. 7a] and transverse [Fig. 7b] to the preferred fiber direction of the moderately aligned networks. The averaging method using the approximate formula for spatially periodic fibers [Eq. 12] agrees very well with the direct calculations for the whole range of volume fractions. The predictions of the averaged permeability when hydrodynamic interactions between the fibers are ignored [Eq. 11] are always higher than the direct calculations, by a factor of 2 at low volume fractions up to a factor of 8 for transverse flow at ϕ=0.14.

Figure 7.

(a) Permeability calculations for flow parallel to the preferred fiber direction of the moderately oriented networks. (b) Permeability calculations for flow transverse to the preferred fiber direction of the moderately oriented networks. The permeability calculated using Eqs. 11, 12 is the average over the five moderately aligned networks.

The permeability calculations for the strongly aligned fiber networks are shown in Figs. 8a, 8b. Figure 8a presents the results for flow parallel to the preferred fiber direction and Fig. 8b the results for transverse flow. Again, when the drag coefficients for spatially periodic fibers [Eq. 12] are used, the averaging predictions agree well with the direct calculations. For parallel and transverse flows, the maximum deviations are 55% and 35%, respectively (at ϕ=0.13). When hydrodynamic interactions are ignored [Eq. 11], the permeability is overpredicted by factors of about 2 at low fiber volume fractions and about 7 at high volume fractions.

Figure 8.

(a) Permeability calculations for flow parallel to the preferred fiber direction of the strongly oriented networks. The permeability calculated using Eqs. 11, 12 is the average over the five highly aligned networks. (b) Permeability calculations for flow transverse to the preferred fiber direction of the strongly oriented networks. The permeability calculated using Eqs. 11, 12 is the average over the five highly aligned networks.

In Fig. 9 we plot the permeability, calculated with the direct-FE method for the five sets of simulations that were performed. From the figure, it is shown that the permeability for flow parallel to the preferred direction of strongly and moderately aligned networks is higher than the permeabilities of the other three sets. This result is expected since the drag force for flow transverse to a fiber is almost twice as much as the drag force for parallel flow.¹⁹ The permeability calculations of the isotropic networks and for flow transverse to the preferred direction of the aligned networks are comparable. Particularly, the less permeable network is the moderately aligned network 2 (see Table 1).

Figure 9.

Dependence of the permeability on the network orientation. (◼) Isotropic networks, (△) moderately aligned networks (parallel flow), (▽) moderately aligned networks (transverse flow), (×) highly aligned networks (parallel flow), and (*) highly aligned networks (transverse flow).

DISCUSSION

Two different methods for permeability calculations in stochastically generated, three-dimensional fiber networks were described. For the first case, the Stokes equations were solved rigorously with the finite element method, and the results were considered to be exact. For the second approach, the network permeability was estimated by adding the contribution of each fiber to the total drag of the network. Both models agreed well with analytical solutions for spatially periodic arrays of fibers. For both isotropic and oriented networks, the averaging method was consistent with the direct-FE results when the drag coefficients for a spatially periodic array of fibers were considered [Eqs. 8, 9, 10, 12]. The maximum deviation of the averaged permeability compared to the exact value was 55% at a volume fraction of 13%. When the assumption of no hydrodynamic interactions between the fibers was made [Eq. 11], the averaging approach significantly overpredicted the permeability for all calculations performed in this study.

The key result of this study is that one can account for the hydrodynamic interactions by adding up independent contributions from each fiber (by treating it as if it was part of a phantom array). The result provides a method to estimate permeabilities of anisotropic random networks based only on the distribution of fibers. In addition, since the drag coefficients for spatially periodic arrays account for the volume fraction but not for detailed structure of the network, we can also conclude that the effects of the volume fraction and fiber orientation on the permeability are more significant than the effect of detailed network geometry.

Correlations of spatially periodic arrays have been used successfully for networks based on random two-dimensional Voronoi diagrams.²⁶ Furthermore, the volume-averaging method we employed in this study is not the only averaging method that have been used. In a recent work, Mattern and Deen⁵³ compared four different methods proposed in the literature, each based on different approximations of the hydrodynamic interactions between the fibers. They found good agreement of one of these methods with experimental data and simulation results for charged fibers and for arrays of uncharged fibers with different radii.

To the best of our knowledge, this is the first time that the effect of fiber alignment on network permeability is examined. From Fig. 9 we see that highly aligned networks are more permeable than moderately aligned networks for flow parallel to their preferred direction. However, the permeability of isotropic networks is comparable to the permeability of networks aligned (moderately or highly) perpendicular to the flow. With increasing isotropy, the average pore size decreases and this in turn decreases the permeability. As it is shown in Table 1, the three sets consist of the same number of fibers and cross-links, and thus differ only in the orientation and the pore size. The increase in the orientation transverse to the flow increases the resistance but at the same time increases also the average pore size, which decreases the resistance. From the results, it seems that the effects of the increase in the orientation and the increase in the pore size cancel out.

We stated in this paper that the results of the direct-FE simulations were exact. It is known, however, that the finite element method provides only an approximation of the analytical solution and, thus, its solution is not theoretically the exact but the converged solution. We repeated the simulations varying the number of the degrees of freedom from 2.5×10⁶ to 4×10⁶ and found that the calculated permeability was mesh independent to within 0.85%. All simulations presented in this study involved approximately 3×10⁶ degrees of freedom, were solved on 24 2.6 GHz AMD Opteron processors, converged after two GMRES iterations, and required a total clock time of ∼8 h. As we mentioned earlier, the true volume fraction of the network [Fig. 1d] was lower than the apparent volume fraction, as calculated from the total fiber length in Fig. 1a and the fiber diameter, because of the inability of the mesh generator to mesh a cylinder exactly and fiber-fiber overlap. To calculate the averaged permeability, the values of the true volume fractions were used. Figure 10 shows that the relationship between the apparent and the true volume fractions is independent of the number of the fibers and the fiber orientation. Incorporation of the apparent values would result in significant changes in the averaged permeability, particularly at low volume fractions, so it is imperative that the true volume fraction be used.

Figure 10.

True vs apparent fiber volume fraction for the networks used in this study.

We saw that adding the drag coefficients of the fibers based on correlations for spatially periodic arrays provides a reasonable estimate of the network permeability, which is of particular importance given the computational demands of the direct calculations. The permeability expression [Eqs. 8, 9, 10, 12] can be useful for existing models of soft tissue biomechanics,^{54, 55, 56} which require the permeability of the underlying fiber network. Many of these models^{55, 56} simply use phenomenological expressions which provide the permeability as a function only of the volume fraction. We have shown here (Fig. 9), however, that not only the volume fraction but also the network orientation affects the permeability. Given the fact that the network orientation varies considerably from tissue to tissue,⁵⁷ the averaging methodology we presented in this paper is potentially more accurate than phenomenological equations. Furthermore, this method can be applied to networks consisting of two or more families of fibers with distinct fiber diameters, as is the case of agarose gels⁸ and collagen-fibrin cogels,⁵⁸ and, in general, can be used as a quick and accurate way to predict the permeability of any fiber network as a function of both volume fraction and orientation.

Finally, the presented methodology of network generation and permeability calculation can be combined with imaging techniques for the prediction of the permeability of real tissues. In previous work, using scanning electron microscopy and polarized light microscopy^{59, 60} the orientation of the tissue was measured and then stochastic networks with similar structure were generated in order to study the mechanical behavior of the tissue. Here, we can repeat the same procedure and use any of the two methodologies presented in the paper to predict the permeability of the tissue.