Abstract
Elastohydrodynamic lubrication over soft substrates is of importance in a number of biomedical problems: From lubrication of the eye surface by the tear film, to lubrication of joints by synovial fluid, to lubrication between the pleural surfaces that protect the lungs and other organs. Such flows are also important for the drug delivery functions of vehicles for anti-HIV topical microbicides. These are intended to inhibit transmission into vulnerable mucosa, e.g., in the vagina. First generation prototype microbicides have gel vehicles, which spread after insertion and coat luminal surfaces. Effectiveness derives from potency of the active ingredients and completeness and durability of coating. Delivery vehicle rheology, luminal biomechanical properties, and the force due to gravity influence the coating mechanics. We develop a framework for understanding the relative importance of boundary squeezing and body forces on the extent and speed of the coating that results. A single dimensionless number, independent of viscosity, characterizes the relative influences of squeezing and gravitational acceleration on the shape of spreading in the Newtonian case. A second scale, involving viscosity, determines the spreading rate. In the case of a shear-thinning fluid, the Carreau number also plays a role. Numerical solutions were developed for a range of the dimensionless parameter and compared well with asymptotic theory in the limited case where such results can be obtained. Results were interpreted with respect to trade-offs between wall elasticity, longitudinal forces, bolus viscosity, and bolus volume. These provide initial insights of practical value for formulators of gel delivery vehicles for anti-HIV microbicidal formulations.
INTRODUCTION
There are many contexts in which elastohydrodynamic flows have biomedical importance.1 Among these are the flow of blood cells in narrow vessels,2 the lubrication of joints by synovial fluid,1 the tear film of the eye,3, 4 the lubrication between pleural surfaces in the chest,5 and numerous flows associated with the digestive tract. These problems typically involve significant deformations of tissue surrounding the flow, little alteration of lubricant physical properties associated with pressure or temperature changes,6 and non-Newtonian lubricant behavior. In these examples, flows are forced by the boundary motion—i.e., relative sliding of solid surfaces. Of interest in the present work is an elastohydrodynamic flow driven by initial distention of elastic surfaces (squeezing) and gravitational acceleration. The goal in this paper is to develop a framework for understanding the trade-offs in squeezing and gravitational acceleration with respect to the coating flows they drive.
An especially compelling application is provided by the problem of the flow of a bolus of anti-HIV microbicide vehicle confined to the vagina. There is now great interest in developing microbicides which, when applied to the lower female reproductive tract, can inhibit infection by sexually transmitted pathogens such as HIV.1, 7, 8, 9, 10 In order to be effective, microbicidal drug delivery vehicles must be sufficiently distributed over vulnerable epithelial surfaces, e.g., the vaginal epithelium, where HIV transmission likely occurs. This distribution facilitates drug delivery to the epithelium and to fluids within the lumen of the vaginal canal and may also provide a physical barrier that retards the rate of transport of pathogens to the epithelium.11 Initial measurements have been made of the distribution of gel coating thickness over the human vaginal epithelium.11, 12, 13 The microbicide vehicle distribution, or coating, process is biomechanically complex.14, 15, 16, 17, 18 As an understanding is developed of the determinants of the coating, such information can be used in the rational design of improved drug delivery vehicles. Unfortunately, there has been little attention to date in developing the science of microbicide vehicle biophysical functionality, i.e., coating, which is a critical input to such design. Clearly, vehicles should be sought which have properties that optimize the extent of coating under biologically relevant conditions (e.g., applied vehicle volume and vaginal geometry).
It is likely that a number of different forces act upon a vehicle once it is inserted vaginally into the lower female reproductive tract.14, 19 These include gravity, transvaginal pressure gradients due to contractility of the supporting viscera, and transverse squeezing forces from the distended epithelium. There have been initial fluid mechanical studies of intravaginal vehicle flows; these have focused on the individual effects of gravity or epithelial squeezing.15, 16, 17 The initial studies are instructive in developing a physical understanding of the mechanisms of intravaginal vehicle deployment flows. However, the true vehicle flow conditions in vivo consist of combinations of multiple types of applied forces. Individual fluid mechanical results for flows due to longitudinally applied forces, e.g., gravity, and transverse forces, e.g., epithelial squeezing, cannot simply be superposed.
The present work begins the exercise of combining the multiple forces. We consider simultaneous effects of a longitudinally directed force along the vaginal canal, e.g., gravity, and transversely directed epithelial squeezing in a lubrication flow analysis. Our goal is to develop an initial formalism for understanding and contrasting the relative effects of tissue elasticity, gravity, and formulation properties on intravaginal coating flows. The simplification of two dimensional flow is actually quite relevant anatomically; the cross section of the undistended human vaginal canal is “H” shaped, with the transverse dimension large compared to the vertical openings on its two sides.20 A bolus of fluid of finite volume (here volume per unit vaginal width, i.e., area in two dimensions) is placed within the vaginal canal, immediately distending it. This initial elastic deformation of the originally flat upper and lower epithelial surfaces constitutes the initial condition for our flow problem. Flow immediately ensues. The factors that determine the extent of the coating driven by this flow are the main focus of the present work. Our analysis begins with consideration of a Newtonian fluid. This is followed by an initial consideration of non-Newtonian fluid behavior in the form of the Carreau constitutive model. The latter has been used in the analysis of actual vaginal microbicidal gels.17
The theory thus developed will find application in other elastohydrodynamic lubrication problems of biomedical interest, mentioned at the start of the introduction. The inclusion of gravitational acceleration and∕or non-Newtonian fluid behavior will improve the physical descriptions of these other phenomena.
PROBLEM FORMULATION
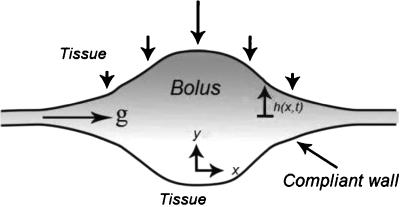
In this section, we derive an evolution equation for the shape of a bolus of non-Newtonian fluid confined between compliant opposed epithelial surfaces. We employ the lubrication approximation and develop the equations in the symmetric domain −h2(x,t)≤y≤h1(x,t) and include a body force in the x direction. In Fig. 1 is shown a definition sketch. In the following, for clarity of presentation, we shall indicate dimensional variables with a tilde. For the constitutive model we take the form (see, for example, Ref. 21)
| (1) |
where one can choose for a Newtonian fluid or, as we do below,
| (2) |
for a Carreau-like fluid which features shear thinning and a finite viscosity at zero-shear rate.
Figure 1.
Definition sketch of the vaginal canal. The introitus is to the right. See also anatomical figures in Ref. 42.
The primary assumption in the lubrication approximation is that the thickness of the bolus is small relative to its longitudinal extent, i.e., , where and are length scales for the transverse (thickness) and longitudinal directions, respectively. The continuity equation is made dimensionless with velocity scales in the longitudinal dimension. The Reynolds number is , where is a representative kinematic viscosity. In the usual way, we take the limits ε Re→0 and ε→0 to obtain the lubrication approximation. Given the limitations on magnitude of the Reynolds number and the thin layer assumption, pressure is made dimensionless by use of a scale constructed from the shear stress, , where is viscosity. After taking the lubrication approximation, the balance of linear momentum in the x direction is integrated with respect to to obtain
| (3) |
By symmetry, on ; hence the constant of integration c1=0. Next we solve this equation for , integrate with respect to , and use the boundary condition . This yields
| (4) |
In order to account efficiently for the absolute value in the constitutive equation 2, we insert a sign parameter β=±1. From the balance of linear momentum, we have
| (5) |
where we choose the sign of β so as to render the absolute value positive.
Next we incorporate a relationship between the fluid pressure and the height of the bolus, which must include the material stiffness of the vaginal wall. As a simple but objective initial approach, we utilize the one dimensional constrained continuum model22 developed for study of elastohydrodynamic lubrication in a roll coating. The accuracy of this approximation has been established.23 Other authors have recently made use of the approximation in a study of lubrication flows between a cavity and a flexible wall.24, 25 Notably, this approximation was earlier employed2 in a first theory for motion of red blood cells squeezing through capillaries. The idea is to relate the fluid pressure near a compliant wall with the local deformation of that compliant wall. In general, for a deformation the fluid pressure is given by . Here, is the elastic (Young) modulus of the compliant layer and is its thickness.
With the absolute value in the constitutive equation and the compliant wall taken into account in this manner, the integral in the solution for the velocity may be performed in closed form. This yields
| (6) |
Now, this result is substituted into the mass conservation equation, which is subsequently integrated with respect to from 0 to . We refrain from writing the lengthy result in dimensional form and turn now to nondimensionalization.
If the total film thickness is h(x,t)≡h1(x,t)+h2(x,t), then in the present problem we define . Here is the compliance of a single surface. In dimensionless terms, this becomes . Because is a derived quantity, the dimensionless number . The dimensionless number E may be interpreted as the ratio of a representative compliance pressure to a shear stress. With this definition, in dimensionless terms, the compliance relationship now reads p=εEh∕2. We define as the dimensionless ratio of the pressure associated with the applied longitudinal stress to a representative shear stress.
The dimensionless numbers, E and W, are both written in terms of the velocity scale . It is not convenient to define this velocity scale in terms of any imposed shear nor in terms of lateral gravitational pressure gradient driven flow because we would like to consider cases where both of these phenomena are absent. Hence we choose for the centerline velocity for flow due to a pressure gradient associated with the compliance of the surfaces. This leads to , where E=8∕ε and . With this definition, in dimensionless terms, the compliance relationship now reads p=4h. To aid in unraveling the dimensional variables in the presentation of results, we note that the time scale is . Hence, the dimensionless number W is, finally, a measure of the relative importance of acceleration and compliance.
Finally, we must consider the constitutive equation rendered in dimensionless variables. The Carreau model can be written as . Here is the shear viscosity, is the zero-shear limit, is the relaxation time scale of the fluid, and is the rate of strain. The power-law exponent is n. We can choose a Carreau-like model in the form
| (7) |
The Carreau and Carreau-like models may be made to match at small and large strain rates by the choices and . The two models are not precisely equivalent, as we will discuss below. In any case, we must introduce a new dimensionless number to account for the relationship between and . We scale Eq. 2 as follows:
where the Carreau number is
In terms of these dimensionless variables, the governing equation is as follows:
| (8) |
Here we have used the notations h,x=∂h∕∂x, etc. The absolute value we earlier incorporated requires choosing the sign of β so that −β(W−4h,x)≥0 in a dimensionless framework.
In the case of a Newtonian fluid, (or n=1 in the Carreau-like model). The governing equation 4 simplifies to read
| (9) |
We note that the condition that determines β is not required in this case.
APPLICATION TO INTRAVAGINAL SQUEEZING
Application of this model requires input values for several parameters including the tissue compliance, viscosity, and longitudinally acting force. There have been qualitative studies of mechanical properties of vaginal tissue explants.26, 27 However, there are, at present, no specific data on the compliance or Young’s modulus for the walls of the human vaginal canal. These walls contain three layers, a relatively thin surface mucosal layer (consisting of stratified squamous epithelium ranging from ∼15 to 200 μm depending on the phase of the menstrual cycle), a middle muscularis layer, and an outer fibrous adventitia layer. The net thickness28, 29 of the vaginal walls can range from ∼0.5 to 2 cm. For the computations here, we therefore consider upper and lower bounds on Young’s modulus based on values for other soft tissues in the body.30, 31, 32 These can range from ∼1 to 100 kPa. Therefore, we consider low and high values of our compliance parameter that are 1–100 kPa∕0.5 cm. We also neglect possible effects of the viscoelastic properties of the vaginal walls, arguing that relaxation times due to such properties would be very small compared to the time scales of biological interest in vaginal bolus flows. Vaginal drug delivery vehicles are commonly polymeric hydrogels with non-Newtonian rheological behavior. Because the initial analysis here is for flow of a bolus of a Newtonian fluid, we consider upper and lower bounds for values of current gels, based on low (∼0.01 s−1) and relatively higher (∼10 s−1) shear rates. Based on our studies of a number of such gels16, 17, 33 we use the values of 1 and 1000 Pa s for viscosity. Longitudinally acting forces on a vehicle bolus within the vaginal canal can be due to gravity and pressure gradients due to visceral contractility throughout the lower reproductive tract.14 Recent measurements have been made of the spatially varying vaginal pressure profile to test the hypothesis that stress urinary incontinence is associated with weak pelvic floor muscles.34 However, these measurements represent the pressure that arises in response to some (uncontrolled) deformation and not the effective compliance of the vaginal wall. For simplicity in this paper, we assume that the vaginal pressure profile derives from variable pressures associated with a uniform wall compliance and gravitational acceleration. We will, again, consider a biologically plausible range for the parameter in the model, with values equal to one and ten times the gravitational acceleration. In Table 1 we list these values and consider six different cases involving the ranges of values for the three parameters , , and . Given the convenient nondimensionalization of results, we are left with four sets of similar cases, i.e., cases 1 and 3, cases 2 and 4, case 5, and case 6. From case to case there is only a change in the dimensionless constant W. We also consider bolus volumes of 2 and 4 ml. These span the range of applied volumes being tested in women in current microbicide research.
Table 1.
Plausible values of tissue compliance, dynamic viscosity, and lateral acceleration, together with associated values of the Reynolds number and the dimensionless ratio of acceleration and compliance as drivers of the flow. The six cases span the interesting range of parameters. In all cases we take ε=1∕6, which implies E=48.
| Case | (Pa s) | (ms−2) | (ms−1) | Re | W | |
|---|---|---|---|---|---|---|
| 1 | 103 Pa∕0.5 cm | 1 | 9.8 | 0.208 | 1.04 | 1.18 |
| 2 | 103 Pa∕0.5 cm | 1 | 49 | 0.208 | 1.04 | 5.9 |
| 3 | 103 Pa∕0.5 cm | 1000 | 9.8 | 2.08×10−4 | 1.04×10−6 | 1.18 |
| 4 | 103 Pa∕0.5 cm | 1000 | 49 | 2.08×10−4 | 1.04×10−6 | 5.9 |
| 5 | 105 Pa∕0.5 cm | 1000 | 9.8 | 2.08×10−2 | 1.04×10−4 | 0.0118 |
| 6 | 105 Pa∕0.5 cm | 1000 | 98 | 2.08×10−2 | 1.04×10−4 | 0.118 |
For the initial condition on the shape of the bolus, we take . As a scale for the height we choose 1 cm; this scale is of the order of magnitude of the maximum height of the bolus at time zero. The analytical form of this expression was taken for convenience in solving Eq. 7. As we will note below, the long time behavior is insensitive to the specific initial shape of the bolus. The volume contained in such a bolus (above ) is , where is the vaginal width. A physically realistic value29 is ; hence, in dimensionless terms when , one obtains for a bolus of 2 ml and for a bolus of 4 ml. Here, we have chosen . This scale characterizes the initial spacing between apposing vaginal walls prior to insertion of the bolus. In other words, the fluid layer is supposed to be perfectly wetting with fully flooded initial conditions. This is a sensible start owing to the likely presence of vaginal fluid before the microbicide is put in place. In reality, vaginal fluid will dilute the microbicide vehicle, which can alter the rheological behavior.18 As this is a paper on coating flows driven by squeezing and gravitational acceleration, we defer consideration of dilution effects to future work.
The equations were solved using MATHEMATICA.35 As a check on the solution, the total volume of the bolus was monitored as a function of time; insufficient temporal or spatial resolution results in a violation of mass conservation. We first consider the parametric study of the Newtonian case 9 and then move on to examine non-Newtonian solutions of Eq. 8.
Newtonian results in dimensionless form
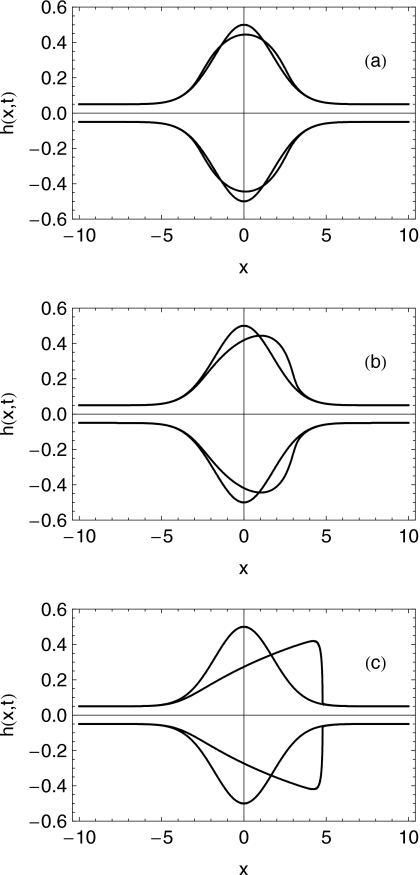
In Figs. 2a, 2b, 2c we show the profiles of the spreading bolus at dimensionless times t=0 and t=20. In each case W is increased, i.e., the applied longitudinal stress increases relative to the wall elasticity. Note from Figs. 2a, 2b, 2c that the shape of the bolus changes little with W unless this number exceeds unity. For W>1 there is a greater amount of spreading and also an increased lateral movement of the bolus. The height profile develops an increasingly steep leading edge—a consequence of the hyperbolic nature of the governing partial differential equation (PDE). Of course, the lubrication approximation would lose validity in such a case.
Figure 2.
Profiles of the shape of the bolus at dimensionless times t=0 s and t=20 s for (a) W=0.118 (e.g., case 6), (b) W=1.18 (e.g., cases 1 and 3), and (c) W=5.9 (e.g., cases 2 and 4). Volume is 2 ml.
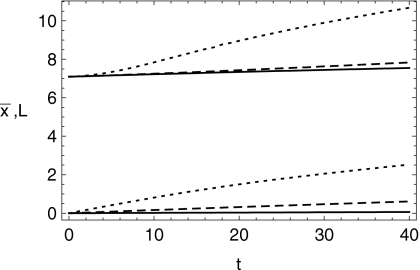
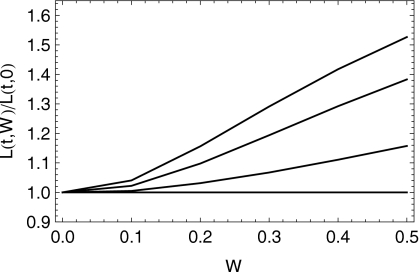
This point is better illustrated in Fig. 3, where the mean position of the bolus and its spread length are shown for 0≤t≤40. The length of spreading of the bolus, which is proportional to the effective surface area coated, is defined as four standard deviations of the bolus height profile. For smaller values of W, the bolus spreads primarily by squeezing flow, and not much longitudinal mean motion occurs. Larger values of W give rise to additional spreading: the bolus becomes longer and its mean displacement along the channel increases. This is illustrated further in Fig. 4, which shows the relative extent to which the spread length increases due to increasing W. At long dimensionless times, there is roughly a 50% increase in spread length as W increases from zero to 0.5.
Figure 3.
Evolution of the dimensionless length of the bolus (four times the standard deviation in x of the bolus height; upper curves) and mean dimensionless longitudinal displacement (lower curves) as functions of dimensionless time for W=0.118 (solid), 1.18 (dashed), and 5.9 (dotted), i.e., cases 1, 2 and 4, and 6. Volume is 2 ml.
Figure 4.
Evolution of the spread length of the bolus divided by the length due to squeezing only (W=0) as a function of W. The relative length is shown at dimensionless times t=0, 1000, 5000, and 10 000 s, reading up from bottom. The volume of the bolus is 2 ml.
Newtonian results in dimensional form
In order to interpret results in a more biologically relevant manner, we next consider the lateral extent of spreading at prescribed values of dimensional time—t=10 s, 1 min, and 5 min. We take 5 min as an upper bound in these computations because, intravaginally, an inserted bolus of gel may begin to become diluted with ambient vaginal fluid by this time, thereby changing its rheological properties.17, 33, 36 We consider twofold differences in the lower and upper bounds for viscosity. Results are shown in Tables 2, 3. Note that for the lower bound of viscosity and a relatively soft wall, doubling viscosity results in a 20% reduction in spreading at 5 min. For the higher viscosity and both soft and stiffer walls, there is negligible difference in spreading at 5 min when viscosity is doubled. These comparisons are true for both the small, 2 ml, and larger, 4 ml, bolus volumes.
Table 2.
The spread length (in cm) of a 2 ml bolus at times 0, 10 s, 1 min, and 5 min. Cases 1, 3, and 5 span the interesting range of parameters. Also shown is the result of doubling the viscosity. In all cases we take and ε=1∕6, which implies E=48.
| Case | (Pa s) | (t=0) | (10 s) | (1 min) | (5 min) | |
|---|---|---|---|---|---|---|
| 1 | 103 Pa∕0.5 cm | 1 | 3.54 615 | 3.86 306 | 5.34 246 | 8.79 664 |
| 103 Pa∕0.5 cm | 2 | 3.54 615 | 3.69 106 | 4.54 799 | 6.97 560 | |
| 3 | 103 Pa∕0.5 cm | 1000 | 3.54 615 | 3.54 640 | 3.54 761 | 3.55 353 |
| 103 Pa∕0.5 cm | 2000 | 3.54 615 | 3.54 627 | 3.54 688 | 3.54 981 | |
| 5 | 105 Pa∕0.5 cm | 1000 | 3.54 615 | 3.56 973 | 3.67 403 | 4.03 676 |
| 105 Pa∕0.5 cm | 2000 | 3.54 615 | 3.55 810 | 3.61 374 | 3.82 883 |
Table 3.
Same as Table 2 but for a 4 ml bolus.
| Case | (Pa s) | (t=0) | (10 s) | (1 min) | (5 min) | |
|---|---|---|---|---|---|---|
| 1 | 103 Pa∕0.5 cm | 1 | 7.09 075 | 7.28 816 | 9.02 082 | 14.07 39 |
| 103 Pa∕0.5 cm | 2 | 7.09 075 | 7.17 257 | 7.94 745 | 11.40 07 | |
| 3 | 103 Pa∕0.5 cm | 1000 | 7.09 075 | 7.09 087 | 7.09 148 | 7.09 446 |
| 103 Pa∕0.5 cm | 2000 | 7.09 075 | 7.09 081 | 7.09 110 | 7.09 259 | |
| 5 | 105 Pa∕0.5 cm | 1000 | 7.09 075 | 7.10 278 | 7.16 063 | 7.40 294 |
| 105 Pa∕0.5 cm | 2000 | 7.09 075 | 7.09 678 | 7.12 635 | 7.25 725 |
Comparison with asymptotic rate of spread when W=0 (Newtonian)
As a partial check on the accuracy of our numerical results, we consider an analytical asymptotic analysis of a closely related problem. For W=0, Eq. 9 is known as the porous medium equation.37, 38 In this case,
| (10) |
For initial conditions composed of a Dirac delta distribution centered at x=0, the solution to the nonlinear equation 9 is
| (11) |
where ϕ+≡max{ϕ,0}. The spread length (four times the standard deviation) is 1.561 29V11∕10t1∕5, where V is the bolus volume per unit depth.
In the case where the initial bolus is not a Dirac delta distribution, then a form similar to Eq. 11 (but time shifted) constitutes an asymptotic approximation,37 with error that decreases to zero as t→∞. The detailed form of the initial distribution does not matter as long as it is non-negative, integrable, and compactly supported (i.e., of finite width).
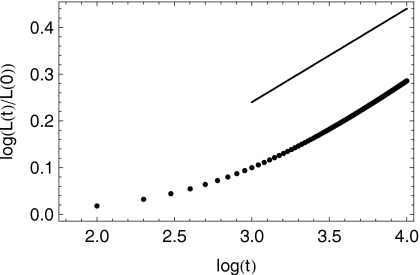
The present numerical solutions reveal a closely similar scaling with t1∕5, as shown in Fig. 5. This is true despite the fact that the bolus does not strictly have a compact support owing to the fact that h∞≠0.
Figure 5.
A comparison against the asymptotic spread rate ∝t1∕5 (upper line) and the simulation results scaled by the original bolus length (lower set of points). Volume is 4 ml.
In the case where W≠0, we note that it is possible to rescale the independent variables (x,t)→(ξ∕W,τ∕W2); in terms of these variables, W≠0 drops out of Eq. 9. This leads to the result that the height of the bolus h(x,t;W)=h(Wx,W2t;W=1) for W≠0, where the solution makes sense—i.e., before shocks form. Hence, we can obtain L(t;W)=L(W2t;W=1)∕W. Of course these results are only valid for initial conditions that are equivalent with respect to the scaling.
Shear-thinning examples
Finally we turn to two examples to illustrate the use of the model in calculations with realistic materials. Cone and plate measurements of the rheological response of different microbicide vehicles—both pure and diluted with vaginal fluid or semen simulants—were made.17 The data were fitted well with the Carreau model; the rheological constants are shown in Table 4. The two cases we consider are “C20V” (Carraguard diluted 20% with vaginal fluid simulant) and “K20S” (K-Y Jelly diluted 20% with seminal fluid simulant). The shear rates spanned the range of 0.2–472.5 s−1.
Table 4.
Rheological constants obtained from experimental data.
| Case | (cP) | (s) | n |
|---|---|---|---|
| C20V | 233 38.9 | 1.93 058 | 0.50 471 |
| K20S | 639 70.9 | 3.63 645 | 0.33 5755 |
For convenience, we consider here only the case W=0, for then the conditional in the derivation of model 8 changes at the symmetry plane x=0. Hence, we need only solve Eq. 8 with β=−1 in the quarter domain (x≥0,y≥0). We chose a bolus with volume of 3.5 ml and a vaginal wall compliance of 100 kPa∕0.5 cm; all other parameters were as before.
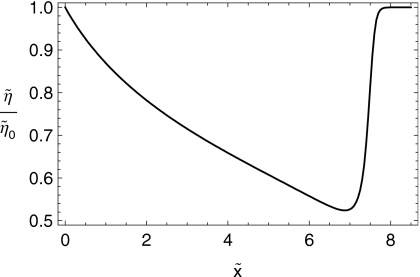
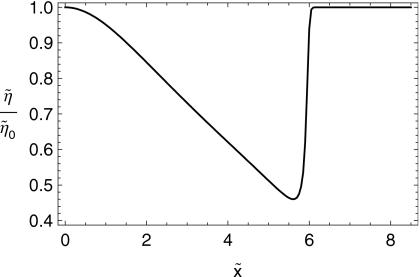
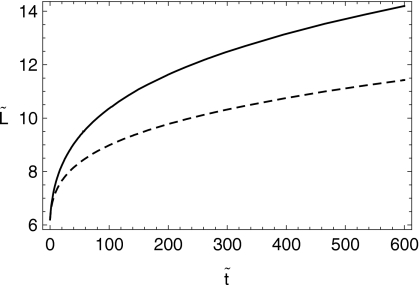
In Figs. 67 we show the shapes of the boluses at the initial time and after 10 min of squeezing-induced spreading have elapsed. In Figs. 89, we plot the effective shear viscosity (i.e., shear stress divided by shear rate) at the epithelial surface after 10 min of spreading. Note that the effective viscosity is much diminished near the leading edge of the spreading boluses. Finally, in Fig. 10 we show the spread length as a function of time for the two cases.
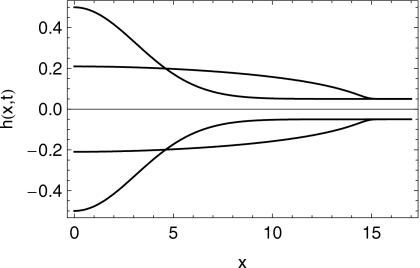
Figure 6.
Profiles of the shape of the right half of the C20V bolus at times t=0 s and .
Figure 7.
Effective shear viscosity at the epithelial surface vs (cm) for the C20V bolus at .
Figure 8.
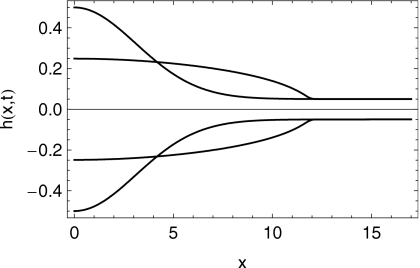
Profiles of the shape of the right half of the K20S bolus at times t=0 s and .
Figure 9.
Effective shear viscosity at the epithelial surface vs (cm) for the K20S bolus at .
Figure 10.
Spread length vs time for the C20V and K20S (dashed) cases.
Briefly we consider the potential for scaling analysis to shed light on the dynamics when W≠0. In this case Eq. 8 permits rescaling to eliminate W only when n=1∕2. Then one can show that the bolus height scales as h(x,t;W,Cr)=h(Wx,W2t;W=1,Cr) and the spread length as L(t;W,Cr)=L(W2t;W=1,Cr)∕W.
DISCUSSION
We have developed a model for the mechanics of spreading of a finite bolus of fluid between two compliant surfaces. Effects of both surface compliance and applied longitudinal stresses are simultaneously taken into account. This analysis builds upon our earlier studies of separate individual effects of gravity or constant force epithelial squeezing on coating flows.15, 16, 17 This new model thus provides a more mechanically complete simulation of coating flow by an anti-HIV microbicidal delivery vehicle between interepithelial surfaces in the vagina. Unlike candidate microbicide delivery vehicles (which are primarily polymeric gels) we focused first on a Newtonian constitutive equation. This simplified solution of the problem and identification of salient dimensionless numbers that characterize flow details. Our goal was to establish a procedure for developing the governing equations and to understand the relative influence of squeezing and longitudinally applied stresses, e.g., gravity or transvaginal pressure gradients, on the spreading rate.
After careful nondimensionalization of the problem, it emerged that a single dimensionless number, , controls the relative influence of squeezing and gravity; here is the formulation density, is the longitudinal stress, is the compliance of the vaginal wall, and ε is a representative width-to-length ratio of the bolus. However, a second (time) scale is required to cast the solutions of the dimensionless problem into dimensional terms, , which involves the formulation viscosity and a representative thickness of the bolus . Notably, the influence of viscosity in this problem is upon the kinetics of flow but not the form of the flow.
When W=0, applied longitudinal stresses are absent and the governing nonlinear PDE simplifies to one for which asymptotic solutions have been developed. We compared numerical solutions of our problem to this asymptotic result and found similar scaling of the bolus spread length with time. We focused primarily upon solutions over a range of values of W which span cases of biophysical interest for microbicide functionality. For different values of the physical parameters, we developed solutions for the extent of spread at times of practical interest.
Heuristically, the results of the flow computations presented here make sense: As the relative effect of the longitudinal applied body force increases, the bolus spreads over a longer distance and its mean displacement increases. Dimensional computations were performed for upper and lower bounds on viscosity. For the lower bound of viscosity and a relatively soft wall, doubling viscosity resulted in a 20% reduction in spreading at 5 min. This is a relatively small difference in coating, suggesting that larger differences in viscosity (when its values are low) are required to effect more significant differences in coating. For the higher viscosity and both softer and stiffer walls, there was a negligible difference in spreading at 5 min when the viscosity was doubled. A thousandfold increase in viscosity resulted in only a twofold reduction in spread length. In general, comparisons were similar for both 2 and 4 ml bolus volumes. Spread lengths for the 4 ml bolus volume were less than twice those of the 2 ml volume, although nearly two times that value. Of course, the greatest shear rate within the flow occurs near the leading edge of the bolus as it spreads. This is a consequence of the fact that the clearance is narrowest there. The higher shear rates near the leading edge would lead to pronounced non-Newtonian behavior when this is included in the model.
The net normal force of the wall on the bolus is obtained by integrating the fluid pressure at the wall with respect to x from minus to plus infinity and by multiplying by the width of the channel. Because pressure is proportional to the local height h of the bolus, we find that the total squeezing force on each wall is simply the wall compliance times the volume of the bolus. For a 2 cm wide channel (and, therefore, bolus) and a bolus volume of 4 ml, we calculate that the net force per wall ranges from 0.8 to 80 N, as wall compliance ranges from 103 to 105 Pa∕0.5 cm (Table 1). There are historical data on net human vaginal forces, albeit measured in varying, semirigorous ways.39 Net normal squeezing forces from both walls were estimated to range from 4.45 to 445 N (see also Ref. 17). There is clearly not a direct correspondence between our calculations of wall force on a finite bolus—we would take twice our values to account for both walls—and the historical data. We do note, however, that the orders of magnitude of the two estimates are comparable.
The present work illustrates the need for data on biomechanical properties of the vaginal environment experienced by a microbicide delivery vehicle. Such data should be obtained for a variety of different postures because the hydrostatic pressure distribution due to the gravitational body force may alter the pressure outside the vaginal barrel—and hence the compliance relationship. Strictly speaking, this is different than the direct influence of gravity on the bolus itself. Nonetheless the present work, by focusing upon upper and lower bounds for the salient physical parameters, e.g., vaginal wall compliance and longitudinally acting forces such as gravity, provides biologically relevant insights about the kinematics of flow of microbicide vehicles. Specifically, the time scale for coating emerges (Tables 2, 3). We see that the extent of coating does not increase appreciably in 5 min of continuous squeezing and longitudinal forcing unless the viscosity is relatively low. Given the relatively high viscosities of candidate microbicide delivery gels, this suggests that those gels may not flow appreciably along the vaginal axes until they begin to become diluted with ambient vaginal fluids (such that their viscosities decrease40 and∕or their flow boundary conditions at the gel-epithelial interface effectively depart from strict no slip). We also found that coating rates are relatively insensitive to changes in viscosity as high as twofold. These findings lend further emphasis to the need to understand the microbicide vehicle dilution process in vivo, so that time dependent viscosity changes, as well as non-Newtonian effects, can be taken into account.
We then went on to examine two very specific cases of microbicide vehicles diluted by vaginal fluid and semen simulants. We proceeded from rheological measurements to obtain rheological parameters in a Carreau model through solution of the governing equations for the evolution of the bolus shape with time. Marked shear thinning was apparent in the simulations, especially near the leading edge of the spreading bolus—even in the case where the spreading is induced only by squeezing arising from the distended, compliant vaginal surfaces. It is clear that non-Newtonian effects will be of paramount importance when one comes to consideration of flow of the microbicide vehicle during coitus.
In the search for effective microbicidal products against HIV, design of the delivery system, as well as selection of the active ingredient, is of paramount importance. Users of microbicides can control details of the applied volume and, in principle, the time interval from application to potential exposure to HIV. Clearly, the properties and applied volume of a microbicidal product are critical factors in the functionality of that product. However, development of microbicidal products to date has involved little attention to the functionality of their delivery systems per se. Such functionality derives from biophysical and biochemical interactions between the products, the vaginal environment (e.g., anatomy, tissue compliance, etc.), a woman’s behavior after application (e.g., posture), concentration and virulence of the inoculum of virus, etc.41 Thus, the model development which here focuses on fluid or fluidlike vehicles provides a preliminary tool for use by formulators in rational design and optimization of microbicide delivery vehicles. Specific ranges of values of rheological properties of prototype vehicles can be targeted via manipulation of the molecular compositions and structures of the vehicles. These, together with data on inserted volume, vaginal compliance, ranges of a woman’s posture (which varies the effects of gravity on spreading), and other physiological, anatomical, and behavioral data, can be input to models such as this initial one, and achievement of targeted coating kinetics can be evaluated. Iterations in vehicle design—e.g., in molecular composition and structure—could occur prior to preclinical human experimental studies (viz., imaging of vaginal coating distributions11, 40), providing significant savings of time and expense. Indeed, parametric analysis of salient factors that govern vaginal coating is practically unprecedented in microbicide research and development.17 The present model provides insights about how to utilize biomechanical analysis in microbicide vehicle design. For example, we illustrated (Tables 2, 3) trade-offs in the effects of doubling viscosity and∕or inserted bolus volume. The fact that increasing viscosity by three orders of magnitude only reduced coating by a factor of about 2 is a finding that might not be intuitive to microbicide formulators, and it exemplifies the role of analyses of the type presented here. Our results are clearly a caveat to microbicide developers of the importance of incorporating biomechanics into the process of microbicide vehicle design.
The goal of this paper was to develop a framework for consideration of the relative importance of boundary squeezing and body forces in driving coating flows of a non-Newtonian fluid. The application we considered had to do with spread of a gel microbicide vehicle between vaginal walls. The physical analysis pointed out along the way a number of properties that must be measured in order to improve the model for use in that application. However, the approach developed here should find application in a number of other biomedical contexts where elastohydrodynamic lubrication and body forces are present.
ACKNOWLEDGMENTS
The authors acknowledge support from NIH Grant No. AI48103 (D.F.K.), including a subaward to the University of California, and from California HIV∕AIDS Research Program Grant No. ID07-B-135 (A.J.S.).
References
- Jin Z. M. and Dowson D., “Elastohydrodynamic lubrication in biological systems,” Proc. Inst. Mech. Eng., Part J: J. Eng. Tribol. 10.1243/135065005X33982 219, 367 (2005). [DOI] [PubMed] [Google Scholar]
- Lighthill M. J., “Pressure-forcing of tightly fitting pellets along fluid-filled elastic tubes,” J. Fluid Mech. 10.1017/S0022112068001795 34, 113 (1968). [DOI] [Google Scholar]
- Holly F. J. and Holly T. F., in Lacrimal Gland, Tear Film, and Dry Eye Syndromes, edited by Sullivan D. A. (Plenum, New York, 1994). [Google Scholar]
- Jones M. B., Fulford G. R., Please C. P., McElwain D. L. S., and Collins M. J., “Elastohydrodynamics of the eyelid wiper,” Bull. Math. Biol. 10.1007/s11538-007-9252-7 70, 323 (2008). [DOI] [PubMed] [Google Scholar]
- Gouldstone A., Brown R. E., Butler J. P., and Loring S. H., “Elastohydrodynamic separation of pleural surfaces during breathing,” Respir. Physiol. Neurbiol. 10.1016/S1569-9048(03)00138-1 137, 97 (2003) [DOI] [PubMed] [Google Scholar]; Loring S. H., Browna R. E., Gouldstone A., and Butler J. P., “Lubrication regimes in mesothelial sliding,” J. Biomech. 10.1016/j.jbiomech.2004.10.012 38, 2390 (2005). [DOI] [PubMed] [Google Scholar]
- Skotheim J. M. and Mahadevan L., “Soft lubrication: The elastohydrodynamics of nonconforming and conforming contacts,” Phys. Fluids 10.1063/1.1985467 17, 092101 (2005). [DOI] [Google Scholar]
- Stone A., “Microbicides, a new approach to preventing HIV and other sexually transmitted infections,” Nat. Rev. Drug Discovery 10.1038/nrd959 1, 977 (2002). [DOI] [PubMed] [Google Scholar]
- Vermani K. and Garg S., “The scope and potential of vaginal drug delivery,” Pharm. Sci. Technol. Today 10.1016/S1461-5347(00)00296-0 3, 359 (2000). [DOI] [PubMed] [Google Scholar]
- Harrison P. F., Rosenberg Z., and Bowcut J., “Topical microbicides for disease prevention: Status and challenges,” Clin. Infect. Dis. 36, 1290 (2003). [DOI] [PubMed] [Google Scholar]
- D’Cruz O. J. and Uckun F. M., “Clinical development of microbicides for the prevention of HIV infection,” Curr. Pharm. Des. 10, 315 (2004). [DOI] [PubMed] [Google Scholar]
- Henderson M. H., Peters J. J., Walmer D. K., Couchman G. M., and Katz D. F., “Optical instrument for measurement of vaginal coating thickness by drug delivery formulations,” Rev. Sci. Instrum. 10.1063/1.1863832 76, 034302 (2005). [DOI] [Google Scholar]
- Henderson M. H., Couchman G. C., Walmer D. K., Peters J. J., Owen D. H., Brown M., Lavine M. L., and Katz D. F., “Optical imaging and analysis of human vaginal coating by drug delivery gels,” Contraception 75, 142 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauck C. K., Katz D. F., Masution M. D., Sandefer E. P., Henderson M. H., Su I., Digenis G. A., and Barnhart K., “Vaginal distribution of Replens and KY Jelly using three imaging techniques,” Contraception 77, 195 (2008). [DOI] [PubMed] [Google Scholar]
- Katz D. F., Henderson M., Owen D. H., Plenys A. M., and Walmer D. K., in Vaginal Microbicide Formulations Workshop, edited by Rencher W. F. (Lippencott-Raven, Philadelphia, 1998). [Google Scholar]
- Kieweg S. L., Geonnotti A. R., and Katz D. F., “Gravity-induced coating flows of vaginal gel formulations: In vitro experimental analysis,” J. Pharm. Sci. 10.1002/jps.20194 93, 2941 (2004). [DOI] [PubMed] [Google Scholar]
- Kieweg S. L. and Katz D. F., “Squeezing flows of vaginal gel formulations relevant to microbicide drug delivery,” J. Biomech. Eng. 10.1115/1.2206198 128, 540 (2006). [DOI] [PubMed] [Google Scholar]
- Kieweg S. L. and Katz D. F., “Interpreting properties of microbicide drug delivery gels: Analyzing deployment due to squeezing,” J. Pharm. Sci. 10.1002/jps.20774 96, 835 (2007). [DOI] [PubMed] [Google Scholar]
- Lai B. E., Xie Y. Q., Lavine M., Szeri A. J., Owen D. H., and Katz D. F., “Dilution of microbicide gels with vaginal fluid and semen simulants: Effects on rheology and coating flow,” J. Pharm. Sci. 10.1002/jps.21132 97, 1030 (2008). [DOI] [PubMed] [Google Scholar]
- Lard-Whiteford S. L., Matecka D., O’Rear J. J., Yuen I. S., Litterst C., and Reichelderfer P., “Recommendations for the nonclinical development of topical microbicides for prevention of HIV transmission: an update,” JAIDS, J. Acquired Immune Defic. Syndr. 10.1097/00126334-200405010-00001 36, 541 (2004). [DOI] [PubMed] [Google Scholar]
- Roy S., Barrier Contraceptives: Current Status and Future Prospects (Wiley, New York, 1994). [Google Scholar]
- Wolff R. and Kubo A., “A generalized non-Newtonian fluid model incorporated into elastohydrodynamic lubrication,” J. Tribol. 10.1115/1.2837095 118, 74 (1996). [DOI] [Google Scholar]
- Coyle D. J., “Forward roll coating with deformable rolls: A simple one dimensional elastohydrodynamic model,” Chem. Eng. Sci. 10.1016/0009-2509(88)80011-3 43, 2673 (1988). [DOI] [Google Scholar]
- Carvalho M. S. and Scriven L. E., “Flow in forward deformable roll coating gaps: Comparison between spring and plane-strain models of roll cover,” J. Comput. Phys. 10.1006/jcph.1997.5826 138, 449 (1997). [DOI] [Google Scholar]
- Yin X. and Kumar S., “Lubrication flow between a cavity and a flexible wall,” Phys. Fluids 10.1063/1.1914819 17, 063101 (2005). [DOI] [Google Scholar]
- Yin X. and Kumar S., “Two-dimensional simulations of flow near a cavity and a flexible solid boundary,” Phys. Fluids 10.1063/1.2204061 18, 063103 (2006). [DOI] [Google Scholar]
- Fu X., Siltberg H., Johnson P., and Ulmsten U., “Viscoelastic properties and muscular function of the human anterior vaginal wall,” Int. Urogynecol J. Pelvic Floor Dysfunct 6, 229 (1995). [Google Scholar]
- Goh J. T. W., “Biomechanical properties of prolapsed vaginal tissue in pre- and postmenopausal women,” Int. Urogynecol J. Pelvic Floor Dysfunct 13, 76 (2002). [DOI] [PubMed] [Google Scholar]
- Forsberg J., “A morphologist’s approach to the vagina,” Acta Obstet. Ginecol. Hisp. Lusit Suppl. 163, 75 (1996). [Google Scholar]
- Hu Y., Chen L., Delancey J. O. L., and Ashton-Miller J. A., “Vaginal thickness, cross-sectional area, and perimeter in women with and those without prolapse,” Obstet. Gynecol. (N.Y., NY, U. S.) 105, 1012 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duck F. A., Physical Properties of Tissue: A Comprehensive Reference Book (Academic, San Diego, 1990). [Google Scholar]
- Fung Y. C., Biomechanics: Mechanical Properties of Living Tissues, 2nd ed. (Springer-Verlag, New York, 1993). [Google Scholar]
- Greenleaf J. F., Fatermi M., and Insana M., “Selected methods for imaging elastic properties of biological tissues,” Annu. Rev. Biomed. Eng. 10.1146/annurev.bioeng.5.040202.121623 5, 57 (2003). [DOI] [PubMed] [Google Scholar]
- Owen D. H., Peters J. J., and Katz D. F., “Rheological properties of contraceptive gels,” Contraception 62, 321 (2000). [DOI] [PubMed] [Google Scholar]
- Peng Q., Jones R., Shishido K., Omata S., and Constantinou C. E., “Spatial distribution of vaginal closure pressures of continent and stress urinary incontinent women,” Physiol. Meas 28, 1429 (2007) [DOI] [PubMed] [Google Scholar]; Guaderrama N. M., Nager C. W., Liu J., Pretorious D. H., and Mittal R. K., “The vaginal pressure profile,” Neurourol Urodyn 24, 243 (2005). [DOI] [PubMed] [Google Scholar]
- Wolfram Research, Inc., MATHEMATICA, Version 5.2, Champaign, IL, 2005.
- Geonnotti A. R., Peters J. J., and Katz D. F., “Erosion of microbicide formulation coating layers: Effects of contact and shearing with vaginal fluid or semen,” J. Pharm. Sci. 10.1002/jps.20386 94, 1705 (2005). [DOI] [PubMed] [Google Scholar]
- Witelski T. P. and Bernoff A. J., “Self-similar asymptotics for linear and nonlinear diffusion equations,” Stud. Appl. Math. 10.1111/1467-9590.00074 100, 153 (1998). [DOI] [Google Scholar]
- Barenblatt G. I., Scaling, Self-similarity and Intermediate Asymptotics (Cambridge University Press, New York, 1996). [Google Scholar]
- Plenys A. M., “Mechanical analysis of topical drug delivery gels for women’s reproductive health,” Ph.D. thesis, Duke University, 2000. [Google Scholar]
- Owen D. H., Lavine M. J., Peters J. J., and Katz D. F., “Effect of temperature and pH on contraceptive gel viscosity,” Contraception 67, 57 (2003). [DOI] [PubMed] [Google Scholar]
- Geonnotti A. R. and Katz D. F., “Dynamics of HIV neutralization by a microbicide epithelial coating layer: Biophysical fundamentals and transport theory,” Biophys. J. 10.1529/biophysj.106.086322 91, 2121 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols D. H., in Vaginal Surgery, edited by Nichols D. H. and Randall C. L. (Williams & Wilkins, Baltimore, 1996), Chap. 1. [Google Scholar]