Flow-structure interaction effects on a jet emanating from a flexible nozzle

Abstract

In recent years, a wide variety of applications have been found for the use of pulsed jets in the area of flow control. The goal of the current study was to identify the flow field and mixing characteristics associated with an incompressible elongated jet emitted from a flexible nozzle. The shape of the nozzle was that of a high aspect ratio jet deforming from a fully opened to a completely closed configuration. The jet was characterized by a pulsatile flow that was self-excited by the motion of the flexible tube. The frequency of excitation was found to be between 150 and 175 Hz and the Strouhal number (nondimensional frequency) varied from 0.17 to 0.45. The jet flow was dominated by vortices that were shed from the nozzle with an axis parallel to the major axis. The vortices in the near field were quasi-two-dimensional so that measurements performed at the center plane represented the dynamics of the entire vortex. The nozzle excited two different modes depending on the tension applied to the flexible nozzle and the volumetric flow through it. The first was a flapping mode, which was associated with alternate shedding of vortices. This caused strong steering of the jet to one side or the other. The second mode was a symmetric mode that was associated with the formation of counter-rotating vortex pairs. Turbulence and jet spread in the measured planes were much larger in the first mode than the second one.

INTRODUCTION

Since Crow and Champagne¹ investigated the orderly structure of turbulent jets, the dynamics of pulsed jets has generated great interest in the scientific community. Crow and Champagne¹ showed the presence of jet column instability at the end of the jet’s potential core. This instability was characterized by a nondimensional frequency [Strouhal number (St)] defined as f^*D∕U₀, where f is the frequency at the end of the potential core, D is the jet diameter, and U₀ is the exit velocity. The instability was excited at St=0.3. Later Gutmark and Ho² showed that the most amplified frequency or preferred mode of a subsonic jet occurs at a normalized frequency (Strouhal number) in the range of 0.25–0.5, depending on the experimental facility. Forcing a subsonic jet at the preferred mode frequency could dramatically alter its growth rate.^{1, 2, 3, 4} The initial jet instability frequency is characterized by a Strouhal number St_θ=f^*Θ∕U₀ in the range of 0.009–0.018,^{3, 4} where f is the initial instability frequency, U₀ is the jet exit velocity, and Θ is the initial shear layer thickness. The growth rates of subsonic flows are dominated by vortex dynamics, and a very low level of forcing can modify the jet’s mixing layers by controlling the vortex formation. Forcing at the initial instability can stabilize the shear layer and prevent growth by stabilizing the small scale Kelvin–Helmholtz vortices that are generated by this initial shear layer instability. Forcing at lower frequencies (subharmonic forcing) accelerates the spreading rate and larger vortex formation by enhancing vortical structure interaction through subharmonic pairing.³ Exciting a jet at a frequency that is lower than the preferred mode causes the vortices to coalesce in a process called collective interaction, thus further enhancing the spreading rate.⁴

A combination of axial and helical excitation was used to generate a unique class of flows known as bifurcating and blooming jets.⁵ Axial forcing caused the shear layer to roll up into distinct vortex rings at the forcing frequency. The helical excitation radially perturbed the rings, producing a small eccentricity in the ring alignment. This initial eccentricity was amplified by mutual ring interaction, leading to dramatic changes in jet evolution. When the axial frequency was exactly twice the helical excitation, the jet bifurcated into two distinct jets with successive rings moving alternately on one of two trajectories. When the ratio of the axial to helical excitation was a noninteger, the jet produced a multitude of vortex rings that increased jet spreading rates in the near field.⁵

Noncircular jets were widely used as a flow control technique for aerospace applications primarily due to their unstable nature as compared to their more stable axisymmetric counterparts. Flow instabilities, self-induction, vortex stretching, vortex evolution, interaction and reconnection, and fine scale turbulence augmentation became the dominating flow characteristics in noncircular jets. Gutmark and Grinstein⁶ provided a comprehensive review of flow control with noncircular jets. A brief, study-relevant discussion of elliptical and rectangular jets is provided below.

The large scale mixing of elliptical and rectangular jets was found to be substantially larger than that of circular jets due to the axis switching associated with the self-deformation of elliptic vortices.⁶ Gutmark and Grinstein⁶ indicated that the mechanism of self-induction was more important in an elliptical or rectangular jet than the vortex interaction and merging that are dominant in circular jets. Austin⁷ measured nearly equal mass entrainment between forced and unforced elliptical jets. Hussain and Husain⁸ studied controlled excitation of elliptic jets, reporting that forcing could dramatically alter the near field turbulence, jet spread, and switching locations of major and minor axes. They also identified that the “preferred mode” of the elliptic jet with moderate aspect ratio scales with the exit equivalent diameter. Schadow et al.⁹ conducted studies on elliptic ducted air jets. They excited the elliptical jets with acoustic resonant pressure waves of the duct. They found that the maximum mixing was achieved when the forcing frequency matched the preferred mode frequency. Husain and Hussain¹⁰ studied a self-excited elliptic jet. The 2:1 aspect ratio self-excited whistler elliptic jet displayed no axis switching, but the near field mass entrainment was found to be 70% greater than the nonwhistler elliptic jet. They attributed this to the evolution of the secondary counter-rotating vortex pair (CVP) that induced tearing of the primary vortices, increasing the jet spread in the major axis that could not be obtained in an elliptic jet without a collar.

In summary, circular jet flow dynamics were found to be governed by the jet vortical structures. Manipulating these vortical structures through forcing could be used to affect the shear layer growth rate and mixing characteristics; however, asymmetric vortex formation and the self-induction process seem to govern noncircular jet flow fields. Forcing the noncircular jet was found to be beneficial for flow control application. Flow modulation of circular and noncircular geometries was used in a wide variety of applications such as jet noise, heat transfer, combustion and mixing control, and thrust vector control. The next section deals with a special class of pulsatile jet flows in which the flow is self-excited through jet flow interaction with the nozzle’s flexible walls. These flows are rich in vortical structures and excite different flow features.

Some engineering applications in which flows interact with flexible walls are summarized here. Thaokar and Kumaran¹¹ conducted stability analysis of laminar flows in flexible tubes and channels and observed three different instability modes. These modes were primarily governed by the Reynolds number and a nondimensional parameter, Σ=elastic force∕viscous force. They also identified the critical Reynolds number that triggered the viscous, inviscid, and wall mode instability for different values of Σ. Sinha¹² used actuated active flexible wall transducer for controlling boundary layer separation. Microflexural vibratory actuation at selected regions of the transducer flexible nozzle was excited at different frequencies to delay separation. At the point of actuation, the transducer used the preseparation velocity gradient to amplify the microvibratory stimuli, causing it to modulate the pressure gradient. This subsequently promoted reattachment by enhancing mixing in the inflectional velocity profiles downstream. Flexible filaments were used by Bhatet al.¹³ to control mixing and noise characteristics in jet noise applications. The centerline velocity and turbulence intensity was reduced by up to 25% with the use of flexible filaments. Their acoustic results showed that the low- and midfrequency noise was reduced with the filament at all measured angles. Greenhalgh et al.¹⁴ and Lorillu et al.¹⁵ studied aerodynamic properties of a two-dimensional flexible airfoil, which has applications in aerodynamic wing, sail, and parachute design. They focused on validating computation, improving aerodynamic efficiency, and extending stall margin for low-speed, high angle of attack operations.

Most channels carrying fluids in a biological system are flexible, and interactions between an internal flow and wall deformation often determine the biological functionality. These interactions involve a rich range of fluid-mechanical phenomena, including nonlinear pressure-drop∕flow rate relations, self-excited oscillations of flows at high Reynolds numbers, and capillary-elastic instabilities of two-phase flow at low Reynolds numbers. A comprehensive review on the biomechanics of flexible tubes is provided in Ref. 16.

The Starling resistor (SR) (Ref. ¹⁷)—a classic biomechanics experimental tool used in the investigation of flexible tubes—and the flexible nozzle flow discussed in the current study both have rich fluid-structure interactions that lead to three-dimensional flow instabilities. The SR is comprised of a segment of elastic tubing mounted between two rigid tubes and is enclosed in a fixed pressure chamber. Bertramet al.^{18, 19} characterized the SR in great detail, specifically identifying the parameter space in which the system exhibited spontaneous and rigorous oscillations. These oscillations arise in distinct frequency bands that are strongly dependent on the properties of the rigid part of the system, and exhibit hysteresis between both steady and dynamic states accompanied by strong evidence of nonlinear phenomena such as mode interactions and chaotic behavior. Both one-dimensional²⁰ and two-dimensional^{21, 22} theoretical analyses have been performed to study flow through the SR or an analogous system. Two-dimensional stability analysis of open flows over compliant surfaces based on Orr–Sommerfeld equation accounting for wall inertia, damping, bending stiffness, tension, and spring backing has revealed multiple instability modes.^{21, 22} The three most common modes based on Benjamin–Landahl energy classification are Tollmien–Schlichting (TS) waves that are stabilized when energy is transferred irreversibly from the flow to the wall, traveling wave flutter (TWF) stabilized by wall damping, and static divergence which is indifferent to the direction of energy transfer. Additional modes could also arise due to the interaction of TS and TWF modes²² or due to strong coupling between longitudinal and transverse wall strain.²³

The current study investigates the flow dynamics of a flexible elongated nozzle. The flow field of a flexible nozzle has many similarities to that of pulsatile jets. Allowing the nozzle shape to deform in response to the fluid flow inside the flexible walls of the nozzle is a special case of unsteady jets. The flow is self-excited and the pulsations are produced by the periodic deformation of the nozzle. The relationship between wall deformations and the flow dynamics in this flexible nozzle is important for medical and engineering applications.

EXPERIMENTAL SETUP

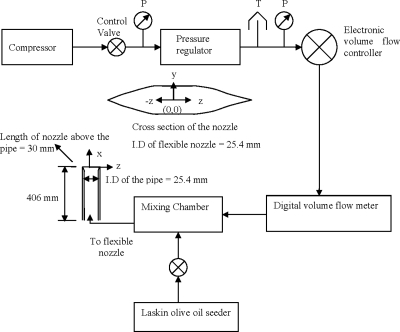
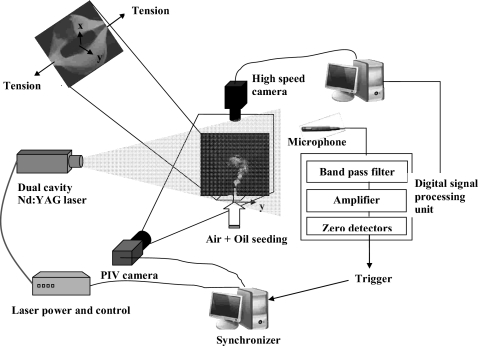
A flexible nozzle was constructed by attaching a 0.25-mm-thick, tube-shaped latex segment to a circular rigid pipe with 26.7 mm outer diameter, 1.3 mm thickness, and 406 mm length (Fig. 1). The unstretched flexible tube length was 37.3 mm, and its inner diameter was 25.4 mm. The flexible tube was fitted over the pipe; 19.5 mm of the unstretched tube length was below the pipe exit. Using two strings that were attached at the tube’s edges, the tube was stretched at its downstream end to form a narrow slot when there was no airflow (Fig. 2). The tension applied to the nozzle was calibrated by connecting weights through pulleys to the strings. Coordinates x and y refer to the streamwise and spanwise directions, respectively. The origin of the nozzle is located at the center of the nozzle (x=0, y=0, z=0).

Figure 1.

Schematic of the flow system.

Figure 2.

Schematic of the setup and coordinate axes.

A pressure regulator, thermocouple, volume flow meter, electronic control valve, and electronic pressure gages were mounted upstream to monitor and regulate airflow. The flow entering the flexible nozzle from the rigid tube was fed by a compressor which was able to produce a maximum volumetric flow rate of 2.5×10⁻³ m³∕s at 35 psi. The airflow was seeded in a settling chamber with 1–5 μm olive oil particles for flow measurements and visualization. Crowe et al.²⁴ and Chein and Chung²⁵ indicated that the Stokes number for flow visualization in incompressible flows should be less than 0.2. Furthermore, they indicate that the error in velocity measurement increases linearly with Stokes number, with approximately 2% error at St=0.2. In the current study maximum Stokes number (St) of the oil droplets could be computed as

$$\text{St}={\tau }_p∕{\tau }_f.$$

Here τ_p and τ_f are the particle and flow time scales, respectively,

$${\tau }_P=\left({\rho }_P{\text{D}}_P^2∕18\mu \right),$$

$${\tau }_f=\delta ∕U_{\text{CL}},$$

where ρ_p is the particle density, D_p is the particle diameter, $\underset{̣}{\mu }$ is the absolute viscosity of the air, $\underset{̣}{\delta }$ is the shear layer thickness at the jet exit (measured as distance from the centerline to where the velocity drops to 80% U_CL), and U_CL is the local streamwise centerline velocity. The upper bound of Stokes number in the present experiment was 0.095. This value is lower than that proposed by Crowe et al.;²⁴ thus, the measurement error due to the effect of Stokes number should be less than 2%.

Nonintrusive measurements of the velocity field were made by using two-dimensional PIV. The LaVision Imager Intense camera used to capture the images has a resolution of 1376 (H) and 1040 (V) pixels with a pixel size of 6.45×6.45 μm² and a maximum frame rate of 10 Hz; it also has 65% quantum efficiency at 532 nm with a 12 bit digital output. The camera was fitted with a Nikon 105 mm F∕1.8 lens and a 532 nm narrow bandpass filter for all the cases. A dual Pentium 4 processor with 1 Gbyte RAM was used to control the data acquisition. The particle image velocimetry (PIV) camera captured an image area of 59.9×44.5 mm² in the physical domain.

To illuminate the flow field, a frequency double Nd:yttrium aluminum garnet laser with dual cavity (New Wave Research Solo-PIV) was used. The output was 50 mJ∕pulse at 532 nm at a pulse rate of 10 Hz. The thickness of the laser sheet during the current set of experiments was 1 mm. The time interval Δt between the two laser pulses was set constant in order to adjust the mean displacement of the particle at the jet centerline to be ∼10 pixels (8 μs in the present study). The arrangement of the laser and the camera is shown in Fig. 2. The viewing plane (x-y) was aligned with the nozzle midplane in the flow direction (refer to Fig. 2). DAVIS software (PIV data processing software from LaVision) was used for image postprocessing to extract velocity vectors. Each of the images was divided into interrogation windows. The interrogation window size limits the spatial resolution of the velocity measurement. An interrogation window size of 64×64 pixels (2.75×2.75 mm² in the physical domain) with 50% overlap was employed in the current study. A conservative estimate of Kolmogorov length scale in the present analysis: η=(ν³∕ε)^1∕4, ν=kinematic viscosity of air (15.11×10⁻⁶ m²∕s at 20 °C), ε=dissipation by turbulence per unit mass [=(u^′3∕l_e)], u^′ is the rms velocity, and l_e is the average size of energy containing eddies. $u_{\max }^{\prime }$ is 4.54 m∕s (for case 5, maximum excitation), l_e∼0.5D_e (equivalent diameter) =8 mm (from time-averaged images). Hence, ε∼11 697. Then η∼0.023 mm.²⁶ This indicates that the Kolmogorov scale is two order magnitude smaller than the resolvable length scale, and hence only the large scales in the flow are resolved.

The cross-correlation function was operated on the intensities inside of each interrogation window and passed through the complete PIV recording with a specified window shift. The evaluation yielded one velocity vector for each interrogation window. For a detailed description of the extraction technique, refer to Kompenhans et al.²⁷

Both time-averaged and phase-locked PIV images were acquired. In a full cycle the open exit area of the flexible nozzle changed from being fully closed at 0° (or 360°) to being fully opened near 180°. This cycle also corresponded to the cycle of the acoustic pressure that was measured in the near field by a microphone [Fig. 5a]. The microphone sensor was placed at x-y plane, 65° from x=0 line at a distance of y=−89 mm (Fig. 2). The acoustic signal was used as a reference source for obtaining the phase-averaged flow field at different phases relative to the flexible nozzle opening cycle.

Figure 5.

(a) Equivalent diameter D_p as a function of phase angle for one cycle. (b) Equivalent diameter D_p as a function of phase angle for one cycle for nonflapping cases (1, 2, 4, and 6) for positive (+y) and negative (−y) nozzle cross sections. (c) Equivalent diameter D_p as a function of phase angle for one cycle for flapping cases (3 and 5) for positive (+y) and negative (−y) nozzle cross sections. (d) High-speed images of the motion of flexible tube at different instances of the microphone cycle for case 2.

The microphone signal was inputted to a Dspace (model DS1104) real-time signal processor. The signal was bandpass (fourth-order Butterworth type) filtered with lower and upper cutoff frequencies of 60 and 400 Hz, respectively. The filtered signal was then amplified before being sent to a threshold detector that outputs a square wave (from −5 to 5 V), depending on the input signal; this signal is positive if the input is greater than the threshold and negative if the input is lower than threshold. The threshold was set high enough so that the trigger was not generated due to noise. This trigger signal was sent as an input to the DAVIS software. Different delays were then generated in the synchronizer to scan through one entire microphone cycle.

One hundred images were acquired at each phase with a total of ten phases. Time-averaged images were constructed by separately obtaining 200 images at each case. There was no time correlation between these images. Because the noncorrelated flow field obtained from 200 images provided a better estimate of the flow field turbulence, the time-averaged sequence was not constructed from the limited phase-averaged images (ten phases).

There are two possible sources of error that can arise in both the time- and phase-averaged flow fields. The first error arises due to the number of flow fields used to compute phase and time averages. We computed a maximum error in the mean and rms of the time-averaged flow field to be less than 1% (for both flapping and nonflapping cases) with 1000 PIV flow fields as compared to 200 flow fields. The second source of error arises due to seeding bias. In the current study only the jet flow was seeded. The maximum error associated with nonuniform seed density was found to be 4.5%. This gave us a total error of 5.5% in the time-averaged cases. A similar analysis gave a total error of less than 6% for the phase-averaged cases, which used 100 flow fields for averaging.

OPERATING CONDITIONS

Figure 3 shows the strain (ξ=Δl∕l, change in length∕original length) percentage of the flexible nozzle as a function of the frequency of vibration obtained at a volumetric flow rate $\left(\dot{Q}={10}^{-3}{\mathrm{m}}^3∕\mathrm{s}\right)$. The strain is attained from l, length of the exit opening when there is no stress at the exit, and Δl, increase in length that is obtained by applying uniform weight stress at the edges of the tube’s exit. Table 1 shows the six different operating conditions that were investigated. Cases 1 and 2 correspond to the conditions in which the nozzle’s strain percentage was 35.94, cases 3 and 4 with nozzle strain percentage of 40.18, and cases 5 and 6 with 43.57. Case 1 (0.3×10⁻³ m³∕s), case 3 (0.22×10⁻³ m³∕s), and case 5 (0.2×10⁻³ m³∕s) correspond to the low volumetric flow rate conditions at which the exit of the tube vibrated for the particular strain, whereas cases 2, 4, and 6 correspond to the higher volumetric flow rate $\left(\dot{Q}={10}^{-3}{\mathrm{m}}^3∕\mathrm{s}\right)$ conditions.

Figure 3.

Percentage strain of the flexible nozzle as a function of excited frequency obtained at $\dot{Q}={10}^{-3}{\mathrm{m}}^3∕\mathrm{s}$.

Table 1.

Operating conditions.

	Range of Re at which the flexible nozzle vibrates	Strain (%)	Volume flow rate,$\dot{Q}\times {10}^6\left({\mathrm{m}}^3∕\mathrm{s}\right)$	Frequency, f (Hz)	Equivalent diameter,De (mm)	Maximum exit velocity over all phases,Umax (m∕s)	Equivalent velocity,$U_e=4\times \dot{Q}∕\pi D_e^2\left(\mathrm{m}∕\mathrm{s}\right)$	Strouhal number, St=fDe∕Ue	Mode
Case 1	Remax=12 800	35.94	333	151	10.8	9.71	3.64	0.45	Nonflapping
Case 2	Remin=1170		1000	153	11.7	17.15	9.3	0.19	Nonflapping
Case 3	Remax=13 300	40.18	217	169	8.9	10.05	3.49	0.43	Flapping
Case 4	Remin=760		1000	173	11.0	15.23	10.52	0.18	Nonflapping
Case 5	Remax=13 600	43.57	200	171	8.6	9.33	3.44	0.43	Flapping
Case 6	Remin=700		1000	175	10.7	15.31	11.12	0.17	Nonflapping

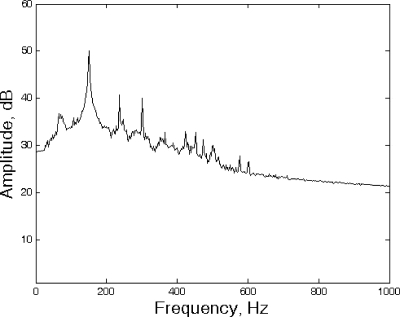
Different weights were applied to the flexible nozzle’s exit through an attached pulley and string in order to achieve the various strains of the nozzle. The limiting Reynolds numbers—recalculated from the diameter of the pipe and the volumetric flow through it, between which the nozzle operated—are also shown in Table 1. The frequency was found to increase with raised volumetric flow rate. Furthermore, for the same strain rate the change in frequency was minimal with increasing flow rate. For example, in cases 5 and 6 there is a fivefold increase in flow rate, but only a 2.3% change in frequency. One period of the microphone cycle corresponded to the flexible tube’s full opening and closing in the direction perpendicular to the slot length. A sample of the filtered (Butterworth fourth-order bandpass with 60–400 Hz) microphone spectrum for case 6 is shown in Fig. 4. Note the appearance of the peak at the frequency of the nozzle operation (∼175 Hz). The spectra also indicate the presence of harmonics at the dominant frequency.

Figure 4.

Filtered microphone spectrum of case 6.

Characterization of the nozzle cyclic motion

Figure 5a shows the cyclic variation in the equivalent nozzle diameter (D_p) at ten phases for all six cases and the microphone time trace that corresponded to case 2. Case 2 was chosen as an example of the similar behavior of the other cases. The equivalent diameter (D_p) was defined based on open equivalent area of the flexible nozzle at the exit for each of the cases. In order to determine the equivalent open diameter for a particular case, ten images of the top surface of the flexible nozzle corresponding to ten phases in a cycle were obtained using a Vision Research high-speed camera (Phantom, Version 7.1). These images were captured at 26 000 frames∕s with a 30 ms exposure time. Image processing software was employed to define the boundary of the nozzle. Using an appropriate scaling factor, the area and the equivalent circle diameter (D_p) were obtained at each phase. The maximum error in computing D_p from the images was less than 3.5%. The average open area (A_e) of all phases of a particular case was used to calculate an average open equivalent diameter (D_e) that was used to normalize length scales (shown in Table 1). The Strouhal number computed from D_e and U_e [where $U_e=4^{*}\text{volumetric}\text{flow}\text{rate}∕\left(\pi D_e^2\right)$] falls within a range of 0.17–0.45 for all cases. The uncertainty associated in measuring volumetric flow rate was less than 1% and the maximum error in computing St was less than 5%. The values of St were found to be within a range of 0.17–0.45 for all cases, which is similar to the range of the preferred mode of a subsonic circular jet.² Because the nozzle did not close completely in cases 2 and 4, the values shown in Fig. 5a for 0° and 360° are nonzero. The flapping cases (3 and 5) have lower open diameter over the entire cycle as compared to the nonflapping cases.

Figures 5b, 5c show the variation in the areas of the two-halves of the nozzle on the two sides of the major axis (z axis) for the symmetric and flapping cases, respectively. Curve +y corresponds to the nozzle section on the positive side of y and −y to the respective negative side. The equivalent diameter of both halves of the nozzles in the symmetric cases 1, 2, 4, and 6 are in phase over the entire cycle, while a relative phase shift was observed for the flapping cases 3 and 5; the peak diameter was shifted by 40°–50° for these two cases. This symmetric or asymmetric variation in the nozzle’s open area on the two sides of the major axis affects the evolution of the vortices shed at these two sides. Cases 1, 2, 4, and 6 show a symmetric pattern of flow vortices (Fig. 16), whereas cases 3 and 5 show asymmetry in the jet evolution pattern (Fig. 17).

Figure 16.

Phase-averaged flow field for case 2.

Figure 17.

Phase-averaged flow field for case 5.

Figures 5d show five high-speed images (phases of 0°, 73°, 145°, 217°, and 323°) of the flexible tube synchronized with the microphone signal for case 2. The portion of the flexible tube that directly interacts with the PIV laser sheet is coated with a fluorescent paint (rhodamine 6G) that absorbs light at 532 nm to avoid saturation of the charge coupled device pixels due to reflection of the laser light from the flexible nozzle. This fluorescent dye gave rise to the black streak in the images of Fig. 5d. A full cycle of the tube motion covers phase angles from θ=0°–360°, where θ=0 corresponds to complete closing and θ=180 to full opening.

RESULTS AND DISCUSSIONS

Time-averaged flow field

The flow dynamics of the flexible nozzle described here occur mostly in planes parallel to the y axis. This is a result of the nozzle’s edges being fixed by the tension of the two supporting strings in the z plane. The flexible nozzle’s edges are free to move only in the y direction, and therefore, the important flow-structure interaction occurs in this plane. Furthermore, it will be shown that in the jet’s near field the flow field is quasi-two-dimensional along the z axis (i.e., the flow structure off the centerline along the z axis is similar to that of the centerline structure). Therefore, most of the data presented here were taken in the y plane on the jet centerline.

The time-averaged, two-dimensional vector flow fields in the center plane x-y at z=0 were computed from PIV images for the six different cases listed in Table 1 and are shown in Figs. 6a, 6b, 6c, 6d, 6e, 6f. The out-of-plane vorticity (ω_z=du∕dy-dv∕dx) is also plotted as contours in the background. Both the streamwise (x) and radial (y) coordinates are normalized by D_e. The flow field was quite symmetric in most of the presented cases. Any slight deviations can be attributed to a possible slight asymmetry in the applied tension. Entrainment of the ambient fluid into the jet was clearly visible in all cases.

Figure 6.

[(a) and (f)] Time-averaged flow field. (a) Case 1, Strain%=35.94, $\dot{Q}=0.3\times {10}^{-3}{\mathrm{m}}^3∕\mathrm{s}$. (b) Case 2, strain %=35.94, $\dot{Q}={10}^{-3}{\mathrm{m}}^3∕\mathrm{s}$. (c) Case 3, strain %=40.18, $\dot{Q}=0.217\times {10}^{-3}{\mathrm{m}}^3∕\mathrm{s}$. (d) Case 4, strain %=40.18, $\dot{Q}={10}^{-3}{\mathrm{m}}^3∕\mathrm{s}$. (e) Case 5, strain %=43.57, $\dot{Q}=0.2\times {10}^{-3}{\mathrm{m}}^3∕\mathrm{s}$. (f) Case 6, strain %=43.57, $\dot{Q}={10}^{-3}{\mathrm{m}}^3∕\mathrm{s}$.

Varying the tension and the volumetric flow rate induced significant effect on the mean flow field. The jet spread was wider at the lower volumetric flow rate when compared to the higher flow rate condition for all three tensions. At the same low flow rate, cases 3 and 5 showed that the jet split into two separate streams. It is shown later in instantaneous images that the split in the mean flow field results from the jet flapping in the x-y plane for these conditions. In case 3 a single jet core was observed up to x∕D_e=0.7 and further downstream; the jet split into two separate streams resulting in a low velocity region along the jet center. Vorticity contours also show two strong shear regions, one in the jet core and the other at the jet circumference past x∕D_e>1.2. The jet split occurred at x∕D_e>0.6 for case 5 and the vorticity generated by the inner shear layer was weaker in case 5 as compared to case 3. Cases 3 and 5 show enhanced entrainment of the ambient stream in the measurement plane as compared to case 1. The jet in case 1 remained unsplit in the entire measurement range. None of the jets with the higher flow rate $\left(\dot{V}={10}^{-3}{\mathrm{m}}^3∕\mathrm{s}\right)$ exhibited any jet split in the time-averaged flow fields. In comparison to case 2, the jet spread was wider for cases 4 and 6. In order to evaluate the behavior of the jet (case 1) off center plane, the flow field was measured in the x-y plane at z=±0.5D_e and on the x-z plane along the jet’s major axis (Figs. 7a, 7b, 7c). All the figures show high vorticity magnitude with opposite signs on either side of the shear layer. Figures 7a, 7b measured on the same x-y plane at z=0 (center plane) show similar vector field to Fig. 6a. Slight asymmetry could be observed in the vorticity contour strengths between the different planes on either side of the shear layer. For example, the boundaries of the vorticity contour level (ω_z∼−7) were found to extend past x∕D_e=1.5 for Fig. 7b, as compared to Fig. 7a. Also, the vorticity magnitude in each plane was found to vary by less than 8% on either side of the shear layer.

Figure 7.

[(a) and (c)] Time-averaged flow field with vorticity contours for case 1 at three different locations. (a) and (b) in the cross sectional plane: (a) 0.5D_e, (b) −0.5D_e, and (c) along the major axis.

Sample instantaneous flow fields superimposed on swirling strength (Γ) are presented in Figs. 89 for cases 5 and 2, respectively. Γ is defined as the angular velocity of the local swirling motion of the jet. It represents the imaginary portion of the complex eigenvalue pair of the local mainstream velocity gradient tensor and has been used as an unambiguous measure of vorticity.²⁸ Swirling strength represents only the intensity of the rotating fluid motion and does not involve any contributions from shear effects; hence, it enables better tracking of the vortical structures. Figure 8a shows the evolution of a single vortical structure on the left side of the jet; at other instances, the vortex structure was found to be present on the right side of the jet [Fig. 8b]. The alternate shedding of the vortices at the two sides of the nozzle is indicative of the flapping motion of the jet. The evolution of these vortices controls the shape and spread of the jet. In contrast, the instantaneous flow field of case 2 shows two symmetric counter-rotating vortices on either side of the jet (Fig. 9). This flow behavior is related to the observations depicted in Figs. 5b, 5c.

Figure 8.

[(a) and (b)] Instantaneous images of case 5.

Figure 9.

[(a) and (b)] Instantaneous images of case 2.

The open area of the two nozzles over one cycle on either side of y=0 was found to be in phase in case 2, whereas they were found to possess a certain phase shift in case 3. This indicates that the displacement of the nozzle moved asynchronously for cases 3 and 5, creating an asymmetric evolution of the flow structures. The flow vortices on either side of the nozzle in cases 1, 2, 4, and 6 were found to be symmetric due to the symmetric motion of the two sides of the nozzle. Also, as shown in Fig. 5, the interaction between the flow and the nozzle’s flexible walls resulted in periodic closing and opening of the nozzle’s exit. This implies that the jet is pulsating. Immediately following the start of exit opening, the jet behaves as an impulsively started turbulent jet in which the velocity field is dominated by a vortex that surrounds the jet head. The starting vortex induces strong entrainment as shown in Fig. 9a.

There is a transient period between the passage of the vortex and the attainment of steady entrainment from the ambient stream.²⁹ The instantaneous images of case 2 shown in Figs. 9a, 9b illustrate the evolution of the symmetric CVP from near the nozzle’s exit in Fig. 9a to the location of its center after being convected to x∕D_e≈1.6 in Fig. 9b. Also noticeable in both Figs. 9a, 9b are the modulations in the jet width that are associated with the wall motion of the flexible nozzle exit. The jet width varies from narrow to wide as the nozzle exit opens and closes periodically. The increased lateral spread in both symmetric and flapping jets (Figs. 89) is located immediately downstream of the front end of the CVP in the symmetric case and the asymmetric vortices shed in case 5, and is induced by these vortices.

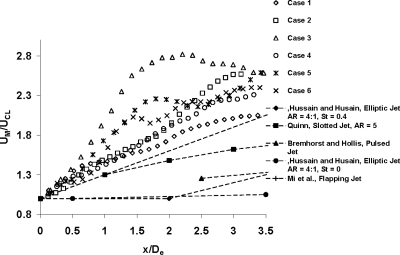
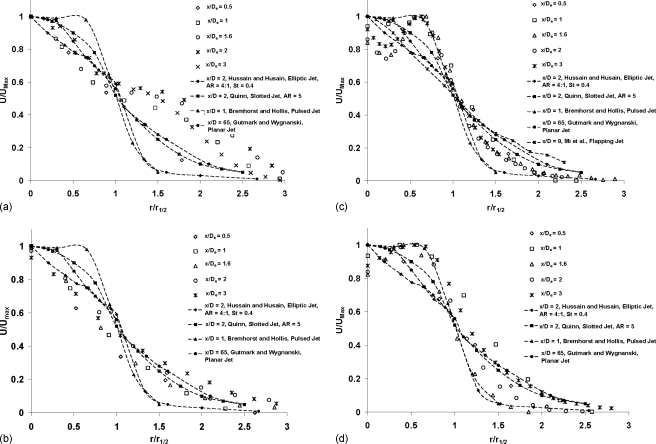
Figure 10 shows the jet half-width (r_1∕2) at different streamwise locations. As observed from the time-averaged flow field, cases 3 and 5 show a rapid increase in slope past x∕D_e=0.5. This arises from the jet flapping motion that results in large entrainment with increased jet spread. For the nonflapping cases 1 and 2, increasing the flow rate resulted in the formation of symmetrical CVPs without alternating steering the jet, thus suppressing the spreading rate of the jet. Figure 9 compares the present results with data from subsonic circular pulsed jet by Bremhorst and Hollis,³⁰ with the 2:1 and 4:1 aspect ratio (AR) elliptic jets along minor axis from Hussain and Husain,⁸ with the 5:1 and 2:1 AR slotted jet along minor axis from Quinn,³¹ and with a 4:1 AR excited elliptic jet (Strouhal number=fD∕U_o=0.4) along the minor axis from Hussain and Husain.⁸ In the current study, the shape of the nozzle for every case varies from an infinitely thin slit to a high AR elongated jet with pinched edges, rendering it difficult to directly compare the current jet growth with the other jets. It is interesting to note, however, that the growth rate of the excited elliptic jet has similar magnitudes to the current self-excited flexible nozzle cases.

Figure 10.

Jet half-width variation in the downstream direction.

It is also clear that the near field growth rate of the jets strongly depends on the shape of the exit nozzle and inlet conditions. A 5:1 AR slotted jet by Quinn³¹ is 50% lower in the first 3.5 jet diameters as compared to a 2:1 unexcited elliptic jet. Also, an excited 4:1 elliptic jet shows 3.5 times increase in jet spread as compared to unexcited jet at 3.5 jet diameters. In addition, the inlet conditions (such as inlet mean and turbulence profile), spectral characteristics of the boundary layer, and contour of the inlet nozzle affect development and growth of the shear layer.³² Hussain and Husain⁸ showed that the effect of initial conditions persisted on both the near field mean and turbulence characteristics of the jet (x<20 jet diameter). Figure 11 shows the decay of the centerline mean velocity along the jet axis. U_M is the maximum velocity in the flow field over all the phases for a particular case (it is a constant for every case and is obtained at the nozzle exit and shown in Table 1), and U_CL is the local streamwise centerline velocity. The flapping cases show an accelerated decay of the centerline velocity up to x∕D_e=1. For cases 3, 5, and 6 the evolution of U_M∕U_CL past 1.5D_e is more complex because of the presence of intermediate low velocity regions. This can result from the presence of secondary modes.

Figure 11.

Centerline velocity decay along the jet axis.

Studies on subharmonic forced shear layers³ indicated that momentum thickness plotted as a function of streamwise distance has regions where the values were observed to reach a plateau. Their spectral measurements show that the momentum thickness reaches a plateau when the fundamental (most amplified wave) equilibrates and the vortex roll up is initiated. This is confirmed by a sharp increase in the subharmonic amplification rate. It is possible in the current study that cases 3, 5, and 6 introduce additional modes that stabilize the jet, which causes the flat zone in the centerline decay plot. Additional spectral measurements would be necessary to support this hypothesis. Similar to Fig. 10, data from elliptic, excited elliptic, slotted, pulsed circular jet, and flapping jet³³ are compared to the current data. Mi et al.³³ induced flapping by a chamber that surrounded the core slit nozzle. A positive feedback generated by the expansion of the slit jet through the entrainment of the surrounding fluid caused the jet to flap in a quasiplanar fashion. The flapping jet, though generated by a different mechanism in the study of Mi et al., shows a much higher decay rate as compared to the other noncircular rigid nozzle geometries and is comparable in slope to the current cases. Clearly the spreading rate and centerline decay associated with the flapping cases is much higher than those of the nonflapping cases in the measured plane. The study of Mi et al. shows similar conclusions, i.e., higher jet spread and decay for flapping jets as compared to their nonflapping jets.

The mean streamwise velocities across the jet were normalized by the maximum axial velocity at the same axial location (U_max) and are presented in Figs. 12a, 12b, 12c, 12d for cases 1, 2, 5, and 6 at several near field streamwise locations. Cases 3 and 4 are not shown here, but have velocity profiles similar to cases 5 and 6. The radial distance from the centerline was normalized by the jet half-width. The present data are compared to those of a fully developed planar jet at a streamwise location of 65 jet diameters,³⁴ a subsonic circular pulsed jet at 1 jet diameter,³⁰ a slotted jet of aspect ratio 5:2 jet diameters,³¹ and an excited elliptic jet of aspect ratio 4:1.⁸ It is worth noting that even though the present data cover only the near field of the jet, cases 2 and 6 show that the streamwise velocity component attains similarity quite close to that of the planar jet. Case 5 shows the peak velocity to be shifted away from the centerline past x∕D_e>0.5 due to jet flapping. The mean jet velocity maximum remains off-axis over the entire measurement domain (3 jet diameters).

Figure 12.

[(a) and (d)] Mean radial profiles of normalized streamwise velocity at different streamwise locations: (a) case 1, (b) case 2, (c) case 5, and (d) case 6.

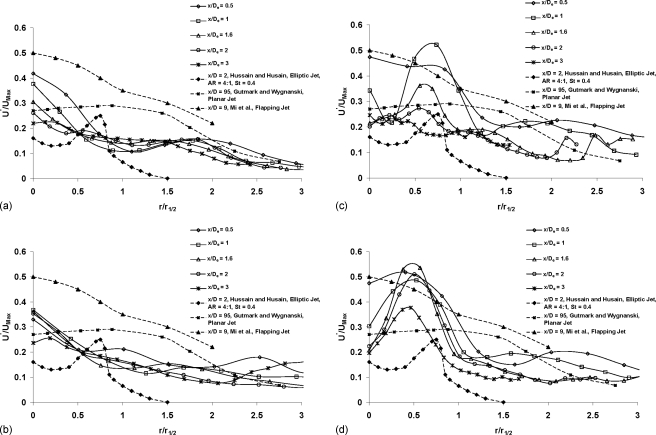
Figures 13a, 13b, 13c show the normalized mean lateral velocity component, V∕U_max for cases 1, 5, and 6 at several streamwise locations. Case 2 is not plotted because the lateral component was less than 5% of the mean streamwise component. This is indicative of the minimal lateral spread of case 2 over the measurement domain. The maximum magnitude of the lateral velocity component at x∕D_e=1.9 is almost twice for the flapping case 5 as compared to the nonflapping case 1. Figure 13b compares the present results with those of Mi et al.³³ for a flapping jet and for a 4:1 excited elliptic jet.⁸ Mi et al. observed that the mean velocity profiles attain self-similarity past 9 jet diameters, and the magnitude of the lateral component of the flapping jet was almost twice that of the nonflapping jet. It was also observed that cases 5 and 6 extend to 3 jet half-widths, whereas case 1 extends only to 2.5r_1∕2. This indicates that the lateral jet spread in the measurement plane is higher for cases 5 and 6 as compared to case 1.

Figure 13.

[(a) and (c)] Mean radial profiles of normalized spanwise velocity at different streamwise locations: (a) case 1, (b) case 5, and (c) case 6.

The radial profiles of the normalized axial component of the turbulence intensity at different streamwise locations are plotted in Figs. 14a, 14b, 14c, 14d for cases 1, 2, 5, and 6. The axial turbulence intensity for all the cases was below 30% of the maximum mean velocity past jet half-width of 1.5. Cases 1 and 2 attain similar levels to that of the elliptic jet profile past x∕D_e>2.5, though with a different radial distribution. The flapping jet (case 5) also approaches the level of the elliptic jet. The flapping jet case from Miet al.³³ is shown in Fig. 14. The centerline streamwise turbulence of the flapping cases in the Mi et al. study at x∕D=9 was at least two times larger in comparison to cases 1, 2, 5, and 6 for x∕D_e<3. The flapping jet study of Mi et al. shows axial turbulence levels as high as 50% on the centerline similar to the current study cases 5 and 6 at x=0.4D_e, for example.

Figure 14.

[(a) and (d)] Radial profiles of normalized streamwise turbulence at different streamwise locations: (a) case 1, (b) case 2, (c) case 5, and (d) case 6.

The normalized Reynolds stress $\left(U^{\prime }{V}^{\prime }∕U_{\max }^2\right)$ for cases 1, 2, 5, and 6 are shown in Figs. 15a, 15b, 15c, 15d. The present data are compared to those of the flapping jet, 4:1 AR excited elliptic jet, 5:1 AR slotted jet, and the planar jet. The maximum turbulence production in cases 1 and 2 were found to be four to five times lower than cases 5 and 6. Also worth noting is the rapid drop off in the maximum U^′V^′ levels from 16% to 1.5%–2.5% within 1 jet diameter. Dual maxima have also been observed in the nonflapping cases (example: at x∕D_e=1.6 in case 1 and at x∕D_e=3 in case 2). Such dual humps have been observed in excited mixing layer studies just before the Reynolds stress becomes negative³⁵ (i.e., when there is a transfer of energy from the turbulence back to the mean flow). The negative turbulence production arises due to changes in the orientation of vortical structures of the mixing layer.³⁶ Additional normal stress measurement downstream of the jet along with flow visualization in the normal plane would be necessary to support the above hypothesis.

Figure 15.

[(a) and (d)] Radial profiles of normalized Reynolds stress at different streamwise locations: (a) case 1, (b) case 2, (c) case 5, and (d) case 6.

Phase-averaged flow field

Phase-averaged mean flow field measurements were acquired at ten phases during a cycle of the pulsed jet based on the variation of the shape of the flexible nozzle. A total of 100 images were averaged at each phase. Flow fields for cases 2 and 5 are presented at different phases in Figs. 1617 to illustrate the evolution of nonflapping and flapping jets, respectively. The x-z coordinates are normalized by the equivalent diameter. For case 2 the formation of the CVP and its convection downstream is shown. The vortex pair formed at two different phases during the cyclic motion of the tube’s exit. The first pair was detected following a short delay after the tube exit opens (36<θ<70). The second vortex pair formed after a short delay (186<θ<216) following the phase when the tube was fully opened. Both vortex pairs were convected downstream in a symmetric manner. For case 5 the flow pattern was quite different. The jet alternately formed single vortices on either side of the jet. Both the flapping (case 5) and nonflapping (case 2) cases had similar convective speed of the vortical structures. The convective Mach number (Ma_c=convective speed∕speed of sound) for cases 2 and 5 was 0.0012.

Figures 18a, 18b, 18c, 18d show the phase-averaged mean flow field and the swirling strength-Γ in gray scale (dark gray is high swirl strength, and light gray is weaker swirling strength) for case 1. Figure 18a shows the flow field in the x-z plane along the major axis, z at Θ=137° for case 1; Figs. 18b, 18c, 18d represent the flow field in the off-axis x-y planes at z=−0.5, 0, and 0.5D_e at Θ=130°, 132°, and 137°, respectively. The rotational direction of the dominant flow eddies is marked. The CVP was observed in all plots with slight variation in location and swirl strength of the vortices. This indicates that the flow structures that dominated the near field are coherent along the circumference of the nozzle; hence, the evolution of the flow vortices at the center plane represents their behavior at off-axis locations.

Figure 18.

[(a)–(d)] Phase-averaged flow field superimposed on swirl strength for case 1. (a) Flow field along the major axis, z, at θ=137°. [(b) and (c)] Flow field along the cross sectional planes, (b) z=−0.5^*D_e, θ=130, (c) z=0, θ=132, (d) z=0.5^*D_e=137. Rotation of the vortices is shown by arrows.

Figures 1920 show instantaneous Mie scattering images at the phase of formation of the vortex pair for cases 2 and 5. Included in these images are the shapes of the flexible tube’s exit at the center span of the nozzle. In case 5 one side of the tube exit is higher than the other and attains a rounded shape. This asymmetry induces an asymmetric vortex formation that is directed alternately to both sides of the jet. The instantaneous seeded images of case 2 (Fig. 19) show a symmetric behavior of the two exit sides of the tube. The two folds come together in a symmetric manner and generate a CVP.

Figure 19.

Instantaneous seeded images of case 2.

Figure 20.

Instantaneous seeded images of case 5.

CONCLUSIONS

Two-dimensional PIV was used to study the flow dynamics at the exit of a flexible tube nozzle. Time-averaged measurements were used to study the turbulence, jet spread, and mean flow field while phase-locked measurements were used to understand the formation and evolution of the vortical structures. The flow-structure interaction was found to vary in the plane parallel to the motion of the flexible nozzle. This was due to the fact that the nozzle edges were constrained and free to move only in one direction in the plane in the nozzle. Further PIV measurement in the near field around the different nozzle circumference showed that the flow structures were coherent with slight variation in their location and rotational strength, indicating that the flow field is quasi-two-dimensional. Based on this observation, the center plane measurements were found to be adequate to describe the important features of the flow dynamics of the jet. However, Nathan et al.³⁷ indicated that even minor changes to a round jet initial profile propagates into the far field; thus, the small variations in the circumferential vortices could amplify in the far field making the flow field highly complex and three dimensional.

The interaction between the nozzle motion, the resulting pulsed jet, and the emitted acoustics were studied for different volumetric flow rates and tensions applied to the nozzle’s exit. The flow was observed to be self-excited, and the nondimensional frequency (Strouhal number) was found to vary between 0.17 and 0.45. The excited Strouhal number was found to inversely scale with inlet velocity. The choice of flow rate, tension applied at the nozzle lips, and the deformation shape of the flexible nozzle acted as inlet conditions which governed the near field flow dynamics.

The jet flow field at the center plane of the minor axis had two different excitation modes: flapping and nonflapping depending on the applied tension and the jet flow rate. Phase-averaged images at the flapping mode indicate that during the first half of the cycle a single vortex was shed on one side, causing the jet to steer to that side. During the second half, the vortex formed on the opposite side. This resulted from the particular motion pattern of the two halves of the flexible nozzle on either side of the major axis; the motion was out of phase in the flapping case and symmetric in the nonflapping case. Time-averaged analysis shows that the flapping motion induced a strong jet spread in the minor axis plane. The maximum jet spread was approximately three times higher for the flapping mode in the x-y plane compared to the nonflapping case. The centerline axial velocity decay was found to drop by 12%–15% for the flapping cases compared to the nonflapping cases, indicating higher jet mixing. The maximum mean radial velocity component for the flapping cases was found to be almost two times that of the nonflapping cases. The symmetric mode featured a CVP that was formed at the beginning of the nozzle exit opening and also at the maximum opening. These vortex pairs yielded a much lower jet spread when compared to the flapping jet.