Comparison of Two Stents in Modifying Cerebral Aneurysm Hemodynamics

Abstract

There is a general lack of quantitative understanding about how specific design features of endovascular stents (struts and mesh design, porosity) affect the hemodynamics in intracranial aneurysms. To shed light on this issue, we studied two commercial high-porosity stents (Tristar stent™ and Wallstent®) in aneurysm models of varying vessel curvature as well as in a patient-specific model using Computational Fluid Dynamics. We investigated how these stents modify hemodynamic parameters such as aneurysmal inflow rate, stasis, and wall shear stress, and how such changes are related to the specific designs. We found that the flow damping effect of stents and resulting aneurysmal stasis and wall shear stress are strongly influenced by stent porosity, strut design, and mesh hole shape. We also confirmed that the damping effect is significantly reduced at higher vessel curvatures, which indicates limited usefulness of high-porosity stents as a stand-alone treatment. Finally, we showed that the stasis-inducing performance of stents in 3D geometries can be predicted from the hydraulic resistance of their flat mesh screens. From this, we propose a methodology to cost-effectively compare different stent designs before running a full 3D simulation.

INTRODUCTION

Endoluminal stenting is a minimally invasive therapy that repairs an intracranial aneurysm by provoking thrombotic occlusions in the aneurysm.^12,18,28,47 A successful stenting treatment is expected to alter intra-aneurysmal hemodynamics enough to create thrombogenic conditions such as reduced flow activity and prolonged stasis, causing the aneurysm to thrombose and occlude. However, the results of the stent-alone treatment to induce aneurysmal occlusion have been inconsistent in many studies.^{10,23,28,35,46}

Stent performance in diminishing aneurysmal inflow is expected to be influenced by the stent design. Lieber et al.²⁹ investigated the effect of the stent strut size on the intra-aneurysmal flow in a sidewall aneurysm model using particle image velocimetry. They found that the stent reduces the aneurysmal vorticity and that the reduction of mean flow circulation varies depending on the strut diameter. Liou et al.³⁴ investigated the effect of stent shapes (helix stent vs. mesh stent) on intra-aneurysmal flow using particle tracking velocimetry measurements and flow visualization. They found that the stented aneurysmal flow varies markedly with the shape of the stent and that the helix stent is more favorable than the (rectangular hole) mesh for endovascular treatment. These experimental studies, however, only provided information on two-dimensional cross-sections of highly three-dimensional aneurysmal flow.

More quantitative studies examining stent effects on three-dimensional aneurysm hemodynamics have been carried out using Computational Fluid Dynamics (CFD). Aenis et al.¹ used a “square mesh” stent with a porosity of 85% and found significantly diminished flow in the stented aneurysm. Stuhne and Steinman⁴⁴ performed mesh convergence analysis using more realistic stent geometry (helical wires with a porosity of 82%) and reported high wall shear stress (WSS) on the stent wire surface and reduced WSS on the aneurysmal wall. Bando and Berger² utilized a stent composed of circular rings with a porosity of 60% and found that the average wall shear rate in the majority of the stented aneurysm was less than 100 s⁻¹. Cebral et al.⁸ simulated the flow passing complex endovascular devices such as coils and stents using a hybrid mesh (body conforming mesh and adaptive embedding mesh) technique. In addition to idealized aneurysm models, they also performed such simulations in patient-specific aneurysm models. These computational studies were limited to the mere demonstration of hypothetical stents in aneurysm flow alteration.

Overall, there is a lack of comparative or systematic study of realistic stents for cerebral aneurysm treatment in scientific literature. In our past work, Meng et al.³⁸ investigated the hemodynamic alterations caused by a realistic stent placed in an in vitro aneurysm model with varying curvature, while Kim et al.²² examined the effect of sequential placement of multiple clinically used stents in a patient’s basilar trunk aneurysm by performing CFD simulations. However, none of these studies attempted to clarify stent design issues, i.e., evaluating the changes in hemodynamics based on stent design parameters. The current work attempts to make a step in this direction.

It is expected that the porosity of a stent is the most important parameter that affects its ability to impede or modify the aneurysmal flow.^22,30 A lower porosity results in more flow blockage, but if the porosity is too low, the stent might inadvertently block perforating vessels or become too rigid for deployment.^4,41 Because of these constraints, the neurovascular stents currently in use are high-porosity stents and, in fact, current FDA-approved endovascular stents for cerebral applications have only slight variations, with porosities between 80% and 90%. On the other hand, these stents do differ widely in the pore shape, size, and the strut shape and size. In this paper, we will systematically evaluate the influence of these differences in design, focusing on two commercial high-porosity stents as examples to establish the methodology for studying any practical stent designs. The detailed comparative analysis of two stents and the focus on the stent design parameters distinguish this work from our earlier study by Meng et al.³⁸ We will further present a novel, cost-effective method to quantify the damping effect of stents on aneurysmal flow using the hydraulic resistance of the mesh. Findings from this study will shed light on how the stent mesh design can differentially influence the hemodynamics in aneurysms.

METHODS

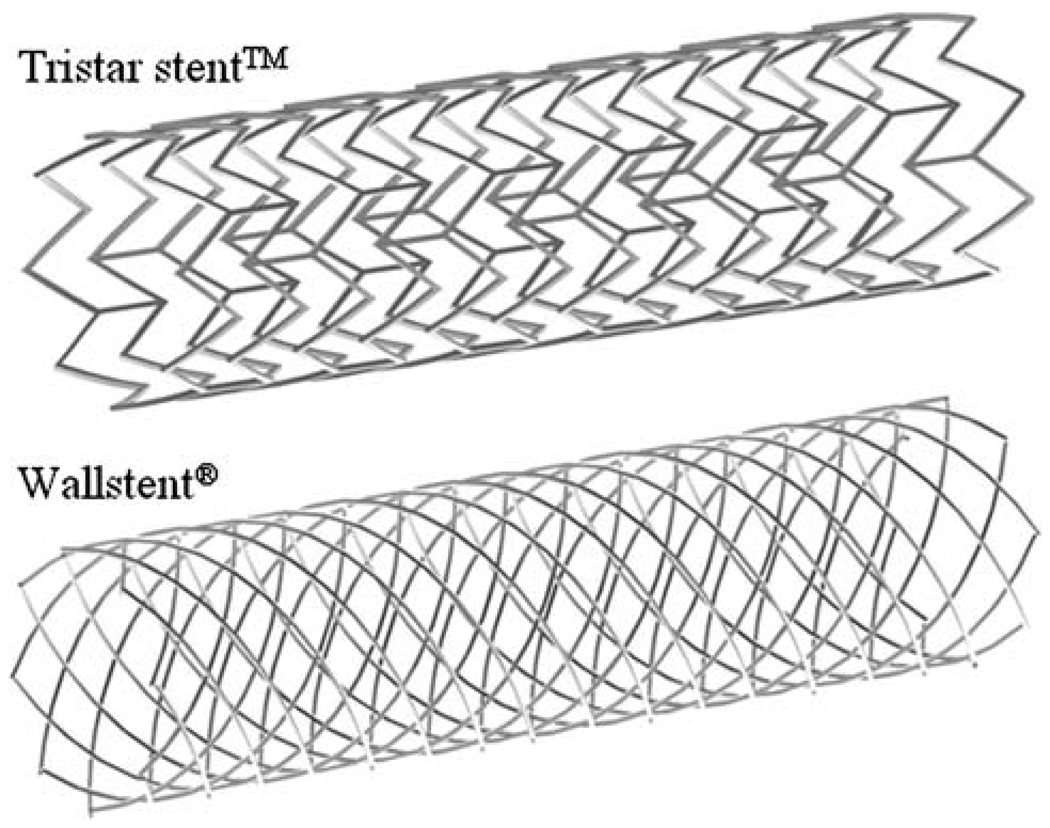
Two high-porosity commercial stent mesh designs are compared in this study. The Tristar stent™ (Guidant, St. Paul, MN) is manufactured by laser-cutting of a thin-wall tube resulting in rectangular strut cross-sections, while the Wallstent® (Boston Scientific/Target, San Leandro, CA) is manufactured by double-helical woven wires with round strut cross-sections. We used the commercial CAD software ProEngineer (PTC, Needham, MA) to reproduce the three-dimensional stents computationally (Fig. 1). The porosities of both stent models were similar, namely 84% for the Tristar stent™ and 82% for the Wallstent®. The stent porosity was calculated by the percent ratio of the void surface to the total surface of the stent cylinder. We validated the CAD stent geometry using micro-CT imaging of the actual stents, bent at specific curvatures in a silicon-based idealized aneurysm phantom. The micro-CT images were captured with 20 µm resolution and a 5 cm maximum field view, and after reconstruction were overlapped with the CAD stent geometry for qualitative comparison. This way, it was assured that the computational stents were bending in a realistic way.

FIGURE 1.

Geometry of the Tristar stent™ andthe Wallstent®.

Flat Screen Models

To evaluate the fundamental effects of stent design damping aneurysmal inflow, we first studied the characteristics of flow passing through infinitely large flat screens of various porosities and strut patterns. For both stent mesh patterns (Tristar stent™ and Wallstent ®), we initially reproduced their original meshes as flat screen models (Screen T and Screen W). From these two basic screens, we then created additional screen models of various hypothetical porosities (50–80%) by varying the distance of the struts while keeping strut angles and hydraulic strut diameters (0.1 mm for both stents) constant. Figure 2 shows the resulting mesh patterns of the Screen T and Screen W models.

FIGURE 2.

Mesh patterns of Screen T and Screen W for various porosities (50, 60, 70, and 80%).

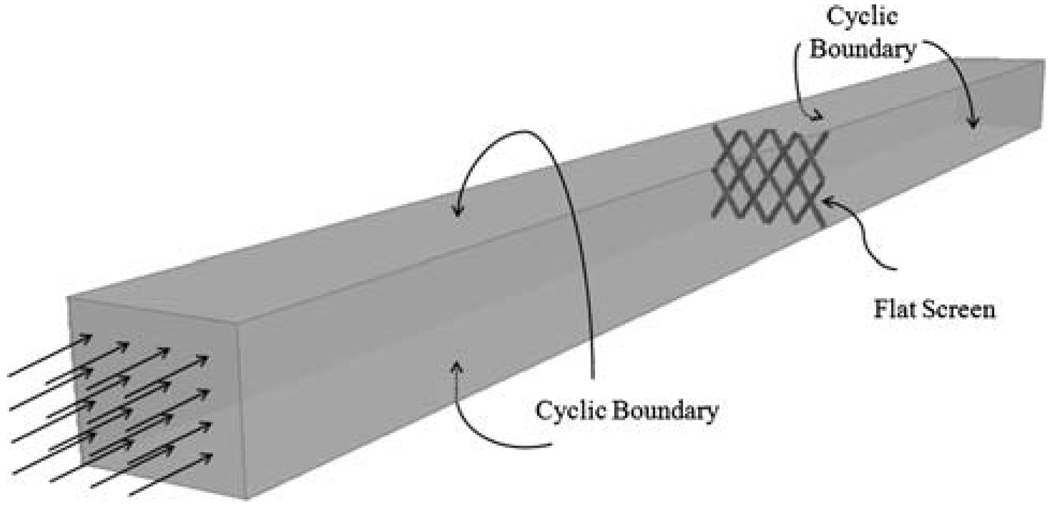
To compare the hydraulic resistances induced by such mesh patterns, each screen was placed in a computational model of an infinitely large wind tunnel with uniform steady flow entering far enough upstream that disturbances due to the screen became negligible at the inlet. The wind tunnel model was created by placing a unit section of the screen into a finite-sized computational domain with side-wall boundaries defined as “cyclic boundaries” to simulate an infinitely large extension of the domain in the screen plane, as shown in Fig. 3. The model was then meshed using the commercial software ANSYS ICEM-CFD (Ansys Inc., Berkeley, CA). Mesh-independent flow through the flat screen models was obtained by increasing the number of elements on the surface of the stent wires until the solution did not vary anymore with element size. The final models consisted of approximately 0.3 million tetrahedral volume elements. The grids were imported into the finite-volume-based CFD code STAR-CD® (CD-adapco, Melville, NY) to solve the Navier–Stokes equations with second-order accuracy under the assumption of incompressible, laminar flow and Newtonian fluid rheology. It should be noted that the laminar flow assumption in cerebral arteries is well justified because of the low Reynolds numbers^21,45 and that it is conventional to neglect the non-Newtonian effects in large arteries where the shear rates are much above 100 s⁻¹.^21,40 The viscosity and the density of blood in the models were 0.0035 kg/(m·s) and 1056 kg/m³, respectively. The outlet at the far end of the tunnel domain was set to be traction-free, which means that flow variables were extrapolated from inside values resulting in zero gradients at the outlet boundary. The outlet was located far enough behind the screen that disturbances due to the screen had dissipated and the flow was uniform at the outlet surface.

FIGURE 3.

Infinitely large wind tunnel model for flat screen resistance calculations.

To characterize the effect of each mesh pattern on the approaching flow, CFD solutions were obtained for a range of normal inflow velocities, i.e., for various Reynolds numbers (Re). Moreover, since the flow approaching a stent mesh in a realistic sidewall aneurysm is at an angle to the stent mesh, we also varied the flow incident angle to the flat screen models. The resistance characteristics of the flow passing through the plane meshes was formulated in terms of the hydraulic resistance coefficient R = ΔP/(ρV²/2) where ΔP is the pressure drop between locations far up- and downstream of the mesh screen (where velocity is uniform), ρ is the fluid density, and V is the velocity. The accuracy of hydraulic resistance coefficients was assessed by comparing the computed results with an empirical formula given by Idelchik,¹⁹

$$R\approx \frac{22}{{\text{Re}}_p}+1.3(1-f)+{\left(\frac{1}{f-1}\right)}^2, \text{when} {\text{Re}}_p<50$$

where Re_p is the pore-size-based (hydraulic diameter) Reynolds number and f is the porosity of the screen.

Idealized Aneurysm Models

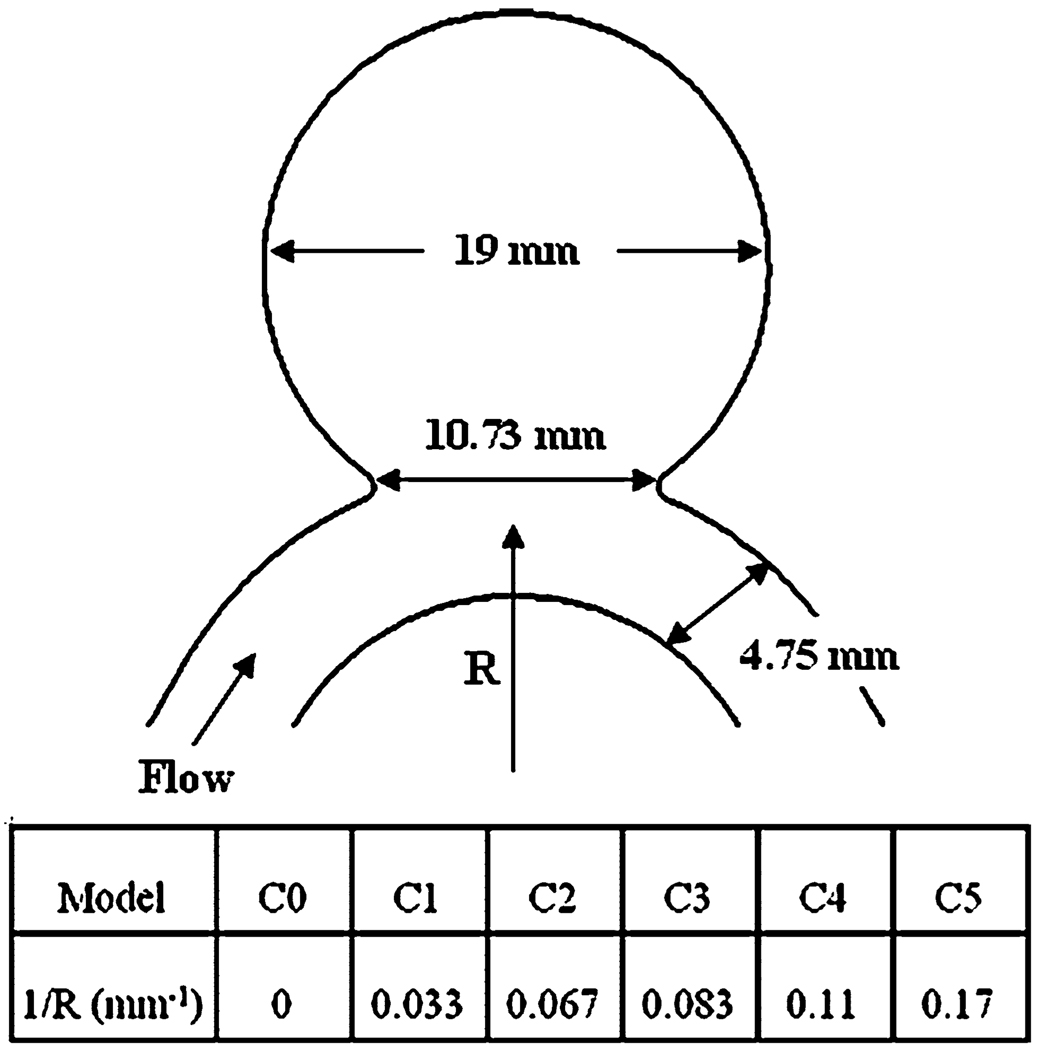
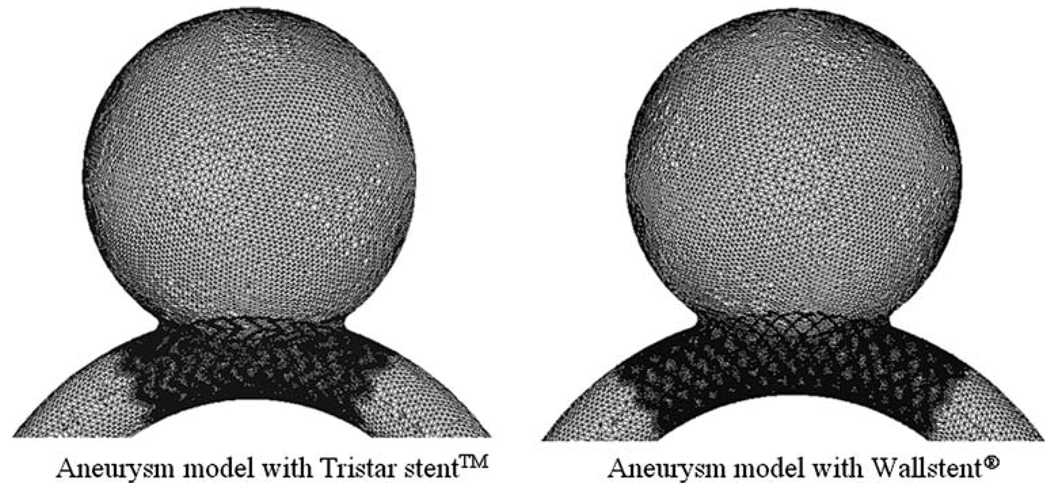
In the next step, we investigated the effect of stent design on various hemodynamic parameters by virtually placing stents in idealized sidewall aneurysm models. The idealized sidewall aneurysm models created in ProEngineer consisted of a spherical sac attached to the side of a parent vessel tube as shown in Fig. 4. The aneurysm was 19 mm in diameter and the artery was 4.75 mm in diameter. The width of the aneurysm neck was 10.7 mm and the aspect ratio (the maximum height of the dome divided by the width of the aneurysm orifice) was 1.68. In this parametric study, we focused on the parent vessel curvature as the varying parameter. Parent vessel curvatures of the idealized aneurysm models were varied from 0.0 mm⁻¹ for case C0 to 0.17 mm⁻¹ for case C5. To deploy the stent in the aneurysm models, the full geometries of the stents were virtually deformed to fit into the parent vessel lumen across the aneurysm neck. The separately reconstructed aneurysm and stent geometries were merged in a single model in ICEM-CFD and meshed. Based on the volume element size in the flat screen models, approximately 470,000 and 2.4 million tetrahedral volume elements were created for the non-stented and stented aneurysm models, respectively, most of which were near perfect tetrahedrons with a quality range of 0.12–0.99. The smallest elements in the model were located on the stent surface and had a size ratio of about 0.05 compared to the artery diameter. As an illustration, Fig. 5 shows the surface grid for the stented aneurysm models at curvature C2.

FIGURE 4.

Schematic diagram of the idealized aneurysm model.

FIGURE 5.

Surface meshes of the idealized aneurysm model with stents.

The no-slip wall of the aneurysm model was assumed to be rigid as in most CFD studies of cerebral aneurysms.^6,16,42,44 Since cerebral arteries are less distensible than large systemic arteries, and since the distensability of the wall only contributes to higher-order errors (the primary error source being the vessel geometry and boundary conditions^6,43), this rigid vessel wall assumption is acceptable for investigating flow in cerebral arteries.^39,40 The CFD simulations were performed with Star-CD under the same fluid property assumptions and traction-free outlet boundary condition as in the flat screen models.

An experimental validation of our CFD method was described in a previous publication,¹⁷ in which simulation results (including local distributions of the 3D velocity field and WSS) were compared with experimental flow measurements obtained by particle image velocimetry (PIV) in a phantom. It was found that as long as the geometry (boundary condition) was well matched, computation results were well validated by experiments.

Since pulsatile flow simulations with fully gridded stent struts would require several weeks of computational time for each aneurysm model, and since we have a series of such models to compare, we followed previous stent studies^{3,24–27,32,48} and used steady-state flow simulations in the current work to keep CPU times reasonable. We want to investigate the blockage effect of stenting on the flow, and in incompressible flow such an effect will manifest itself at each moment of the pulsatile heart cycle, especially at the highest vessel velocities. Therefore, a single steady-state solution at the peak systole is sufficient to investigate the effect of stenting, provided that the following two conditions are met: (1) The steady-state solution accurately represents the pulsatile solution at the momentary inflow velocity (quasi-steadiness of the flow). (2) The pulsation only causes a change in magnitude of flow parameters like velocity and pressure, but not a change in flow features (vortex patterns or spatial distributions).

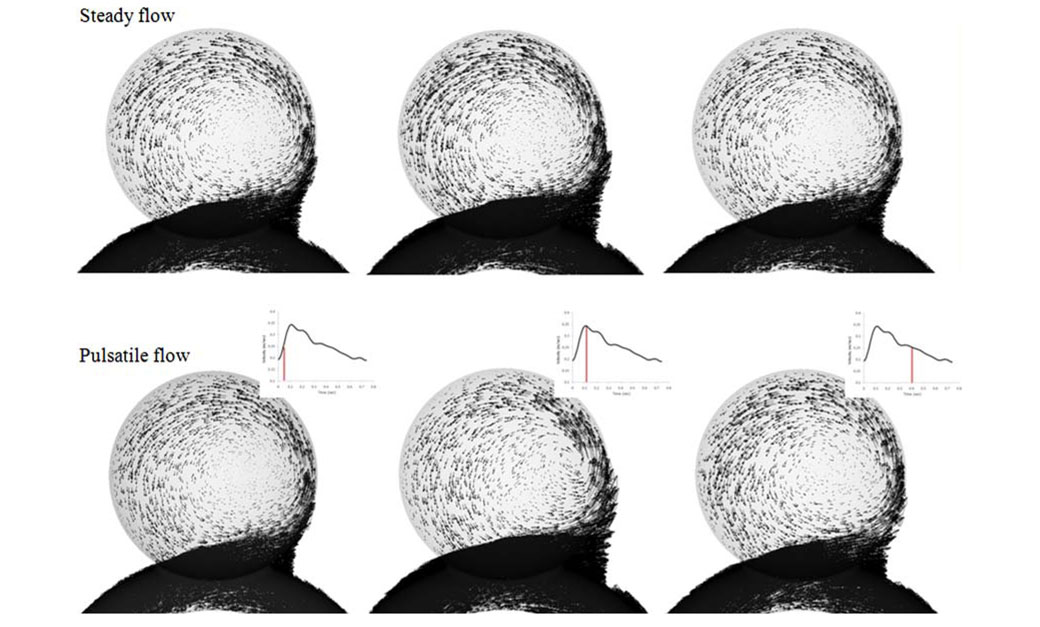
To check if these two conditions are met in the current study, we performed preliminary simulations for an unstented aneurysm model under both pulsatile and steady-state flow conditions. The inlet velocity wave of the pulsatile flow simulation (shown in Fig. 6) was obtained by phase-contrast MRI from a patient, resulting in a Womersley number in the inlet tube of 2.83 with an average Re of 363 and a peak systole Re of 490. Under these conditions, the uniform flow at the feeding vessel was fully developed at about twenty-five diameters downstream of the inlet, before reaching the aneurysm. Figure 7 shows the results of the preliminary simulations for three different time points in the pulsatile wave. The vectors in the figure are scaled to the same length range for each time point, so that flow features can be easily compared. From visual inspection, it is evident that the aneurysmal flow at mid-systole, peak systole, and diastole is indeed quasisteady, i.e., the steady-state solution is a good representation of the pulsatile snapshot. We quantified this at peak systole by calculating the aneurysmal inflow rate for the pulsatile and steady-state simulations, which differed by only 8.6%. From Fig. 7 it is also evident that flow features are virtually identical for all three time points investigated, which means that variations during the cycle are mostly changes in velocity magnitude, but not in vortex patterns or spatial distributions. Based on these preliminary results, we concluded that a steady-state simulation at peak systole is sufficient to characterize the aneurysmal flow, and in all subsequent 3D model runs we performed steady-state flow simulations at peak systole. The simulations required approximately 18 h of CPU runtime for each of the 3D models on a 2 GHz PC. We concede, however, that such steady-state simulations cannot capture the effect of stenting on time-dependent flow parameters like temporal WSS gradient or Oscillatory Shear Index (OSI). Such transient parameters will be investigated in a future paper.

FIGURE 6.

Inlet velocity wave used for preliminary pulsatile flow simulations.

FIGURE 7.

Comparison of pulsatile and steady-state simulations (at the same momentary inflow velocity) for three different time points in the cycle. Velocity vectors are scaled to the same length range for easy comparison of flow features.

From the simulated flow fields in the aneurysms, we calculated various hemodynamic quantities that potentially relate to biological responses such as thrombus formation and further aneurysm growth and rupture. The intra-aneurysmal flow activity was qualitatively examined by velocity contour plots in the center-plane. The flow stasis in the aneurysm was quantified by turnover time, which was calculated by dividing the aneurysm volume by the aneurysmal inflow rate. The aneurysmal inflow rate was obtained by integrating all entering flow over a cross-sectional plane slightly above the stent struts in the aneurysm. It was always compared with the outflow rate at the same plane to insure mass conservation.

The wall shear stress (WSS), a tangential drag force per unit area acting on the endothelial surface, is an important factor which influences arterial wall remodeling.^14,37,42,46 In this study, the WSS distribution was illustrated by surface contour plots, while the extent of flow impingement on the aneurysm wall was quantified by calculating the area of elevated aneurysmal WSS. Following the methodology of Hoi et al.¹⁶, this area, referred to as the impact zone, is defined as the area where the WSS is higher than the normal physiological arterial value of 20 dyne/cm².³⁶ It should be noted that, since we based the inlet conditions on a typical Reynolds number (not WSS value) in human cerebral arteries, the upstream/inlet WSS value was not equal to 20 dynes/cm² in our 3D models. For this reason, the area of impact zone (IZ) given in this paper should only be interpreted as a qualitative parameter to compare the performance of the stents relative to each other.

Patient-Specific Aneurysm Model

The modeling techniques used in this study were applied to an anatomically realistic aneurysm geometry, which was reconstructed from Computed Tomographic Angiography (CTA) images of a 52-year-old female patient’s right anterior communicating artery. The images were composed of 512 × 512 pixels at 16 bits. The resolution between planes was 0.4 mm. During the geometry reconstruction process, bone detail was subtracted, and the resulting vascular structure was segmented by the region-growing method. For stent insertion, we first determined the vessel centerline and deformed the stent according to this curve. The deformed stent geometry was then virtually deployed across the aneurysm neck with ProEngineer, and its location was adjusted for an optimal fit. Once the stent was placed in the right location, both aneurysm and stent geometries were merged for mesh generation. To achieve a smooth surface representation, different element sizes were created on the surfaces of the stent and the artery, respectively. Approximately 3.5 million tetrahedral volume elements were then generated in ICEM-CFD and the flow solution was obtained using Star-CD with the same fluid properties and boundary conditions as before (rigid no-slip wall, steady-state inlet condition at peak systole, Re = 490, traction-free outlet boundary). The hemodynamic changes caused by the stents were compared with non-stented results, and interpreted in light of the flat screen results obtained earlier.

RESULTS

Hydraulic Resistance Coefficient

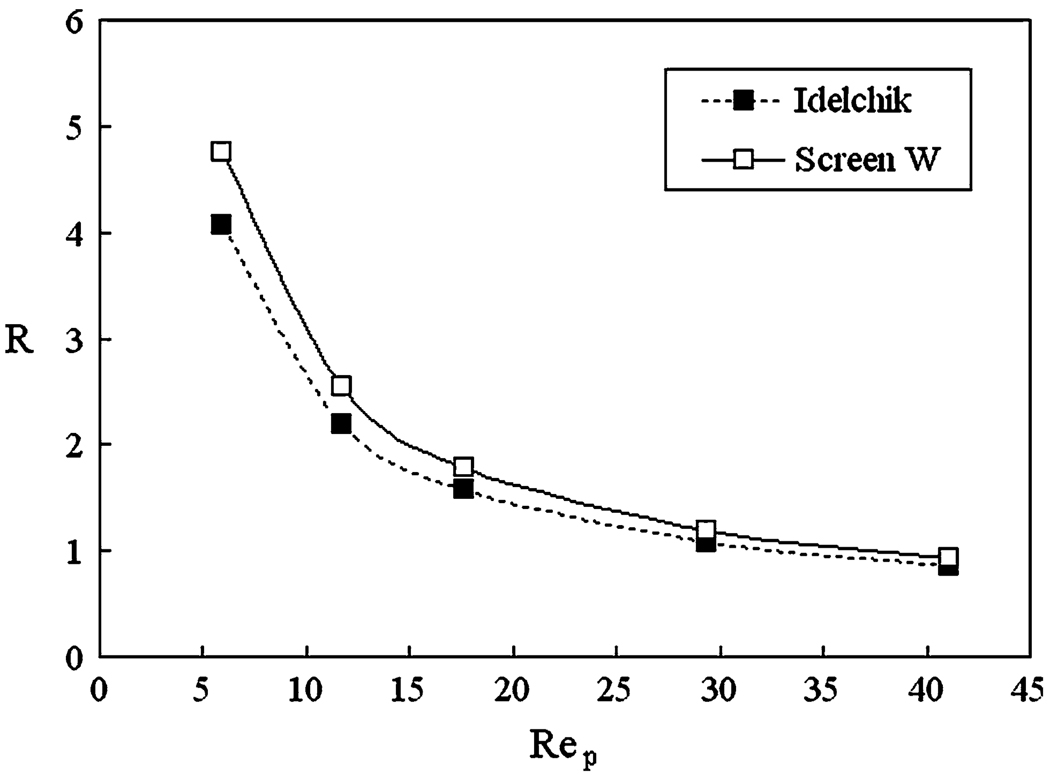
Shown in Fig. 8 is the CFD-calculated hydraulic resistance coefficient (R) for the 80% porous Screen W. It is seen that the hydraulic resistance generally decreases with increasing Re_p, which is the Reynolds number based on the pore size. In the same figure we also plot the resistance for an 80% porous woven mesh (with the same thread angles and diameters as Screen W), obtained empirically by Idelchik in experimental measurements. We note that the resistance from the CFD simulation is generally close to the empirical formula, which confirms the validity of the computational model. However, the CFD simulation gave somewhat higher resistances than the experiment, which can be attributed to the difference of the strut intersection points between the computational and experimental screen models: The screen in Idelchik’s experiments consisted of a woven wire mesh (separated struts at cross-over points) while the model of Screen W was latticed (fused struts at cross-over points).

FIGURE 8.

Hydraulic resistance as a function of Re_p (Reynolds number based on mesh pore size) for Screen W at 80% porosity, compared with Idelchik’s experimental data.

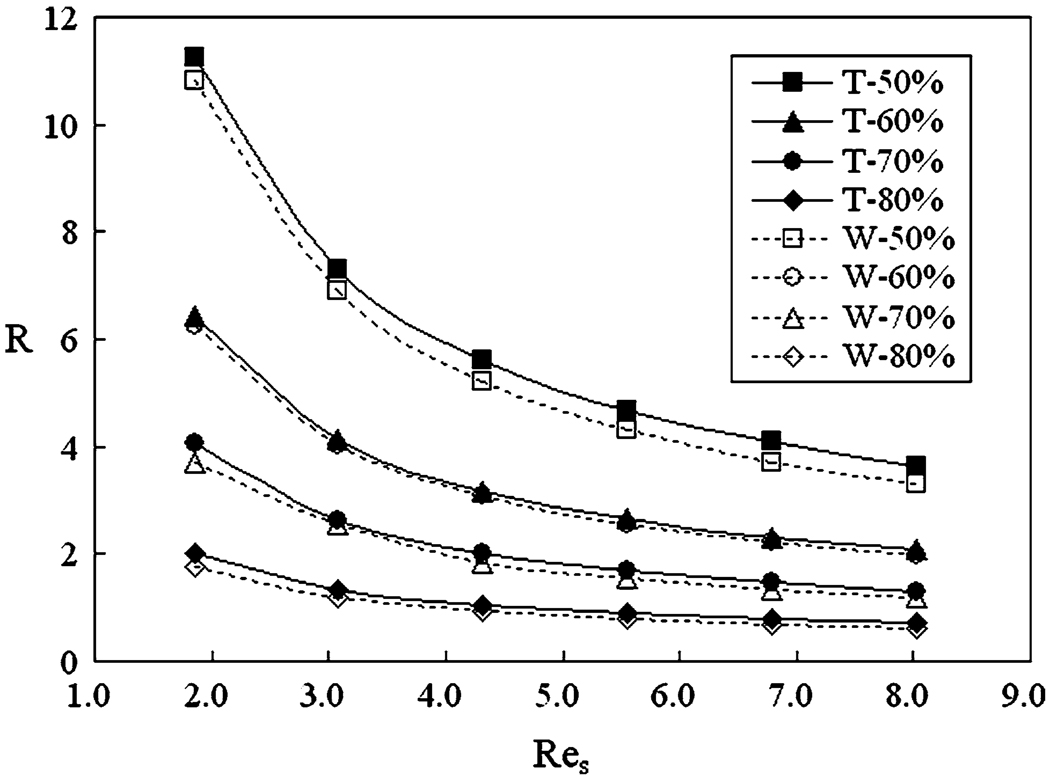
To obtain a general understanding about the influence of the porosity and stent design, we plot the hydraulic resistance coefficients (R) for Screens T and W at various hypothetical porosities in Fig. 9, where Re_s is the Reynolds number based on the strut wire hydrodynamic diameter (identical for both screens). For a given porosity, both screens have the same pore-size hydrodynamic diameter, so that a single Re_s corresponds to a single Re_p. The range of Re_s in Fig. 9 is typical for stent wires in aneurysmal flow. From Fig. 9, we see that the porosity has a major influence on the hydraulic resistance, which increases with decreasing porosity. We also observe that Screen T always has a greater resistance (3.2–16.0% higher, depending on porosity) than Screen W. It should be emphasized that the observed difference in resistance between the two stents are not due to computational errors, but rather due to the flow change induced by the different mesh designs. Since the CFD models in this study were grid-independent, and since the same base flow conditions and boundary conditions were used for all simulations, computational errors (round-off error and truncation error) were extremely small and undetectable.

FIGURE 9.

Hydraulic resistance as a function of Re_s (Reynolds number based on mesh strut size) for screens with various porosities (expressed as percentages).

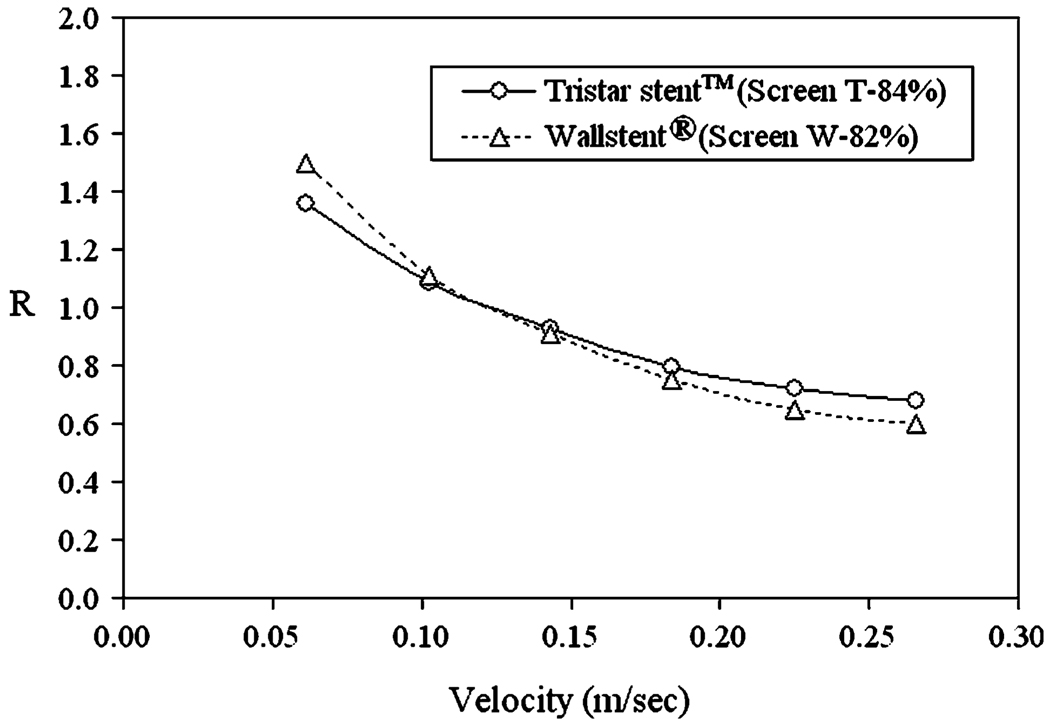
Figure 10 shows hydraulic resistance as a function of velocity for the screens based on the original stent designs, i.e. the original Tristar stent™ screen (84% porous Screen T) and the original Wallstent® screen (82% porous Screen W). We see that at high normal velocities, the Tristar stent™ has a greater resistance than the Wallstent®. At lower velocities, flow pattern influence is weaker and the difference in porosity becomes dominant, resulting in a higher resistance of the less porous Wallstent® screen.

FIGURE 10.

Resistance of the original screens based on the porosities of the original stents, for various inflow velocities.

Although the flat screen results can provide insight into flow damping by stents being approached by an inflow from a parent vessel, it should be kept in mind that when the stent is bent for insertion into a curved vessel, not only will the mesh pattern become distorted, but also the incident angle of the flow approaching the stent mesh to enter the aneurysm will vary along the curve, as illustrated in Fig. 11a. To investigate the effect of changing incident angle α, we plot in Fig. 11b the pressure drop across 80% porous screens for an inclined uniform flow approaching the screen as a function of incident angle α. The inflow velocity magnitude μ, corresponding to a pore-size based Reynolds number of 150, was kept constant. In the same graph we also plot the pressure drop ΔP for the normal velocity component μ cos α at each incident angle. From this figure, we make three observations as follows: (1) The pressure drop decreases when the incident angle changes from 0° to 90°, corresponding to a decreasing normal velocity component. (2) Consistent with the hydraulic resistance results (Fig. 9), the pressure drop generated by Screen T is higher than that of Screen W. (3) We also note that at each incident angle, the pressure drop for the inclined flow is nearly identical to that for the normal component only. This means that the pressure drop across a screen is only due to the perpendicular velocity component. The tangential component of the velocity vector has no appreciable contribution.

FIGURE 11.

(a) The definition of flow incident angle, α. (b) Pressure drop across 80% porous screens for a uniform flow of velocity μ and incident angle α. For comparison, the pressure drop for a perpendicular inflow velocity of μ cos α is also shown.

Stenting Hemodynamics in Idealized Aneurysms

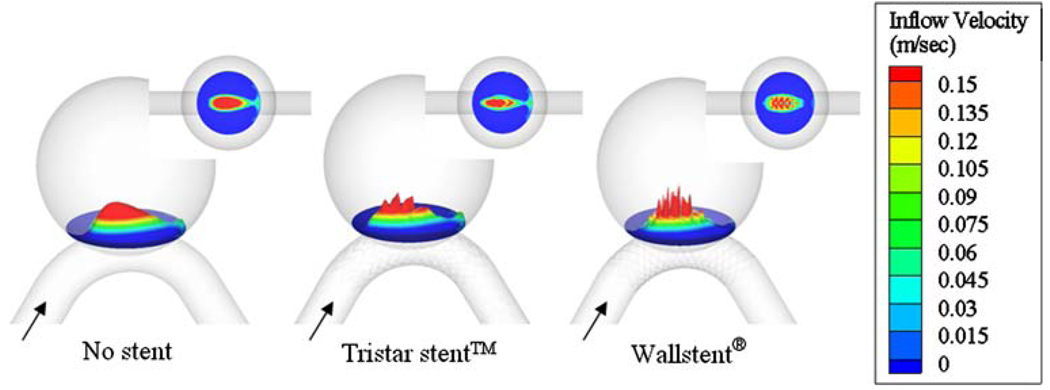
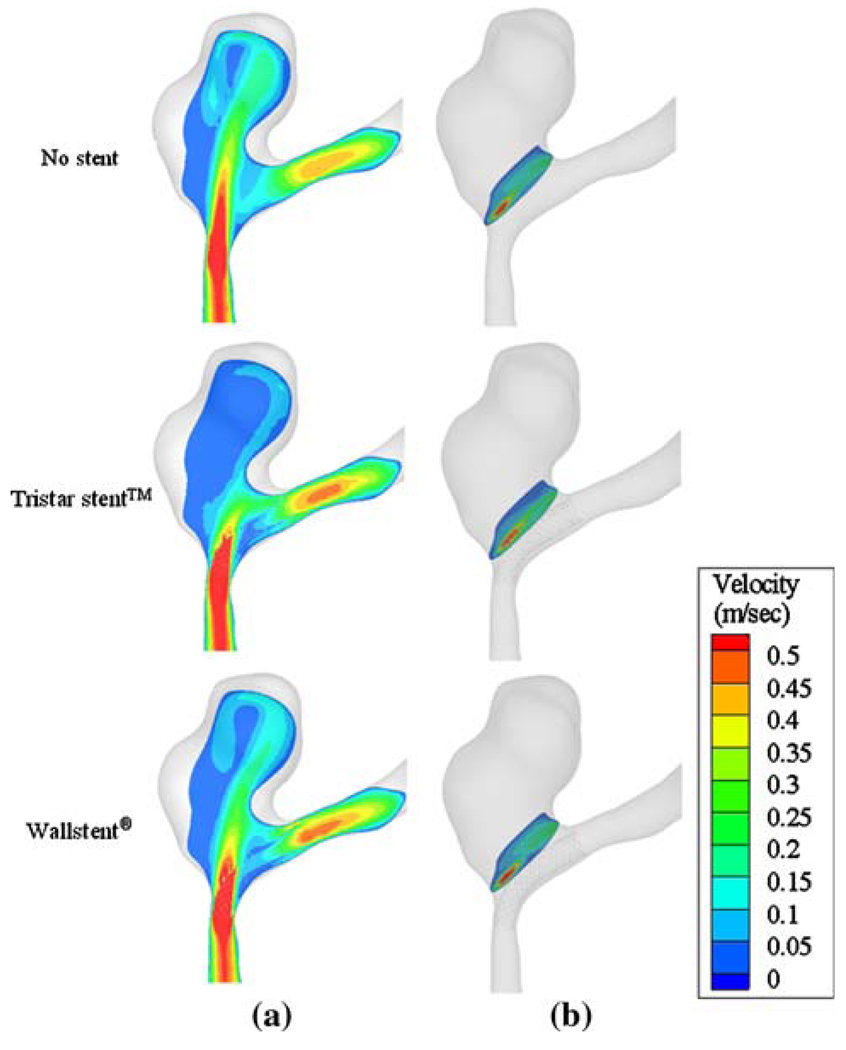
The full three-dimensional flow of stented idealized aneurysm models is first illustrated in a 2D plane in Fig. 12, which shows the velocity magnitude distribution in the center-plane of idealized aneurysm models of various parent vessel curvatures. Both Tristar stent™ and Wallstent® are seen to provide impedance to the inflow to various degrees, but the impedance is decreased at higher vessel curvatures.

FIGURE 12.

Velocity contours on the center plane (idealized aneurysm model).

The flow entering the aneurysm orifice actually interacts with the stent in a three-dimensional manner. To examine how different stent patterns alter the inflow, we show the 3D contour of the perpendicular velocity component of inflow at the orifice of the aneurysm with medium vessel curvature C4 in Fig. 13. It is seen that the Wallstent® breaks up the aneurysmal inflow jet into smaller segments than the Tristar stent™.

FIGURE 13.

Contour of the perpendicular velocity component of inflow at the aneurysm orifice for vessel curvature C4. The inflow is more dispersed by the Wallstent® than by the Tristar stent™.

The detailed flow pattern around the stent struts is given in Fig. 14 for the aneurysm model on a straight parent vessel (C0) with Wallstent®. Around individual struts, we can see local vortical flow in reverse direction to the global aneurysmal vortex, as observed in experiments by Lieber et al.²⁹ at the peak systole. Such localized reverse vortices do not contribute to the inflow for the aneurysm, and hence were excluded from our region of interest for turn-over time calculation by positioning the plane defining the aneurysm neck slightly above this strut-induced vortex region.

FIGURE 14.

Center-plane velocity vectors at the aneurysm neck for straight parent vessel (C0).

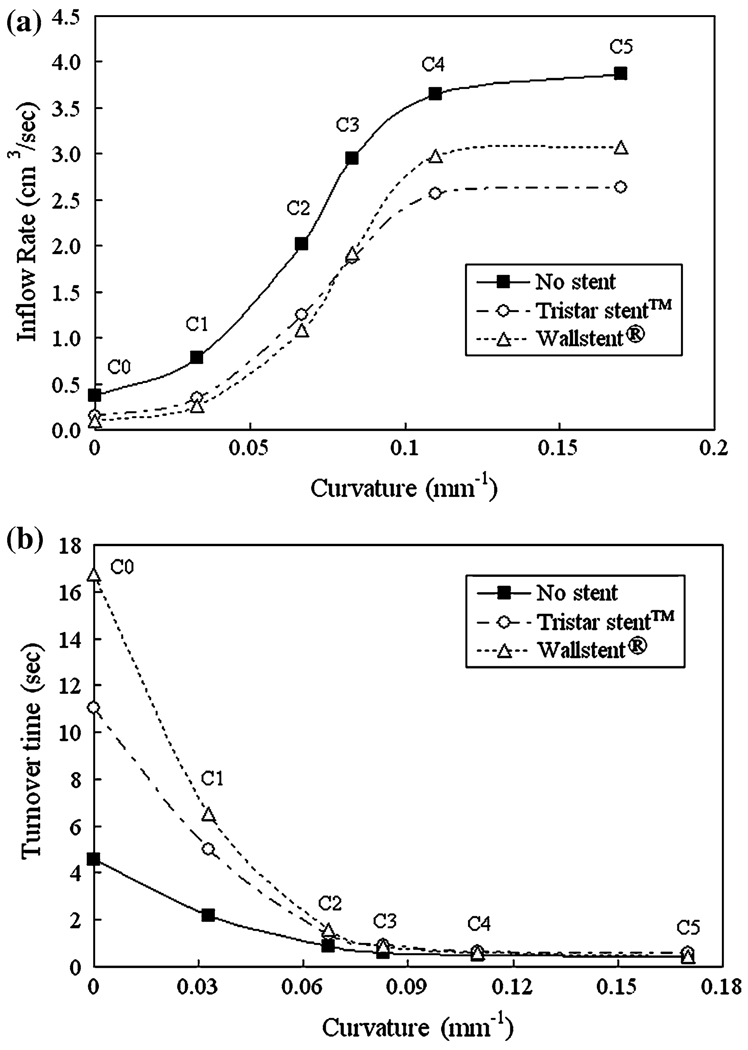
The aneurysmal inflow rate is shown in Fig. 15a as a function of curvature. With increasing vessel curvature, the blockage effect of the stents diminishes and the aneurysmal inflow rate increases, which is consistent with the results in Fig. 12. In Fig. 15a, we also see that the aneurysmal inflow is blocked more effectively by the Tristar stent™ in strongly curved vessels, while it is blocked more by the Wallstent® in weakly curved vessels. It is important to note, again, that computational errors (round-off error and truncation error) for the results in Fig. 15a are negligibly small.

FIGURE 15.

(a) Variation of the aneurysmal inflow rate for various parent vessel curvatures. (b) Variation of the aneurysmal turnover time for various parent vessel curvatures.

We quantified the flow stasis in the aneurysm by calculating turnover time. As seen in Fig. 15b, both stents cause large turnover times for smaller vessel curvatures, the Wallstent® being more effective due to its higher hydraulic resistance in this case (see Fig. 10). For larger curvatures the stented inflow rates are too high to achieve long turnover times, and both stents are essentially ineffective, with turnover times nearly as small as those for the unstented aneurysm.

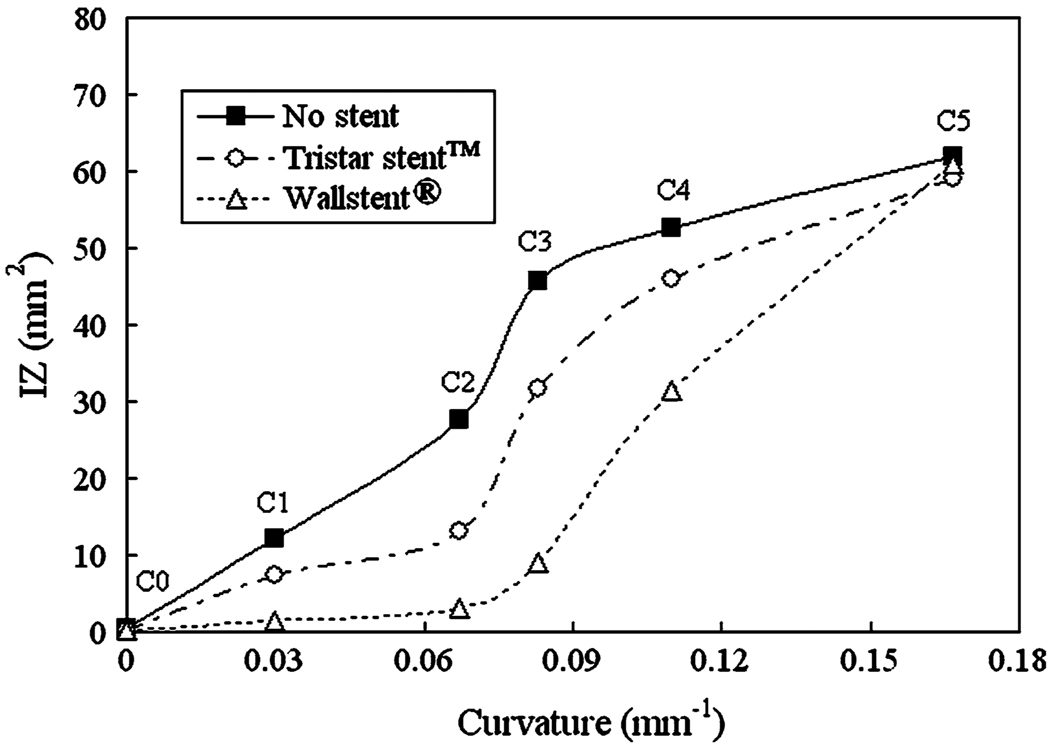
Figure 16 shows the WSS distribution for vessel curvatures C0, C2, and C5 in the non-stented and stented case, and Fig. 17 shows the impact zone size as a function of the vessel curvature. Generally, we note that increased vessel curvature results in a larger impact zone since the parent vessel flow has a more direct path toward the distal wall. Although both Tristar stent™ and Wallstent® reduce the impact zone, the reduction is greater for the Wallstent®, except at C5 where both stents have approximately the same impact zone.

FIGURE 16.

WSS contour variation at the distal wall of the aneurysm for different vessel curvatures.

FIGURE 17.

Variation of impact zone (IZ) with curvature of parent vessel.

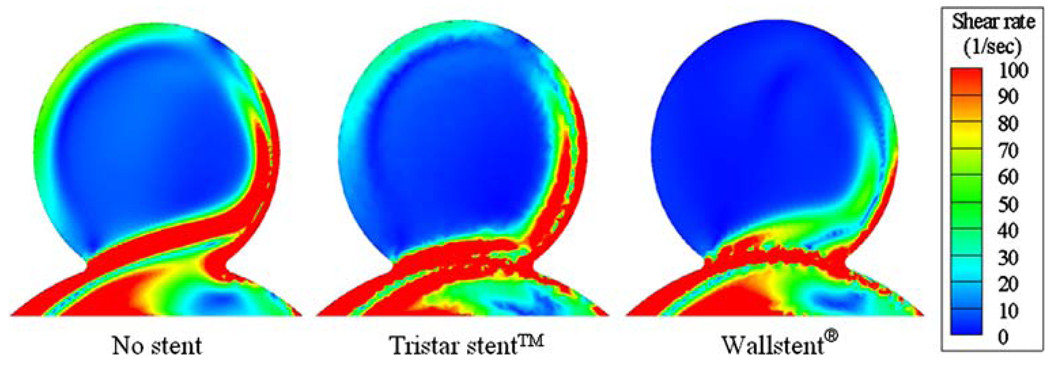
Shown in Fig. 18 are the principal shear rate distributions on the center-plane of the stented and non-stented idealized aneurysms for a medium vessel curvature (C2). High shear rate zones are visible near the aneurysm orifice and the distal wall. These zones become broader with increasing vessel curvature (not shown in the figure). Placing a stent across the aneurysm orifice generally reduces the shear rate and increases the regions of low shear rate (<100 s⁻¹), where thrombosis might take place.^13,15 For the considered vessel curvature (C2), the region of low shear rate is larger for the Wallstent® than for the Tristar stent™, which is consistent with the lower inflow rate for the Wallstent® at this curvature.

FIGURE 18.

Contour plot of the principal shear rate in an aneurysm on a curved vessel (C2).

Patient-Specific Aneurysm Model

Figure 19 shows the velocity field in a plane passing through the anatomical aneurysm without stent, with the Tristar stent™ and with the Wallstent®, respectively. The local vessel curvature near the distal neck of the anatomical geometry in this study is approximately 0.13 mm⁻¹ (which is higher than C4), while the curvature at the proximal side of the orifice is even larger. In the unstented case, the flow enters through the proximal side of the aneurysm neck resulting in a jet-like flow which directly impinges on the distal wall. After implanting the stent, the strong inflow is attenuated and the aneurysm hemodynamics changes significantly. The volumetric inflow rate through the aneurysm neck is reduced to 91.9% and 61.1% of the unstented value by the Wallstent® and the Tristar stent™, respectively. For the above calculation, the aneurysm was, again, defined as the volume above a plane on top of the stent just above the local vortices induced by the stent struts. Consistent with Fig. 15a at high curvature (and therefore with the flat screen results), the Tristar stent™ blocks more inflow than the Wallstent®. The volume-averaged intra-aneurysmal flow velocity magnitudes are 39.5%, 27.1%, and 20.7% of average vessel velocity for no stent, the Wallstent® and the, Tristar stent™, respectively.

FIGURE 19.

Effect of a virtual stent in an anatomical geometry. (a) Inflow velocity contours in the middle plane of the aneurysm. (b) Inflow velocity contours in the plane of the aneurysm neck.

DISCUSSION

Hydraulic Resistance

In fluids engineering applications, a wire mesh is frequently modeled as a porous medium which exerts a hydraulic resistance to the incoming flow. This type of modeling, although rather crude, provides a simple and cost-effective means to evaluate flow modification by meshes of different designs. Borrowing this approach, we evaluated the hydraulic resistance of stent meshes. By numerically simulating flat screens with mesh designs taken from the two real stents and artificially varying their porosity (Fig. 9), we have found that the porosity plays the most crucial role in determining the hydraulic resistance of the meshes. However, when porosity is fixed, stent performance is dependent on detailed mesh design, and Screen T consistently gives a higher hydraulic resistance than Screen W. The higher resistance of Screen T is mainly contributed by its quadratic struts, which produces larger drag due to flow separation, as opposed to the round struts of Screen W.

Effects of Porosity and Strut Design Dominate Different Flow Regimes

The Tristar stent™ (84% porosity) and the Wallstent® (82% porosity) are evaluated in terms of hydraulic resistance of their flat mesh screens in Fig. 10, where we notice a cross-over of the two corresponding resistance vs. velocity curves. At low normal flow velocities, the Wallstent® screen gives higher resistance, while at high normal flow velocities, the Tristar stent™ screen gives higher resistance. This difference can be accounted for by noticing the difference in stent design and identifying what features contribute to higher hydraulic resistance, as shown in Table 1. From this result, we infer that porosity has a stronger influence at lower flow velocities, while strut shape exerts a stronger influence at higher flow. This observation is supported by Fig. 9, where the resistance curves of various porosities are more separated from each other at the low end of Reynolds number (thus lower velocities), showing the dominant role of porosity at lower velocities. We further notice a cross-over of the inflow rate curves for the idealized aneurysm models in Fig. 15a consistent with that of the hydraulic resistance curves for the two corresponding stent screens (Fig. 10). At high vessel curvature, the Tristar stent™ impeded the flow more than the Wallstent®, and vice-versa for low vessel curvatures (Table 2). This is not a coincidence, since a higher curvature corresponds to a higher normal velocity with respect to the stent mesh (as can be inferred from the illustration in Fig. 11a). From the analogy of the two tables, we submit that the blockage effect of different stents on the aneurysmal inflow rate is directly reflected by the hydraulic resistance of simple flat screens with the same mesh designs as the stents. We also note that the flat screen results were consistent with the patient-specific geometry investigated in this study. Here, the vessel curvature was high (i.e., high normal velocity with respect to the stent mesh) and, as expected from the flat screen results, the Tristar stent™ reduced the inflow rate through the aneurysm neck more than the Wallstent®.

TABLE 1.

Relationship between screen performance and mesh feature.

	Low normal velocities	High normal velocities
Screen with higher hydraulic resistance	Wallstent®	Tristar stent™
Contributing feature	Lower porosity	Square struts (higher drag)

TABLE 2.

Relationship between screen performance and mesh feature.

	Low vessel curvatures	High vessel curvatures
Stent with lower aneurysmal inflow	Wallstent®	Tristar stent™
Contributing feature	Lower porosity	Square struts (higher drag)

Since in anatomic geometries, feeding vessels might be distorted and bent out of the plane, the following methodology should be followed when intending to evaluate two stents in real geometries based on the hydraulic resistance of their meshes. First, the correct curvature of the feeding vessel directly ahead of the aneurysm needs to be determined. It must be measured in the plane in which the neck is shown laterally (as a line) and in which the feeding vessel directly upstream has the lowest inclination angle with regard to the neck. The curvature thus measured correlates with the normal velocity with regard to the stent mesh at the neck, regardless of out-of-plane bending of vessels at a further upstream location. The normal velocity in turn determines the hydraulic mesh resistance and thus the performance of the stent in terms of aneurysmal inflow rate and turnover time. Therefore, the relative performance of two stents can be evaluated in real anatomies based on the vessel curvature, provided that the hydraulic resistance characteristics of the flat stent screens have been determined beforehand and are known.

Using the above methodology, stent performance with respect to aneurysmal inflow rate and turnover time can be evaluated in real anatomies by simply using the flat screen analysis, without performing a full 3D simulation. It is important to note that the flat screen models are much cheaper to simulate numerically. Thus, several stent designs can be cost-effectively compared to narrow down the selection of stents that might be ultimately used in an intervention. Once this pre-selection process is finished, full 3D simulations should be run with the remaining stent candidates to determine the details of the stented flow field (for example, the WSS distribution).

Effect of Vessel Curvature on Aneurysmal Inflow

Aneurysm geometry is an important factor in determining aneurysmal flow characteristics.⁶ In addition to the geometry of the aneurysm sac, the curvature of the parent vessel also has a critical influence on aneurysm hemodynamics,^16,38 and the effectiveness of a stent.^33,34,38

From our study, it is evident that the flow-impeding effects of stenting for both stent designs are compromised by increasing parent vessel curvature. Higher curvature is associated with diminished ability of the stents to reduce inflow rate (Fig. 15a), increase stasis (Fig. 15b), and reduce impact zone/maximal WSS (Fig. 16 and Fig 17). This has been attributed to the dominance of inertia-driven flow at high vessel curvatures. ³⁸

We have also seen (above a certain curvature) rapid increases in inflow rate (Fig. 15a) and impact zone (Fig. 17) regardless of stenting, and cease of reduction of impact zone by stenting at the highest curvature (C5). Such changes can be interpreted from flow dynamics. At low curvatures, the inflow jet impinges on and splits at the distal neck, with only little change in inflow rate as the curvature increases (Fig. 15a). At medium to high curvatures, there is a transition from a split inflow at distal neck to whole-jet inflow, so that the curves of inflow rate vs. vessel curvature (in both unstented and stented aneurysm models) take a rapid rise and then level off once the whole jet enters the aneurysm.

Stasis/Turnover Time

The goal of aneurysm treatment is to prevent rupture. It is expected that stenting can potentially accomplish “exclusion” of the aneurysm from the arterial circulatory system, preventing rupture by increasing stasis and thereby stimulating aneurysmal thrombosis.³³ Researchers^{5,13,15,28,47} have shown that increasing aneurysmal flow turnover time (which is an indicator of stasis^13,31) can induce thrombus formation in cerebral aneurysms. Figure 15b shows that at low parent vessel curvatures, both stents increase aneurysmal turnover time (and thus stasis), and the Wallstent® is twice as effective as the Tristar stent™ in this regard. However, at high curvatures (greater than about 0.07 mm⁻¹), the increase in turnover time by stenting is greatly diminished, and both stents are essentially ineffective, with turnover times similar to the unstented case. Thus, neither the Wallstent® nor the Tristar stent™ are adequate as a stand-alone treatment to induce thrombotic occlusion of aneurysms at these high parent vessel curvatures. At such curvatures, only a far less porous stent could possibly be able to achieve long turnover times, but such a stent was not part of our study.

It should be pointed out that an increased stasis does not guarantee whole-sac thrombosis. Partial thrombosis could do more harm to the aneurysm by increasing the risk of rupture through inflammatory or atherosclerotic responses or causing stroke in the parent vessels if the thrombus is washed out of the aneurysm. Additional studies investigating the relationship between aneurysmal blood flow and thrombosis/healing of aneurysm should be carried out to clarify this issue.

Wall Shear Stress

An important hemodynamic factor that influences vascular remodeling, aneurysm growth and aneurysm rupture is WSS. Highly elevated WSS may provoke the initiation and further growth of cerebral aneurysms by destructive vascular remodeling.^{6,7,14,33,34,37} In contrast to this high-WSS-mediated destructive remodeling pathway, an inflammatory and atherosclerotic pathway triggered by low WSS has also been implicated in aneurysms.^{9,11,14,16,36,49} Very low WSS (<4 dyne/cm²) within the aneurysm sac could lead to atherosclerotic inflammatory infiltration, causing deterioration of the aneurysm wall that could ultimately lead to rupture. From this standpoint, not all effects of stenting on the aneurysm wall are desirable; a reduction in maximum WSS and impact zone could be accompanied by an increase of the low WSS areas in the aneurysm sack. Much research in this area is needed in order to delineate the mechanisms for aneurysm wall deterioration and rupture, thereby clarifying the role of stenting. In this study, we focus on the areas of elevated WSS in the aneurysm because these regions are more readily altered by stent placement (affecting the wall-impinging jet) than low WSS areas.

We found that both stents reduce impact zone at all curvatures except C5, the highest vessel curvature studied (Fig. 17). Between the two stents we studied, the Wallstent® results in a greater reduction of impact zone size than the Tristar stent™, again for all vessel curvatures except for C5. The same trend was true for the maximum WSS value (not shown here). Why the Wallstent® produces a greater reduction of impact zone and maximum WSS for these curvatures may be explained by Fig. 13 which shows that the inflow jet is more dispersed by the Wallstent® than by the Tristar stent™ at the aneurysm orifice, possibly due to its double-helical woven wire pattern where holes are less elongated in the flow direction than for the Tristar counterpart. This produces less focused impingement on the distal wall, and smaller WSS values (and impact zone) for the Wallstent®. At the highest curvature (C5), the elongation of the holes is less relevant as the flow direction becomes more perpendicular to the stent mesh. This reduces the difference in jet dispersion between the Tristar stent™ and the Wallstent®, and causes a similar impact zone for both. It should be noted that the WSS results in Fig. 17 do not directly correlate with the aneurysmal inflow rate results in Fig. 15a, since WSS depends on the velocity near the wall, while the aneurysmal inflow is calculated from the volume of flow entering the aneurysm neck per second.

Stent Design Improvement

From our CFD results we suggest that for a given porosity a better stent design entails a double-helical woven mesh pattern like the Wallstent® and a rectangular strut cross-section like the Tristar stent™. The double-helical woven mesh provides stronger dispersion of the inflow to achieve more reduction of impact zone/maximal WSS, while the rectangular strut cross-section produces higher hydraulic resistance, which reduces inflow rate and increases turnover time, thus increasing potential for thrombotic occlusion at low vessel curvatures. If the vessel curvature is so large that the turnover time (stasis) and WSS are essentially insensitive to stenting, then a highly porous stent alone (as those investigated in this study) is not an adequate treatment, and coiling^20,23 or additional stents²² should be added as a complementary measure. Alternatively, a very low-porosity stent could achieve long turnover times without coiling at high vessel curvature, but care would have to be taken in the design of such a low-porosity stent to assure the necessary flexibility for successful delivery, and to retain an adequate patency of the peripheral vessels.

Results given in this paper are, strictly speaking, only valid for the flow condition tested, which is peak-systole flow. Although we would not expect major differences in the results, it is certainly desirable to perform whole pulsatile flow simulations and compare the stent performance at each instant in the cycle. Due to the extraordinary CPU time required and limited space of the current work, we would defer such a comprehensive pulsatile study to future research. Furthermore, there are large variations in anatomic aneurysm geometries as well as a great variety of stent designs on the market. More stents (and geometries) could be tested in order to gain more experience with the method presented here and to explore its full potential as well as to establish its limitations.

CONCLUSION

We evaluated two stent designs using the hydraulic resistance of their flat screen meshes and proposed that this methodology can be used to predict the damping effect of stents in real geometries without the need to run costly 3D simulations. We found that at low vessel curvatures, the Wallstent®—owing to its higher hydraulic resistance (which results from its lower porosity)—can damp the aneurysmal inflow and produce larger stasis in the aneurysm more effectively than the Tristar stent™. Additionally Wallstent® is more effective at breaking up the inflow jet and reducing the impact zone for all but the largest vessel curvatures. At high vessel curvatures, the Tristar stent™ has a higher hydraulic resistance owing to its square struts. However, the resulting increase in stasis over unstented aneurysms for both stents is marginal due to the strong inertia-driven flow at high curvatures.