Transient binding patches: a plausible concept for drug binding

Abstract

Dose–response curves for inhibitors (drugs) generally are analyzed by means of four-parameter fits, yielding IC₅₀, background, amplitude, and Hill coefficient. Hill coefficients ≠1 contradict 1:1 competition. If binding of substrates to proteins is a stepwise process where initial binding to initial locations (patches) leads to strong binding on defined sites, then drugs (non-endogenous inhibitors) may bind to those presumably larger patches and need not follow a 1:1 stoichiometry for specific inhibition. This concept was translated into three computable models and successfully fitted to 1,282 phosphatase dose–response curves. The models only required four parameters, namely, the equilibrium dissociation constant K_D(1) of the first inhibitor binding step, background, amplitude, and a compound interaction factor to quantify the interaction of inhibitors on those patches. Binding of one established inhibitor to the vaccinia virus VH1-related (VHR) phosphatase was directly measured with microcalorimetry, confirming multiple inhibitor binding with equilibrium constants obtained from corresponding inhibition curves.

Electronic supplementary material

The online version of this article (doi:10.1007/s12154-008-0011-5) contains supplementary material, which is available to authorized users.

Introduction

Drug development [1] typically involves screening of large compound libraries [2]. Those compounds which display significant inhibition in one or more significant cellular or biochemical assays are identified as hits; their potencies are given as IC₅₀ values. These are the concentrations of compounds required to inhibit an activity or other signal in a given assay by 50%. In most cases, IC₅₀ values are derived from four-parameter fits (4PL) [3, 4] of enzymatic activity measured as a function of inhibitor concentration I₀:

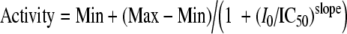This yields a symmetric sigmoid curve when activity is plotted versus the logarithm of I₀. The four parameters derived from a fit of that curve to experimental data are Min and Max for background and 100% activity, IC₅₀ for the inflection point, and slope as a measure for the maximal slope in the half logarithmic sigmoid representation. These four parameters are statistically not correlated and therefore ideal for data fitting. For I₀ = IC₅₀, Activity is equal to Min + (Max − Min)/2, as expected and indicated by the name.

The molecular interpretation of 4PL curves has always been a problem [5]. If the response is proportional to compound binding [6], Eq. 1 would correspond to simultaneous binding of n agonist molecules (A) to a receptor (R):

With the exception of n = 1, this scheme is not plausible [5] since it postulates the simultaneous binding of n molecules without intermediates such as A₁R, A₂R, A₃R…. When Eq. 1 is applied for the calculation of reaction scheme 2, the parameter slope corresponds to the number n of molecules A in scheme 2. This parameter is called Hill coefficient n_H. Fitting real data yields non-integer slopes, but non-integer n_H does not conform to scheme 2. Hill coefficients usually are regarded as an indication for the lower limit of the number of interacting small molecules on a receptor. For n_H > 1, the corresponding binding curve would be sigmoid and indicative of a “cooperative” binding mechanism.

To our best of knowledge, most experimental dose–response curves obtained from high throughput screens yield varying Hill coefficients, independent of the assay or the compound library. And conversely, variations in Hill coefficients are the underlying reason for four-parameter fits, since true 1:1 competition could be fitted with three parameters. Publication of absolute IC₅₀ measurements [7, 8] avoids commitment to a nonplausible molecular mechanism but does not explain the underlying binding process. This contribution now will address possible molecular mechanisms leading to Hill coefficients other than one. It will employ these mechanisms to fitting a consistent body of inhibition experiments. Although only enzymes, substrates and inhibitors have been measured, the underlying mechanisms are of general interest for pharmacology where one traditionally considers receptors, agonists, and inhibitors. Therefore, the general symbol A (“Agonist”) will also denote substrate, and the general symbol R (“Receptor”) will also stand for enzymes used in competition assays.

Materials and methods

All phosphatase assays were performed by means of automated systems consisting of Tecan EvoWare robots and Genios Pro MTP readers. The twofold dilution series were obtained from 10 μl of a buffered enzyme solution containing 200 μM of inhibitor. Of this, 5 μl was removed and mixed with 5 μl buffered enzyme solution resulting in a twofold dilution. This step was repeated nine times. Five microliters of the final dilution was removed, so that 11 wells consisted of 5 μl buffered enzyme with twofold inhibitor dilutions. The last two columns were left for controls. After a pre-incubation period of 10 min, the reaction was started by the addition of 5 μl p-nitrophenyl phosphate. This gave a reaction volume of 10 μl and inhibitor concentrations of 100, 50, 25… μM. All experiments were performed in quadruplicates with eight different inhibitors on one 384 microtiter plate. Reaction velocity was determined from the slope of the absorbance change of the substrate (p-nitrophenyl phosphate) at 405 nm and related to control without enzyme for 0% activity and without inhibitor for 100% activity. The substrate concentration was 50 mM in the case of CDC25A, 5 mM in the case of vaccinia virus VH1-related (VHR) phosphatase, and 1 mM for all other phosphatases; the reactions were observed at 405 nm in a spectrophotometer kept at 37 °C. These relatively high concentrations were chosen to be between two- and threefold above the respective K_m values [9]. For all enzymes, their concentration was adjusted to an initial absorbance change between 0.5 and 1 OD₄₀₅ during the measuring time of 30 min.

Epigallocatechin-3-monogallate (compound 172) was obtained from Microsource Discovery; bis(4-trifluoromethylsulfonamidophenyl)-1,4-diisopropylbenzene (compound 281, also named “Protein Tyrosine Phosphatase Inhibitor IV,” which was routinely run as standard in all plates) was obtained from Calbiochem CAT# 540211.

The phosphatases PTP1b, MPTPA, MPTPB, and SHP2 were donated from Prof. Schwalbe, Frankfurt. The phosphatases VHR and CDC25A were produced by Kirill Alexandrov, Max-Planck-Institute Dortmund. Vascular endothelial protein tyrosine phosphatase (VE-PTP) was a gift from Prof. Vestweber, Max-Planck-Institute Münster. All reaction mixtures contained 1 mM 1,4-dithio-d,l-threitol (DTE; added on the day of the experiment from 100 mM stock) and 0.0125% (v/v) of the detergent NP-40 (Calbiochem 492015). The buffers consisted of 50 mM Tris, 50 mM NaCl, 0.1 mM ethylenediamine tetraacetic acid (EDTA), pH 8.0 in the case of CDC25A; or 25 mM 4-(2-hydroxyethyl)piperazine-1-ethanesulfonic acid (HEPES), 50 mM NaCl, 2.5 mM EDTA, pH 7.2 in the case of PTP1b, SHP2, MPTPA, and MPTPB; 50 mM Tris, 50 mM NaCl, 0.1 mM EDTA, pH 8.0, 40 mM Tris, 30 mM MgCl₂, 20 mM KCl, pH 8.1, or 25 mM 3-(N-morpholino)propanesulfonic acid, 5 mM EDTA, pH 6.5 in the case of VHR.

Isothermal Titration Calorimetry The thermodynamic parameters of the VHR phosphatase interaction with compound 281 were determined by isothermal titration calorimetry (ITC; VP-ITC, MicroCal). Purified VHR phosphatase was diluted to a concentration of 25 μM in ITC buffer [50 mM HEPES, pH 7.4, 40 mM NaCl, 1 mM EDTA, 1 mM DTE, 0.025% NP-40, 1% dimethyl sulfoxide (DMSO)] and thermostated in the sample cell at 15 °C, 25 °C, and 37 °C, respectively. The inhibitor was solubilized with DMSO to a concentration of 100 mM and diluted with ITC buffer without DMSO in 1:100 ratio. This solution was injected stepwise by volumes of 8 μl from syringe into sample cell containing the phosphatase solution. Control measurements where performed by injecting inhibitor into buffer without phosphatase. The change in heating power was observed for 4 min until equilibrium was reached before the next injection was started. The control data were subtracted from the binding data to deplete data from injection effects. Further data evaluation was performed using the manufacturer’s analysis software, yielding equilibrium constants and ΔH° values.For model calculations, three non-linear equations follow from the summation of total enzyme, total substrate, and total inhibitor concentration and the complexes following from the respective reaction schemes. The complexes were calculated from the free concentrations and the respective equilibrium dissociation constants, e.g., 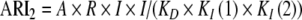. The resulting three equations only have three unknowns, namely, the free concentrations A, R, and I. All calculations were done with the program Matlab R2007b and its optimization toolbox (Mathworks.com). The routine fsolve was employed for solving the set of non-linear equations, and lsqcurvefit was used for multiparameter nonlinear fits. For inhibition experiments, only the ratio of substrate concentration to K_m value is relevant for the calculation of complexes. Since the experiments were performed at A₀/K_m of roughly a factor 2 [9], a total substrate concentration of 100 μM and a K_m value of 50 μM could be used for the calculation of all experiments alike. Likewise, for all experiments, the total enzyme concentration R₀ was set to 0.01 μM, i.e., one order of magnitude lower than the lowest inhibitor concentration. This ensured that both relations, A₀/R₀ and I₀/R₀, were 10,000 or less, and therefore, numerical rounding artifacts were avoided. Fitting routines require initial parameters, which were set to 10 μM for all equilibrium inhibition dissociation constants and 1 for the compound interaction factor CIF (Eq. 7) and the Hill coefficient. The lower limit of these parameters was set to 0.001, the lower limit for Min to 20%, and the lower limit for Max to 60%. The residual sum of squares (the value of the squared 2-norm of the residual) was returned from the function lsqcurvefit, which also was employed for 4PL fitting (Eq. 1). This sum of squares is a measure for the goodness of fit and should be as low as possible.Correlation coefficients of the resulting parameters were calculated with the program Benchware Data Miner, version 1.6 (Tripos L.P.). This program was also employed to calculate the molecular properties (AlogP98, polarizability, pLC50, volume, hydrogen bond donors, hydrogen bond acceptors, and rings) of the compounds.The quality of the fits could only be compared with relative residuals, since absolute residuals also reflect the noise of single experiments. For this, noisy experiments (Z′-factor <0.5) [10] or experiments with fits out of range (Min < −19%, Max < 61%) were discarded. Having sorted the residuals according to their 4PL Hill coefficient, their values were replaced by the average of next ±3 neighbors (non-biased noise-filter with n = 7). Then relative residuals were calculated in relation to the 4PL residuals. Eleven of the resulting 1,138 experiments had relative residuals of model C6 > 350 for n_H > 1. These experiments also were discarded, so that 1,127 experiments were finally selected for the calculations shown in Fig. 3. One note on errors: Errors which can be obtained from curve-fitting algorithms generally differ from experimental errors. This is the reason why errors for single fits are only given in the supplementary material and only for Fig. 5. Variations of repeated experiments [indicated by Quad(rant) 1 to 4 for the same enzyme and compound number] are more significant and are shown in table FitANCH6 of the supplementary material.

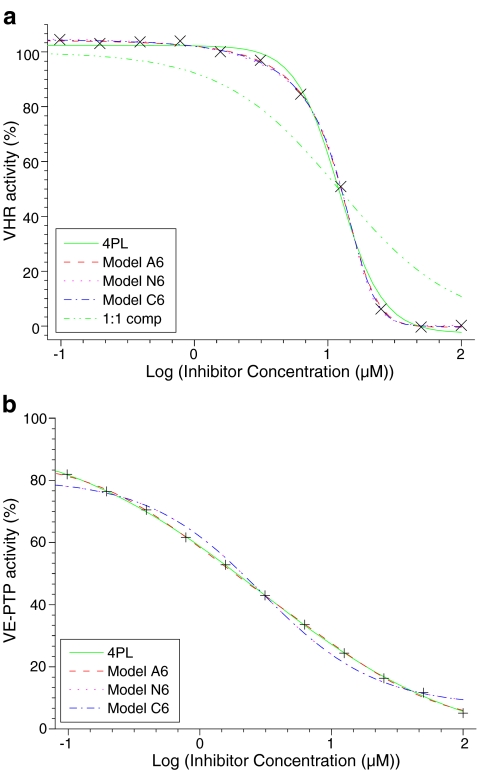
Fig. 3.

Dose–response curves. Phosphatase activity was measured at 37 °C in the presence of inhibitors as initial velocity and was related to independent 100% and 0% controls. The resulting percent activity is shown vs. inhibitor concentrations. The data were fitted to the four-parameter logistic model (4PL) and to the models A6, N6, and C6. a The phosphatase VHR was inhibited with compound 281. The Hill coefficient was 2.7. Other parameters obtained from fitting are shown in row 1,282 of table FitANCH6.xls of the supplementary material. The green (…-) dotted line does not result from data fitting but illustrates the case of simple competitive binding (C1), with IC50 taken from 4PL. Models A6, N6, and C6 could fit the data equally well for Hill coefficients ≥1. b The phosphatase VE-PTP was inhibited with compound 172. The Hill coefficient was 0.55. Other parameters obtained from fitting are shown in row 1,182 of table FitANCH6.xls of the supplementary material. Model A6 (not C6 or N6) could fit the data when the Hill coefficient was significantly smaller than 1

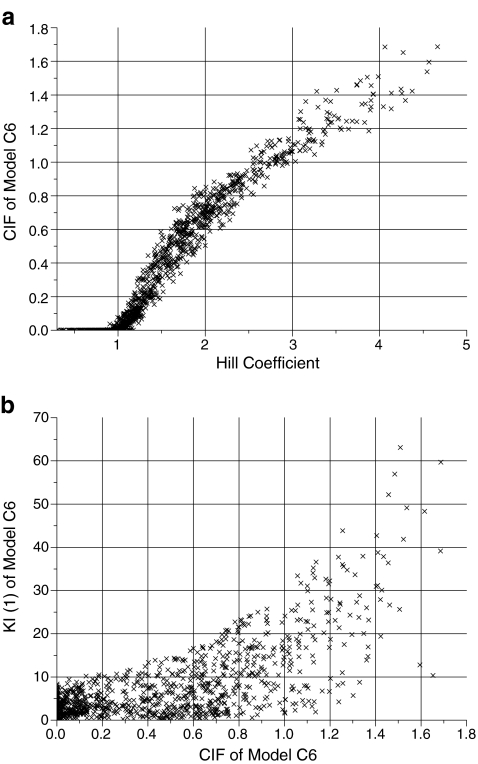
Fig. 5.

Dot plots of selected parameters derived from data fitting to model C6 and 4PL. a Factor CIF (Eq. 7) vs Hill coefficient; correlation coefficient 0.96. This plot may be used to derive the compound interaction factor CIF from a known Hill coefficient. b First K_I(1) vs. CIF (Eq. 7), correlation coefficient 0.71. This plot shows that both parameters are not independent

Results

Classical description of inhibition curves by means of four-parameter fits

The enzymatic activities of the phosphatases MPTPA, MPTPB, CDC25A, PTP1b, VHR, VE-PTP and SHP2 were analyzed after addition of 280 different selected compounds. For each of these compounds, dilution series (11 concentrations, differing by a factor 2 each) were performed in quadruplicates. That gave a body of 7,840 individual inhibition curves measured between 0.1 and 100 μM of inhibitor. Of these, 1,282 experiments showed IC₅₀ values between 0.5 and 25 μM and thus were ideal for the concentration range of the experiments.

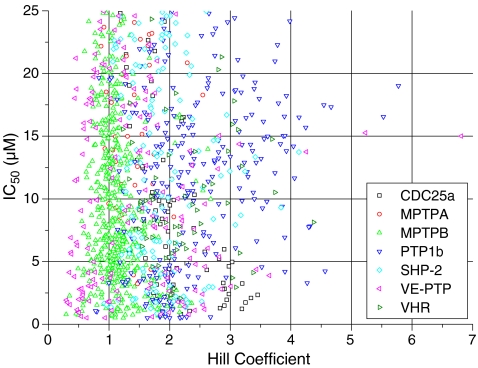
Figure 1 shows a dot plot of IC₅₀ values and Hill coefficients n_H obtained from 4PL (Eq. 1) fits of these experiments. Two features are noteworthy: (1) The distributions for IC₅₀ are not correlated to the distributions of n_H. (2) The distributions of Hill coefficients n_H depend on the enzyme investigated. For example, the phosphatase VE-PTP showed the largest variety in the slopes of inhibition curves with Hill coefficients ranging from 0.3 to 6.8 (factor 22). More than 57% of all Hill coefficients were either lower than 0.7 or larger than 1.3. Thus, a large proportion of the experiments of Fig. 1 clearly did not conform to 1:1 inhibition which should always give a Hill coefficient of one. A new molecular concept was required for the analysis of these experiments. This concept has to allow for variations of Hill coefficients and is shown below.

Fig. 1.

IC₅₀ versus the Hill coefficient derived from four-parameter fits (Eq. 1). Two hundred eighty substances were tested for their inhibition of seven phosphatases (CDC25a, MPTPA, MPTPB, PTP1b, SHP-2, VE-PTP, and VHR) in quadruplicates. Only experiments with IC₅₀ values between 0.5 and 25 μM are shown. Hill coefficients are a measure of the steepness (slope) of dose–response curves (Fig. 3). The IC₅₀ value is the inhibitor concentration, where 50% of activity is maintained

Model development

Reversible binding of compound A to a receptor R generally is described as:

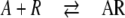The receptor concept [6] states that activity is proportional to the concentration of the occupied receptor AR. For enzymes, activity is measured as the rate of product formation, which itself is proportional to the concentration of the enzyme–substrate complex AR and thus need not be discussed separately. Structural studies had shown that similar molecules which bind to the same site may find different arrangements of microscopic interactions (H-bonds, etc.) on the protein [12, 13]. Molecular dynamics of proteins show that a binding site of a protein is by no means rigid. It is therefore plausible to assume that there are binding patches on a protein where compounds initially bind weakly to first interaction points or to hydrophobic surfaces from where they will find energetically more favored states involving multiple interactions. If they do not dissociate during this process, then 2-dimensional diffusion on those patches will act like a funnel or an antenna, increasing the binding cross section. For endogenous substrates, initial binding will lead to stable binding at the active site and thus could only be detected transiently. This need not be the case for inhibitors, in particular not for those which are no transition state analogues. Some may have a higher affinity toward the initial patches; some may show multiple binding there. Inhibition would be observed when binding patches involved in substrate binding are occupied with inhibitors.

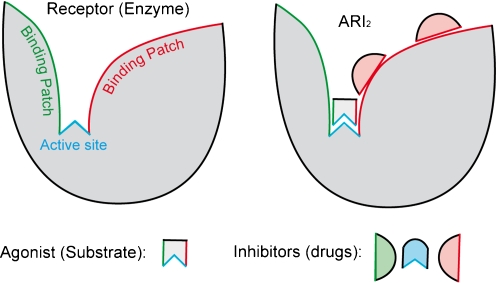
Figure 2 illustrates such a molecular model: An agonist may bind transiently to binding patches (green or red) on the receptor but will eventually bind to the active site (blue). Different inhibitors may interact with any of those patches and/or with the active site. In general, all inhibitors I would bind to those patches on a protein R just as they would bind to distinct sites:

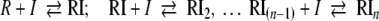Fig. 2.

Molecular model. A simplified molecular model of a receptor R is drawn with one active site (blue) and two different binding patches (green and red). The agonist A may initially bind with its corresponding ‘side’ (green or red) to one binding patch. Diffusion will lead to predominant binding to the active site (blue). Different inhibitors (drugs drawn as green, blue, or red) may be specific for the active site (blue) but also for a corresponding binding patch (green or red). Binding of agonist A and one type of inhibitors I to the receptor R is illustrated for one possible complex ARI₂. A classical model for 1:1 competition would be similar and simply would not consider binding patches as drug targets

Note that complexes RI, RI₂, RI₃… will generally not be unique, but will be dynamic ensembles where the compounds may be bound to different locations and with different numbers of microscopic interactions (hydrogen bonds, etc.). Such transient states are only relevant for the analysis of kinetic experiments. For the calculations of equilibrium dose–response curves, however, the only valid difference between complexes is the number of bound inhibitor molecules I. Unlike for the classical models with fixed sites, one need not consider a finite number of arrangements (or the statistical degeneracy, as it is sometimes called for equivalent sites) for such a dynamic distribution. Nota bene: For n equivalent fixed sites with intrinsic equilibrium dissociation constants K_Di, such a statistical degeneracy would correspond to

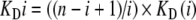where K_D(i) would denote the equilibrium dissociation constants of scheme 4. Equation 5 is not required for dynamic ensembles and is given here only for reference.

Reaction schemes 3 and 4 are sufficient to calculate competitive binding models. More general mechanisms should also consider binding of inhibitors to the protein–substrate complex AR:

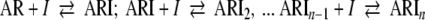These mixed complexes of substrate, receptor, and inhibitor again need not be static but will be ensembles only characterized by the number of bound small compounds. Ternary complexes ARI_i may be active when inhibitors do not interfere with the mechanism or may be inactive for uncompetitive inhibitors. Employing schemes 3–5 for curve fitting would require 2 × n equilibrium constants and n unknown activities of ternary complexes. Obviously, 3 × n parameters cannot be determined from 11 data points. Therefore, one has to make further assumptions in order to reduce the number of parameters. Plausible simplifications led to models C, N and A, as described below.

Model C (Competitive binding) Binding of inhibitor is calculated according to scheme 4. No mixed complexes of enzyme, substrate, and inhibitor are considered. The number of fitting parameters is reduced when the interactions of inhibitors are generalized, postulating that the affinity for the ith inhibitor depends on the affinity of the (i – 1)th inhibitor:

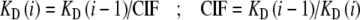With equilibrium dissociation constants K_D(i) for the respective steps. The compound interaction factor CIF quantifies the interaction of inhibitors: For CIF = 0, only one inhibitor molecule can bind, and the stoichiometry of inhibitor and substrate is 1:1. For 0 < CIF < 1, binding of one inhibitor decreases the affinity for the next. CIF > 1 indicates increase in affinity for subsequent binding steps. This would require induced conformational changes of the receptor or intermolecular interactions of bound inhibitors. Note that the parameter CIF is not the same as the Hill coefficient, and for CIF = 1, model C corresponds to classical “cooperative” binding, taking classical degeneracy (5) into account. Model C only has four parameters for curve fitting, namely K_D(1) and the compound interaction factor CIF, as well as Min and Max for adjusting experimental variations.

Model N (Non-competitive binding) Binding of inhibitor is calculated according to schemes 4 and 6. All ternary complexes ARI_i are inactive. The affinity of the inhibitor for free and substrate-bound enzyme is assumed to be identical. The generalized compound interaction 7 is assumed to hold for schemes 4 and 6. Model N also requires only four parameters, namely K_D(1) and CIF as well as Min and Max.

Model A (Active ARI) Binding of inhibitor is calculated according to schemes 4 and 6. The first ternary complex ARI is assumed to be fully active. All other complexes with bound inhibitor are assumed to be inactive. The first affinities of the inhibitor for free or substrate-bound enzyme are different. The simplification 7 holds for schemes 4 and 6. Model A requires five parameters, namely KIA1 = K_D(1) for scheme 4, and KIA2 = K_D(1) for scheme 5, CIF for the interactions of inhibitors 7, as well as Min and Max.Each of the schemes A, C, and N require a given maximal number of bound inhibitors to fit the data. In initial calculations, the number was varied between 2 and 8 but was set to 6 for most calculations shown below. This is in the order of the highest Hill coefficients present in our data and thus did not impose additional restrictions to curve fitting. This number by no means indicates that there are six well-defined inhibitor binding sites on these patches: Only the agonist (substrate) binding site must be a well-defined active site (Fig. 2).

Analyzing inhibition curves on the basis of molecular models

Figure 3a shows enzymatic activity of VHR versus the logarithm of inhibitor (compound 281) concentration1. For this figure, the standard phoshatase inhibitor bis(4-trifluoromethylsulfonamidophenyl)-1,4-diisopropylbenzene (CalBiochem, PTP Inhibitor IV) was selected. The data were fitted to models A6, N6, and C6. In that notation, A, N, and C denote the type of model, whereas the number denotes the maximal number of inhibitors which are considered. The solid green line (4PL) shows a four-parameter fit (Eq. 1) and has a symmetric sigmoid type of shape in this half-logarithmic representation. Note that the experimental data are not symmetrical. At low concentrations (between 0.1 and 1 μM), the experimental data show a slight decrease at a concentration range where the 4PL fit remains unchanged. At high concentrations (50 and 100 μM), the experimental data have reached their minimum of 0% activity, whereas the 4PL fit still shows a decrease. The (…-) dotted green line shows a theoretical curve for 1:1 competition and IC₅₀ from 4PL. Visual inspection of this experiment does not allow one to distinguish between the three models A6, N6, and C6.

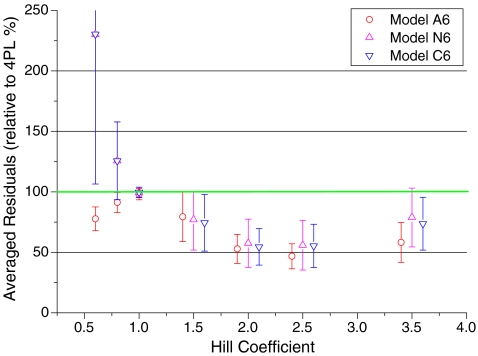
All fitting routines try to minimize the sum of squares, which is the sum of the squared difference from theoretical to experimental values. The residual sum of squares is a measure of the goodness of fit and can be used to compare models. When the residual sum of squares simply was averaged for all 1282 experiments, models A6, C6, and N6 gave smaller residuals (69%, 88%, and 87%, indicating better fits) than the residuals of the four-parameter fit (taken as 100%). Figure 4 shows relative residuals (relative to 4PL) as a function of the Hill coefficients. The experimental section describes the removal of outliers and smoothing, leading to the error bars of Fig. 4. Since all residuals were calculated as percent of 4PL residuals, four-parameter fits are represented by the solid line of 100% in Fig. 4. For n_H > 1, models A6, N6, and C6 differed only within their standard deviation, but all were significantly better than 4PL, the 100% value. For n_H = 1, the error bars are very small (<5%). This does not indicate that the experiments were less noisy in that range but that the calculated curves of all models were identical to single-site competition. For these curves, the parameter CIF fitted to the lower limit (0.001) of the fitting routine and thus numerically ruled out multiple binding in the models A6, N6, and C6. For Hill coefficients n_H < 1, models C6 and N6 were not adequate to fit the data.

Fig. 4.

Quality of the fits. Residual sums of squares (%) calculated for models A6, N6, and C6 related to 4PL (green line, 100%) were plotted against the Hill coefficient n_H. Averaged residuals were related to averaged residuals of four-parameter fits for 1,127 selected experiments as described in “Materials and methods.” Adjacent averaged ranges are represented by averages with Hill coefficients of the center of the averaged range. The error bars indicate standard deviations for the values of these ranges. For Hill coefficients larger than one, models A6, N6, and C6 fitted the data equally well within their error range and were better than the corresponding four-parameter fits (green line). For n_H = 1, all dose–response curves were identical, independent of the model. For n_H < 1, the theoretical curves N6 and C6 did not fit the data, and model A6 gave a better fit than the reference 4PL

An experiment with n_H < 1 is illustrated in Fig. 3b, fitting the inhibition of VE-PTP activity with the inhibitor epigallocatechin-3-monogallate (compound 172). Models C6 and N6 gave identical bad fits, so that their curve patterns were superimposed and gave the impression of one sinusoidal-shaped line meandering around the data. Models C6 and N6 therefore are not applicable for n_H < 1. Note that the inhibitor concentration range was not sufficient to cover the full range from 100% to 0% activity for inhibitors with low Hill coefficients such as in Fig. 3b.

Some other models which were applied to fit the data also should be mentioned. When models C2, C4, C6, and C8 were fitted to experiments with n_H > 1, C2 could not fit experiments with n_H > 1.5. C6 showed the lowest residual sum of squares but only within the experimental error as compared to C4 and C8. The fitted value of CIF decreased with increasing numbers of inhibitors.

Multi-parameter fitting generally will give ambiguous results when the parameters are correlated, that is, if an increase of parameter 1 leads to the same effect as an increase of parameter 2. That correlation is quantified by means of correlation coefficients [11] which would be 1 for linear functions and 0 for independent parameters. For independent fits or independent observations, high correlation coefficients indicate a functional relation, whereas correlation factors of 0 indicate no correlation. The correlation coefficients for models A6, N6, C6, and 4PL are shown in Table 1. For example, the correlation coefficient of 0.06 for IC₅₀ and Hill coefficient indicates no significant correlation. This is reflected in the dot plot of Fig. 1, where indeed no correlation between these parameters is visible. The compound interaction factor CIF is correlated to the Hill coefficient for all models. This relation is shown in the dot plot of Fig. 5a for model C6. It can be used to extrapolate the compound interaction factor CIF from the Hill coefficient. If one would have identified distinct sites, that plot can be used in conjunction with Eq. 5 to calculate the average affinities for these sites. Note that for Hill coefficient <1, the parameter CIF was fitted to its lower limit of 0.001, indicating that the binding of one inhibitor molecule effectively blocks the binding of a second one. The compound interaction factors CIF and the equilibrium dissociation constants K_I(1) were correlated for all models. This is illustrated for model C6 in Fig. 5b. Parameters with a correlation coefficient of 0.67 are not orthogonal and thus not ideal for curve fitting.

Table 1.

Correlation coefficients for selected parameters obtained from non-linear fitting of 1,282 experiments (shown in FitANCH6 of the supplementary material)

	KIA1-A6	KIA2-A6	CIF-A6	KI1-N6	CIF-N6	KI1-C6	CIF-C6	IC50	nH
KIA1-A6	1	0.28	0.45	0.68	0.46	0.73	0.49	0.25	0.53
KIA2-A6		1	0.61	0.67	0.57	0.65	0.59	0.46	0.51
CIF-A6			1	0.67	0.97	0.69	0.98	0.11	0.96
KI1-N6				1	0.67	0.99	0.69	0.66	0.67
CIF-N6					1	0.68	0.99	0.13	0.95
KI1-C6						1	0.71	0.59	0.71
CIF-C6							1	0.13	0.96
IC50								1	0.06
nH									1

Multiple binding of inhibitors might be nonspecific and might be related to general molecular properties like solubility, polarizability, or hydrogen bonds. However, when correlation coefficients were determined, none of the parameters AlogP98, polarizability, pLC50, volume, hydrogen bond (HB) donors, HB acceptors, or number of rings were correlated to the Hill coefficient n_H. Note that all experiments were done in the presence of 0.0125 of the non-denaturing detergent NP-40 in order to avoid hydrophobic unspecific interactions leading to promiscuous binding [14].

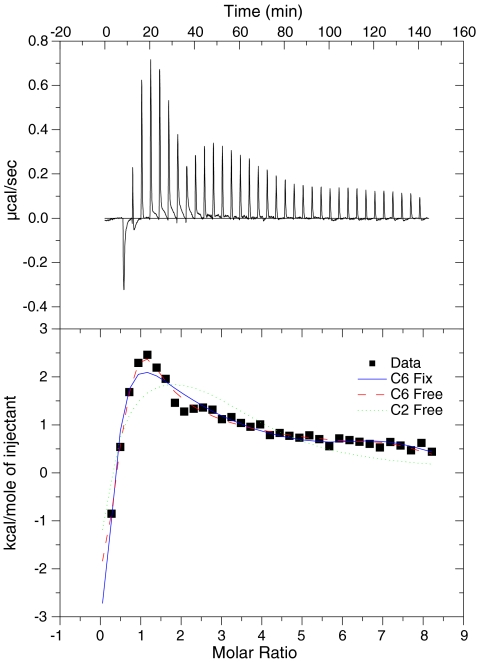
Models A6, N6, and C6 alike predict multiple sequential binding of inhibitor according to scheme 4. In order to verify this prediction, binding of the well-known “PTP Inhibitor IV” from CalBiohem (compound 281) to the phosphatase VHR was measured directly by means of isothermal titration calorimetry at 15 °C, 25 °C, and at 37 °C (Fig. 6). The buffer effect (dilution of the corresponding amount of DMSO into buffer with detergent) was subtracted but consisted of the same peak between the second and the eighth injections, which is visible in Fig. 6. The corresponding inhomogeneity in Fig. 6 therefore may be attributed to a dilution artifact. When the equilibrium constants from model C6 of the competition experiment in Fig. 3a were used to calculate the ITC experiment (blue solid line), the fit was reasonable, at least better than for a fit assuming two sites (green dotted line). This is remarkable, since both experiments were done with slightly different buffer and different charges of VHR and compound 281. If all 12 parameters (six affinity constants and six entropies) were allowed to vary, the fit was better (red dashed line), although 12 parameters cannot be deduced from that experiment. The obtained parameters are only listed for reference in the supplementary material.

Fig. 6.

Isothermal titration calorimetry of 25 μM of the phosphatase VHR with compound 281. A solution of 1 mM compound 281 was titrated in 8 μl steps into a solution of VHR phosphatase at 37 °C. The heat absorbed/released upon their interaction (ΔH) was monitored over time (top panel). The heats from each injection is integrated and plotted against the ratio of compound 281 and VHR phosphatase in the cell (closed squares). These data were fitted with model C6 and equilibrium constants from inhibition experiments (blue solid line), C6 without restriction (red dashed line), and model C2 (green dotted line). The parameters obtained from the fitting procedures were compiled in a table shown in the supplementary material. The binding mechanism deduced indirectly from Fig. 3a thus could be confirmed with direct measurements

Discussion

The concept of inhibitor binding patches with transient non-defined sites was translated into three molecular models for reversible inhibitor binding. These models were successfully employed to fit a consistent body of dose–response curves. For Hill coefficients larger than one, a model of competitive inhibition (C6) and a model of non-competitive inhibition (N6) both gave better fits than the standard four-parameter fit employing the same number of four parameters for the fitting process. Dose–response curves obviously are not adequate for the distinction between competitive and non-competitive inhibition. Interactions of bound drugs with each other or with the binding patch may lead to facilitated binding or steric hindrance for inhibitors and/or to induced conformational changes of the target macromolecule. All this is quantified as variations in the compound interaction factors CIF. Similar reasoning extends to Hill coefficients smaller than one, where different interactions may allow or prohibit an active ternary complex ARI. For larger Hill coefficients, all models predict multiple inhibitor binding with increasing inhibitor concentration. This prediction was confirmed with microcalorimetry. The concept of binding patches is not based on mechanistic models of the phosphatases studied here and therefore should be generally applicable.

Classical molecular mechanisms assume unique interactions between inhibitor and enzyme. Competitive inhibition in classical models would indicate that the inhibitor binds exactly to the substrate pocket and thus competes for that site [15]. This is plausible for 1:1 competition and, thus, for experiments with Hill coefficients n_H exactly equal to one. Any experiment with Hill coefficient significantly other than one violates 1:1 stoichiometry, no matter how small the deviation. For binding curves with Hill coefficients larger than one, allosteric models, such as for oxygen binding to hemoglobin [16], had been applied. But how could one account for variation in n_H? Could one seriously imagine different numbers of subunits interacting with different inhibitors acting on the same enzyme? And even when one tries to calculate formal schemes involving one, two, three, four, five… sites as indicated from the distribution of Hill coefficients in Fig. 1: How could it be that one inhibitor fits to a specific mechanism involving the high number of three (or four?) specific binding sites, whereas a similar compound inhibits with a different stoichiometry? Answering those questions for classical mechanisms may not be impossible for single, well-defined cases [17] but would be extremely difficult in the general case or even for the limited set of experiments described here.

The concept of transient non-defined sites contradicts all schemes where sites are an intrinsic feature of the molecular mechanism [18–20]. It is, however, very similar to multiple binding of calcium antagonists to the L-type calcium channel [21]: Dihydropyridines are potent established and specific drugs for the treatment of heart failure, yet at higher concentrations they will act as local anesthetics and generally block cationic ion channels. Conversely, local anesthetics interact with dihydropyridine binding [22]. These mechanisms are difficult to reconcile with classical inhibition and led to the postulation of allosteric effects [23, 24]. The underlying mechanism simply may be multiple binding to transient overlapping patches, just as postulated here for models N. Note that such a mechanism can be confirmed by means of independent kinetic displacement experiments when “accelerated” [25] or “facilitated” [26] dissociation would be expected.

Bioactive compounds seem to conform to certain structural requirements which are common to natural products and can be applied to “biology-oriented synthesis” [7]. It is feasible that those bioactive compounds have some general affinity towards proteins or patches on proteins. In view of this, bioactive inhibitors may generally bind to substrate binding patches of the protein from where they would inhibit the active site specifically. Any general binding step would increase the probability for side effects. Following this reasoning, inhibitors with high Hill coefficients should be scrutinized for pharmacological side effects.

In conclusion, the reaction scheme 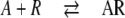is a simplification, when the binding of compounds to macromolecules is concerned. The simplification is justified for natural substrates, when a stepwise association process leads to a final bound state. This need not be the case for non-endogenous compounds (drugs) which may well interact with parts of the protein (patches) which are involved in the association process of substrates, but which need not be the active site. Whenever inhibition curves are fitted with Hill coefficients larger than one, classical 1:1 competition for an active site can be ruled out, and multiple drug (inhibitor) binding must be considered. Drug design based on docking programs to the active site of a rigid protein structure should only yield inhibitors (blue in Fig. 2) which bind with Hill coefficients of 1. Flexible docking programs such as MODOR [27] consider transient molecular interactions of ligands with macromolecules and thus allow the identification of binding patches and corresponding inhibitors. Discrimination of molecular inhibition mechanisms can be supported by Hill coefficients, which therefore should be published along with the IC₅₀ values for high throughput screens.