What do diffusion measurements tell us about membrane compartmentalisation? Emergence of the role of interprotein interactions

Abstract

The techniques of diffusion analysis based on optical microscopy approaches have revealed a great diversity of the dynamic organisation of cell membranes. For a long period, two frameworks have dominated the way of representing the membrane structure: the membrane skeleton fences and the lipid raft models. Progresses in the methods of data analysis have shed light on the features and consequently the possible origin of membrane domains: Inter-protein interactions play a role in confinement. Innovative developments pushing forward the spatiotemporal resolution limits are currently emerging, which are likely to provide in the future a detailed understanding of the intimate functional dynamic organisation of the cell membrane.

Overview

The main function of membranes is to generate close compartments: The cell itself (by the plasma membrane) and also the nucleus (by nuclear envelope), the Golgi apparatus, the endoplasmic reticulum, various organelles or the vesicles which are involved in transport processes. Membranes delimit these structures and allow them to have a different composition from the rest of the cell by restricting the diffusion of ions and macromolecules. The specific transport of molecules or information across the membrane is devoted to membrane proteins. Membranes are essentially composed of lipid and proteins, each of them representing about 50% in weight. Lipids are amphiphilic molecules that spontaneously form a bilayer in water. Among the variety of lipids, cholesterol has a specific place since it is particularly abundant in eukaryotic cells. Cholesterol can modify the lipid molecular order [1] and is presumed to participate in lipid micro-phase separation (rafts) [2–5].

Since the structure of biological membranes is maintained by non-covalent bonds, they have first been considered as a fluid lipid bilayer in which embedded proteins are free to diffuse [6]. After the advent of this fluid mosaic model postulating a random distribution of membrane molecules [6], experimental evidence showed that the proteins and lipids are distributed heterogeneously in the membrane. For example, incomplete recoveries were systematically observed in fluorescence recovery after photobleaching (FRAP; see “Appendix 1”) experiments. The first indication of the presence of micrometer-sized domains was obtained by FRAP. Yechiel and Edidin found a decrease of the mobile fraction with increasing radius of the bleaching spot ([7, 8] and see “Appendix 1”).

The huge diversity of lipids and proteins implies that a very large number of combinatorial interactions can occur between them [9]. Since all lipids and proteins do not present the same hydrophobic thicknesses, it has been demonstrated that some interactions will be favoured to form domains where their size can vary from a few nanometres to several microns. The formation of these domains can be induced either by lipid–lipid interactions [4, 10, 11], lipid–protein interactions [12, 13] or protein–protein interactions [14, 15]. Interactions of membrane proteins with the cytoskeleton or with the glycocalyx can also affect the membrane organisation and are likely to play a confining role [16]. A significant challenge of cell biology is to characterise and to understand not only the origin but also the role of these micrometric and sub-micrometric domains. One of the main goals is to propose a realistic model of the forces involved in membrane organisation.

For the further understanding of membranes organisation, optical methods have revealed to be an essential alternative to the classical biochemical ones. Until recently, the Rayleigh limit made it impossible to obtain images with a resolution higher than the wavelength of light and only electron microscopy presented a resolution that allowed observation of sub-micrometric structures. Alternatively, the study of the diffusion of membrane constituents has been successfully used to provide valuable insight into the membrane structure. While the initial approaches consisted of global measurements, single-molecule tracking (SMT) methods have recently been developed, allowing direct visualisation of individual behaviours of molecules and molecular interactions. In contrast to biochemical techniques and global measurement, which have average properties, single-molecule methods present the advantage to detect rare (sub-dominant) events. Despite this, a synthetic picture of membrane organisation is still not available. Although some particular mechanisms have been correctly documented, some of them are still the object of active or controversial debates.

The scope of this review is not only to provide the reader with an overview of the successes of the different diffusion techniques but also to discuss unanswered questions. We will also show that the use of these techniques must be accompanied by modelling to interpret experimental data that require a combination of biological, biophysical and physical approaches. Furthermore, the precise signature of a given mechanism is often subtly concealed in the background, especially in single-molecule experiments, and mathematical analysis is a powerful tool to extract these signatures.

In this study, we highlight novel concepts and results in the active field of membrane dynamic organisation. Thus, after a short survey of the well-documented fence-and-picket and lipid raft models, we develop the emerging idea that inter-protein interactions play a role as a source of compartmentalisation. In addition, two inserts are dedicated to describe the different methodological tools and to detail the various forces involved in protein–protein interactions.

The cytoskeleton meshwork is a barrier to diffusion

The prevailing “fence-and-picket” model, involving the cortical cytoskeleton in the membrane compartmentalisation proposed by Kusumi’s group [17], is the result of successive upgrades of the initial “corral model” by Sheetz [18] (see Fig. 1a). Indeed, FRAP measurements on erythrocytes membrane (see also [19]) suggested that membrane proteins are confined by steric interaction of their cytoplasmic part with spectrin cytoskeleton. This model was reinforced by electron microscopy imaging of the sub-membrane region that showed unambiguously that spectrin forms a meshgrid tightly attached to the membrane via transmembrane band-3 proteins [20]. Since the erythrocytes are anuclear and specialised cells, the extrapolation of the above model to a generic eukaryotic cell is not straightforward. Nevertheless, single-particle tracking (SPT) observations revealed a similar scheme at the plasma membrane of other cell types. Jumps between adjacent compartments were observed, and the size of the compartments increased upon cytoskeletal destabilisation. The “membrane-skeleton fence model” has been proposed as a paradigm. It accounts for slow diffusion at longer times due to occasional jumps between adjacent domains allowed by the fluctuations of either the membrane or the cytoskeletal filaments [16]. In these SPT experiments, the mean square deviation MSD(t) (see “Appendix 1”) exhibited two different diffusion modes. At short times, the diffusion with coefficient D_M is confined in a domain of diameter L. At longer times, it resembles free diffusion with a much smaller diffusion coefficient, D_M.

Fig. 1.

Schematic representations of the main confinement sources in the plasma membrane associated to their expected diffusion behaviour. a Membrane skeleton pickets-and-fences model: the cytoskeleton (brown) generates barriers through the filaments and the anchored proteins (not represented in this study) to the diffusion of proteins and lipids. The diffusion of a protein is represented with a red arrow. Escapes from the compartments are possible giving rise to a “hop-diffusion” [17]. b Lipid rafts assemble preferentially cholesterol and saturated lipids in a liquid-ordered phase represented by the circles. Some proteins have an affinity for these domains as revealed by transient confinement zones in their trajectories (red arrows). c Protein–protein interactions generate stable cluster phases characterised by dynamic nanodomains of proteins (circles). These nanodomains can interact into larger domains (in grey). Proteins are confined in these nanoclusters. Red arrows represents the trajectory of a protein, while gray arrow represents the trajectory of the whole cluster

Similarly, a compartmentalisation has been observed for lipids at the external membrane leaflet that do not interact with the cytoskeleton. The “membrane-skeleton fence” model [17] was amended to account for these findings. This led to the “fence and picket” model [17] assuming that integral membrane proteins anchored to the cytoskeleton generate cages confining membrane molecules.

The merits of these models were to provide the cell biology community with a first post-Singer-and-Nicolson model of the membrane dynamic organisation. However, this “fence-and-picket” model could not explain the origin of all observed confinements, and the refinements of the model became a necessity.

Lipid microdomains and membrane rafts

Lipid microdomains commonly known as rafts were first proposed on the basis of biochemical studies performed by Simons and van Meer [2]. They observed structures in the Golgi apparatus that were sorted to the apical pole of epithelial cells. These structures were found to be enriched in cholesterol and sphingolipids. Due to their high level of cholesterol and saturated lipids, these domains were assumed to be in a liquid-ordered phase that rendered them resistant to detergent extractions [4]. Many papers suggested that lipid rafts were involved in various cellular processes such as signal transduction, apoptosis or protein sorting [20, 21]. They have also been shown to play a role in HIV or influenza viruses infection processes [22–24].

Model membrane experiments have shown that liquid-ordered microdomains in fluid membranes can exist and that proteins can preferentially segregate into the fluid or the ordered phase domain [25, 26]. However, biological membranes are much more complex than synthetic membranes, and the presence of lipid rafts in intact cells still remains to be proved. The typical method to detect rafts in cells is based on their resistance to solubilisation by non-ionic detergents and on their sensitivity to cholesterol depletion [27, 28]. Since these techniques are aggressive, the interpretations of these experiments are controversial. Furthermore, raft composition appeared to heavily depend on the method used to isolate them (e.g. temperature and nature of the detergent) [29, 30]. It has even been proposed that detergent-resistant membranes could be promoted by the detergent itself without necessarily existing in the membrane before extraction [31]. Several attempts have been performed to directly observe lipid rafts on living cells using fluorescent markers. Since these data generally showed a homogeneous distribution of these markers within the membrane [20], Simons and Toomre [32] proposed that “rafts are too small to be resolved by standard light microscopy”. This size limitation raised another issue. When domains were observed in giant unilamelar vesicles, at equilibrium, the lipid-phase separation formed lipid domains of approximately several microns. Thus, it is unclear why the same structures remain sub-micrometric or nanometric in live cells. Several theories have been proposed to explain this observation. For instance, one reason may be due to the out-of-equilibrium thermodynamics of the cell [33–35] or the effect of the lipid composition on membrane rigidity and curvature [36]. It has also been proposed that rafts may result from a rapid liquid-to-solid local phase transition. This would be nucleated by a protein seed, since the liquid state of the membrane would be metastable [37].

To study such small structures, the use of dynamic techniques is the method of choice. By using FRAP, SPT, or fluorescence correlation spectroscopy (FCS), different laboratories verified whether proteins or lipids could be confined in small patches at the plasma membrane. From these experiments, a series of converging results were obtained. Using FRAP, some authors deduced that raft markers were either not compartmentalised or they were in dynamic partitioning between domains and the bulk of the plasma membrane [38]. However, studies that were carried out by SPT showed transient confinement zones of 200-nm diameter (see example in Fig. 1b) related to the presence of cholesterol [39]. Due to the difficulty of direct domain observation, heterogeneity in domain size, composition and lifetime [5], the characterisation of rafts in living cells is still an open question [5, 40].

A consensus definition of membrane rafts emerged from the Keystone Symposium on Lipid Rafts and Cell Function (March 23–28, 2006): “Membrane rafts are small (10–200nm), heterogeneous, highly dynamic, sterol- and sphingolipid-enriched domains that compartmentalise cellular processes. Small rafts can sometimes be stabilised to form larger platforms through protein–protein and protein–lipid interactions” [41]. Consequently, efforts are now being made to advance the development of new tools for studying dynamic nano-scale microdomains technically and theoretically [42].

Independently, it is well admitted that clustering of lipids in functional domains is likely to be present in most biological membranes and could regulate protein activity [43].

Protein–protein interactions generate confinement

Proteins are densely packed in their two-dimensional membrane environment, and this feature is known to slow down their diffusion by more than one order of magnitude compared to a model membrane with low protein to lipid ratio [44, 45]. This high density must be taken into account for the correct description of cell membrane dynamics.

Additionally, proteins interact not only at short range because of their specific chemical nature but also at intermediate or long distances due to physical interactions. The insertion of a protein in the membrane induces a perturbation of the lipid bilayer, which results in free-energy cost. When two proteins are inserted in the membrane, the variation of free energy is dependent on their inter-distance and induces a force between both proteins. Several mechanisms can lead to such a membrane-mediated protein–protein interaction. Depending on whether they are attractive or repulsive forces, they facilitate or prevent protein aggregation.

Pink et al. [45] and Abney et al. [46] were the first to argue that high protein density at the membrane causes crowding effects that favour interactions between proteins. In addition to the reduction of the diffusion rate, this was expected to generate density fluctuations and formation of protein-rich or protein-poor regions. The authors modelled the membrane as a two-dimensional medium where proteins diffuse in a “lipid sea”. The movement of proteins was therefore governed by a random force due to the thermal agitation and by the interactions with their neighbours [47].

Interacting Brownian particle model

Recently, a thorough statistical analysis of the SPT trajectories of the μ opioid receptor at the surface of stably transfected NRK cells revealed that most receptors exhibited a “walking confined diffusion” mode [15]. This corresponds to the superposition of a short-term confined diffusion and a slower long-term free diffusion. At first sight, this behaviour could be interpreted in the context of a fence-and-picket model (described in Fig. 1a). It appeared that, for a collection of receptors, the microscopic diffusion coefficient of the confined protein and the size L of confining domain were following the simple law of ∼ L². Furthermore, this was also observed in trajectories where both quantities fluctuated significantly with time. Such behaviour cannot be understood in the frame of a fence-and-picket model, where is a local quantity that only depends on the immediate environment of the receptor and not on the distance between the confining obstacles. Even at a short time range, a protein “feels” the size of its confining domain, which suggests the occurrence of collective effects. In the work performed on the μ opioid receptor, it was also observed that the macroscopic diffusion coefficient, D_M, is correlated to L²: D_M ∼ L². The detection of jumps by a new algorithm (see “Appendix 1”) showed that the trajectories do not display enough jumps over actin-like barriers to account for the observed relationship [48].

An alternative mechanism known as “interacting Brownian particle” model was proposed to explain the observed diffusion behaviours [15]. It stated that attractive long-range interactions can be sufficiently strong to ensure the stability of small confined assemblies of proteins without invoking external barriers (see Fig. 1c). It should be emphasised that, within this assembly, the proteins do not need to be of identical nature.

A hypothesis of the “interacting Brownian particle” model states that, according to earlier observation of Peters and Cherry [49], the microscopic diffusion of the protein is inversely proportional to the protein concentration within the assembly. As a consequence, assuming that the number of proteins within an assembly is constant, both the microscopic and macroscopic diffusion coefficients remain proportional to L² [15].

Moreover, in different systems using different tracking techniques, similar observations were made [50–53]. Frick et al. [54] have recently given additional evidence supporting the previous interpretation by using FRAP on four different proteins. They concluded that (1) the cytoskeleton plays a limited role on diffusion coefficients, since diffusion in cytoskeleton-free blebs is not increased as compared to normal plasma membrane and (2) “protein density has a significant effect on the observed rates of diffusion”.

The “cluster phase” model

As stated above, the “interacting Brownian particle” model requires the microscopic diffusion coefficient to be inversely proportional to the local protein concentration. A recent theoretical study [55] proposed a simple physical mechanism leading to this behaviour. It is reminiscent of the cluster phases, a current and active field in physics of colloidal suspensions [56]. In these phases, colloidal particles are found to condense in small clusters. It has been shown that the average cluster size grows proportionally to the colloid concentration [56–59], and it can be demonstrated that the average diffusion coefficient of colloids is inversely proportional to the cluster size and consequently to the colloid concentration. This model has been shown to be valid in two dimensions for membrane proteins [55]. Proteins clusters in cell or model membranes can result from a combination of non-specific short-range attractions and longer-range weaker repulsions (see “Appendix 2” for details) [60].

Currently, molecular dynamics simulates natural systems whereby several proteins are embedded in a lipid bilayer [61]. Despite the short time scale of these simulations (a few microseconds), Periole and collaborators [62] have simulated a quasi-all-atom description of rhodopsin in a phosphatidylcholine bilayer containing more than 1,000 lipids and up to 16 proteins. Since proteins self-assembly was found to be modulated by lipid-mediated interactions their findings are compatible with the cluster phase model.

Examples of observed protein confinements

The wide variety of protein–protein interactions could explain the diversity of the observed behaviours of protein assemblies at the cell surface. For example, the recruitment of dynamin by clathrin-coated vesicles has been modelled by membrane-mediated long-range forces [63, 64]. The non-clathrin-dependent endocytotic process of Shiga toxin has been shown to be driven by interplay between membrane curvature, hydrophobic mismatch and protein aggregation [65]. The lateral organisation of photosystems in thylakoid membranes has been described by a combination of attractive and repulsive forces [66].

Further support for the involvement of protein–protein interactions in the generation of confinement has been provided by Sieber and collaborators [67, 68]. The authors have shown by stimulated emission depletion microscopy and numerical simulations that syntaxin clusters of 70nm were formed by the competition of short-range attractions and long-range steric repulsions. Furthermore, in agreement with the “cluster phase” model, the overexpression of syntaxin did not affect the mean domain size but only the number of domains [69].

Biological functions require composition specificity of protein assemblies: role of specific interactions

Cell membranes are hypothesised to contain numerous compartments or micro-domains, such as reaction centres or signalling platforms, which are involved in specialised tasks. Since each task requires the involvement of a precise set of proteins, a specific protein composition is needed in these compartments.

For example, by regrouping different proteins involved in a transduction pathway, compartmentalisation would enhance the rapidity of response. For example, it has been demonstrated that in hippocampus neurons, β₂ adrenergic receptor, calcium channels, G protein, adenyl cyclase and other proteins are co-localised [70]; however, these clusters of proteins are not recognised as partitioning into rafts. The authors conclude that “co-localisation of GPCRs with their ultimate targets in macromolecular complexes could be a general mechanism to ensure that signalling is both specific and fast” [70]. Note that due to the indirect methodologies used to reach this conclusion one cannot infer the microscopic mechanism responsible for co-localisation.

More direct methodologies such as near-field scanning optical microscopy (NSOM) have shown that β1- and β2-adrenergic receptors in cardiac cells are localised in distinct sub-micrometric clusters of about 100nm in diameter [71]. This suggested that compartmentalisation favours a “rapid and high fidelity” signalling mechanism in a “crowded and active cell membrane” [71]. This notion that distinct compartments should have different compositions to achieve specialised tasks is also raised by the work of Sieber et al. [68] where syntaxin 1 and syntaxin 4 segregate in distinct clusters.

These examples suggest that, in addition to non-specific associations, specific protein interactions allow the formation of specialised domains [55]. As stated previously, the lipid raft and fence-and-picket model can only explain to certain extent the diversity of these specialised domains [67]. Rafts are enriched in cholesterol and sphingolipids [20]. With this restricted composition, it is inconceivable that they can sort proteins into many different domains. As for barriers, they can only form sub-micrometric domains with very similar nature. Interestingly, the cluster phases model may basically account for a specificity by introducing a modulation of the short-range attraction depending on the nature of proteins [55].

Future challenges

Recent experimental and theoretical pieces of evidence have enabled to place the organisation of the membrane more coherently. The challenge now will be to understand how the various pieces of this organisation are assembled. To enable this, cutting-edge optical methodologies are being developed to analyse in situ membrane dynamics and organisation.

In the field of fluorescence, efforts are being made to improve the brightness and the photostability of the fluorescent proteins [72, 73]. This should allow a more accurate detection of the molecules in a longer time and could circumvent the main drawbacks of single-molecule tracking (see “Appendix 1”). The emergence of nanodiamonds is also a promising alternative since these particles emit bright fluorescence in the absence of photobleaching and, unlike quantum dots, they do not blink [74]. The improvement of fluorescent molecules will also benefit to Förster resonance energy transfer to detect interactions on a molecular scale [75].

For SPT, the use of photothermal interference contrast [76, 77] allows the usage of gold colloids of 2.5nm. This affects the movement of the protein less compared to when it is bound to a 40-nm colloid.

Atomic force microscopy (AFM) has the advantage of not requiring the molecule to be labelled. This method consists of a cantilever with a sharp tip at the end that scans the sample surface and thereby contouring its profile. Single protein can be observed in the membrane with this methodology since the resolution is 0.1nm vertically and 0.5nm horizontally. For example, AFM has provided an understanding of oligomeric Rho protein structure in native membranes [78]. Recent progress in time-lapse AFM showed, in real time, the change in height of the pore protrusion from the membrane of cytolysin within its formation [79]. Scheuring and Sturgis [80] have even managed to image photosynthetic membranes with a spatial resolution of 1nm. They have analysed and modelled its composition and architectural modifications in response to light.

AFM cannot be used to study all types of cell membranes. Consequently, a derivative of AFM in optical imaging has been developed to access the membrane structure at a sub-wavelength scale. NSOM consists of a laser beam passing through an aperture smaller than the wavelength of the laser to illuminate a sample at a distance much less than the wavelength of the beam (a few nanometres). This probe scans the surface of the sample to obtain images with a 50-nm xy resolution and a 10-nm z resolution. This methodology has been successfully used to demonstrate that free heavy chains and class I HLA heterodimers co-cluster in B cells [81]. It has also been used to observe nanometre domains of β-adrenergic receptor complexes on the surface of cardiac myocytes [71, 82], clustering of the pathogen receptor DC-SIGN on dendritic cells [83] and T cell receptor re-organisation induced by antigenic stimulation [84].

These high resolution methodologies share a common drawback of a low time resolution as they rely on scanning the surface of interest. In a perpetually moving landscape, this would not provide a reliable image at a given instant. The image will be distorted at all positions that have not been acquired simultaneously.

In conclusion, the highly complex structures of membranes, their nano/microdomain organisation, heterogeneity, dynamics and functions are still far from being understood clearly. Multidisciplinary approaches, conceptual breakthroughs and innovative technological advances should give more precise insight on the questions raised in this review.

Appendix 1. Methods for the analysis of diffusion

The analysis of the diffusion of molecules in cells is usually performed by optical microscopy. FRAP and FCS provide average measurements, while single-particle or single-molecule tracking methods (SPT or SMT) address the individual behaviours of the molecules. Although single-molecule approaches directly detect and analyse sub-populations, they present drawbacks discussed in the following section that make the global measurement methods FRAP and FCS still of valuable interest.

For global measurement of molecule dynamics within the membrane, methods such as variable radius FRAP or variable waist FCS are advantageous over the single-molecule methods. For a detailed description of these methods, see [85]. For the scope of this review, we discuss how these methods have been exploited to characterise the compartmentalisation of lipids and proteins in the membrane.

Fluorescence recovery after photobleaching

The fluorescence intensity is monitored in a geometrically defined zone after having photobleached the probes by the application of an intense and extremely brief light pulse (Fig. 2). The analysis of the fluorescence recovery curve due to the diffusion of the intact fluorescent molecules derived from outside of this zone determines the diffusion coefficient D of the molecules (the accessible range is between 10⁻³ and 10μm²/s) and the fraction of mobile molecules M. These parameters are deduced from the fit of the normalised fluorescence intensity recovery curve by the expected solution of the diffusion equations that are dependent on the intensity profile of the bleaching beam. This has been established, in the case of a uniform illumination disk of radius R by Soumpasis [86].

where R is the radius of illumination; τ_D = R²/4D and I₀ and I₁ are the modified Bessel functions of the first order.

Fig. 2.

Principle of a fluorescence recovery after photobleaching experiment. a The initial fluorescence intensity I_o of the labelled molecules (green “sparks”) is measured in a defined illuminated region of the membrane (blue zone). b A bleaching pulse is applied leading to a reduced fluorescence intensity I_b. c Due to the diffusion of the molecules, a fluorescence recovery is observed. d The recording of the fluorescence intensity as a function of time is then used to determine both the diffusion coefficient and the mobile fraction of the labelled molecules

Microdomains that are smaller than 1μm down to about 200 nm can be characterised by varying the illumination radius from 1 to 5μm. As seen in Eq. 2, M and D are then expected to vary as a function of R [87].

where M_p is the permanent mobile fraction. Depending on the M_p value, two cases can be considered:

• If M_p ≈ 0, there is a single population of tracers confined in closed domains. The measured diffusion coefficient is an apparent one (D_app) and the real diffusion coefficient inside the domains D_conf can be evaluated from Eq. 3.

  

The validation of the analysis can then be obtained by verifying the invariance of D_conf with R.

• If M_p > 0, the tracers are either inside juxtaposed but in open domains or distributed both inside and outside isolated closed domains.

An analysis of the recovery curves assuming two sub-populations of tracers is then necessary, leading to the determination of weight and diffusion coefficient of each population. Confined tracers present a diffusion coefficient, D_conf, varying according to Eq. 3, while non-confined tracers present a diffusion coefficient, D_free, invariant with R. This last population corresponds to tracers with a long-range free diffusion.

If D_free > D_conf, tracers are distributed both inside and outside isolated closed domains. Note that the relevance of the two diffusion coefficients analysis requires that the weight of the free diffusion population should be in the same range as M_p.

Such an approach was first developed by Yechiel and Edidin [7] and Edidin and Stroynowski [8] and has been applied in the analysis of dynamic compartmentalisation of the NK2, hMOR, CCR5 and CD4 receptors [88, 89].

Fluorescence correlation spectroscopy

The fluorescence intensity is measured inside a small volume defined by a focalised laser beam (Fig. 3). The fluctuations of the fluorescence intensity result from the molecules that enter and escape the confocal volume. These fluctuations are recorded with a temporal resolution ranging typically from 1 ns to 1 min.

Fig. 3.

Principle of a fluorescence correlation spectroscopy measurement. a Labelled molecules (green “sparks”) diffusing in the membrane enter and leave a small observation zone defined by a focused laser beam. b The autocorrelation function of the fluorescence intensity is calculated from the fluctuations of fluorescence recorded over time

For a free Brownian diffusion, the diffusion time, τ_d, is obtained from the autocorrelation function in Eq. 4

where N is the average number of molecules in the observation volume. The diffusion coefficient D of the molecule can then be deduced according to Eq. 5

where w corresponds to the transversal waist of the focused laser beam.

One of the principal advantages of FCS is its ability to measure diffusion constants lower than 0.001μm²/s and its accuracy for analysing fast diffusing molecules [90].

Currently, FCS is exploited at variable waist [91, 116]; therefore, the variation of D with w allows us to easily discriminate between two different diffusing populations.

Pure Brownian diffusion obeys the linear diffusion law τ_d = f (w²) equation. A negative value of the intercept at w = 0 corresponds to a compartmentalisation of proteins inside domains delineated by a meshwork. A positive intercept at w = 0 corresponds to a dynamic partition of molecules between isolated domains.

Typical FCS instruments have a spatial resolution of approximately 300nm that is determined by optical diffraction limit. However, by using metallic nano-apertures, 30-nm domains can be characterised [92]. Other variations of FCS instruments with multiple-colour cross-correlation have been developed [93].

Single-particle or single-molecule tracking

This methodology allows the direct observation of individual molecules at the surface of living cells with a nanometre scale precision in the position measurement by video-microscopy coupled to image analysis (Fig. 4).

Fig. 4.

Principle of the single-particle tracking and single-molecule tracking methodologies. a The molecule of interest is specifically labelled by a fluorophore (green “spark”) or a nanoparticle (usually attached via an antibody). b The trajectory of the labelled molecule is determined by video-microscopy coupled to image analysis

Probes used in SPT are nanometre particles such as latex spheres, gold colloids or nanocrystals. Generally, these particles are attached to the molecule of interest by means of antibodies or fragments of antibodies. This permits one to observe endogenously expressed proteins or receptors [94, 95]. Particular care must be taken to avoid non-specific binding and multiple attachments of multiple target molecules. This is circumvented in SMT, where the molecules of interest are fused to naturally fluorescent proteins. However, the use of Halo tag® or Snap tag® labelling, which restrict the labelling to proteins expressed at the membrane, ought to be preferred.

Both for SPT and SMT, the acquisition frequencies are comparable and can be decreased to a few milliseconds. Nevertheless, due to photobleaching, the duration of the acquisition with SMT cannot exceed more than 10s, while in the case of SPT it can vary between 1 and 30min.

After the establishment of the trajectories [96], the mean square displacement is calculated according Eq. 6.

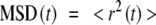where r is the vector between two positions separated by a time interval t and brackets denote a discrete average over images.

Diffusion modes are determined by the analysis of the MSD(t) best fits [97]:

• A linear MSD(t) is characteristic from a random-free diffusion

  

  where D is the diffusion coefficient of the protein.
• A MSD(t) presenting a saturation at long term is characteristic of a pure confined diffusion

  

  where τ = L²/12D, L is the size of the domain and D the diffusion coefficient of the protein. For fast diffusing molecules, the detector time-averaging effect can be corrected by the use of a mathematical formula detailed in [60].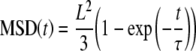

• More complex behaviours such as transient confinement or other combinations of simple modes, that require a thorough statistical analysis can be evidenced. Algorithms have been developed for detecting confinement and jumps between adjacent domains [48, 60], directed motion [98] and multi-type motion [99].

Single molecule versus collective measurements

An interesting comparison between the collective and individual approaches has been recently performed by Bates et al. [100] who studied, under identical conditions, the dynamics of the transmembrane protein CFTR using FRAP, SPT and image correlation spectroscopy (ICS, the imaging analogue of FCS). They first observed differences between FRAP and ICS measurements: The diffusion coefficient obtained with FRAP was fourfold larger than that obtained by ICS. SPT experiments revealed complex movements of the proteins with a rapid diffusion of CFTR interspersed by intermittent trapping. Such behaviour remained unravelled by FRAP or ICS that are addressing populations of molecules instead of single molecules.

Owing to the extensive duration of the observations accessible to the single-particle tracking approach compared to single-fluorophore tracking, it is likely to be an unavoidable tool to address the membrane organisation. Nevertheless, efforts must be concentrated in the understanding of the effects of nanoparticles on the labelled molecules. The role of their nature, of their size and their interaction with the underlying membrane and the glycocalix will have to be rigorously quantified.

Appendix 2. Nature of protein–protein interactions

There is a rich variety of non-specific interactions between membrane proteins. Their nature is either electrostatic or thermodynamic. Thermodynamic interactions are mediated by the membrane. Note that the following discussion does not only concern transmembrane proteins but also peripheral proteins.

1. Short-range interactions

Short-range interactions are typically in a range of 1nm and involve energies of the order of magnitude of the thermal energy k_BT. Dipole–dipole, Van der Waals forces always contribute to the short-range attraction between proteins. They decay rapidly at large distances (as 1/r⁶) and add a binding energy of a fraction of k_BT at short distance [66].

If the thickness of the hydrophobic core of a transmembrane protein is significantly different from the thickness of the membrane, the membrane will adjust so that the acyl chains of the lipids are not exposed to the aqueous medium. When the protein core is thicker than the membrane, the mismatch is said to be positive; conversely, it is negative. Membrane deformation costs a certain amount of elastic energy. Therefore, when two proteins inserted in the membrane [101] have the same mismatch sign, they attract. Conversely, they repulse if they present a different mismatch sign [101]. For instance, the activation of a receptor after ligand binding can change its hydrophobic thickness [102] and consequently the interaction potential with neighbouring proteins.

Furthermore, the shape of the protein can modulate hydrophobic interactions by deforming differently the lipid bilayer of the membrane [103]. Cell membranes are a mixture of many different lipids, with various fatty acid chain lengths. Therefore, lipids can be sorted by the protein to match its hydrophobic core. Mouritsen [20] and Gil et al. [104] have shown that an additional attraction between membrane proteins can occur to minimise the lipid/protein interface. This attraction leads to the formation of protein-rich domains. However, it is unclear why these domains are limited in size, i.e. why a single macro-domain does not recruit the majority of proteins. As in the case of the lipid rafts, this limitation in size may be due to the out-of-equilibrium thermodynamics of the cell [105].

Another short-range interaction known as the “depletion interaction” [106] occurs because the diameters of membrane proteins in the plane of the membrane are greater than the lipids [106]. The lipids surrounding an isolated protein exert an osmotic pressure that is parallel to the plane of the membrane. Due to the symmetry, the total force vanishes. However, if the distance between two proteins is smaller than the lipid diameter, the interval between the proteins will be devoid of lipids. Under these circumstances, the resulting force brings both proteins close to one another. The amplitude and range of this interaction are of the orders of one k_BT and one nanometre [66].

1. Long-range interactions

The long-range interactions extend beyond ten nanometres. These interactions occur because embedded membrane proteins impose constraints on the membrane. Variations in entropy and elastic energy contribute to long-range interactions [107, 108].

Effects on long-range interactions of purely entropic origin are known as Casimir interactions. These Casimir attractive forces are related to the thermal fluctuations of the membrane [107]. Moreover, the influence of elastic energy on long-range interactions is due to the conical shape of the transmembrane proteins (with an aperture angle θ). This shape imposes a curvature on the membrane, inducing a repulsive force [107, 109]. Forces resulting from entropic and elastic energies decay slowly at the same rate, and their sum can be attractive or repulsive. This resulting force is repulsive if the protein curvature is superior to 5°. Given that the hydrophobic core of most transmembrane proteins, in particular G-protein coupled receptors (GPCRs), consists of several α-helices, it is unlikely that their shape can be approximated by a cylinder. For example, the average contact angle estimated for rhodopsin is greater than 10° [110, 111]. Peripheral proteins are also affected by both Casimir attractive force and elastic repulsion, since they impose an intrinsic local curvature when they bind to the membrane. The curvature anticipated in [63] is large enough to override the entropic attraction. Thus, it can be considered, in a first approximation, that all membrane proteins experience repulsion at long distances.

A more refined analysis of these longer range forces should also take into account that proteins structure is anisotropic (e.g. their cross-section in the plane of the membrane is not circular). This is achieved by modelling proteins by ellipses. It has been shown [108] that this can decrease the long-distance repulsion and even lead to attraction [110]. Finally, it has been argued that a torque applied to the proteins is also susceptible to affect the long-range pair potentials and even to enhance them [112]. This torque is, for example, the result of the electric field due to the difference of ion concentrations on both sides of the membrane.

To sum up, the coupling between the membrane curvature and the protein intrinsic curvature generically leads to a weak repulsive force. It is worth noting that this coupling enhances the protein rate of diffusion [113].

1. Effects of short- and long-range interactions

Short- and long-range interactions result in attractive or repulsive forces between two proteins. Figure 5 illustrates the energetic profile of protein–protein interactions. Hard-core repulsion occurs at distances shorter than a few nanometres and, at intermediate distances, a short-range binding potential well, of a few k_BT, forms. At longer distances, repulsive forces dominate [55]. This model only takes into account pairwise interaction potentials. A more refined analysis should include many-body interactions [106, 108]. For instance, it has been shown that, under certain circumstances, repulsive forces between pairs of proteins can be counter-balanced by the attractive forces due to many-body attractions [114, 115].

Fig. 5.

Typical shape of the interaction potential between membrane proteins. F(r) is the free energy, in units of the thermal energy k_BT; r is the distance between the proteins in nanometres. A hard-core repulsion occurs for distances inferior or equal to the protein diameter. Then, a narrow attraction, with a binding energy of a few k_BT, occurs due to different short-range interactions discussed in “Appendix 2”. Beyond an energy barrier of a fraction of k_BT, the potential decreases. The values chosen in this example are those used in [55]