Probing airway conditions governing ventilation defects in asthma via hyperpolarized MRI image functional modeling

Abstract

Image functional modeling (IFM) has been introduced as a method to simultaneously synthesize imaging and mechanical data with computational models to determine the degree and location of airway constriction in asthma. Using lung imaging provided by hyperpolarized ³He MRI, we advanced our IFM method to require matching not only to ventilation defect location but to specific ventilation throughout the lung. Imaging and mechanical data were acquired for four healthy and four asthmatic subjects pre- and postbronchial challenge. After provocation, we first identified maximum-size airways leading exclusively to ventilation defects and highly constricted them. Constriction patterns were then found for the remaining airways to match mechanical data. Ventilation images were predicted for each pattern, and visual and statistical comparisons were done with measured data. Results showed that matching of ventilation defects requires severe constriction of small airways. The mean constriction of such airways leading to the ventilation defects needed to be 70–80% rather than fully closed. Also, central airway constriction alone could not account for dysfunction seen in asthma, so small airways must be involved.

asthma is a disease in which airway hyper-reactivity can cause increases in the lung's resistive (Rl) and elastic (El) properties to levels that make it very difficult to breathe mechanically and to adequately distribute the inhaled air to the gas exchanging regions of the lung. Measures of Rl and El over a range of frequencies surrounding breathing are consistent not only with increased levels of Rl and El but also with heterogeneous airway constriction (2, 6, 10). Imaging approaches such as positron emission tomography (PET) (13) or hyperpolarized ³He MRI (HP ³He) (1) show that such heterogeneous constriction leads to substantial heterogeneities in ventilation distribution. Unfortunately, there is no practical approach for imaging airways in human subjects to identify which airways are responsible for degradation in mechanical and ventilation function, especially if these airways are small. Controversies remain regarding which airway sizes are highest priority for treatment in asthma and, most recently, whether treatment of larger airways alone would be sufficient (5).

Tgavalekos et al. (15) introduced a modality to address this called image functional modeling (IFM). In IFM, a three-dimensional (3-D) computational model is synthesized with oscillatory mechanics and PET imaging data to determine the constriction conditions necessary to match both the location of ventilation defects and changes in airway mechanics. The Tgavalekos study implicated severe constriction in small airways as a major cause for functional defects. However, the PET imaging did not allow imaging of the entire lung, only a middle section. Also, PET imaging is not attractive from a clinical perspective or even for routine research use because it requires injecting the subject with a radioactive tracer.

The current study has advanced IFM in two important ways. First, we now incorporate nonradioactive HP ³He lung imaging data. With HP ³He, we can image the entire lung field, and the benign tracer is inhaled rather than injected, making the procedure less invasive and safer for the subject. Second, we now can take advantage of a recently published technique for quantifying specific ventilation throughout the lung (19) during our IFM approach. In previous studies, ventilation in imaging data was often quantified in a binary fashion with a threshold set to determine areas of the lung that are being ventilated versus those that are not. The current study incorporates visual and statistical comparisons between real ventilation images and simulated ventilated images. By incorporating quantitative comparisons of model specific ventilation in 3-D with data, we can advance the prediction of peripheral airway constriction conditions (<2-mm diameter) required to create ventilation defects.

METHODS

Experimental Protocol

The Health Insurance Portability and Accountability Act-compliant research protocol in this study was approved by both Boston University and Brigham and Women's Hospital Institutional Review Boards. HP ³He imaging data and oscillatory mechanics were collected for four healthy and four asthmatic subjects before and after bronchial challenge with methacholine (Table 1). Before the first study visit, all subjects participated in a screening day in which a standard methacholine challenge was given to determine their PC₂₀ dose (20% drop in baseline forced expiratory volume in 1 s). If the subject's PC₂₀ value was >16 mg/ml and the subject had no history of asthma, the subject was enrolled as a healthy participant. If the PC₂₀ value was <8 mg/ml and the subject had been previously diagnosed with asthma, the subject was enrolled as an asthmatic participant. On the day of the study, a physician inserted an esophageal balloon into the subject to estimate pleural pressure. Baseline mechanics measurements were taken via the optimal ventilator waveform (OVW) technique, and a baseline image was taken of the lung using HP ³He MRI (9). A five-breath methacholine challenge was then administered to induce bronchoconstriction until the PC₂₀ was reached. After bronchoconstriction, mechanics and imaging data were acquired again within 5–10 min of the end of the methacholine challenge.

Table 1.

Subject demographics

Subjects	Sex	Age, yr	Baseline FEV1, %Pred	PC20, mg/ml
Healthy
H1	F	25	108	>16
H2	M	22	84.1	>16
H3	F	31	90.6	>16
H4	M	23	95.3	>16
Asthmatic
A1	F	29	83.9	1.25
A2	F	21	63.8	0.12
A3	M	32	83.0	4.10
A4	F	22	91.5	3.32

FEV₁, forced expiratory volume in 1 s, where %Pred is the percentage predicted at baseline measured with subject in the upright position; PC₂₀, methacoline dose causing a 20% decrease in FEV₁; F, female; M, male.

Oscillatory Mechanics

Rl and El were measured as a function of frequency by using the OVW technique as previously described in detail (9). A linear motor delivers a waveform consisting of seven sine waves with frequencies ranging from 0.1 to 8 Hz, which can adequately ventilate the subject. The subject is instructed to relax and allow the ventilator to breath for them for a period of 40–60 s to eliminate any artifacts created by the subject's natural breathing frequency. Flow (V̇_ao) and pressure (P_ao) are measured at the airway opening, and esophageal pressure (P_es) is also measured through a latex balloon catheter inserted into the esophagus. Transpulmonary pressure (P_tp) is estimated as the difference between P_ao and P_es (Eq. 1). V̇_ao and P_tp are transformed into frequency domain and used to calculate Rl and El over the range of frequencies using Eqs. 2–4:

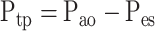(1)

(2)

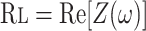(3)

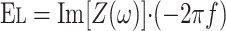(4)

where Re is the real part of impedance [Z(ω)] and Im is the imaginary part of impedance.

HP ³He MRI Imaging

Imaging data were collected in conjunction with the Hyperpolarized Noble Gas MRI Laboratory at Brigham and Women's Hospital. The ³He gas is polarized in a room adjacent to the MRI, via a collision spin exchange with optically pumped rubidium (8) using a polarizer built in-house. When polarization reaches a level of 10–20%, one-third liter of gas is released into a Tedlar plastic bag, and nitrogen gas is added to the bag to bring the total volume to 1 liter at 1 atm. The bag is then quickly brought into the MRI area, where the subject breathes in the 1 liter of gas and holds their breath for 10–15 s while the images are acquired. We obtained 9–14 coronal slices, each 13 mm in thickness. With a 46-cm MRI scan field of view and images zero-padded to 256 × 256 pixels, the in-slice resolution is 1.8 mm.

At each study visit, it is only possible to take three images, due to the limitations of polarizing only 1 liter of gas every 7 h. Four stages of the experiment include baseline, postmethacholine challenge, post-deep inspiration, and postalbuterol. For this study, the baseline or postalbuterol image is used as a reference image for analysis of the postchallenge image. In healthy subjects, the entire lung field appears homogenously ventilated with clear boundaries of the lung periphery. However, if a subject is severely bronchoconstricted, the ³He gas will not reach all areas of the lung due to some airways experiencing excessive constriction, if not complete airway closure. These severely constricted airways will in turn create ventilation defects in the lung field, and several studies have shown that the defects always occur heterogeneously (1).

HP ³He MRI Image Processing

Between each image set, the subject must be removed from the MRI scanner for the methacholine challenge and the albuterol delivery. As a result, the images from each data set are misaligned as the subject shifts position for the subsequent image. We first align the images using a rigid registration algorithm, which shifts the lung regions to obtain the optimum overlay with the baseline or postalbuterol image. For each coronal slice, the images are coregistered to the corresponding baseline image by identifying the maximum of the normalized correlation function within a ±32-pixel translation in the superior-inferior direction and a ±16-pixel translation in the left-right direction. The baseline or postalbuterol image is used as the reference image because it provides the clearest definition of the bounds of the lung, particularly in asthmatic subjects. Some information may be lost due to the fact that even at baseline/postalbuterol, asthmatics may have mild constriction; however, the registration algorithm finds the location of maximum correlation between image sets and is robust when ventilation defects are small.

Using the aligned images, we were able to quantify the ventilation in several ways. First, we identified a threshold value that effectively removed the background noise without losing lung information. Using this threshold, we created a binary mask with the areas of the lung that are above the threshold, which are described as ventilated, whereas the areas that are below the threshold are described as not ventilated. This method was used to define the lung boundaries at baseline and the location of severe ventilation defects after bronchoconstriction.

The second method used to quantify ventilation, published recently by Tzeng et. al (19), allowed us to describe specific ventilation throughout the lung field, not just where the defects were located. For every voxel in the image set, we calculated the percentage of that voxel that was filled with the ³He gas. The mean noise level was found first and subtracted from all the pixels. Next, if we assume that signal decay is negligible, the sum of all the pixel intensities (P_i) will be linearly proportional to the amount of gas inhaled (1 liter). We calculated this signal intensity to volume scaling factor (C) using Eq. 5:

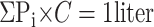(5)

By multiplying C to every pixel, we obtained an estimate for the amount of gas in that particular pixel. Furthermore, since we knew the size of every voxel (1.8 × 1.8 × 13 mm), we could calculate the percentage of the voxel that was filled with the ³He and nitrogen gas mixture. This calculation is summarized by Eq. 6,

(6)

where G_i,j,k is the fraction of voxel i,j,k that is filled with gas, V_voxel is the volume of the voxel, and S_i,j,k is the signal intensity. The total amount of gas inhaled is 1 liter, although the amount of actual hyperpolarized ³He inhaled is on the order of 70 ml. We assumed that the gas and signal were evenly mixed so that the signal intensity is proportional to the total amount of gas in the voxel.

Computational Models

We used the 3-D asymmetric computational model of the airway tree developed by Tgavalekos et al. (15). The model is grown into a host space defined by computerized tomography (CT) or MRI data, with mean airway diameters and lengths that are consistent with human airway morphometry. The airway tree consists of 57,801 airways with 28,901 terminal airways. Tgavalekos et al. (16) have described in detail how lung mechanical function is predicted using the 3-D model. Each airway is modeled as a function of diameter and thickness and to account for resistive and inertial pressure losses due to laminar flow. The airway walls are modeled as compliant rather than rigid, allowing shunting of flow. Input impedance of the entire airway tree is calculated using a stack-based algorithm to traverse the tree and combine the individual impedances of the airways in series and parallel. Terminal airways lead to ventilated acini, which is added in series by using a viscoelastic tissue element of a constant-phase model. The original mechanical model only contains information from the trachea and below in the airway tree. All of our data, of course, included the impedance of the upper airway. Using an anatomically based model of the upper airway combined with computational fluid dynamics, we can estimate the impedance of the upper airway as a function of frequency (12). These impedances are added in series to the remainder of the airway tree to calculate total respiratory system impedance.

Various constriction patterns are then applied to the model to alter the airway diameters to try and match measured data. A random draw from a Gaussian distribution with a user-defined mean and standard deviation is used to determine the degree of constriction of a particular airway. Impedance of each individual airway can then be recalculated with its new diameter, and the impedance of the entire airway tree is found.

Ventilation distributions.

For any particular airway condition, we also are able to predict a specific ventilation distribution out to the terminal airways. We assume that flow is laminar and that any air being shunted into the airway walls is negligible compared with the flow delivered to acini, particularly at low frequencies. A flow divider relationship is used to determine the fraction of flow entering each daughter branch from a parent branch based on the downstream impedances of the two daughters. Fractional ventilation delivered to each terminal airway is equivalent to the fraction of flow that each acini would receive if the lung were completely homogenous, which is then characterized as to how much that acini is under- or overventilated (F_acini). This method is described in more detail by Tgavalekos et al. (15).

However, this simulated ventilation cannot be compared with the real ventilation image for several reasons. First, the model predicts the relative ventilation of each terminal airway (compared with the homogenous case), whereas the real ventilation is calculated in terms of the fraction of the voxel filled with the ³He gas mixture. Furthermore, the model only predicts the ventilation to the acini subtended by the model terminal airways. This results in a nonuniform grid consisting of ventilation data only where terminal airways happen to exist in each 2-D slice (Fig. 1B). In reality, alveolar sacs (acini) fed by these airways would cause space filling for a ventilation field, but the model does not account for such. In contrast, an actual ventilation image contains ventilation data for each pixel in a uniform grid throughout the 2-D slice. Hence, visual comparisons are difficult.

Fig. 1.

Schematic depiction of process to create a model-predicted image slice of ventilation distribution at the same resolution as an actual image. An actual ventilation image (A) is used to determine where there are data in the lung field. A corresponding model slice (B) depicts predicted ventilation to each terminal airway in the slice. The terminal airway slice is converted to the same resolution as the data by averaging the nonzero pixels in the surrounding box, as shown at right. This is repeated recursively for the entire model slice (C).

To convert the model predictions to the same units as the real data, we first must calculate, after a 1-liter inhalation, the percentage of total gas subtended by each terminal airway that is occupied by HP ³He gas. Average functional residual capacity (FRC) for supine healthy adults has been found to be ∼3.05 liters and is slightly higher in asthmatics (3). Using this information, we assumed that the FRC lung volume is 3 liters and is distributed homogenously among the terminal airways. We chose to use the same FRC for all subjects regardless of size or sex, because this would have resulted in only minor variations of 3 liters. Since we had no extremely tall or short subjects, this would have little or no impact on our primary results. The fraction of gas in the acini that is HP ³He after inhalation is calculated using Eq. 7.

(7)

After both the simulated and real ventilation distributions are expressed in the same units, statistical comparisons can be done between the two “ventilation image” data sets.

To visually compare real and predicted images, the predicted image must be converted to the same resolution as the real image. The real image contains ventilation information for the entire lung field (Fig. 1A), whereas the predicted image does not (Fig. 1B). The predicted image must be smoothed to estimate ventilation everywhere in the lung field, not just where there is a terminal airway. Both image sets contain the same number of slices with the same number of voxels in each slice. Utilizing this, we can overlay the two images and find the precise voxels that contain information in the real ventilation image. Moving to the predicted image, these same voxels are identified and are then assigned a value based on the average of intensities of all the nonzero voxels surrounding it in a 3 × 3 grid. This is repeated recursively until all voxels in the lung field have an estimated value for the simulated image. Figure 1C shows an example of the smoothed predicted image process where ventilation is estimated for the entire lung field.

Image Functional Modeling

Using IFM, we can predict the specific airway constriction conditions that effectively recreate both the location of the ventilation defect seen in the imaging data and the measured oscillatory mechanics data. Briefly, the locations of ventilation defects are spatially mapped into the airway tree model to determine the terminal airways that are not being ventilated due to bronchoconstriction. Next, we move up the airway tree from these terminal airways to identify the highest generation (i.e., largest airway) that could be responsible for these image-located unventilated terminal units without creating new model ventilation defects inconsistent with the images. Finally, constriction patterns are applied outside of these defects to explore airway conditions necessary for simultaneously mapping oscillatory mechanical data.

Model mapping.

The spatial locations of the terminal airways are defined explicitly in the tree model. Using these 3-D coordinates, we divide the computational model into the same number of 2-D coronal slices of the particular MRI image set. For each 2-D slice, we then morph the terminal airways that are located in that model slice into a grid space of 256 × 256 pixels. Next, this terminal airway model must be scaled into the bounds defined by the image. The lung boundaries in the baseline/postalbuterol mask (Fig. 2A) are determined, and the terminal airway model is then scaled into this region defined by the image (Fig. 2B). The postchallenge mask (Fig. 2C) can then be multiplied by the baseline terminal branch model to identify which terminal branches are now no longer being ventilated due to the methacholine. This allows us to accurately identify which terminal airways are no longer being ventilated due to the induced bronchoconstriction (Fig. 2D).

Fig. 2.

A binary baseline mask (A) is used to map the terminal branch locations into the lung region defined by the mask. This terminal branch map (B) is then multiplied by the postchallenge mask (C) to determine the ventilated (white) and nonventilated (orange) terminal branches postchallenge (D).

Baseline.

A baseline airway tree model is created for each subject as follows. The generic airway tree model contains lengths and diameters for all airways at total lung capacity (TLC). With the approach of previous computational models, a generation-dependent airway pressure-area relation is used to scale the diameters and lengths of all airways down to FRC (7, 10, 15). Often, measured baseline mechanics data are elevated, so it is necessary to apply constriction to the airways to match baseline Rl and El. To find the baseline constriction conditions, we begin by applying random constriction with a mean of 0% and a standard deviation of 10% to generations 4 and below in the airway tree. The means and standard deviations of constriction are then individually incremented, and the process is repeated until we have applied random constriction patterns with means of 0–50% (10% increments) and standard deviations of 0–50% (10% increments). This approach is again repeated for different generations in the airway tree: generations 6 and below, generations 8 and below, and so on through generation 18 and below in the tree. In total, this provides us with 288 combinations of random constriction patterns (8 airway generations × 6 means × 6 standard deviations). A performance index (PI) is calculated by comparing the measured mechanics to the mechanics predicted by each random constriction pattern. The PI is a measure of how closely the predicted mechanics matches the measured, with lower PI values indicating a better match. Equation 8 describes how the PI is calculated,

(8)

where subscript d represents measured data and subscript m is model data, Re is the real part of impedance, Im is the imaginary part of impedance, and nf is the number of frequencies. For each constriction pattern, a PI is calculated, and the pattern that produces the minimum PI is found. The generic airway tree is then scaled according to the constriction pattern that best matches the measured baseline mechanics.

Postchallenge.

These scaled airway tree diameters are then used as the baseline tree for the postchallenge conditions. The terminal airways that are not being ventilated postchallenge are identified as described previously. At each “closed” terminal airway, we move up the airway tree, closing larger and larger airways until we reach a point where closing an airway produces an additional ventilation defect that is not identified by the image. We then move one generation below this airway and identify that as the maximum-size airway that must be highly constricted to produce the ventilation defect identified in the image. We begin by constricting these airways with a mean of 90% and a standard deviation of 10%. On top of this severe constriction to defect areas, random constriction patterns with means and standard deviations of 0–80% (in 10% increments) are applied to all remaining airways below a specified generation. Again, this is applied to generations 4–18 in the airway tree. The PI is calculated for each pattern, and the constriction pattern that produces the best match to measured data is identified. This constriction pattern is chosen because it can spatially match the ventilation defects seen in the image, as well as match the mechanical measurements.

With this pattern in place, ventilation was predicted for all the terminal airways. Often, it was observed that the ventilation predicted to the defect areas was significantly less than seen in real data. Therefore, the degree of constriction applied to the “closed” airways was reduced by steps of 10% (e.g., to 80% and then to 70%, and so on) until a match to both mechanics and ventilation was found.

RESULTS

Airway Closures/Constriction

We first identified the largest airway that was highly constricted to recreate in the airway tree model only those ventilation defects identified in 3D by the postchallenge image. Figure 3 shows an airway tree model for an asthmatic subject (A2) postbronchoconstriction and postalbuterol. Ventilated airways are plotted in black, whereas nonventilated airways identified by imaging data as described are shown in red. After bronchial challenge, there were a substantial number of unventilated airways, and albuterol was able to relieve some of this constriction, but not all. These defects appear to occur heterogeneously.

Fig. 3.

Model airway tree for asthmatic subject A2 postbronchoconstriction with methacholine (left) and postalbuterol (right). In black are airways that are ventilated; in red are airways that are not being ventilated due to methacholine. Visually, there are a large number of airways that are unventilated; after albuterol, some airways are recovered, but not all.

The diameters of these airways were characterized for all subjects. The range, mean, and standard deviation of diameters for these airways for the healthy subjects are shown in Table 2, and results for the asthmatic subjects are shown in Table 3. For both healthy and asthmatic subjects, the average diameter of airways that needed to be highly constricted to match imaging data was <0.5 mm. In addition, all airways that needed to be highly constricted were smaller than 2.9 mm in diameter. These results are consistent with previous studies by Tgavalekos et al. (15).

Table 2.

Distribution of maximum-size airway closures in healthy subjects

Subject	Maximum Diameter of Airway, mm
	Range	dmean	dstd
H1	0.22–2.56	0.40	0.24
H2	0.22–2.25	0.45	0.32
H3	0.22–2.30	0.44	0.33
H4	0.22–2.95	0.47	0.35
Mean ± SD		0.44±0.03	0.31±0.05

Values are range, mean diameter (d_mean), and SD (d_std) of diameter of airways that need to be closed or highly constricted in the model to match the location of ventilation defects seen in imaging data in healthy subjects.

Table 3.

Distribution of maximum-size airway closures in asthmatic subjects

Subject	Maximum Diameter of Airway, mm
	Range	dmean	dstd
A1	0.22–2.22	0.42	0.27
A2	0.22–2.36	0.45	0.31
A3	0.22–2.56	0.42	0.27
A4	0.22–2.56	0.42	0.30
Mean ± SD		0.43±0.02	0.29±0.02

Values are range, d_mean, and d_std of diameter of airways that need to be closed or highly constricted in the model to match the location of ventilation defects seen in imaging data in asthmatic subjects.

Matching MRI and Mechanics

An example of lung mechanics of an asthmatic subject (A2) before and after a methacholine challenge is shown in Fig. 4. After we challenged the lungs, there was an increase in resistance and elastance as well as an overall increase in frequency dependence of both, indicating heterogeneity (10). At low frequencies there was an upward shift of the dynamic lung elastance, which modeling studies have shown is indicative of highly constricted airways effectively creating a smaller lung (10, 11, 17). After this shift, there was an initial “slow” frequency-dependent increase with frequency consistent with the presence of heterogeneous airway constriction, followed by a faster and more dramatic increase with frequency that is indicative of airway wall shunting due to high peripheral airway heterogeneous constriction (10). If we assume a 90% constriction in the airways leading to ventilation defects, we simulate resistance and elastance (Fig. 4, dashed lines). We were able to match mechanics well by applying a mean constriction of 10% with a 20% standard deviation to all airways at generations 10 and below in the airway tree on top of the constriction applied to ventilation defects. Subsequent assessment of model-predicted ventilation indicated that optimal match to the imaging ventilation data occurred with only 70% constriction in the airways leading to the defects (see below). Figure 4 shows that if we apply a 70% constriction to ventilation defects and a 40% mean and 0% standard deviation to airways in generations 16 and below, we also obtain an excellent match to the oscillatory mechanics data, indeed a slightly better one (PI = 2.52 and 1.43 for 90 vs. 70%, respectively).

Fig. 4.

Measured and predicted lung resistance (Rl) and elastance (El) as a function of frequency for asthmatic subject A2. Data were measured at baseline data and postchallenge, and the postchallenge model was fit with 90% constriction applied to ventilation defects vs. 70% constriction.

With these patterns in place, we could simulate ventilation images and compare them both quantitatively and visually to the real image. We expressed the impact of constriction level in the defect subtending airways in a quantitative fashion by plotting the cumulative distribution of ventilation of all the voxels for the real postchallenge data and the simulated data (Fig. 5). First, at baseline, the model predicts a homogenous ventilation distribution where the majority of the pixels are filled with 25% ³He gas (dashed-dotted line). Postchallenge, if we use a 90% constriction applied to airways leading to ventilation defects (dotted line), we find a distribution quite inconsistent with the real data postchallenge (solid line) with substantially more low-ventilated areas and less highly ventilated areas. However, by imposing only 70% constriction to these defect airways (dashed line), we obtain a much better fit to the low-ventilating units of the postchallenge data. In neither model simulation are we able to precisely match the high-ventilating areas seen in real data.

Fig. 5.

Cumulative distribution function of ventilation for a real image postchallenge and for several model predictions. Without any constriction imposed (baseline), the model predicts nearly homogenous ventilation distribution with the majority of the pixels around 0.25. In the postchallenge model, when 90% constriction is applied to ventilation defects, the model substantially overpredicts the amount of low-ventilated voxels compared with real data. When constriction leading to defects is reduced to 70%, there is a better match to low-ventilating units.

Visually, it is difficult to see differences between model simulations. Figure 6 is an example of three slices from the same asthmatic subject postchallenge. We show the real data and the model predictions when assuming 90 or 70% constriction in the airways leading to ventilation defects and after imposing the optimal constriction pattern to the rest of the airway tree for matching the mechanics (Fig. 4). The real ventilation image (Fig. 6, top) shows clear areas of ventilation defects located heterogeneously; some of these defects have been highlighted with red circles to help with visual comparisons. The simulated image with 90% mean constriction with a 10% standard deviation leading to the defects (Fig. 6, middle) maintains the locations of the defect areas; however, consistent with the cumulative distribution function, it does not have as many high-ventilating units as the real image. Also, the predicted image predicts much less ventilation to the defect areas than seen in real data. In comparison, when only 70% constriction with a 10% standard deviation is assumed (Fig. 6, bottom), there is still no match to high-ventilating areas, but the ventilation to defect areas more closely matches the real image.

Fig. 6.

Real and predicted images of 3 middle lung slices for asthmatic subject A2. The real image (top) has a diversity of bright colors representing high ventilation and less darker colors representing poor ventilation (i.e., clear heterogeneous ventilation). The simulated image with 90% constriction to defects (middle) has more poorly ventilating units than the real image. Simulating an image with 70% constriction (bottom) to defects does not change the image much from that for 90%. Red circles highlight differences between the model predictions.

Using the above approach applied to all subjects, we calculated the average constriction needed to be applied to match both measured ventilation and mechanics data postchallenge. Shown in Fig. 7 are the mean and standard deviation of constriction applied to the airways causing ventilation defects alone, to all airways outside these defects, and to all airways in the tree for both healthy and asthmatic subjects. We found that on average in healthy subjects postchallenge, a 73 ± 12% diameter reduction in airways leading to defects was optimal for matching ventilation image data, whereas in asthmatics, a slightly higher constriction was necessary (80 ± 12%). For airways not leading to ventilation defects, asthmatics required a mean of ∼21 ± 20%, whereas healthy subjects constricted with a mean of 15 ± 17%. Also, these constrictions were applied to primarily smaller airways (generations 12 ± 5.7 and below for asthmatics and 13 ± 4.1 and below for healthy subjects). Finally, when we calculated the degree of constriction for the entire airway tree, asthmatics constricted to a slightly higher degree (μ = 28%, σ = 21%) compared with healthy subjects (μ = 20%, σ = 23%).

Fig. 7.

Pooled results of image functional modeling (IFM) for the best match to both mechanics and ventilation for healthy and asthmatic subjects. The mean and standard deviation of constriction are shown for airways leading to ventilation defects, airways outside of ventilation defects, and all airways in the tree. Slightly larger mean constriction was seen in all asthmatic airways; however, no significant differences were seen between healthy and asthmatic subjects.

DISCUSSION

Distilling out the airway constriction conditions and airway sizes most responsible for degradation of mechanical and ventilation dysfunction during human asthmatic provocation remains a challenging and unanswered issue. Imaging technology remains unable to probe small airways (<2–3 mm) with sufficient time resolution to capture the nature of the disease. Using a variety of loosely supported rationale, several studies have continued to convey that the larger airways bare the brunt of responsibility (4, 14), and hence, if one can prevent these airways from constricting (e.g., via bronchial thermoplasty), one can prevent or at least alleviate much of the severity of asthma. This rationale, however, contradicts intuition regarding the extraordinary number of small airways and the fact that the material properties, reported remodeling, and inflammation in such airways in asthmatics should greatly facilitate over constriction of small compared with large airways when the smooth muscle around them is activated (6). In 2003, Tgavalekos et al. (16) proposed an alternative approach to probing the airway conditions that likely contribute to asthma. They synthesized imaging data of ventilation dysfunction with oscillatory mechanics data, sensitive to the degree and pattern of airway constriction within anatomic models that were forced to match both sets of data. This provocative approach resulted in two major conclusions. First, they concluded that ventilation defects had to derive from severe constriction of primarily very small airways (<1 mm). If larger airways were severely constricted, model ventilation defects became much larger and more spatially distributed than the data supported. Second, to also match oscillatory mechanics, airway constriction had to occur throughout the airway tree and had to include small airways (i.e., constriction of larger airway alone could never explain both mechanics and ventilation imaging data). The current work extended this approach by using ventilation data covering the entire lung field via HP ³He MRI and by forcing the model to also match the specific ventilation to all lung units in an image-based voxel.

Our primary conclusions are unchanged from the original Tgavalekos study but have become more refined and applicable to recently proposed treatment approaches for upper airways. Unlike our previous study with PET imaging (15), the current study provided imaging of the entire lung field. Thus, although the PET IFM analyses had to assume some statistical properties of the airways outside the image field that were consistent with the in-field data, the current study mapped the entire lung explicitly. Several new findings also have emerged. First, by using the quantitative ventilation distribution data during our IFM approach, we found that recreation of the so-called ventilation defects in the model does not require absolute closure of the airways leading to them. Certainly, visual inspections of the images reveal heterogeneous clusters of what appear to be very poorly ventilation lung regions. Our current IFM approach indicated that such reasons are likely subtended by airways that have constricted by ∼70% of their baseline diameter and hence are not actually closed or collapsed. In short, these regions are ventilated, but with a likely time constant that makes them operate as functionally closed from a gas exchange perspective.

The second interesting new result is that the model always underestimated the specific ventilation of well-ventilated units and confined them to a narrow range (Fig. 5). We consider several possible reasons. First, although the model is anatomically consistent down to the level of the acini, it is not a precise 3-D replica of the entire airway tree. In fact, there are only some 29,000 terminal airways in the entire model. Thus the actual lung might be able to distribute highly ventilated regions more so than such a model. Second, the model assumes that the baseline FRC is 3 liters and is evenly distributed over all the terminal airways. Gravitational forces and nonlinearities of inherent stress-strain properties of lung tissue most likely cause this not to be the case, especially postprovocation and in asthmatics. This assumption limits the amount of overventilation that can occur in a particular acini. Hence, we often underestimate the true ventilation in areas outside of the ventilation defects. Third, after airway provocations, some airways may actually dilate while others constrict. In a real lung, this would enhance the fraction of tidal volume entering the acini subtended by the dilated airways. In our model analysis we allowed airways to dilate up to 10% of their baseline diameter based on the random Gaussian draws; however, we did not impose dilation in airways explicitly leading to ventilated acini or allow dilation of more than 10%. It is possible that airways leading to well-ventilated areas need to be more dilated to accurately match ventilation images. In fact, dilation in some airways during lung constriction has occurred in other computational models as a consequence of the complex relation between smooth muscle and airway geometry (2, 20). Also, some recent imaging data revealed airway dilations do occur in some larger airways postmethacholine (18). Future applications might try and explicitly match more highly ventilated regions by imposing such dilations in a manner similar to how we identified severe constriction necessary to match the ventilation defects in the images.

To match the final lung mechanical and ventilation conditions following airway provocation in an asthmatic, one must include substantial and heterogeneous constriction in small airways. This is not to say that large airways do not constrict (indeed, they can and do), but our prediction is that large airway constriction alone is incapable of matching our data.

Recent studies by Venegas et al. (20) suggest some coupling between constriction that occurs in larger airways and the conditions in small airways that cause heterogeneous clusters of ventilation defects. Regardless of such coupling, our study expanded the approach of Tgavalekos et al. to the entire lung field and continues to predict that heterogeneous and substantial constrictions of small airways are essential phenotypes of asthma postprovocation. Future studies are needed to connect potential mechanisms implied from the studies of Venegas et al. to the results from our work. It is conceivable that the conditions in the small airways require some initial threshold of constriction in the larger airways. Future modeling studies can address this, but if this were the case, it could explain some level of efficacy for treatments that target large airways.

Our study is based on the validity of the anatomic model, and there remain some important limitations that could impact our results. First, the same airway tree was applied to all subjects. We do not know whether a “generic” airway tree would distort the necessary airway conditions compared with a tree personalized for a particular subject's thoracic space. Generally, we anticipate that the morphometry of a human lung would be consistent from subject to subject. The main concern, though, is whether a lack of a one-to-one 3-D match in the lung peripheral airways would necessarily result in an overestimation of the number of very smaller airways needed to constrict to recreate ventilation defects. Tgavalekos et al. (15) explored this issue somewhat and showed that the mismatch is not likely to cause more than a generation or two of larger airway sizes that could explain our data. However, their analysis still used the generic tree, and this issue remains open if additional constraints were imposed such as whether the growth of the airway tree into a particular thoracic volume should consider the locations of the defects a priori. For example, if defects could only derive from a single parent, perhaps a larger number of upper generations would require closure. Such conditions would still need to be able to also match oscillatory mechanics data. A second limitation is our small sample size. The scope of this project was to advance IFM to engage an imaging modality that captures the entire lung in a clinically compatible fashion and with image processing that permits us to incorporate specific ventilation distributions into the resulting airway constriction predictions. We believe that our results confirm viability of this approach, and moreover, our results were remarkably consistent among subjects within each group (normal or asthmatic). Consequently, we believe that although the subject pool was small, it is unlikely that adding data from additional subjects would alter our studies predictions regarding the role of small airways, in general, and the relative degree of constriction in those airways leading to ventilation defects.

In summary, we have shown that to apply a generic but still morphometically consistent 3-D airway tree to match both oscillatory mechanical and ventilation imaging data, small airways (<2 mm) must be constricted by ∼70% of their baseline diameter, consistent with results from Tgavalekos et al. (15). This result at first would predict that therapies targeting only larger airways such as bronchial thermoplasty would not be effective. However, it is unknown whether these airways constrict independently or rely on a coupling mechanism with airways upstream, as recently modeled (20). If improvements are seen in asthma severity as a result of bronchial thermoplasty, coupling between the constriction in large and small airways must occur.

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Grant R01 HL62269-04.