Skip to main content
NCBI home page
Journal of Computational Biology logoLink to Journal of Computational Biology
. 2008 Sep 1;15(7):737–754. doi: 10.1089/cmb.2007.0130

Deterministic Pharmacophore Detection via Multiple Flexible Alignment of Drug-Like Molecules

Dina Schneidman-Duhovny 1,*, Oranit Dror 1,*, Yuval Inbar 1,*, Ruth Nussinov 2,,3, Haim J Wolfson 1
PMCID: PMC2699263  NIHMSID: NIHMS115304  PMID: 18662104

Abstract

We present a novel highly efficient method for the detection of a pharmacophore from a set of drug-like ligands that interact with a target receptor. A pharmacophore is a spatial arrangement of physico-chemical features in a ligand that is essential for the interaction with a specific receptor. In the absence of a known three-dimensional (3D) receptor structure, a pharmacophore can be identified from a multiple structural alignment of ligand molecules. The key advantages of the presented algorithm are: (a) its ability to multiply align flexible ligands in a deterministic manner, (b) its ability to focus on subsets of the input ligands, which may share a large common substructure, resulting in the detection of both outlier molecules and alternative binding modes, and (c) its computational efficiency, which allows to detect pharmacophores shared by a large number of molecules on a standard PC. The algorithm was extensively tested on a dataset of almost 80 ligands acting on 12 different receptors. The results, which were achieved using a set of standard default parameters, were consistent with reference pharmacophores that were derived from the bound ligand-receptor complexes. The pharmacophores detected by the algorithm are expected to be a key component in the discovery of new leads by screening large databases of drug-like molecules. A user-friendly web interface is available at http://bioinfo3d.cs.tau.ac.il/pharma. Supplementary material can be found at http://bioinfo3d.cs.tau.ac.il/pharma/reduction/.

Key words: computer-aided drug design (CADD), rational drug discovery, 3D molecular similarity, 3D molecular superposition

1. Introduction

A pharmacophore is the three-dimensional (3D) arrangement of features that is essential for a ligand molecule in order to interact with a target receptor in a specific binding mode. Once identified, a pharmacophore can serve as an important model in rational drug design, since it can aid in the discovery of new lead compounds that can bind to a target receptor. Many computational methods for pharmacophore identification have been developed (Dror et al., 2006; Güner, 2000). The methods are classified into direct and indirect methods. Direct methods use both ligand and receptor structural information. However, often the 3D structure of the receptor is unknown. In such cases, only indirect methods, which derive a pharmacophore only from a set of ligands that have been experimentally observed to interact with the receptor, are applicable. Generally, given a set of active ligands, the indirect methods search for the largest or highest scoring 3D pattern of features responsible for binding that is shared by all or most of the input ligands. If we represent the ligands by the 3D positions of the features that they possess, then a simpler variant of the problem is the largest common point set (LCP) problem in computational geometry, which is known to be NP-hard even when the input consists of only three 3D point sets (Akutsu and Halldorsson, 2000; Shatsky et al., 2006). The pharmacophore identification problem is further complicated by the fact that drug-like molecules are flexible, mainly due to rotatable bonds. As a result, they may have many possible conformations. The specific ligand conformations that bind in the active site of the receptor are unknown. Thus, all the feasible conformations of each input ligand have to be considered.

Due to the hardness of the problem, no indirect method finds the optimal solution in polynomial-time. The various existing approaches mainly differ in (i) the chosen feature descriptors and structure representation, (ii) their technique for addressing the ligand flexibility, and (iii) the pattern identification algorithm (Dror et al., 2006). The different feature descriptors mainly depend on the desired level of resolution. At the highest level, a feature is defined as the 3D position of an atom associated with the atom type (Holliday and Willet, 1997; Handschuh et al., 2000; Finn et al., 1998). At the next (coarser) level, atoms are grouped into topological features such as phenyl ring and carbonyl group (Chen et al., 1999). Finally, at the lowest level of resolution, spatially adjacent atoms are grouped into physico-chemical functional features that are important for ligand-receptor binding, such as aromaticity, charge, hydrogen bonding and hydrophobicity (Güner et al., 2004; Clement and Mehl, 2000; Barnum et al., 1996; Li et al., 2000). The ligands as well as the searched pharmacophore pattern are then described by the features that they possess, and their structures are represented mainly as 3D point sets (Finn et al., 1998), distance matrices (Crandell and Smith, 1983; Brint and Willett, 1987), graphs (Takahashi et al., 1987; Brint and Willett, 1987), or trees (Hessler et al., 2005). Most indirect methods treat the conformational search in a separate initial stage. A discrete set of conformations is generated with the goal of sampling the whole conformational space of each ligand (Martin et al., 1993; Barnum et al., 1996; Clement and Mehl, 2000; Güner et al., 2004; Finn et al., 1998; Holliday and Willet, 1997; Richmond et al., 2006; Dixon et al., 2006). The main drawback of this approach is that the number of conformations required to cover the whole conformational space might be extremely large, especially for highly flexible compounds. An alternative approach is to combine the conformational search within the pattern identification process. The main advantage of this approach is that the search space is not limited to a precomputed discrete number of conformations. However, to date the methods that adopt this approach are based on a random search (Chen et al., 1999; Jones et al., 1995; Handschuh et al., 2000; Cottrell et al., 2004). Furthermore, even for the simplified problem of superimposing only a pair of (and not multiple) ligands, deterministic algorithms that do incorporate the conformational search within their superposition process are rare. Two such methods are FlexS (Lemmen and Lengauer, 1997) and fFLASH (Krämer et al., 2003). The most common techniques for identifying pharmacophore patterns are clique-detection (Martin et al., 1993; Holliday and Willet, 1997; Baum, 2005), exhaustive search (Güner et al., 2004; Chen et al., 1999), and genetic algorithms (Holliday and Willet, 1997; Jones et al., 1995; Handschuh et al., 2000; Cottrell et al., 2004).

Here, we present a new indirect method named Pharmagist for pharmacophore detection. The main novelty of the method lies in its explicit consideration of ligand flexibility in the pattern identification stage. The algorithm is highly efficient, as demonstrated in Results. Another key advantage of the method is its ability to find candidate pharmacophores shared by non-predefined subsets of the input ligands. This makes the method tolerant to outliers and to several binding modes. The performance of the method has been successfully evaluated on a benchmark dataset taken mainly from the FlexS dataset (Lemmen et al., 1998). This dataset consists of 74 ligands that are classified into 12 cases according to the protein receptor to which they bind.

2. Methods

2.1. Problem definition

General

Given a set of ligands, the goal is to find candidate pharmacophore, namely the largest (or highest scoring) 3D patterns of features responsible for binding that are shared by a significant number of input ligands. If we consider the ligands as rigid bodies represented by the 3D positions of their features, then a simpler optimization task is to search for the maximal cardinality 3D set of features that is shared by all ligands. This task is equivalent to the largest common point set (LCP) problem in computational geometry, which is NP-hard even for the case of only three 3D point sets (Akutsu and Halldorsson, 2000; Shatsky et al., 2006). The pharmacophore detection task is even more complicated, since drug-like ligands are flexible and thus can adopt many conformations. As shown in the supplementary material, even the simplest case of finding the largest common set of features shared by a pair of molecules, one rigid and one flexible, is NP-Hard.

There are two other related requirements that are expected from a robust method for pharmacophore detection. The first requirement is motivated by the fact that, due to alternative binding modes, the same set of ligands may share several pharmacophores. Thus, the aim is to detect not only the largest (or highest scoring) candidate pharmacophore, but also other candidates, as long as their score is larger than a predefined threshold. Additionally, in order to overcome outlier ligands and to be able to deal with several binding sites of the target receptor, it is important to find candidate pharmacophores shared by only some of the ligands. This requirement complicates the problem since the number of ligand subsets is exponential in the number of input ligands. Furthermore, since there is a trade-off between the number of ligands and the number of features in their common 3D pattern, the exact definition of the requirement is quite vague mathematically. One possible approach, which we have adopted, is to find for any possible number of r input ligands, candidate pharmacophores shared by exactly r input ligands for which the score is greater than a predefined threshold.

Our approach

The input is a set of ligands, each given by the 3D coordinates of its atoms’ centers and the covalent bonds between them. To avoid explicit conformational search, we assume that one of the ligands, called the pivot, is given in its active conformation and thus considered as rigid. In contrast, the other (target) ligands are treated as capable of exhibiting torsional flexibility about their rotational bonds. Informally, the goal is to find the highest scoring 3D pattern of pivot features that can be aligned to most of the target ligands. We approach this task by searching for conformations of the target ligands and their superpositions on the pivot such that the score of the superimposed common features is maximized. Note that the pivot ligand may be selected by the user as the ligand with highest affinity to the receptor or the ligand with the smallest number of degrees of freedom. However, the default assumption is that the identity of the pivot ligand is unknown. Thus, the method iteratively selects each one of the input ligands to serve as a pivot.

Formally, we consider a feature of a molecule to be a set of atoms with a physico-chemical property important for ligand-receptor binding (aromaticity, charge, hydrogen bonding, or hydrophobicity). Let S(f p, f t) be a given scoring function for measuring the similarity between a pair of features, f p of the pivot and f t of a target ligand. We associate each feature with its center of mass and define the following terms:

Definition 1. Potentially Matched Features. A pair of features, f p of the pivot and f t of the target ligand t, are said to be potentially matched if their Euclidean distance is below a predefined threshold ϵ and their similarity score S(f p, f t) is positive.

Definition 2. Flexibly Matched Feature Sets. Two equal-sized sets of l features, one of the pivot and one of a target ligand, Inline graphic and Inline graphic, are said to be flexibly matched if there are a feasible conformation of the target ligand and a 3D pose (position and orientation) for it, such that the corresponding features, Inline graphic and Inline graphic (for any 1 ≤ i ≤ l) are potentially matched. The score of a pair of flexibly matched feature sets, F p and F t, is defined as the sum of the similarity scores of the corresponding features, that is Inline graphic.

Definition 3. m-Matched Feature Set. A set of features of the pivot, Inline graphic is said to be m-matched if there are m sets of target features, F t (1 ≤ t ≤ m), each belonging to a different ligand, such that F p and F t are flexibly matched. The score of an m-matched set of pivot features is defined as the center-star score of all matched feature pairs with the m target molecules, that is Inline graphic.

Definition 4. Pharmacophore Detection Problem. Given a pivot, a set of M target ligands, and a distance error ϵ ≥ 0, the goal is to find for any number of m ligands (1 ≤ m ≤ M) the highest scoring sets of pivot features that are m-matched. In case that the pivot is not selected explicitly by the user (the default scenario), an iteration over all input ligands is performed and the goal is generalized to selecting the best pivot as well.

2.2. Method outline

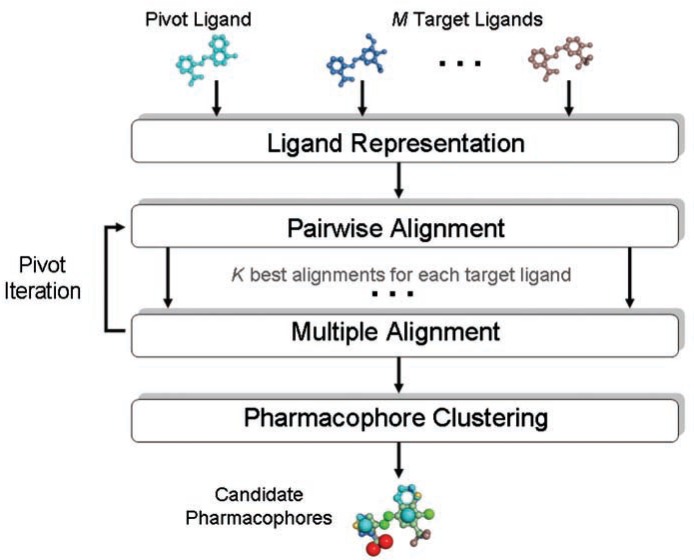
The method consists of four stages: (i) Ligand Representation, (ii) Pairwise Alignment, (iii) Multiple Alignment, and (iv) Pharmacophore Clustering (Fig. 1). In the first stage, each ligand is partitioned into rigid groups connected by rotatable bonds and is assigned a set of physico-chemical features. In the second stage, pairwise flexible alignments between the pivot and each target ligand are computed. In the third stage, we combine pairwise alignments into multiple alignments between the pivot and at least two target ligands. In the fourth stage, all candidate pharmacophores are clustered to produce a non-redundant set of solutions. While the second and the third stages are invoked for each possible pivot separately, the clustering stage is invoked only once to cluster solutions generated by all pivot iterations.

FIG. 1.

FIG. 1.

Open in a new tab

Method flow.

2.3. Ligand representation

A ligand is represented by an atom graph. The vertices of the graph are the atoms of the ligand and the edges are the covalent bonds between them (Fig. 2a). The rotatable bonds of the ligands are identified and each ligand is divided into rigid groups. A bond is considered rotatable if it is not: (i) double, (ii) a ring bond (detected by DFS as an edge on a cycle in the atom graph of the ligand), (iii) a bond connecting a single (leaf) atom, or (iv) a peptide bond. A rigid group of a ligand is defined as a set of atoms between rotatable bonds (including their atoms). To determine the rigid groups of a ligand, the connected components of a graph identical to the atom graph of the ligand but without the rotatable bonds are detected by DFS. Then, a rigid group is specified as the set of atoms of such a connected component and the atoms of the rotatable bonds to which it is connected in the atom graph. This definition ensures at least three atoms in a rigid group (in the extreme cases, a rigid group consists of a leaf atom connected to a rotatable bond or two adjacent rotatable bonds). It also ensures that adjacent rigid groups are not disjoint, but share the atoms of the rotatable bond between them. Note that including both atoms of a rotatable bond in the same rigid group does not violate the rigidity of the group, since when rotating the bond, its atoms remain in the same position relative to the other atoms in the group. The decomposition of a ligand into rigid groups is represented by a directed tree called rigid group tree (Fig. 2b). The vertices of the tree are the rigid groups of the ligand and the edges connect adjacent rigid groups. By DFS, the vertices (rigid groups) are topologically sorted and the edges are directed so that the out-degree of each vertex is at most one.

FIG. 2.

FIG. 2.

Open in a new tab

Ligand representation. (a) An example for an atom graph of a ligand. The vertices of the graph are the atoms of the ligand and the edges are the covalent bonds between them. The rotatable bonds of the ligand are colored in green. Two rigid groups of the ligand are circled. (b) An illustration of the rigid group tree that represents the ligand in (a). The vertices of the tree are the rigid groups of the ligand and the edges connect adjacent rigid groups. The vertices (rigid groups) are topologically sorted and the edges are directed so that the out-degree of each vertex is at most one (the directionality of the edges is not displayed for simplicity). (See this paper online for Fig. 2 in color.)

Finally, we compute for each ligand the features that it possesses. A feature is a set of atoms with a physico-chemical property that is important for binding, namely it is one of the following types: (i–ii) a hydrogen-bond acceptor/donor atom; (iii–iv) an anion/cation atom; (v) a set of atoms of an aromatic ring (detected by a variant of BFS applied on the atom graph of the ligand); and (iv) a pair of adjacent hydrophobic atoms. All features are represented by their center of mass, where aromatic rings are represented by their normals as well.

Applying this stage to a single ligand takes linear time in the size of the ligand, that is O(n) if n is the maximal number of atoms in an input ligand. This is due to the fact that we apply several variants of DFS and BFS on the atom graph of the ligand.

2.4. Pairwise alignment

The input is the pivot and a single target ligand. The pivot is considered as rigid, while the target ligand is treated as flexible. The goal is to simultaneously find feasible conformations of the target ligand and their superpositions on the pivot such that the score of their aligned features is maximized. The algorithm consists of two stages, Rigid Group Alignment and Rigid Group Assembly into a Flexible Alignment. In the first stage, a set of transformations is generated for each rigid group of the target ligand. Each transformation superimposes a target rigid group on the pivot and yields a new candidate pose for the rigid group. In the second stage, we combine candidate poses of the target rigid groups. The result is a set of feasible conformations of the target ligand superimposed on the pivot such that the score of the aligned features is maximized.

2.4.1. Rigid group alignment

The goal is to generate candidate transformations for superimposing the rigid groups of the target ligand onto the pivot. For this purpose, we apply a hybrid technique of Pose-Clustering (Stockman, 1987) and Geometric Hashing (Lamdan and Wolfson, 1988).

In the pre-processing stage, we store all the non-collinear triplets of atoms of the pivot in a 3D hash table. The hash key of a triplet is the triple of side lengths of the triangle that it forms and is invariant to 3D translation and rotation. In the recognition stage, for each rigid group of the target ligand we query the hash-table by all its non-collinear triplets of atoms. The result for each query with a target triplet is a list of all the triplets on the pivot that are almost-congruent to it.

Each pair of almost-congruent triplets, one of the pivot and one of a target rigid group, uniquely defines a transformation that superimposes the target triplet onto the pivot triplet with minimal RMSD (Kabsch, 1978). Different pairs of almost-congruent triplets can lead to nearly identical transformations. Thus, for each target rigid group, we cluster similar transformations and join their matched triplets of atoms into one list. The clustering method is similar to the one used in Rarey et al. (1996) and is based on the RMSD distance between the images of the transformations on the atoms of the target rigid group.

Finally, for each cluster we compute a representative transformation with minimum RMSD between the matched atoms in the joined list in linear time in the size of the list (Kabsch, 1978). These transformations when applied on the target rigid group represent new poses for it on the pivot. For each new pose we compute the highest-scoring feature match list. This is a list of pairs of matched features, one of the pivot and one of the target rigid group. Two such features can be matched if (i) they have an identical physicochemical property,1 and (ii) the distance between their centers of mass, on the pivot and on the new pose of the target rigid group, is less than a predefined threshold ϵ. Each feature match list is associated with a feature score (S(F p, F t) as defined in Section 2.1). Given a new pose of a target rigid group, the feature match list with the highest score is found by an exact algorithm for finding maximal matching in a bipartite graph (Mehlhorn, 1999). The vertices of the graph are the features of both the pivot and the target rigid group. The edges connect potential pairs of matched features and are efficiently constructed by using a 3D look-up grid as follows. The features of the pivot are stored in the grid by their centers. The centers of the features on the pose of the target rigid group are then used to query the grid and find all pivot features in a ball of radius ϵ. Since different features of a molecule cannot be too close in space, the number of pivot features that can be matched to a target feature is bounded by a small constant and the number of edges is thus linear in the number of vertices.

Let n be the maximal number of atoms in a ligand. In the worst case, the target ligand is also rigid and the number of atom triplets that are constructed for each of the two ligands is O(n3). Thus, the maximal number of transformations for superimposing the target ligand on the pivot is O(n6) and clustering them takes O(n12 log n) time (Rarey et al., 1996). The representative transformation of each cluster is computed in O(n) time (Kabsch, 1978), and its feature match list is computed in Inline graphic time (Mehlhorn, 1999). The overall theoretical time complexity is thus O(n12 log n). In practice, since the atoms of a molecule are not random 3D points and cannot penetrate each other, the number of atoms that are close in space is bounded. Thus, by considering only triplets of spatially close atoms, we get a linear number of atom triplets per ligand, O(n2) poses, and an overall complexity of O(n4 log n).

2.4.2. Rigid group assembly into a flexible alignment

The input to this stage is a set of candidate poses for each rigid group of the target ligand. We define a feasible flexible alignment of the whole target ligand on the pivot as an assembly of input poses that fulfills the following criteria: (i) there is exactly one pose for each rigid group; (ii) poses of two adjacent rigid groups are consistent, namely they agree on the location of their two shared atoms2 and cause no steric clashes between non-shared atoms; and (iii) there are no steric clashes between poses of atoms on non-adjacent rigid groups. The goal is to find K feasible flexible alignments of the target ligand on the pivot with the highest feature scores of the associated feature match lists under the assumption of an additive score. This problem is NP-Hard (see Supplementary Material). Below, we first present a graph-theory algorithm that solves the problem in polynomial time under the relaxation that: (*) steric clashes between poses of non-adjacent rigid groups are allowed (condition iii). Then, we explain how to use this algorithm to find the K highest-scoring feasible flexible alignments that fulfill all the three conditions.

Assembly Graph Construction. We construct a weighted N-partite DAG, called assembly graph, where N is the number of rigid groups in the target ligand (Fig. 3). Each partition is associated with all the candidate poses of a specific rigid group. A vertex represents one pose for the respective rigid group. A pair of vertices in two different partitions are connected by an edge if they represent consistent poses of adjacent rigid groups. The rationale behind this construction is that any feasible flexible alignment of the target ligand on the pivot is represented by a tree in the graph and its feature score is the sum of the weights of all its vertices and edges. The weight of a vertex is the feature score of the represented rigid group pose. Adjacent rigid groups share the two atoms of the connecting rotatable bond and thus may have common features. To avoid double scoring of these features, we assign to each edge a non-positive weight computed as follows. We merge the feature match lists of the two connected rigid group poses and define the weight of the edge as the feature score of the resulting list minus the sum of the scores of the two separate feature match lists. The partitions of the assembly graph are ordered according to the order of the rigid groups in the rigid group tree of the target ligand (see Section 2.3). The edges of the assembly graph are directed according to this order, from the vertex in the partition with the lower index (source partition) to the vertex in the partition with the higher index (target partition). The directionality of the edges ensures that all the out-edges that start from a specific source partition always end at the same target partition. This ordering is exploited in the next stage of the algorithm.

FIG. 3.

FIG. 3.

Open in a new tab

Assembly graph. An example for an assembly graph of a target ligand with five rigid groups. The graph is a DAG with five partitions. The vertices of each partition are circled and represent different poses of the same target rigid group on the pivot. Edges exist between consistent poses of adjacent rigid groups. An example for an assembly tree is depicted in red. (See this paper online for Fig. 3 in color.)

Search for the K-Best Assembly Trees. Our aim is to find the K-best (highest-scoring) trees in the assembly graph that include at most one vertex from each partition. Such an assembly tree represents a feasible flexible alignment of the target ligand with the pivot (under relaxation *), since at most one pose is selected for each rigid group and the edges in the tree connect consistent poses of adjacent rigid groups. The K-best assembly trees are computed by dynamic programming in a bottom-up manner from the leaves to the root. In each step, the K-best assembly trees rooted at vertices in a particular partition are computed. Specifically, the K-best assembly trees rooted at vertex υ in the current partition are computed based on the K-best assembly trees rooted at vertices in source partitions that have out-edges to υ. The order of the partitions and the directionality of the edges ensures that the K-best assembly trees of all vertices in source partitions with out-edges to υ have already been computed in previous steps.

An assembly tree rooted at vertex υ is computed by combining assembly subtrees rooted at vertices in source partitions and the corresponding in-edges of υ such that at most one subtree is selected from each source partition. This guarantees that in the resulting tree only one pose is selected for each rigid group. Each vertex υ holds a sorted list of the K-best assembly trees rooted at υ. For a vertex with no in-edges, the only possible assembly tree consists of the vertex itself. For a vertex υ with in-edges from D source partitions, the K-best trees are computed in two stages: Source Partition Merge and Tree Union (Fig. 4). In the first Source Partition Merge stage, we select for each source partition of υ all the vertices that have out-edges to υ and merge their sorted list of K-best trees into one sorted list with the K-highest scoring trees. The score of each tree in the merged list is the sum of the score of the original tree and the score of the connecting edge to υ. In the second, Tree Union, stage the input is the merged list of K-best assembly trees for each source partition of υ. Any combination of subtrees, each taken from a different input list, defines an assembly tree of υ. The K-best assembly trees of υ are computed by selecting the K-highest scoring combinations of assembly subtrees. The score of such tree is the sum of the scores of the combined subtrees and the score of υ. There are KD such possible combinations. However, since we are interested only in the K highest scoring ones, there is no need to enumerate all of them. This problem can be generally stated as: given D sorted arrays of numbers, find the K D-tuples of array indices with the highest sum of numbers. This problem can be efficiently solved as follows (Huang and Chiang, 2005). In an initialization stage we insert the highest-scoring D-tuple into a heap. This D-tuple is the tuple that points to all the first elements in the input sorted arrays. As long as less than K highest-scoring D-tuples have been reported, we report the highest-scoring D-tuple in the heap. Then, we extract this tuple from the heap and insert to the heap all its child tuples, where a child-tuple is a D-tuple similar to its parent tuple, but with the next index in one of its entries. We have further enhanced this procedure by inserting a tuple to the heap only after all its parents have been reported. Once the lists of K-best assembly trees for all the vertices are computed, we merge the lists of all vertices into one list and retain the K highest scoring trees.

FIG. 4.

FIG. 4.

Open in a new tab

Search for the K-best assembly trees. (a) A subgraph of the assembly graph depicted in Figure 3. (b) An illustration for the computation of the K-best assembly trees rooted at vertex υ of partition 3 by dynamic programming. This vertex has four in-edges from two source partitions, 1 and 2. The order of the partitions and the directionality of the edges ensures that the K-best assembly trees rooted at vertices w1, w2, u1, and u2 have already been computed in previous steps of the dynamic programming algorithm and are stored in sorted lists, one list for each node. The computation of the K-best assembly trees rooted at vertex υ consists of two stages. In the first, Source Partition Merge, stage a sorted list of K best assembly trees is computed for partition 1 based on the sorted lists of K best assembly trees of its two vertices, w1 and w2. A similar list is also computed for partition 2. In the second, Tree Union, stage a sorted list of K-best assembly trees for vertex υ is computed based on the two lists computed for partitions 1 and 2 in the previous stage.

The construction of the assembly graph ensures that any two connected vertices represent consistent poses of two adjacent rigid groups in the target molecule. However, a tree in the assembly graph might present inconsistency (steric clashes) between atoms of non-adjacent rigid groups. Thus, not all the K-best trees found by the algorithm represent feasible flexible alignments. Due to the geometry of drug-like molecules, the number of trees with inconsistent poses is usually much smaller than that of the consistent trees. Therefore, we iteratively increase the number of searched assembly trees until K feasible flexible alignments with a positive score are found (if exist).

An assembly tree does not necessarily contain poses for all the rigid groups of the target ligand. To obtain a feasible conformation for the whole target ligand, for each missing rigid group in the assembly tree, we set its pose according to the transformation of its predecessor rigid group (in DFS order) in the rigid group tree of the target ligand. Finally, for each new conformation of the target ligand, we update the list of matched features with the pivot by applying a maximum cardinality matching algorithm as described in Section 2.4.1.

The algorithm works separately on each vertex in the assembly graph G(V, E). Let υ be a vertex with d in-edges from D source partitions. Let di be the number of in-edges of υ from source partition i. That is, Inline graphic. The first, Source Partition Merge, procedure of the algorithm is applied several times, one time for each partition with out-edges to υ. The time complexity of this procedure on partition i is O(K log di), since it merges di sorted lists. The time complexity of the second, Tree Union, procedure is O(KD log D + K log K) (Huang and Chiang, 2005). The overall complexity for vertex υ is thus O(Kd log d + K log K), resulting in an Inline graphic time complexity for all vertices, where Inline graphic is the maximum degree of a vertex. According to Section 2.4.1 |V|, which is the number of poses, is O(n2), where n is the maximal number of atoms in a ligand. Thus, in the worst case, Inline graphic is O(n2) and |E| is O(n4). This leads to an overall time complexity of O(Kn4 log n + n2 K log K). In practice, the assembly graph is sparse, |E| = |V| = O(n2) and the time complexity is lower.

2.5. Multiple matching

The input is the pivot, M target molecules and K pairwise alignments between each target molecule and the pivot. Each pairwise alignment matches a set of pivot features Fp to a set of features Fi of a target molecule with score S(Fp, Fi). A selection of m (2 ≤ m ≤ M) target molecules and exactly one pairwise alignment for each one of them defines a multiple alignment. The consensus (m-matched) pivot feature set Inline graphic of a multiple alignment is defined as the intersection of the pivot feature sets matched by all its pairwise alignments. The score of a multiple alignment is the sum of the fractions of the scores of its pairwise alignments with respect to the consensus pivot feature set, that is Inline graphic, where Inline graphic is the feature set matched to Inline graphic in the ith target molecule. The goal is to find for each m (2 ≤ m ≤ M) the highest scoring multiple alignments consisting of exactly m target molecules. The consensus pivot feature sets of these multiple alignments are candidate pharmacophores. This problem is NP-Hard even for K = 1 (proved by a reduction from the maximum k-intersection problem [Staal, 2004]).

There is an exponential number of O((K + 1)M) combinations to construct a multiple alignment from K pairwise alignments for each of the M target molecules. An enumeration over all these possible combinations is impractical. Moreover, we are interested in a method that will be scalable in the number of input molecules. Therefore, a more applicable approach is to enumerate the possible subsets of pivot features that can be matched by multiple alignments. If n is the number of pivot features, then there are O(2n) such subsets. An enumeration over all these subsets is practical since the number of atoms, and thus the number of features, in a typical drug-like molecule is small. We have adopted this approach and enumerate only relevant pivot feature subsets. These are subsets of pivot features that are matched by at least two input pairwise alignments.

A relevant pivot feature subset can be matched by several multiple alignments depending on the selected target molecules and the selected pairwise alignment for each one of them. Given a relevant pivot feature subset Fp, the method represents all the multiple alignments for which Fp is part of their consensus pivot features in a bitwise data structure called combinatorial bucket (CB) (Fig. 5). Specifically, the CB of Fp holds for each target molecule all the pairwise alignments for which the set of matched pivot features includes Fp. Selecting at most one pairwise alignment for each target molecule in the CB defines a multiple alignment for which Fp is part of their consensus pivot features.

FIG. 5.

FIG. 5.

Open in a new tab

Combinatorial bucket (CB). A combinatorial bucket is a bitwise data-structure that represents for a specific pivot feature subset Fp all the multiple alignments for which Fp is part of the consensus set of pivot features. The CB data structure consists of three parts. The first part (on the left) is a bit array that represents the pivot feature subset Fp. Each bit in this array stands for a pivot feature and the bit is on if the corresponding feature is in Fp. The second part (on the bottom right side of the figure) is an K × M 2D bit array. This 2D array represents the K-best pairwise alignments for each of the M target ligands. A bit in this array is on if the represented pairwise alignment matches the pivot feature subset Fp. The third part of the CB is a bit array for which each bit stands for one of the M target ligands. A bit i in this array is on if there is some pairwise alignment for target ligand i for which the set of matched pivot features includes Fp (this is the result of a logical or operation on the bits of column i in the K × M 2D array). When two combinatorial buckets are combined, their pivot feature subsets are united (by a logical or operation) and their 2D arrays of pairwise alignments are intersected (by a logical and operation)). To speed up the intersection of the 2D arrays, the bit arrays of matching target ligands is used.

The method computes the relevant pivot feature sets and their CBs incrementally. First, all the relevant sets of size one and their CBs are created. In each of the following steps, all the relevant sets of size i are computed from relevant sets of size i − 1. Specifically a relevant set of size i can be computed as the union of two relevant sets of size i − 1. However, not every union of two sets of size i − 1 leads to a set of size i. Additionally, different pairs of sets of size i − 1 may lead to multiple copies of the same set of size i. Thus, a naive enumeration over all the pairs of sets of size i − 1 is inefficient. Instead, an efficient enumeration based on the following observation is applied. Let Inline graphic be a relevant set with i pivot features sorted by their indices. We can uniquely build this set as the union of two relevant pivot feature sets of size i − 1, one without the first feature Inline graphic and the other without the last feature Inline graphic. Thus, in step i the method enumerates over all the relevant pivot feature sets of size i − 1. For each such set Inline graphic, the method looks for another relevant pivot feature set Inline graphic of size i − 1 without the first feature Inline graphic and with an additional feature Inline graphic, that is Inline graphic. To find all the possible sets Inline graphic for a given Inline graphic, the method enumerates over all the pivot features indexed from ki−1 + 1 to n and checks if there is a relevant pivot feature set Inline graphic as required. The CBs of Inline graphic and Inline graphic are then combined by intersecting their sets of pairwise alignments for each target molecule, meaning that the resulting CB of the union pivot feature set contains a pairwise alignment if and only if it is present in both original CBs.

The many union and intersection operations of sets are efficiently performed using a bitwise representation of both the pivot feature subsets and the CBs. Assuming that the number of features in a drug-like molecule is smaller than the number of bits in a word (a standard of 64 bits), a pivot feature subset is represented by a single integer word. This allows us to keep all the pivot feature subsets in a hash table with a bitwise representation key. A molecule possesses O(n) features, where n is its number of atoms. Thus, the complexity of the stage is O(n|S|MK), where S is the set of all relevant pivot subsets. In the worst case, S = O(2n) and the overall complexity is O(n2n MK).

2.6. Pharmacophore clustering

This stage receives, as an input, the candidate pharmacophores from all pivot iterations. Different pivot iterations may lead to similar candidate pharmacophores. These are similar spatial arrangements of the same feature types. Moreover, in case of intra-molecular symmetry, the same pharmacophore may be detected in different regions of the pivot molecule. Therefore, the goal of this stage is to cluster the input candidate pharmacophores and to produce a set of non-redundant representatives.

A cluster of candidate pharmacophores is attributed with a feature key and a representative pharmacophore. The feature key is simply the set of feature types (e.g., 2 aromatic, 3 acceptors, and 1 anion), which is the same for all the candidate pharmacophores in the cluster. The representative pharmacophore is the highest scoring candidate pharmacophore in the cluster. The clusters are constructed by iterating the input candidate pharmacophores according to their score in descending order. In each iteration, a feature key for the current pharmacophore candidate is generated. All the clusters with the same feature key are identified (using a hash table) and their representative pharmacophores are compared to the current candidate pharmacophore. If there is a cluster for which the representative pharmacophore has an almost congruent spatial arrangement of features as the current candidate pharmacophore, then the current pharmacophore candidate is added to the cluster. Otherwise, a new cluster is created with the current candidate pharmacophore as its representative.

2.7. Overall time complexity

The most time-consuming stages are the pairwise alignment and the multiple alignment stages. For a single pivot ligand and M target ligands, the two stages together take O(M(Kn4 log n + n2 K log K) + n2n MK) time, where n is the maximal number of atoms in a ligand and K is the number of pairwise alignments produced between the pivot and each target ligand. Since we try all the input ligands as pivots, the overall time complexity is O(M2 Kn(n3 log n + n log K + 2n). As elaborated in Section 2.4.2, this analysis is based on the worst-case assumption that the degree of a vertex in the assembly graph G(V, E) is O(|V|) = O(n2). In practice, the vertex degree is much lower. Let Inline graphic be the maximal vertex degree in the assembly graph. Using this notation, the time complexity of the assembly stage is Inline graphic resulting in Inline graphicInline graphic time for the whole algorithm.

2.8. Web server

A webserver for the Pharmagist program is freely available at http://bioinfo3d.cs.tau.ac.il/pharma. Its user interface is very simple and intuitive. It requires the user to fill a form with only two mandatory fields: molecules in Sybyl Mol2 format and an email address. Other advanced parameters of the algorithm, like setting a pivot ligand, can also be configured via the form. After submitting the form, the pharmacophore detection algorithm starts running. When the job completes, the user is notified by an email that the prediction results are ready. The email contains a link to a web page in which the top-scoring candidate pharmacophores are presented for different numbers of input ligands. The candidate pharmacophores are organized in tables by the number of aligned ligands. In each table, the candidate pharmacophores are sorted by their score in descending order. For a candidate pharmacophore, in addition to the score, the following data are presented: (i) the name of the participating ligands, (ii) the number of common features and their type distribution, and (iii) a link to a page that display the candidate pharmacophore. The candidate pharmacophore page supplies a 3D visualization of the pharmacophore and the multiple flexible alignment that it is based on. The page consists of three parts: (i) a summary of the attributes of the pharmacophore, (ii) a Jmol3 display of the alignment and the common pharmacophore, and (iii) a panel for controlling the Jmol display.

3. Results

3.1. Evaluation procedure

We evaluated the method on a diverse dataset of drug-like ligands that are divided into several test cases. Each test case included several (crystal structure) complexes of the same protein receptor with different ligands. The ligands were separated from their complexes and their structures were minimized. We then applied our method on the minimized ligand structures of each test case (enumerating over all the possible pivots). The resulting candidate pharmacophores were compared to the superposition of the ligand structures in their bound modes. This reference superposition of the ligands was computed by superimposing the structures of the receptor from the different complexes. The rationale behind this evaluation approach is that a pharmacophore of a receptor is the 3D pattern of features shared by the active conformations of its ligands.

The evaluation procedure consists of two stages: (i) preparation of reference pharmacophores from the reference superposition and (ii) comparison of the candidate pharmacophores produced by our method to the reference pharmacophores. The reference pharmacophores are computed from the reference superposition as follows. We iteratively select each ligand to serve as a pivot. In each iteration, based on the reference superposition, we compute the maximal set of matched features between the pivot and each of the other M target ligands. This is carried out by applying a maximal bipartite matching algorithm (Mehlhorn, 1999), where a pair of features can be matched if they have the same type and their distance in the reference superposition is below ϵ. The result is M pairwise alignments (one for each target ligand) that are given as an input to the multiple alignment algorithm. Since this algorithm performs an exhaustive enumeration over all subsets of matched pivot features, it will produce all the possible reference pharmacophores that can be extracted from the reference superposition, including pharmacophores based on subsets of ligands. In the second stage, a candidate pharmacophore matched by r input ligands is first compared to all reference pharmacophores of exactly r ligands. If there are less than three spatially distinct common features, we compare the candidate pharmacophore to all reference pharmacophores of r − 1 ligands and so on, in an attempt to find a significant set of common features. In each comparison, we apply Geometric Hashing (Lamdan and Wolfson, 1988) to produce a transformation that superimposes the candidate pharmacophore onto the reference pharmacophore such that the type of matched features is the same and their distance is below a predefined threshold ϵ. A feature of the candidate pharmacophore is considered as a hit if, after applying the transformation, there are at least two features from different ligands in the reference superposition with the same feature type and at distance below ϵ. The number of hits compared to the total number of features in both the candidate pharmacophore and the reference pharmacophore is used as a measure for evaluating the candidate pharmacophore.

3.2. Benchmark dataset

Our benchmark is mainly based on the FlexS dataset (Lemmen et al., 1998). This dataset consists of 77 x-ray complexes that are classified into 14 test cases according to their receptor. We have considered all cases, except for three cases that are unsuitable for testing multiple alignments since each includes only two complexes. In addition, we have considered another test case of three ACE inhibitors, which was used to evaluate MTree (Hessler et al., 2005). Overall, our benchmark dataset consists of 12 different test cases, each with 3–12 ligands. The ligands vary from small molecules with only several heavy atoms, to peptides that have dozens of rotatable bonds (Table 1).

Table 1.

Benchmark Dataset

Receptor No. of ligands No. of atoms No. of rotatable bonds
Glycogen phosphorylase 4 27 (29) 3 (3)
Carboxypeptidase-A 5 42 (74) 9 (17)
Thrombin 3 66 (71) 10 (11)
Streptavidin 5 34 (39) 4 (5)
Immunoglobulin 5 57 (67) 3 (6)
Endothiapepsin 5 125 (159) 25 (33)
Rhinovirus 8 51 (57) 9 (11)
ACE 3 48 (63) 8 (12)
HIV-protease 10 111 (134) 23 (31)
Elastase 7 55 (70) 11 (15)
Thermolysin 12 45 (69) 9 (15)
Trypsin 7 27 (59) 3 (8)
Open in a new tab

The dataset consists of 74 drug-like ligands that are classified into 12 test cases according to their receptor. The data provided for each test case consists of (i) the name of the receptor, (ii) the number of input ligands, (iii) the average (maximal) number of atoms in a ligand, and (iv) the average (maximal) number of rotatable bonds in a ligand.

The method was applied on the ligands of each test case using the same parameter set. No specific ligand was used as a pivot. Therefore, the algorithm iteratively selected each ligand to serve as a pivot. The score for matching a pair of features of different types was set to 0. The score for matching a pair of features of the same type was set to 1, except for aromatic rings and hydrophobic features for which the score was set to 3.0 and 0.3 respectively. The value of K given to the Flexible Pairwise Alignment algorithm was 1500. The value of the maximal distance error ϵ between two matched features was set to 1.5 Å. In order to account for inaccuracies in the crystal structures, the value of ϵ in the evaluation procedure was set to 1.5–2.0 Å. All computations were performed on a single processor PC workstation (Pentium© 4, 3.20-GHz processor with 3-GB RAM).

A summary of the results for all test cases is given in Table 2. Specifically, this table provides a comparison between the top scoring candidate for every number of input ligands to the reference pharmacophores. A candidate pharmacophore is compared to a reference pharmacophore by (i) the number of common features (hits) out of the total number of features in the candidate pharmacophore; and (ii) the RMSD between the superimposed common features. In addition, we give the maximal number of features in the reference pharmacophore for the same number of molecules as in the evaluated candidate. Below, we first discuss the simple test cases, where a significant reference pharmacophore exists for all ligands. Next, we discuss the more complicated cases, where a significant reference pharmacophore exists for only subsets of the ligands due to outliers or several binding modes.

Table 2.

Benchmark Results

graphic file with name inl-25.gif
Open in a new tab

The data provided for each test case consists of the name of the receptor, the number of input ligands, the runtime (mm:ss, on a standard PC) and details on the top-scoring candidate pharmacophore for different number of input ligands. These details are (i) the number of ligands that match the candidate pharmacophore (# lig); and if the number of ligands in the reference pharmacophore it was compared to is different, this number is specified in brackets; (ii) the number of hits out of the total number of features in the candidate pharmacophore; (iii) the RMSD between the features common to the candidate pharmacophore and the reference pharmacophore; (iv) the maximal number of features (# ref) among reference pharmacophores for the same number of ligands; and (v) the maximal rank of the pairwise alignments (maxK) used in the multiple alignment.

Glycogen Phosphorylase. The four ligands of glycogen phosphorylase share a candidate pharmacophore with eleven features, where nine of them are hits. Furthermore, a candidate pharmacophore with 13 features has been found for three out of the four ligands. All these features match the features of the reference pharmacophore with an RMSD of 0.77 Å. The increase in the number of features in the top-scoring candidate pharmacophores for four and three ligands may suggest that one ligand is an outlier. Indeed, the outlier ligand (PDB:1gpy) is slightly longer than the others and occupies a different region in the active site of the protein receptor (Lemmen et al., 1998).

Carboxypeptidase-A. The five ligands binding to carboxypeptidase-A are very different and possess 21–74 atoms. Nevertheless, the top-ranking candidate pharmacophore found for all five ligands contains all the six features of the reference pharmacophore with an RMSD of 0.19 Å. In addition, a candidate pharmacophore of 10 features was found for a subset of three molecules.

Thrombin. For the thrombin receptor, the reference pharmacophore of the three ligands has only three features, while the top-ranking pharmacophore candidate has two additional hits.

Streptavidin. Similarly, in the case of the streptavidin ligands, the top-scoring candidate pharmacophore for all five ligands includes two additional feature hits. For three molecules, the top-scoring candidate pharmacophore is similar to the one for five molecules, with an additional hydrophobic feature.

Immunoglobulin. The ligands binding to immunoglobulin consist of several hydrophobic rings. These ligands are characterized by a small number of relatively large rigid groups (on average a rigid group consists of twenty atoms). Thus, in this test case the bottle neck of the algorithm is the Rigid Group Alignment procedure of the Pairwise Alignment stage. This is due to the fact that many almost congruent triplets of atoms are generated and matched. Two of the ligands are cholic-acid type (PDB: 1dbj, 1dbk), and three are steroid type (PDB: 1dbm, 2dbl, 1dbb) (Lemmen et al., 1998). The method has successfully found the common hydrophobic core of all five ligands, which consists of 16 hydrophobic features and one HB-acceptor. The method has also found the subset of three steroid type ligands with 18 common features (16 hydrophobic features and two acceptors).

Endothiapepsin. The five ligands binding to endothiapepsin are peptidic inhibitors. Thus, they are quite large (87–159 atoms) and with up to 33 rotatable bonds. The top-scoring candidate pharmacophore for all ligands contains seven features, where five of them are hits. Moreover, candidate pharmacophores with nine and thirteen features have been detected for four and three ligands respectively.

Rhinovirus. The rhinovirus case is interesting since the eight ligands can bind to Rhinovirus in two alternative modes (Fig. 6a,b). The top-scoring candidate pharmacophore for all eight ligands has seven features, where all of them are hits (Fig. 6c). Due to a reversed orientation of half of the ligands in the crystal structures, the candidate pharmacophore was compared to the reference pharmacophore of four ligands. For five ligands, the top-scoring candidate pharmacophore is larger with ten features (Fig. 6d).

FIG. 6.

FIG. 6.

Open in a new tab

(a,b) The two binding modes of Rhinovirus ligands can be distinguished by the relative location of their aromatic ring (a cyan sphere) in the protein binding site (blue). (c) The top-scoring candidate pharmacophore of all eight ligands contains seven features. (d) The top-scoring candidate pharmacophore for five ligands contains ten features. In all figures, green, cyan, and gray spheres represent HB-acceptor, aromatic and hydrophobic features, respectively. (See this paper online for Fig. 6 in color.)

ACE. The top-scoring pharmacophore candidate found for all ligands, ACE, consists of six out of the eight features of the reference pharmacophore.

HIV-Protease. HIV-protease is a symmetric dimer and thus has two symmetric binding modes in the pocket between the two monomers. Its ten ligands are quite large with an average size of 111 atoms. The ligands are also highly flexible with up to 31 rotatable bonds. The method has found that all ten ligands share a candidate pharmacophore with four features, where three of them are hits. In this test case one can clearly see that the number of features grows as the number of ligands decreases.

Elastase. The elastase binding site contains four specificity pockets. The tripeptidic structure of the elastase inhibitors allows them to occupy several of these pockets. Therefore, a reference pharmacophore exists for only three out of seven input ligands. Nevertheless, the method has detected that all seven ligands share a candidate pharmacophore. This candidate pharmacophore consists of an aromatic ring and two HB-acceptors, which are important for binding to one of the specificity pockets (Fig. 7a). The top-scoring pharmacophore candidates found for five ligands is more significant and includes all the features of the reference pharmacophore for three ligands (Fig. 7b). In addition, our candidate pharmacophore for three ligands consists of eleven features, seven of which are hits with an RMSD of 0.83 Å (Fig. 7c).

FIG. 7.

FIG. 7.

Open in a new tab

The Elastase test case. (a–c) The top-scoring candidate pharmacophore for seven, five, and three input ligands consist of three, six, and eleven features, respectively. Cyan, gray, green, and blue spheres represent aromatic, hydrophobic, HB-acceptor and positively charged features, respectively. (See this paper online for Fig. 7 in color.)

Thermolysin. The thermolysin inhibitors can adopt several binding modes. Therefore, a reference pharmacophore exists for only nine out of the twelve input ligands. Nevertheless, the method has detected candidate pharmacophores for different number of input ligands, where their number of features increases from three to ten as the number of aligned ligands decreases.

Trypsin. The trypsin inhibitors are small molecules with an average number of 27 atoms. Consequently, they possess a very small number of physico-chemical features and no significant pharmacophore can be found. Nevertheless, the method has found three common features for a subset of three ligands.

Summary

In all test cases, we have found candidate pharmacophores, where most of their features are hits with an RMSD of at most 1.03 Å. In some cases, the candidate pharmacophores found by the method are shared by more input ligands compared to the reference pharmacophores. These examples (especially the rhinovirus and elastase test cases) show that the method is capable of handling different binding modes of the input ligands. Additionally, for the top-scoring candidate pharmacophore of each test case, we have computed the maximal rank of the pairwise alignments that take part in the respective multiple alignment (maxK in Table 2). This parameter helps us to evaluate the number of pairwise alignments (K) required by the multiple alignment algorithm in order to find the correct solution. In all cases, the value of maxK was less than 1000. The running times of the test cases are between 2 seconds for the three ACE inhibitors and less than 3 minutes for the 10 HIV-protease inhibitors, which possess only few rotatable bonds.

4. Conclusion

We have described a fully automated indirect method for pharmacophore elucidation by multiple flexible alignment of (acyclic) drug-like ligands. This problem is NP-hard with respect to the number of ligands, the number of features and the number of degrees of freedom. The method provides a heuristic solution. Its time complexity is exponential in the number of features, but polynomial in the number of ligands and the number of degrees of freedom. In practice, since the number of atoms, and, thus, the number of features in most drug-like ligands is small, the runtime of the method is immensely satisfying (between a few seconds to a few minutes on a standard PC).

The performance of the method has been successfully evaluated on a benchmark dataset consisting of 74 drug-like ligands divided into 12 test cases. The results show the ability of the method to deal with different types of drug-like ligands including peptides with more than 30 rotatable bonds. The ligand flexibility is fully taken into account in a deterministic manner, an attribute that, to the best our of knowledge, is unique to our pharmacophore detection method. The results also demonstrate that the method is capable of detecting candidate pharmacophores that are shared by non-predefined subsets of input ligands. This makes the method tolerant to the presence of outlier ligands and may aid in distinguishing between pharmacophores of different binding modes. In all test cases no prior knowledge on the receptor was assumed and the default parameters were used. However, in “real-life” drug-design practice, some data on the receptor binding site or on the affinity of the ligands may be available and can be easily taken into account by setting the parameters.

In future work, we intend to improve the method so it will be able to find pharmacophore patterns that are present on non-adjacent rigid groups of the ligands. We would also like to generalize the definition of the searched candidate pharmacophores to deal with cases where a ligand is active despite lacking an important feature for binding that other ligands possess. The method can be strengthened by taking into account ring conformations, deriving a pharmacophore shape as the negative image of the receptor binding site, and the definition of excluded volumes. The presented pharmacophore detection method will be a key component in the selection of new leads for drug design by virtual screening of large databases of compounds.

Acknowledgments

We would like to thank D. Fishlovitch, A. Oron, and H. Senderowitz for their useful advice. The research of O. Dror and Y. Inbar has been supported by the Eshkol Fellowship funded by the Israeli Ministry of Science. The research of H.J.W. has been supported in part by the Israel Science Foundation (grant no. 281/05) and by the Hermann Minkowski-Minerva Center for Geometry at TAU. The research of H.J.W. and R.N. has been supported by the NIAID, NIH (grant no. 1UC1AI067231), and by the Binational U.S.–Israel Science Foundation (BSF). This project has been funded in whole or in part with Federal funds from the National Cancer Institute, NIH (contract no. N01-CO-12400). The content of this publication does not necessarily reflect the view of the policies of the Department of Health and Human Services, nor does mention of trade names, commercial products, or organization imply endorsement by the U.S. Government. This research was supported in part by the Intramural Research Program of the NIH, National Cancer Institute, Center for Cancer Research.

Disclosure Statement

No competing financial interests exist.

1

In principle, the method can match features of different types and maximize their overall score.

2

The validity of the bond angles and the torsional angle are checked as well.

3

Jmol: an open-source Java viewer for chemical structures in 3D (http://www.jmol.org).

References

  1. Akutsu T., and Halldorsson M.M. 2000. On the approximation of largest common subtrees and largest common point sets. Theoret. Comput. Sci. 233, 33–50 [Google Scholar]
  2. Barnum D., Greene J., Smellie A., et al. 1996. Identification of common functional configurations among molecules. J. Chem. Inform. Comput. Sci. 36, 563–571 [DOI] [PubMed] [Google Scholar]
  3. Baum D. 2005. Multiple semi-flexible 3D superposition of drug-sized molecules. Lect. Notes Comput. Sci. 3695, 198–207 [Google Scholar]
  4. Brint A., and Willett P. 1987. Algorithms for the identification of three-dimensional maximal common substructures. J. Chem. Inform. Comput. Sci. 27, 152–158 [Google Scholar]
  5. Chen X., Rusinko III A., Tropsha A., et al. 1999. Automated pharmacophore identification for large chemical data sets. J. Chem. Inform. Comput. Sci. 39, 887–896 [DOI] [PubMed] [Google Scholar]
  6. Clement O.A., and Mehl A.T. 2000. Pharmacophore Perception, Development, and Use in Drug Design. International University Line, La Jolla, CA
  7. Cottrell S.J., Gillet V.J., Taylor R., et al. 2004. Generation of multiple pharmacophore hypotheses using multiobjective optimisation techniques. J. Comput. Aided Mol. Des. 18, 665–682 [DOI] [PubMed] [Google Scholar]
  8. Crandell C., and Smith D. 1983. Computer-assisted examination of compounds for common three-dimensional substructures. J. Chem. Inform. Comput. Sci. 23, 186–197 [Google Scholar]
  9. Dixon S., Smondyrev A., Knoll E., et al. 2006. PHASE: a new engine for pharmacophore perception, 3D QSAR model development, and 3D database screening: 1. Methodology and preliminary results. J. Comput. Aided Mol. Des. 20, 647–671 [DOI] [PubMed] [Google Scholar]
  10. Dror O., Shulman-Peleg A., Nussinov R., et al. 2006. Predicting molecular interactions in silico: I. An updated guide to pharmacophore identification and its applications to drug design. Front. Med. Chem. 3, 551–584 [DOI] [PubMed] [Google Scholar]
  11. Finn P.W., Kavraki L.E., Latombe J.-C., et al. 1998. RAPID: randomized pharmocophore indentification for drug design. Comput. Geom. Theor. Appl. 10, 263–272 [Google Scholar]
  12. Güner O.F., ed. 2000. Pharmacophore Perception, Development, and Use in Drug Design. International University Line, La Jolla, CA
  13. Güner O.F., Clement O., and Kurogi Y. 2004. Pharmacophore modeling and three-dimensional database searching for drug design using catalyst: recent advances. Curr. Med. Chem. 11, 2991–3005 [DOI] [PubMed] [Google Scholar]
  14. Handschuh S., Wagener M., and Gasteiger J. 2000. The search for the spatial and electronic requirements of a drug. J. Mol. Model. 6, 358–378 [Google Scholar]
  15. Hessler G., Zimmermann M., Matter H., et al. 2005. Multiple-ligand-based virtual screening: methods and applications of the MTree approach. J. Med. Chem. 48, 6575–6584 [DOI] [PubMed] [Google Scholar]
  16. Holliday J., and Willet P. 1997. Using a genetic algorithm to identify common structural features in sets of ligands. J. Mol. Graphics Model. 15, 203–253 [DOI] [PubMed] [Google Scholar]
  17. Huang L., and Chiang D. 2005. Better k-best parsing. Proc. Ninth IWPT 53–64 [Google Scholar]
  18. Jones G., Willett P., and Glen R. 1995. A genetic algorithm for flexible molecular overlay and pharmacophore elucidation. J. Comput. Aided Mol. Des. 9, 532–549 [DOI] [PubMed] [Google Scholar]
  19. Kabsch W. 1978. A discussion of the solution for the best rotation to relate two sets of vectors. Acta Cryst. A34, 827–828
  20. Krämer A., Horn H., and Rice J. 2003. Fast 3D molecular superposition and similarity search in databases of exible molecules. J. Comput. Aided Mol. Des. 17, 13–38 [DOI] [PubMed] [Google Scholar]
  21. Lamdan Y., and Wolfson H. 1988. Geometric hashing: a general and efficient model-based recognition scheme. Proc. IEEE Int. Conf. Comput. Vision 238–249 [Google Scholar]
  22. Lemmen C., and Lengauer T. 1997. Time-efficient flexible superposition of medium-sized molecules. J. Comput. Aided Mol. Des. 11, 357–368 [DOI] [PubMed] [Google Scholar]
  23. Lemmen C., Lengauer T., and Klebe G. 1998. FlexS: a method for fast flexible ligand superposition. J. Med. Chem. 41, 4502–4520 [DOI] [PubMed] [Google Scholar]
  24. Li H., Sutter J., and Hoffmann R. 2000. Pharmacophore Perception, Development, and Use in Drug Design. International University Line, La Jolla, CA
  25. Martin Y., Bures M., Dahaner E., et al. 1993. A fast new approach to pharmacophore mapping and its application to dopaminergic and benzodiazepine agonists. J. Comput. Aided Mol. Des. 7, 83–102 [DOI] [PubMed] [Google Scholar]
  26. Mehlhorn K. 1999. The LEDA Platform of Combinatorial and Geometric Computing. Cambridge University Press, Cambridge, UK
  27. Rarey M., Wefing S., and Lengauer T. 1996. Placement of medium-sized molecular fragment into active sites of protein. J. Comput. Aided Mol. Des. 10, 41–54 [DOI] [PubMed] [Google Scholar]
  28. Richmond N., Abrams C., Wolohan P., et al. 2006. GALAHAD: 1. Pharmacophore identification by hypermolecular alignment of ligands in 3D. J. Comput. Aided Mol. Des. 20, 567–587 [DOI] [PubMed] [Google Scholar]
  29. Shatsky M., Shulman-Peleg A., Nussinov R., et al. 2006. The multiple common point set problem and its application to molecule binding pattern detection. J. Comput. Biol. 13, 407–442 [DOI] [PubMed] [Google Scholar]
  30. Staal A.V. 2004. Privacy: a machine learning view. IEEE Trans. Knowledge Data Eng. 16, 939–948 [Google Scholar]
  31. Stockman G. 1987. Object recognition and localization via Pose Clustering. J. Comput. Vision Graphics Image Process. 40, 361–387 [Google Scholar]
  32. Takahashi Y., Satoh Y., Suzuki H., et al. 1987. Recognition of largest common structural fragment among a variety of chemical structures. Anal. Sci. 3, 23–28 [Google Scholar]

Articles from Journal of Computational Biology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES