Modeling a Cross-Sectional Response Variable with Longitudinal Predictors

Abstract

We wish to model pulse wave velocity (PWV) as a function of longitudinal measurements of pulse pressure (PP) at the same and prior visits at which the PWV is measured. A number of approaches are compared. First, we use the PP at the same visit as the PWV in a linear regression model. In addition, we also use the average of all available PP’s as the explanatory variable in a linear regression model. Next, a two-stage process is applied. The longitudinal PP is modeled using a linear mixed-effects model. This modeled PP is used in the regression model to describe PWV. An approach for using the longitudinal PP data is to obtain a measure of cumulative burden, the area under the PP curve (AUC). This AUC is used as an explanatory variable to model PWV. Finally, a joint Bayesian model is constructed similar to the two-stage model.

A. Introduction

In this paper we discuss different methodologies to approach the problem of modeling a response variable that is available at a single time point while the explanatory variable is available at multiple time points. In particular, we wish to model pulse wave velocity (PWV) as a function of pulse pressure (PP = systolic blood pressure — diastolic blood pressure). PWV data is available at only the most recent visit while PP values are available at the same and previous visits.

Methods like panel data analysis, econometric modeling, and time series cross-sectional regressions are some approaches that handle similar situations but the data has to be either balanced or equally spaced.

A class of econometric models called dynamic models explores the relationship when the independent variable is a time series and the dependent variable is measured at a certain time t. i.e. when Y is modeled as a function of the current and lagged X’s. These are called dynamic models because the effect of a unit change in the value of the explanatory variable is felt over a number of time periods. The equation for this kind of model has the following form (Gujarati, 1999):

$${\mathrm{Y}}_t=\mathrm{A}+{\beta }_0{\mathrm{X}}_t+{\beta }_1{\mathrm{X}}_{t-1}+{\beta }_2{\mathrm{X}}_{t-2}+{\mathrm{U}}_{t.}$$

The time series cross-sectional regression analysis (TSCSREG) procedure analyzes linear econometric models that often arise when cross-sectional and time series data are combined. The TSCSREG procedure analyzes panel data sets that consist of a number of sets of time series data on each of several individuals. The performance of an estimation procedure for the model regression parameters depends on the error components chosen to be in the model. The TSCSREG procedure estimates the regression parameters in the model under several error structures (SAS/ETS, 1999).

Panel data usually consist of two dimensions: the cross-sectional or between subjects dimension and the time-series or longitudinal dimension. Generally the time series component is measured at regular intervals. In our case we have a number of subjects with repeated measurements on the covariates which are measured periodically. Hsiao (2003) presents a number of approaches for analyzing panel data.

Each of the methods described above requires balanced data (the same number of observations at common time points). Given the nature of our study, the data are unequally spaced and subjects have varying numbers of repeated measurements. Consequently these approaches cannot be applied in this case.

In section 2 we describe the data to be used in this study. In section 3 we list the approaches to be used to estimate the effect of PP on PWV. In section 4 we present the results of the study and section 5 presents a simulation study to investigate the relative merits of the approaches used. We present our conclusions in section 6.

B. Data

The data consists of 183 male participants from the Baltimore Longitudinal Study of Aging (BLSA). Participants in the BLSA are volunteers who return every 2 years for approximately two and a half days of clinical examinations. In addition to the other variables measured on these participants, pulse wave velocity (PWV), a measure of arterial stiffness was measured on these subjects at some point in time. Earlier, arterial stiffness was roughly estimated by using pulse pressure (PP). Pulse pressure is the difference of systolic and diastolic blood pressures. We wish to model the cross-sectional PWV based on longitudinal pulse pressure (PP) values.

C. Methods

We use a number of approaches to address this problem. The approaches are based on classical methods like linear regression, linear mixed-effects models, and area under the curve (AUC) to analyze this data. We have also used a Bayesian approach and we compare the results obtained from the Bayesian approach with the linear mixed effects model approach. In addition to PP, all the models include age as a covariate as PWV is related to age. An assumption of linear regression models is that the residuals exhibit normality. In this case, when PWV is used in the analyses, the residuals were quite strongly skewed to the right with some minor heteroscedasticity. To overcome these problems, we perform all analyses using ln(PWV). This leads to normal residuals and homoscedastic errors.

C.1 Linear Regression

This is the most naive approach where we model ln(PWV) using multiple regression. Here we initially use PP values at the same visit as PWV and ignore the PP measurements at all previous visits. The linear regression model is:

$$\ln \left({\mathrm{PWV}}_{\mathrm{i}}\right)={\beta }_0+{\beta }_1\times {\mathrm{PP}}_{\mathrm{i}}+{\beta }_2\times {\mathrm{LAge}}_{\mathrm{i}}+{\epsilon }_{\mathrm{i}}$$

where LAge_i is the last age for participant i, the age at which PWV is measured. β₀ is the model intercept, β₁ is the effect of PP on ln(PWV) and β₂ is the effect of last age on ln(PWV). That is, for a unit change in PP, ln(PWV) is expected to change by β₁ and for a unit change in LAge, ln(PWV) is expected to change by β₂. In addition, the average of all the repeated PP values for each participant are used as the predictor in the regression model. There is a mean of 4.62 PP measurements per participant (ranging from 2 to 6). About 50% of participants have six PP measurements while the remaining values (2 to 5) are approximately uniformly distributed.

C.2 Linear Mixed Effects/Regression Approach

Stanek et al. (1999) point out that it is often beneficial to use best linear unbiased predictors (BLUPs) in place of the actual value of a variable, especially when the variable is measured with error. In this case, BLUPs are subject-specific predictions from a mixed-effects model. These predictions are computed using both the fixed- and random-effects to obtain the fitted values. Morrell et al. (2003) use this approach to obtain improved parameter estimates in a logistic regression model. They use the mixed-effects model to predict systolic blood pressure. These predicted blood pressure values are used as explanatory variables in the logistic regression model to predict the occurrence of coronary heart disease. The paper shows that this approach yields more unbiased estimates of the parameters than the naïve approach of just using a single blood pressure value and also produces appropriate inferences. Here we apply their two-step approach to this situation. In the first step, a better estimate of PP is obtained by modeling all available PP data using a linear mixed effects (LME) model. Next, using this LME model, PP is predicted at the time point at which PWV is available. In the second step, ln(PWV) is modeled using the predicted PP from the first step along with last age. The models used in the two-step approach are:

1. PP_LME,ij = θ₀+b_i0 + θ₁×LAge_i + θ₂×LAge_i² + (θ₃+b_i1)×Time_ij + θ₄×Time_ij² + θ₅×LAge_i×Time_ij + δ_ij.

2. ln(PWV_i) = β₀ + β₁× PP̂_LME,i + β₂×LAge_i + ε_i, where in this step PP_LME is the value predicted from step 1.

In the first step, the longitudinal PP data are modeled using a mixed-effects model. The PP depends on the age of the participant at the same visit as the PWV measurement as well as the time of the measurement. Note that to allow for curvature, a quadratic in LAge is used. The longitudinal trends are modeled with a quadratic in Time (measured as time before the PWV visit). Finally, there is an interaction between LAge and Time to allow the longitudinal changes to depend on the participant’s age. The θ parameters are the fixed-effects regression parameters. The random effects, b_i0 and b_i1, allow the intercept and Time-slope to vary among participants. Consequently, each participant will have their own intercept and Time-slope which will lead to participant-specific predictions of PP. At the second step, the model for ln(PWV) is the same as in section C.1 but with the observed PP replaced by the predicted value from the mixed-effects model in step 1, PP̂_LME,i’ , predicted at the visit where PWV is measured. The interpretation of the regression parameters is the same as in section C.1.

C.3. Area under the curve or cumulative burden analysis

The area under the curve (AUC) can be used as a way of assessing the cumulative burden of an explanatory variable on a response variable. For example, Li et al. (2003) use the area under the curve “as a measure of cumulative risk burden from childhood to adult.” In this two-step approach, the longitudinal PP is again modeled using the LME model as in section C.2. Then the area under the curve (AUC) is calculated from the fitted model for each subject. The AUC is the integral of the fitted mixed model with respect to time. Since the fitted model is a quadratic function in time, a formula for the AUC is derived and used to compute an AUC value for each participant (see below). These AUCs are used as the explanatory variables in the regression model along with LAge. Since participants have different lengths of followup, the cumulative burden will depend on this length of followup. Consequently, the AUC is divided by the length of the time interval over which the participant has data. In what follows, AUC means AUC/Time. In addition, the AUC’s are calculated in two ways: for the entire time-span (from the participant’s first visit to the PWV visit); and for a fixed time period (the most recent 2 yrs) to eliminate any effect of different lengths of followup on the results. In the second stage, the transformed PWV is modeled using the AUC calculated from stage 1 along with last age. For this approach, the formula for calculating the AUC and the regression model used to model ln(PWV) in this two-step approach are:

1. PP _AUC,i = -{(θ₀+b_i0 + θ₁LAge_i + θ₂LAge_i²) Time +( θ₃+b_il + θ₅LAge_i) Time ²/2 + θ₄Time³/3}, where the parameter estimates are obtained from the LME model in Step-1 of section C.2 and Time is the length of followup where either the entire followup is used or Time = 2 when the followup is restricted to 2 years.

2. ln(PWV)_i = β₀ + β₁ PP_AUC,i + β₂ LAge_i + ε_iwhere PP_AUC,i is the AUC value computed in step 1 for participant i. The interpretation of the regression parameters in step 2 is similar to the interpretations given in section C.1.

C.4 Bayesian Approach

Guo and Carlin (2004) describe a Bayesian joint model for longitudinal and survival data. Here we follow their approach to jointly model the longitudinal pulse pressure with the regression modeling of ln(PWV) as a function of pulse pressure. The Bayesian joint model first describes the longitudinal pulse pressure data in an identical way to the first part of the two-step LME/Regression approach. The longitudinal model for pulse pressure is:

$${\text{PP}}_{i,j}={\theta }_0+b_{i,0}+{\theta }_1\times {\mathrm{LAge}}_i+{\theta }_2\times {\mathrm{LAge}}_i^2+({\theta }_3+b_{i,1})\times {\text{Time}}_{i,j}+{\theta }_4\times {{\text{Time}}_{i,j}}^2+{\theta }_5\times {\mathrm{LAge}}_i\times {\text{Time}}_{i,j}+{\delta }_{i,j}$$

where δ_ij∼ N(0, σ²_δ) and b_i ∼ N(0, D). Note that the model for PP is the same as the longitudinal mixed-effects model in section C.2. In addition, the normal assumptions on the error term and random effects vector, b_i = (b_i,0, b_i,1)^T , are the standard assumptions for the mixed effects model. σ²_δ is the variance of the random error term and D is a 2×2 positive-definite covariance matrix of the random effects. Next the regression model for the PWV data is specified as:

$$\text{ln}\left({\mathrm{PWV}}_i\right)={\beta }_0+{\beta }_1\times \mathit{P}{\widehat{P}}_{\mathrm{Bayes},i}+{\beta }_2\times {\mathrm{LAge}}_i+{\epsilon }_{i,}$$

where, since time = 0 at the PWV visit, the predicted pulse pressure from the longitudinal model at the PWV visit is

$$\mathit{P}{\widehat{P}}_{\text{Bayes},\mathit{i}}={\theta }_0+{\mathrm{b}}_{\mathrm{i},0}+{\theta }_1{\mathrm{LAge}}_{\mathrm{i}}+{\theta }_2\times {\mathrm{LAge}}_{\mathrm{i}}^2$$

where the parameters and random effects are replaced by their estimates and ε_i ∼ N(0, σ²_ε). Once more, following Guo and Carlin (2004), the vague proper prior distributions are: θ∼ N₆(0, Σθ), 1/σ²δ ∼ gamma(0.2, 0.2),${\mathrm{D}}^{-1}~\text{Wishart}(\left[\begin{array}{cc}\hfill 1000\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 10\hfill \end{array}\right],23),$ β ∼ N₃(0,Σ_β), and 1/σ²_ε ∼ gamma(0.2, 0.2) where Σθ = diag(0.0001, 0.01, 0.01, 0.01, 0.01, 0.01)^-1, and Σ_β = diag(0.0001, 0.0001, 0.001)^-1 These distributions provide relatively flat prior information about the mixed-effects and regression parameters, θ and β. In addition, the Gamma and Wishart priors chosen for the inverses of the three variance/covariance parameters in the models, 1/σ²,_δ D^-1, and 1/σ²_ε, are standard priors for these parameters. The parameters of the prior distributions are again chosen to provide little influence on the posterior estimates of the parameter values.

D. Results

D.1 Results of Approaches using Classical Statistics Models

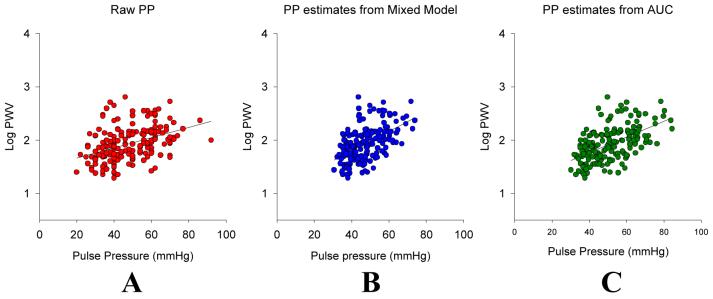
The parameter estimates of pulse pressure obtained from the regression analyses are compared along with their standard error and their 95% confidence intervals among the various approaches. In Table 1 we note that the estimates range from 0.00315 m/s for the linear regression method to 0.0072 m/s for the mixed model approach. For the AUC approach, when we use the entire follow up period, the estimate is 0.0053 m/s while for a fixed time period of 2 years the estimate is 0.00681 m/s, close to the mixed model approach. It is not clear from these results whether linear regression provides underestimates or mixed models are providing overestimates. The R² for all models are very similar. Figure-1 illustrates the pulse pressure estimates obtained from the mixed model approach (Panel-B) as well as the area under the curve approach (Panel-C) in comparison to the observed pulse pressure measures (Panel-A). The slope of pulse pressure in the mixed model approach is much steeper and is in accordance with the result obtained from the model. To enable us to evaluate which approach is best, we conducted a simulation study (see Section E.).

Table I.

Comparison of regression estimates obtained from the classical methods.

Method β1	β1	se(β1)	95% CI	Model R2
LR (same visit)	0.00315	0.00157	0.000041, 0.00625	0.388
LR (average)	0.00584	0.00232	0.00126, 0.01042	0.388
Mixed Model	0.00723	0.00288	0.00154, 0.01291	0.395
AUC(entire follow- up)	0.00539	0.00225	0.00094, 0.00983	0.387
AUC (2 yrs follow- up)	0.00681	0.00277	0.00135, 0.01227	0.388

(Position of Table-I: Should be in the results section at the end of section D.1 and before the beginning of section D.2)

Figure-1.

(Position of the figure should be before part E --the simulation study)

D.2 Results of Bayesian Approach

WinBUGS (Lunn, Thomas, Best, and Spiegelhalter, 2000) was used to fit the Bayesian model to the data. We used 5 chains and thinned the results by 5. After omitting 1000 iterations for burnin, the next 5000 values are used to obtain the posterior distributions and parameter estimates. To check for convergence of the chains to a stable posterior distribution, we examined the history plots, autocorrelations, posterior densities, Brooks-Gelman-Rubin plots, quantile plots, as well as the impact of the priors on the posterior distributions. Based on these checks, the chains of all parameters appear to exhibit a stationary process so that these chains may be used to estimate the posterior distributions of each parameter. Tables 2 and 3 present the means and standard deviations of the MCMC values and compare them to the LME/regression estimates and standard errors. For the longitudinal pulse pressure model, the estimates/mean of posterior distributions and standard errors/posterior standard deviations are almost identical except for some slight differences with the components of the random-effects covariance matrix (Table 2) for the intercept and covariance. For the regression model, the values are also very similar (Table 3). Thus the LME/Regression and Bayes approaches provide very similar results for this data.

Table II.

Comparison of the LME estimates with the posterior mean and standard deviation of the parameters in the longitudinal pulse pressure model.

	LME/Regression Approach			Bayesian Approach
	Estimate	se	95% CI	Estimate	se	95% CI
Fixed Effects
Intercept	52.1	5.9	40.5, 63.8	52.0	6.0	40.3, 63.7
Lage	-0.70	0.22	-1.13, -0.28	-0.69	0.22	-1.13, -0.26
Lage2	0100	0019	0062, .0137	0099	0020	0061, .0138
Time	-1.01	0.40	-1.79, -0.22	-0.98	0.43	-1.81, -0.15
Time2	0.036	0.010	0.016, 0.057	0.040	0.012	0.018, 0.063
Lage×Time	0.033	0.006	0.020, 0.046	0.033	0.007	0.020, 0.046
Random Components
σ2ε	75.34			75.3	4.50	66.93, 84.56
Intercept	53.89			44.92	7.79	31.51, 61.61
Time	0.38			0.40	0.10	0.25, 0.62
Covariance	3.28			1.75	0.77	0.43, 3.43

(Position of Table-II: Should be in the results section at the end of section D.2)

Table III.

Comparison of the regression estimates (from LME/Regression approach) with the posterior mean and standard deviation of the parameters in the regression model of the predicted pulse pressure on the PWV.

	LME			Bayes
	Estimate	se	95% CI	Estimate	se	95% CI
Fixed Effects
Intercept	5.700	0.095	5.513, 5.887	5.683	0.102	5.476, 5.879
LAge	0.00875	0.00162	0.00555, 0.01195	0.00849	0.00177	0.00497, 0.0119
PP	0.00723	0.00288	0.00154, 0.01291	0.00789	0.00327	0.00153, 0.0144
Random Component
σ2ε	0.06239			0.06398	0.00699	0.05154, 0.07891

(Position of Table-III: Should be in the results section after table-II)

E. Simulation Study

To assess which of the methods provides the best approach to estimating the regression parameters a simulation study was conducted. For the purpose of the simulation, the regression model was simplified to contain only the pulse pressure variable and the longitudinal model contains only a linear time term. This will not affect the results since the LAge and Age terms in the longitudinal and regression models, respectively, only affect the level for each subject. Excluding them will not affect the relationship between the longitudinal trend in PP and its association with ln(PWV). The simulation study used 183 subjects with an average of 4 observations per subjects (with 2, 3, 4, 5, or 6 observations). As described in section C.1, in the actual data used in this study there tended to be more participants with 6 observations while the remaining numbers of observations are approximately uniformly distributed. We do not anticipate that using a uniform distribution of the number of observations in the simulaton study will invalidate the results. To generate the data we used the following procedure:

1. Pick “true” PP₀ values, values of pulse pressure at the same visit as the PWV value.

2. Compute ln(PWV) values from the true model: ln(PWV) = β₀ + β₁PP₀ + ε where β₀ = 0, β₁ = 0.005, and ε ∼ N(0, 0.25²).

3. To make sure the longitudinal model has the correct value at the PWV visit, compute random effect: b_i0 = PP₀ + θ₀ where θ₀ = 46.67 (the mean of the true PP₀ values).

4. Generate b_i1 from conditional distribution of $b_{i1}\mid b_{i0}~\mathit{N}(d_{12}∕d_{11}+\mathcal{Z}\times \sqrt{d_{22}-d_{12}^2∕d_{11}})$ where $z\sim N(0,1)\text{and}\mathrm{D}=\left[\begin{array}{cc}\hfill 54\hfill & \hfill 2.718\hfill \\ \hfill 2.718\hfill & \hfill 0.38\hfill \end{array}\right]$.

5. Compute the “observed” PP values: PP=(θ₀ + b_i0) + (θ₁ + b_i1)×T + δ_iT where θ₁ = 0.5 and δ_iT ∼ N(0, 50).

This procedure will create data sets that contain longitudinal PP data and the corresponding ln(PWV) values that will allow us to compare the properties of a number of estimation procedures.

It is assumed that ln(PWV) follows a regression model with PP as the explanatory variable. In particular,

$$\ln \left({\mathrm{PWV}}_{\mathrm{i}}\right)={\beta }_0+{\beta }_1\times {\mathrm{PP}}_{\mathrm{i}}+{\epsilon }_{\mathrm{i}}$$

where the values PP_i will be chosen in 5 different ways leading to different estimates of the regression parameter, β₁. Initially, the true PP₀ values and the “observed” pulse pressures (with error) at the PWV visit are used in the regression models. Using PP₀ will provide the standard against which the other procedures may be compared since the true (but in practice unknown) PP values are used. In this case we know we are fitting the correct model to the data. The other approaches use a number of different ways of replacing the unknown true PP value with an estimate. Fitting the models with the observed PP values (with error) mimics what would happen if the researcher just used a single PP value measured with error at the same visit as PWV to fit the model (as was done in section C.1). Next, predicted values of PP from the mixed effects model are used (as in section C.2) and finally the cumulative burden or AUC value from both the subject’s entire follow-up and restricted to a two-year period is used (as in section C.3).

The results of the simulation are presented in Table 4. The bias due to the estimation procedure is measured by how far the mean of the simulated parameter estimates is from the true parameter value. The mean square error (MSE) measures how much the estimates deviate from the true value by accounting for the variability in the estimates. It is not surprising that using the true PP₀ values leads to the smallest bias and mean squared errors (MSE) for both the intercept and slope. As mentioned above this is the standard against which all other procedures can be compared. The LME/Regression approach is the best among the methods where error is added to the PP values in terms of both bias and MSE. The AUC over a fixed two year time frame is only slightly worse than the LME/Regression approach in terms of MSE. It is perhaps not surprising that the AUC method performs quite well as the AUC values are calculated from the LME model. Interestingly, the mean of the parameter estimates from the AUC method is on the opposite side of the true parameter value compared to the means obtained using the true PP₀ and LME approaches. Using the “observed” PP at the PWV visit leads to the most biased parameter estimates. In particular the slope estimate is severely biased downward towards 0 while the intercept is biased by having the largest mean intercept among the five approaches. Interestingly, the AUC approach over the entire time span (so that different subjects are integrated over different time spans) provides the worst estimates in terms of MSE. However the bias is much better then the “observed” PP for both the intercept and slope. Consequently, when additional data is available one can obtain improved regression parameter estimates using the LME/Regression approach over only using the explanatory variable at the same visit as the response variable as this removes some of the measurement error that may be present in the data.

Table IV.

Results of Simulation Study (number of replications = 1000)

	β0 (True value = 0)			β1 (True value = 0.005)
Method	Mean	Std. Dev.	MSE	Mean	Std. Dev.	MSE×106
True PP0	0.0019	0.1180	0.01394	0.00496	0.00252	6.34
PP at Time = 0	0.1100	0.0856	0.01943	0.00260	0.00181	9.03
LME	0.0029	0.1343	0.01804	0.00494	0.00289	8.36
AUC over entire time	-0.0150	0.1440	0.02096	0.00544	0.00317	10.02
AUC over 2 years	-0.0059	0.1387	0.01926	0.00518	0.00302	9.13

(Position of Table-IV: Should be after the conclusions)

F. Conclusions

In this paper we have investigated the problem of choosing how to represent an explanatory variable in a regression model with a response variable when repeated measurements on the explanatory variable are available. With the help of a simulation study we are able to draw some conclusions about which approach leads to the best estimates of the parameter in the regression model. The analyses suggest that if multiple values of the explanatory variable are available it is not advisable to use a single time point. Among the different methods that were used to model the pulse pressure data, using a linear mixed-effects model to estimate the value of the explanatory variable leads to the best estimates of the regression parameters. Area under the curve could also be used as a reasonable approach as long as the AUC is computed from a common time frame. A unified longitudinal-regression model was estimated using a Bayesian approach. The Bayesian analysis produced similar results to the LME/regression approach.