Abstract
We explore the effects of thermostats in replica exchange molecular dynamics (REMD) simulations. For thermostats that do not produce a canonical ensemble, REMD simulations are found to distort the configuration-space distributions. For bulk water, we find small deviations of the average potential energies, the buildup of tails in the potential energy distributions, and artificial correlations between the energies at different temperatures. If a solute is present, as in protein folding simulations, its conformational equilibrium can be altered. In REMD simulations of a helix-forming peptide with a weak-coupling (Berendsen) thermostat, we find that the folded state is overpopulated by about 10% at low temperatures, and underpopulated at high temperatures. As a consequence, the enthalpy of folding deviates by almost 3 kcal/mol from the correct value. The reason for this population shift is that non-canonical ensembles with narrowed potential energy fluctuations artificially bias toward replica exchanges between low-energy folded structures at the high temperature and high-energy unfolded structures at the low temperature. We conclude that REMD simulations should only be performed in conjunction with thermostats that produce a canonical ensemble.
1 Introduction
Replica exchange molecular dynamics (REMD)1,2 is a widely used method to enhance the conformational sampling of molecular dynamics (MD) simulations.3 In typical REMD simulations, several “replicas” i (i.e., copies of a physical system) are simulated in parallel at different temperatures Ti. At regular intervals, attempts are made to exchange the structures of different replicas to increase the conformational sampling efficiency at the lower temperatures. 1 The exchange of a structure X of a replica at temperature T1 with a structure Y of a replica at temperature T2 is accepted with probability pacc(XY → Y X) = min{1; exp(ΔβΔU)}, where ΔU = U(Y) – U(X) is the potential energy difference, and Δβ = β2 – β with βi−1 = kBTi and kB being Boltzmann's constant. This acceptance criterion is designed to maintain canonical probability distributions in configuration space, pi(X) ∝ e−βiU(X), at each temperature Ti, as follows from the detailed balance relation
| (1) |
After an accepted exchange, particle velocities can be re-assigned from a Maxwell-Boltzmann distribution at the new temperatures T1 and T2, respectively. Alternatively, the old velocities can be scaled by factors (T1=T2)1/2 and (T2=T1)1/2, respectively. 1,2
Here, we explore the effects of combining REMD with thermostats that do not produce canonical ensembles. The weak-coupling (W-C) thermostat4 (often referred to as “Berendsen” thermostat) is widely used in biomolecular simulations because of its stability and efficiency, but produces a non-canonical phase-space distribution.5-8 As a consequence, the detailed balance relation, eq 1, is not satisfied. Problems with ergodicity in W-C simulations combined with REMD were identified previously in an insightful study by Cooke and Schmidler.9 We show that for bulk water at near-ambient conditions the effects of using a W-C thermostat in REMD simulations are relatively small. In contrast, the folding/unfolding equilibrium of a small peptide in water is shifted significantly by the thermostat, resulting in an overpopulation of the folded state at low temperatures and an underpopulation at high temperatures. The reason for this population shift is that the narrowed potential energy distributions in the non-canonical ensembles artificially favor replica exchanges between low-energy folded structures of the high-temperature replica and high-energy unfolded structures of the low-temperature replica.
We discuss possible ways to address the artificial population shift in REMD simulations with W-C thermostats. In principle, the acceptance criterion could be adjusted to maintain the energy distributions created by the thermostat, as implemented previously for microcanonical dynamics. 10 In practice, prior knowledge about the energy distributions, including their tails, is normally not available. We thus conclude that REMD simulations with a standard acceptance criterion, eq 1, should only be performed in conjunction with thermostats that preserve a canonical ensemble, such as Langevin thermostats,11 Andersen thermostats,12 Nosé-Hoover chains13,14 based on the Nosé-Hoover thermostat,15,16 or hybrid Monte Carlo.17
2 Methods
2.1 Water simulations
MD simulations are widely used to study water and aqueous solutions. Even for relatively large solutes such as proteins, the main contribution to the heat capacity of the system, and thus to the potential energy fluctuations, typically comes from the water solvent. To explore the effects of combining REMD with thermostats, we thus first study bulk TIP3P water18 at near-ambient conditions with a particle density of ρ = 33:0 nm−3 and at temperatures of T = 300 and 310 K. We compare the results of regular equilibrium MD and REMD simulations using a Langevin thermostat11 with a collision frequency of 2 ps−1, W-C thermostats4 with coupling constants of 0.5 and 5 ps, and simulations run at constant energy (NVE ensemble; only regular MD). In all simulations, the system contains 1024 water molecules in a cubic, periodically replicated box of constant volume. Both regular MD and REMD simulations are performed using the sander module of Amber 919 with a time step of 0.002 ps, particle-mesh Ewald (PME) summation20 with a grid width <1 Å, a real-space cutoff of 10 Å, and production times of 5 ns for each combination of thermostat and temperature, including the REMD runs. Two replicas are used in the REMD runs at temperatures of 300 and 310 K, respectively, with replica exchange attempts every 1 ps. In the NVE runs, the average kinetic energies correspond to temperatures of 299.9 and 310.1 K, respectively.
2.2 Protein folding
To quantify the thermostat effects on the folding/unfolding equilibrium of a protein, we performed simulations of a helix-forming peptide Ala5 in water.3,21 In these simulations, the GROMACS molecular dynamics package22 was used to run both standard MD (GROMACS version 3.3.0) and REMD simulations (GROMACS version 3.3.1) of the folding of blocked Ala5 (CH3CO-Ala5-NHCH3) in TIP3P water.18 For the peptide, we used the AMBER-GSS force field23 ported to GROMACS.24 The simulations were performed with periodic boundary conditions and PME electrostatics20 using a real-space cutoff distance of 10 Å and a grid width <1 Å. REMD simulations were performed both with a W-C thermostat (coupling constant of 1 ps) 4 and a Langevin thermostat (collision frequency of 1 ps−1).22 Standard MD simulations were performed with a W-C thermostat. The pressure was held constant at p = 1 bar using a W-C barostat with a coupling constant of 5 ps.4 The replica-exchange acceptance criterion was adjusted for simulations in an NPT ensemble by replacing the energy difference ΔU in eq 1 with the enthalpy difference ΔH, where H = U + pV with V the fluctuating system volume. Since the compressibility of water is low near ambient conditions, and pressure has little effect on the helix-coil equilibrium, 25 we expect that any deviations between MD and REMD simulations are caused primarily by the use of a W-C thermostat in the REMD runs, and to a lesser degree by using a barostat that produces non-Boltzmann enthalpy distributions. A time step of 2 fs was used in conjunction with constrained bonds of hydrogen atoms.26 The simulation box contained 1050 TIP3P water molecules.18 Four independent trajectories starting from different initial conformations were created for each of the three setups (MD/W-C, REMD/W-C, and REMD/Langevin, respectively). The standard MD runs 21 were performed for 4× 250 ns at 300 and 350 K, and 4 × 200 ns at 310, 325, and 340 K. REMD simulations of 150 ns duration (per replica) were run for each thermostat and each of the four initial conditions. We used 12 replicas spanning the 295−350 K temperature range, for a combined simulation time of 4 × 150 ns at each temperature.3 Coordinates were saved every 1 ps and REMD exchanges were attempted every 5 ps.
3 Results and Discussion
3.1 Bulk water
MD
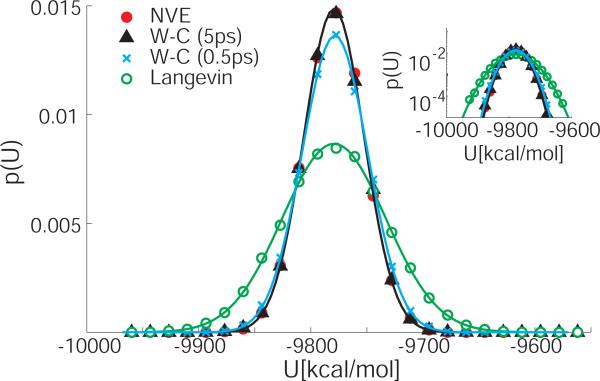
Figure 1 shows the potential energy distributions for bulk TIP3P water obtained from regular MD with W-C and Langevin thermostats, and in the NVE ensemble. We find that at a given temperature all distributions are well approximated by Gaussians of nearly identical means. However, the widths of the distributions vary considerably, with the W-C and NVE simulations producing narrower distributions than the Langevin simulations, consistent with results from earlier studies.5-7 As shown in Table 1, the variances in the potential energy distributions differ by up to a factor of three.
Figure 1.
Potential energy distributions for simulations of TIP3P water at ambient conditions using Langevin (green circles) and W-C thermostats4 with coupling constants of 0.5 ps (black triangles) and 5 ps (blue crosses), and in an NVE simulation (red dots). The continuous lines show Gaussians of corresponding means and variances. The inset shows the same distributions on a semi-logarithmic scale.
Table 1.
Potential energy distributions using constant energy (NVE) dynamics, Langevin dynamics and W-C thermostats. Energies are in units of kcal/mol. The numbers in parentheses are the estimated statistical errors in the last digit (one standard deviation). Italic numbers indicate deviations between REMD and MD results that exceed twice the combined statistical errors. τ is the thermostat coupling time. The skew coefficient is defined as skew = is the ratio of the excess heat capacities calculated from the temperature derivative and the canonical fluctuation formula. C12 is the normalized cross-correlation coefficient.
| 300 K |
310 K |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Thermostat | τ[ps] | 〈U〉 | σ2 | skew | 〈U〉 | σ2 | skew | g | C12[10−4] | |
| |
NVE |
|
−9779.3(2) |
709(7) |
−0.01(2) |
−9665.7(2) |
757(8) |
−0.01(2) |
2.9 |
−2(3) |
| Langevin | 2.0 | −9779.3(7) | 2120(30) | 0.00(2) | −9665.8(7) | 2110(30) | −0.01(2) | 1.0 | −3(3) | |
| MD | Weak coupling | 5.0 | −9779.4(4) | 722(8) | −0.03(2) | −9665.9(3) | 767(7) | −0.01(2) | 2.8 | 0(3) |
| |
Weak coupling |
0.5 |
−9778.5(4) |
858(9) |
−0.01(2) |
−9665.5(4) |
900(10) |
−0.01(2) |
2.4 |
−2(3) |
| Langevin | 2.0 | −9777.8(7) | 2110(30) | −0.01(2) | −9666.7(8) | 2150(30) | −0.01(2) | 1.0 | −1(2) | |
| REMD | Weak coupling | 5.0 | −9773.4(7) | 910(10) | 0.26(3) | −9671.2(7) | 940(10) | −0.31(2) | 2.0 | −55(3) |
| Weak coupling | 0.5 | −9775.2(5) | 990(10) | 0.17(2) | −9669.0(5) | 1000(10) | −0.18(3) | 2.0 | −42(4) | |
To test whether the potential energy distributions are consistent with a canonical distribution, we compare the excess heat capacity at constant volume calculated (1) from the temperature derivative of the average potential energy, CV = ∂ 〈U〉/∂T, and (2) from the fluctuations in the potential energy, where σ 2 = 〈U2〉 – 〈U〉2 is the variance in the potential energy. For a canonical ensemble, the two expressions are identical, . However, we will show in the following that in the non-canonical ensembles created by W-C thermostats, differs from CV because of the narrowed potential energy distributions. To estimate the temperature derivative in the expression for CV, we use the difference between the average potential energies at 310 K and 300 K, CV ≈ (〈U〉2 – 〈U〉1)/(T2 – T1). The variance in is averaged over the two temperatures, σ2 ≈ (σ12 + σ22)/2. As listed in Table 1, we find that the ratio of the two expressions for the excess heat capacity, , is 1.0 for the Langevin simulations, consistent with canonical distributions. In contrast, for the W-C and NVE simulations g varies between 2.4 and 2.9, indicative of strong deviations from the canonical distribution.
REMD
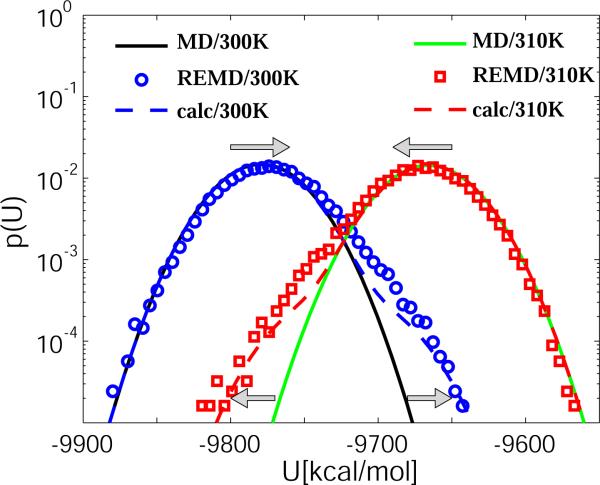
Figure 2 compares the potential energy distributions of bulk water at 300 and 310 K obtained from MD and REMD simulations using W-C thermostats with a coupling constant of 5 ps. The results for different thermostats are summarized in Table 1. We find that in REMD with a Langevin thermostat, the distributions do not change compared to those from MD simulations. In contrast, REMD significantly changes the potential energy distributions when a W-C thermostat is used: the mean energies at the two temperatures move together, the variances increase, and the distributions become skewed with pronounced non-Gaussian tails. Table 1 also lists the normalized cross-correlation coefficient C12 = 〈(U1 – 〈U1〉)(U2 – 〈U2〉)〉/(σ1σ2) between the instantaneous potential energies of the two replicas. We find that in the REMD simulations with a Langevin thermostat, the energies are uncorrelated (C12 = 0). In REMD with a W-C thermostat, we find small but significant correlations, C12 ≈ −0:0050±0:0004. We conclude from these results that REMD with a W-C thermostat can significantly alter the potential energy distributions.
Figure 2.
Comparison of bulk TIP3P water potential energy distributions from MD and REMD simulations (semi-logarithmic scale). The blue circles and red squares show the REMD results for the replicas at 300 and 310 K, respectively. The blue and red dashed lines are calculated from iterated numerical solutions of eq 2 at 300 and 310 K, respectively. For reference, Gaussian approximations to the MD results using a W-C thermostat4 with a coupling time of 5 ps are shown as black (300 K) and green lines (310 K). The arrows indicate the change in the energy distributions of REMD simulations compared to MD, in particular the buildup of artificial tails and the small shifts in the means.
Model of thermostat effects in REMD
The effects of thermostats in conjunction with REMD can be understood from a simple model, similar to the ones used previously 27,28 to study the efficiency of REMD. With (U) the potential energy distribution at temperature Ti, the joint probability distribution of the potential energies U and W at the two temperatures T1 and T2 is . Let us consider how replica exchange alters this distribution. After an attempted replica exchange, a given pair of energies U and W is obtained either from an accepted move starting with W and U or from a rejected move starting with U and W . Replica exchange thus transforms pMD(U, W) to:
| (2) |
where pacc(U, W ) is the probability that a replica exchange is accepted if U and W are the potential energies of the structures in replicas 1 and 2, respectively. If the acceptance probabilities satisfy detailed balance, pacc(U ,W)pMD(U, W) = pacc(W, U)pMD(W, U), then replica exchange preserves the distribution, pREMD(U, W) = pMD(U, W); otherwise, the distribution will be distorted. In our model, we iterate eq 2 to self-consistency and then calculate the marginal distributions by integration, and . In the numerical calculations we approximate the potential energy distributions by Gaussians with means and variances taken from the MD results in Table 1. As shown in Figure 1, Gaussians provide excellent approximations to the actual distributions over the whole range of potential energies sampled in the simulations.
Figure 2 compares the potential energy distributions obtained by iteration of eq 2 to those of the REMD simulations. We find that the model can account almost quantitatively for the effects of the W-C thermostat on the energy distributions. The distribution at the low temperature is shifted upward and has a pronounced tail towards the higher energies. The energy distribution at the high temperature is modified in the opposite direction: it is shifted towards lower energies and has a tail skewed to the left. The cross-correlation coefficient C12 predicted by the model is about −0:09, of the same sign and roughly the same magnitude as the C12 ≈ −0:005 obtained from the W-C REMD simulations (Table 1). The smaller correlations in the REMD simulations can be explained by the randomizing effect of the thermostatted MD runs between replica exchanges.
The distortions seen in Figure 2 arise because the potential energy distributions of the thermostat are inconsistent with the acceptance criterion eq 1. For the narrowed energy distributions produced by the W-C thermostat, as compared to the wider canonical distributions, replica exchange is relatively more likely to be accepted for conformations in the high-energy tail at the low temperature, and in the low-energy tail at the high temperature. We will show in the following that this bias can result in distortions of the conformational equilibrium of a solute.
3.2 Protein folding
REMD is widely used to study the folding of peptides and proteins. Protein folding can often be described by using only two dominant states, with a folded state being enthalpically stabilized against an entropically favored unfolded state. In the following, we explore how simulations of protein folding are affected by replica exchange when W-C thermostats are used. We analyze the simulation data from Refs.3 and21 for blocked Ala5 in water, which folds into a short helical peptide for the force field used.
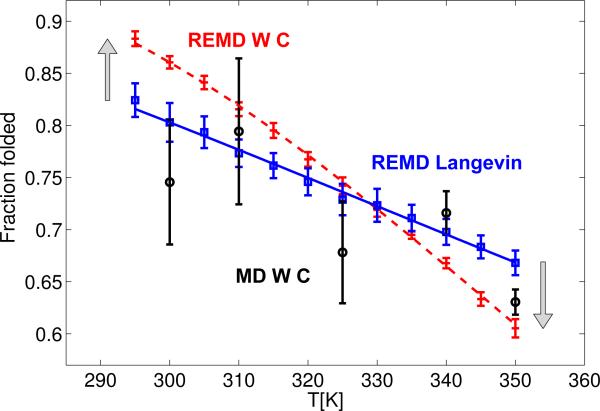
Figure 3 compares the relative populations of the folded (helical) state obtained from long MD runs at 300 K and 350 K, and from REMD simulations using Langevin and W-C thermostats, respectively, with 12 replicas equally spaced in temperature between 295 and 350 K. The folded state is defined as in Refs.3 and.21 We find that the equilibrium populations of the folded state agree for standard MD simulations using a W-C thermostat and REMD simulations using a Langevin thermostat. In contrast, the folded populations obtained from REMD simulations using a W-C thermostat differ significantly from both the standard MD results and the REMD/Langevin results. In the REMD runs with the W-C thermostat, the population of the folded (helical) peptide is increased at the low temperatures, and decreased at the high temperatures, with ∼10% shifts in the folded populations at 300 K and at 350 K.
Figure 3.
Relative populations of the folded (helical) state of Ala5 as a function of temperature (red crosses: REMD with W-C thermostat; blue squares: REMD with Langevin thermostat; black circles: MD). The dashed line (REMD with W-C) and solid line (REMD with Langevin) are fitted melting profiles. The error bars correspond to one estimated standard deviation and were estimated from four independent runs. In case of the MD simulations, the standard deviations agree well with the estimate using the kinetic rate coefficients of folding and unfolding 21 in a two-state kinetic model.29 Vertical arrows indicate the population changes in the REMD W-C simulations.
For a quantitative comparison, we fit the relative populations pf(T) of the folded state to a melting profile pf(T) = 1/[1 + exp(ΔH/kBT – ΔS/kB)] where ΔH and ΔS are the enthalpy and entropy of folding, respectively, which are assumed to be independent of temperature in the range of 295 to 350 K. The results are shown in Table 2. We find that both the enthalpy and entropy of folding from the Langevin-thermostatted REMD and the MD simulations are in excellent agreement. In contrast, both the enthalpy and entropy obtained from REMD/W-C and REMD/Langevin simulations differ by about 7 times their respective combined standard deviations. For the small peptide, the systematic error in the enthalpy of folding is almost 3 kcal/mol. We conclude from these inconsistencies that REMD with a W-C thermostat significantly alters the temperature dependence of the folded population.
Table 2.
Enthalpy ΔH and entropy ΔS of folding obtained from fits to the melting profiles (Figure 3). The last column lists the difference in average total potential energy of the folded and unfolded states. The estimated statistical errors (one standard deviation) are also given.
| ΔH [kcal/mol] | ΔS [cal/(mol K)] | 〈U〉f-〈U〉u [kcal/mol] | |
|---|---|---|---|
| MD | −3.20±1.00 | −8.0±2.9 | −3.00±0.10 |
| REMD (Langevin) | −2.93±0.26 | −7.0±0.8 | −3.13±0.10 |
| REMD (W-C) | −5.74±0.14 | −15.5±0.4 | −3.68±0.07 |
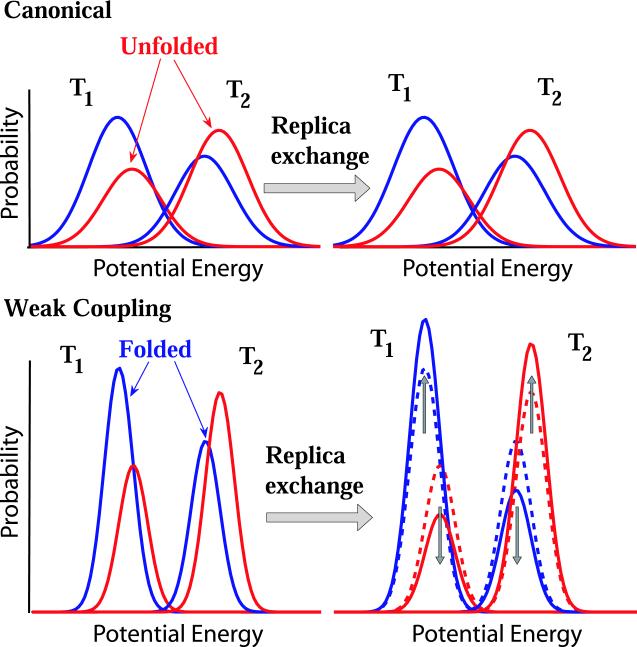
Qualitatively, the change in the folded populations induced by combining REMD with a W-C thermostat can be explained by using a simple model, as illustrated in Figure 4. In this model, we assume that the folded state has lower enthalpy than the unfolded state. The blue (red) lines show the potential energy distribution of the folded (unfolded) states. In the canonical case, replica exchange leaves the distributions unchanged, thus preserving equilibrium. For a W-C thermostat (bottom), the distributions are narrower, reducing the overlap of the distributions at different temperatures. As a consequence, the probability of acceptance of replica exchange moves is reduced. In addition, in the W-C REMD there are relatively more accepted replica exchanges between the unfolded state at the lower temperature T1 and the folded state at T2. As a result, the population of the folded states artificially increases at T1 and decreases at T2. In Appendix A we implement such a model, and show that it can account for the observed population shifts. Interestingly, this model also explains the observation of Cooke and Schmidler9 that in their simulations of alanine dipeptide in vacuum using REMD with a W-C thermostat, the C7ax configuration was not populated in the lowest-temperature replica: C7ax has higher energy than C7eq, and should thus have an artificially low population in the replicas at low temperatures.
Figure 4.
Schematic of the effect of REMD with W-C thermostats on folding probabilities. Potential energy probability distributions of folded (blue) and unfolded (red) states are shown at two temperatures before and after replica exchange. For classical canonical distributions (upper panel), REMD does not affect the distributions. However, for the narrowed distributions in W-C REMD (lower panel), replica exchange alters the relative populations of folded and unfolded states. Folded states become overpopulated at low temperatures and underpopulated at high temperatures, as indicated by the vertical arrows.
For further validation of our model, we also calculate ΔH directly from the difference in the average total potential energies of the system with the peptide in the folded and unfolded state, respectively (see Table 2; the small pV contribution is ignored). The potential energy differences between folded and unfolded states averaged over all temperatures and all four initial conditions are listed for both the MD and REMD simulations with Langevin and W-C thermostats. Errors are estimated from the 5 × 4 = 20 and 12 × 4 = 48 independent MD and REMD simulations, respectively. ΔH obtained from the potential energy differences in REMD/Langevin and in standard MD simulations are consistent with the values obtained from the fit of the melting profile. In contrast, for the REMD simulations with the W-C thermostat the energy difference and the value of ΔH are inconsistent, differing by ∼10 combined standard deviations. ΔH obtained from the potential energy distributions of the REMD W-C simulations is significantly closer to the values obtained from the MD and REMD Langevin data, as expected from our model illustrated in Figure 4.
4 Conclusions
We showed that thermostats can significantly affect the outcome of REMD simulations, consistent with the results of earlier studies.9 W-C thermostats produce potential energy distributions that are narrower than those expected for a canonical ensemble. If a standard replica-exchange acceptance criterion is used, replica exchange will distort these distributions, and as a result shift the configuration-space populations. For bulk TIP3P water18 at near-ambient conditions, the effects are statistically significant but overall small. We found that in W-C simulations the mean potential energies are shifted, become artificially correlated, and develop distributions with enhanced tails. No such effects were seen in REMD simulations using a Langevin thermostat that preserves the canonical distribution.
For protein folding, REMD with non-canonical thermostats is expected to result in more pronounced effects. Simulations of a small helix-forming peptide using a W-C thermostat showed that the folding probabilities are artificially enhanced by ∼10% at the low temperatures, and reduced at the high temperatures. For thermostats that produce a higher variance than the canonical energy distribution, the opposite effects are expected.
We have used simple models to estimate the effects of thermostats on the energy distributions and folding equilibria. As input, these models use the energy differences between folded and unfolded states, and the means and variances of the potential energy. We found that the thermostat-induced changes in the energy distributions and folding equilibria could be predicted nearly quantitatively, suggesting that the models can be used to assess and possibly correct W-C REMD simulation results.
For non-canonical simulations (e.g., at constant energy or with W-C thermostats), the replica-exchange acceptance criterion, eq 1, has to be modified.10 Without exact explicit expressions for the configuration-space distribution, such modifications are not easily possible in practice. We therefore conclude that REMD simulations should be carried out with thermostats that preserve canonical distributions, such as Langevin thermostats,11 Andersen thermostats,12 Nosé-Hoover chains13,14 based on the Nosé-Hoover thermostat15,16 (which by itself is not guaranteed to produce a canonical distribution9,30), or the hybrid Monte Carlo method.17
Acknowledgement
We thank Dr. Attila Szabo for many helpful and stimulating discussions and Dr. Nicolas Fawzi for his valuable comments. This research used the Biowulf Linux cluster at the National Institutes of Health (NIH), and the Irish Centre for High-End Computing (ICHEC). E.R. and G.H. were supported by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases, NIH.
A Appendix: Protein folding in REMD simulations
We use a simple model to analyze the effects of using W-C thermostats in protein-folding REMD simulations. In this model, the protein is assumed to have two states, a low-energy folded state and a high-energy unfolded state, Uf < Uu, with relative populations pf(Ti) at temperature Ti. For simplicity, we first consider only two replicas at two temperatures, T1 < T2. There are four distinct folding states overall: ff, fu, uf, and uu, where the first position indicates the folding state at T1 and the second at T2. At equilibrium, the populations of the four states are pff, pfu, puf, and puu, respectively. An accepted replica exchange switches the states X ∈ {f, u} and Y ∈ {f, u} at temperatures T1 and T2. After an exchange attempt, the probability distribution of the four states changes to :
| (3) |
where in the canonical case. The acceptance probabilities pacc of replica exchanges depend on the potential energy difference. For simplicity, we assume that the solvent-energy distributions at each temperature Ti are Gaussians, gi(U), with means 〈U〉i and standard deviations σi, independent of the state of the protein. We thus ignore the non-Gaussian tails of the distributions. The distributions of the potential energies at temperature Ti in the folded and unfolded states are then pi(U|f ) = gi(U – Uf) and pi(U|u) = gi(U – Uu), respectively. If the solvent-energy fluctuations are fast relative to folding and unfolding, they can be integrated out. The probability of accepting an exchange XY→YX then becomes
| (4) |
This model can easily be extended to more than two replicas. As in the model for bulk water, the coupled equations corresponding to eq 3 can be iterated to self-consistency.
We applied this model to the REMD simulations of Ala5 folding in water. To calculate the replica-exchange acceptance probabilities, we assumed a constant enthalpy difference of folding, ΔH, and linear temperature dependences of s and 〈U〉. The parameters were extracted from MD simulations of Ala5 using a W-C thermostat with a 1 ps coupling constant at 300 K and 350 K, respectively. ΔH and the folding probabilities at different temperatures were determined from the folding and unfolding rates extracted from the MD simulations 3,21 using a two-state model and assuming an Arrhenius temperature dependence. As in the REMD simulations, we used 12 temperatures spaced equally between 295 K and 350 K. The iterative scheme corresponding to eq 3 was applied by alternating exchange attempts between replicas at neighboring temperatures. Consistent with the REMD simulations, the converged model led to an increase in the folded population at low temperatures and a decrease at high temperatures. However, the magnitude of the effect was smaller, resulting in ∼5% changes in the folded population at the two extreme temperatures.
References
- 1.Sugita Y, Okamoto Y. Chem. Phys. Lett. 1999;314:141–151. [Google Scholar]
- 2.García AE, Sanbonmatsu KY. Proc. Natl. Acad. Sci. U.S.A. 2002;99:2782–2787. doi: 10.1073/pnas.042496899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Buchete NV, Hummer G. Phys. Rev. E. 2008;77:030902. doi: 10.1103/PhysRevE.77.030902. [DOI] [PubMed] [Google Scholar]
- 4.Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
- 5.D'Alessandro M, Tenenbaum A, Amadei A. J. Phys. Chem. B. 2002;106:5050–5057. [Google Scholar]
- 6.Morishita T. J. Chem. Phys. 2000;113:2976–2982. [Google Scholar]
- 7.Allen M, Tildesley D. Computer Simulation of Liquids. Clarendon Press; Oxford: 1989. [Google Scholar]
- 8.Frenkel D, Smit B. Understanding Molecular Simulation. From Algorithms to Applications. Academic Press; San Diego: 2002. [Google Scholar]
- 9.Cooke B, Schmidler SC. J. Chem. Phys. 2008;129:164112. doi: 10.1063/1.2989802. [DOI] [PubMed] [Google Scholar]
- 10.Calvo F, Neirotti JP, Freeman DL, Doll JD. J. Chem. Phys. 2000;112:10350–10357. [Google Scholar]
- 11.Pastor RW, Brooks BR, Szabo A. Mol. Phys. 1988;65:1409–1419. [Google Scholar]
- 12.Andersen HC. J. Chem. Phys. 1980;72:2384–2393. [Google Scholar]
- 13.Martyna GJ, Klein ML, Tuckerman M. J. Chem. Phys. 1992;97:2635–2643. [Google Scholar]
- 14.Tobias DJ, Martyna GJ, Klein ML. J. Phys. Chem. 1993;97:12959–12966. [Google Scholar]
- 15.Nosé S. J. Chem. Phys. 1984;81:511. [Google Scholar]
- 16.Hoover W. Phys. Rev. A. 1985;31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 17.Duane S, Kennedy AD, Pendleton BJ, Roweth D. Phys. Lett. B. 1987;195:216–222. [Google Scholar]
- 18.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 19.Case DA, Cheatham T, III, Darden T, Gohlke H, Luo R, Merz KM, Jr, Onufriev A, Simmerling C, Wang B, Woods RJ. J. Comput. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. J. Chem. Phys. 1995;103:8577. [Google Scholar]
- 21.Buchete NV, Hummer G. J. Phys. Chem. B. 2008;112:6057–6069. doi: 10.1021/jp0761665. [DOI] [PubMed] [Google Scholar]
- 22.Lindahl E, Hess B, van der Spoel D. J. Molec. Model. 2001;7:306–317. [Google Scholar]
- 23.Nymeyer H, García AE. Proc. Natl. Acad. Sci. U.S.A. 2003;100:13934–13939. doi: 10.1073/pnas.2232868100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sorin EJ, Pande VS. Biophys. J. 2005;88:2472–2493. doi: 10.1529/biophysj.104.051938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Paschek D, Gnanakaran S, García AE. Proc. Natl. Acad. Sci. U.S.A. 2005;102:6765–6770. doi: 10.1073/pnas.0408527102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hess B, Bekker H, Berendsen HJC, Fraaije JGEM. J. Comput. Chem. 1997;18:1463–1472. [Google Scholar]
- 27.Sindhikara D, Meng YL, Roitberg AE. J. Chem. Phys. 2008;128:024103. doi: 10.1063/1.2816560. [DOI] [PubMed] [Google Scholar]
- 28.Zheng W, Andrec M, Gallicchio E, Levy RM. Proc. Natl. Acad. Sci. USA. 2007;104:15340–15345. doi: 10.1073/pnas.0704418104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Berezhkovskii AM, Szabo A, Weiss GH. J. Chem. Phys. 1999;110:9145–9150. [Google Scholar]
- 30.Tuckerman ME, Liu Y, Ciccotti G, Martyna GJ. J. Chem. Phys. 2001;115:1678–1702. [Google Scholar]