Female-biased sex allocation of offspring by an Apodemus mouse in an unstable environment

Abstract

We investigated the effects of population fluctuation on the offspring’s sex allocation by a weakly polygynous mouse, Apodemus argenteus, for 3 years. In acorn-poor seasons, heavier mothers invested more in sons, and lighter mothers invested more in daughters. In acorn-rich seasons, heavier mothers invested more in daughters, and lighter mothers invested more in sons. Maternal body condition and litter size affected the sex allocation. Furthermore, there was a maternal investment trade-off between a son’s birth mass and the number of daughters. Based upon the effect of population fluctuation on the lifetime reproductive success of each sex, we proposed the new “safe bet hypothesis”. This hypothesis predicts that frequent and unpredictable change in female distribution, which is often caused by abrupt fall in food condition, favors female-biased maternal investment to offspring by polygynous mammals and is applicable to many small mammals inhabiting in unstable environments.

Introduction

Since Fisher (1930) predicts equal sex ratios in most species with separate sexes, many speculations and predictions have been proposed to explain biased sex ratios from a fitness perspective. Trivers and Willard (1973) first proposed a verbal model for polygynous mammals in which a mother may allocate offspring to different sexes according to her condition: male-biased investment when she is in good condition and female-biased investment when she is in bad condition. In polygynous mammals, high-quality mothers should get much larger fitness returns (number of grand-offspring) from high-quality sons than high-quality daughters by their extra investment because of strong male–male competition for mating (Clutton-Brock et al. 1984; Clutton-Brock and Iason 1986).

The Trivers and Willard (hereafter abbreviated as TW) hypothesis has been supported by a number of empirical and laboratory studies in various mammals (reviewed by Clutton-Brock and Iason 1986; Hiraiwa-Hasegawa 1993; Sheldon and West 2004). These studies, however, have also produced many inconsistent results, such as no conditional sex ratios (Krackow 1997; Fernández-Llario et al. 1999), as well as effects that contradict the predictions of the TW hypothesis (Clutton-Brock and Iason 1986; Hewison et al. 2005). Recent reviews of sex ratios in many mammals have highlighted the potential constraints on sex ratio adjustment (West and Sheldon 2002; Sheldon and West 2004; West et al. 2005). The TW hypothesis was originally applied to species in which the litter (clutch) size is one. Whether the TW hypothesis is applicable to polytocous species (species that produce several offspring per litter) is unclear (Williams 1979).

Murid rodents include mice and voles. Because of their large litter size, short periods until sexual maturity, multiple reproduction cycles within a year, and quick saturation of populations due to short life spans, they are a suitable group in which to investigate the effect of litter size variation on the adaptive sex allocation of offspring. Murid rodents generally show great fluctuations in population density that is often due to drastic changes in habitat conditions. These features cause various intraspecific variations on life history traits, including mating system, litter size, and sex ratio within a litter (Clutton-Brock and Iason 1986; Boonstra et al. 1987; Wright et al. 1988; Dobson and Myers 1989; Ostfeld 1990; Lambin 1994; Krackow 1997; Cochran and Solomon 2000; Singleton et al. 2001).

Most studies on birth sex ratios in murid rodents, however, have been restricted to laboratory conditions (e.g., Sikes 1996; Krackow 1997; Wright et al. 1988). This is because sex ratio and litter size at birth are almost impossible to determine in wild populations, owing to the animals’ secretive nesting habits (e.g., giving birth and nursing young in underground nests).

The small Japanese field mouse, Apodemus argenteus, which is endemic to Japan, is a common omnivorous mouse in forested areas. To some degree, A. argenteus exhibits arboreal activity (Doi et al. 1982; Shioya 1996). This species often uses tree cavities and birdhouses (nest boxes) for giving birth and nursing young (Oka 1992). In order to obtain reproductive data and information about its natural habitat, we adopted a new method that involves the use of nest boxes as well as radio-frequency identification (RFID) chips. Adult mice in nest boxes were individually identified with an RFID chip reader, and the date of parturition was documented by audible observations of newborn trebles; both observations were made through the nest box wall, with minimum disturbance. A. argenteus shows marked seasonal and annual variations in population density (Nishikata 1979; Nakata 1998), individual variations in litter size (range: 2–9; Shibata 2006), and intraspecific variation in its mating system from monogamy to polygyny (Oka 1992; Ohnishi et al. 2000; Shibata 2006); these factors create ideal conditions in which to examine sex allocation of offspring under natural conditions.

Our aim in this paper is to examine how habitat saturation affects maternal investment in offspring in a weakly polygynous mouse with large litter sizes, A. argenteus. We investigated (1) the relationship between the sex allocation of offspring and maternal condition for 3 years, and (2) the effects of habitat saturation (mouse density and food condition) on birth sex ratios.

Methods

Study area and nest boxes

Our study was conducted at Mt. Asama (36°23′N, 138°31′E, elevation 1,450–1,700 m) in central Honshu, Japan. The 31-ha study area consisted of two types of forest: a natural broad-leaved forest dominated by oaks (Quercus crispula; 19 ha) and a Japanese larch plantation (Larix leptolepis; 12 ha; see Fig. 1). A detailed description of the vegetation was given by Shibata et al. (2004).

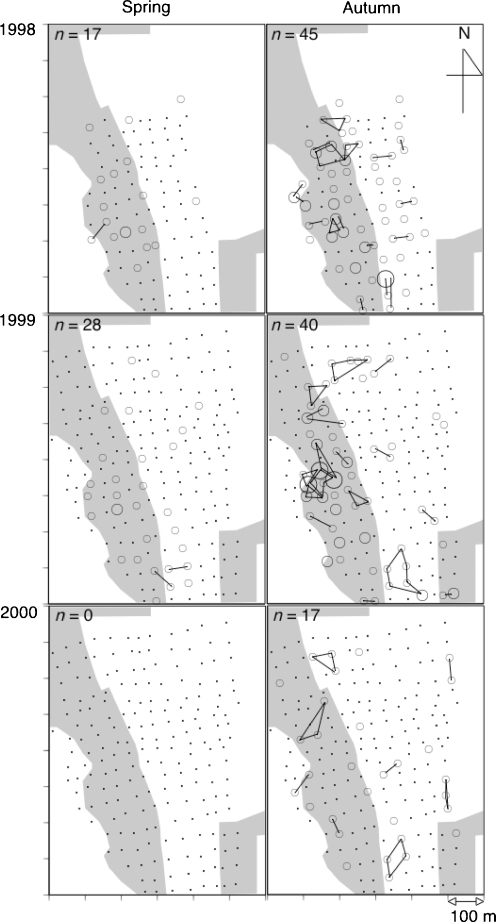
Fig. 1.

Distribution of nest boxes used by adult females in each reproductive season (spring or autumn) of 1998–2000. Nest boxes used by females (open circles) are indicated. Size of the circle (three grades) shows the number of females (one to three) using the box. Nest boxes used by the same individual are bound with a line. Small solid circles indicate investigated nest boxes used by no female. n is the number of identified adult females. Shaded area indicates larch forest and open area indicates oak forest. In 1998, only nest boxes in the center of the study area (15 ha) were investigated

In the study area, 197 nest boxes were set to provide reproductive and daytime rest chambers for A. argenteus, and also, as a means of live-capture. Each wooden nest box was 150 × 150 × 110 mm³ in internal dimensions, and the walls were 20 mm thick. A single round entrance (30 mm in diameter) was opened at the upper part of the wall. The nest boxes were fixed at a height of 1.0–1.5 m above ground on the tree trunk closest to a cross point of a 40 × 40 m grid that covered the whole study area (6.4 nest boxes/ha).

Inspection and measurement procedure

Our daily routine included the inspection of nest boxes (more than 100 nest boxes/day), which usually began before 8:00 a.m. and ended by 3:00 p.m. Inspections of all nest boxes were conducted every day or every other day, from April to October in 1999–2000. A portable reader (model LID 500, Trovan Ltd., UK) was used outside the boxes to detect RFID chips implanted in mice that were resting inside the nest boxes. When no signals were recorded from the RFID chips, we opened the nest boxes to capture unmarked A. argenteus. Live-captured mice were placed in a textile bag and weighed, aged, and sexed without anesthesia; reproductive condition (examination of the vulva for estrus and parturition, palpation for pregnancy, and teat condition for sucking) was also examined for females on every capture. In 1998, only 100 nest boxes in the center of the study area (15 ha) were investigated by the same method.

Age was determined according to the body mass and fur color of the captured mice. All mice with gray neotenous fur were juveniles (approximately less than 2 months of age; Koyama 1994). Among mice with brownish fur, those weighing less than 12.0 g were classified as juveniles born in that year (see Ohnishi et al. 2000), and the others were classified as adults.

An RFID chip (Trovan model ID 100) was implanted on the dorsal shoulder. In order to avoid the influence of RFID chips (0.1 g weight and 1.2 cm length) on behavior, RFID chips were implanted in captured mice weighing 12.0 g or more, including all adult mice.

After finding new nest materials within a nest box (a sign of reproductive nests), we carefully listened for a whisper of trebles emitted by newborns from outside the nest box. On the day that a whisper was observed, we captured the newborns and their mother. When parturition occurred during the intervals when inspection took place every few days, the day of birth was estimated using the developmental stage of newborns, unless a taint of bleeding would otherwise indicate the day of parturition. All newborns were sexed and weighed. We analyzed data from the mothers and their newborns; they were measured within 1 day after the day of birth/parturition. Only for analyzing litter sex ratio, data from mothers and their newborns measured within 2 days after birth/parturition were also analyzed.

Data analyses

Two reproductive seasons, spring (April–June) and autumn (August–October), were observed each year during 1998–2000. The autumn reproductive seasons were investigated fully for 3 years (1998, 1999, and 2000). In the spring reproductive seasons, data from the initial part of 1998 were lacking because of the delayed investigation. The whole period during the spring season of 2000 was observed, but no mice were found in nest boxes across the entire study area.

A total of 72 litters (n = 7 in spring of 1998, 23 in autumn of 1998, 18 in spring of 1999, 10 in autumn of 1999, and 14 in autumn of 2000) were measured within 2 days after birth. Among them, a total of 51 litters (n = 6 in spring of 1998, 10 in autumn of 1998, 16 in spring of 1999, 9 in autumn of 1999, and 10 in autumn of 2000) were measured on the day of birth (within 1 day after birth). In 43 of 51 litters measured on the day of birth, litter size, sex ratio (proportion of males) within a litter, birth mass, and maternal body mass were fully recorded. Data of all 51 litters measured on the day of birth were fully used for analyzing. The other 21 litters were measured within 1 or 2 days after birth, but their precise days of birth were not determined. Therefore, data of them were only for analyzing litter sex ratio. Of the 51 litters measured on the day of birth, 42 (82.4%) were produced by 37 individually marked females, and the other nine (17.6%) were produced by unmarked females. Of the other 21 litters measured within 1 or 2 days after birth, 14 (66.7%) were produced by seven marked females, and the other seven (33.3%) were produced by unmarked females. In 51 litters measured on the day of birth, almost all newborns (199 of 206 newborns) were weighed on the day of birth (within 1 day after birth); these measurements were used as the birth mass of each sex.

Maternal body mass, local density of adult females, acorn harvest (poor or rich), and most dominant tree species (oak or other) were accepted as factors that likely affect litter size and sex allocation within a litter. Furthermore, litter size was accepted as a factor that likely affects litter sex ratio. As factors that likely affect the birth mass of offspring, maternal body mass, litter size, litter sex ratio, and sex of offspring were accepted.

The local density of adult females was defined as the density of mice in circle area (0.79 ha) with a 50-m radius from the nest box. The local density was estimated in the reproductive season by the number of different adult females found in nest boxes (four to five nest boxes) distributed in the circle area. The density was not estimated for the nest boxes in the periphery of the study area. Unmarked adult females were counted as one if we could not discriminate among them.

Mast production was classified by eye as acorn-rich or acorn-poor seasons. In an acorn-poor season, oak acorns were rarely found on the ground or on trees throughout the study area. In an acorn-rich season, abundant acorns were found. The springs of 1998 and 1999 were classified as acorn-poor seasons, although acorns produced in the previous autumn were still abundant on the ground in the spring of 1999. Quercus acorns cannot survive until the following spring unless they germinate in winter as acorns rarely exhibit dormancy and thus germinate soon after falling (Arai 1982; Saito 1992). Most dominant tree species around a nest box (oak or other) will affect acorn harvest in a mouse’s home range. Therefore, it was accepted as the factor that likely affects the sex allocation.

Statistical analyses

Factors affecting the sex allocation of offspring within a litter were analyzed through the generalized linear models (GLMs) using the “glm” procedure in R (version 2.8.0 GUI 1.26 (5256); R Foundation for Statistical Computing, 2008) and the generalized linear mixed models (GLMMs) using the “lmer” procedure of library “lme4” in R. Litter size was analyzed through the GLM with a quasi-Poisson error distribution and log-link function. A GLM with a quasi-binomial error distribution and logit-link function was used for analyzing litter sex ratio. A GLMM with a normal error distribution and identity-link function was used for analyzing the birth mass of offspring. The “maximum-likelihood ratio” method was used in the GLMM for the birth mass of offspring. In the GLMM, litter’s identity was designated as a random effect. Among the 37 marked females measured within 1 day after parturition, five females (13.5%) produced two litters (10 of 51 litters; among the 44 marked females measured within 2 days after birth, ten females produced two or three litters (22 of 56 litters)), and litters produced by the same female are not independent. However, we found little variance in the sex allocation among females. Therefore, female individuality was not designated as a random effect in the GLMM.

Beginning with the interactions, GLMs and a GLMM were reduced by stepwise deletion of non-significant terms, with the numerically smallest coefficients from models including all the factors and all interaction terms using the procedure “anova” in R (Crawley 2005). A reduced model was compared with a non-factor model with only interception using the analysis of deviance test by the procedure “anova”. The effects of factors in the reduced GLMs were examined through the F tests (Krackow and Tkadlec 2001; Faraway 2006) using the procedure “anova” of library “car” in R. The effects of factors in the reduced GLMM were examined by comparing the GLMM to the model in which one factor was removed from the GLMM, with the χ²-test using the procedure “anova”. If significant interaction effect was found among several factors, each effect of the factor was not analyzed.

A Kruskal–Wallis test combined with a sequential Bonferroni test (Rice 1989) was used to analyze the differences in the mean local density between reproductive seasons, using the software package JMP ver. 6.03J (SAS Institute Inc., Cary, NC, USA).

Results

Population fluctuation and female distribution

In the spring reproductive season, 17 females in the center of the study area (15 ha) in 1998 and 28 females in the entire study area (31 ha) in 1999 were identified (Fig. 1). In the spring of 1998, the mean local density of adult females was 3.4 ± 0.4 (SE) mice/ha (n = 16 nest boxes examined), and it was 3.3 ± 0.3 mice/ha (n = 26) in 1999. No significant difference was found between these years (Kruskal–Wallis test; χ² = 0.04, df = 1, P = 0.85). In the spring of 2000, however, no adult females were found throughout the entire study area (Fig. 1).

In the autumn reproductive season, 45 females in 1998, 40 females in 1999, and 17 females in 2000 were identified (Fig. 1). The mean local density of adult females was 5.5 ± 0.3 mice/ha (n = 53) in 1998, 5.2 ± 0.4 mice/ha (n = 39) in 1999, and 1.7 ± 0.6 mice/ha (n = 17) in 2000. A significant yearly difference in the local density was found among these three autumn seasons (Kruskal–Wallis test; χ² = 33.8, df = 2, P < 0.0001). The density in the autumn of 2000 was significantly lower than in the other two, although there was no significant difference between 1998 and 1999 (sequential Bonferroni test; 1998 vs 2000, χ² = 34.8, P < 0.0001; 1999 vs 2000, χ² = 21.5, P < 0.0001; and 1998 vs 1999, χ² = 0.70, P = 0.40). In the autumns of 1998 and 1999, many adult females were aggregately distributed, and some females communally shared one nest box with one another (Fig. 1). In the autumn of 2000, however, females were sparsely distributed, and no adult females communally used nest boxes. Therefore, population disruption apparently occurred during the winter of 1999.

Environmental factors affecting litter size and sex allocation of a litter

The effects of environmental factors (acorn harvest, dominant tree species, and local density of females) and those of maternal conditions (body mass and litter size) on the sex allocation within a litter were analyzed using GLMs. Food and maternal body conditions affected the sex allocation of offspring of A. argenteus.

Across all litters measured on the day of birth, the mean litter size was 4.0 ± 0.2 (n = 51, range: 2–9), and large individual and seasonal variations in litter size were observed (Table 1). For litter size, two factors (acorn harvest and maternal body mass) were identified in the GLM (Table 2: n = 44, F = 24.0, df = 2,41, P < 0.0001). In the GLM, acorn harvest and maternal body mass had significantly positive effects on litter size. Females produced larger-sized litters in acorn-rich seasons (i.e., autumns of 1998 and 2000; n = 20, 5.1 ± 0.2 for litter size, Table 1) than in acorn-poor seasons (springs of 1998 and 2000, and autumn of 2000; n = 31, 3.4 ± 0.2), and heavier females produced larger-sized litters than lighter females (Fig. 2).

Table 1.

Sex allocations of offspring within a litter in five reproductive seasons

		Male offspring	Female offspring	Litter size	Sex ratio
Seasons	Number (N)	Mean ± SE	Mean ± SE	Mean ± SE	Mean ± SE
Acorn-poor seasons
Spring of 1998	6	1.7 ± 0.5	1.8 ± 0.5	3.5 ± 0.4	0.46 ± 0.11
Spring of 1999	16	1.6 ± 0.3	1.6 ± 0.3	3.2 ± 0.2	0.50 ± 0.07
Autumn of 1999	9	1.9 ± 0.4	1.7 ± 0.4	3.6 ± 0.3	0.51 ± 0.09
Acorn-rich seasons
Autumn of 1998	10	2.1 ± 0.4	2.4 ± 0.4	4.5 ± 0.3	0.45 ± 0.08
Autumn of 2000	10	2.6 ± 0.4	3.1 ± 0.4	5.7 ± 0.3	0.47 ± 0.08

Means of the number of each sex, litter size, and sex ratio within a litter are indicated. The reproductive seasons are classified into acorn-poor seasons (springs of 1998 and 1999 and autumn of 1999) and acorn-rich seasons (autumns of 1998 and 2000). Data are collected from litters measured on the day of birth

N is the sample size

Table 2.

Statistical results of F tests for factors potentially affecting litter size in a GLM

	Litter size
Terms	F value	df value	P value
Acorn harvest	39.1	1	<0.0001
Maternal body mass	5.15	1	0.029

The GLM with a quasi-Poisson error and a log-link function for litter size (n = 44) was used

Significant P values are in italics

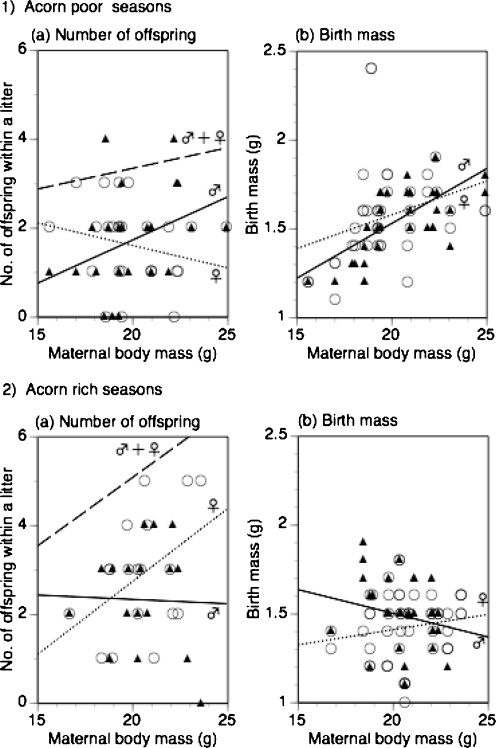
Fig. 2.

Effects of maternal body mass on (a) number of each sex and (b) birth mass of offspring, within a litter in (1) acorn-poor seasons (springs of 1998 and 1999 and autumn of 1999) and in (2) acorn-rich seasons (autumns of 1998 and 2000). Male offspring are indicated with solid triangles and a solid regression line, and female offspring with open circles and a dotted regression line. Broken regression lines are fitted to litter size (a). Data were collected from 44 litters for the number of offspring, and 177 offspring from 43 litters for birth mass, measured on the day of birth. In the acorn-poor seasons, maternal body mass positively correlated with the number of male offspring and the birth mass of offspring. In the acorn-rich seasons, however, maternal body mass positively correlated with the number of female offspring and weakly the birth mass of female offspring. Furthermore, the birth mass of male offspring negatively correlated with the maternal body mass

The mean litter sex ratio was 0.48 ± 0.04 (n = 51) across litters measured on the day of birth (Table 1). In the acorn-poor seasons (the springs of 1998 and 1999 and the autumn of 1999), maternal body mass positively correlated with the number of male offspring within a litter, while it negatively correlated with the number of female offspring within a litter (in 1a in Fig. 2). Therefore, heavier females produced more male offspring and lighter females, more female offspring. In the acorn-rich seasons (the autumns of 1998 and 2000), however, heavier females invested more in female offspring, and lighter females invested more in male offspring (in 2a in Fig. 2). Maternal body mass positively correlated with the number of female offspring within a litter, while it did not correlate with that of male offspring.

Litter size variation depending on the acorn harvest affected the offspring’s sex allocation depending on the maternal body condition. Across the litters measured on the day of birth, we did not identify any significant factors in the GLM for litter sex ratio. Across litters measured within 2 days after birth, however, two factors (maternal body mass and litter size) and their interaction were identified in the reduced GLM for the sex ratio (Table 3: n = 58, F = 2.79, df = 3,54, P = 0.049). Furthermore, across litters measured on the day of birth, similar correlations were also found (Fig. 3).

Table 3.

Statistical results of F tests for factors potentially affecting litter sex ratio in a GLM

Terms	F value	df value	P value
Maternal body mass (MB)	0.82	1	0.37
Litter size (LS)	0.31	1	0.58
MB*LS	7.47	1	0.0085

The GLM with a quasi-binomial error and logit-link function was used. Data were collected from litters and their mothers measured within 2 days after birth (n = 58)

Significant P values are in italics

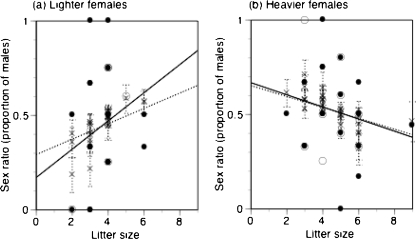
Fig. 3.

Litter sex ratios in relation to litter size in (a) lighter females than the mean maternal body mass (20.3 ± 0.2 g) and in (b) heavier females with the mean maternal body mass or heavier. Data were collected from litters and their mothers measured within 2 days after birth (n = 28 for lighter females and n = 30 for heavier females). Litters measured on the day of birth are indicated with solid circles and a dotted regression line. The other litters are indicated with open circles. A solid regression line is fitted to all litters including litters measured on the day of birth. Crosses indicate predicted sex ratios with a GLM with a quasi-binomial error and logit-link function for litter sex ratio. Error bar is SE for the predicted sex ratio. With litter size, sex ratio positively correlated in lighter females, but negatively correlated in heavier females

A significant interaction effect on litter sex ratio was found between maternal body mass and litter size in the GLM for litters measured within 2 days after birth (Table 3). Across litters produced by the lighter females (n = 28) lighter than the mean maternal body mass (20.3 ± 0.2 g), litter sex ratio positively correlated with litter size (Fig. 3a). However, across litters produced by the heavier females (n = 30) with the mean body mass or heavier, litter sex ratio decreased from male-biased one (sex ratio > 0.5) to female-biased one as litter size increased (Fig. 3b).

Relationship between offspring’s number and birth mass

The mean birth mass of offspring was 1.51 ± 0.02 g (n = 199 from 51 litters: male offspring, n = 96, 1.53 ± 0.02 g; female offspring, n = 103, 1.48 ± 0.02 g). In the acorn-poor seasons, both the birth masses of male and female offspring positively correlated with the maternal body mass (in 1b in Fig. 2). In the acorn-rich seasons, however, the birth mass of male offspring negatively correlated with the maternal body mass, while the birth mass of female offspring did not correlate or weakly positively correlated with the maternal body mass (in 2b in Fig. 2).

Correlations of the birth mass of offspring with the maternal body mass, litter size, litter sex ratio, and sex of offspring were analyzed through a GLMM. In the reduced GLMM for the birth mass of offspring, all the four factors and their interactions were identified (Table 4: χ²-test; n = 177 (43 litters), χ² = 43.3, df = 10, P = 0.0000044). Predicted values with the reduced GLMM highly fitted to the observed birth mass (Fig. 4a).

Table 4.

Summary of a GLMM for offspring’s birth mass

Terms	Estimate ± SE	t value
Maternal body mass (MB)	0.10 ± 0.07	1.52
Litter size (LS)	0.02 ± 0.33	0.07
Sex ratio (SR)	−1.31 ± 0.37	−3.50
Sex of offspring (SX)	−1.68 ± 0.86	−1.95
LS*SR	0.29 ± 0.09	3.06
SR*SX	0.25 ± 0.10	2.63
MB*LS	−0.01 ± 0.02	−0.72
MB*SX	0.07 ± 0.04	1.74
LS*SX	0.45 ± 0.21	2.14
MB*LS*SX	−0.02 ± 0.01	−2.06

The GLMM with a normal error and identity-link function was used (n = 177 from 43 litters). Litter’s identity was designated as a random effect in the GLMM

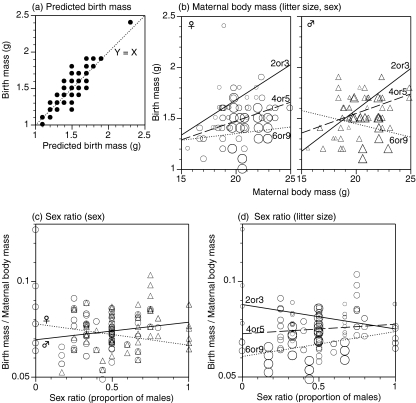
Fig. 4.

Birth masses of offspring in relation to (a) predicted birth mass with a GLMM, (b) maternal body mass, and (c, d) litter sex ratio. In a, a solid line is Y = X. In c and d, the birth masses of offspring per the maternal body mass are indicated. In b and c, male offspring are indicated with open triangles, and female offspring with open circles. In b and d, size of the symbol (three grades) indicates litter size (2 or 3, 4 or 5, and 6 or 9). A solid regression line is fitted to offspring from the small litters (two or three), a broken line to offspring from the middle-sized litters (four or five), and a dotted line to offspring from the large litters (six or nine). In c, a solid regression line is fitted to male offspring and a dotted regression line to female offspring. Data were collected from 177 offspring from 43 litters and their mothers measured on the day of birth. In b, the maternal body mass positively correlated with the birth mass of offspring, excepting male offspring from large litters. This positive correlation became weakened in larger litters. The birth mass of male offspring from large litter negatively correlated with the maternal body mass. In c, sex ratio positively correlated with the birth mass of male offspring but negatively correlated with the mass of female offspring. In d, negative effect of litter size on the birth mass decreased with the sex ratio

Maternal body mass positively correlated with the birth mass of offspring, excepting the mass of male offspring from large litters (litter size equal to six or nine; Fig. 4b). However, this positive correlation between the birth mass of offspring and the maternal body mass became weaker in larger litters. Furthermore, the birth mass of male offspring from large litters (six or nine) negatively correlated with the maternal body mass. In the GLMM, there was a significant interaction effect on the birth mass among the maternal body mass, litter size, and the sex of offspring (χ² = 4.19, df = 1, P = 0.041).

The sex composition of offspring within a litter also affected the quality of offspring. Litter sex ratio positively correlated with the birth mass of male offspring per the maternal body mass, but negatively correlated with the birth mass of female offspring (Fig. 4c). There was a significant interaction effect between litter sex ratio and the sex of offspring in the reduced GLMM (Table 4: χ² = 6.79, df = 1, P = 0.0092). Furthermore, a significant interaction effect between the sex ratio and litter size was observed (χ² = 8.59, df = 1, P = 0.0034). In litters with lower sex ratio, the birth mass of offspring per the maternal body mass decreased with litter size (Fig. 4d). However, this negative correlation between litter size and the birth mass was lower in litters with higher sex ratio.

Discussion

Population disruption and acorn harvest

A serious decline in the population density of A. argenteus was observed after the autumn reproductive season of 1999. We could not find any mice throughout the entire study area in the following spring. It should be noted that a failure of mast production occurred in the autumn of 1999. Oak acorns are thought to be important food resources for forest-dwelling mice (e.g., the large Japanese field mouse, Apodemus speciosus; Wada 1993). Studies on the stomach contents of A. speciosus have revealed that acorns or other seeds are the most dominant food items from autumn to winter (Ohta et al. 1976; Sone et al. 1986).

A. argenteus also depends on oak acorns in autumn to winter, as indicated by the number of adult females (Shibata 2006): in the acorn-poor autumn of 1999, 27 were found in the larch forest (3.9 mice/ha), while only six were found in the oak forest (0.8 mice/ha) in the central part of the study area (8.0 ha oak forest and 7.0 ha larch forest). In the previous autumn (i.e., the acorn-rich season of 1998), adult females were found equally in both forests: 21 in the larch forest (3.0 mice/ha) and 24 in the oak forest (3.0 mice/ha). Therefore, the population disruption was presumably caused by the failure of mast production.

Female-biased sex allocation and “safe bet hypothesis”

A. argenteus has previously been thought to be a monogamous species, and one in which males directly care for their offspring (Oka 1992; Shioya 1992). However, using DNA analysis, Ohnishi et al. (2000) showed frequent extra-pair copulation and polygynous mating. Even if males are socially monogamous, they may copulate with extra-pair mates, which may produce a genetically polygynous mating system that increases the variance of male reproductive success (Westneat et al. 1990). Interestingly, male A. argenteus did not exhibit direct care for offspring during the lactation period in our study area; the larger or older males were accessible to more females than smaller or younger males (Shibata 2006), suggesting that male body size (body mass) may positively affect male mating success, although we have no data indicating that mouse’s body condition at birth affects its body condition at reproduction.

In our study, females in good condition invested more in sons, and females in bad condition invested more in daughters in the acorn-poor seasons. Thus, the investigated population appeared to fit the TW hypothesis. In the acorn-rich seasons, however, heavier females produced more offspring and invested more in daughters, and lighter females invested more in sons, which is inconsistent with the prediction of the TW hypothesis.

In many species in which the TW hypothesis could be applied to, limited dispersal by females can lead to the local resource competition (LRC) between related females (Clark 1978; Clutton-Brock et al. 1982; Silk 1983). In primates, high-ranking females were reported to bias the sex ratio towards daughters (Simpson and Simpson 1982). Under the LRC and rank-inheritance from mothers to their daughters, the TW hypothesis predicts that high-ranking females should benefit greatly from producing daughters, while females of lower rank should benefit more from producing sons (the advantaged daughter hypothesis: Altmann and Altmann 1991). Therefore, if the quality of a female positively correlate with the quality of a patch where the female inhabits and females inherit their patches to their daughters, the TW hypothesis may predict females in good condition produce more daughters and females in bad condition produce more sons, as A. argenteus in the acorn-rich seasons. Wild and West (2007) model predicts conditional sex ratio adjustment in either direction, with high-quality females producing a higher proportion of either sons or daughters when both LRC and conditions of the TW hypothesis can occur simultaneously in the same species. Their model also predicts that mothers in good condition produce daughters in cases where the advantages given to males born on high-quality patches is not appreciably greater than those given to females born on high-quality patches. This prediction might fit to the weakly polygynous species as A. argenteus. However, our finding that low-quality females produced more daughters in the acorn-poor seasons cannot support the advantaged daughter hypothesis because LRC should be higher in poor patches where low-quality females might inhabit.

Lambin (1994) found female-biased sex ratios in Microtus townsendii in spring at low population density. For an adaptive explanation, Lambin adopted the local resource enhancement (LRE) hypothesis (Emlen et al. 1986), which predicts that if philopatric offspring of one sex improved maternal reproductive success more than dispersing offspring of the other sex, the mother will show biased investment to philopatric offspring. Ohnishi et al. (2000) and our previous study (Shibata 2006) suggested that males tend to disperse from their natal areas, and females tend to be philopatric such that the LRE hypothesis (Emlen et al. 1986) is adoptable to sex allocation by females in A. argenteus.

However, the occurrence of philopatry for young female A. argenteus is probably restricted in saturated environments. Most of the communal nesting in young females and adult females (their probable mothers) was observed after the reproductive seasons in years of high population density (Shibata 2006). In a year of the lowest density and good acorn harvest, however, this communal nesting was rarely observed, although females produced more daughters than in the highly saturated seasons. Thus, Lambin’s hypothesis is not likely to explain why female A. argenteus produced more daughters at low habitat saturation.

Here, we propose a new hypothesis, the “safe bet hypothesis”, which predicts female-biased parental investment to offspring in polygynous small mammals that inhabit unstable environments. In polygynous mammals, intra-sexual competition for mates is expected to be greater among males than among females, which presumably results in a wide variance of reproductive successes among conspecific males. Thus, the reproductive success of young males is expected to generally be much lower than those of both older males and young females if body mass and age positively affect male reproductive success in polygynous animals with multiple reproductive events over their lifetime (as A. argenteus). However, in several murid rodent species that experience general instability in their natural populations, mating is usually facultative, varying from monogamous at low population levels to polygynous or promiscuous at high population levels, depending on female distribution (e.g., Mus musculus: Bronson 1979; M. townsendii: Lambin and Krebs 1991). In those species, the reproductive success of dominant males will not be much higher than those of subordinate younger males and of females at low population levels because sparse distribution of females should force males to mate monogamously (as A. argenteus). If the population level abruptly changes from high to low in a non-isolated population, this disruption will seriously decrease future reproductive success of young males settling at high population levels and should more seriously lower the lifetime reproductive success for males than for females. On the other hand, a relatively gradual increase of population density from the low population level is not likely to greatly affect the sexual differences in their lifetime reproductive success. Furthermore, males of most mammal species tend to disperse farther from their natal areas than females (Greenwood 1980). Thus, parents cannot predict the level of populations where their sons settle. This situation favors for mothers invested more in daughters as “a safe bet” than sons in unpredictable environments.

Litter size variations will affect the prediction of our “safe bet hypothesis”. Even in polygynous mammals under unstable environments, male-biased sex allocation by mothers in good condition will be predicted when females produce only a few offspring at once as A. argenteus in acorn-poor seasons, because individual variation in the lifetime reproductive success should be higher across males than across females (Trivers and Willard 1973). In acorn-rich seasons, however, heavier female A. argenteus produced larger-sized litters and invested more in daughters. Frank (1987, 1990) predicts that as the number of offspring per reproductive attempt increases across species, fitness returns from investing in male and female offspring will become equivalent because fitness returns scaling with numbers of offspring will outweigh differences between the fitness returns of having male or female offspring. In polygynous small mammals under unstable environments, however, our hypothesis predicts that the mean of the lifetime reproductive success of daughters will be higher than that of sons. Therefore, it is predicted that as litter size increases, fitness returns from investing in multiple daughters within a litter will become higher than fitness returns from investing in multiple sons within a litter, and mothers will invest in daughters more than sons. Our hypothesis looks like the strategy for playing at a horse race: a rich gambler (high-quality females) bets a lot of money (resources) on a sure thing (daughters), but a poor one bets all on a dark horse (sons).

In murid rodents, female-biased litter sex ratios at low population levels (e.g., the house mouse M. musculus: Evans 1949; the meadow vole Microtus pennsylvanicus: Clutton-Brock and Iason 1986; and the Townsend’s vole M. townsendii: Lambin 1994) and the negative correlation between litter size and sex ratios (M. musculus: Krackow and Hoeck 1989; the guinea pig Cavia porcellus: Peaker and Taylor 1996) have been reported. Female-biased parental investment at low population levels may be common in murid rodents, where the largest litter sizes have been reported, often at low population levels in wild populations (e.g., Nakata 1986; Dobson and Myers 1989; Singleton et al. 2001), although evidence showing female-biased sex allocation of offspring has so far not been reported in species of Apodemus other than the one studied here. Our “safe bet hypothesis” may explain the female-biased sex allocation of offspring in those murid rodents.

Trade-off between quality and number of offspring and sex allocation

Several researchers have noted that possible trade-offs between size, number, and sex of offspring complicate the test of the TW hypothesis in polytocous species (Williams 1979; McGinley 1984; Gosling 1986; Carranza 2004; Servanty et al. 2007). If survival of a mother is affected by her reproductive effort and sons are more costly than daughters per maternal investment, female-biased sex allocation is predicted by the evolutionary stable strategy (ESS) theory when litter size is fixed (Pen and Weissing 2002). In the same situation, if the lifetime reproductive success of sons and daughters has affected maternal investment per offspring in polygynous mammals, a high-quality mother may invest more in daughters in lowly saturated habitats when the adaptive litter size is determined by habitat saturation and maternal body condition. McGinley (1984) argues that the TW hypothesis may explain the negative correlation between litter size and sex ratio (percentage of males per litter) that is sometimes observed in polytocous mammals, because offspring from larger litters usually are weaned at lighter weight (Mendl 1988). Accordingly, increased proportions of males in relatively small litters have been considered adaptive in rodents (Krackow and Hoeck 1989, Peaker and Taylor 1996). In A. argenteus, however, increase in litter size prompted low-quality mothers to invest more in sons. This is inconsistent with the prediction of the ESS theory and McGinley’s argument.

In our study, litter size negatively correlated with litter sex ratio and the birth mass of offspring produced by high-quality mothers. However, this negative correlation between litter size and the birth mass was not observed in male-biased litters and litters produced by low-quality mothers. These results indicate a maternal investment trade-off between quality of sons and number of daughters. In polygynous animals, a negative correlation between body size and the number of offspring within a litter will favor mothers who improve either the quality of a son or the number of daughters, because a decline in the body mass of offspring probably decreases fitness returns to investing in sons more than those from investing in daughters (Trivers and Willard 1973). Thus, fitness returns investing in daughters will increase with their number within a litter, while fitness returns investing in sons will increase with the quality of sons, but this is not so in the increase or decrease with the number of offspring. However, LRC between related females will reduce the marginal fitness gain of producing philopatric daughters (Clark 1978). This LRC will also be affected by habitat saturation (food condition and density). Therefore, if a maternal investment trade-off between quality of sons and the number of daughters exists in polygynous animals, small litter (clutch) size and/or strong LRC between related females may favor dominant mothers investing in one or a few high-quality sons (as in A. argenteus in the acorn-poor seasons), while a large litter size and weak LRC may favor dominant mothers producing as many daughters as they can (as in A. argenteus in the acorn-rich seasons).

We conclude that unstable environments and a maternal investment trade-off between a son’s birth mass and the number of daughters prompt female-biased sex allocation by high-quality mothers in acorn-rich seasons in A. argenteus. Unstable environments and variation in litter size will complicate the predictions of adaptive models such as the TW hypothesis. Our “safe bet hypothesis” will be applicable to the female-biased sex allocation of offspring by many small mammalian species that experience drastic population fluctuations. Furthermore, if a negative correlation exists between the quality and the number of offspring within a litter, conventional hypotheses on adaptive sex allocation should be used carefully in examining the offspring’s sex allocation for small mammals with large litter.