Theoretical Study of Excitation Energy Transfer in DNA Photolyase

Abstract

Photolyase (PL) is a DNA repair enzyme which splits UV light-induced thymine dimers on DNA by an electron transfer reaction occurring between the photoactivated FADH⁻ cofactor and the DNA dimer in the DNA/PL complex. The crystal structure of the DNA/photolyase complex from Anacystis nidulans has been solved. Here, using the experimental crystal structure, we re-examine the details of the repair electron transfer reaction and address the question of energy transfer from the antenna HDF to the redox active FADH⁻ cofactor. The photoactivation of FADH⁻ immediately preceding the electron transfer is a key step in the repair mechanism that is largely left unexamined theoretically. An important butterfly thermal motion of flavin is identified in ab initio calculations; we propose its role in the back electron transfer from DNA to photolyase. Molecular dynamics simulation of the whole protein/DNA complex is carried out to obtain relevant cofactor conformations for ZINDO/S spectroscopic absorption and fluorescence calculations. We find that significant thermal broadening of the spectral lines, due to protein dynamics, as well as the alignment of the donor HDF and the acceptor FADH⁻ transition dipole moments both contribute to the efficiency of energy transfer. The geometric factor of Förster’s dipolar coupling is calculated to be 1.82, a large increase from the experimentally estimated 0.67. Using Förster's mechanism, we find that the energy transfer occurs with remarkable efficiency, comparable with the experimentally determined value of 98%.

1. Introduction

Photolyase (PL) is an enzyme that catalyzes photorepair of thymine dimers on UV damaged DNA.^1,2 The structure of the enzyme has been known for over a decade, however, the structure of DNA/photolyase complex has been solved only recently.³ The enzyme repair mechanism presents a number of intriguing questions that are of interest to physical chemistry.⁴ For example, the molecular mechanism by which photolyase recognizes the dimer on DNA appears to be very intricate since the dimer by itself is not flipped out of the DNA structure and is “poorly visible” on the surface of DNA, unless photolyase is bound to it. How exactly does a PL find the dimer is not clear. The mechanism of sliding/diffusion of photolyase along DNA is poorly understood as well. The work on a similar system has demonstrated the nontrivial nature of the search process.⁵ In our previous work,^6,7 we have shown that, upon binding of photolyase to a dimer on DNA, the latter is flipped out of the DNA helix and gets in a position deep inside the catalytic cavity of photolyase, close to the key redox cofactor flavin adenine dinucleotide (FADH⁻). In the repair reaction, this cofactor becomes electronically excited upon photoexcitation energy transfer from a chromophore antenna that captures photons and transfers an electron to the dimer; the dimer splits, after which the transferred electron returns back to FADH⁻. The mechanism by which photolyase flips the dimer is unknown; however, our prediction of the structure of DNA/PL complex with a flipped dimer has been recently confirmed experimentally.³ The details of the repair reaction which leads to the splitting of the dimer have been extensively studied, including computationally,⁴ although some questions still remain open. In contrast, the mechanism of energy transfer between the photolyase antenna and the FADH⁻ cofactor has not been examined in depth theoretically. A detailed discussion of these and other issues of the enzyme function as well as the current status of experimental and theoretical studies of the enzyme can be found in recent papers.^1–4,8–14

In this paper, we use the now available experimental crystal structure of the DNA/PL complex from Anacystis nidulans to re-examine the details of electron transfer between the enzyme FADH redox cofactor and the thymine dimer of DNA and to study the electronic energy transfer between 7,8-didemethyl-8-hydroxy-5-deazariboflavin (HDF) antenna and FADH⁻ cofactor, a key step in the catalytic function that has a puzzling, almost 100%, efficiency.

Energy transfer in photolyase has been experimentally studied in the past by Heelis and co-workers^15,16 using time-resolved and steady-state fluorescence spectroscopy. The Förster mechanism was postulated to explain the observed exchange of excitation energy between HDF antenna and FADH⁻ cofactor. With the new crystallized DNA/PL complex, we re-examine this process by using molecular dynamics simulation and spectroscopic calculations. One of the interesting aspects of energy transfer in this system is that the emission spectrum maximum is shifted to the red with respect to the local absorption maximum; therefore, a significant broadening of the emission and absorption spectra is required to produce the spectral overlap for an efficient energy transfer to take place. We examine the nature of the motions of the protein that result in such broadening. In the process, a peculiar butterfly thermal motion of flavin is identified in ab initio calculations; we propose its role both in spectral broadening and in the back electron transfer from DNA to photolyase. Molecular dynamics simulation of the whole PL/DNA complex is carried out to obtain relevant conformations for ZINDO/S spectroscopic absorption and fluorescence calculations. We find that both the significant thermal broadening of the spectral lines and the alignment of the transition dipole moments of the antenna HDF and FADH⁻ contribute to the efficiency of energy transfer. The geometric factor of the Förster theory is calculated to be 1.82, a large increase from the experimentally estimated 0.67. Using Förster dipolar coupling mechanism, we find that the energy transfer occurs with a remarkable efficiency, comparable with the experimentally determined value of 98%.

The paper is organized as follows: in section 2, we present the system setup and theoretical methods that were used in the calculations; in section 3, we present computational results and their discussion; finally, in section 4, we summarize the conclusions from this work.

2. Methods and Calculation Details

2.1. System Setup. Molecular Dynamics Simulations

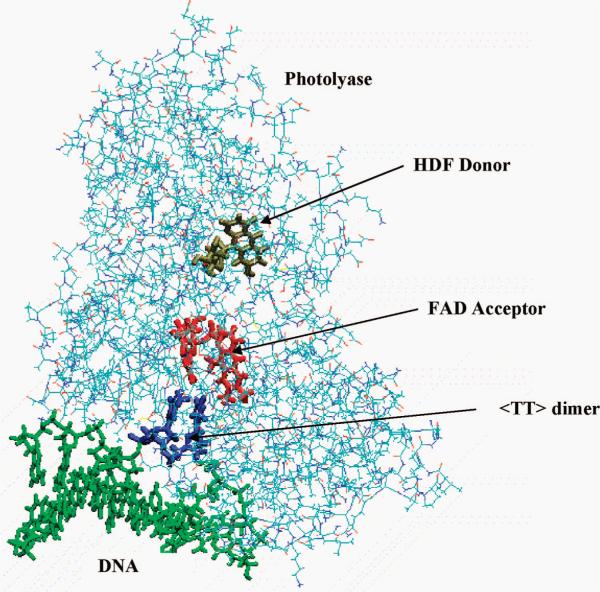
The calculations were based on the crystal structure of the DNA photolyase from Anacystis nidulans bound to a DNA oligomer containing a TT dimer, recently obtained by Mees et al.³ at 1.8 A resolution (Protein Data Bank code 1TEZ). In the reported tetramer structure, only units A and B are in the bound confirmation; the unit A was chosen for this study. In a natural DNA, the adjacent thymine bases are linked by a phosphate bridge. However, in the crystallized structure of the DNA/PL complex, this phosphate group is modified into a formacetal group.³ In the simulation, we retained the formacetal linking group, as was in the crystal structure. In the dynamics simulations, the DNA/PL complex was placed within a solvation shell of water which is 8 A thick; see Figure 1. Overall, the system contained 19 416 atoms and a total of 4239 residues.

Figure 1.

Molecular dynamics simulation system setup. Shown are photolyase enzyme attached to DNA with a TT dimer, and two cofactors: HDF (antenna) and FAD (electron donor). In the simulation, the entire DNA/photolyase complex is treated (see text for details). The complex is solvated in water (not shown) as described in the text.

Molecular dynamics simulations were performed using the AMBER 6.0 suites of programs¹⁷ and Amber94 force field.¹⁸ Nonstandard force constants including those of improper dihedral angles for flavins and formacetal groups were constructed using templates from various sources such as CHARMM;¹⁹ nonstandard charges were calculated by the quantum chemical program ZINDO,²⁰ as previously done.²¹ Standard protonation states for titratable groups of the protein and DNA were assumed and the counterions Na+ were added by XLEAP to obtain system neutrality. In all stages of the simulation, the movable parts included the DNA dimer, the redox active FADH⁻, the antenna HDF and their neighboring protein residues in the proximity of 12 A, and all of the water molecules within 7 A from any atoms of these entities. In the simulation procedure, we first performed energy minimization up to 1.0 × 10⁻⁴ in rms deviation, then equilibration of 400 ps, with 0.5 fs integration step and 300 K in constant temperature dynamics using Berendsen's coupling algorithm.²² After equilibration, the dynamics runs were typically 0.5 ns long, sufficient for our purposes. The equilibrium properties of the system were shown to remain unchanged as the simulation times were extended to as long as 10 ns²³ (see Supporting Information).

2.2. Quantum Chemical Calculations

The Geometry optimization and normal-mode analysis of flavin chromophore were performed using DFT B3LYP/6−31G* by the Gaussian 03 program.²⁴ The electronic spectra were calculated using the ZINDO/S CIS method implemented in the ZINDO program.^20,25 In these quantum chemical calculations, to account for spectroscopic shift due to the electrostatic protein environment, all atoms within a 12 A distance from the chromophore were represented by point charges, same as in the dynamics simulation. Solvent shift due to the protein dielectric is accounted for by self-consistent reaction field (SCRF) theory developed within the ZINDO/S CIS methodology for electronic absorption spectra.²⁶ For the fluorescence spectra, a similar method was used, but special formulation of the theory allows for the relaxation both electronically and geometrically of the excited state.^26,27

2.3. Energy Transfer

Due to the long distance separating HDF and FADH⁻, which preclude electronic exchange, and the large transition dipole moments of donor and acceptor, the Förster mechanism²⁸ was postulated to explain the energy transfer in this system.^1,29 In these calculations, we follow this model. In the Förster mechanism, the transfer efficiency is expressed as

$${\Phi }_{\mathrm{ET}}=\frac{R_0^6}{R_0^6+R^6}$$ (1)

where R is the separation of the donor and acceptor (point dipoles are assumed in the standard Förster model; here, we follow this model without modifications), and the parameter R₀, known as the “critical distance”, is defined as follows¹⁵:

$$R_0=(9.79\times {10}^3)\times {\left(J{K}^2{Q}_F{n}^{-4}\right)}^{1∕6}$$ (2)

In the above formula, overlap J with the units cm³ M⁻¹ is defined as

$$J={\int }_0^{\infty }{F}_D\left(\lambda \right){∊}_A\left(\lambda \right){\lambda }^4\mathrm{d}\lambda ∕{\int }_0^{\infty }{F}_D\left(\lambda \right)\mathrm{d}\lambda$$ (3)

Q_F is the fluorescence quantum yield, n is the index of refraction, and K is the unitless geometric factor describing the orientation of the donor and acceptor transition dipoles.^30,31

In determining the geometric factor K, the transition dipole moments were taken from the spectroscopic ZINDO/S CIS calculations; the same calculations were used to obtain the spectroscopic overlap J.

3. Results and Discussions

3.1. Flavin Geometry, Vibrations, and Excited States

The redox active flavin in FAD can take the free radical form (i.e., FADH⁻ looses an electron and becomes FADH) which is not catalytically active. In order to be able to split the thymine dimmers, the flavin has to be in its reduced form, FADH⁻, bearing a negative charge. Due to the important dual role of the flavin as the energy acceptor from the antenna and electron donor–acceptor with respect to the thymine dimer, we choose to study its geometry first. The geometry of reduced flavin (in vacuum) was found to be nonplanar; see Figure 2. Namely, the two hexagonal rings from the center of the two-electron reduced isoalloxazine assume a bent geometry with an angle close to 30°, forming a buckled butterfly structure. In the experiment performed by Mees et al.,³ the reduced form of flavin is indeed found bent, but it assumes a smaller bending angle of approximately 9° under the conditions of brilliant synchrotron radiation for X-ray measurement. According to our calculation, the bent structure of flavin has the highest projection of a normal mode vibration with a frequency of 34 cm⁻¹, the lowest of a series of ring-bending modes in the IR active vibrations. The molecular dynamics equilibrium geometry for flavin takes this butterfly form as well. It appears that this structure is not unique to photolyase. For example, reduced flavin in bent conformation with an angle of 27° was also found in a different species as well.³² In addition to this bending mode, several other floppy vibrational normal modes are low-lying, and they are expected to mix with the lowest bending mode in the course of thermal motion of the molecule.

Figure 2.

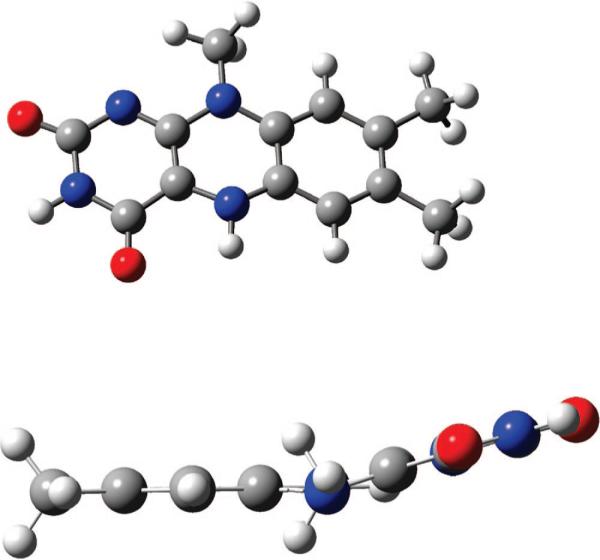
Butterfly bending of the fully reduced flavin molecule, calculated using DFT B3LYP method and 6−31G* basis set in Gaussian03.

We have examined the effect of the bending motion described above on the UV absorption spectrum of FADH⁻ for three lowest-frequency transitions in the molecule. The data for several most important transitions are shown in Figures 3 and 4. We find that LUMO is localized on the heterocyclic ring of the flavin, and electron density is shifted toward the phenyl ring on the other side of the molecule, in agreement with ref 10. The HOMO orbital with electron density concentrated on N, and O atoms has an overall bonding character. When the electron is promoted to the LUMO by photoexcitation, the excited-state orbital is largely centered on the benzene ring on the other side of the isoalloxazine, with an overall character of a nonbonding molecular orbital, indicating that this electron is free to be transferred out as far as its contribution to chemical bonding of the flavin delocalized ring system is concerned. The lowest transition, largely due to HOMO to LUMO excitation, is most sensitive to the bending, yielding a shift and broadening of the order of some 20 nm due to thermal motions of the bending mode. In ZINDO/CI formalism, higher transitions still have contributions from HOMO and LUMO configurations (due to orbital mixing). In our calculation, these contributions diminish as the spectral transitions get higher. As such, the spectroscopic shift due to the flavin ring bending becomes smaller, yielding some 10 nm for the second transition and a few nanometers for the third highest spectroscopic excitation, as shown in Figure 4.

Figure 3.

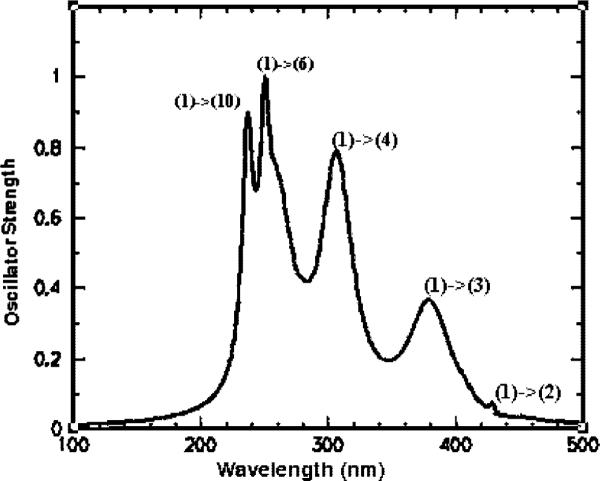
Overall absorption spectrum of FADH⁻ obtained with ZINDO/S program using DFT B3LYP/6−31G* geometry.

Figure 4.

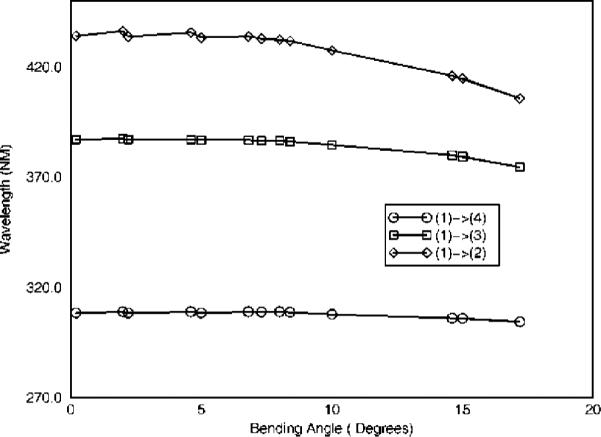
Bending angle dependence of flavin absorption frequency for the first three transitions shown in Figure 3.

In the reduced form, flavin remains catalytically inactive until it is promoted to its first excited state. As this transition is most sensitive to flavin bending motion, spectroscopic shift originated by this thermal vibration is expected to broaden the flavin absorption and thus increase the spectroscopic overlap with the antenna HDF, whose spectral maximum is shifted from that of flavin, an effect that we discuss in the following subsections.

3.2. Absorption Spectrum of FADH⁻

The electron transfer of the repair reaction occurs only from the excited state of the reduced flavin (FADH^−*). The activation is achieved through energy transfer from the antenna HDF cofactor. The excited state can be described as a single electron excitation within the configuration interaction singles (CIS) theory. The semiempirical quantum mechanical method ZINDO/S can calculate with reasonable accuracy such excited states and their absorption transition moments. The overall absorption spectrum calculated in this way is shown in Figure 3.

Careful consideration here must be given to the DNA/protein environment that may cause noticeable spectroscopic shift due to electrostatic interaction with the chromophores. We set a radius of 12 A within which all atoms of the protein/DNA complex represented by point charges are moving according to the molecular dynamics simulation, and as such produce spectral shift and broadening of the absorption spectra. For this radius, the overall net charge for the quantum system remains reasonably close to zero for the antenna and remains −1 for FADH⁻. Spectral analysis is performed as follows. We first compute the spectral transition without the protein environment, then the same calculations are carried out with the inclusion of protein environment represented by the point charges. The difference of the transition frequencies represents the spectroscopic shift due to environment.

The spectroscopic shift due to protein electrostatic environment, when averaged over the MD trajectories, has the largest value 25 nm for transitions largely corresponding to HOMO–LUMO excitation, whereas it becomes 17 nm for the second excited state and 6 nm for the third excited state; see Figure 5.

Figure 5.

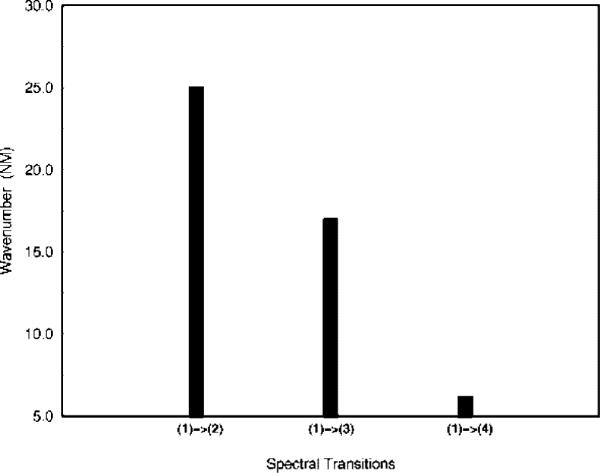
Average shift of absorption frequency due to protein electrostatics.

The shift and broadening of the spectra due to solvation is accounted for by the inclusion of the self-consistent reaction field (SCRF) in our calculations. This is necessary due to the highly polar dielectric environment of the chromophores in the protein. In SCRF treatment, the electric multipole moments of a chromophore are allowed to interact with the protein dielectric medium which gets polarized; the induced reaction field then is included in the electronic structure calculations of the chromophores.

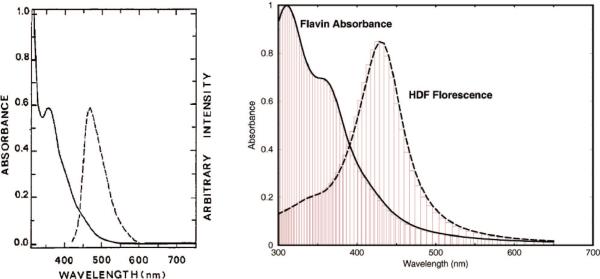
The spectroscopically significant electronic transitions take place largely among the π orbitals near the HOMO–LUMO gap. The most intense transition band is generated by the HOMO–LUMO transition. These transitions are shown in Figure 3, where the Lorentzian line-shapes were used to describe the line broadening. Overall, both the maximum of absorption and a minor shoulder of (1) → (2) and (1) → (3) transitions agree well with the experimental measurement;¹⁶ see Figure 6.

Figure 6.

Experimental (left, from ref 16 by ACS copyright permission) and theoretical (right, from this calculation) absorption and emission spectra of FADH⁻ and HDF, respectively, and their overlap.

3.3. Fluorescence Spectrum of HDF Antenna

The emission transitions were calculated using the same procedure as was used for the absorption and involved trajectory data collection, evaluation of the electrostatic environment effects, and solvation spectroscopic calculation using ZINDO/S CI SCRF methodology.²⁷ However, here the excited state is allowed to fully relax. The antenna chromophore HDF, apart from its difference with FADH⁻ in the peripheral groups, has an identical flavin structure with that of FADH⁻ which accounts for all of the spectroscopic transitions. Yet, the spectroscopic transitions in HDF, whether calculated as absorption or emission, are markedly different from those in FADH⁻. The calculated fluorescence band for HDF is shown in Figure 6. As in FADH⁻ absorption spectra, the fluorescence involves mostly π orbitals that are LUMO, HOMO, and orbitals downward from HOMO.

3.4. Energy Transfer Process

The overall efficiency of donor–acceptor energy transfer is an averaged-overtime quantity. To calculate the Förster parameters in PL, the average geometry was determined over the same dynamical trajectories as those used to generate the electronic spectra. Early work in computing donor and acceptor transition dipole moments involved uncertainties in their relative orientation.²⁹ To overcome this problem, here, separate calculations were carried out for both the donor and the acceptor, keeping them positioned in the same molecular frame coordinate system. This strategy eliminates the uncertainty and possible errors that were encountered in earlier work.²⁹

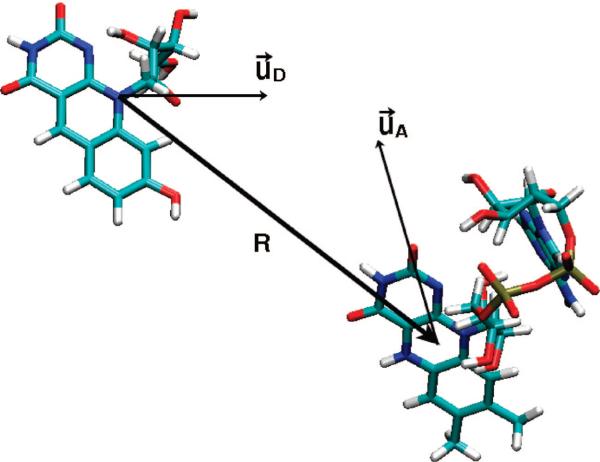
The donor (HDF) and acceptor (FADH⁻) are separated by a distance of 17.1 A (center of mass to center of mass) as measured in the protein structure. The position vector of this separation forms a dot product with the donor and acceptor transition dipole moments, yielding the values of 0.897 and 0.610, respectively, while the mutual dot product of the dipoles is 0.293; see Figure 7. The transition dipolar vectors were determined from the ZINDO quantum chemical calculations. With these results, for geometric factor K in eq 2 we obtain the value of 1.82. This value is significantly larger than previously estimated 0.67 from the experimental arguments,¹⁶ but it is close to a previous calculation based on crystal structure.³³

Figure 7.

Relative orientation of HDF donor (D) and FADH acceptor (A) in energy transfer process, and orientation of transition dipole moments.

The absorption and emission spectra calculated in the last two subsections have an appreciable overlap J as shown in Figure 6. By numerical integration, it was found to be approximately 5 times the estimated 3.6 × 10⁻¹⁵ M⁻¹ cm³ of ref 16. With these results and assuming the refraction index to be 1.36, from eq 1, we derive the energy transfer efficiency of 99.6%. This is a remarkably high efficiency, given the distance between donor and acceptor is about 17 Å.

From the fluorescence lifetime measurements, the efficiency of energy transfer was previously estimated to be 98%.¹⁶ However, with the Förster parameters deduced from the same data, theoretical estimate yielded the efficiency of 95%. In our present estimate, both the broadening of the spectral lines leading to spectral emission/absorption overlap and the geometrical factor contributed to a slightly higher efficiency of energy transfer compared with earlier estimates. The higher efficiency in our estimate is largely due to the red-shift broadening of the absorption spectra due to flavin ring bending mode (since absorption is on the “blue” side of the fluorescence, red shift brought the absorption in closer overlap with fluorescence) and better than previously estimated alignment of transition dipole moments and the chromophore separation vector.

Both the previously estimated experimental values and the current theoretical results agree on the remarkably high efficiency of energy transfer in PL over a long distance.

4. Conclusions

With the recently solved crystal structure of DNA/PL complex from Anacystis nidulans, we have examined the dynamic behavior of the photolyase cofactors and evaluated the efficiency of energy transfer between PL antenna HDF and electron donor FADH. The redox active flavin experiences butterfly-like ring buckle as the electron is transferred in and out of FADH. The thermal motion of this mode, in combination with other low lying floppy vibrations, results in significant spectral broadening for both the emission of the antenna HDF and the absorption of FADH⁻. Our MD simulation together with ZINDO/S calculated spectra has revealed a significant spectral overlap between HDF donor and FADH⁻ acceptor which allows one to rationalize the experimentally observed high efficiency of energy transfer in this system. The major factor responsible for spectral broadening of the flavin appears to be its butterfly-like thermal motion.

The same butterfly mode may, among other reasons,¹ be responsible for slowing down back electron transfer from the <TT> DNA dimer to FADH cofactor of photolyase, because, in order to receive an electron back from DNA, the oxidized redox cofactor, which has a plane geometry in the ground state, must reorganize and assume a structure resembling one in the final state, that is, one in which FADH is highly bent. The restricted energy supply required for such reorganization may therefore contribute to decreasing the rate of back electron transfer. The slow rate of back electron transfer is crucial for the overall mechanism of DNA repair by photolyase, since electron must not be transferred back to FADH until the repair reaction is finished and the dimer on DNA is split. Further study is underway to examine in greater detail the effect of thermal motion of this mode on electron transfer. Overall, the described role of thermal fluctuations of catalytic cofactors in photolyase is yet another example of a system where the thermal conformational dynamics is crucial for its function.