Theoretical and computational analysis of the membrane potential generated by cytochrome c oxidase upon single electron injection into the enzyme

Abstract

We have developed theory and the computational scheme for the analysis of the kinetics of the membrane potential generated by cytochrome c oxidase upon single electron injection into the enzyme. The theory allows one to connect the charge motions inside the enzyme to the membrane potential observed in the experiments by using data from the “dielectric topography” map of the enzyme that we have created. The developed theory is applied for the analysis of the potentiometric data recently reported by the Wikström group [I. Belevich, D.A. Bloch, N. Belevich, M. Wikström and M.I. Verkhovsky, Exploring the proton pump mechanism of cytochrome c oxidase in real time, Proc. Natl. Acad. Sci. U. S. A.104 (2007) 2685–2690] on the O to E transition in Paracoccus denitrificans oxidase. Our analysis suggests, that the electron transfer to the binuclear center is coupled to a proton transfer (proton loading) to a group just “above” the binuclear center of the enzyme, from which the pumped proton is subsequently expelled by the chemical proton arriving to the binuclear center. The identity of the pump site could not be determined with certainty, but could be localized to the group of residues His326 (His291 in bovine), propionates of heme a₃, Arg 473/474, and Trp164. The analysis also suggests that the dielectric distance from the P-side to Fe a is 0.4 or larger. The difficulties and pitfalls of quantitative interpretation of potentiometric data are discussed.

1. Introduction

Time-resolved measurements of the membrane potential generated by proteins upon single-electron injection have been one of the most fruitful techniques in studies of charge translocation in membrane proteins such as cytochrome c oxidase (CcO) and reaction centers [1–10]. Although such measurements provide valuable data that reflect charge transfer processes in proteins, getting molecular insights from these experiments has been difficult because of lack of the theory for proper quantitative interpretation of the data. The main problem is related to the dielectric inhomogeneity of the membrane-protein system, which complicates the relationship between the observed membrane potential and the distances traveled by charges in the protein.

The goal of the present paper is to establish a connection between the measured amplitudes of the kinetic phases and charge transfer processes in the protein taking into account the actual inhomogeneous dielectric properties of the system. To this end, we have developed a continuum electrostatic model that directly relates the computed potentials of different groups of the protein to the membrane potential generated when the charges are transferred in the enzyme. The result of such calculations is what can be termed the dielectric topography map of the protein. Each residue is assigned a normalized potential, which is a measure of the dielectric depth of the residue measured from one side of the membrane, so that the difference between the corresponding values of two groups is directly proportional to the membrane potential observed in the potentiometric experiments.

We have created such a map for Paracoccus denitrificans CcO, and have applied our theory for the analysis of the potentiometric kinetic data on the O to E transition reported recently by Belevich et al. [9]. In their experiment, three protonic kinetic phases were observed. Using their data, we have attempted to establish the identity of the groups that exchange charges and generate the observed potentials. Of our particular interest is the so-called Proton Loading Site (PLS) of the pump. We will show that although the identity of PLS cannot be precisely established, this site can be localized to a small group of residues located just “above” the Binuclear Center (BNC) of the enzyme. Both the dielectric model of the enzyme and the experimental data contain uncertainties that prevent an unambiguous molecular interpretation of the potentiometric data. The limitations of the theory are discussed.

The insights obtained in the analysis are discussed in the context of other potentiometric experiments and proposed proton pumping models of CcO. This paper demonstrates the usefulness of the developed approach and with further improvements can provide a quantitative method for interpretation of potentiometric data not limited to CcO, but for other proton pumps as well.

The plan of the paper is as follows. In the next section we present theory that describes how the potentials observed in the experiment can be calculated and connected to specific groups inside the enzyme that exchange charges; the sequential kinetic model that is typically used in the analysis of potentiometric data is described next. We then present the results of the calculations on the P. denitrificans enzyme, and apply the developed theory for the analysis of the experimental data by Belevich et al. We examine the extent to which identity of the proton loading site of the pump can be determined from the data. We conclude the paper with a discussion of the results for other systems, including Rhodobacter sphaeroides mutant N139D. Limitations of the potentiometry are discussed and suggestions are made as to how to improve the accuracy of the method.

2. Theory

2.1. Relation between the measured membrane potential and calculated potentials of individual groups in the protein

For interpretation of the experimental results we need to calculate the potentials generated by moving charges in inhomogeneous dielectric medium. The system consists of a protein molecule embedded in an infinite planar hydrophobic membrane of thickness L separating two aqueous electrolyte solutions with ionic strength of I. The membrane planes together with the outer protein surfaces can be considered as two plates of a capacitor, a and b. The protein region is inhomogeneous dielectrics with a coordinate-dependent dielectric constant ε(r). In order to formulate the problem numerically, we cut on the membrane a circle of a large radius R with its center at the protein, such that ε(r) is constant outside the circle x²+y²=R² (the z-axis is perpendicular to the membrane with its origin at the membrane center), where the potential created by a voltage difference between two plates of the capacitor has the form

$${{\varphi }^m(\mathbf{r})\equiv {\varphi }^m(x,y,z)=\frac{\mathrm{\Delta }{V}_m}{L}\left(z+\frac{L}{2}\right)\mid }_{x^2+y^2\ge R^2}.$$ (1)

Here, ΔV_m = V_{plate b} − V_{plate a} is the potential difference between the N-side plate b (z=L/2) and the P-side plate a (z=−L/2). Boundary conditions require that potential be constant at the plates,

$${{\varphi }^m(\mathbf{r})\mid }_{\mathbf{r}={\mathbf{r}}_a\in a}=0,{{\varphi }^m(\mathbf{r})\mid }_{\mathbf{r}={\mathbf{r}}_b\in b}=\mathrm{\Delta }{V}_m.$$ (2)

Below we will show that the normalized potential,

$${\varphi }^0(\mathbf{r})={\varphi }^m(\mathbf{r})/\mathrm{\Delta }{V}_m,$$ (3)

obeying the modified linearized Poisson–Boltzmann equation [11,12],

$$-\nabla ·[\epsilon (\mathbf{r})\nabla {\varphi }^0(\mathbf{r})]+{\epsilon }_w{\kappa }^2(\mathbf{r})[{\varphi }^0(\mathbf{r})-f(\mathbf{r})]=0,$$ (4)

directly represents the required “dielectric topography” of the protein, that is, φ⁰(r) is the dielectric distance traveled by the electron moving from the P-side to a given point r inside the protein and 1−ϕ⁰(r) is the distance traveled by the proton from the N-side to r. In Eq. (4), ε_w is the dielectric constant of water, κ(r) is a constant equal to the Debye–Hückel screening parameter κ outside the membrane–protein system and zero inside it, and f(r) is 1 on the N-side and 0 everywhere else. The term with f(r) is introduced in order to satisfy the boundary conditions at z → ± ∞. The normalized potential ϕ⁰(r) ranges from 0 at z → −∞ to 1 at z → + ∞.

The voltage ΔV_m is expressed in terms of the capacitance C and the total charge,

$$Q_a=-Q_b\equiv Q,$$ (5)

accumulated at each plate, so that

$${\varphi }^m(\mathbf{r})=(Q/C){\varphi }^0(\mathbf{r}).$$ (6)

In the limit of R→∞, both Q and C are increasing, whereas their ratio remains finite. The function ϕ⁰(r) is independent of the cut-off radius R when R is significantly larger than the protein dimensions. The charges are inhomogeneously distributed over the plates, so that

$$Q_{a,b}=\underset{a,b}{\int }\text{d}{Q}_{a,b}.$$ (7)

Now let us consider the experimental setup. When a single electron is injected into the protein and is transferred between the redox centers, it causes translocation of protons. It is a change in the potential difference between the plates induced by a single-electron injection that is measured in experiment. Therefore, the problem is formulated differently in this case.

Let ψ(r) be the potential at point r when a single point charge q′ is placed at a point r′. If both r and r′ belong to the protein interior, ψ(r) satisfies the Poisson equation,

$$-\nabla \epsilon (\mathbf{r})\nabla \psi (\mathbf{r})=4\pi q^{\prime }\delta (\mathbf{r}-{\mathbf{r}}^{\prime }),$$ (8)

with boundary conditions (1) and (2), where now ΔV_m is an unknown constant. The potential induced by q′ can be written in a general form as

$$\psi (\mathbf{r})=q^{\prime }G(\mathbf{r},{\mathbf{r}}^{\prime }),$$ (9)

where G(r,r′) is the potential created at r by a unit charge placed at r′. We note that this is not the Green function as defined in common textbooks (see, e.g. [13,14]) since it does not obey homogeneous boundary conditions. It is important, however, that it is symmetric with respect to its arguments. In order to prove this statement, we consider the total energy change, ΔW, when two charges, q and q′, are placed at points r and r′, respectively. It consists of three terms, ΔW=A +A′ +B, where A is the interaction energy of q with the medium, A′ is the same for q′, and B is the interaction between q and q′. The latter can be calculated either as the energy of charge q in the potential of Eq. (9), B=qq′G(r,r′), or as the energy of charge q′ in the potential created by charge q, B=q′qG(r′r). Since both equations represent the same quantity, we obtain

$$G({\mathbf{r}}^{\prime },\mathbf{r})=G(\mathbf{r},{\mathbf{r}}^{\prime }).$$ (10)

We will use this property in order to connect our calculated function ϕ⁰(r) with the measured trans-membrane potential generated by a single-electron injection.

Consider charge q placed at point r. According to Eq. (9), the potential generated by this charge at plate a is

$$qG({\mathbf{r}}_a,\mathbf{r})\equiv q{G}_a(\mathbf{r}),$$ (11)

where G(r_a,r) is independent of the location of the point r_a on the surface of the conductor a and is therefore designated simply as G_a(r). For the potential difference between plates a and b we obtain

$$\mathrm{\Delta }\psi (\mathbf{r})=q[G_a(\mathbf{r})-G_b(\mathbf{r})]\equiv q\phi (\mathbf{r}).$$ (12)

If several charges q_k move from the initial locations ${\mathbf{r}}_k^{(i)}$ to the final locations ${\mathbf{r}}_k^{(f)}$, the change in the potential difference is given by

$$V_{fi}=n_m\sum _k{q}_k\left[\phi \left({\mathbf{r}}_k^{(i)}\right)-\phi \left({\mathbf{r}}_k^{(f)}\right)\right],$$ (13)

where n_m is the number of enzymes on the membrane and summation is over charges in a single enzyme. Thus, in order to calculate the amplitudes of the kinetic phases observed in experiments, we have to relate φ(r) with ϕ⁰(r), the latter being obtained as a numerical solution to a different electrostatic problem discussed at the beginning of this section. This relationship can be obtained as follows.

Consider again the first problem where there are no charges, but instead a known potential difference ΔV_m is maintained between the capacitor plates. The solution given by Eq. (6) can now be written in terms of function φ. First of all, the potential created by a surface charge dQ_a at a point r is dQ_aG(r,r_a). Furthermore, G(r,r_a)= G(r_a,r) ≡ G_a (r) is independent of r_a due to its symmetry, see Eq. (10). Hence, integration over surface a gives Q_aG_a(r), and the same applies to surface b. With this and Eq. (5), we obtain that the total potential created at a given point r by both plates is Qφ(r). Comparing it with Eq. (6), we obtain the equation

$$C\phi (\mathbf{r})={\varphi }^0(\mathbf{r}),$$ (14)

which relates the function needed for interpretation of experiment with the one calculated numerically. It is worthwhile to note that the capacitance of our system, C, tends to infinity when the cut-off radius, R, increases infinitely. Therefore, any changes of the potential generated by a single charge must disappear, i.e., φ(r) → 0 when R → ∞, whereas the product on the left of Eq. (14) remains finite. From Eqs. (13) and (14), we obtain

$$V_{fi}=C_V\sum _k{q}_k\left[{\varphi }^0\left({\mathbf{r}}_k^{(i)}\right)-{\varphi }^0\left({\mathbf{r}}_k^{(f)}\right)\right].$$ (15)

If charges are measured in atomic units, i.e., q_k = −1 for electron and +1 for proton, then the coefficient of proportionality, C_V = en_m/C, is the potential generated by a unit charge crossing the full membrane (from the measured value of C_V =2.5 mV, see footnote to Table 2, one obtains C/n_m =6.4×10⁻¹⁷ F). The k-th term on the right represents the relative, dimensionless dielectric distance covered by charge q_k moving from ${\mathbf{r}}_k^{(i)}$ to ${\mathbf{r}}_k^{(f)}$, which is equal to the potential generated due to this movement. For instance, the electron moving from the P-side (ϕ⁰=0) to a point r inside the protein generates the potential C_Vϕ⁰(r), and the proton moving from the N-side (ϕ⁰=1) to r generates C_V[1 − ϕ⁰(r)].

Table 2.

The inverse rates (in ms) and normalized cumulative amplitudes of four kinetic phases (V₄ =2) found by four-exponential fitting of the experimental kinetics of the potential generated upon single-electron injection into CcO from P. denitrificans [9]

Set number	$k_1^{-1}$	$k_2^{-1}$	$k_3^{-1}$	$k_4^{-1}$	V1	V2	V3	SD (0.1μV)
1	0.020	0.140	0.636	2.28	0.336	1.06	1.62	5.82
2	0.021	0.150	0.716	2.37	0.350	1.09	1.66	5.91
3	0.022	0.155	0.758	2.41	0.358	1.11	1.68	6.00
4	0.026	0.189	0.824	2.16	0.418	1.20	1.68	6.85
5	0.010	0.149	0.769	2.21	0.259	1.11	1.68	7.75
6	0.010	0.15	0.8	2.6	0.24	1.08	1.68	10.5

Sets 1–4, Our fittings of the original experimental data file provided by Belevich et al. The rate of the first phase was kept constant, other three rates and four amplitudes were optimized. The merit function is the sum of relative deviations squared. C_V is the same as in set 5.

Set 5, Inverse rates, amplitudes U_i (recalculated in terms of V_i), and C_V =2.477 mV are from Belevich et al. (private communication).

Set 6, Inverse rates and amplitudes U_i (recalculated in terms of V_i) are from Fig. 2B caption of Ref. [9]; we assumed C_V =2.512 mV in order to obtain the minimum SD shown.

Thus, in order to predict the potential that a charge transfer between groups A and B inside the enzyme will generate, one needs to know the potentials ϕ⁰(A) and ϕ⁰(B) of these groups. The observed membrane potential is proportional to the difference between ϕ⁰(A) and ϕ⁰(B), as Eq. (15) states. The potentials ϕ⁰(g_i) of different groups g_i of the P. denitrificans enzyme will be calculated in the following section.

2.2. Sequential kinetic model

The observed potential generated across the measuring membrane upon single-electron injection is usually represented in the form

$$V_{\text{obs}}(t)=C_V{\sum }_{i=1}^N{A}_i\left(1-e^{-k_{i}t}\right),$$ (16)

where N is the number of kinetic phases, k₁ > k₂ > … >k_N are rate constants, A_i are the amplitudes normalized such that their sum is equal to the total number of charges translocated across the full membrane at $t\gg k_N^{-1}$, and C_V is the potential generated by unit charge crossing the full membrane.

It will be assumed that the above potential is generated by a sequence of charge transfer processes of the form:

$$S_0(V_0=0)\to S_1(V_1)\to S_2(V_2)\to \dots \to S_N(V_N),$$ (17)

where S₀ is the initial state of the enzyme before electron injection, S_N is the final state when all charge translocations have occurred, and S_i are intermediate states. Each intermediate state is characterized by a specific charge distribution in the enzyme and a specific potential V_i accumulated when the system reaches state S_i. As the system undergoes a sequence of transitions from state S₀ to state S_N, the membrane potential is changing from V₀ to V_N.

If the potentials V_i are normalized such that V_N is the total charge translocated across the membrane, the evolution of the membrane potential can be represented as follows:

$$V(t)=C_V{\sum }_{n=0}^N{V}_n{p}_n(t),$$ (18)

where p_n(t) are populations of states S_n. The time-dependent populations of a general sequential kinetic model, such as in Eq. (17), with N+1 states are given by

$$p_n(t)={\sum }_{i=1}^{n+1}{K}_{ni}{e}^{-k_{i}t},0\le n\le N-1,$$ (19)

where k_i are the rates of sequential transitions, K₀₁ =1, and

$$K_{ni}=\frac{{\displaystyle \prod _{j=1}^n}{k}_j}{{\displaystyle \prod _{\underset{j\ne i}{j=1}}^{n+1}}(k_j-k_i)},1\le n\le N-1,1\le i\le n+1$$ (20)

(for derivation, see Supplementary information, section S1). Substituting Eq. (19) into Eq. (18) and comparing the resulting expression with the experimental fitting curve, Eq. (16), one finds the relationship between the observed apparent amplitudes of the N kinetic phases and the membrane potentials V_n that characterize the intermediate kinetic steps. The relationships are

$$A_i={\sum }_{n=i-1}^{N-1}(V_N-V_n)K_{ni}.$$ (21)

It should be noticed that the observed amplitudes A_i depend not only on the potentials of the intermediate states V_n but also on the transition rates k_i. It is only when the time-scales of successive kinetic phases are well separated, k_i ≫ k_{i + 1}, that the observed amplitudes A_i become equal to potential increments (V_i − V_{i − 1}) between the successive steps. In general, the kinetic phases are not separable —the next phase begins while the previous one is not completely finished. Hence, the kinetic overlap is critical for the correct analysis of the experimental kinetics [8,15].

Inverting the above equation, one can express the potentials V_i in terms of the observed amplitudes of the kinetic phases A_i and rates k_i. A specific relation between A_i in Eq. (16) and V_i in Eq. (18) for N =4 that corresponds to one electronic and three protonic phases, as in experiment of Belevich et al., is given in section S1 of Supplementary information, see also [8,15].

Wikström and co-workers [6,9,16] used another equivalent representation for the observed potential,

$$U_{\text{obs}}(t)=C_V{\sum }_{i=1}^N{U}_i{F}_i(t),$$ (22)

where F₁(t)=1 − p₀(t), F₂(t)=1 − p₀(t) − p₁(t),…, F_N(t)= p_N(t). Comparing Eqs. (18) and (22) one finds that the newly-defined “amplitudes” U_i (not to be confused with the commonly used amplitudes A_i) represent the increments of the potential between the successive phases, that is,

$$U_i=V_i-V_{i-1},i=1,\dots N.$$ (23)

Note that both V_i and U_i are the actual potentials due to charge displacements; hence, in contrast to A_i, they are independent of the rate constants. When the rates of successive phases differ more than an order of magnitude, the overlap effect is negligible, and one has A_i = U_i.

Experimental data typically include sets of rate constants and amplitudes, either A_i [4,5,7,8] or U_i [6,9,16]. The theory of the previous section allows one to directly connect the charge transfer processes inside the enzyme with the amplitudes derived from the experimental kinetic curves.¹ In order to do this, one only needs to know the potentials corresponding to different groups. We next discuss the calculations of such potentials for P. denitrificans CcO.

3. Computational methods

3.1. Electrostatic calculations

The electrostatic calculations described in section 2 were performed using a modified version of Adaptive Poisson–Boltzmann Solver (APBS), ver. 0.3.2 [17–19]. The details are given in section S2 of Supplementary information. The structure of CcO from P. denitrificans determined by Harrenga and Michel [20] (PDB code 1QLE, all redox centers oxidized) was used in the calculations. The first three subunits containing all redox and other important groups were included in the calculations (see related ref. [21]). The membrane was modeled as a planar low-dielectric slab, see Fig. 1. The orientation of the membrane with respect to the molecular frame of the protein was assumed to be the same as for bovine enzyme, for which calculations involving the membrane were performed by us earlier [22].

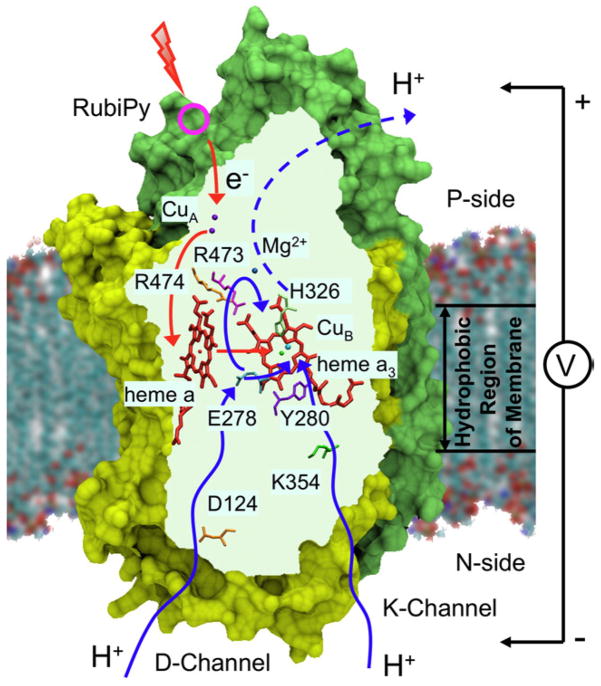
Fig. 1.

Schematics of CcO incorporated in the membrane and major groups involved in proton pumping activity. The photo-injection of an electron into the enzyme results in the development of the membrane potential examined in this paper.

3.2. Membrane parameters

The coordinates of 1QLE were transformed to have the best overlap with the structure of 1V55 [23](bovine CcO). The transformation was performed by the Swiss-PDB Viewer [24] best fit with the so-called structure alignment function, which minimizes RMSD of C_α atoms of homologous residues in the first two subunits. The coordinate system of 1 V55 has the xy-axes in the plane of the membrane and the z-axis perpendicular to it, directed from the P-side to the N-side. The resulting orientation of the membrane with respect to protein body can be described in a coordinate system fixed in the molecular frame of CcO. This frame was defined by three unit vectors e₁, e₂, and e₃ connecting Cu_B with Fe a, Fe a₃, and His326/ND1, respectively; the orientation of the membrane was then defined by a unit vector u normal to the membrane surface and aligned along the z-axis of 1 V55 structure. In the molecular frame of CcO, the normal vector u has the following form: u=0.832e₁ −0.469e₂ −1.178e₃. Throughout the paper, we describe the membrane position, M.P., as the z-coordinate of the membrane center in the coordinate system of 1V55. Then, M.P.=194.0 Å corresponds to the membrane center located at distance 3.42 Å from Cu_B in the direction of vector u; hence, the z-coordinate of Cu_B is 190.58 Å.

The membrane width was taken to be 26 Å, which is the accepted value for the low-dielectric part of the membrane [25,26]. We also varied it between 25 and 32 Å [27,28] and found that potential variations for all key residues around the catalytic center were small, within ±0.02.

Taking into account that the membrane width=26 Å corresponds to the membrane potential=1 and that the uncertainty of the atomic positions in the X-ray structure is about 0.5 Å (from their b-value, which is around 20), we find that the uncertainty in the membrane potential due to small thermal fluctuations should be about ±0.02.

3.3. Dielectric constants

The internal water cavities in the protein were determined by an in-house geometry-based program, details are given in the Supplementary information.

Dielectric constants assigned for the membrane and the external solvent regions were ε_m =2 and ε_w =80, respectively. For the bulk protein and the internal cavities, the dielectric constants were varied in the ranges ε_p =4–16 and ε_cav =4–80, respectively, to explore various degrees of hydration and polarizability of the protein [29].

The major factor was the ratio ε_p:ε_cav, whereas the absolute value of ε_p was less important. Thus, changing ε_p at a given ε_p:ε_cav =1:2 or 1:5 shifted the potentials of Cu_A, PropA/a₃, Arg474/HH11, and Trp272/HE by about 0.02, and less for other sites. The internal cavities that belong to the first two subunits, where all charge translocations are taking place, were included in the calculations. Temperature and ionic strength were 300 K and 0.1 M, respectively. Within the physiological range, variations in these two parameters had very little effect on the results.

4. Results

4.1. The dielectric topography map of CcO

In order to determine the potentials of different groups of CcO, the following continuum electrostatic calculations have been performed. The protein structure of CcO from P. denitrificans was incorporated into a membrane, which was modeled as a dielectric slab, see Fig. 1. The potential difference=1 was set across the membrane, and the distribution of the electric potential ϕ⁰(r) inside the protein was calculated by solving the modified Poisson–Boltzmann equation (Eq. (4) with appropriate boundary conditions), see [11,22] and Supplementary information. The potential ϕ⁰(r) varying from 0 to 1 is a measure of the “dielectric depth” inside the membrane. As shown in section 2, the experimentally observed membrane potential V_fi generated by a point charge q transferred from point r⁽ⁱ⁾ to point r^(f) is proportional to the difference between the electric potentials ϕ⁰(r) in points r⁽ⁱ⁾ and r^(f), see Eq. (15). In a homogeneous planar membrane, the potential V_fi would be proportional to the geometric distance between the points projected onto the normal across the membrane, i.e., the difference of the geometric depths of the two points. In a real system this is not the case; the potential is proportional instead to the difference of the dielectric depths. The potentials of the most interesting groups in CcO are shown in Table 1 (we show only a few groups of interest; the extended version of the Table, in the same format, is given in the Supplementary information).

Table 1.

Dielectric topography map of CcO^a

		Membrane center (Å)				Variation
Residue	Atom	190.0	194.0	197.0	200.0	Diel.	Width
Metal sites
CuA	(top)	0.09	0.06	0.05	0.04	±0.01	±0.01
	(bottom)	0.12	0.09	0.07	0.05	±0.01	±0.01
Heme a	Fe	0.53	0.44	0.38	0.32	±0.01	±0.01
Heme a3	Fe	0.52	0.43	0.37	0.31	±0.01	±0.02
CuB	Cu	0.51	0.42	0.35	0.29	±0.01	±0.02
BNCb		0.52	0.43	0.36	0.30	±0.01	±0.02
PLS candidatesa
His326	HD1	0.38	0.31	0.25	0.21	±0.02	±0.02
Heme a3	HA1	0.32	0.25	0.21	0.17	±0.01	±0.01
	HA2	0.30	0.23	0.19	0.15	±0.01	±0.01
	HD1	0.39	0.31	0.26	0.22	±0.01	±0.01
	HD2	0.36	0.29	0.24	0.19	±0.02	±0.01
Arg473	HE	0.34	0.27	0.22	0.18	±0.01	±0.01
Arg474	HE	0.29	0.23	0.19	0.15	±0.02	±0.01
Trp164	HE	0.46	0.38	0.32	0.27	±0.01	±0.01
Trp272	HE	0.34	0.26	0.21	0.17	±0.01	±0.01
PLS-related sites
Asp399	OD2	0.30	0.23	0.18	0.14	±0.01	±0.02
Waterc	O	0.36	0.29	0.24	0.19	±0.01	±0.02
K-channel residuesa
D-channel residuesa

The normalized potentials of the atoms shown have the meaning of the dielectric depth measured from the P-side of the membrane. The charge transfer between any of the atoms shown will produce membrane potential proportional to the difference of the potentials of the atoms. The shown data are discussed in the text.

^aThis is an abbreviated version of the data. A more complete table is given in the Supplementary information.

^bBNC is defined as the midpoint between Heme a₃/Fe and Cu_B/Cu.

^cThe water molecule located between the two propionates of heme a₃ and His326. Its position is estimated from the crystallography structure 1 V55[23].

4.1.1. Effects of dielectric inhomogeneity, membrane width, and the position of the membrane

The electrostatic computational model of the protein employed to produce the data shown in Table 1 involves several unknown parameters: the width of the membrane, the position of the membrane with respect to the protein, and the dielectric composition of the protein itself. By the width of the membrane we mean the width of the hydrophobic and low-dielectric part (ε_m ≈ 2) of the lipid bi-layer which affects the electrostatic calculations. Roughly, the boundaries of this part of the membrane coincide with the position of carbonyl groups of the lipids. The orientation of the membrane plane with respect to the protein was discussed in section 3, and appears to be well-defined by the structure of the protein. However, the position of the center of the low-dielectric part of the membrane is more difficult to determine from the published structural data and considered here as an unknown parameter. Finally, the dielectric composition of the protein is determined by the internal water cavities of the protein, which are filled with ill-defined number of water molecules. These regions of the protein should have higher dielectric constant. However, the exact value of the dielectric constant is not known. In this subsection, we examine how the results of our calculation depend on these parameters.

We assume that the thickness of the low-dielectric part of the membrane is in the range of 25–32 Å; for example for L-lecithin [16] the width of the low-dielectric part is close to 25–27 Å. The potential calculations were performed for various values of the membrane width; we find that the potentials of the most interesting groups located in the middle part of the membrane are not very sensitive to the membrane thickness in the range of 25–32 Å. Table 1 lists the data for membrane of 26 Å and the variation of the potential (last column) for each of the group due to uncertainty in the membrane width is reported in a separate column.

Similarly, the dependence of the results on the dielectric composition of the protein was found to be relatively unimportant within the range of reasonable variation of the dielectric constant of the protein, ε_p =4–16 and dielectric of the water cavities, ε_cav =4–20. The data shown in Table 1 were obtained for ε_p =4 and ε_cav =10, and the variations of the potentials with changing dielectric of the cavities in the range of 4–20, as well as with various dielectric constants for the protein are also shown for each group in Table 1 in the second column from the right.

The most significant parameter, however, that is crucial for the electrostatic topography of the protein was found to be the position of the membrane center, M.P. In Fig. 2, dielectric distances (difference of potentials) between some important sites of the protein calculated as functions of membrane position are shown for various values of ε_cav. The total dielectric distance between two sides of the membrane is set to unity. As seen from Fig. 2, dielectric inhomogeneity of the protein–membrane system has relatively minor effect on the dielectric distances. This agrees with our previous estimates [15]. The potential and distances, however, are quite sensitive to the position of the membrane center with respect to the protein. Hence, any analysis of the data on the amplitudes of various kinetic phases observed in experiment requires precise determination of the “optimal” membrane position using some additional information independent of experimental data, which would permit such determination. In the following section we will demonstrate how this can be accomplished in practice using experimental data by Belevich et al.

Fig. 2.

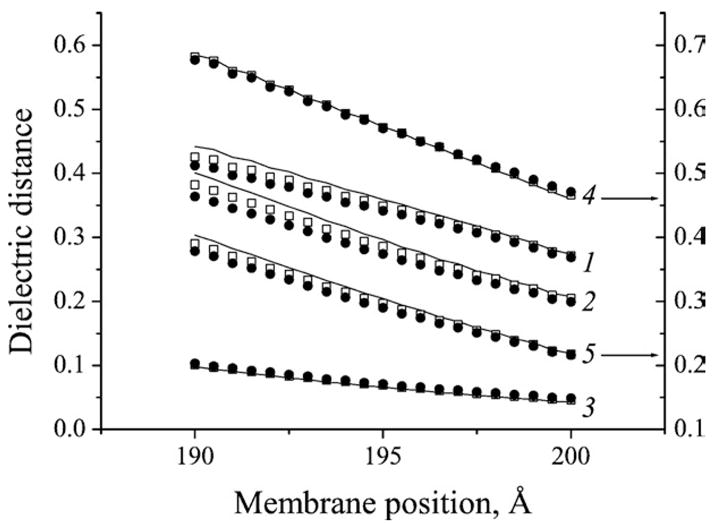
Calculated dielectric distances for P. denitrificans. Membrane width 25 Å, ε_p =4, ε_cav =4 (line), 10 (open squares), 20 (full circles). 1, from Cu_A to Fe_a; 2, from P-side to His326; 3, from P-side to Cu_A; 4, from P-side to Glu278; 5, from P-side to PropD1/Fea₃. Left ordinate, data sets 1, 2, and 3. Right ordinate, data sets 4 and 5. For definition of the membrane position, see Methods section.

As will be shown later in the paper, the requirement of self-consistency of the model and consistency with experimental data can be utilized to reduce the degree of uncertainty in the position of the membrane, M.P. Also, there are indirect structural data that also allow one to make a reasonable estimate of the range of possible values of this important parameter. Namely, the low-dielectric part of the membrane is localized in the region roughly between the carbonyl groups of the fatty acids of the membrane lipids; some of these lipids have been recently reported by Yoshikawa and co-workers for bovine enzyme [30]. In Fig. 3, the position of some of the carbonyl groups on the bovine structure (subunits I and II) are shown, and the corresponding range of possible positions of the low-dielectric part of the membrane, assuming its width 26 Å, is schematically indicated; for these positions of the membrane, the low-dielectric part of the membrane would be localized between the carbonyl groups found in the structure. Although the interface between the membrane and the enzyme is unlikely to be identical for bacterial and bovine enzymes, the positions of redox centers in two species are amazingly similar (the z-component of the coordinates of the redox centers, normal to the membrane surface, differ only by less than 0.2 Å). If we assume that the position of the membrane center in the bovine structure is about the same as in Paracoccus structure (although the membrane width may be somewhat different), the bovine structural data can be used for an estimate of the possible positions of the membrane in the bacterial enzyme. Based on these considerations, we assume that the position of the membrane center should be expected to be between 194 and 200 Å (for the description of the coordinate system utilized in our calculations see section 3), and the position of the membrane center outside the window 194–200 Å will be considered as unlikely.

Fig. 3.

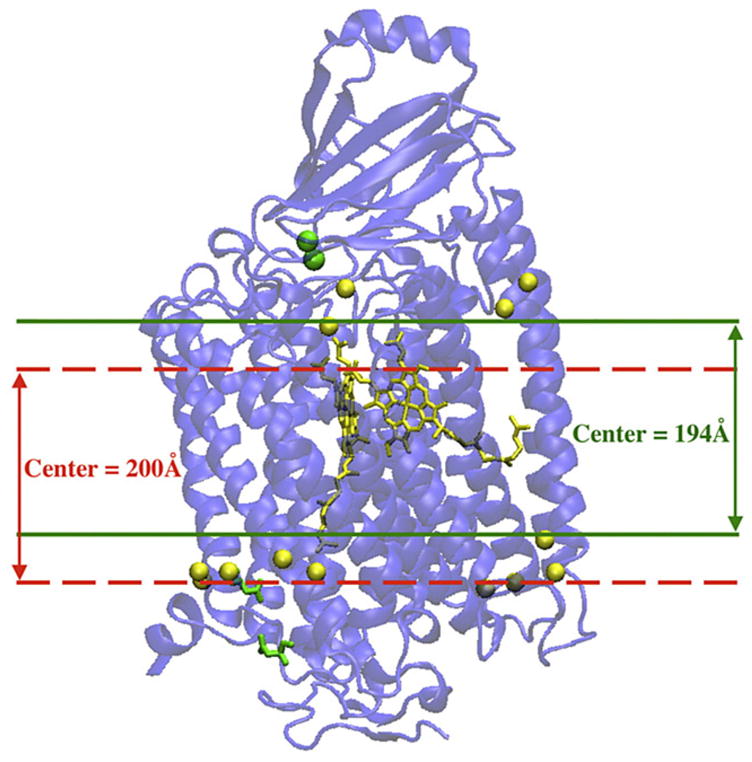
The structure of the bovine enzyme, subunits I and II [30] (PDB ID=2DYR), and possible range of membrane center positions. The coordinate system employed is described in the text. The light balls correspond to carbonyl groups of the phospholipids of the membrane, which are considered to be the boundaries of the low-dielectric (insulating) part of the membrane.

In Table 1, the potentials of CcO are shown for three possible positions of the membrane in this range, 194, 197, and 200 Å. It is noteworthy that at the membrane position 200 Å the potential of BNC is about one third of the total. We also show data for one additional position of the membrane, 190 Å, for the following reason. In the next section we will be looking for a combination of the parameters of the model including the position of the membrane M.P. that is most consistent with the potentiometric data. As we will see, the best fit to experimental data is provided for three positions of the membrane: 190, 194, and 197 Å. Based on the arguments of this section, the position of 190 Å can be discarded as it is in the conflict with structural data, however, for completeness purposes, and also to demonstrate details of our analysis these data are also included in Table 1. Thus, as we will see later, only data shown for positions 194 and 197 Å are fully consistent with structural and potentiometric data of Belevich et al. These data are shown in Table 1 in bold, and will be further discussed in the following sections of the paper.

4.1.2. Potential of Cu_A center

The results for the Cu_A center shown in Table 1 deserve special consideration. The calculated dielectric distance from Cu_A to the P-side of the membrane is appreciably non-vanishing in contrast to the commonly accepted opinion that it is zero because Cu_A does not reside within the membrane domain, but instead belongs to the part of the protein that is exposed to the aqueous solution on the P-side of the membrane. We notice, however, that Cu_A is buried inside the low-dielectric part of the protein and appears from the structure to be isolated from the solution, therefore there must be some non-zero potential drop from the P-side solution to Cu_A center. On the other hand (M. Wikström and M. Verkhovsky, private communication), when the photo-activated RubiPy donates its electron to the Cu_A center in less than 0.5 μs, the potential should show significant initial jump, up to about one third of the amplitude of the fast (electronic) phase, which had not been observed in the experiment. This disagreement between the theory and experiment might be due to the fact that when RubiPy complex is docking in the vicinity of the Cu_A center, it partially deforms the protein surface, allowing for some additional water molecules and ions to penetrate into the structure, and therefore reduces the isolation of the Cu_A center. In our calculations, we used the intact CcO structure since the structure of the CcO/RubiPy complex is unknown.

Allowing for possibility that the structure of the CcO/RubiPy complex involves additional “connectivity” between the P-side and Cu_A center, not seen in the X-ray structure of CcO, in the following analysis of the pumping mechanism of CcO, we will consider the case when the potential of Cu_A is set to be zero, in addition to actual data from our calculations shown in Table 1.

4.2. O to E transition in P. denitrificans. Experiment of Belevich et al. [9]

In a recent paper, Belevich et al. [9] have presented the results of the most detailed electrometric study yet on CcO from P. denitrificans, in which the kinetics of the membrane potential generated by the enzyme upon single-electron injection in the O to E transition was measured. In addition to a pure electronic kinetic phase, three protonic phases have been resolved, for which the rates k_i and the corresponding amplitudes U_i were reported.

The experimental details are described in Ref. [9]. Briefly, the enzyme was incorporated into a measuring membrane. With use of RubiPy as photo-sensitized donor, an electron was injected into the enzyme prepared in the “pulsed” oxidized state O (or O_H, using notation of [6]), and the membrane potential generated by the enzyme, as it made the O to E transition, was monitored with a time step of ≥1 μs. In a separate experiment, changes of the redox state of the enzyme were also monitored by optical spectroscopy. Three phases of the redox kinetics of heme a were revealed with rates k_1,2,3 shown in Table 2. The kinetics of the membrane generation was analyzed in Ref. [9] with use of Eq. (22) with N=4 and rates k_1,2,3 fixed at their values from the optical data whereas k₄ and four amplitudes were varied to get the best fit to the experimental kinetics. It was obtained $k_4^{-1}=2.6\text{ms}$, U₁ =0.24, U₂ =0.84, U₃ =0.60, and U₄ =0.32. Instead of U_1,2,3,4, we will use the cumulative amplitudes V_1,2,3 of Eq. (18) shown in Table 2.

4.2.1. Qualitative interpretation

According to Ref. [9], phase 1 (10 μs) corresponds to electron transfer from Cu_A to heme a, see Fig. 1. Only a “fraction of electron”, β=0.70, is transferred to heme a in this phase. Further electron redistribution between Cu_A, heme a, and the heme a₃/Cu_B binuclear center (BNC) is coupled to three proton transfers, which generate three additional kinetic phases. The spectroscopic data indicate that, by the end of the 150 μs phase, 60% of the electron is transferred to the heme a₃/Cu_B site, while 40% still remains on heme a. This electron transfer is coupled to the transfer of the pumped proton from the N-side of the membrane to an unknown proton-loading site (PLS) “above” BNC. The proton transfer occurs via Glu278, which is deprotonated and reprotonated in a concerted manner since a stepwise process would require overcoming a large barrier inconsistent with the observed kinetics [31]. The next 800 μs phase corresponds to the transfer of the remaining 40% of the electron from heme a to BNC and an accompanying transfer of the chemical proton to BNC. Finally, the last 2.6 ms phase is associated with the displacement of the pumped proton from PLS to the P-side of the membrane. Presumably, this happens due to repulsion between the chemical proton arrived to BNC and the pumped proton preloaded to PLS [32]. Overall two unit charges are crossing the membrane during the transition, therefore V₄ =2.

The sequence of events — 1) electron transfer to BNC, 2) loading the pumped proton to PLS via Glu278 in the D-channel, 3) transfer of the chemical proton to BNC, and 4) ejection of the pumped proton from PLS to the P-side of the membrane due to Coulomb repulsion between the pumped and chemical protons — exactly corresponds to the scheme described earlier in Ref. [33] (see also [32]), where it was proposed, based on ab initio and electrostatic calculations, that the role of PLS is played by one of the ligands of the Cu_B center, His326. The identity of PLS, however, has never been directly probed experimentally. Below, making use of the above data of Belevich et al., we will examine the proposed mechanism and will try to establish likely candidates for PLS.

4.2.2. Quantitative analysis

4.2.2.1. Analysis of the kinetics data. Uncertainty of exponential fittings

There is an intrinsic uncertainty in the rates and amplitudes of individual kinetic components that are found from the decomposition of the experimental signal. This is a well-known difficulty of exponential decomposition of the kinetic data. While for qualitative interpretation these uncertainties may not be of any significance, our goal is to explore the extent to which potentiometric data can be used for understanding molecular specifics of the charge transfer in the enzyme. Belevich et al. have kindly provided us with their original raw experimental data (and their own precise fitting parameters) so that we could explore various fittings. Some results obtained are shown in Table 2, Sets 1–4. Set 5 is provided by Belevich et al. in their private communication, and Set 6 is the original set of parameters from Ref. [9], we only added standard deviations (SDs). Both these fittings used a fixed rate of k₁ that was determined from the optical experiment. Since the ET driving force of Cu_A to Fe a transition is close to zero, this transition rate k₁ may be different in the enzyme incorporated in the membrane, in particular when some potential exists on the membrane. It is appropriate to stress that the details we are considering at the moment were not important for Belevich et al. in their analysis of the experimental data. For instance, small changes of k₄ and V₁ between Sets 5 and 6 do not affect any conclusions of Ref. [9]. On the contrary, our approach requires more quantitative evaluation of the parameters. Therefore, we explored additional fittings with different rate constants $k_1^{-1}$ varied in the range of 10 to 26 μs. It is worth mentioning that for the rate of the electronic phase of the O to E and E to R transitions in CcO from P. denitrificans, Ruitenberg et al. [4,5] reported the values of 20 and 27 μs, respectively, which fall in the range of our values. As seen from Table 2, several different fittings could be obtained, with quite significant (for our quantitative analysis) variation of the amplitudes V₁–V₃.

4.2.2.2. Pumping model, identity of PLS

Our model is identical to what is qualitatively described by Belevich et al., see Fig. 4. We now provide a quantitative description of this model, and examine possible candidates for PLS. In this scheme, we have three intermediate states, S₁–S₃, and corresponding membrane potentials, V₁–V₃.

Fig. 4.

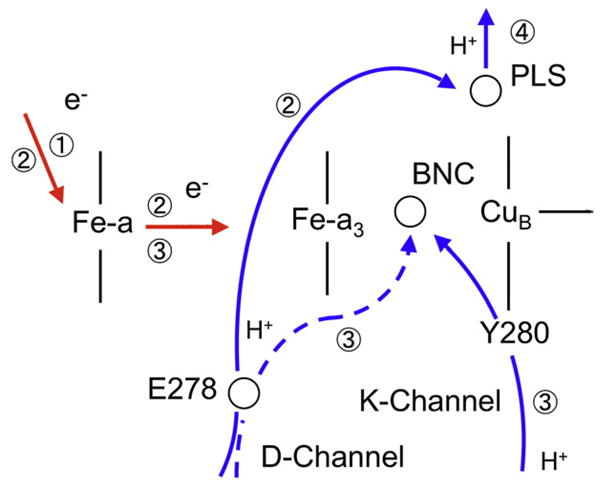
Schematics of the considered pumping model (c.f. [33]). The numbers correspond to the kinetic phase order observed in the experiment. BNC is the binuclear catalytic center, PLS is the Proton Loading Site of the pump. For O to E transition discussed in the text, the third phase presumably corresponds to proton transfer to BNC along the K-channel; in other transitions, the same transition may occur along the D-channel.

Phase 1, in which the first intermediate state S₁ is formed, is associated with the transfer of the injected electron via the Cu_A center to heme a. As established experimentally, only a fraction of electron β=0.70 moves to heme a in this phase. Therefore, the potential generated by the enzyme when state S₁ is formed can be written as

$$V_1=V_{\text{CuA}}+\beta (V_a-V_{\text{CuA}}),$$ (24)

where V_CuA and V_a are normalized potentials (i.e., dielectric depths) of Cu_A and heme a, respectively, measured from the P-side of the membrane, obtained from our electrostatic calculations, Table 1, whereas V₁ is obtained from the kinetic analysis of the experimental data, Table 2. In a similar way we obtain the relationships for other two phases.

Phase 2 corresponds to the S₁ to S₂ transition, where the second intermediate state S₂ is formed. This phase is associated with the transfer of the pumped proton from the N-side of the membrane to an unknown group PLS, via the D-channel and Glu278, and simultaneous redistribution of the injected electron between the redox centers of the enzyme. By the end of this phase fraction (1−γ)=0.6 of the electron is localized on the a₃/Cu_A binuclear center and fraction γ=0.4 remains on heme a. Hence, this intermediate generates the potential

$$V_2=\gamma V_a+(1-\gamma )V_{\text{BNC}}+(1-V_{\text{PLS}}).$$ (25)

The contribution of the proton is written in such a way as to reflect the fact that the proton moves from the N-side of the membrane, which is assigned the potential of +1, to Glu278 and further to PLS in a concerted manner [31].

Phase 3, S₂ → S₃, is the transfer of the chemical proton and the remaining fraction of the electron to BNC. The corresponding potential is

$$V_3=V_{\text{BNC}}+(1-V_{\text{BNC}})+(1-V_{\text{PLS}})=2-V_{\text{PLS}},$$ (26)

where the first term corresponds to a complete electron transfer to BNC, the second term is due to the chemical proton transfer to BNC, and the third term is due to the pumped proton from the previous phase.

The above three equations relate the potentials that we found from the kinetic analysis of the experimental data (V₁,V₂, and V₃, Table 2) to the potentials of the specific groups of the enzyme that we calculated by solving the Poisson–Boltzmann equation, Table 1. The identities of all groups are known, except for that of PLS.

If we knew the exact values of V₁–V₃, and if there were no ambiguity in the electrostatic model and we could calculate the potentials of different groups unambiguously, then we could use Eq. (26) to find V_PLS, and then look up the table of potentials of different groups of the protein, such as Table 1, and find the group that has the “target” value V_PLS – thus, the identity of the PLS would be revealed. Unfortunately, there are ambiguities both in the membrane potentials, i.e., left-hand-sides of Eqs. (24)–(26), found from the decomposition of the experimental data (Table 2), and in the electrostatic model, which determines the potentials of the groups in the right-hand-side of Eqs. (24)–(26). Thus, the identity of PLS cannot be easily determined.

With such uncertainties both on the right- and left-hand-sides of Eqs. (24)–(26), one might think that there is no hope to find a unique solution to the problem, since there will be always a combination of parameters such that Eqs. (24)–(26) would be satisfied. It turns out, however, that the situation is not as hopeless as it appears to be.

The overall situation that we deal with resembles that in the branch of mathematics which considers so-called “ill-posed” problems, where the data are not known exactly, and there is no unique solution to the problem. In this case, one attempts to identify the “most likely” solution that best satisfies a given set of conditions. In our case, we have several independent conditions, Eqs. (24)–(26), and certain requirements on the membrane position. Therefore we proceed as follows.

We have multiple combinations of amplitudes V₁–V₃ that all satisfy the experimental data, some of which are shown in Table 2. Without additional conditions, one cannot choose one set of parameters over another. We consider our Eqs. (24)–(26) as these additional conditions that should be satisfied. Therefore, we will be looking for such a set of experimental parameters V₁–V₃, a position of the membrane, and a PLS group that best satisfy all three equations. To estimate the quality of the solution we introduce a statistical parameter χ² as follows:

$${\chi }^2={\sum }_{i=1}^3{\left(\frac{{\mathrm{\Delta }}_i}{{\sigma }_i}\right)}^2,$$ (27)

where Δ_i is the difference between left- and right-hand-side of Eqs. (24)–(26), and σ_i is a typical uncertainty with which the right-hand-side of Eqs. (24)–(26) could be calculated. This uncertainty is due to small variations of the membrane composition and width, as well as the accuracy with which parameters β and γ could be determined in the experiment. We assume β =0.7±0.05 and γ =0.4±0.05. For computed potentials (other than that of Cu_A) the maximum error (for a given membrane position) is roughly 0.02 and maximum error due to uncertainty in the atom’s position is also roughly 0.02. Overall, in our estimate the σ_i are 0.034, 0.049, and 0.030 for Eqs. (24), (25), and (26), respectively.

We then introduce the likelihood parameter,

$$P(k,m,p)=exp(-{\chi }^2(k,m,p)),$$ (28)

which is evaluated for each kinetic fitting k, membrane position m, and PLS candidate p. The parameter P is a statistical measure of the quality of a given set of parameters of the model.

Table 3 lists several best combinations of kinetic parameters, membrane positions, and PLS candidates. We examined both the case when the potential of Cu_A is calculated from our electrostatic model (non-zero potential), and the case when the potential of Cu_A is set to zero, for reasons explained in section 4.1. Despite the uncertainty of the parameters of the model, we find that the number of PLS candidates turns out to be rather small. The reason for such a selection is the large number of conditions that the model should satisfy for self-consistency: three equations, Eqs. (24)–(26), and an additional condition for a specific window for the membrane position. The analysis with this method yields the following results. (The Supplementary information provides details of the analysis of PLS candidates. Table 3 gives only the summary of the results).

Table 3.

PLS candidates for six different kinetic fitting sets shown in Table 2

Set	Most likely PLS candidates (P-value, M.P.)
A. VCuA ≠ 0
1	Trp164 (81% at 194.0 Å)
2	a3/D1 (52% at 193.0 Å) and His326 (39% at 193.0 Å)
3	His326 (41% at 193.5 Å) and a3/D1 (41% at 194.0 Å)
4	a3/A1 (55% at 190.5 Å), a3/A2 (45%), Trp272 (42%)
5	Trp164 (7.9% at 197.0 Å)
6	Trp164 (3.5% at 197.5 Å)
B. VCuA =0
1	Trp164 (35% at 193.5 Å)
2	a3/D1 (22% at 193.0 Å) and His326 (21% at 192.5 Å)
3	His326 (14% at 193.5 Å) and a3/D1 (13% at 193.5 Å)
4	a3/A2 (20% at 189.0 Å), a3/A1 (17%), Trp272 (12%)
5	Trp164 (20% at 197.0 Å)
6	Trp164 (14% at 197.0 Å)

In (A), the PLS analysis was done with V_CuA predicted by our electrostatic model, which in general gives non-zero potential, see Table 1; (B) same as in (A), but with the potential of Cu_A set to zero. P is the likelihood parameter, Eq. (28), and M.P. is the membrane position that was found for a given set of kinetic parameters.

As can be seen in Table 3, only three positions of the membrane, around 190, 194, and 197 Å are consistent with experimental data and with the pumping model considered – that is only these positions of the membrane yield any PLS groups. Only positions 194 and 197 Å however are in the window of realistic values. Hence, the PLS candidates found for the membrane position of 190 Å should be considered as unlikely. There was no PLS found for the position of the membrane at 200 Å. Some kinetic fitting sets do not provide any candidates for PLS at any position of the membrane in the interval of expected values between 194 and 200 Å.

For the membrane positions in the interval of expected values, i.e., between 194 and 200 Å, the analysis yields several PLS residues which are clustered in the region just “above” BNC. We first consider the case of V_CuA ≠ 0. Here, the best candidates are: Trp164, P=0.8, Set 1; His326, PropD/heme a₃, P =0.5–0.4, Set 2 and 3; naturally, the sites with close potential, such as propionate D of heme a, a water molecule between the two propionates of heme a₃ and His326, and Arg 473/474, cannot be excluded as PLS candidates on the basis of potentiometry data.

In Set 4, PropA/a₃ and Trp272 were identified as PLS candidates with likelihood P=0.4; however, in this case the membrane position turns out to be around 190 Å, i.e. out of the range of the expected values; hence, these candidates should be considered as unlikely. For Sets 5 and 6 (Belevich et al.) the only PLS candidate is Trp164 with a very low likelihood values, P=0.08 and 0.04. All other groups, for all kinetic parameter sets produce the likelihood parameter much smaller that what we considered above (for more quantitative details, see extended Table 3 in the Supplementary information).

When the assumption V_CuA =0 is imposed, the results are as follows. PLS candidates of Sets 1–4 remain the same, however, the likelihood parameter becomes significantly smaller: Trp164 (Set 1, P=0.35), His326 and PropD/a₃ (Set 2, P =0.22); PropA/a₃ and Trp272 (Set 4, P =0.2) appeared here as well, but only for membrane position around 190 Å and therefore should be considered less likely candidates than others. Sets 5 and 6 now yield Trp164 as the best candidate for PLS, with P=0.2 at M.P. around 197 Å.

We see that both cases of zero and non-zero potential of Cu_A result in the same group of PLS candidates, which are clustered in a small region just above BNC. The likelihood parameter P allows one to qualitatively compare the candidates. It is hardly possible, however, to make a strong case for one specific candidate from this group on the basis of potentiometric data alone. Obviously, the above results are maximum that one can expect from the present theory and current data.

4.3. N139D non-pumping mutant of R. sphaeroides, Siletsky et al. [7]

While we did not make electrostatic calculations for this bacterium, data of section 4.1 can still be used for semi-quantitative discussion. In the experiments on F→O transition in N139D mutant recently reported by Siletsky et al. [7], only one electronic and one protonic phases were observed with the amplitude ratio of A₂/A₁ =1.3. Since the time constants of the two phases differ significantly (15 and 600 μs), the measured amplitudes directly represent the intrinsic dielectric distances, that is, A₁ = U₁ = V₁ and A₂ = U₂ = V₂ − V₁. The total charge transferred across the full membrane is V₂ =1, which gives V₁ =0.435. By its physical meaning, the amplitude of the electronic phase, V₁, is approximately equal to the dielectric distance from the P-side to Fe a, or equivalently from the P-side to BNC (Fe a₃ or Cu_B), see Eq. (24) where β =0.84 [8]. For P. denitrificans, we found that for most likely M. P.=194 Å the potential of BNC is 0.43, instead of the usually assumed “geometric” value 0.33. If this is also approximately valid for R. sphaeroides, the above experimental amplitude ratio and the resulting value of V₁ =0.435 can be rationalized.

It is instructive to calculate the value of V₁ using geometric considerations. Inserting V_CuA = 0, V_a − V_CuA = 0.33, and β = 0.84 into Eq. (24), we obtain V₁ =0.28, which is significantly smaller than the one found above. The geometric value predicts the amplitude ratio A₂/A₁ =2.6, that is, two times as large as the observed value. Thus, our explanation of the experimental result implies that, “dielectrically”, heme a and catalytic center are buried deeper into CcO, closer to the N-side, than they are “geometrically”.

5. Discussion

5.1. Uncertainties, dielectric map

The electrostatic calculations presented above indicate that the major factor influencing the dielectric topography of a protein incorporated in a membrane is the relative position of the membrane center with respect to the protein body. Other factors, such as the dielectric constants for protein cavities and the width of the hydrophobic part of the membrane, have relatively minor effects. Therefore, it is important to know the actual membrane position (M.P.) with respect to the body of the protein in order to be able to calculate the dielectric distances between key sites, which could be further used to analyze experimental data on the kinetics of the potential generation. In the absence of direct structural data, here we attempted to reduce the uncertainty of the membrane position by using indirect structural data for bovine enzyme.

There is a generic uncertainty in the decomposition of a kinetic signal into individual exponential components [34]. In our case the major uncertainty of the fitting procedure arises due to the first kinetic phase. As seen from Table 2, the amplitude V₁, which mainly affects the membrane position, fluctuates by about 50% among various fittings whereas other amplitudes are stable within a few percent. This is because the experimental counts are taken with a long time step of 1 μs, which results in 150 and more counts during the lifetimes of the second and subsequent phases but only 10 counts during the first phase, which is insufficient for accurate determination of V₁. To reduce this uncertainty, it would be desirable that the fast part of the kinetics within, say, the initial 100 μs be measured with a short time step on the order of 0.1 μs.

It cannot be excluded, indeed it is expected, that each of the three protonic phases observed in the experiment of Belevich et al. consists of several components; by its nature, proton translocation is always a multi-step process. The fitting of a kinetic signal with larger number of exponential components is possible, but highly numerically unstable. For example, we could fit the experimental kinetic data with five exponentials instead of four; in this fit the intermediate phase with lifetime k⁻¹ =0.57 ms splits into two components with lifetimes 0.52 and 0.71 ms. The quality of overall fitting is about the same as for four kinetic components. However, our analysis suggests that these refinements can hardly be reliable enough to be utilized for identification of the groups involved.

5.2. BNC potential 0.4

We found that the dielectric distances between the sites participating in the catalytic cycle of CcO differ significantly from the values based on the geometry. For example, the binuclear center is located at approximately one third of the membrane width from the P-side, which implies the geometric distance of 0.33, but the dielectric depth of Cu_B and Fe a₃ from the P-side were found to be at least 0.4 (for the membrane positions that are consistent with both the structural data and kinetic potentiometry data of Belevich et al.) This result helps to rationalize the experimental data of Siletsky et al. [7] for N139D non-pumping mutant of R. sphaeroides enzyme. It is interesting to note that the “electric distance” between heme a and the P-phase had been originally estimated on the basis of equilibrium studies (effect of the imposed membrane potential on a redox equilibrium between cytochrome c and heme a in mitochondria) by P. Hinkle and P. Mitchell almost 40 years ago[35], who obtained a value of ~0.4–0.5. The present work appears to reconcile the Hinkle and Mitchell’s results with the structural data.

5.3. Cu_A potential

Another redox center to be noted is Cu_A. It is generally assumed that its dielectric distance from the P-side is zero because Cu_A is located outside the membrane region. However, this center is located inside the low-dielectric protein region generally isolated from the P-side solution, therefore our electrostatic calculations yield non-zero potential of Cu_A. The question arises with respect to the electron transfer from the primary electron donor, RubiPy, to Cu_A. This very fast transfer should generate an appreciable initial jump of potential that had not been observed in experiment. The nature of this disagreement is not clear. It well may be that the protein structure is deformed in the vicinity of RubiPy docking site, so that water and ions penetrate closer to Cu_A thereby decreasing the dielectric distance of this center from the P-side. In such a case, our electrostatic problem should be solved with a new boundary condition at the P-side, and this would result in decreasing the calculated potential not only at Cu_A but also at Fe a and other sites (to a lesser extent). There are no structural data at present to undertake such calculations. Instead, we examined an artificial condition when the potential of Cu_A was set to be zero. There was no major qualitative difference in the PLS candidates produced by the procedure.

5.4. PLS candidates

The computational approach developed in this paper, together with detailed potentiometric data such as obtained by Belevich et al. [9], opens the door for quantitative analysis aiming at determining specific residues that exchange charges inside the membrane protein and produce changes of the membrane potential observed in the experiment. Even though a specific residue that plays the role of the loading site of the pump (PLS) could not be identified, due to uncertainties both in the experimental data and in the theory, it is still remarkable that the PLS could be localized to a relatively small group of candidates. All these candidates: Trp164, His326, PropD, A/a₃, Arg473/474 for PLS are located “above” BNC (that is, closer to the P-side).

Recently, Siegbahn and Blomberg [36] have analyzed the rates of the four kinetic phases measured by Belevich et al. [9]. These authors derived energy levels and barriers for likely intermediate states of the pumping process using the reaction mechanism proposed by Belevich et al. and considered in this paper. They concluded that propionate A of heme a₃ is the best candidate for PLS. Our analysis shows that PropA of heme a₃ is indeed in the group of possible candidates, but less likely candidate for PLS compared with Trp164, His326, Arg474, PropD of heme a₃.

5.5. BNC-first model

Brzezinski with coauthors [37–39] have proposed an alternative mechanism where the first proton goes from Glu278 to BNC rather than to PLS. Their studies were on the P to F transition in R. sphaeroides. We have considered such a possibility for the O to E transition in P. denitrificans discussed in section 4.2 and found that it is not supported by our data. Since the only change is that (1 − V_PLS) term in V₂ is replaced with (1 − V_BNC), one should formally consider BNC to be potentiometrically equivalent to PLS in our model. In this case, however, we could not agree quantitatively with the data of Belevich et al. because all our PLS candidates turned out to be “above” BNC. One should keep in mind of course that all these considerations are based on the assumption of equivalence of different transitions in different enzymes.

6. Conclusions

1. The relative position of the membrane with respect to the protein is a critical factor affecting the dielectric distances in CcO. The lack of structural information about the membrane is a significant impediment for computational analysis of the potentiometric data.

2. The dielectric distances from the P-side to Fe a and to BNC are larger than 0.33 suggested by geometry/structure. Our estimate is approximately 0.4 or higher; the exact number is difficult to pinpoint, but our estimate in any case is significantly larger than the usually assumed 0.33. The new estimate explains the ratio of the amplitudes of two kinetic phases observed in a non-pumping CcO mutant.

3. In the proton-pump model with a single proton-loading site (PLS), the most probable candidates for PLS belong to a group of closely related residues above BNC: Trp164, propionate D of heme a₃, His326, Args 473/474; while Trp272 and propionate A of heme a₃ also cannot be excluded.

4. Obtaining more definitive predictions with respect to the identity of PLS might be possible if more detailed experimental data for the first 100 μs of the potential kinetics were available. The data should be obtained with a shorter time-step, say 0.1 μs, for better resolution of the kinetic parameters of the signal.

5. Despite the inherent uncertainties, it is clear that potentiometry in combination with the computational analysis demonstrated here is a powerful technique for characterization of protonpumps. It would be interesting to perform such experiments and analyses on Complex I of the respiratory chain, the proton pumping mechanism of which remains a complete mystery [40,41].

As a final remark, it is worthwhile to mention that impossibility of strict identification of the proton loading site may also be an indication that there is no single PLS for the proton pump in CcO; rather, several residues within the above-found group may serve as PLS with various degrees of participation.

Abbreviations

CcO

cytochrome c oxidase

BNC

binuclear center

PLS

proton-loading site

N-side

negative side of the membrane

P-side

positive side of the membrane

M.P

membrane position

SD

standard deviation

Appendix A. Supplementary data

Supplementary data associated with this article can be found, in the online version, at doi:10.1016/j.bbabio.2008.05.006.