Abstract
Detection of remote sequence homology is essential for the accurate inference of protein structure, function and evolution. The most sensitive detection methods involve the comparison of evolutionary patterns reflected in multiple sequence alignments (MSAs) of protein families. We present PROCAIN, a new method for MSA comparison based on the combination of ‘vertical’ MSA context (substitution constraints at individual sequence positions) and ‘horizontal’ context (patterns of residue content at multiple positions). Based on a simple and tractable profile methodology and primitive measures for the similarity of horizontal MSA patterns, the method achieves the quality of homology detection comparable to a more complex advanced method employing hidden Markov models (HMMs) and secondary structure (SS) prediction. Adding SS information further improves PROCAIN performance beyond the capabilities of current state-of-the-art tools. The potential value of the method for structure/function predictions is illustrated by the detection of subtle homology between evolutionary distant yet structurally similar protein domains. ProCAIn, relevant databases and tools can be downloaded from: http://prodata.swmed.edu/procain/download. The web server can be accessed at http://prodata.swmed.edu/procain/procain.php.
INTRODUCTION
Recent progress in structural biology, including structural genomics initiatives (1) has significantly increased the coverage of existing protein folds by representatives with solved 3D structures (2). According to some analyses (3), this coverage is close to completion, which means that any given protein is likely to have a structure similar to a solved one. The existence of such structural templates opens the opportunity for structure modeling and potential function prediction for a majority of protein sequences. However, as demonstrated by the recent Critical Assessment of Techniques for Protein Structure Prediction, CASP8 (4), the presence of homologs with known a structure does not warrant the quality of sequence-based structure prediction. The largest current challenge in the prediction process is the ability to detect a distant homolog and to construct an accurate alignment between this homolog and the target sequence. Thus, there is a strong demand for more powerful automated methods for remote homology detection and alignment construction.
Historically, most progress in sequence-based homology detection was made by considering sequence patterns that reflect evolutionary, structural and functional constraints in protein families. Introduction of numerical profiles (5) and hidden Markov models (HMMs) allowed comparing a sequence to a multiple sequence alignment (MSA) rather than its single representative (6–8). As a further improvement, methods for profile-profile (9–12) and HMM–HMM (13) comparison were aimed at detecting similarities in amino acid preferences at sequence positions in two distant families. In addition to the residue substitution preferences (‘vertical’ signals), MSA can reveal patterns of interdependence between amino acid content at different positions (‘horizontal’ signals). These patterns, dictated by structure and function, are often preserved better than the sequence and thus can help detecting protein similarity where individual sequence positions diverged beyond recognition. Currently, such ‘horizontal’ information is used by only a few methods (13,14), mainly in the form of secondary structure (SS) prediction.
Here, we complement sensitive profile–profile comparison with the consideration of various structure- and function-related patterns revealed by MSA: similarity in SS, amino acid conservation and MSA motifs. The resulting tool for MSA comparison, PROCAIN, improves homology detection and alignment quality beyond the range of current state-of-the-art methods.
METHODS
Multiple sequence alignments
Profiles are generated as described elsewhere (9) from multiple sequence alignments that are constructed and processed using a program (buildali.pl) generously provided by J. Soding. Starting from a single sequence, this program runs up to eight iterations of PSI-BLAST, filtering PSI-BLAST alignments at each iteration. We find that this filtering results in better homology detection by resulting profiles.
Score for similarity of residue content in MSA columns
To measure the positional similarity of residue content, we use the formula originally implemented in the COMPASS method (9).
where n1i and n2i are effective counts (15) of residue type i in the compared columns 1 and 2; Q1i and Q2i are estimated target residue frequencies (16) of the two columns; pi is the background residue frequency. c1 and c2 are scaling factors calculated as follows:
 |
 |
Sequence motif score
In the alignments of homologous protein sequences, matches of similar positions tend to cluster together along the sequence (17). These clusters often correspond to similar functional motifs (18). Thus, we introduce a simple additional score that rewards such clusters, i.e. diagonals of positively scoring matches in the dynamic programming matrix. If a pair of profile positions has a positive score for residue content, and both immediate neighbors of this pair also score positively, then the score of the central pair is increased by the sum of these three sequence similarity scores, sm, multiplied by a weight wm = 0.5.
Residue conservation score
Strong residue conservation normally indicates important functional positions, such as binding sites; therefore matches and mismatches of such positions should be of special importance for homology detection (19). In order to further emphasize similarity between conserved positions, we introduce a separate conservation score. Residue conservation is calculated using an entropy-based method (17), with the final measure normalized to the range [0;1]:
 |
Here fi is the total residue frequency in the compared columns 1 and 2. This conservation value is then combined with the sequence similarity score as follows:
where wc = 0.5 is the weight for the conservation score. This term additionally rewards the matches between highly conserved positions if these positions are similar and penalizes these matches if the positions are dissimilar.
Secondary structure score
PROCAIN incorporates SS information in the form of SS prediction by PSIPRED (20). A 3 × 3 secondary structure substitution matrix derived from structural alignment of SCOP domains is used for this purpose. The confidence levels of secondary structure prediction are considered as follows:
Here Sseqmean is the average of all positions to all positions sequence similarity scores. wss is the weight factor, a constant for all query sequences after it is trained. CD1 and CD2 are the secondary structure prediction confidence levels (0–9) of columns 1 of the query profile and columns 2 of the subject profile. SS12 is the secondary structure substitution value of the two columns. n and m are the lengths of the query protein sequence and subject protein sequence. Sseqij is the sequence similarity scores of columns i of the query profile and columns j of the subject profile.
An important characteristic of how PROCAIN incorporates these three types of information is that sequence similarity scores or its average value are involved in every additional score.
Database
A calibration database of 935 protein SCOP domains is formed by picking a representative protein domain from each SCOP fold (13). The subject database is composed of 4147 SCOP protein domains. MSAs are formed for all the protein sequences for both databases by running buildali.pl and then converted into numerical profiles. SS is predicted for all the proteins in both databases using PSIPRED (20). An all-to-all profile comparison is performed within the subject database; for each protein domain, the average score to nonhomologs is calculated. Similarly, each protein profile of the calibration database is compared to all the profiles of the subject database using PROCAIN. The corresponding average scores are calculated and recorded. The average scores for both calibration and subject database profiles serve as rough measures of their propensity to produce a large score in a random comparison.
Statistical significance estimation
As part of database construction, we precompute and store background score distributions for profiles of the searching database. First, for every profile A we calculate the set of similarity scores (21) against all nonhomologous profiles B in the same database and find the mean value of this set, <s>A. Then we process this set by subtracting the mean score of the counterpart profile B from each score sAB: s′AB = sAB – <s>B. The resulting distribution of scores {s′AB} for profile A is stored and used during the search.
For every profile C in the calibration database, we precompute the set of similarity scores {sCA} against entries of the searching database and then calculate the mean value of this set, <s>C. When the query profile Q is compared to profiles in the calibration database, the mean score of each profile C is subtracted from its similarity score to the query sQC: s′QC = sQC – <s>C.
During the actual search, when query Q is compared to profile A in the searching database, the distribution of adjusted calibration scores for the query, {s′QC}, is combined with the distribution of adjusted background scores for the subject, {s′AB}. The resulting distribution is fitted with EVD to estimate EVD parameters k and λ, which are then used in the Karlin–Altschul formula to calculate the E-value: E = kmne−λS, where m and n are effective lengths of the two profiles and S = sQA – 0.5(<s>QC +<s>A) is the adjusted score for query against the database profile A.
Quality of homology detection by individual queries
We construct sorted lists of hits for each query domain, and consider sensitivity (sensitivity = recall = TP/(TP + FN), where TP and FN are the numbers of true positives and false negatives, respectively) at a given level of selectivity (selectivity = precision = TP/(TP + FP), where FP is the number of false positives). These sensitivity values for the evaluated methods are compared using paired t-test and nonparametric paired Wilcoxon rank test. We find that a 50% level of selectivity reveals the most significant differences between the compared methods, and results are similar for the t-test and Wilcoxon test.
RESULTS
Numerical profiles describe amino acid content at MSA positions and reflect, in a simple way, evolutionary process in a protein family at the level of individual residues in polypeptide chain. However, profile comparison position by position cannot detect subtler yet powerful sequence features that are dictated by structural or functional constraints and remain preserved long after the divergence of two homologous sequence families. One obvious example of such feature is the conservation of SS: as a rule, even extremely distant homologs share SS elements that are part of their common structural fold. We find that two more features significantly improve the quality of homology detection: the level of amino acid conservation at individual positions and the presence of similar extended motifs without insertions or deletions.
Alignment construction and scoring
Given MSA for a query protein family, PROCAIN performs a search in a profile database, constructs profile–profile alignments and reports significant similarities. We introduce new approaches to both alignment construction and estimating statistical significance of these alignments (Figure 1). Profile–profile alignments are based on the scores for similarity between individual positions of compared MSAs. These scores include four terms (Figure 1): a standard measure for the similarity in residue composition (9) combined with three additional measures that reflect local similarity in secondary structure, amino acid conservation and sequence motifs:
where sseq is the score for similarity of residue content at the two compared MSA columns [the same measure as used in COMPASS (9)], C is a measure of total conservation in the two columns, normalized to the range [0;1], wc is the constant weight for the conservation term; sss and wss are the score for similarity in predicted SS and the corresponding constant weight. The last term rewards aligned motifs: δm = 1 if the two aligned positions have a positive residue content score and belong to a longer alignment segment that includes at least one position with a positive score on each side, δm = 0 otherwise; sm is the sum of scores for similarity of residue content for the given pair of positions and for its two immediate neighbors (see Methods for details). Importantly, the motif score is always non-negative: it rewards positive-scoring segments of profile–profile alignment without indels but does not additionally penalize gaps or mismatches. The resulting positional scores s are used for the construction of the optimal local Smith–Waterman alignment (22) of the two profiles.
Figure 1.
Schema of PROCAIN procedures for construction of sequence alignments (green) and estimation of their statistical significance (orange). For the two compared multiple sequence alignments (MSAs), scores between individual positions are calculated by combining the standard measure for the similarity of residue content in the alignment columns (step 3a) with the motif (3b), conservation (3c) and secondary structure (3d) terms. The resulting scores for positional matches are used to construct the optimal local alignment by Smith–Waterman algorithm. To estimate the statistical significance of the optimal alignment score, we perform comparisons to unrelated profiles for both the query and subject MSAs. The query is compared to the calibration database, whereas the subject is compared to unrelated profiles in the searching database. The combined distribution of the resulting random scores is approximated with extreme value distribution (EVD) and used to calculate E-value.
Estimating statistical significance
Accurate estimation of statistical significance of the optimal alignment score (P-value or E-value) is essential for the confident discrimination of even most distant homologs from nonhomologs. In this respect, profile–profile comparison presents a particular challenge: the optimal alignment scores strongly depend on residue composition, secondary structure, and other features of specific pairs of compared profiles. As a remedy, Soding (13) suggested constructing individual distributions of random alignment scores for each query, based on the query's comparison to a calibration database. This database includes a single protein representative from each structural fold and thus should not contain more than one protein homologous to the query; therefore the produced set of scores should represent random comparisons of the query to unrelated profiles. The resulting score distribution is used to estimate statistical significance of a score between the query and any given family.
Although this calibration adjusts statistical estimates to individual properties of each query, it does not distinguish between various families present in the database. These families also differ in their propensity to produce random high-scoring alignments with nonhomologs. We develop this approach further and consider individualized distributions on each side of the comparison, for both the query and the database profiles. The most straightforward way to construct a distribution of random scores for a database profile would be to perform a calibration on the same representative database as for the query. We find, however, that the quality of homology detection benefits from considering the composition of the specific database where an actual search is performed. A typical search would be aimed at 3D structure prediction and would therefore involve a database of protein families with known structures, for example, MSAs of sequence homologs for PDB, SCOP or CATH representatives. In such a database, we take advantage of knowing the actual relationships between database entries. For each database profile, we precompute the set of similarity scores to nonhomologs in the same database. We then use the means of these sets to further compensate for the different properties of database entries: each score for a given database profile A against another profile B is individually adjusted by subtracting the mean score of B (see ‘Methods’ section for details). The resulting distribution of adjusted scores for profile A is later used for the E-value estimation in the actual search.
Similarly, for every profile in the calibration database we precompute the mean score against all profiles in the searching database. When the query is compared to the calibration profiles, the corresponding means are subtracted from the similarity scores, producing the calibration distribution. Finally, when the actual search is performed, we combine calibration distributions for the query and the database profiles and estimate the E-value using approximation (23) of the combined distribution by extreme value distribution (EVD) (24,25) (see ‘Methods’ section for details).
Quality of homology detection
To assess PROCAIN's performance from different angles, we use a number of evaluation tests. These tests are based on a statistically balanced set of divergent protein domains from SCOP (26), whose relationships are defined by complementing SCOP annotation with a rigorous Support Vector Machine (SVM)-based algorithm (2) and combining a number of metrics for sequence and structure similarity. Our evaluation of detection quality includes complementary approaches to the definition of true/false positives: reference-dependent approaches use ‘gold standard’ domain relationships, whereas reference-independent approaches focus on the quality of structural matches predicted by the sequence alignment (2).
Results of several evaluations are shown in Figure 2. Each plot includes ROC curves (27) for two versions of PROCAIN (with and without consideration of SS), PROCAIN's predecessor COMPASS (9) and the current state-of-the-art method employing SS prediction, HHsearch (versions with and without consideration of SS). In Figure 2a, true positives are defined as all domain pairs that share the same SCOP superfamily or have a significant similarity detected by our evaluation system using Support Vector Machine (SVM) (2). Comparison of these plots leads to important conclusions. First, PROCAIN without SS significantly outperforms COMPASS, the method based only on the residue similarity at the profile positions. Moreover, performance of PROCAIN without SS is similar to that of HHsearch with SS (Figure 2a). This improvement is due to considering residue conservation and motif matches, as well as the new estimates of statistical significance. Second, introducing the comparison of SS in either PROCAIN or HHsearch further improves detection quality, especially in the area of remote homologs (the right part of the plot). Indeed, conservation of SS becomes more important for highly diverged proteins with low sequence similarity. Third, performance of PROCAIN with SS is significantly higher than that of HHsearch, which is considered a current standard in the field (Figure 2a).
Figure 2.
Quality of homology detection by PROCAIN compared to other methods. ROC plots are shown for PROCAIN and HHsearch, both with and without consideration of SS, and for PROCAIN predecessor COMPASS. Light and dark green, PROCAIN without and with SS, respectively. Blue and purple, HHsearch without and with SS, respectively. Red, COMPASS. (a) True positives include all homologs as annotated by SCOP and predicted by a combination of similarity measures (see text for details). (b) True positives defined only as close homologs. (c) True positives defined as in (a), with additional requirement for the level of alignment accuracy. (d) True positives defined in a reference-independent fashion, as alignments corresponding to meaningful structural superpositions (GDT_TS > 0.15).
Although information about SS improves the discrimination between homologs and nonhomologs, it might potentially scramble the ranking of evolutionary distances between detected homologs and the query. If overemphasized, SS similarity to a distant relative might bring this protein to the top of the list of detected homologs, above the query's immediate relatives. This effect would diminish the method's value for evolutionary analysis and prediction of structure and function. As a control for this effect, we evaluate the quality of detecting only closest homology relations, by disregarding more remote homologs as false positives. Figure 2b shows ROC curves where true positive matches are defined as sharing the same SCOP superfamily, which generally corresponds to the similarity detected by PSI-BLAST. Notably, in this range of evolutionary distances PROCAIN and HHsearch have similar quality of homolog ranking, unaffected by the addition of SS information (Figure 2b).
For the purpose of structure and function prediction, a method should not only correctly rank the detected similarities but also provide meaningful sequence alignments. Figure 2c shows the quality of detecting all homologs, including remote, with additional requirement for the accuracy of produced alignments. Similarity to a homolog is considered a true positive only if the corresponding alignment has a certain level of quality, either reference-dependent (matching a ‘gold-standard’ structural alignment) or reference independent (generating a reasonable structural superposition). In this experiment, alignments are required to either correctly reproduce ≥5 residue matches in the reference DALI (28) alignment, or to generate structure superposition with GDT_TS (29) score ≥0.15 (see ‘Methods’ section for details). According to these criteria both versions of PROCAIN have a higher detection quality than HHsearch version with SS, which indicates improvement in the alignment accuracy for the detected homologs (Figure 2c).
As a more direct evaluation of structure modeling, we use an approach conceptually similar to the one in the Critical Assessment of Techniques for Protein Structure Prediction (CASP) (30). We define true positives according to their value for structure prediction rather than to a fixed reference of protein relationships and alignments. In this reference-independent evaluation (Figure 2d), any detected protein superpositions with GDT_TS ≥ 0.15 are considered true positive; all others false positives. Both versions of PROCAIN show a significantly higher reference-independent detection quality than other methods (Figure 2d).
Homology detection by individual queries
Evaluation based on all-to-all comparisons (Figure 2) might be biased if a subset of queries produces many highly significant hits that dominate the beginning of the ROC curve. To control for such a bias, we compare the performance of the methods query by query. For each query in our set, we consider the sorted list of hits and calculate sensitivity at a given level of selectivity (see ‘Methods’ section in Supplementary Data). For a pair of methods, sensitivity values for each query are compared using the paired t-test. Table 1 shows t-test P-values for sensitivity at 50% selectivity; data for other sensitivity levels are included in SI Table S8 and S9. Consistent with the results of all-to-all comparisons (Figure 2), at the level of individual queries PROCAIN performs significantly better than other methods.
Table 1.
Paired tests for detection quality on individual queries
| 50% sensitivity | COMPASS | HHsearch_ noss | ProCAIn_ noss | HHsearch_ ss |
|---|---|---|---|---|
| HHsearch_noss | 9.01e-46 | |||
| −4.6e-36 | ||||
| 8.3e-04 | ||||
| 0e+00 | ||||
| ProCAIn_noss | −2.24e-146 | −1.28e-194 | ||
| −6.23e-54 | −8.52e-05 | |||
| −1.31e-126 | −1.94e-113 | |||
| 1.22e-105 | −0e+00 | |||
| HHsearch_ss | −3.77e-171 | −0e+00 | 8.09e-01 | |
| −1.03e-60 | −7.43e-28 | −4.05e-02 | ||
| −7.96e-76 | −5.69e-242 | 1.46e-06 | ||
| 0e+00 | −0e+00 | 0e+00 | ||
| ProCAIn_ss | −6.43e-300 | −1.27e-261 | −1.63e-189 | −3.73e-94 |
| −8.45e-87 | −1.21e-12 | −3.59e-15 | −1.39e-03 | |
| −3.32e-298 | −3.6e-252 | −3.47e-191 | −3.73e-121 | |
| −6.01e-66 | −0e+00 | −0e+00 | −0e+00 |
Methods are compared by sensitivity values at 50% selectivity, calculated separately for each query. The cell for each pair of methods contains P-values of paired t-test for four criteria of true/false positive distinction, the same as used in Figure 2a–d (from top to bottom): reference dependent, close homologs only, reference dependent with alignment quality, and reference independent. Plus and minus signs by the P-values denote, respectively, positive and negative difference between the method on the left and the method on the top.
Homology detection in protein classes
PROCAIN performs differently in different major protein classes. Results of evaluation of homology detection quality within the main SCOP classes (all α, all β, α/β and α + β) can be found in Supplementary Figures S3–S6. PROCAIN performance in the α/β class is very similar to the overall performance, whereas the other three classes show significant differences. Similar, yet somewhat smaller, differences are observed for HHsearch (see Supplementary Figures S3–S6). We hypothesize that these differences may reflect the composition of the training set that is used to optimize the weights (wc, wss and wm) of additional terms in PROCAIN score. This set consists of domains randomly chosen from the total evaluation set, and therefore shows a similar distribution of representatives among the main classes. As the protein world in general, this set is dominated by the homologs from the α/β class (47.9%), whereas all α, all β and α + β classes are less represented (17.6%, 9.6% and 8.9%, respectively).
The observed difference in performance suggests that adjustment of scoring parameters according to the query's class may be a plausible further direction to increase the detection quality. For example, for all α or all β proteins, the improvement introduced by considering SS is smaller compared to the whole set (Supplementary Figures S3 and S4). Indeed, an SS prediction string that consists mainly of a single SS type bears less additional information for an aligner than a string with clearly delimited SS elements of different types. Therefore, in all α and all β proteins, using a lower relative weight for the SS score may put more emphasis on the direct amino acid similarity, which might be more important to detect.
Alignment quality
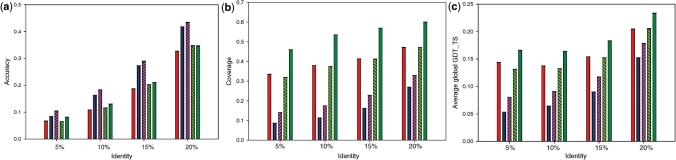
Similar to the evaluation of homology detection, we use both reference-dependent and -independent criteria for the assessment of alignment quality. Figure 3 shows the quality of alignments produced by COMPASS, HHsearch and PROCAIN evaluated by three measures. Accuracy with respect to the reference alignment is defined as the fraction of correctly aligned positions among all aligned residue pairs. Coverage is the ratio of alignment length to the overall length of the reference structural alignment. As a reference-independent measure, we use GDT_TS (29) of the structural superposition guided by the alignment under evaluation.
Figure 3.
Quality of alignment between homologs. Color-coding is the same as in Figure 2: light and dark green, PROCAIN without and with SS, respectively; blue and purple, HHsearch without and with SS, respectively; red, COMPASS. Average parameters of alignment quality are shown for several bins of remote sequence identity: 0–5%, 5–10%, 10–15% and 15–20%. (a) Reference-dependent accuracy. (b) Coverage. (c) GDT_TS of alignment-guided structure superposition. See text for details.
PROCAIN generally produces much longer alignments with coverage of 40% larger than COMPASS and almost 200% larger than HHsearch (Figure 3b). Manual inspection of alignments suggests that PROCAIN aligns the same relatively easy sequence segments as HHsearch or COMPASS, and additionally extends the alignment in both directions. These extended regions often have lower similarity and are harder to align. Lower accuracy in these regions reduces the overall alignment accuracy (Figure 3a). However, the less accurate alignments that include more divergent protein parts may better reflect structural and functional protein similarities. Such alignments may be especially beneficial in structure modeling, being more informative than clear-cut yet short alignments covering only a few SS elements. Accordingly, PROCAIN alignments are favored by reference-independent evaluation based on structure superposition (Figure 3c).
Subtle homology relations detected by PROCAIN
In our SCOP data set, PROCAIN confidently (E-value <0.01) detected 405 pairs of distant homology relationships between SCOP domains that belong to different superfamilies while structurally similar. These relationships were missed by HHsearch (HHsearch probability <0.20). On the other hand, approximately 68% fewer distant relationships (129 domain pairs) are detected by HHsearch (probability >0.91, which corresponds to PROCAIN E-value of 0.01) and missed by PROCAIN (E-value >2.13, which corresponds to HHsearch probability of 0.20). Full lists of these similarities are included in Supplementary Data. The considerable amounts of remote homologs uniquely detected by either of the methods reflect conceptual differences between PROCAIN and HHsearch. Thus, as is often the case in sequence analysis, a user searching for distant protein similarities would benefit from combining both methods.
Figure 4 shows two examples of subtle homology relationships detected by PROCAIN. The nitrilase Nit domain of NIT-FHIT fusion protein from Caenorhabditis elegans (PDB ID 1emsA, domain 2, Figure 4a) is similar to the mre11 nuclease from achreon Pyrococcus furiosus (PDB ID 1ii7A, Figure 4b), with a significant PROCAIN E-value of 9.9 10−3. Mre11 is a central component of a protein complex responsible for homologous recombination, telomere length maintenance and DNA double-strand break repair in eukariotes (31). The NIT-FHIT protein is involved in purine metabolism (32). In vertebrates, Nit and Fhit homologs are expressed as two separate interacting proteins. Fhit is a nuleotide-binding domain strongly associated with carcinogenesis and tumor suppression (32), whereas the substrate and cell biology of Nit are unknown. SCOP assigns mre11 and Nit to different superfamilies within metallo-dependent phosphatase fold of α + β class (carbon-nitrogen hydrolases and metallo-dependent phosphatases, respectively), noting that these superfamilies share ‘some topological similarities’ in structure but not establishing homology. The detected sequence similarity should have significant implications for the evolution and biology of both double-strand DNA repair and purine metabolism in eukaryotes.
Figure 4.
Subtle homology relations detected by PROCAIN. (a, b) Similarity between a Nit domain (PDB ID 1emsA, domain 2) and mre11 nuclease (PDB ID 1ii7A). (c, d) Similarity between CelF endocellulase (PDB ID 1g9gA) and squalene-hopene cyclase (PDB ID 2sqcA, domain 1). Matched protein regions corresponding to blocks in PROCAIN alignments are shown in the same color, from blue to red. Unmatched regions are colored gray. Sequence alignments are colored according to predicted secondary structure, with α-helices and β-strands shown in red and cyan, respectively.
As another example, PROCAIN predicts homology (with E-value = 3.0 10−3) between two bacterial all-α proteins: processive endocellulase CelF from Clostridium cellulolyticum (PDB ID 1g9gA, Figure 4c) and squalene-hopene cyclase from Alicyclobacillus acidocaldaris (PDB ID 2sqcA, domain 1, Figure 4d). These domains share a significant structure similarity (DALI Z-score = 16.7) yet belong to different SCOP superfamilies: six-hairpin glycosidases and terpenoid cyclases/protein prenyltransferases, respectively. CelF is a component of cellulosome, protein complex responsible for the degradation of cellulose and similar substrates outside the cell. Squalene-hopene cyclase is a membrane protein with the active site located in a large central cavity (33,34). The detected homology between these domains may suggest a similar functional role of the internal cavity in enzymatic activity of CelF.
DISCUSSION
Here we present a new method for sequence profile comparison that complements ‘vertical’ context of MSA, i.e. substitution constraints at individual sequence positions, with ‘horizontal’ context, i.e. patterns of residue contents at multiple positions. We find that the additional ‘horizontal’ information, in the form of similarity in predicted SS and local sequence motifs, significantly expands the range of detected remote protein relationships. Combining this information with the new approach to the estimation of statistical significance, PROCAIN provides the quality of homology detection beyond the capabilities of current state-of-the-art methods.
Contribution of SS prediction
Similar to others (13,14), we find that considering SS prediction leads to significant improvement in both similarity detection (Figure 2) and alignment accuracy (Figure 3). As expected, this improvement is more pronounced for extremely distant homologs, where direct sequence signals are weak yet SS is conserved. SS prediction itself (20) involves the analysis of various types of information derived from sequence profiles: periodic patterns of hydrophobicity, residue propensities for occurrence in SS elements, specific sequence motifs, and so on. Thus, for the purposes of homology detection, similarity between SS predictions, regardless of their accuracy, may be considered as a simple representation of ‘horizontal’ sequence patterns in the compared protein families. After testing different ways of including SS predictions in the profile comparison, we find that the best performance results from a simple addition of the weighted substitution score for SS types. The optimal weight value, wss = 0.1, appears to be similar to that used in HHsearch (13), suggesting that this might be a general optimal ratio of mixing residue and SS information.
Contribution of additional non-SS features
Although the comparison of SS predictions is a major contributor to the increased quality of homology detection (Figure 2), it does not dominate the improvement as much as reported for HHsearch, a conceptually similar method based on the comparison of HMMs (13). Interestingly, inclusion of simple profile features (positional conservation and the presence of ungapped segments in profile alignment), as well as the new protocol of statistical estimation, results in a performance comparable to that of HHsearch with SS included (Figure 2a). HHsearch (13) is based on HMM–HMM comparison allowing for flexible gap penalties in alignment construction, and is considered among the best performing methods for homology detection. We find that a similar detection quality can be achieved by a simpler profile aligner with fixed gap penalties and no SS consideration (Figure 2). Addition of SS improves the quality of PROCAIN detection further, beyond the previously achievable levels (Figure 2). The simplicity of profile–profile comparison makes it more tractable for analyzing contributions of different score terms and procedures, providing potentially an easier platform for finding directions of major improvement. However, evaluation of the effects of additional PROCAIN procedures on HMM comparison would be extremely interesting.
An important PROCAIN feature that differs from previously reported methods is the score that rewards clusters of positive matches in continuous motifs but does not penalize for their absence. In such a cluster, each positional match receives additional score input from neighboring matches. This scheme boosts the importance of longer stretches of similar sequence positions, which are typical in homologs, and evens out the scores within a stretch, so that the signals from extremely conserved positional matches are further distributed over their closest neighbors.
E-value estimation based on symmetrized calibration
A significant contribution to PROCAIN's performance comes from the new approach to the estimation of statistical significance of detected similarities. In our symmetrized calibration scheme, the background score distributions are derived for both query and its database counterparts. When used as queries, different profiles are known to differ in the heaviness of the tail of random score distribution: the same score value may be quite significant for one query and marginal for another. These differences are caused by variations in profile properties, some of which are easier to model separately (length, sequence diversity), whereas others are more difficult (residue composition, SS content, etc.) In the same fashion, profiles in the searching database have different propensity to appear as highly scored matches when compared to an unrelated query. Thus, a random model of individual comparison between a query and a database profile would be more accurate if the background distributions for both query and subject are considered. Our scheme does not affect the computational speed of the search, since all distributions for the database profiles are pre-computed and analytically approximated in advance. Given the power of today's computational resources, building distributions based on comparisons of unrelated entries in the search database is feasible and may be beneficial for various other search applications.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
The National Institute of Health (grant number GM67165 to N.V.G.). Funding for open access charge: Howard Hughes Medical Institute.
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENT
The authors acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing high-performance computing resources.
REFERENCES
- 1.Chandonia JM, Brenner SE. The impact of structural genomics: expectations and outcomes. Science. 2006;311:347–351. doi: 10.1126/science.1121018. [DOI] [PubMed] [Google Scholar]
- 2.Qi Y, Sadreyev RI, Wang Y, Kim BH, Grishin NV. A comprehensive system for evaluation of remote sequence similarity detection. BMC Bioinformatics. 2007;8:314. doi: 10.1186/1471-2105-8-314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhang Y, Hubner IA, Arakaki AK, Shakhnovich E, Skolnick J. On the origin and highly likely completeness of single-domain protein structures. Proc. Natl Acad. Sci. USA. 2006;103:2605–2610. doi: 10.1073/pnas.0509379103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Moult J, Fidelis K, Kryshtafovych A, Rost B, Tramontano A. 8th Community Wide Experiment on the Critical Assessment of Techniques for Protein Structure Prediction. Available at http://predictioncenter.org/casp8/
- 5.Gribskov M, McLachlan AD, Eisenberg D. Profile analysis: detection of distantly related proteins. Proc. Natl Acad. Sci. USA. 1987;84:4355–4358. doi: 10.1073/pnas.84.13.4355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Altschul SF, Madden TL, Schaffer AA, Zhang J, Zhang Z, Miller W, Lipman DJ. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Eddy SR. Profile hidden Markov models. Bioinformatics. 1998;14:755–763. doi: 10.1093/bioinformatics/14.9.755. [DOI] [PubMed] [Google Scholar]
- 8.Karplus K, Barrett C, Cline M, Diekhans M, Grate L, Hughey R. Predicting protein structure using only sequence information. Proteins. 1999;(Suppl. 3):121–125. doi: 10.1002/(sici)1097-0134(1999)37:3+<121::aid-prot16>3.3.co;2-h. [DOI] [PubMed] [Google Scholar]
- 9.Sadreyev R, Grishin N. COMPASS: a tool for comparison of multiple protein alignments with assessment of statistical significance. J. Mol. Biol. 2003;326:317–336. doi: 10.1016/s0022-2836(02)01371-2. [DOI] [PubMed] [Google Scholar]
- 10.Schaffer AA, Wolf YI, Ponting CP, Koonin EV, Aravind L, Altschul SF. IMPALA: matching a protein sequence against a collection of PSI-BLAST-constructed position-specific score matrices. Bioinformatics. 1999;15:1000–1011. doi: 10.1093/bioinformatics/15.12.1000. [DOI] [PubMed] [Google Scholar]
- 11.Pietrokovski S. Searching databases of conserved sequence regions by aligning protein multiple-alignments. Nucleic Acids Res. 1996;24:3836–3845. doi: 10.1093/nar/24.19.3836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yona G, Levitt M. Within the twilight zone: a sensitive profile-profile comparison tool based on information theory. J. Mol. Biol. 2002;315:1257–1275. doi: 10.1006/jmbi.2001.5293. [DOI] [PubMed] [Google Scholar]
- 13.Soding J. Protein homology detection by HMM-HMM comparison. Bioinformatics. 2005;21:951–960. doi: 10.1093/bioinformatics/bti125. [DOI] [PubMed] [Google Scholar]
- 14.Chung R, Yona G. Protein family comparison using statistical models and predicted structural information. BMC Bioinformatics. 2004;5:183. doi: 10.1186/1471-2105-5-183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sunyaev SR, Eisenhaber F, Rodchenkov IV, Eisenhaber B, Tumanyan VG, Kuznetsov EN. PSIC: profile extraction from sequence alignments with position-specific counts of independent observations. Protein Eng. 1999;12:387–394. doi: 10.1093/protein/12.5.387. [DOI] [PubMed] [Google Scholar]
- 16.Tatusov RL, Altschul SF, Koonin EV. Detection of conserved segments in proteins: iterative scanning of sequence databases with alignment blocks. Proc. Natl Acad. Sci. USA. 1994;91:12091–12095. doi: 10.1073/pnas.91.25.12091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pei J, Grishin NV. AL2CO: calculation of positional conservation in a protein sequence alignment. Bioinformatics. 2001;17:700–712. doi: 10.1093/bioinformatics/17.8.700. [DOI] [PubMed] [Google Scholar]
- 18.Siddharthan R, Siggia ED, van Nimwegen E. PhyloGibbs: a Gibbs sampling motif finder that incorporates phylogeny. PLoS Comput. Biol. 2005;1:e67. doi: 10.1371/journal.pcbi.0010067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Durbin R, Eddy S, Krogh A, Mitchison G. Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge, UK: Cambridge University Press; 1998. [Google Scholar]
- 20.McGuffin LJ, Bryson K, Jones DT. The PSIPRED protein structure prediction server. Bioinformatics. 2000;16:404–405. doi: 10.1093/bioinformatics/16.4.404. [DOI] [PubMed] [Google Scholar]
- 21.Doolittle RF. Stein and Moore Award address. Reconstructing history with amino acid sequences. Protein Sci. 1992;1:191–200. doi: 10.1002/pro.5560010201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Smith TF, Waterman MS. Identification of common molecular subsequences. J. Mol. Biol. 1981;147:195–197. doi: 10.1016/0022-2836(81)90087-5. [DOI] [PubMed] [Google Scholar]
- 23.Eddy SF. Maximum Likelihood Fitting of Extreme Value Distributions. 1997. Available at ftp://selab.janelia.org/pub/publications/Eddy97b/Eddy97b-techreport.pdf. [Google Scholar]
- 24.Karlin S, Altschul SF. Methods for assessing the statistical significance of molecular sequence features by using general scoring schemes. Proc. Natl Acad. Sci. USA. 1990;87:2264–2268. doi: 10.1073/pnas.87.6.2264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gumbel EJ, editor. Statistics of Extremes. New York: Columbia Univeristy Press; 1958. [Google Scholar]
- 26.Murzin AG, Brenner SE, Hubbard T, Chothia C. SCOP: a structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol. 1995;247:536–540. doi: 10.1006/jmbi.1995.0159. [DOI] [PubMed] [Google Scholar]
- 27.Schaffer AA, Aravind L, Madden TL, Shavirin S, Spouge JL, Wolf YI, Koonin EV, Altschul SF. Improving the accuracy of PSI-BLAST protein database searches with composition-based statistics and other refinements. Nucleic Acids Res. 2001;29:2994–3005. doi: 10.1093/nar/29.14.2994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Holm L, Sander C. Mapping the protein universe. Science. 1996;273:595–603. doi: 10.1126/science.273.5275.595. [DOI] [PubMed] [Google Scholar]
- 29.Zemla A. LGA: a method for finding 3D similarities in protein structures. Nucleic Acids Res. 2003;31:3370–3374. doi: 10.1093/nar/gkg571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Das R, Qian B, Raman S, Vernon R, Thompson J, Bradley P, Khare S, Tyka MD, Bhat D, Chivian D, et al. Structure prediction for CASP7 targets using extensive all-atom refinement with Rosetta@home. Proteins. 2007;69(Suppl. 8):118–128. doi: 10.1002/prot.21636. [DOI] [PubMed] [Google Scholar]
- 31.D'Amours D, Jackson SP. The Mre11 complex: at the crossroads of DNA repair and checkpoint signalling. Nat. Rev. Mol. Cell Biol. 2002;3:317–327. doi: 10.1038/nrm805. [DOI] [PubMed] [Google Scholar]
- 32.Pace HC, Brenner C. The nitrilase superfamily: classification, structure and function. Genome Biol. 2001;2 doi: 10.1186/gb-2001-2-1-reviews0001. REVIEWS0001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Full C, Poralla K. Conserved tyr residues determine functions of Alicyclobacillus acidocaldarius squalene-hopene cyclase. FEMS Microbiol. Lett. 2000;183:221–224. doi: 10.1111/j.1574-6968.2000.tb08961.x. [DOI] [PubMed] [Google Scholar]
- 34.Wendt KU, Poralla K, Schulz GE. Structure and function of a squalene cyclase. Science. 1997;277:1811–1815. doi: 10.1126/science.277.5333.1811. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.