Local and global effects of strong DNA bending induced during molecular dynamics simulations

Abstract

DNA bending plays an important role in many biological processes, but its molecular and energetic details as a function of base sequence remain to be fully understood. Using a recently developed restraint, we have studied the controlled bending of four different B-DNA oligomers using molecular dynamics simulations. Umbrella sampling with the AMBER program and the recent parmbsc0 force field yield free energy curves for bending. Bending 15-base pair oligomers by 90° requires roughly 5 kcal mol⁻¹, while reaching 150° requires of the order of 12 kcal mol⁻¹. Moderate bending occurs mainly through coupled base pair step rolls. Strong bending generally leads to local kinks. The kinks we observe all involve two consecutive base pair steps, with disruption of the central base pair (termed Type II kinks in earlier work). A detailed analysis of each oligomer shows that the free energy of bending only varies quadratically with the bending angle for moderate bending. Beyond this point, in agreement with recent experiments, the variation becomes linear. An harmonic analysis of each base step yields force constants that not only vary with sequence, but also with the degree of bending. Both these observations suggest that DNA is mechanically more complex than simple elastic rod models would imply.

INTRODUCTION

DNA molecules can undergo strong bending in many protein/DNA complexes (1–3), in looped DNA (4) and in nucleosomal complexes (5,6). The predisposition of certain DNA sequences to adopt the particular shapes required for complex formation with proteins or smaller, ligands, notably curvature, contributes to specific recognition via so-called indirect readout (7–10). Recent cyclisation experiments on short DNA fragments indicated that significantly stronger bending than expected from a simple elastic rod model of DNA could occur spontaneously (11). Other experimental techniques including molecular force sensors (12), fluorescence energy transfer (13), and atomic force microscopy (14) have also suggested that strong bending of DNA is easier than expected and theoretical models have been developed that attempt to reproduce this behaviour (14–17). These results make it important to understand the molecular mechanism of strong DNA bending and, in particular, to determine whether such bending results in sharp kinks or rather involves a smoothly distributed deformation of DNA.

Sharp kinking of DNA was first proposed by Crick and Klug in 1975 on the basis of physical models of the double helix (18). Strong bending has also been proposed to occur via a series of smoother deformations with 45° bending to the major groove (19) or 22.5° bending towards both grooves, alternating with the helix phase (20). Other propositions invoked flipped-out bases (21,22) or the formation of local bubbles (17,23). The Crick–Klug type kink was observed in recent simulations of DNA minicircles (24,25) and termed a type I kink. It is characterized by a high roll (of the order of 90°) at a particular junction leading to the unstacking of a single base pair (bp) step, with little disturbance of the neighbourhood. A second type of kink, also observed in the minicircle simulations and termed a type II kink involves three successive base pairs. In this case, the Watson–Crick hydrogen bonding of the central base pair is broken and each base stacks on its 5′ neighbour. This base pair disruption is characterized by very large propeller (roughly 120°) and stagger parameters.

Bent and kinked DNA molecules correspond to non-equilibrium conformations of DNA that may occur only transiently and are therefore difficult to study experimentally. Molecular dynamics simulations are in principle well suited to study such deformations at high spatial and temporal resolution. However, at current timescales (typically tens of ns) unrestrained MD simulations are not really sufficient to sample the bending fluctuations of free DNA and are certainly incapable of reproducing the severe bends seen in some protein–DNA complexes. These restrictions can however be overcome by using restraints to induce sampling to the desired conformations.

The present study has two objectives. First, we use our recently developed bending restraint approach (26) to obtain the bending free energy of short DNA fragments as a function of base sequence and, secondly, we characterize DNA bending dynamics at the base pair level. Interestingly, in the regime of weak bending (up to 50°), the bending free energy closely follows a quadratic curve which is consistent with the experimentally measured DNA persistence length. For larger bend angles the slope of the free energy as a function of the bending angle decreases and is consistent with recent AFM experiments (14). This bending regime is accompanied by the creation of sharp, sequence-dependent kinks.

MATERIALS AND METHODS

DNA oligomers

The present study involves four B-DNA 15-mers, d(CGCGCGCGCGCGCGC), d(CATATATATATATAC), d(CGCGCAAAAACGCGC) and d(CGCGCGCGCAAAAAC) referred to as [GC], [AT], [Atract-1] and [Atract-2] oligomers, respectively. In each case, simulations were started using standard B-DNA structures.

DNA bending restraint

The geometric variable associated with global DNA bending has been presented in detail in a previous publication (26). Briefly, the global bend angle θ of a given DNA oligomer is calculated as an angle between helical axes defined at either end of the oligomer and referred to as handles. To obtain each axis, we first calculate screw rotation vectors corresponding to the helical transformation between successive bases along each strand within a short fragment of n base pairs (n = 4 in this study). The average of these vectors yields the best approximation to the local helical axis and is used as the ‘handle’. During simulations global bending can then be controlled by a quadratic restraint on θ. In the present study the direction of bending is not imposed and the oligomers can bend according to their sequence dependent preferences.

It has been shown previously (26) that θ correlates very well with global bend angle calculated with the program Curves (27,28), frequently used as the standard method to define helical and global properties of DNA. The main advantage of our bending restraint is that it leaves the intervening base pair steps (seven in the present case, see below) free to adopt their energetically preferred conformations in terms of the regularity/irregularity of bending and in terms of bending direction. At the same time, this restraint leaves the ends of the oligomer free to change their helical conformation, however it will only function correctly if these ends remain helical. Base unpairing in the ends would clearly damage this helicity and so the quality of base pairing was analysed throughout the simulations. Base pairing in the ends of the oligomers studied here was well-maintained for all bending angles, with the exception of strong bending of the [AT] oligomer (see below).

Molecular dynamics umbrella sampling

All simulations used the AMBER ff99 with the parmbsc0 modifications (29), standard Amber 8.0 MD protocols (30) and the weighted histogram analysis method (31) for potential of mean force (PMF) calculations. Explicit solvation with TIP3P water molecules and neutralizing K⁺ ions was used as in the original publication on this force field (29). Further details of protocol can also be found in (32,33). Bending was induced using a quadratic biasing potential V(θ)= k(θ – θ_ref)² with a force constant k = 0.2 kcal mol⁻¹ degree⁻², where θ is the angle between two handle vectors described above and θ_ref is the reference value for a given sampling window. Windows were sampled every 5° from 0° to 150° (26). In order to obtain sufficient statistics, each window was sampled for 3 ns after an initial equilibration period (comparison was made with 2 ns sampling to check convergence). Conformations were recorded every 2 ps. The total production time for each oligomer was 124 ns (producing almost a quarter of a million conformational snapshots). Helical analysis of the conformations was performed with the program Curves (27,28). The conformations along the MD trajectories were scanned for significant deviations of local roll, propeller, opening and stagger from canonical values and selected conformations were then analysed in more detail.

In order to characterize changes in the stiffness of base pair junctions with respect to increasing bending, we also calculated the effective force constant k_i,j for every base pair junction i, in each umbrella window j. k_i,j was derived from a simplified harmonic analysis, similar to that used in (3,34,35) using the inverse of the variance of the local bending angles a_i,j (36,37), defined as:

a_i,j corresponds to the bending angle for the junction i over the window j which generally presents unimodal (Gaussian) distributions as discussed in the results section. a0_i,j corresponds to its most probable value. Angular brackets denote averaging over a given sampling window.

RESULTS AND DISCUSSION

DNA bending free energies

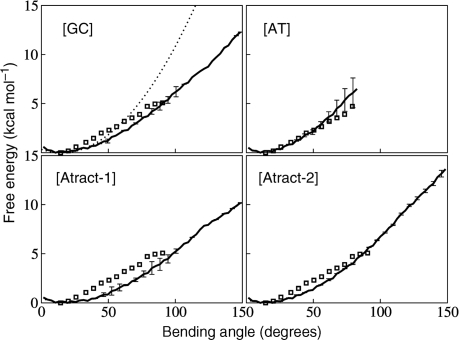
The free energy changes associated with the global bending of each DNA duplex were calculated for 2 ns and 3 ns sampling for each 5° step (Figure 1). The overlapping of the distributions in the consecutive windows was carefully checked (Figure 1S in Supplementary Data). The curves for both simulation times are very similar suggesting good convergence of the conformational ensembles. Partial studies of unbending were also performed by decreasing the bending restraint, again in 5° steps, with limited 1 ns sampling per window. It was found that unbending followed the same free energy curves, with the exception of the [AT] sequence (see below), if unbending began from 100°, again suggesting good convergence (Figure 2S in Supplementary Data). Beyond this point, all unbending curves showed hysteresis due to base pair disruption.

Figure 1.

Calculated free energy for bending the four DNA oligomers are plotted for 3 ns sampling per 5° window (bold full lines), with corresponding error bars. The bending free energy deduced from AFM experiments (14) is shown by open squares. A quadratic energy function derived from the experimental equilibrium persistence length is shown for the [GC] oligomer (dotted line). Note the departure from quadratic energy variation for larger bending angles.

Sequence effects are already visible for small bending angles. For the [GC] and [AT] oligomers the global free energy minimum occurs at 10° bending, while for [Atract-1] and [Atract-2] it is shifted to roughly 20°. This is in agreement with experiments indicating intrinsic bending of such sequences in solution (38). The overall shape of the bending free-energy curves is similar for the four sequences. For small bending angles (up to 50°) the free energy curves are close to being quadratic and correspond well to the curve derived from the persistence length of DNA (indicated as dotted line for [GC] in Figure 1).

Global bending beyond this point is clearly not quadratic and flattens out to an almost linear increase of the free energy with the bending angle. It is interesting to note that this almost linear dependence for strong bending of DNA corresponds to recent experimentally measured values for individual DNA molecules on same length scale (50 Å) obtained with high resolution atomic force microscopy (14). In Figure 1 squares indicate the data reproduced from Figure 2c of ref. (14), omitting first two points. The agreement between the experimental results and our values is very good, especially for the alternating sequences which are expected to behave like an ‘average’ DNA. This would suggest that amber ff99 with parmbsc0 modifications is capable of reproducing the dynamic behaviour of the B-DNA double helix. Bending up to 90° requires a total free energy change of ∼4.5 kcal mol⁻¹ for A-tract sequences and ∼5.5 kcal mol⁻¹ for alternating [GC] and [AT] sequences, compared to 5 kcal mol⁻¹ from the AFM measurements (14). For higher bending, up to 150°, which was not probed by the AFM experiments, we obtained the values of roughly 12 kcal mol⁻¹ for [GC] and [Atract-2] and 10 kcal mol⁻¹ for [Atract-1]. A structural explanation for this difference in bending free energy between the two A-tract containing oligomers is given in the next section. Note that the [AT] oligomer could not be bent beyond 80° because of AT base pair disruption at one end of the oligomer. This unpairing (despite the CG capping base pairs) indicates that for strong bending, breaking the terminal base pairs to escape the imposed restraint becomes energetically favourable.

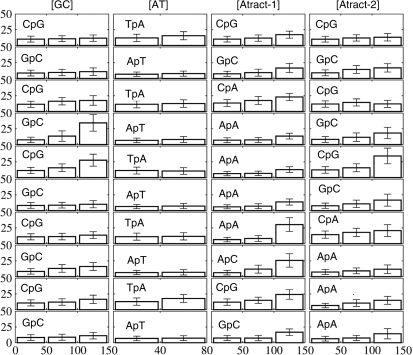
Figure 2.

Mean hinge angle a (vertical axis, scale 0–50°) and its standard deviation (cross-bars) for the 10 central junctions of the four oligomers (that is, X3pY4, at the top of the figure, through X12pY13 at the bottom) and for three bending angle regimes (weak: 0–50°, medium: 50–100°, strong: 100–150°). No values for [AT] are given beyond 80° due to base unpairing at one end and the breakdown of the bending restraint.

It is possible to make a linear fit to the free-energy curves for bending angles in the roughly linear regime above 60°. We obtain slopes of 7.4 [Atract-2], 6.9 [GC] and 5.7 [AT] and [Atract-1] in kcal mol⁻¹ radian⁻¹ (the corresponding values in kcal mol⁻¹ degree⁻¹ are 0.13, 0.12 and 0.09 respectively). These values are in good agreement with the experimental value of 6.8 kcal mol⁻¹ radian⁻¹, found by averaging over a large number of samples with diverse base sequences (14). They can be used for describing sequence-specific bending elasticity in the sub-elastic chain (SEC) models of DNA recently developed (16,17).

Weak bending of DNA

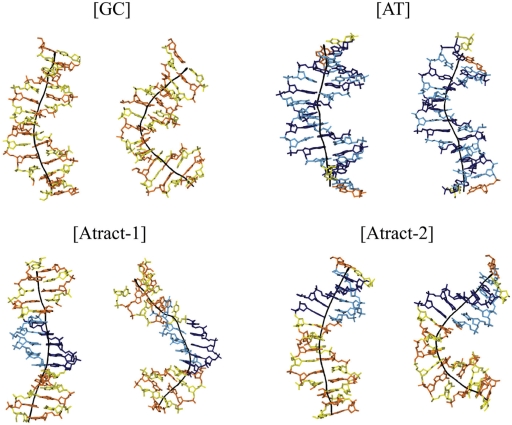
For each DNA oligonucleotide, bending up to 100° (or 80° for [AT]) can be considered as ‘smooth’ since it mainly involves coupled base pair rolls with roll angles limited to 20°. This is illustrated in Figure 2, which shows the local bend angle at each base pair step (mostly roll, since tilt is energetically more costly). For global bending up to 50°, one can see a clear pattern with pyrimidine–purine steps (CpG, TpA, CpA) contributing more than purine-pyrimidine steps (20). This pattern can also be clearly seen in the central region of the [Atract-2] duplex, which contains CG and GC steps. For bending in the 50–100° range, the AA steps at the center of the [Atract-1] show only small local bend angles (Figure 2). This result points towards a fundamentally different bending mechanism for this oligomer. Weak bending of [Atract-1] occurs towards the minor groove at the center, with contributions towards the major groove mainly at the junctions with the flanking GC-rich sequences (Figure 3). This is in agreement with earlier studies of A-tract bending (38–40). In contrast, as the snapshots in Figure 3 show, weakly bent [GC], [AT] and [Atract-2] duplexes show bending preferentially towards the major groove towards the center of the oligomers.

Figure 3.

Representative conformational snapshots of the four duplexes for weak bending, <50° (left panel for each duplex) and strong induced bending, >100° (75° for [AT]) (right panel for each duplex). The nucleotides are colour coded (cytosine in yellow, guanine in orange, thymine in pale blue and adenine in dark blue). The global helical axis (black line) was calculated using curves (27,28).

Strong bending and analysis of base pair kinking

For bending angles beyond 100°, localized kinks at individual base pair steps are observed. As described earlier, recent molecular dynamics simulations of short DNA minicircles (24,25) led to two types of kinks: ‘classical’ type I kinks which unstack a single base pair step and type II kinks which involve the three base pairs, with disruption of the hydrogen bonding for the central pair. Both kinks lead to strong bending (90° or more) towards the major groove. In our simulations, which use the recent parmbsc0 force field (29), type I kinks were not observed. We believe that this is due to changes introduced in the new force field, aimed at reducing artefacts associated with α/γ transitions in the phosphodiester backbone (33,41), and, notably, the artificial stabilization of γ trans which occurs during type I kinking (24). In order to verify this assumption we analysed a simulation of the [GC] oligomer made with the parm94 force field. Type I kinks were indeed found to occur in this case. With the new parmbsc0 force field, although no type I kinks are seen, incomplete and reversible base pair unstacking frequently occurs (Figure 4). In particular, kinks with mean rolls of 20–50°, directed toward the major groove (and opening the minor groove) are a frequent, and slowly relaxing, deformation.

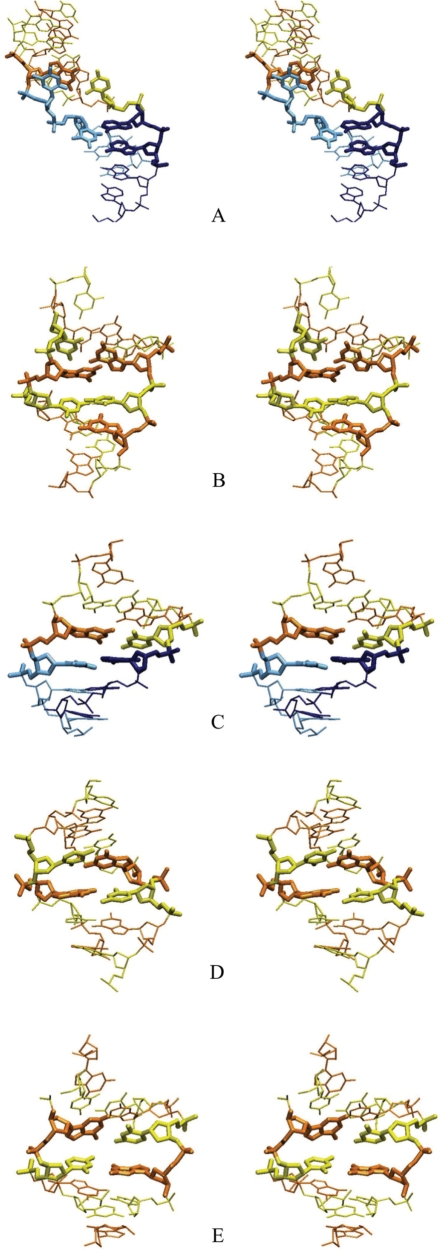
Figure 4.

Stereo view of DNA kinks observed during MD simulations. The central nucleotides around the kink site are shown by bold lines: (A) Type II kink at A₉A₁₀C₁₁ in [Atract-1], directed towards the minor groove, (B) Type II kink at G₆C₇G₈ in [GC], directed towards the major groove, (C) small kink (with a 45° roll) towards the major groove at C₅G₆ in [GC]. These kinks can be compared to typical small rolls at pyrimidine–purine steps: (D) 20° roll towards the major groove at C₅pA₆ in [Atract-1], (E) 20° roll towards the minor groove at C₁₁pG₁₂ in [GC]. The same colour coding as in Figure 3 is used (cytosine in yellow, guanine in orange, thymine in pale blue and adenine in dark blue).

Type II kinks do however occur in our simulations, as can be seen at base pairs G₆C₇G₈ in [GC] for bending beyond 130° and for A₉A₁₀C₁₁ in [Atract-1] for bending beyond 120° (illustrated in Figure 4, see also Figure 2). In the case of the GCG motif, the average propeller is 60°, the kink closes the local major groove and can induce bifurcated hydrogen bonds within the base triplet (Figure 4B). In contrast, the AAC triplet (Figure 4A), closes the local minor groove, similarly to that found at a, AGG sequence in earlier work (24). Type II kinking induces both roll and tilt deformations of neighbouring base pair steps. A linear axis fitted with Curves to four base pairs on either side of the motif gives a local bend for type II kinks of 91° for GCG and 87° for AAC. Figure 4 shows also a small kink towards the major groove, corresponding to roll of 45°, at C₅G₆ within [GC] oligomer (Figure 3).

A-tract bending

As indicated above, ApA steps within A-tracts show particularly small junction bending (mainly roll) for global bending up to 120° for [Atract-1] and up to 150° for [Atract-2]. A similar result has already been observed in a simulation using the parm94 force field (26). At 120° bending for [Atract-1], a transition occurs which fundamentally alters the pattern of helical parameters. The first three AA junctions of the A-tract become rolled by roughly 25° towards the major groove. This corresponds to a transition from the classical mechanism of A-tract bending with smooth and phased local bends at specific junctions, as described in (26), to a new pattern with small kinks towards the major groove at the 5′-end of the A-tract and a type II kink at the 3′-end, which closes the minor groove.

It is interesting to note that when the A-tract block is shifted away from the centre of the oligomer in [Atract-2], bending arises from small rolls towards the major groove at the central GpC junctions and towards the minor groove at the 5′-end of the duplex. Comparing the sequences of [GC] and [Atract-2] shows that an important difference results from the replacement of a C₉pG₁₀ junction in the former with C₉pA₁₀ in the latter (see Figure 2). The CpA junction should be easier to unstack since the experimental stacking energy for CA is about −0.55 kcal mol⁻¹ compared to –0.91 for CG (42). Unstacking indeed occurs in [Atract-2], thus avoiding the II kink that appears upstream in the [GC] oligomer.

Helical parameters and phosphodiester backbone

It is interesting to see that small kinks (local bending angle of 20–50°) occur not only at pyrimidine–purine junctions (CpG, TpA, CpA), but also at some purine–pyrimidine steps (GpC, ApT), as well as at ApA. An inverse correlation of roll versus twist (20,43,44) was systematically observed for all kinked base-pair steps. Anisotropic DNA bending, favouring bending toward the grooves (2) was also systematic, with tilt close to zero except within type II kinks. Base pair disruption (excluding the breakdown of pairing at one end of strongly bent [AT] discussed above), is easily observable via the helical parameters and was limited to the central base pairs of the type II kinks in the [GC] and [Atract-1] oligomers.

Concerning the phosphodiester backbone, we found no coupling between strong base pair bends and BI/BII backbone transitions, as suggested earlier (45). We however observed some sequence effects on these transitions, with a higher population of BII states for GpC junctions. γ backbone dihedral angles (C4′–C5′) in trans conformations, predicted (18) and observed (24) to be associated with type I kinks and with the 5′-CA of an A-tract (46) were not observed in our study.

Harmonic analysis of base pair hinges

Bending stiffness, described by effective force constants for each base pair junction along our oligomers as a function of global bending, are shown in Figure 5. The quasi-normal distribution of the amplitudes of the local bending angle (a_i,j) for each junction was checked by several techniques for each a_i,j histogram, including quantile-quantile normal probability plots, chi-square and Shapiro–Wilk statistical tests (data available on request). A simplified quasi-harmonic analysis of local bending angles (3,34,35) was then performed in each global bending window (see ‘Materials and Methods’ section).

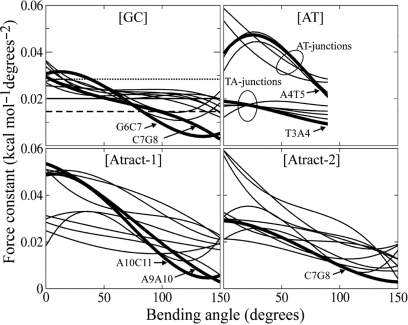
Figure 5.

Bending force constants k_i,j of each junction for the four oligomers for each simulation window. k_i,j is obtained from a harmonic approximation to the junction hinge angle defined as √(roll² + tilt²). The results have been smoothed using a cubic polynomial. Junction force constants discussed in the text are highlighted by bold lines. For a CpG several values from other studies are shown in the figure for [GC]: thermal stability data (50) (pointed line); X-ray crystallography (3) (solid line) and EPR (51) (dashed line).

The effective force constants obtained from this analysis (Figure 5) show several interesting features. First, for all oligomers, the force constants decrease with increasing global bending. This corresponds to the linear dependence of the free energy on the bending angle, beyond small deformations, as shown in Figure 1 and observed experimentally. For relaxed structures, and for the [GC] oligomer, both GpC and CpG junctions have similar force constants around 0.03 kcal mol⁻¹ deg⁻². In contrast, for the [AT] oligomer, the two types of junctions are clearly distinguishable, and the ApT force constants can reach 0.06 kcal mol⁻¹ deg⁻², whereas the TpA values group around 0.02 kcal mol⁻¹ deg⁻². In the two A-tracts, the lower values for the GC segments and the A-tracts themselves can easily be distinguished.

There are a few junctions that reduce their force constants dramatically with bending. In the case of the [GC] oligomer, these involve the two junctions of the type II kink G₆pC₇pG₈. The decreased force constants for these steps are coupled to increases for the neighbouriong steps C₅pG₆ and G₁₀pC₁₁, starting from 120° to 130° of global bending. The [AT] oligomer presents a different picture. The ApT steps have much higher force constants than the TpA steps. While the TpA steps show only small increases in force constants most of the ApT steps show larger sigmoidal variations. In [Atract-1], the two descending lines in Figure 5 correspond to the type II kink formation at A₉pA₁₀pC₁₁, while G₄pC₅ shows a sigmoidal variation. Most interestingly in this oligomer, the central junction A₉pA₁₀ shows the highest reduction. Finally, in [Atract-2] the ApA junctions loose their stiffness very rapidly with bending, but the strongest decrease in stiffness corresponds to a CpG junction and is linked to the generation of the series of small kinks discussed above.

Note that both junctions of the type II kink in [Atract-1], A₉pA₁₀ and A₁₀pC₁₁, show a roughly 10-fold reduction in stiffness when the kink forms. The smaller 5-fold reduction for the G₆pC₇ and C₇pG₈ junctions of the type II kink in [GC] can be explained by the additional rigidity of the undeformed A-tract.

CONCLUSIONS

By controlling the overall bending of short DNA oligomers during molecular dynamics simulations we have been able to calculate the bending free energy of four oligomers with different base sequences. The results are analyzed in conformational detail and lead to a better understanding of bending mechanisms.

The energy change required to form a global bend of 90° for the oligomers we study (which are roughly 50 Å in length) is close to 4.5 kcal mol⁻¹ for sequences containing A-tracts and 5.5 kcal mol⁻¹ for alternating [GC] or [AT] sequences. This agrees with earlier simulations using the parm94 force field (26,47). For bending up to 150°, the free energy cost is 12 kcal mol⁻¹ for [GC] and [Atract-2] and 10 kcal mol⁻¹ for [Atract-1]. Beyond small bending angles, we find linear energy dependence on bending and we have been able to extracted linear coefficients for different base sequences that could be used in refining sub-elastic chain models of DNA (14,16).

The structural analysis of oligomer bending shows that for moderate global bending angles, curvature is distributed smoothly over the whole oligomer. For strong global bending, the oligomer behaviour depends on its sequence: [GC] and [Atract-1] oligomers produce type II kinks, while [Atract-2] produces a series of small kinks in the GC part of its sequence.

We do not observe type I kinks, whose appearance in earlier simulations appears to be related to problems in representing the behavior of the α/γ backbone angles in the parm94 force field. At the moment it is difficult to say whether the parmbsc0 modifications of the parm99 perfectly represent the DNA backbone, the trans conformation of γ being strongly disfavoured. The Type II kinks were observed in both the [GC] and the [Atract-1] oligomers and produce bending of roughly 90°. In [GC] the kink is associated with local bending towards the major groove. In [Atract-1], it induces sharper local bending towards the minor groove. We note that the bending mechanism of the two oligomers containing A-tracts depends on the position of the tract.

We have lastly made a harmonic bending analysis of each oligomer to extract force constants for each base pair step as a function of overall bending. These values are commonly used in elastic rod models of DNA (3,35,48) to interpret large-scale mechanics and dynamics (49). Recent experimental measurements of DNA flexibility on short length scales (11–14) have questioned this harmonic treatment and suggested that non-linear terms may be necessary to account for local structural changes (14–17). Our results on short oligomers show that individual junctions indeed behave differently as a function of their sequence context, even before extreme local deformations occur and as a function of the extent of bending.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

VolkswagenStiftung PhD grant (to M.Z.); Universite Franco-Allemande (UFA), cotutelle agreement between Université Paris 7 and Jacobs University. ANR grant ALADDIN ANR-O8-BLAN-0154-01 (to K.Z., R.L.). Funding for open access charge: ANR.

Conflict of interest statement. None declared.