Global potential for wind-generated electricity

Abstract

The potential of wind power as a global source of electricity is assessed by using winds derived through assimilation of data from a variety of meteorological sources. The analysis indicates that a network of land-based 2.5-megawatt (MW) turbines restricted to nonforested, ice-free, nonurban areas operating at as little as 20% of their rated capacity could supply >40 times current worldwide consumption of electricity, >5 times total global use of energy in all forms. Resources in the contiguous United States, specifically in the central plain states, could accommodate as much as 16 times total current demand for electricity in the United States. Estimates are given also for quantities of electricity that could be obtained by using a network of 3.6-MW turbines deployed in ocean waters with depths <200 m within 50 nautical miles (92.6 km) of closest coastlines.

Wind power accounted for 42% of all new electrical capacity added to the United States electrical system in 2008 although wind continues to account for a relatively small fraction of the total electricity-generating capacity [25.4 gigawatts (GW) of a total of 1,075 GW] (ref. 1; www.awea.org/pubs/documents/Outlook_2009.pdf). The Global Wind Energy Council projected the possibility of a 17-fold increase in wind-powered generation of electricity globally by 2030 (ref. 2; www.gwec.net/fileadmin/documents/Publications/GWEO_2008_final.pdf). Short et al. (3), using the National Renewable Energy Laboratory's WinDs model, concluded that wind could account for as much as 25% of U.S. electricity by 2050 (corresponding to an installed wind capacity of ≈300 GW).

Archer and Jacobson (4) estimated that 20% of the global total wind power potential could account for as much as 123 petawatt-hours (PWh) of electricity annually [corresponding to annually averaged power production of 14 terawatts (TW)] equal to 7 times the total current global consumption of electricity (comparable to present global use of energy in all forms). Their study was based on an analysis of data for the year 2000 from 7,753 surface meteorological stations complemented by data from 446 stations for which vertical soundings were available. They restricted their attention to power that could be generated by using a network of 1.5-megawatt (MW) turbines tapping wind resources from regions with annually averaged wind speeds in excess of 6.9 m/s (wind class 3 or better) at an elevation of 80 m. The meteorological stations used in their analysis were heavily concentrated in the United States, Europe, and Southeastern Asia. Results inferred for other regions of the world are subject as a consequence to considerable uncertainty.

The present study is based on a simulation of global wind fields from version 5 of the Goddard Earth Observing System Data Assimilation System (GEOS-5 DAS). Winds included in this compilation were obtained by retrospective analysis of global meteorological data using a state-of-the-art weather/climate model incorporating inputs from a wide variety of observational sources (5), including not only surface and sounding measurements as used by Archer and Jacobson (4) but also results from a diverse suite of measurements and observations from a combination of aircraft, balloons, ships, buoys, dropsondes and satellites, in short the gamut of observational data used to provide the world with the best possible meteorological forecasts enhanced by application of these data in a retrospective analysis. The GEOS-5 wind field is currently available for the period 2004 to the present (March 20, 2009) with plans to extend the analysis 30 years back in time. The GEOS-5 assimilation was adopted in the present analysis to take advantage of the relatively high spatial resolution available with this product as compared with the lower spatial resolutions available with alternative products such as ERA-40, NECP II, and JRA-25. It is used here in a detailed study of the potential for globally distributed wind-generated electricity in 2006.

We begin with a description of the methodology adopted for the present study. The land-based turbines envisaged here are assumed to have a rated capacity of 2.5 MW with somewhat larger turbines, 3.6 MW, deployed offshore, reflecting the greater cost of construction and the economic incentive to deploy larger turbines to capture the higher wind speeds available in these regions. In siting turbines over land, we specifically excluded densely populated regions and areas occupied by forests and environments distinguished by permanent snow and ice cover (notably Greenland and Antarctica). Turbines located offshore were restricted to water depths <200 m and to distances within 92.6 km (50 nautical miles) of shore.

These constraints are then discussed, and results from the global analysis are presented followed by a more detailed discussion of results for the United States.

Methodology

The GEOS-5 analysis uses a terrain-following coordinate system incorporating 72 vertical layers extending from the surface to a pressure level of 0.01 hPa (an altitude of ≈78.2 km) (5). Individual volume elements are defined by their horizontal boundaries (latitude and longitude) and the pressures at their top and bottom. The horizontal resolution of the simulation is 2/3° longitude by 1/2° latitude (equivalent to ≈66.7 km × 50.0 km at midlatitudes). The model provides 3D pressure fields at both layer centers and layer edges in addition to wind speeds (meridional and zonal) and temperatures at the midpoint of individual layers with a time resolution of 6 h. The 3 lowest layers are centered at approximate altitudes of 71, 201, and 332 m. The 6-h data for the 3 lowest layers are used in the present analysis by using an interpolation scheme indicated as follows to estimate temperatures, pressures, and wind speeds at 100 m, the hub height for the 2.5- and 3.6-MW turbines considered here.

Knowing pressures at the lower and upper edges of individual layers together with temperatures and pressures at the midpoints of the layers, altitudes corresponding to the midpoints of the layers are calculated based on an iterative application of the barometric law by assuming a linear variation of temperature between the midpoints of individual layers. The barometric law was also used to calculate the pressure at 100 m. Wind speeds and temperatures at 100 m were computed by using a cubic spline fit to data at the midpoints of the 3 lowest layers.

The kinetic energy of the wind intercepted by the blades of a turbine per unit time (P) depends on the density of the air (ρ), the area swept by the rotor blades (πr²), and the cube of the wind speed (V³) reduced by an efficiency or power factor (f_p) according to the formula (6):

The efficiency with which kinetic energy intercepted at any given wind speed is converted to electricity by the turbine depends on details of the turbine design specified by what is referred to as the turbine power curve. Typically, conversion to electricity varies as the cube of the wind speed at low wind speeds, asymptoting to a constant value for moderate to higher wind speeds, dropping to 0 at the highest wind speeds when the blades of the turbine are normally feathered to prevent damage. For the present purpose, we chose to use power curves and technical parameters for 2.5- and 3.6-MW turbines marketed by General Electric (GE) (http://gepower.com/businesses/ge_wind_energy/en/index.htm).

These power curves assume an air density of 1.225 kg/m³ under conditions corresponding to an air temperature of 15 °C at a pressure of 1 atmosphere (7). To account for the differences in air density at the rotor elevations as compared with this standard, wind speeds in the published power/wind speed curves were adjusted according to the formula

where P and T identify the air pressures and temperatures at the hub height and R denotes the atmospheric gas constant, 287.05 N·m/(kg·K) for dry air.

Optimal spacing of turbines in an individual wind farm involves a tradeoff among a number of factors, including the costs of individual turbines, costs for site development, and costs for laying power cables, in addition to expenses anticipated for routine operations and maintenance (O&M). Turbines must be spaced to minimize interference in airflow caused by interactions among individual turbines. This process requires a compromise between the objective to maximize the power generated per turbine and the competing incentive to maximize the number of turbines sited per unit area (8). Restricting overall power loss to <20% requires a downstream spacing of >7 rotor diameters with cross-wind spacing of >4 diameters (9, 10). Applying this constraint to the 2.5-MW GE turbines (rotor diameter 100 m, r = 50 m) requires an interturbine areal spacing of 0.28 km². Similar restrictions apply to the spacing of offshore turbines (rotor diameter 111 m, r = 55.5 m). For present purposes we assume an area for individual offshore turbines of 5 × 10 rotor diameters corresponding to an occupation area per turbine of 0.616 km². The greater spacing for offshore turbines was selected to ensure that the overall power loss should be limited to 10% compensating for the presumed higher cost of installation and greater O&M expense for turbines operating in the more hostile marine environment (8, 9). Subject to these constraints, we propose to calculate the electricity that could be generated potentially every 6 h on the scale of the individual grid elements defined by the GEOS database (≈66.7 km × 50.0 km) subject to the additional spatial limitations identified below.

In addition to providing an estimate for the maximum potential power generation, we propose to evaluate also the power yield expressed as a fraction of the rated power potential of the installed turbines, i.e., to account for the anticipated variability of the wind over the course of a year. This quantity is referred to as the capacity factor (CF), defined by the relation

where P_real denotes the power actually realized (neglecting potential interference between neighboring turbines), and P_rated refers to the power that could have been realized had conditions permitted the turbine to operate at maximum efficiency for 100% of the time. We assume in this context that downtime for maintenance accounts for loss of only a small fraction of the total potential power that could be generated by the installed turbines reflecting the fact that maintenance is normally scheduled for periods of relatively low wind conditions (11). We restrict attention in this analysis to regions with capacity factors >20%.

Geographic Constraints

The Moderate-Resolution Imaging Spectroradiometer (MODIS) provides a useful record of the spatial distribution of different types of land cover for 2001, with a horizontal resolution of ≈1 km × 1 km. This record will be used to exclude from our analysis areas classified as forested, areas occupied by permanent snow or ice, areas covered by water, and areas identified as either developed or urban.

Wind speeds are generally lower over forested areas, reflecting additional surface roughness. Consequently, turbines would have to be raised to a higher level in these environments to provide an acceptable economic return. Although it might be reasonable for some regions and some forest types, we elected for these reasons to exclude forested areas in the present analysis.

The exclusion of water-covered areas is more problematic. Wind speeds are generally higher over water as compared with land. However, it is more expensive to site turbines in aquatic as compared with terrestrial environments. Public pressures in opposition to the former are also generally more intense, at least in the U.S.

Topographic relief data for both land and ocean areas were derived from the Global Digital Elevation Model (GTOPO30) of the Earth Resources Observation and Science Data Center of the U.S. Geological Survey. The spatial resolution of this data source for offshore environments (bottom topography) is ≈1 km × 1 km (12). A number of factors conspire to limit the development of offshore wind farms. Aesthetic considerations, for example, have limited development of wind resources in the near-shore environment in the U.S. although objections to near-shore development in Europe appear to have been less influential. There is a need to also accommodate requirements for shipping, fishing, and wildlife reserves and to minimize potential interference with radio and radar installations. Accounting for these limitations, Musial and Butterfield (13) and Musial (14), in a study of offshore wind power potential for the contiguous U.S., chose to exclude development of wind farms within 5 nautical miles (nm) (9.3 km) of shore and restrict development to 33% of the available area between 5 and 20 nm (9.3–37 km) offshore, expanding the potential area available to 67% between 20 and 50 nm (37–92.6 km).

For purposes of this study, following Dvorak et al. (15), we consider 3 possible regimes for offshore development of wind power defined by water depths of 0–20, 20–50, and 50–200 m. Somewhat arbitrarily, we limit potential deployment of wind farms to distances within 50 nm (92.6 km) of the nearest shoreline, assuming that 100% of the area occupied by these waters is available for development.

Wind Power Potential Worldwide

Approximately 1% of the total solar energy absorbed by the Earth is converted to kinetic energy in the atmosphere, dissipated ultimately by friction at the Earth's surface (16, 17). If we assume that this energy is dissipated uniformly over the entire surface area of the Earth (it is not), this would imply an average power source for the land area of the Earth of ≈3.4 × 10¹⁴ W equivalent to an annual supply of energy equal to 10,200 quad [10,800 exajoules (EJ)], ≈22 times total current global annual consumption of commercial energy. Doing the same calculation for the lower 48 states of the U.S. would indicate a potential power source of 1.76 × 10¹³ W corresponding to an annual yield of 527 quad (555 EJ), some 5.3 times greater than the total current annual consumption of commercial energy in all forms in the U.S. Wind energy is not, however, uniformly distributed over the Earth and regional patterns of dissipation depend not only on the wind source available in the free troposphere but also on the frictional properties of the underlying surface.

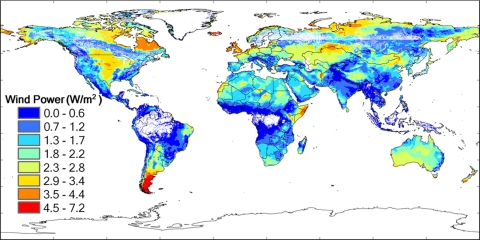
We focus here on the potential energy that could be intercepted and converted to electricity by a globally distributed array of wind turbines, the distribution and properties of which were described above. Accounting for land areas we judge to be inappropriate for their placement (forested and urban regions and areas covered either by water or by permanent ice), the potential power source is estimated at 2,350 quad (2,470 EJ). The distribution of potential power for this more realistic case is illustrated in Fig. 1. We restricted attention in this analysis to turbines that could function with capacity factors at or >20%.

Fig. 1.

Global distribution of annual average onshore wind power potential (W/m²) for 2006 accounting for spatial limitations on placement without limitations on potential realizable capacity factors.

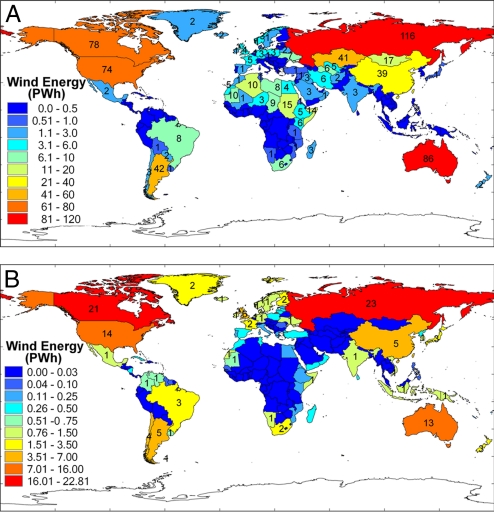
Results for the potential electricity that could be generated using wind on a country-by-country basis are summarized in Fig. 2 for onshore (A) and offshore (B) environments. Placement of the turbines onshore and offshore was restricted as discussed earlier. Table 1 presents a summary of results for the 10 countries identified as the largest national emitters of CO₂. The data included here refer to national reporting of CO₂ emissions and electricity consumption for these countries in 2005. An updated version of the table would indicate that China is now the world's largest emitter of CO₂, having surpassed the U.S. in the early months of 2006. Wind power potential for the world as a whole and the contiguous U.S. is summarized in Table 2.

Fig. 2.

Annual wind energy potential country by country, restricted to installations with capacity factors >20% with siting limited. (A) Onshore. (B) Offshore.

Table 1.

Annual wind energy potential, CO₂ emissions, and current electricity consumption for the top 10 CO₂-emitting countries

Country	CO2 emission, million tonnes	Electricity consumption, TWh	Potential wind energy, TWh
			Onshore	Offshore
U.S.	5,956.98	3,815.9	74,000	14,000
China	5,607.09	2,398.5	39,000	4,600
Russia	1,696.00	779.6	120,000	23,000
Japan	1,230.36	974.1	570	2,700
India	1,165.72	488.8	2,900	1,100
Germany	844.17	545.7	3,200	940
Canada	631.26	540.5	78,000	21,000
U.K.	577.17	348.6	4,400	6,200
S. Korea	499.63	352.2	130	990
Italy	466.64	307.5	250	160

CO₂ emission and electricity consumption are for 2005; data are from the Energy Information Administration (http://tonto.eia.doe.gov/country/index.cfm).

Table 2.

Annual wind energy potential onshore and offshore for the world and the contiguous U.S.

Areas	Worldwide, PWh		Contiguous U.S., PWh
	No CF limitation	20% CF limitation	No CF limitation	20% CF limitation
Onshore	1,100	690	84	62
Offshore 0–20 m	47	42	1.9	1.2
Offshore 20–50 m	46	40	2.6	2.1
Offshore 50–200 m	87	75	2.4	2.2
Total	1,300	840	91	68

Analysis assumes loss of 20% and 10% of potential power for onshore and offshore, respectively, caused by interturbine interference. Analysis assumes offshore siting distance within 50 nm (92.6 km) of the nearest shoreline.

The results in Table 1 indicate that large-scale development of wind power in China could allow for close to an 18-fold increase in electricity supply relative to consumption reported for 2005. The bulk of this wind power, 89%, could be derived from onshore installations. The potential for wind power in the U.S. is even greater, 23 times larger than current electricity consumption, the bulk of which, 84%, could be supplied onshore. Results for the contiguous U.S. will be discussed in more detail in the next section. If the top 10 CO₂ emitting countries were ordered in terms of wind power potential, Russia would rank number 1, followed by Canada with the U.S. in the third position. There is an important difference to be emphasized, however, between wind power potential in the abstract and the fraction of the resource that is likely to be developed when subjected to realistic economic constraints. Much of the potential for wind power in Russia and Canada is located at large distances from population centers. Given the inevitably greater expense of establishing wind farms in remote locations and potential public opposition to such initiatives, it would appear unlikely that these resources will be developed in the near term. Despite these limitations, it is clear that wind power could make a significant contribution to the demand for electricity for the majority of the countries listed in Table 1, in particular for the 4 largest CO₂ emitters, China, the U.S., Russia, and Japan. It should be noted, however, the resource for Japan is largely confined to the offshore area, 82% of the national total. To fully exploit these global resources will require inevitably significant investment in transmission systems capable of delivering this power to regions of high load demand.

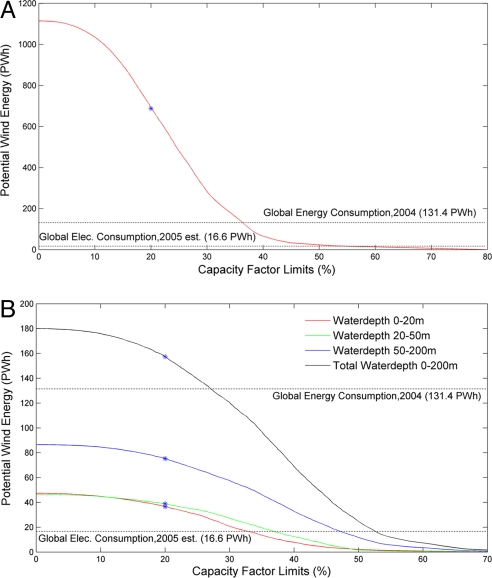
The electricity that could be generated potentially on a global basis by using wind, displayed as a function of an assumed capacity factor cutoff on installed turbines, is presented in Fig. 3 for onshore (A) and offshore (B) environments. The results in Fig. 3A suggest that total current global consumption of electricity could be supplied by wind while restricting installation of land-based turbines to regions characterized by most favorable wind conditions, regions where the turbines might be expected to function with capacity factors >53%. If the cutoff capacity factor were lowered to 36%, the energy content of electricity generated by using wind with land-based turbines globally would be equivalent to total current global consumption of energy in all forms. Cutoff capacity factors needed to accommodate similar objectives with offshore resources would need to be reduced as indicated in Fig. 3B. To place these considerations in context, we would note that capacity factors realized by turbines installed in the U.S. in 2004 and 2005 have averaged close to 36% (18).

Fig. 3.

Annual wind energy potential as a function of assumed limits on capacity factors. Results corresponding to the capacity factor limit of 20% assumed in this study are indicated by *. (A) Global onshore. (B) Global offshore.

Wind Power Potential for the United States

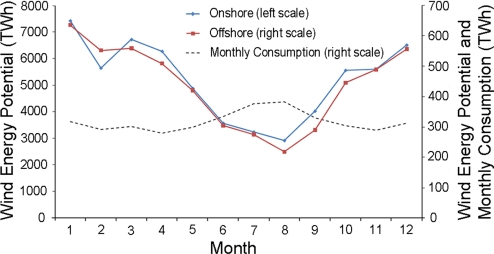
An estimate of the electricity that could be generated for the contiguous U.S. on a monthly basis (subject to the siting and capacity limitations noted above) is illustrated for both onshore and offshore environments in Fig. 4. Results presented here were computed by using wind data for 2006. Not surprisingly, the wind power potential for both environments is greatest in winter, peaking in January, lowest in summer, with a minimum in August. Onshore potential for January, according to the results presented in Fig. 4, exceeds that for August by a factor of 2.5: the corresponding ratio computed for offshore locations is slightly larger, 2.9.

Fig. 4.

Monthly wind energy potential for the contiguous U.S. in 2006 with monthly electricity consumption for the entire U.S.

Fig. 4 includes also monthly data for consumption of electricity in the U.S. during 2006. Demand for electricity exhibits a bimodal variation over the course of a year with peaks in summer and winter, minima in spring and fall. Demand is greatest in summer during the air-conditioning season. Summer demand exceeds the minimum in spring/fall demand typically by between 25% and 35% on a U.S. national basis depending on whether summers are unusually warm or relatively mild. The correlation between the monthly averages of wind power production and electricity consumption is negative. Very large wind power penetration can produce excess electricity during large parts of the year. This situation could allow options for the conversion of electricity to other energy forms. Plug-in hybrid electric vehicles, for example, could take advantage of short-term excesses in electricity system, while energy-rich chemical species such as H₂ could provide a means for longer-term storage.

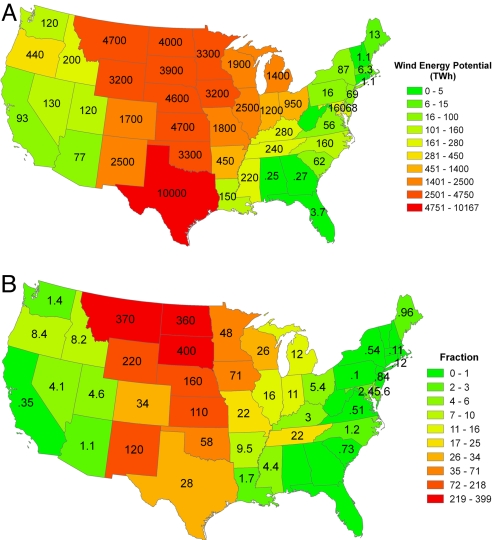
Potential wind-generated electricity available from onshore facilities on an annually averaged state-by-state basis is presented in Fig. 5A. Note the high concentration of the resource in the central plains region extending northward from Texas to the Dakotas, westward to Montana and Wyoming, and eastward to Minnesota and Iowa. The resource in this region, as illustrated in Fig. 5B, is significantly greater than current local demand. Important exploitation of this resource will require, however, significant extension of the existing power transmission grid. Expansion and upgrading of the grid will be required in any event to meet anticipated future growth in electricity demand. It will be important in planning for this expansion to recognize from the outset the need to accommodate contributions of power from regions rich in potential renewable resources, not only wind but also solar. The additional costs need not, however, be prohibitive (ref. 18; www.nrel.gov/docs/fy08osti/41869.pdf). The Electric Reliability Council of Texas, the operator responsible for the bulk of electricity transmission in Texas, estimates the extra cost for transmission of up to 4.6 GW of wind-generated electricity at ≈$180 per kW, ≈10% of the capital cost for installation of the wind power-generating equipment (ref. 19; www.ercot.com/news/presentations/2006/ATTCH_A_CREZ_Analysis_Report.pdf.).

Fig. 5.

Annual onshore wind energy potential on a state-by-state basis for the contiguous U.S. expressed in TWh (A) and as a ratio with respect to retail sales in the states (2006) (B). For example, the potential source for North Dakota exceeds current total electricity retail sales in that state by a factor of 360. Data source for total electricity retail sales was www.eia.doe.gov.

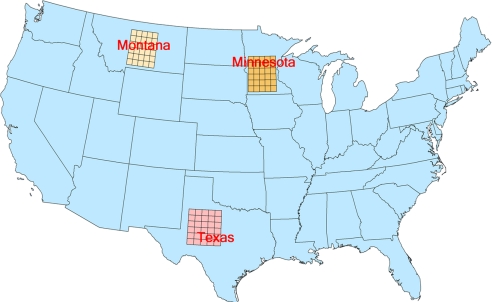
An important issue relating to the integration of electricity derived from wind into a grid incorporating contributions from a variety of sources relates to the challenge of matching supply with load demand, incorporating a contribution to supply that is intrinsically variable both in time and space and subject to prediction errors. This challenge can be mitigated to some extent if the variations of wind sources contributing to an integrated transmission grid from different regions are largely uncorrelated. An anomalously high contribution from one region can be compensated in this case by an anomalously low contribution from another. To investigate the significance of this potential compensation, we examined the covariance of wind resources from 3 specific regions, one in Montana, the second in Minnesota, and the third in Texas, as indicated in Fig. 6. Analysis of 6-h averaged potential wind-generated supplies of electricity from the 3 regions over the 4 seasons, winter, spring, summer, and fall, yielded the results summarized in Table 3. Contributions from the 3 regions are essentially uncorrelated during the winter months (October through March) with r values of <0.07. Correlation coefficients (r values), however, are relatively high in summer (July through September) with values ranging from 0.28 (Montana versus Texas) to 0.37 (Montana versus Minnesota) with intermediate values in spring. The analysis suggests that wind power could make a relatively reliable contribution to anticipated base load demand in winter. It may be more difficult to incorporate wind power resources into projections of base load demand for other seasons, particularly for summer.

Fig. 6.

Locations of regions in Montana, Minnesota, and Texas selected to explore the spatial correlation of wind resources.

Table 3.

Correlations of wind power potential between selected regions of Montana (MT), Minnesota (MN), and Texas (TX) in different seasons for 2006

Region	Correlation coefficient, r
	Jan.–March	April–June	July–Sept.	Oct.–Dec.
MN–MT	0.027	0.11	0.37	−0.15
MN–TX	0.069	0.29	0.29	−0.060
MT–TX	0.065	0.26	0.28	−0.0024

Concluding Remarks

The GEOS-5 winds used here were obtained through assimilation of meteorological data from a variety of sources, in combination with results from an atmospheric general circulation model. Transport in the boundary layer was treated by using 2 different formalisms, one applied under conditions when the boundary layer was stable, the other under conditions when the boundary layer was either unstable or capped by clouds. The variation of wind speed with altitude was calculated in the present study by using a cubic spline fit to the 3 lowest layers (central heights of 71, 201, and 332 m) of the GEOS-5 output to estimate wind speeds at the rotor heights of the turbines considered here (100 m). Wind speeds so calculated were used in deriving all of the results presented above.

The rotors of the turbines modeled in this study are of sufficient size that as the blades rotate they traverse significant portions of the 2 lowest layers of the GEOS-5-simulated atmosphere. Use of wind speed for a single level (100 m) must be consequently subject to some uncertainty. To assess this uncertainty we explored results derived with an alternate approach. The power intercepted by the blades of the rotors passing through the separate layers was calculated initially on the basis of the reported average wind speeds for the involved layers. Adopting a typical value of ≈135 m for the height of the boundary between the first 2 layers, given a rotor diameter of 100 m as appropriate for the assumed onshore turbines, it follows that 99% of the area swept out by the rotors would intercept air from the first layer, with only 1% encountered in the second layer. The power intercepted by the rotors may be calculated in this case by averaging appropriately the power intercepted in the 2 layers. Implementing this approach yielded results that differed typically slightly lower, by <15% for the onshore results presented above, by <7% for the offshore results.

The GEOS-5 data had a spatial resolution of ≈66.7 km × 50.0 km. It is clear that wind speeds can vary significantly over distances much smaller than the resolution of the present model in response to changes in topography and land cover (affected in both cases by variations in surface roughness). In general, we expect the electricity yield computed with a low-resolution model to underestimate rather than overestimate what would be calculated by using a higher-resolution model. The GEOS-5 data are expected to provide a useful representation of winds on a synoptic scale as required for example to describe the transport between adjacent grid elements. They would not be expected to account for subgrid scale variations in wind speeds even though the latter might be expected, at least under some circumstances, to make a significant contribution to the potentially available wind power. To test this hypothesis we explored the implications of a high-resolution wind atlas available for an altitude of 100 m for Minnesota (20). Wind speeds indicated by the high-resolution database are higher than the wind speeds indicated by GEOS-5, supporting our hypothesis. The close association of wind speed with surface land classification implied by the high-resolution Minnesota wind atlas suggests that land classification data could provide a useful basis for at least a preliminary downscaling of the relatively coarse spatial resolution of the potential wind resources in the present study.

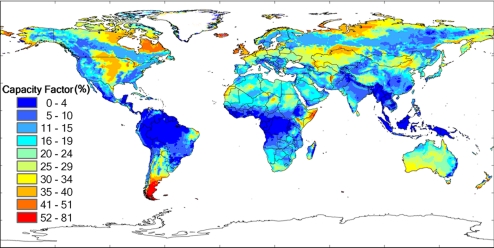
We elected in this study to exclude forested, urban, permanently ice covered, and inland water regions. Given the relatively coarse spatial resolution of the GEOS-5 database, it is possible that this approach may have failed to identify localized environments where wind resources may be unusually favorable and where investments in wind power could provide an acceptable economic return. To explore this possibility, we developed a global land-based map of the efficiencies with which turbines with rotors centered at 100 m might be capable of converting wind energy to electricity. We included all land areas with the exception of regions identified as permanently ice-covered (notably Greenland and Antarctica). Results, stated in terms of relevant capacity factors, are presented in Fig. 7. Regions with particularly favorable capacity factors, even though forested, urban, or occupied by extensive bodies of inland waters, might be considered as potential additional targets for development.

Fig. 7.

Global distribution of onshore capacity factor (%) for winds at 100 m with exclusion of permanent snow/ice-covered areas such as Antarctic and Greenland.

It is apparent, for example, that the low-resolution GEOS-5 record underestimates the wind resource available in Spain and Portugal (a consequence most likely of the complex terrains present in these regions). Sweden is another example where wind resources indicated with an available high-resolution wind atlas (21) are significantly higher than those implied by GEOS-5. The discrepancy in this case may be attributed to the extensive forest cover of the region and the a priori decision to neglect such regions in the present global study. Assessment of the potential of mountainous or hilly regions is also problematic. On average, wind speeds in these regions may be relatively low. Particularly favorable conditions may exist, however, on mountain ridges or in passes through mountainous regions. The Appalachian mountain range in the U.S. offers a case in point. In general the low-resolution results tend to slightly overestimate wind resources in regions of flat terrain, while underestimating the potential for regions defined by more complex topography.

The analysis in this article suggests that a network of land-based 2.5-MW turbines operating at as little as 20% of rated capacity, confined to nonforested, ice-free regions would be more than sufficient to account for total current and anticipated future global demand for electricity. The potential for the contiguous U.S. could amount to >16 times current consumption. Important additional sources of electricity could be obtained by deploying wind farms in near-shore shallow water environments.

An extensive deployment of wind farms may be considered as introducing an additional source of atmospheric friction. For example, if the entire current demand for electricity in the U.S. were to be supplied by wind, the sink for kinetic energy associated with the related turbines would amount to ≈6% of the sink caused by surface friction over the entire contiguous U.S. land area, 11% for the region identified as most favorable for wind farm development [the region indicated in red in Fig. 5A defined by wind resources >280 terawatt hours (TWh)]. The potential impact of major wind electricity development on the circulation of the atmosphere has been investigated in a number of recent studies (22, 23). Those studies suggest that high levels of wind development as contemplated here could result in significant changes in atmospheric circulation even in regions remote from locations where the turbines are deployed. They indicate that global dissipation of kinetic energy is regulated largely by physical processes controlling the source rather than the sink. An increase in friction caused by the presence of the turbines is likely to be compensated by a decrease in frictional dissipation elsewhere. Global average surface temperatures are not expected to change significantly although temperatures at higher latitudes may be expected to decrease to a modest extent because of a reduction in the efficiency of meridional heat transport (offsetting the additional warming anticipated for this environment caused by the build-up of greenhouse gases). In ramping up exploitation of wind resources in the future it will be important to consider the changes in wind resources that might result from the deployment of a large number of turbines, in addition to changes that might arise as a result of human-induced climate change, to more reliably predict the economic return expected from a specific deployment of turbines.