A multiscale model linking ion-channel molecular dynamics and electrostatics to the cardiac action potential

Abstract

Ion-channel function is determined by its gating movement. Yet, molecular dynamics and electrophysiological simulations were never combined to link molecular structure to function. We performed multiscale molecular dynamics and continuum electrostatics calculations to simulate a cardiac K⁺ channel (I_Ks) gating and its alteration by mutations that cause arrhythmias and sudden death. An all-atom model of the I_Ks α-subunit KCNQ1, based on the recent Kv1.2 structure, is used to calculate electrostatic energies during gating. Simulations are compared with experiments where varying degrees of positive charge—added via point mutation—progressively reduce current. Whole-cell simulations show that mutations cause action potential and ECG QT interval prolongation, consistent with clinical phenotypes. This framework allows integration of multiscale observations to study the molecular basis of excitation and its alteration by disease.

The current carried by ion channels during the action potential (AP) in excitable tissues is determined by dynamic changes of the ion channel conformation during gating. Recently determined crystal structures of ion channel proteins (e.g., ref. 1) provide a structural basis for computer simulations of the ion-channel protein molecular dynamics (MD) during conformational changes. In parallel, recently acquired experimental data on ion-channel electrophysiological function have provided the basis for detailed Markov models of channel electrical function during gating (2, 3). These models can be used to link cellular consequences of genetic mutations in cardiac ion channels that alter channel kinetics to cardiac arrhythmias [see ref. 4 for review]. Although consistent in reproducing the kinetics of channel opening and closing, the molecular conformations represented by the states of these Markov models are not identified.

In this article, we develop a multiscale computational approach that combines molecular dynamics simulations and Poisson-Boltzmann continuum electrostatic calculations with electrophysiological modeling for establishing structure-function relationships between ion channel movement during gating, its function as a carrier of transmembrane ionic current, and its role in the whole-cell AP. Detailed understanding of these relationships is necessary for the development of effective genetic/molecular therapies and specific drug treatment of disease states that involve abnormal electrical function of excitable tissues. We present an example of a cardiac ion channel, the slow delayed rectifier I_Ks, which participates in AP repolarization and its rate dependence (4). We consider mutations to its alpha subunit, KCNQ1, that lead to reduction of I_Ks current and prolongation of the AP. The clinical phenotype associated with such mutations is the Long-QT syndrome type 1, LQT1; it presents as QT interval prolongation on the ECG and predisposes patients to cardiac arrhythmia and sudden death.

Results and Discussion

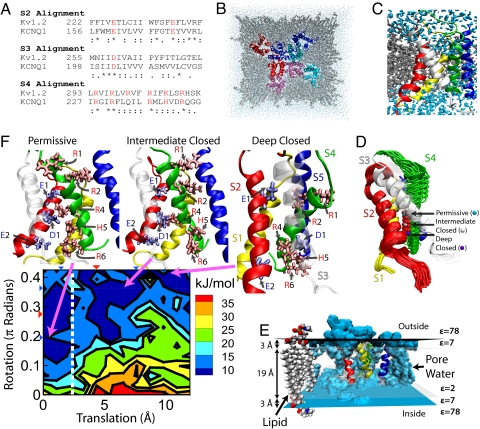
Several charged residues that participate in Kv1.2 (Shaker homolog) gating are conserved in KCNQ1 (Fig. 1A). We focus on the voltage sensing region of each of the 4 channel subunits, which contains transmembrane segments S1-S4 (Fig. 1B). Negatively charged residues on S2 and S3 can interact with positive charges on S4, forming energetically favorable salt bridges between oppositely charged residues during channel activation. The S4 residues in KCNQ1 are highly conserved and, as in most K⁺ channels, enable channel opening and closing in response to transmembrane potential, V_m. The molecular KCNQ1 model is constructed by aligning the KCNQ1 sequence with Kv1.2 (Fig. 1A) using its open state as a template. The model is then refined with MD (SI Appendix, Section 1, Figs. S1 and S2). The resulting KCNQ1 configuration is shown in Fig. 1B. Close examination (Fig. 1C) shows that water penetrates and interacts with charged S4 residues. In Shaker, the ability of water to solvate part of the voltage sensor has been implicated in its ability to transport protons when R2 and R3 are mutated to histidine (5). Additionally, a single point mutation to R1, such as R1C, enables ionic current (omega current) to pass through the voltage sensing region (6).

Fig. 1.

KCNQ1 model and energy landscape. (A) Kv1.2/KCNQ1 alignment. Symbols: * identical, : conserved, and . semiconserved substitutions. Red residues are charged. (B) Top-down (extracellular) view of the all atom system. Each of the 4 channel subunits (consisting of S1–S6 segments) is color coded. Pore regions (S5–S6) of one subunit interact with the adjacent subunit voltage-sensing region (S1–S4). (C) Voltage-sensing region with lipid of the 4 channel subunits (consisting of S1–S6 segments) (gray) and water (light blue) solvent molecules. (D) S4 translation and rotation. β-carbon of R4 labeled with red beads shows motion. Arrows indicate stable configurations (labeled). S1, Yellow; S2, Red; S3, White; S4, Green; S5, Blue. (E) Implicit membrane. Isocontours at dielectric constant ε = 78 (blue) and ε = 2 (transparent) show the transition region representing the lipid esters. Water (blue) can penetrate the protein as in C and is represented by ε = 78. (F) Energy landscape at V_m = 0 mV and associated conformations. Increasing translation corresponds to movement toward the intracellular space; increasing rotation is counterclockwise as viewed from extracellular space. Left of dotted white line is permissive state. Positively/negatively charged residues are labeled with red/blue letters. Energy landscape minima (deep blue) correspond to stable configurations; right to left: deep closed state, intermediate closed state, permissive state. In the deep closed state conformation, interactions occur between R2 and E1 and between R4 and E2. Intermediate closed state shows interactions between R4 and D1 and E2. In the permissive state, interactions are observed between R6 and E2 and between R4 and E1. Views of conformations were selected to show the interactions between residues. For movement of S4 during gating, see Movie S1.

To simulate S4 motion during channel gating, we translated it 12 Å [experiments suggest 7–13 Å (7, 8)] from the permissive state (or up state) down toward the intracellular space and rotated it 90° counterclockwise (observed from extracellular space) about its axis (Fig. 1D) (SI Appendix, Section 2). The probability that S4 resides at a given position is primarily determined by the electrostatic energy, which is computed with the Poisson-Boltzmann Equation (PBE) to generate a 2-dimensional energy landscape as a function of S4 movement, Fig. 1F (9–11). For the energy contributed by V_m(calculated below) to determine channel opening and closing, we needed to scale the solvation and coulombic energy contributions. This scaling had the effect of reducing barriers between minima corresponding to stable channel states [Details can be found in SI Appendix, Section 4]. We label the minima (right to left) as a deep closed state, an intermediate closed state and a permissive state of the voltage sensors. These labels are associated with specific protein conformations, of which representatives are shown in Fig. 1F. Channels can open only when all voltage sensors are in the permissive state. The presence of multiple closed states (minima) is consistent with the sigmoidicity of KCNQ1 and I_Ks activation, which facilitates participation in AP rate adaptation (3).

Although a crystal structure of the closed state of Shaker is not available, experiments suggest spatial constraints that localize R1 on S4 between E1 on S2 and near another residue close to the top of S1 (12). A second study, examining site-specific fluorescence, indicates a rotation of 180° (8) and translation of 6–8 Å with an additional degree of freedom for S4 that tilts its axis as it moves intracellularly. Applying 90° rotation from the open to the closed state in our KCNQ1 simulations implies that R2 moves near E1 whereas R1 has only long distance interactions with it. Data suggesting otherwise in KCNQ1 have not been published. However, Cd²⁺ bridge formation (12), fluorescence mapping, and site specific mutations (8), could examine this proposed model as done in Shaler.

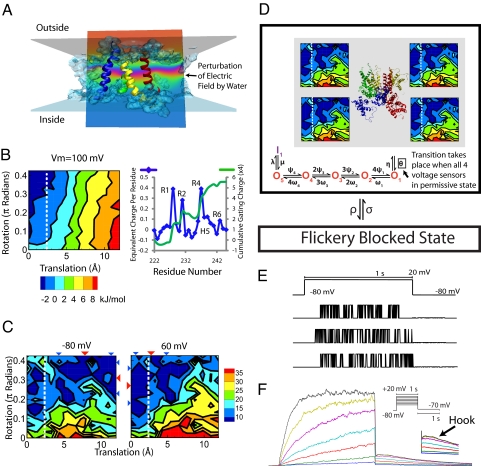
The movement of positive charges on S4 (R1-R6) across the membrane during channel opening and closing, causes gating to depend on V_m. The energy landscape in the presence of V_m (Fig. 2A) is computed with a modified PBE (often referred to as the PB-V) (13) (SI Appendix, Section 5). The presence of water that penetrates into the voltage sensor focuses the electric field, reducing the distance that S4 positive charges need to travel to cause gating, as shown experimentally (5, 6, 14) and computationally (15). The energy because of charges moving through the electric field (V_m = 100 mV) is shown in Fig. 2B (Left); it shows permissive state stabilization of ≈10 kJ/mol per 100 mV relative to the deep closed state. Since residues in S4 are translated, we plot (Fig. 2B, Right) their individual gating charge contribution (calculated as in ref. 13) at opposite ends of the translated region. The dominant role of R1-R4 in conferring voltage dependence is observed experimentally in Shaker (16); however, the total gating charge in our model is less (≈6 charges move across the field vs. ≈13 in Shaker), which is to be expected because the R3 position in KCNQ1 is filled with a glutamine. Additional gating charge may also be generated by movement of residues that we did not translate such as S2 and other segments that have been suggested to participate in gating (17).

Fig. 2.

V_m effect and kinetic model of KCNQ1. (A) Transmembrane potential. Water penetration causes significant perturbation of the electric field (ripples in the potential lines, arrow). (B) (Left) Membrane potential (Vm = 100 mV) causes stabilization of the open state and introduces a net difference of ≈10 kJ/mol between closed and open configurations. (Right) Gating charge contribution, as calculated in ref. 13, for each residue in S4 caused by moving across energy landscape (blue, left axis), and cumulative gating charge for whole channel (green, right axis). (C) Energy landscape at positive and negative V_m. Triangles are mean S4 position (red) and standard deviation (blue). (D) KCNQ1 Markov model. Energy landscapes of 4 subunits determine residency in permissive state. All 4 subunits in the permissive state (left of dotted white line) enables open state (O1–O5) transitions. Inactivated state, I, is only accessible from O5. Flickery blocked state is available from any conformation (32). (E) Single channel currents; traces show random nature of opening. (F) Macroscopic KCNQ1 current is the sum of 1000 single channels. A hook (arrow), characteristic of KCNQ1, is observed upon repolarization and is caused by channel recovery from inactivation.

Adding the contribution of V_m to the energy landscape shown in Fig. 1F, allows us to visualize its effect on the minima that define the 3 stable states of the model. In the presence of a negative V_m = −80 mV, stabilization of the closed states occurs (Fig. 2C). Applying a positive potential (+60 mV), causes the stable region to shift toward the permissive state. The scheme in Fig. 2D utilizes the energy landscapes of the 4 voltage-sensing domains and their voltage dependence to compute the probability of their residency in the permissive state using a Monte Carlo simulation. For these simulations, each voltage sensor is allowed to perform a random walk on its own energy landscape, and if all 4 reach the permissive state the channel can transition to the open states (Fig. 2E). This current is then calculated as the sum of many (1,000) single channel currents (Fig. 2F). This current is then compared with experimentally recorded currents. As shown in Fig. 3, simulated current traces at varying pulse potentials are similar to experimental traces with some slowing of activation rate at lower potentials, indicating that the simulated activation barrier is higher than that in the oocyte-expressed KCNQ1 channels in the experiment.

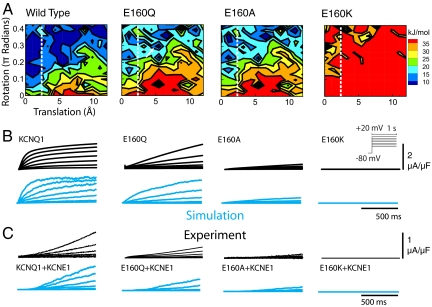
Fig. 3.

Mutation effects. (A) Energy landscapes for wild-type KCNQ1 and mutants E160Q, E160A, and E160K at V_m = 0 mV. (B) Comparison of macroscopic current between experiment (black) and simulation (cyan) for homomeric KCNQ1 and mutants. (Protocol in Inset). (C) I_Ks (KCNQ1 + KCNE1) is accurately simulated by slowing S4 movement. Mutations cause slowing of activation, in addition to KCNE1 effect.

Further validation of the model and its predictive capability is obtained by introducing (simulating) mutations at the molecular level. We examined mutations at E160 (E1) on S2 that is the site of E160K, a naturally occurring LQT1 mutation. We tested 3 mutations: Q (polar side chain), A (neutral) and K (positively charged). These mutations progressively reduce the negative charge carried by glutamic acid (E) and correspondingly slow activation, as observed experimentally. For E160Q, slowing is caused by a higher energy barrier for reaching the permissive state. Additionally, fewer channels reside in the permissive state, because R4 no longer interacts with a fully negative charge to stabilize the open configuration (R4 stabilization by E160Q is 30% less than WT). In the deep closed state, the same is true for R2. However, in the intermediate state, where neither R2 nor R4 of S4 are near E1 of S2, the energy minimum is not as affected by mutation. Consistent with a previously published model of I_Ks, destabilization of the deep closed state reduces the sigmoidicity of the simulated macroscopic current (3).

As expected, the E160A energy landscape closely resembles E160Q, because the residues only differ by side-chain polarity. However, E160A activation kinetics are modestly slower than E160Q (as in experiment). This difference is caused by the absence of a minimum near the intermediate closed state in the E160A landscape that is present for E160Q (Fig. 3A, arrow). Experiments also show a significant reduction in total E160A current because of reduced channel expression and/or conductance, which is accounted for in the model. For E160K an electrostatic repulsion is present between R4 and the substituted K at E1. Experimentally, these channels do not generate membrane current, so macroscopic conductance is set to 0.

Native I_Ks is carried by a heteromeric channel that consists of KCNQ1 and a modulatory subunit KCNE1 that slows activation (18). We account for the slowing of S4 motion by KCNE1 through a decrease in the diffusion constant between points on the energy landscape. With this change, we reproduce the voltage dependent activation of I_Ks and that of the mutant channels, in the presence of KCNE1 (Fig. 3C). This result is consistent with experiments showing proximity of KCNE1 and S4, supporting the idea that KCNE1 directly affects S4 motion.

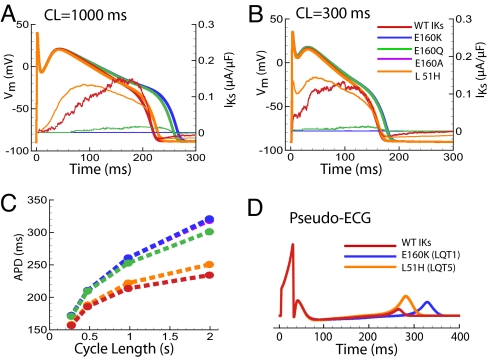
To simulate the whole-cell phenotype, we insert the channel into a recently updated Hund-Rudy canine ventricular myocyte model (19). Whole-cell WT and mutant currents at different rates are shown in Fig. 4. In the absence of current (most severe LQT1 mutation E160K), the AP is significantly prolonged. As rate increases, the AP shortens, a process termed adaptation. The slower activation of the mutant currents E160Q and E160A also results in a prolonged AP and a severe phenotype. Note that AP prolongation increases at slow heart rate (Fig. 4C), a hallmark of LQT Syndrome. The KCNE1 mutation L51H reduces the amount of expressed KCNQ1 by 30% (20). In our simulations (Fig. 4, orange) this mutation causes moderate AP prolongation, as seen clinically for LQT5 patients (21).

Fig. 4.

AP and ECG. V_m and I_Ks currents are color coded. All currents, with the exception of L51H, are in the presence of KCNE1. (A) Slow cycle length (CL = 1000 ms). (B) Fast rate (CL = 300 ms). (C) Adaptation curves, which plot AP duration (APD) dependence on CL (time between beats). (D) Simulated pseudoECGs. LQT1 mutation E160K shows significant QT interval prolongation, compared with mild prolongation by LQT5 mutation L51H, consistent with clinical phenotypes (21) (E160A closely overlaps E160K).

The duration of the ECG QTc interval (QT corrected for rate) in patients reflects the time between ventricular depolarization and repolarization, and nominally has a duration of 348 to 467 ms (22). In patients with LQT1, QTc is prolonged significantly to an average 493 ms. QTc in patients with LQT5 is much less prolonged at 457 ms (21). To evaluate the potential ECG changes of the simulated mutations, we calculate pseudo ECGs (23) (Fig. 4D), showing QT prolongation similar to the clinical phenotypes in the absence of βadrenergic stimulation.

Dramatic alteration of channel kinetics caused by charge switching and neutralization mutations in Shaker and KCNQ1 suggest that the electrostatic energy is a primary component of the channel free energy, which determines opening and closing rates. However, several additional factors may also contribute, including: intramolecular interactions, solvent rearrangement, entropic terms, nonpolar energies, and the force required to move the channel gate. A simulation estimating such contributions is provided (Fig. S3). In addition to S4, the surrounding S2 and S3 helices may also move, and S4 may have more degrees of freedom in addition to translation and rotation (24). Experimental clarification of the S4 pathway will enable more complete MD simulations to provide a better picture of the channel molecular dynamics. Our primary contribution is to provide a framework that links molecular structural dynamics to function in excitable tissues. As additional observations are made about the structure and function of different ion channels, this framework will enable us to examine the functional effects of molecular alterations at the level of whole-cell physiology and to link genotype and phenotype in the context of pathology.

Materials and Methods

A detailed description of methods is provided in the SI Appendix. Briefly, the homology model is built with Modeller (25) using the Kv1.2 open-state crystal structure as a template (26). This model is refined using molecular dynamics in the NAMD simulation package (27). Visualization of these molecular models is accomplished with VMD (28). Poisson Boltzmann calculations are computed with APBS (11), which is modified to compute the PB-V equation to include V_m effects (13). These modifications also enable computation of gating charges as in ref. 13. The adjoint form of the Smoluchowski equation (29) is used to calculate transition rates between points on the energy landscape (9, 30), which are incorporated into macroscopic Markov models of the current. Macroscopic current models are incorporated into the Hund-Rudy canine ventricular action potential model (HRd) (31). PseudoECG traces are calculated from a strand as in ref. 23.