Abstract
Background and Purpose
The use of endo-rectal balloons as immobilisation devices in external beam radiotherapy for prostate cancer has lead to improved target position reproducibility and a decrease in rectal toxicity. The air cavity created by an endo-rectal balloon in photon radiotherapy perturbs the dose distribution. In this study, the effect of the balloon cavity on the dose distribution and the accuracy to which two treatment planning systems calculate the dose distribution was investigated.
Materials and Methods
Single beams as well as 3D conformal, conventional IMRT and helical tomotherapy treatment plans were investigated using a specifically constructed phantom. Radiochromic film was used to measure the cavity wall doses and cavity wall DVHs.
Results
For a 70Gy prescription dose both the Pinnacle and TomoTherapy TPSs over-predicted the anterior cavity wall dose by 1.43Gy, 3.92Gy and 2.67Gy for 3D conformal, conventional IMRT and helical tomotherapy respectively. The posterior cavity wall dose was under-predicted by 2.62Gy, 2.01Gy and 4.79Gy for 3D conformal, conventional IMRT and helical tomotherapy respectively. An over-prediction by the Pinnacle RTPS of the V50, V60, V65 and V70 values for the cavity wall DVH was measured for the 3D conformal and conventional IMRT cases. These reductions may lead to a less than expected rectal toxicity. The TomoTherapy RTPS under-predicted the V50, V60, V65 and V70 values which may lead to higher rectal toxicity than predicted.
Conclusion
Calculation of dose around an air cavity created by an endo-rectal balloon provides a challenge for radiotherapy planning systems. Various electronic disequilibrium situations exist due to the cavity, which can lead to a lower anterior rectal wall and higher posterior rectal wall dose than calculated by planning systems. This has consequences for comparisons of dose volume constraints between different modalities.
Keywords: endo-rectal balloon, cavity, radiochromic film, tomotherapy, IMRT
Introduction
Local control and disease free survival rates are known to increase with increased dose in prostate radiotherapy [1-3]. The ability to increase dose however is limited by toxicity to surrounding tissues, mainly the rectum [4, 5]. Rectal toxicity is directly related to the dose received by the rectal wall [6, 7]. Reduction in planning target volume (PTV) margins allows reduction of normal tissue toxicity by reducing the dose delivered to the rectum, which in turn allows an increase in prescribed dose. The ability to reduce the PTV margins in prostate radiotherapy requires management of target motion and the ability to reduce the volume of the rectal wall receiving high doses.
Endo-rectal balloons are employed in prostate radiotherapy by a number of institutions as a means of immobilizing the prostate and reducing the volume of the rectal wall in the high dose region [8-12]. Target immobilization is achieved through the balloon forcing the prostate against the pubic symphysis. The volume of the rectal wall receiving high doses is reduced by forcing the posterior rectal wall away from the target and reducing the rectal wall thickness by expanding the rectal volume. The use of endo-rectal balloons during treatment delivery has been shown to decrease the delivered rectal dose [9]. Decreased rectal toxicity when using an endo-rectal balloon has also been reported [11, 13, 14].
Endo-rectal balloons are commonly filled with air in photon radiotherapy, with volumes of up to 100cm3 used. The volume of air will perturb the dose distribution in the surrounding tissue, particularly in the rectal wall [15, 16]. The perturbation of dose due to air cavities has been shown to be amplified for smaller fields [17, 18]. Any dosimetric effects of the endo-rectal balloon cavity may thus be increased when using intensity modulated radiotherapy (IMRT) and helical tomotherapy, where multiple small segments are used in place of the larger open fields seen in 3D conformal and box techniques. Multiple small segments incident from multiple angles surrounding an air cavity creates an interesting dosimetric situation. How commercial treatment planning systems calculate the dose in these situations requires investigation.
This paper investigates the convolution/superposition dose calculation algorithm [19] with the collapsed cone convolution method [20] used by both the Pinnacle RTPS and the TomoTherapy Hi-Art RTPS. The convolution/superposition algorithm involves the superposition of the energy imparted by primary photons (usually called the TERMA – Total Energy Released per unit MAss) with polyenergetic primary and scatter dose deposition kernels. These kernels represent the dose deposited from primary and secondary radiation around a primary interaction site and are generated using Monte Carlo simulations [21]. For heterogeneous regions, the kernels are scaled according to the electron density based on the average density between the primary interaction site and the voxel of interest [22]. This rectilinear density scaling has been shown to introduce errors in the dose calculation in regions of heterogeneous density [22, 23]. These errors may be observable in the rectal balloon cavity situation and may lead to inaccurate calculation of the dose to the wall of the balloon cavity.
Recent studies have reported that the α/β-ratio for prostate cancer is lower than the conventional value of 10 Gy for tumour [24-26]. Some studies have reported values as low as 1.5 Gy which is lower than the α/β-ratio for late rectal complications (α/β ∼ 3 Gy) [24-28]. To maximise the benefit of a lower prostate α/β-ratio than that for late rectal complications hypofractionation regimes have been introduced [29-31]. In conventional fractionation the prolonged delivery will lead to repair of the rectal mucosa however with hypofractionation the same may not apply. In fact some hypofractionated regimes have reported comparable but slightly higher rectal toxicity rates than standard fractionation [32, 33].
The accuracy to which treatment planning systems calculate dose in the presence of an endorectal balloon cavity must be known to ensure that rectal toxicity data is correlated with the correct dose. In this phantom study the dose to the rectal wall in the presence of an endorectal balloon was measured using radiochromic film. The dose distributions were measured for a 3DCRT plan, an IMRT plan and a helical tomotherapy plan. The results were compared with calculations from two commercial radiotherapy treatment planning systems (RTPS).
Methods
I. Phantom Setup
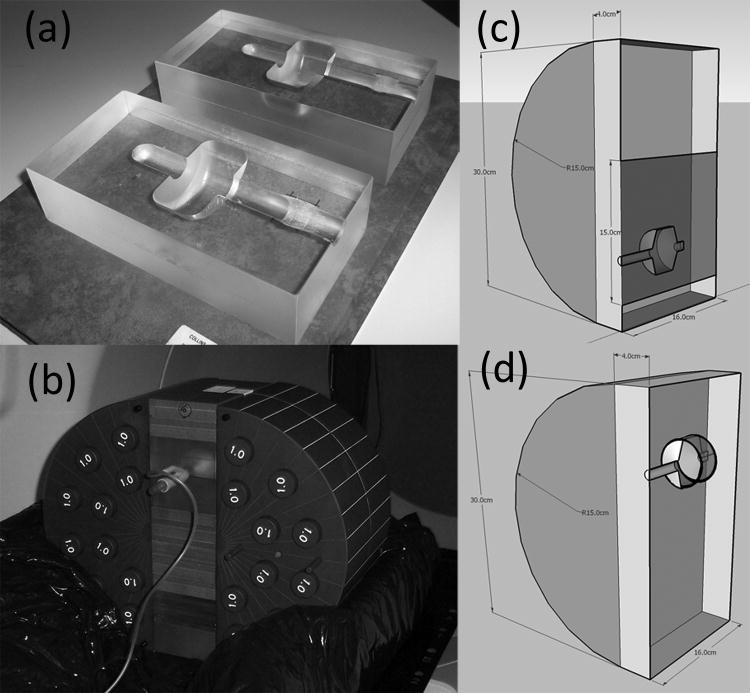
An 8×8×16cm3 phantom was constructed from acrylic to match the external contours of an EZ-EM balloon catheter. This is shown in Figure 1a. This phantom was then sandwiched between slabs of solid water and placed between the two halves of a circular phantom having a 36cm diameter yielding an ellipsoid with a short axis of 36cm and a long axis of 44cm approximating the pelvis anatomy. The rectal balloon insert was placed in either the lower (sagittal geometry) or upper (spiral geometry) half of the resulting pelvic phantom. This was then placed in an alpha cradle. The whole setup for the spiral geometry case is seen in Figure 1b.
Figure 1.
Phantom setup a) acrylic phantom to hold EZ-EM rectal balloon catheter b) full phantom setup in prone position c) schematic diagram showing the location of the sagittal film (in blue) d) schematic diagram showing the location of the film spiral (black lines wrapping around inside of balloon cavity)
Sagittal Geometry
The film was set up in two different geometries. The first termed ‘sagittal geometry’, had the balloon phantom with the two halves aligned such that a sheet of radiochromic (Gafchromic EBT, International Specialty Products, Wayne, NJ, USA) film was placed in the sagittal plane. No balloon was in place for these measurements however the air cavity created by the Perspex phantom remained, representing the balloon cavity. The sheet of EBT film was 15×16cm2 and covered the region extending over the whole balloon phantom cross section and 8 cm above the balloon phantom through the target. The sagittal geometry setup is shown in Figure 1c.
Radiochromic film has been shown to be an excellent dosimeter in cavity situations [18, 34, 35]. Paelink et al. [35] however showed that radiochromic film (Gafchromic MD-55) in a cavity in the central axis of a beam irradiated edge-on can under-respond at the distal cavity edge due to attenuation in the film through the cavity. The under-response was 6-7% for this particular type of film and is present only when the film is in the beam's central axis and irradiated edge on. This effect was investigated for the Gafchromic EBT film by comparing the sagittal geometry setup for a single anterior-posterior beam with and without film in the cavity. An under-response of 5.3% was found for the anterior-posterior beam when there was film in the cavity.
Spiral Geometry
The second geometry, termed ‘spiral geometry’ had the phantom in the prone position with the endorectal balloon in place. Three strips of EBT film were cut and taped together to give a strip sized 76.2×1.5cm2. This was then wrapped around the inflated balloon in a spiral fashion. The length of the film strip wrapped around the balloon, inflated with 60cc of air, approximately 4.7 times. This gave a layer of film 1.2mm thick around 70% of the balloon diameter. The spiral geometry setup is shown in Figure 1d.
II. Treatment Plans
A planning CT was taken of the phantom in both geometry setups. In the sagittal geometry no balloon was in place during image acquisition. For the spiral geometry the balloon was in place and a ‘dummy’ film spiral was put in place for the CT scan which allowed the film spiral to be visible on the scan and able to be contoured as a region of interest (ROI). Seven field IMRT and 3DCRT Treatment plans were generated on the Pinnacle RTPS (Philips Radiation Oncology Systems, Fitchburg, Wl, USA) for a Varian Trilogy linear accelerator (Varian, Palo Alto, CA). Beam angles (IEC convention [36]) of 120°, 80°, 40°, 0°, 320°, 280° and 240° were used. Helical tomotherapy plans were also generated using the TomoTherapy Hi-Art planning system, version 2.2.4.1.1, (TomoTherapy Inc, Madison, Wl, USA). A field width of 2.5cm and pitch of 0.215 was used. Optimization parameters for IMRT and helical tomotherapy plans are given in Table 1.
Table 1. IMRT and Helical Tomotherapy optimization parameters.
| Structure | Weight | Max dose | Max dose penalty | DVH Vol (%) | DVH dose | Min dose | Min dose penalty | DVH penalty |
|---|---|---|---|---|---|---|---|---|
| PTV | 300 | 70 | 100 | 98 | 98 | 70 | 70 | 2000 |
| Rectum | 40 | 70 | 150 | 20 | 25 | - | - | 700 |
| Bladder | 10 | 70 | 70 | 20 | 40 | - | - | 25 |
| Femurs | 5 | 40 | 2 | 20 | 20 | - | - | 5 |
For each 3DCRT, IMRT and helical tomotherapy plan three measurements were taken for both the spiral and vertical geometries. The results presented are the mean of the three measurements and error bars represent the 95% confidence interval (CI) of the mean. In our case the 95% CI of the mean is obtained by adding and subtracting the product of the standard error of the mean times the †* value corresponding to a p-value of 0.05 and 2 degrees of freedom from the mean.
The under-response of the film when irradiated edge-on was investigated for the measured films from the treatment plan deliveries. As stated, this effect is only present for the anterior-posterior beam which carries a beam weighting of 10% for the 3DCRT and IMRT plans. Therefore an under-response of 5.3% for this field will lead to an under-response of 0.53% in the 3DCRT and IMRT deliveries which has been applied to the posterior rectal wall doses. This will be even less for the helical tomotherapy delivery due to the much greater number of beam angles used. As an exact anterior-posterior beam weighting is not known for the helical tomotherapy delivery no correction was applied however this is expected to be a small fraction of the 95% CI range.
III. Single fields
So as to understand the effect of the cavity on individual fields, single field measurements were performed. An anterior-posterior and a lateral field were investigated. The film was in the sagittal geometry with the jaw (8×9cm2) and SSD settings used in the A-P and lateral fields in the 3DCRT plan. Each field was irradiated individually with three films taken for each separate beam. The results presented are the average of the three measurements and the error bar represent the 95% confidence interval of the mean.
IV. Film Calibration
Two sets of calibration films were taken for the EBT film, one for the 3DCRT, IMRT and single field irradiations and a second set for the helical tomotherapy delivery. The first calibration was performed by plotting 5th order polynomial curve to ten dose points from 0-3.5 Gy that were measured on separate films on a Varian Trilogy linac. For the second calibration set a 5th order polynomial curve was fitted to nine dose points from 0-4.3 Gy that were measured on separate films using the TomoTherapy beam using the following method. A procedure was set up that delivered radiation for a given length of time. The dose was measured using an ionization chamber to obtain the dose delivered for a given beam-on time. Integer multiples of this beam-on time were then used to deliver varying doses. The EBT films were scanned on an Epson Perfection V700 flatbed scanner. All films were scanned at least 24 hours post irradiation to minimize post-irradiation colour effects [37]. All films were scanned in landscape orientation with a scanning resolution of 75dpi. The resultant images were 32-bit colour from which the red channel chosen was for analysis. Background corrections were made to remove spatial non-uniformities by scanning each EBT film prior to irradiation. All analysis was performed on a desktop PC using ImageJ and Matlab software with the Computational Environment for Radiotherapy Research (CERR, University of Washington in St. Louis) package [38].
Results
I. Sagittal Geometry
For both the single field and treatment plan sagittal film measurements the measured and calculated doses at the posterior and anterior cavity walls were compared. The calculated dose was taken as the dose in the voxel with a CT number between that of air and water at each border. For the 3DCRT and IMRT plan this was a voxel 2mm wide in the anterior-posterior direction and for the TomoTherapy plan 1.875mm wide. The measured dose was taken as the average of all the pixels in the region covered by the planning system voxel.
Single Fields
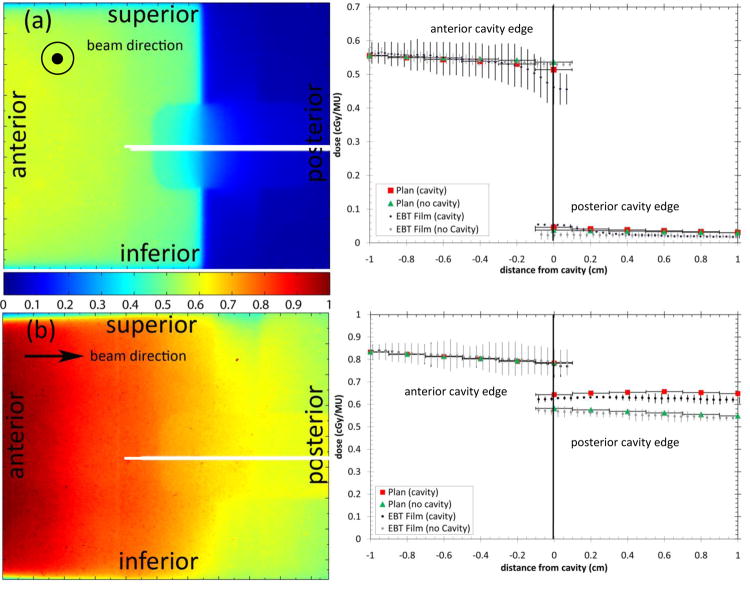
The results of single field irradiations are shown in Figure 2. Figure 2a shows the resultant digitized sagittal film image from a single laterally incident beam. Figure 2b shows the resultant digitized sagittal film image from a single anterior-posterior beam. Table 2 summarises the measured and RTPS calculated doses to the anterior and posterior rectal wall with and without the cavity. For the LAT beam the cavity reduced the anterior rectal wall dose and increased the posterior rectal wall dose. For the LAT beam the RTPS accurately calculated the anterior rectal wall dose (within 95% CI of the mean) both with and without the cavity. The posterior rectal wall dose was over-predicted with no cavity. This region is outside of the treatment beam and is dependent on the accuracy of the RTPS model outside of the field. In practice doses in this region are of limited importance due to their low value. The posterior rectal wall dose was under-predicted when the cavity was present. For the single AP beam the cavity had no effect on the anterior rectal wall dose but increased the posterior rectal wall dose. For the AP beam the RTPS calculated the anterior rectal wall dose within the 95% CI of the measurement both with and without the cavity. The posterior rectal wall dose was calculated within the 95% CI of the measurement with no cavity but was over-predicted when the cavity was present. When the film was removed from the cavity and placed only on the outside for a single AP beam, the effect of the attenuation in the film through the cavity is evident; the posterior rectal wall dose increased relative to the measurement with the film in the cavity. When compared to the RTPS calculation, the measured dose at the posterior rectal wall was higher, showing an under-prediction by the RTPS.
Figure 2.
Sagittal film results from (a) single laterally incident beam and (b) single anterior-posterior beam with and without a cavity. The white lines show the location of the profiles. The arrows show the beam direction. Horizontal error bars on the plan data show the width of the planned dose voxels.
Table 2. Single field measurements and RTPS calculations of anterior and posterior rectal wall doses with and without rectal balloon cavity. All errors are the 95% confidence interval of the mean.
| Beam | anterior cavity wall | posterior cavity wall | ||||
|---|---|---|---|---|---|---|
| Measured (Gy) | Planned (Gy) | Difference (Gy) | Measured (Gy) | Planned (Gy) | Difference (Gy) | |
| LAT – No Cavity | 0.530 ± 0.010 | 0.537 | -0.007 | 0.024 ± 0.011 | 0.038 | -0.014 |
| LAT – Cavity | 0.468 ± 0.053 | 0.514 | -0.046 | 0.053 ± 0.003 | 0.046 | 0.007 |
| AP – No Cavity | 0.790 ± 0.060 | 0.786 | 0.004 | 0.570 ± 0.020 | 0.582 | -0.012 |
| AP - Cavity | 0.776 ± 0.049 | 0.784 | -0.008 | 0.625 ± 0.011 | 0.643 | -0.018 |
| AP – Cavity (no film in cavity) | 0.785 ± 0.006 | 0.784 | 0.001 | 0.659 ± 0.004 | 0.643 | 0.016 |
Treatment Plans
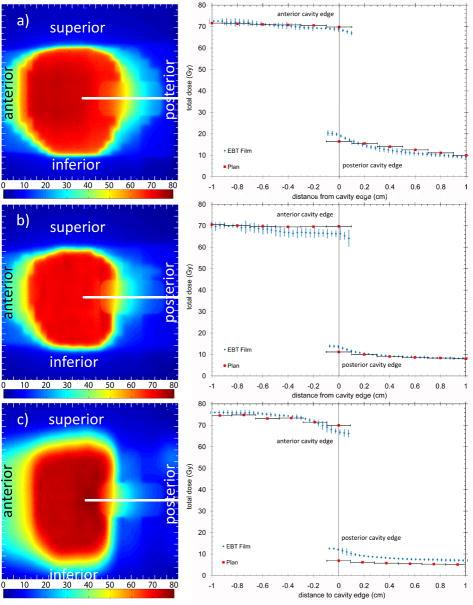
Figure 3 shows the digitized film images and the resultant dose profiles taken in the anterior-posterior direction for the 3DCRT, IMRT and helical tomotherapy plans. In all three treatment techniques the rectal balloon cavity was seen to perturb the dose distribution. For all three plans the anterior cavity wall dose was over-predicted and the posterior cavity wall dose under-predicted by the relevant planning systems. The measured and calculated doses are given in Table 3.
Figure 3.
Sagittal digitized film images and resultant dose profiles for a) 3DCRT b) IMRT and c) helical tomotherapy (HT) delivery techniques. The colour bar is in absolute dose in Grays. All measurements were scaled to represent the dose delivered over the total treatment (28 fractions). The error bars are the standard error of three measurements.
Table 3. Measured and planned cavity wall doses. Percentage differences are measured-planned normalized to measured dose. Errors quoted are the 95% confidence interval.
| technique | anterior cavity wall | posterior cavity wall | ||||
|---|---|---|---|---|---|---|
| Measured (Gy) | Planned (Gy) | difference (Gy) | Measured (Gy) | Planned (Gy) | difference (Gy) | |
| 3DCRT | 68.39 ± 1.06 | 69.82 | -1.43 | 19.16 ± 0.98 | 16.44 | 2.72 |
| IMRT | 65.80 ± 2.47 | 69.72 | -3.92 | 13.26 ± 0.85 | 11.18 | 2.08 |
| Helical Tomotherapy | 67.31 ± 1.73 | 69.98 | -2.67 | 11.64 ± 1.07 | 6.85 | 4.79 |
II. Spiral Geometry
Treatment Plans
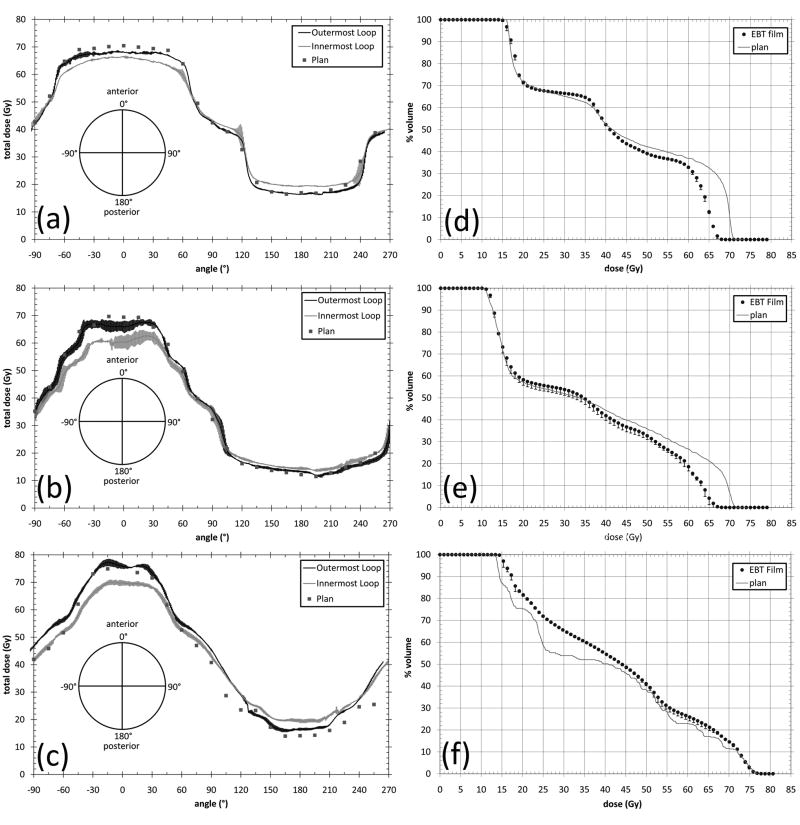
The spiral film strips, which represent a surrogate for the rectal wall were scanned and converted into absolute dose. Two analyses were performed. In the first, a line profile was taken across the centre 1 cm of the film along the length of the spiral. This averaged all of the pixels across the central 1 cm of the film strip at each point along the length of the film. The dose projection tool in CERR (CERR, University of Washington in St. Louis) was then used to get the average dose across the film contour in the superior-inferior direction, at each point around the rectal balloon cavity. The measured and calculated doses were then plotted as a function of angle around the cavity. The outermost loop and innermost full loop only were plotted for clarity. These constitute the two extremes of the dose gradient across the thickness of the film spiral. The outermost loop is the dose to a 0.040mm thick strip centred at 0.117mm from the outside of the balloon cavity and the innermost loop is the dose to a 0.040mm thick strip centred 0.819mm from the outside of the cavity. The planning system represents the dose averaged over a 1.5mm thick voxel around the outside of the cavity. Each loop of the film spiral is thus measuring a different point contained within the film ROI. The measured and calculated profiles are shown in Figure 4a.
Figure 4.
Measured and planned rectal wall doses and resultant DVH from spiral film geometry. (a) represents the dose to the outermost and innermost loop of the film spiral and the planned dose to the film spiral for the 3DCRT plan (f) represents the resultant rectal wall DVH from the film spiral and the planned rectal wall DVH for the 3DCRT plan. (b) and (e), and (c) and (f) represent the same for the IMRT and helical tomotherapy plans respectively.
Dose-volume histograms (DVHs) were generated from the digitized film images. This was done by obtaining histograms of the digitized film images and normalizing the volume approximating the pixels as volume elements. This is valid since an individual pixel can be considered the dose measured in a voxel whose dimensions are the resolution of the digitized film image (0.034×0.034cm2 at 75dpi) by 40μm (the thickness of the active layer in Gafchromic EBT film). The measured voxels constitute a fraction of the total volume of the film spiral however due to the geometry the voxels can be considered as a representative volume of the total film spiral. The film spiral was visible on the CT scans as a layer one CT voxel thick (1.5mm) around the inside of the cavity. This was contoured as the film spiral ROI. The volume of the film spiral ROI (3.42cm3) was different to that of the actual film spiral (2.68cm3) due to the size of the CT scan voxels. The differences in the volume were due to differences in dimensions between the actual film spiral and the film spiral ROI, primarily in the thickness of the film spiral (the actual film spiral is 1.2mm thick and the film spiral ROI is 1.5mm thick). The actual film spiral was contained completely by the film ROI. There is some uncertainty in the location of the film spiral within the film ROI. This may lead to discrepancy between the measured and planned dose that depends on whether the film spiral is at the centre, outside or inside of the film ROI. This difference in measurement location is ≤ 0.3mm and as such will be within the experimental error of the three measurements. The measured DVHs were compared with those calculated by the planning systems for the film spiral region of interest (ROI). The volumes were normalised to percentage volumes to aid comparison. The measured versus planned DVHs are shown in Figure 4b.
Both the 3DCRT and IMRT planned DVHs match their respective measured DVHs in the lower dose region (< 35Gy). However for doses >35Gy the measured volumes for doses up to 70Gy are less than planned. Slight differences exist in the dose range 15-20Gy which represents the dose at the posterior cavity edge. The measured doses were higher than the planned doses as seen in Figure 3 which is then represented by higher volumes receiving 15-20Gy. For both the 3DCRT and IMRT plan large discrepancies were found between the planned and measured DVH for doses between 60 and 70Gy. The measured DVH shows much lower rectal wall volumes receiving dose between 60 and 70Gy.
For the helical Tomotherapy plan discrepancies occurred between the measured and planned DVH in the dose region between 15Gy and 72Gy, where the measured volumes receiving a given dose were more than the planned volumes by varying amounts. Volumes receiving doses > 72Gy were accurately calculated. The V25, V50, V60, V65 and V70 values for the three treatment techniques are summarised in Table 4.
Table 4. Measured and planned rectal wall percentage volumes receiving specified doses. Reported error is the 95% confidence interval of the mean of three measurements.
| Parameter | 3DCRT | IMRT | HT | |||
|---|---|---|---|---|---|---|
| Measured | Planned | Measured | Planned | Measured | Planned | |
| V25 (%) | 67.66 ± 0.36 | 67.56 | 55.65 ± 2.53 | 54.11 | 71.93 ± 0.48 | 58.76 |
| V50 (%) | 39.11 ± 0.38 | 42.30 | 32.71 ± 1.72 | 35.86 | 41.11 ± 0.92 | 38.28 |
| V60 (%) | 32.89 ± 0.55 | 36.94 | 18.62 ± 1.94 | 26.68 | 26.24 ± 1.73 | 22.91 |
| V65 (%) | 12.62 ± 0.79 | 32.65 | 4.26 ± 2.95 | 21.16 | 21.23 ± 1.52 | 16.98 |
| V70 (%) | 0.00 ± 0.01 | 10.48 | 0.01 ± 0.02 | 6.70 | 14.58 ± 0.58 | 11.59 |
Discussion
In this report the dosimetric effect of an endorectal balloon cavity and the accuracy two commercial RTPSs in calculating the dose around the cavity was investigated. Single lateral and anterior-posterior fields were initially investigated. For the lateral beam the impact of the cavity is to reduce the dose to the anterior rectal wall and increases the dose to the posterior rectal wall. The posterior rectal wall dose was increased due to the greater electron range through the cavity leading to a higher fluence of lateral electrons at the posterior rectal wall. The RTPS accurately models the dose to the anterior rectal wall within error but in the measurements there is a clear trend of decreasing dose in the 2mm proximal to the anterior cavity wall that is not seen in the RTPS calculation. At the posterior rectal wall the RTPS under-predicted the dose.
There are similarities between these lateral field results and other reports investigating head and neck and lung cavities. The phenomenon of lateral electron disequilibrium has been experimentally characterized in lung by several investigators. The main observations for small fields in lung are dose voids in the central axis and small secondary build up regions beyond the lung tissue interface [39-41]. For larger fields while central axis dose voids are reduced, penumbral flaring is still an observable phenomenon [42, 43]. With the relatively large fields used in this study there was only a slight dose reduction at the anterior cavity wall but penumbral flaring was inferred by the decreased anterior rectal wall dose and increased posterior rectal wall dose. The penumbral flaring is because the electron range extends in low density regions, causing the penumbral width to broaden. The effect of lateral electron disequilibrium on dose beyond air cavities in the head and neck region has been discussed [44-46]. In this report we have not investigated higher energy photon beams but previous studies in lung cavities suggest that penumbral flaring will increase with energy [41-43]. As higher energies such as 10MV and 18MV are often used for lateral fields the penumbral flaring effect may increase in these cases.
For the anterior-posterior beam the cavity had no effect on the anterior rectal wall but increased the posterior rectal wall dose. No build-down effect was seen, as observed by Li et al. [17], mainly due to the relatively large field size compared with the cavity size. The increased posterior rectal wall dose was due to the reduced attenuation through the cavity meaning higher photon fluence at the posterior edge of the cavity. A slight secondary build-up is seen distal to the posterior cavity edge, however this effect is minimal due again to the relatively large field size used and the depth of the cavity. This is in agreement with Li et al. [17] who found a secondary build-up at the distal cavity edge whose magnitude was reduced with increased field size and cavity depth. The RTPS calculated the dose to the anterior rectal wall within the 95% CI of the measurement but over-predicted the dose to the posterior rectal wall.
Multiple fields and segments were combined in the 3DCRT, IMRT and helical tomotherapy plans. With the sagittal film geometry both the Pinnacle RTPS and TomoTherapy RTPS over-predicted the anterior rectal wall dose (by 1.43Gy, 3.92Gy and 2.67Gy for 3DCRT, IMRT and helical tomotherapy respectively) and under-predicted the posterior rectal wall dose (by 2.62Gy, 2.01 Gy and 4.79Gy for 3DCRT, IMRT and helical tomotherapy respectively). These two effects are similar to that seen in the single lateral field irradiation which is expected, since the majority of the radiation for the three plans was delivered from angles oblique to the anterior cavity wall.
For the spiral film geometry for the 3DCRT and IMRT plans, the Pinnacle RTPS calculated dose was seen to agree with the measured dose to the outermost loop in the film spiral with the exception of the dose to the anterior 60° of the cavity wall. The Pinnacle RTPS over-predicted the dose to the anterior 60° of the cavity wall. When compared with the innermost loop of the film spiral the Pinnacle RTPS over-predicted the dose to the anterior 60° of the cavity wall and under-predicted the dose to the posterior 120° of the cavity wall. These results were reflected when the film spiral was converted to a DVH and compared with the film ROI DVH calculated by the planning system. The Pinnacle RTPS accurately calculated the volumes receiving < 35Gy but over-predicted the volumes receiving > 35Gy.
The accuracy of the TomoTherapy RTPS when compared with films in the spiral geometry varied around the cavity. It should be emphasised that although higher doses are being delivered to the rectal wall than in the 3DCRT and IMRT plans, we are not judging the quality of the plan, but the agreement between the RTPS calculated and the measured dose. The RTPS calculated anterior cavity wall dose lies between that of the outermost and innermost loops of the film spiral; once the planned doses and film spiral doses are converted to a DVH this averages out giving an accurate calculation of the volumes receiving high doses. The TomoTherapy RTPS then under-predicts the intermediate and low doses, leading to the reduced volumes receiving these doses in the DVH.
It is clinically significant that for the 3DCRT and IMRT plans the V70, V65, V60 and V50 values are over-predicted by the Pinnacle RTPS. The V70, V65, V60 and V50 parameters are correlated with incidence of rectal bleeding [47-49]. Any reduction in these parameters should result in a decreased incidence of rectal bleeding under that predicted by the planning system. This has been observed in other studies [11, 13, 14]. Conversely, the TomoTherapy RTPS under-predicted the V70, V65, V60 and V50 values but accurately predicted volumes receiving higher doses than 70Gy. Any under-prediction of these values could lead to an unexpected increase in rectal toxicity, particularly if delivering a hypofractionated schedule. Given this observation one may want to consider a reduction in dose volume objectives placed on the rectal wall when employing helical tomotherapy.
The results from the spiral film geometry suggest that the Pinnacle RTPS over-estimates the dose to the anterior rectal wall, but the TomoTherapy RTPS is accurately calculating or slightly under-predicting the anterior rectal wall dose. The consequence of this is that dose volume constraints for the rectal wall acquired from 3DCRT and IMRT studies may have been over-estimated, where as for tomotherapy they might have been correct or even under-predicted. Any dose-volume constraints deemed ‘safe’ from 3DCRT and IMRT studies that have subsequently been applied to tomotherapy cases may need to be reconsidered.
The effect of the rectal balloon cavity on treatment plan delivery has been investigated in other reports [15, 16] but the accuracy of the convolution/superposition algorithm has not been investigated with regard to the rectal balloon cavity. Teh et al. [16] measured the dose to the rectal cavity wall for a single 2×2cm field as well as a serial tomotherapy delivery. A 15% reduction in the dose to the anterior cavity wall due to the presence of the rectal balloon cavity was observed. Song et al. [15] used Monte Carlo simulations to investigate the accuracy of the Eclipse RTPS (with no heterogeneity corrections) in the presence of a rectal balloon. The Eclipse RTPS was found to over-predict the volumes receiving > 96% of the prescription dose and an under-prediction of the rectal volumes receiving < 22% of the prescription dose. It was determined that the differences at these two ends of the dose range were due to inaccurate calculation of the dose from two lateral beams. The results presented in this investigation agree with these two reports.
The important issue is that if heterogeneity correction is used in the RTPS then the convolution/superposition algorithms [19, 50, 51] used by both Pinnacle and TomoTherapy RTPSs effectively model these disequilibrium situations. These models suffer from some small electron range scaling issues [52] that can lead to inaccurate modelling of cavity interface doses as seen in this report. The magnitude of these inaccuracies in the high dose region is small but may be clinically significant considering evidence suggests most disease is likely to be found in the transitional zone i.e. in the lobes and close to the rectal border [53]. They do however accurately show the qualitative effect of this disequilibrium region. The utility of Monte Carlo simulations in these situations becomes apparent [15]. Monte Carlo accurately models disequilibrium situations and may provide clinicians with more precise dosimetry. The importance of in vivo dosimetry also becomes evident; accurate measurements of the dose received by the rectal wall will provide more accurate data for toxicity correlations.
Conclusion
This report details the effect of an air cavity created by an endorectal balloon and the accuracy of two commercial treatment planning systems in calculations surrounding the cavity. When irradiated with single fields of the same size as that seen clinically, the cavity was seen to perturb the dose at the cavity walls. For a single lateral beam the cavity lead to a decrease in the anterior rectal wall dose and an increase in the posterior cavity wall dose. This was due to penumbral flaring through the air cavity. For a single anterior-posterior beam the cavity was seen to increase the posterior dose. The Pinnacle RTPS predicted the qualitative effects of the cavity but under-estimated the effect of the cavity.
For clinically relevant treatment plan delivery, the Pinnacle and TomoTherapy RTPSs both over-predicted the anterior rectal wall dose and under-predicted the posterior cavity wall dose for 3DCRT, IMRT and helical tomotherapy deliveries. This was visible on the sagittal film geometry. For the spiral film geometry the Pinnacle RTPS was seen to over-predict the high dose region at the anterior rectal wall. The dose to the posterior rectal wall was under-predicted by the Pinnacle RTPS. The TomoTherapy Hi-Art RTPS under-predicted the low and intermediate doses to the rectal wall but accurately calculated the high dose region at the anterior cavity wall adjacent to the prostate. If the Pinnacle RTPS over-predicts but the TomoTherapy RTPS accurately calculates the anterior rectal wall dose then dose volume constraints carried into tomotherapy treatments from 3DCRT and IMRT treatments may need to be reconsidered.
Acknowledgments
The authors would like to thanks the Australian Rotary Health Research Fund and the NSW Cancer Institute Clinical Leaders program for funding for this research.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Hanks GE, Hanlon AL, Schultheiss TE, et al. Dose escalation with 3D conformal treatment: five year outcomes, treatment optimization, and future directions. Int J Radiat Oncol Biol Phys. 1998;41:501–510. doi: 10.1016/s0360-3016(98)00089-3. [DOI] [PubMed] [Google Scholar]
- 2.Pollack A, Zagars GK, Smith LG, et al. Preliminary results of a randomized radiotherapy dose-escalation study comparing 70 Gy with 78 Gy for prostate cancer. J Clin Oncol. 2000;18:3904–3911. doi: 10.1200/JCO.2000.18.23.3904. [DOI] [PubMed] [Google Scholar]
- 3.Zelefsky MJ, Leibel SA, Gaudin PB, et al. Dose escalation with three-dimensional conformal radiation therapy affects the outcome in prostate cancer. Int J Radiat Oncol Biol Phys. 1998;41:491–500. doi: 10.1016/s0360-3016(98)00091-1. [DOI] [PubMed] [Google Scholar]
- 4.Marzi S, Arcangeli G, Saracino B, et al. Relationships between rectal wall dose-volume constraints and radiobiologic indices of toxicity for patients with prostate cancer. Int J Radiat Oncol Biol Phys. 2007;68:41–49. doi: 10.1016/j.ijrobp.2006.12.003. [DOI] [PubMed] [Google Scholar]
- 5.Vavassori V, Fiorino C, Rancati T, et al. Predictors for rectal and intestinal acute toxicities during prostate cancer high-dose 3D-CRT: results of a prospective multicenter study. Int J Radiat Oncol Biol Phys. 2007;67:1401–1410. doi: 10.1016/j.ijrobp.2006.10.040. [DOI] [PubMed] [Google Scholar]
- 6.Storey MR, Pollack A, Zagars G, Smith L, Antolak J, Rosen I. Complications from radiotherapy dose escalation in prostate cancer: preliminary results of a randomized trial. Int J Radiat Oncol Biol Phys. 2000;48:635–642. doi: 10.1016/s0360-3016(00)00700-8. [DOI] [PubMed] [Google Scholar]
- 7.Tucker SL, Dong L, Cheung R, et al. Comparison of rectal dose-wall histogram versus dose-volume histogram for modeling the incidence of late rectal bleeding after radiotherapy. Int J Radiat Oncol Biol Phys. 2004;60:1589–1601. doi: 10.1016/j.ijrobp.2004.07.712. [DOI] [PubMed] [Google Scholar]
- 8.McGary JE, Teh BS, Butler EB, Grant W., 3rd Prostate immobilization using a rectal balloon. J Appl Clin Med Phys. 2002;3:6–11. doi: 10.1120/jacmp.v3i1.2590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Patel RR, Orton N, Tome WA, Chappell R, Ritter MA. Rectal dose sparing with a balloon catheter and ultrasound localization in conformal radiation therapy for prostate cancer. Radiother Oncol. 2003;67:285–294. doi: 10.1016/s0167-8140(03)00056-2. [DOI] [PubMed] [Google Scholar]
- 10.Teh BS, Mai WY, Uhl BM, et al. Intensity-modulated radiation therapy (IMRT) for prostate cancer with the use of a rectal balloon for prostate immobilization: acute toxicity and dose-volume analysis. Int J Radiat Oncol Biol Phys. 2001;49:705–712. doi: 10.1016/s0360-3016(00)01428-0. [DOI] [PubMed] [Google Scholar]
- 11.van Lin EN, Kristinsson J, Philippens ME, et al. Reduced late rectal mucosal changes after prostate three-dimensional conformal radiotherapy with endorectal balloon as observed in repeated endoscopy. Int J Radiat Oncol Biol Phys. 2007;67:799–811. doi: 10.1016/j.ijrobp.2006.09.034. [DOI] [PubMed] [Google Scholar]
- 12.Wachter S, Gerstner N, Dorner D, et al. The influence of a rectal balloon tube as internal immobilization device on variations of volumes and dose-volume histograms during treatment course of conformal radiotherapy for prostate cancer. Int J Radiat Oncol Biol Phys. 2002;52:91–100. doi: 10.1016/s0360-3016(01)01821-1. [DOI] [PubMed] [Google Scholar]
- 13.D'Amico AV, Manola J, McMahon E, et al. A prospective evaluation of rectal bleeding after dose-escalated three-dimensional conformal radiation therapy using an intrarectal balloon for prostate gland localization and immobilization. Urology. 2006;67:780–784. doi: 10.1016/j.urology.2005.10.008. [DOI] [PubMed] [Google Scholar]
- 14.Sanghani MV, Ching J, Schultz D, et al. Impact on rectal dose from the use of a prostate immobilization and rectal localization device for patients receiving dose escalated 3D conformal radiation therapy. Urol Oncol. 2004;22:165–168. doi: 10.1016/j.urolonc.2004.02.002. [DOI] [PubMed] [Google Scholar]
- 15.Song JS, Court LE, Cormack RA. Monte Carlo calculation of rectal dose when using an intrarectal balloon during prostate radiation therapy. Med Dosim. 2007;32:151–156. doi: 10.1016/j.meddos.2006.11.002. [DOI] [PubMed] [Google Scholar]
- 16.Teh BS, Dong L, McGary JE, Mai WY, Grant W, 3rd, Butler EB. Rectal wall sparing by dosimetric effect of rectal balloon used during intensity-modulated radiation therapy (IMRT) for prostate cancer. Med Dosim. 2005;30:25–30. doi: 10.1016/j.meddos.2004.10.005. [DOI] [PubMed] [Google Scholar]
- 17.Li XA, Yu C, Holmes T. A systematic evaluation of air cavity dose perturbation in megavoltage x-ray beams. Med Phys. 2000;27:1011–1017. doi: 10.1118/1.598966. [DOI] [PubMed] [Google Scholar]
- 18.Martens C, Reynaert N, De Wagter C, et al. Underdosage of the upper-airway mucosa for small fields as used in intensity-modulated radiation therapy: a comparison between radiochromic film measurements, Monte Carlo simulations, and collapsed cone convolution calculations. Med Phys. 2002;29:1528–1535. doi: 10.1118/1.1487421. [DOI] [PubMed] [Google Scholar]
- 19.Mackie TR, Scrimger JW, Battista JJ. A convolution method of calculating dose for 15-MV x rays. Med Phys. 1985;12:188–196. doi: 10.1118/1.595774. [DOI] [PubMed] [Google Scholar]
- 20.Ahnesjo A. Collapsed cone convolution of radiant energy for photon dose calculation in heterogeneous media. Med Phys. 1989;16:577–592. doi: 10.1118/1.596360. [DOI] [PubMed] [Google Scholar]
- 21.Mackie TR, Bielajew AF, Rogers DW, Battista JJ. Generation of photon energy deposition kernels using the EGS Monte Carlo code. Phys Med Biol. 1988;33:1–20. doi: 10.1088/0031-9155/33/1/001. [DOI] [PubMed] [Google Scholar]
- 22.Hoban PW, Murray DC, Metcalfe PE, Round WH. Superposition dose calculation in lung for 10MV photons. Australas Phys Eng Sci Med. 1990;13:81–92. [PubMed] [Google Scholar]
- 23.Woo MK, Cunningham JR. The validity of the density scaling method in primary electron transport for photon and electron beams. Med Phys. 1990;17:187–194. doi: 10.1118/1.596497. [DOI] [PubMed] [Google Scholar]
- 24.Brenner DJ, Hall EJ. Fractionation and protraction for radiotherapy of prostate carcinoma. Int J Radiat Oncol Biol Phys. 1999;43:1095–1101. doi: 10.1016/s0360-3016(98)00438-6. [DOI] [PubMed] [Google Scholar]
- 25.Brenner DJ, Martinez AA, Edmundson GK, Mitchell C, Thames HD, Armour EP. Direct evidence that prostate tumors show high sensitivity to fractionation (low alpha/beta ratio), similar to late-responding normal tissue. Int J Radiat Oncol Biol Phys. 2002;52:6–13. doi: 10.1016/s0360-3016(01)02664-5. [DOI] [PubMed] [Google Scholar]
- 26.Fowler J, Chappell R, Ritter M. Is alpha/beta for prostate tumors really low? Int J Radiat Oncol Biol Phys. 2001;50:1021–1031. doi: 10.1016/s0360-3016(01)01607-8. [DOI] [PubMed] [Google Scholar]
- 27.Chappell R, Fowler J, Ritter M. New data on the value of alpha/beta--evidence mounts that it is low. Int J Radiat Oncol Biol Phys. 2004;60:1002–1003. doi: 10.1016/j.ijrobp.2004.06.204. [DOI] [PubMed] [Google Scholar]
- 28.King CR, Fowler JF. A simple analytic derivation suggests that prostate cancer alpha/beta ratio is low. Int J Radiat Oncol Biol Phys. 2001;51:213–214. doi: 10.1016/s0360-3016(01)01651-0. [DOI] [PubMed] [Google Scholar]
- 29.Kupelian PA, Reddy CA, Klein EA, Willoughby TR. Short-course intensity-modulated radiotherapy (70 GY at 2.5 GY per fraction) for localized prostate cancer: preliminary results on late toxicity and quality of life. Int J Radiat Oncol Biol Phys. 2001;51:988–993. doi: 10.1016/s0360-3016(01)01730-8. [DOI] [PubMed] [Google Scholar]
- 30.Kupelian PA, Willoughby TR, Reddy CA, Klein EA, Mahadevan A. Hypofractionated intensity-modulated radiotherapy (70 Gy at 2.5 Gy per fraction) for localized prostate cancer: Cleveland Clinic experience. Int J Radiat Oncol Biol Phys. 2007;68:1424–1430. doi: 10.1016/j.ijrobp.2007.01.067. [DOI] [PubMed] [Google Scholar]
- 31.Logue JP, Cowan RA, Hendry JH. Hypofractionation for prostate cancer. Int J Radiat Oncol Biol Phys. 2001;49:1522–1523. doi: 10.1016/s0360-3016(00)01565-0. [DOI] [PubMed] [Google Scholar]
- 32.Arcangeli S, Strigari L, Soete G, et al. Clinical and Dosimetric Predictors of Acute Toxicity after a 4-Week Hypofractionated External Beam Radiotherapy Regimen for Prostate Cancer: Results from a Multicentric Prospective Trial. Int J Radiat Oncol Biol Phys. 2008 doi: 10.1016/j.ijrobp.2008.04.005. [DOI] [PubMed] [Google Scholar]
- 33.Leborgne F, Fowler J. Acute Toxicity After Hypofractionated Conformal Radiotherapy for Localized Prostate Cancer: Nonrandomized Contemporary Comparison with Standard Fractionation. Int J Radiat Oncol Biol Phys. 2008 doi: 10.1016/j.ijrobp.2008.01.023. [DOI] [PubMed] [Google Scholar]
- 34.Paelinck L, Reynaert N, Thierens H, De Neve W, De Wagter C. Experimental verification of lung dose with radiochromic film: comparison with Monte Carlo simulations and commercially available treatment planning systems. Phys Med Biol. 2005;50:2055–2069. doi: 10.1088/0031-9155/50/9/009. [DOI] [PubMed] [Google Scholar]
- 35.Paelinck L, Reynaert N, Thierens H, De Wagter C, De Neve W. The value of radiochromic film dosimetry around air cavities: experimental results and Monte Carlo simulations. Phys Med Biol. 2003;48:1895–1905. doi: 10.1088/0031-9155/48/13/303. [DOI] [PubMed] [Google Scholar]
- 36.International Electrotechnical Commission. IEC1217: Radiotherapy equipment - Coordinates, movements and scales. 1996. [Google Scholar]
- 37.Cheung T, Butson MJ, Yu PK. Post-irradiation colouration of Gafchromic EBT radiochromic film. Phys Med Biol. 2005;50:N281–285. doi: 10.1088/0031-9155/50/20/N04. [DOI] [PubMed] [Google Scholar]
- 38.Deasy JO, Blanco AI, Clark VH. CERR: a computational environment for radiotherapy research. Med Phys. 2003;30:979–985. doi: 10.1118/1.1568978. [DOI] [PubMed] [Google Scholar]
- 39.Mackie TR, el-Khatib E, Battista J, Scrimger J, Van Dyk J, Cunningham JR. Lung dose corrections for 6- and 15-MV x rays. Med Phys. 1985;12:327–332. doi: 10.1118/1.595691. [DOI] [PubMed] [Google Scholar]
- 40.Metcalfe PE, Battista JJ. Accuracy of inhomogeneity corrections in lung irradiated with high energy X-rays. Australas Phys Eng Sci Med. 1988;11:67–75. [PubMed] [Google Scholar]
- 41.Metcalfe PE, Wong TP, Hoban PW. Radiotherapy X-ray beam inhomogeneity corrections: the problem of lateral electronic disequilibrium in lung. Australas Phys Eng Sci Med. 1993;16:155–167. [PubMed] [Google Scholar]
- 42.Kornelsen RO, Young ME. Changes in the dose-profile of a 10 MV x-ray beam within and beyond low density material. Med Phys. 1982;9:114–116. doi: 10.1118/1.595059. [DOI] [PubMed] [Google Scholar]
- 43.Young ME, Kornelsen RO. Dose corrections for low-density tissue inhomogeneities and air channels for 10-MV x rays. Med Phys. 1983;10:450–455. doi: 10.1118/1.595392. [DOI] [PubMed] [Google Scholar]
- 44.Massey JB. Dose distribution problems in megavoltage therapy. I.The problem of air spaces. Br J Radiol. 1962;35:736–738. doi: 10.1259/0007-1285-35-419-736. [DOI] [PubMed] [Google Scholar]
- 45.Nilsson B, Schnell PO. Build-up effects at air cavities measured with thin thermoluminescent dosimeters. Acta Radiol Ther Phys Biol. 1976;15:427–432. doi: 10.3109/02841867609131777. [DOI] [PubMed] [Google Scholar]
- 46.Wong TP, Metcalfe PE, Kron T, Emeleus TG. Radiotherapy x-ray dose distribution beyond air cavities. Australas Phys Eng Sci Med. 1992;15:138–146. [PubMed] [Google Scholar]
- 47.Fiorino C, Cozzarini C, Vavassori V, et al. Relationships between DVHs and late rectal bleeding after radiotherapy for prostate cancer: analysis of a large group of patients pooled from three institutions. Radiother Oncol. 2002;64:1–12. doi: 10.1016/s0167-8140(02)00147-0. [DOI] [PubMed] [Google Scholar]
- 48.Huang EH, Pollack A, Levy L, et al. Late rectal toxicity: dose-volume effects of conformal radiotherapy for prostate cancer. Int J Radiat Oncol Biol Phys. 2002;54:1314–1321. doi: 10.1016/s0360-3016(02)03742-2. [DOI] [PubMed] [Google Scholar]
- 49.Jackson A, Skwarchuk MW, Zelefsky MJ, et al. Late rectal bleeding after conformal radiotherapy of prostate cancer. II.Volume effects and dose-volume histograms. Int J Radiat Oncol Biol Phys. 2001;49:685–698. doi: 10.1016/s0360-3016(00)01414-0. [DOI] [PubMed] [Google Scholar]
- 50.Boyer A, Mok E. A photon dose distribution model employing convolution calculations. Med Phys. 1985;12:169–177. doi: 10.1118/1.595772. [DOI] [PubMed] [Google Scholar]
- 51.Mohan R, Chui C, Lidofsky L. Differential pencil beam dose computation model for photons. Med Phys. 1986;13:64–73. doi: 10.1118/1.595924. [DOI] [PubMed] [Google Scholar]
- 52.Keall PJ, Hoban PW. Superposition dose calculation incorporating Monte Carlo generated electron track kernels. Med Phys. 1996;23:479–485. doi: 10.1118/1.597679. [DOI] [PubMed] [Google Scholar]
- 53.Chen ME, Johnston DA, Tang K, Babaian RJ, Troncoso P. Detailed mapping of prostate carcinoma foci: biopsy strategy implications. Cancer. 2000;89:1800–1809. doi: 10.1002/1097-0142(20001015)89:8<1800::aid-cncr21>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]